Enhanced Adaptive Sine Multi-Taper Power Spectral Density Estimation for System Performance Evaluation in Low-Frequency Gravitational Wave Detection
Abstract
:Featured Application
Abstract
1. Introduction
2. Optimization Model for the Adaptive Sine Multi-Taper Algorithm
2.1. Adaptive Sine Multi-Taper Power Spectral Density Estimation
2.2. Focus of Optimization for the Adaptive Sine Multi-Taper Algorithm
- 1.
- Initial Setup:
- The adaptive sine multi-taper algorithm starts by initializing the tapering parameter, setting all frequencies to a degree of 20.
- 2.
- Spectral Estimate Processing:
- For frequencies below 1 mHz (f < 1 mHz): The value of K(f) is set to 1.
- For frequencies between 1 mHz and 0.01 Hz (1 mHz < f < 0.01 Hz): A robust filtering technique is applied to smooth K(f).
- For frequencies above 0.01 Hz (f > 0.01 Hz): K(f) is determined using parabolic weighting as specified in Equation (11).
- For frequencies ranging from 0.01 Hz to 1 Hz (0.01 Hz < f < 1 Hz): A mild filtering technique is applied to further enhance the smoothness of K(f).
- 3.
- Outlier Removal and Iteration:
- Outliers are identified and removed through linear interpolation. The K(f) values are smoothed over three iterations. The PSD estimation process is iterated 15 times to yield optimal estimates for both the PSD and the amplitude spectral density (ASD).
3. Algorithm Simulation Comparison
3.1. Focus of Algorithm Research
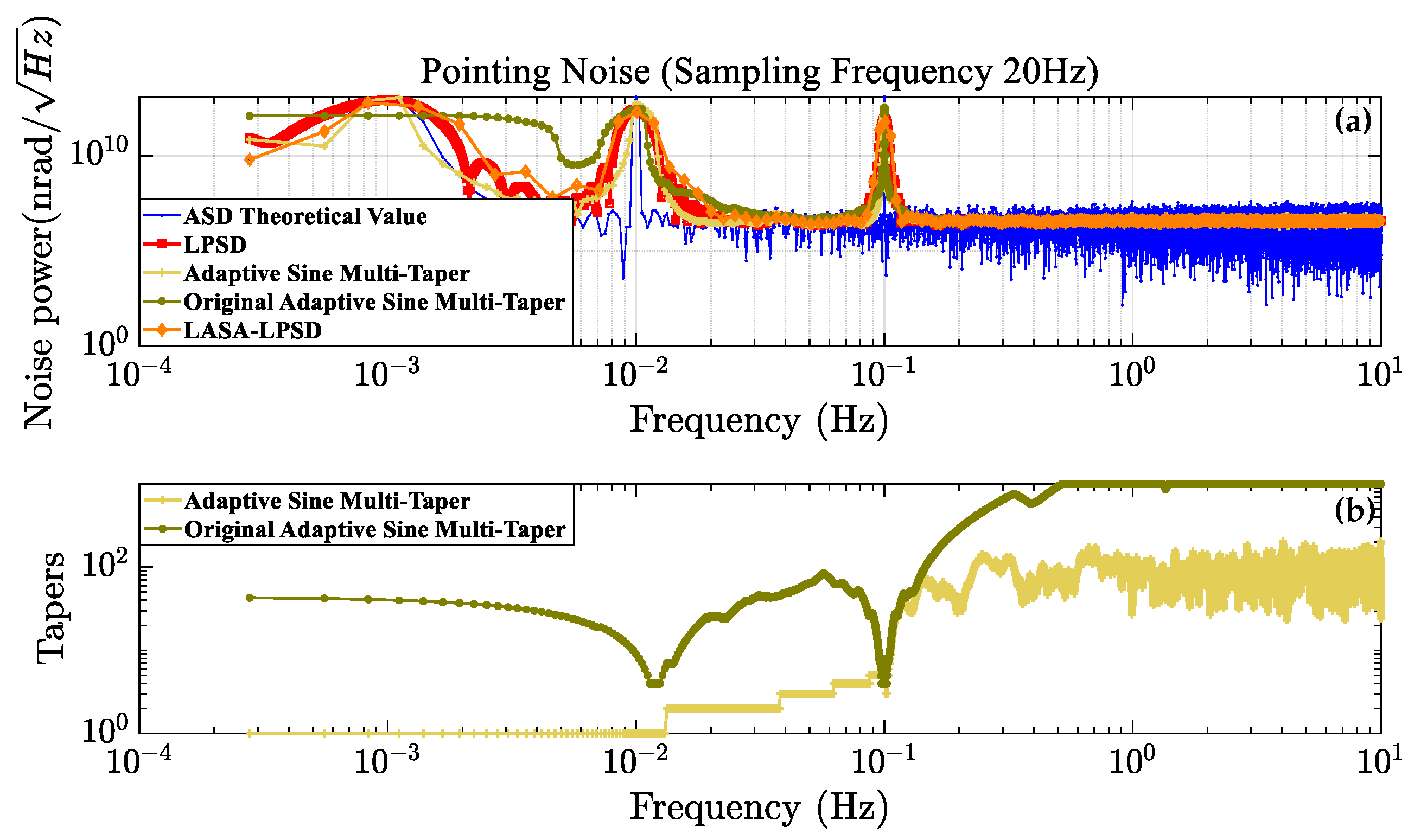
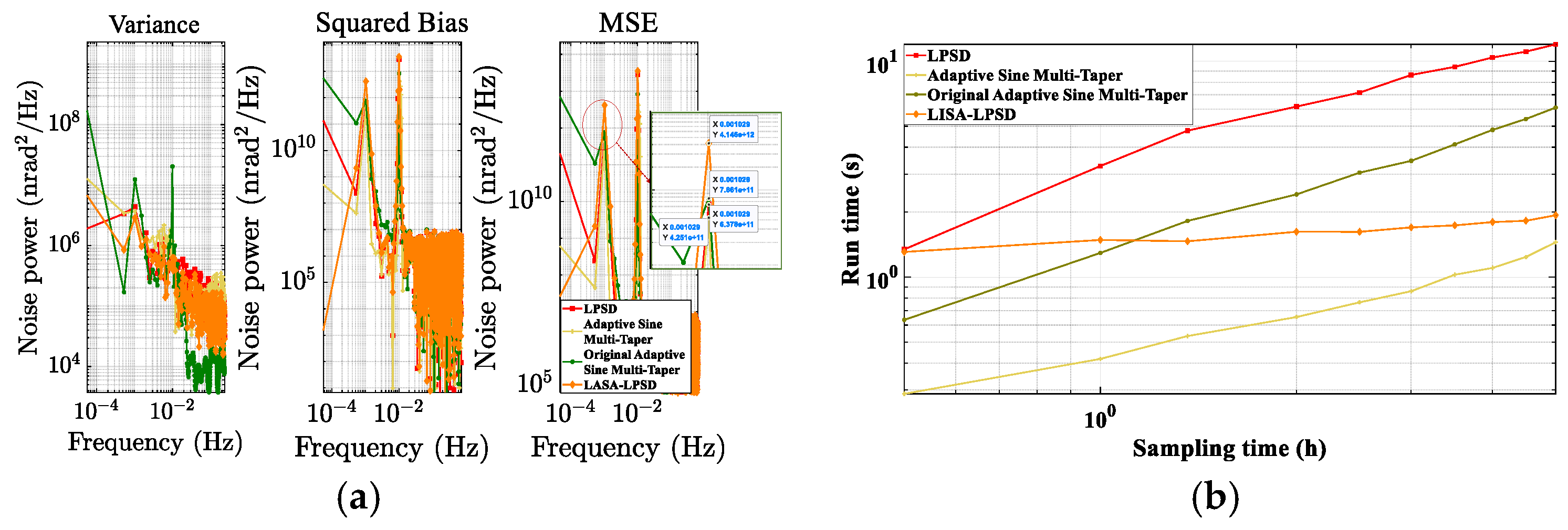
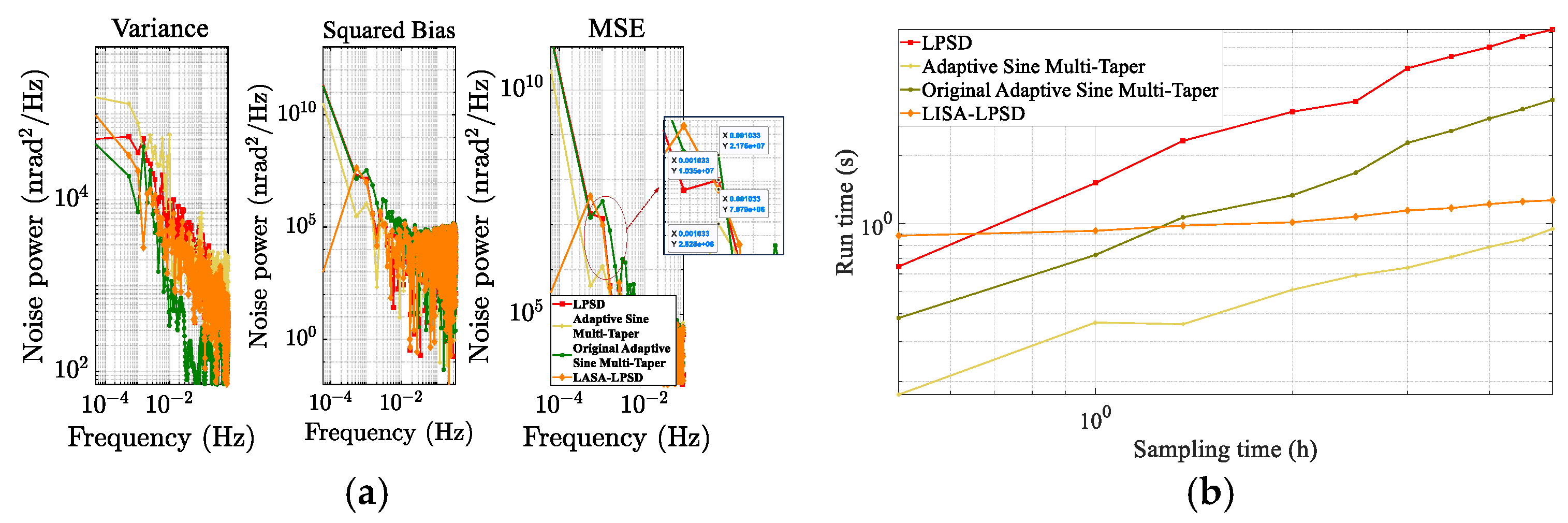
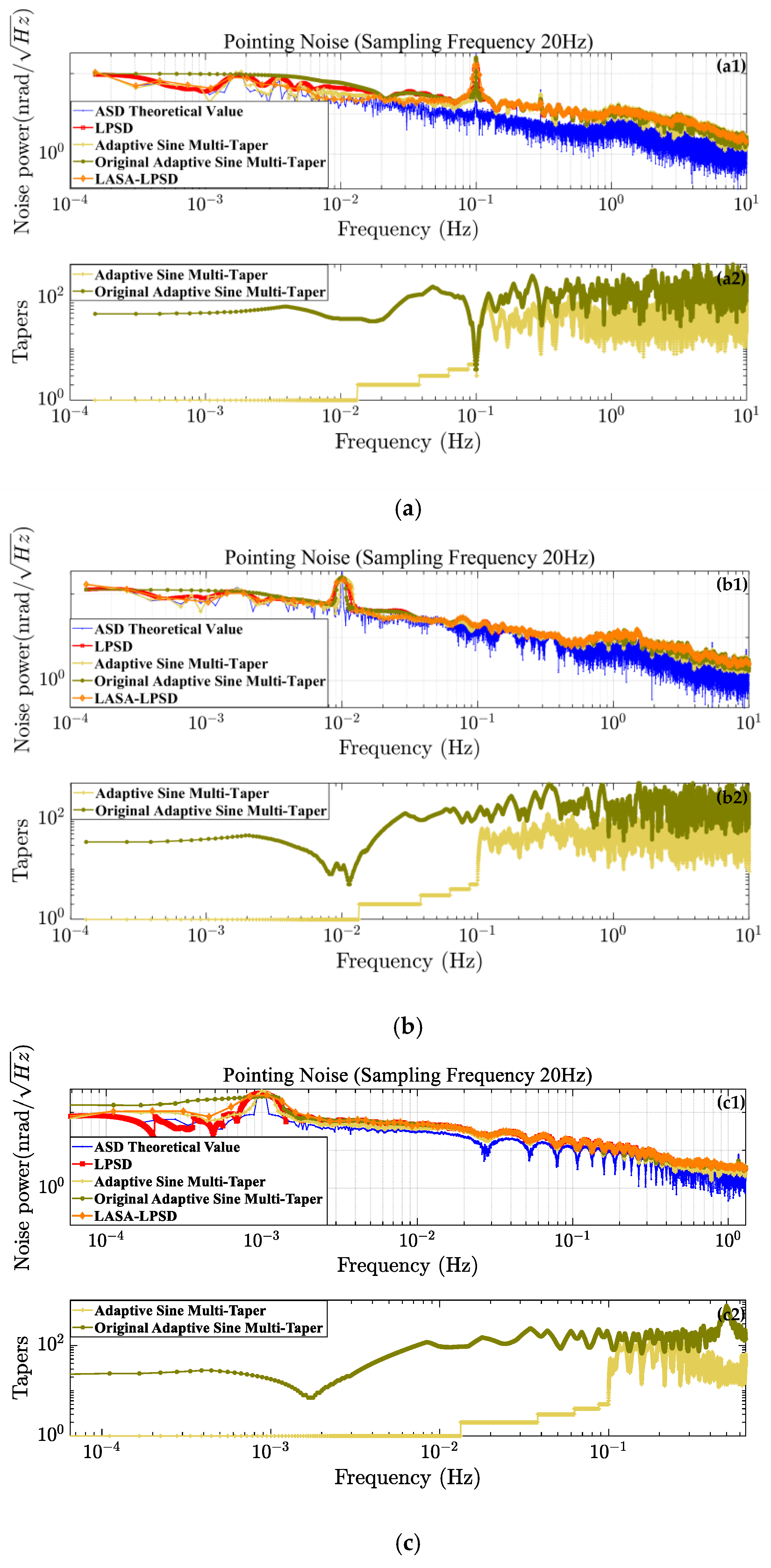
3.2. Simulation Comparison of ASD Estimation Algorithms
4. Validation and Discussion
5. Conclusions
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gong, Y.; Luo, J.; Wang, B. Concepts and Status of Chinese Space Gravitational Wave Detection Projects. Nat. Astron. 2021, 5, 881–889. [Google Scholar] [CrossRef]
- Cyranoski, D. Chinese Gravitational-Wave Hunt Hits Crunch Time. Nature 2016, 531, 150–151. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Wang, J.-W.; Gao, Z.-C.; Li, J.-B.; An, B.-N.; Li, R.-X.; Bai, Y.; Yin, W.-B.; Tian, L.; Zheng, Y.-H. Laser Intensity Noise Evaluation System for Space-Based Gravitational Wave Detection. Acta Phys. Sin. 2022, 71, 209501. [Google Scholar] [CrossRef]
- Amaro-Seoane, P.; Andrews, J.; Arca Sedda, M.; Askar, A.; Baghi, Q.; Balasov, R.; Bartos, I.; Bavera, S.S.; Bellovary, J.; Berry, C.P.L.; et al. Astrophysics with the Laser Interferometer Space Antenna. Living Rev. Relativ. 2023, 26, 2. [Google Scholar] [CrossRef]
- Percival, D.B.; Walden, A.T. Spectral Analysis for Physical Applications: Multitaper and Conventional Univariate Techniques; Cambridge University Press: Cambridge, UK, 1993; pp. 368–370. [Google Scholar]
- Wang, W.; Li, F.; Li, J.; Ju, M.; Zheng, L.; Tian, Y.; Yin, W.; Tian, L.; Zheng, Y. Research on Low-Noise Balanced Zero-Phasing Detection System for Space Gravitational Wave Detection (Invited). Infrared Laser Eng. 2022, 51, 20220300. [Google Scholar] [CrossRef]
- Stoica, P.; Moses, R.L. Spectral Analysis of Signals; Pearson/Prentice Hall: Upper Saddle River, NJ, USA, 2005; pp. 1–2. [Google Scholar]
- Welch, P. The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging over Short, Modified Periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef]
- Thomson, D.J. Spectrum Estimation and Harmonic Analysis. Proc. IEEE 1982, 70, 1055–1096. [Google Scholar] [CrossRef]
- Riedel, K.S.; Sidorenko, A. Minimum Bias Multiple Taper Spectral Estimation. IEEE Trans. Signal Process. 1995, 43, 188–195. [Google Scholar] [CrossRef]
- Tröbs, M.; Heinzel, G. Improved Spectrum Estimation from Digitized Time Series on a Logarithmic Frequency Axis. Measurement 2006, 39, 120–129. [Google Scholar] [CrossRef]
- Guo, J.; Ma, S.; Zhou, C.; Liu, J.; Wang, B.; Pan, D.; Mao, H. Vibration Compensation for a Vehicle-Mounted Atom Gravimeter. IEEE Sens. J. 2022, 22, 12939–12946. [Google Scholar] [CrossRef]
- Miller, A.L.; Badaracco, F.; Palomba, C. Distinguishing Between Dark-Matter Interactions With Gravitational-Wave Detectors. Phys. Rev. D 2022, 105, 103035. [Google Scholar] [CrossRef]
- Joo, K.-N.; Clark, E.; Zhang, Y.; Ellis, J.D.; Guzman, F. A Compact High-Precision Periodic-Error-Free Heterodyne Interferometer. J. Opt. Soc. Am. A 2020, 37, B11. [Google Scholar] [CrossRef]
- Barbour, A.J.; Parker, R.L. psd: Adaptive, Sine Multitaper Power Spectral Density Estimation for R. Comput. Geosci. 2014, 63, 1–8. [Google Scholar] [CrossRef]
- Welford, B.P. Note on a Method for Calculating Corrected Sums of Squares and Products. Technometrics 1962, 4, 419–420. [Google Scholar] [CrossRef]
- Haley, C.L.; Anitescu, M. Optimal Bandwidth for Multitaper Spectrum Estimation. IEEE Signal Process. Lett. 2017, 24, 1696–1700. [Google Scholar] [CrossRef]
- Karnik, S.; Romberg, J.; Davenport, M.A. Thomson’s Multitaper Method Revisited. arXiv 2022, arXiv:2103.11586. [Google Scholar] [CrossRef]
- Huang, Z.; Xu, Y.L. A Multi-Taper S-Transform Method for Spectral Estimation of Stationary Processes. IEEE Trans. Signal Process. 2021, 69, 1452–1467. [Google Scholar]
- Huang, Z.; Xu, Y.L.; Tao, T. Multi-Taper S-Transform Method for Evolutionary Spectrum Estimation. Mech. Syst. Signal Process. 2022, 168, 108667. [Google Scholar]
- Prieto, G.A.; Thomson, D.J.; Vernon, F.L.; Shearer, P.M.; Parker, R.L. Confidence Intervals for Earthquake Source Parameters Using Multitaper Spectral Analysis. Bull. Seismol. Soc. Am. 2007, 97, 163–177. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Huang, Z.; Xia, Y. An Adaptive Multi-Taper Spectral Estimation for Stationary Processes. Mech. Syst. Signal Process. 2023, 183, 109629. [Google Scholar] [CrossRef]
- Negri, E.; Fuscaldo, W.; Burghignoli, P.; Galli, A. An Overview of Design Techniques for Two-Dimensional Leaky-Wave Antennas. Appl. Sci. 2025, 15, 1854. [Google Scholar] [CrossRef]
- Nawaz, W.; Albert, K.; Jouvet, P.; Noumeir, R. Acute Respiratory Distress Identification via Multi-Modality Using Deep Learning. Appl. Sci. 2025, 15, 1512. [Google Scholar] [CrossRef]
- Buzzicotti, M.; De Santis, A.; Tantalo, N. Teaching to Extract Spectral Densities from Lattice Correlators to a Broad Audience of Learning-Machines. Eur. Phys. J. C 2024, 84, 32. [Google Scholar] [CrossRef]
- Valadão, M.D.M.; Costa, A.L.A.D.; Silva, É.R.D.; Mateus, A.C.; Júnior, W.S.S. Noise Power Density Estimation Based on Deep Learning Using Spectrograms Extracted from Wireless Signals. In Proceedings of the XLII Simpósio Brasileiro de Telecomunicações e Processamento de Sinais, Belém, Brazil, 1–4 October 2024. [Google Scholar] [CrossRef]
- Qiao, D.; Jia, F.; Li, X.; Zhou, X. A Review of Orbital Mechanics for Space-Based Gravitational Wave Observatories. Space Sci. Technol. 2023, 3, 0015. [Google Scholar] [CrossRef]
- Shen, J.; Wang, Q.; Zhao, M.; Hu, J.; Wang, J.; Shu, M.; Liu, Y.; Guo, W.; Qiao, H.; Niu, Q.; et al. Mapping Maize Planting Densities Using Unmanned Aerial Vehicles, Multispectral Remote Sensing, and Deep Learning Technology. Drones 2024, 8, 140. [Google Scholar] [CrossRef]
- Zhang, Q.; Peng, Z.; Song, Y. Performance Analysis of Spectrum Sensing Algorithms in Cognitive Radio: A Statistical Approach. Sensors 2023, 23, 1942. [Google Scholar] [CrossRef]
- Nakamura, M.; Yokota, K.; Ozawa, M. Numerical Calculation Optimization for Particulate Matter Trapping and Oxidation of Catalytic Diesel Particulate Filter. Appl. Sci. 2025, 15, 2356. [Google Scholar] [CrossRef]
- Hansson, M. Optimized Weighted Averaging of Peak Matched Multiple Window Spectrum Estimators. IEEE Trans. Signal Process. 1999, 47, 1141–1146. [Google Scholar] [CrossRef]
- Almstrom, M. Optimizing Weighting Factors for Multiple Window Spectrum Estimates. Bachelor’s Thesis, Lund University, Lund, Sweden, 2021. [Google Scholar]
- Wang, L.; Ma, L. Multi-Window Spectral Estimation Based on the Minimum Mean Square Error (MMSE) Criterion. Off. Autom. 2010, 16, 23–25. [Google Scholar]
- Lindgren, G.; Rootzen, H.; Sandsten, M. Stationary Stochastic Processes for Scientists and Engineers; Chapman and Hall/CRC: Boca Raton, FL, USA, 2013. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, T.; Zhou, J. Spectrum Estimation Techniques for Cognitive Radio: Beyond Traditional Methods. Sensors 2024, 24, 1456. [Google Scholar] [CrossRef]
- Percival, D.B.; Walden, A.T. Spectral Analysis for Physical Applications; Cambridge University Press: Cambridge, UK, 1993; pp. 20–40. [Google Scholar]
- Walden, A.T. A Unified View of Multitaper Multivariate Spectral Estimation. Biometrika 2000, 87, 767–788. [Google Scholar] [CrossRef]
- Babadi, B.; Brown, E.N. A Review of Multitaper Spectral Analysis. IEEE Trans. Biomed. Eng. 2014, 61, 1555–1564. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Tan, Y.; Mu, H.; Li, Y.; Wang, J.; Jin, J. Laser Interferometry Multi-Degree-of-Freedom Measurement Technology in Space Gravitational Wave Detection. Laser Optoelectron. Prog. 2023, 60, 0312006. [Google Scholar] [CrossRef]




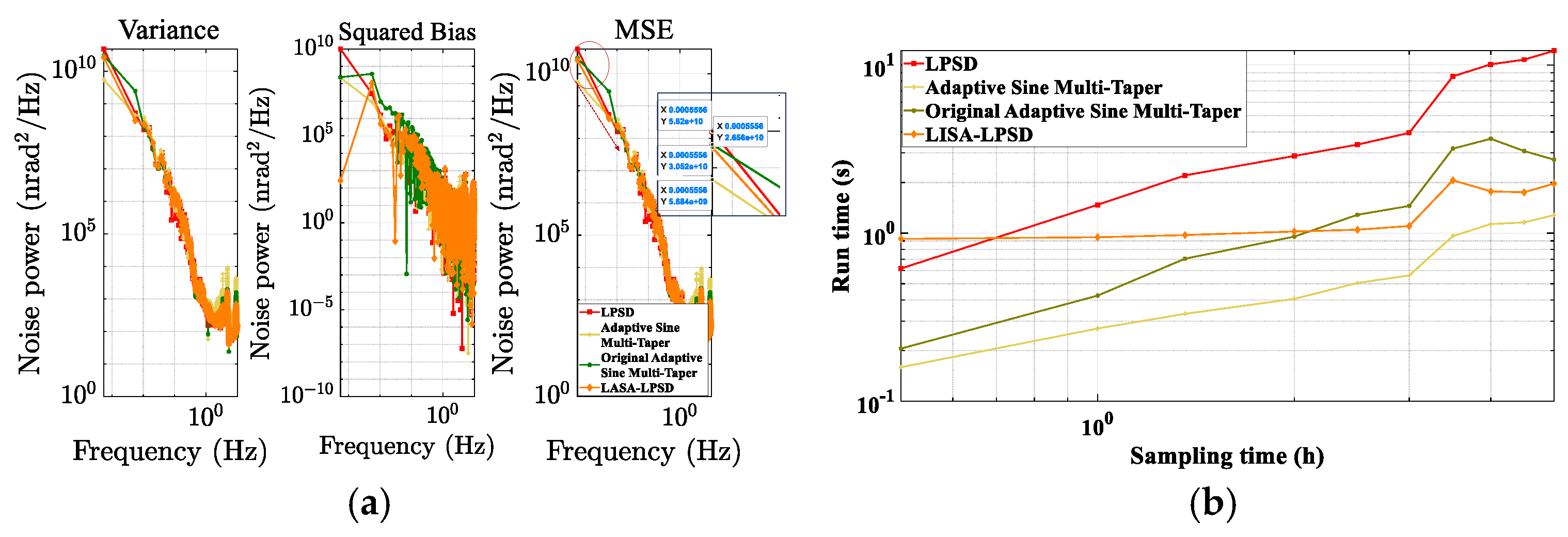

| Algorithm | In Sinusoidal Simulation Adaptive Sine Multi-Taper vs. Others | Under Noise Metric Simulation Adaptive Sine Multi-Taper vs. Others | ||
|---|---|---|---|---|
| MSE Reduction(%) | Runtime Reduction(%) | MSE Reduction(%) | Runtime Reduction(%) | |
| Original Adaptive Sine Multi-taper | 45 | 76 | 85 | 68 |
| LPSD | 34 | 88 | 64 | 86 |
| LISA-LPSD | 90 | 25 | 64 | 31 |
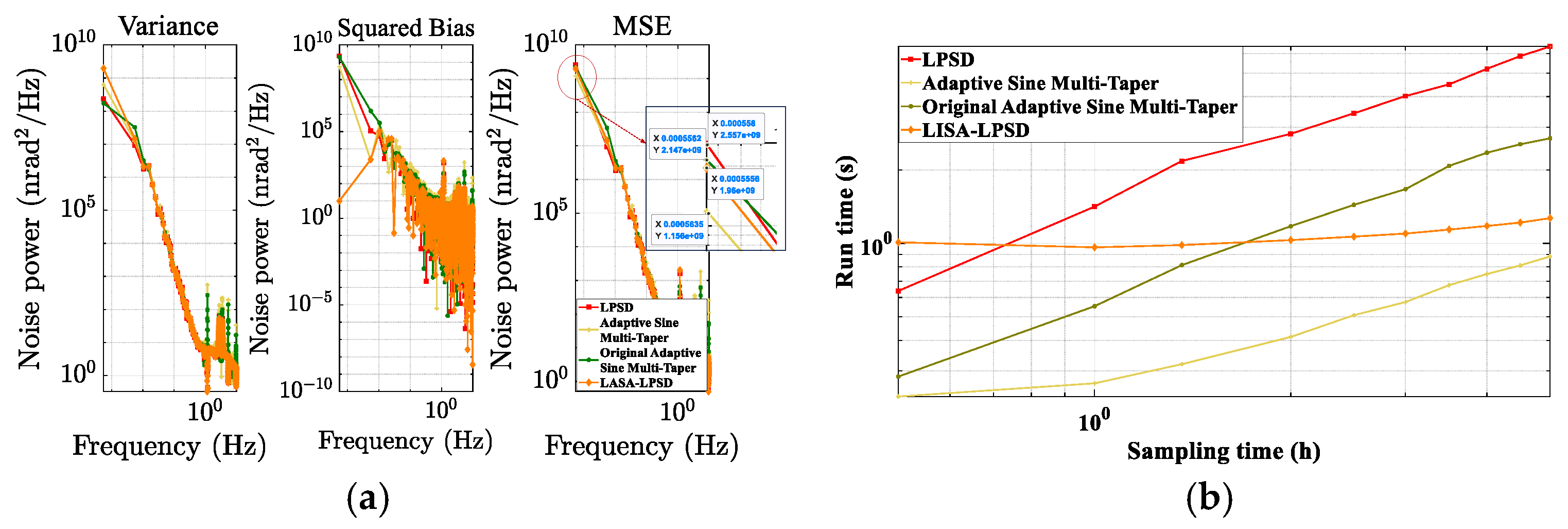
| Algorithm | In sinusoidal Excitation Experiment Adaptive Sine Multi-Taper vs. Others | Under Noise Metric Experiment Adaptive Sine Multi-Taper vs. Others | ||
|---|---|---|---|---|
| MSE Reduction (%) | Runtime Reduction (%) | MSE Reduction (%) | Runtime Reduction (%) | |
| Original Adaptive Sine Multi-taper | 81 | 53 | 46 | 67 |
| LPSD | 90 | 90 | 55 | 86 |
| LISA-LPSD | 79 | 35 | 41 | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Li, Y.; Fu, C.; Zhang, H.; Wang, Q.; He, D.; Huang, Y. Enhanced Adaptive Sine Multi-Taper Power Spectral Density Estimation for System Performance Evaluation in Low-Frequency Gravitational Wave Detection. Appl. Sci. 2025, 15, 3919. https://doi.org/10.3390/app15073919
Liu C, Li Y, Fu C, Zhang H, Wang Q, He D, Huang Y. Enhanced Adaptive Sine Multi-Taper Power Spectral Density Estimation for System Performance Evaluation in Low-Frequency Gravitational Wave Detection. Applied Sciences. 2025; 15(7):3919. https://doi.org/10.3390/app15073919
Chicago/Turabian StyleLiu, Caiyun, Yang Li, Changkang Fu, Hongming Zhang, Qiang Wang, Dong He, and Yongmei Huang. 2025. "Enhanced Adaptive Sine Multi-Taper Power Spectral Density Estimation for System Performance Evaluation in Low-Frequency Gravitational Wave Detection" Applied Sciences 15, no. 7: 3919. https://doi.org/10.3390/app15073919
APA StyleLiu, C., Li, Y., Fu, C., Zhang, H., Wang, Q., He, D., & Huang, Y. (2025). Enhanced Adaptive Sine Multi-Taper Power Spectral Density Estimation for System Performance Evaluation in Low-Frequency Gravitational Wave Detection. Applied Sciences, 15(7), 3919. https://doi.org/10.3390/app15073919






