Thermo-Mechanical Behavior Simulation and Experimental Validation of Segmented Tire Molds Based on Multi-Physics Coupling

Abstract

To address the challenges of unclear thermo-mechanical coupling mechanisms and unpredictable multi-field synergistic effects in segmented tire molds during vulcanization, this study focuses on segmented tire molds and proposes a multi-physics coupling numerical model. This model integrates fluid flow dynamics into heat transfer mechanisms. It systematically reveals molds’ heat transfer characteristics, stress distribution and deformation behavior under combined high-temperature and mechanical loading. Based on a fluid-solid-thermal coupling framework and experimental validations, simulations indicate that the internal temperature field of the mold is highly uniform. The global temperature difference is less than 0.13%. The temperature load has a significant dominant effect on the deformation of key components such as the guide ring and installation ring. Molding forces play a secondary role in total stress. The error between multi-field coupling simulation results and experimental results is controlled within 6%, verifying the model’s reliability. This research not only provides a universally applicable multi-field coupling analysis method for complex mold design but also highlights the critical role of temperature fields in stress distribution and deformation analysis. This lays a theoretical foundation for the intelligent design and process optimization of high-temperature, high-pressure forming equipment.

1. Introduction

Tires, as the sole components in direct contact between vehicles and road surfaces, critically determine vehicular handling, safety and fuel efficiency. With the rapid advancement of the automotive industry, tire manufacturing technologies have undergone continuous improvements, particularly in the design and optimization of tire molds, which are a pivotal element in enhancing tire performance [1,2,3]. During the vulcanization process, tire molds must simultaneously withstand high-temperature conditions and molding forces while ensuring precise dimensional accuracy and structural integrity of tire products. The temperature distribution, stress characteristics and deformation behavior of molds exert profound influences on vulcanization efficacy and final product quality. Research has demonstrated that deviations in vulcanization temperature, whether excessive or insufficient, significantly impair tire performance. Suboptimal thermal conditions during curing manifest distinct failure mechanisms: insufficient vulcanization compromises the rubber’s physical-mechanical properties through inadequate cross-link formation, while over-vulcanization induces excessive cross-linking networks that detrimentally affect elastic resilience and thermal stability [4]. During the vulcanization process, molds are subjected to dual operational demands: exposure to elevated temperatures and the application of molding forces. The strategic implementation of molding forces serves to maintain dimensional precision and structural integrity during tire formation. Nevertheless, this synergistic loading induces concurrent thermal and mechanical stresses within mold components, precipitating deformation phenomena and progressive fatigue damage [5]. Such cumulative deterioration mechanisms will further influence both product quality and manufacturing throughput efficiency [6]. Therefore, comprehensive investigation into the heat transfer, stress characteristics and deformation behavior of molds during vulcanization processes holds paramount theoretical and practical significance.

In recent years, numerous studies have investigated the heat transfer and mechanical behavior of segmented tire molds through numerical simulation methods. Sun et al. [7] investigated the heat transfer mechanisms and temperature distribution characteristics on the inner surfaces of pattern blocks in X1188 segmented tire molds through numerical simulations of their thermal processes. This research provides theoretical guidance for optimizing tire production processes and vulcanization molding. Tang et al. [8] conducted temperature analysis on the internal structure of molds by developing a simulation platform integrating finite element simulation and ANSYS Workbench 14.5. Their study determined the optimal curvature value, outer surface length and base inner diameter of the pattern blocks. Subsequent structural modifications reduced temperature differentials between the upper and lower points of the pattern blocks, resulting in more uniform thermal distribution and enhanced tire vulcanization quality. Shi et al. [9] established a finite element transient heat transfer model for tire molds. By analyzing the effects of factors such as convective heat transfer coefficients and contact thermal resistance on the heat transfer efficiency and temperature distribution uniformity of tire segment molds, they improved the heat transfer analysis model for tire molds.

Although significant advancements have been achieved in heat transfer and stress analysis of tire molds, certain limitations persist in existing research. Most studies in heat transfer simulation directly assign temperature values to the heat source (heating plate and guide ring) in order to save computational costs, without considering that the hot plate and guide ring are heated by internal steam and the impact of fluid flow on heat transfer [10]. Moreover, existing research has largely focused on the analysis of a single physical field, whereas systematic studies are lacking on the heat transfer, stress, and deformation of molds under the coupled effect of multiple fields.

Building upon existing research, this study focuses on segmented tire molds and proposes a multi-physics coupled simulation model that comprehensively integrates flow fields, temperature fields and structural fields. By incorporating heat transfer analysis of fluid domains, the work refines the simplified method of direct heat source assignment in traditional mold thermal simulations. Furthermore, it investigates mold deformation behavior under multi-physics coupling by integrating mechanical stresses induced by molding forces. This research advances methodologies for analyzing heat transfer, mechanical loading and deformation in complex segmented tire molds, offering a novel approach to enhancing vulcanization efficiency and product quality in tire manufacturing.

2. Theoretical Foundations

2.1. The Control Equations of the Fluid Domain

The flow of steam within the mold channels exhibits turbulent characteristics, with heat transfer governed by the energy conservation law. Due to the presence of sudden expansion and contraction geometric features in the heating plate’s flow channels, the SST k-ω turbulence model is employed to simulate vapor-mediated heat transfer, thereby improving the computational accuracy of turbulence–heat transfer coupling. The governing equations describing the turbulent flow and heat transfer processes of steam in the mold channels are formulated below, providing thermal boundary conditions for the solid domain [11,12],

$${\displaystyle \frac{\partial \left(\rho \mathbf{u}\right)}{\partial t}}+\nabla ·\left(\rho \mathbf{u}\otimes \mathbf{u}\right)=-\nabla p+\nabla ·\mathsf{\tau }+\rho \mathbf{g}$$

(1)

$${\displaystyle \frac{\partial \left(\rho E_{total}\right)}{\sigma t}}+\nabla ·\left(\rho \mathbf{u}{E}_{total}\right)=\nabla ·\left(k_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{a}\mathrm{m}}\nabla T\right)+S_{energy}$$

(2)

$${\displaystyle \frac{\partial \left(\rho k\right)}{\partial t}}+\nabla ·\left(\rho \mathbf{u}k\right)=\nabla \left[\left(\mu +{\sigma }_k{\mu }_t\right)\nabla k\right]+P_k-{\beta }^{\mathrm{*}}\rho \omega k$$

(3)

$${\displaystyle \frac{\partial \left(\rho \omega \right)}{\partial t}}+\nabla ·\left(\rho \mathbf{u}\omega \right)=\nabla ·\left[\left(\mu +{\sigma }_{\omega }{\mu }_t\right)\nabla \omega \right]+{\displaystyle \frac{\gamma }{v_t}}{P}_k-\beta \rho {\omega }^2+2(1-F_1){\displaystyle \frac{\rho {\sigma }_{\omega 2}}{\omega }}\nabla k·\nabla \omega$$

(4)

where $\rho$ is the density of steam, $\mathbf{u}$ is the velocity vector, $p$ is the static pressure of the fluid, $\mathsf{\tau }$ is the viscous stress tensor, $\mathbf{g}$ is the gravitational acceleration vector, $E_{total}$ is total energy (including internal and kinetic energy), $k_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{a}\mathrm{m}}$ is the thermal conductivity of steam, $S_{energy}$ is the energy source term, $k$ is the turbulent kinetic energy, $\mu$ is the dynamic viscosity of the fluid, ${\sigma }_k$ is the turbulent Prandtl number, assigned a value of 1, ${\mu }_t$ is turbulent viscosity, $P_k$ is the turbulent kinetic energy production term, ${\beta }^{\mathrm{*}}$ is dissipation coefficient, set to 0.09, $\omega$ is the specific dissipation rate, ${\sigma }_{\omega }$ is the turbulent Prandtl number for $\omega$, $\gamma$ is the production term coefficient with a value of 0.44, $v_t$ is the turbulent kinematic viscosity, $\beta$ is the dissipation coefficient, fixed at 0.075, $F_1$ is the blending function, and ${\sigma }_{\omega 2}$ is the second set of Prandtl numbers in the blending model, assigned a value of 1.168.

2.2. Governing Equations for the Solid Domain

The mold structure predominantly employs steel as the primary material, with its heat transfer behavior adhering to Fourier’s law. The following equations integrate Fourier’s law with thermoelastic equations to characterize thermal conduction within the solid domain and the resultant thermal stress induced by temperature gradients. Superimposing mechanical stresses from molding forces yields the total stress distribution across the mold assembly [13],

$$\mathrm{Thermal} \mathrm{Conduction}: \nabla ·\left(k_{steel}\nabla T\right)+Q=\rho c_p{\displaystyle \frac{\partial T}{\partial t}}$$

(5)

$$\mathrm{Thermal} \mathrm{Stress}: {\mathit{\sigma }}_{thermal}=\alpha E_{clastic}(T-T_0)\mathit{I}$$

(6)

$$\mathrm{Equilibrium} \mathrm{Equations}: \nabla ·\left({\mathit{\sigma }}_{mechanical}+{\mathit{\sigma }}_{thermal}\right)+\mathit{F}=0$$

(7)

where $k_{steel}$ is the thermal conductivity of steel, $Q$ is the internal heat source, $c_p$ is the specific heat capacity, $\alpha$ is the coefficient of thermal expansion, $E_{clastic}$ is the elastic modulus, $T_0$ is the initial temperature, ${\mathit{\sigma }}_{thermal}$ is the thermal stress tensor, ${\mathit{\sigma }}_{mechanical}$ is the mechanical stress tensor, and $\mathit{F}$ is the body force.

2.3. Fluid–Solid Coupling Boundary Conditions

To ensure the continuity of the temperature field and displacement field at the interface between the fluid domain and the solid domain, at the internal flow channel wall surface (the fluid–solid interface) of the mold, the following conditions should be met [14,15],

$$\mathrm{energy} \mathrm{conservation}: {\left.k_{steam}{\displaystyle \frac{\partial T}{\partial n}}\right|}_{fluid}={k_{steel}\left.{\displaystyle \frac{\partial T}{\partial n}}\right|}_{solid}$$

(8)

$$\mathrm{displacement} \mathrm{continuity}: {\mathbf{u}}_{fluid}={\mathbf{u}}_{solid}$$

(9)

where ${\displaystyle \frac{\partial T}{\partial n}}$ is the normal component of the temperature gradient, and ${\mathbf{u}}_{fluid}$ and ${\mathbf{u}}_{solid}$ are the displacement vectors of the fluid and solid at the interface, respectively.

The accuracy of the convective heat transfer coefficient $h$ directly governs the interfacial heat flux density. Within the ANSYS Fluent framework, $h$ is automatically computed via wall functions. The convective heat transfer between steam and the steel surface is defined by Newton’s law of cooling:

$$q_{conv}=h(T_{steam}-T_{steel})$$

(10)

where $h$ is the convective heat transfer coefficient, and $T_{steam}$ and $T_{steel}$ denote the surface temperatures of the steam and steel, respectively.

3. Numerical Simulations

3.1. Establishment of Simulation Model

A three-dimensional model was constructed based on the CB12 segmented tire mold, applicable to the majority of complex segmented tire molds. Figure 1 is the structural schematic diagram of the segmented tire mold. The basic structure of the segmented tire mold comprises the mold shell and forming components. The mold shell includes the upper cover, mounting ring, guide ring, guide strip, slide block, lower base, etc. The forming components, which directly contact the tire, include the upper side plate, tread segment and lower side plate. The upper heating plate and lower heating plate in the figure are components of the vulcanizer, serving as heat sources in direct contact with the mold.

The workflow of the mold involves preheating, mold opening, placement of the green tire, mold closing, pressurization, vulcanization and subsequent mold opening for tire removal. The mold is preheated by injecting 180 °C steam into the cavities of the upper heating plate, lower heating plate and guide ring, transferring heat to internal structures via conduction.

During preprocessing, fillets and chamfers were appropriately simplified to enhance computational efficiency without compromising accuracy.

For meshing, since the forming components such as the upper side plate, tread segment and lower side plate directly contact the tire, they critically affect the tire’s quality. And considering subsequent stress analysis requirements, structured grids were employed for these components to achieve precise meshing. The average element quality was 0.83, with an average aspect ratio of 2.5, meeting stress analysis requirements. Irregularly shaped internal components were meshed with unstructured grids. The hybrid meshing strategy ensured both precision and computational efficiency, yielding an average element quality of 0.81 (Figure 2).

To replicate actual conditions, gravity (9.8 m/s²) was applied to the internal flow field. The fluid domain’s inlet was set as a pressure inlet (180 °C, 1.15 MPa gauge pressure), and the outlet as a pressure outlet. Fluid simulation results were used as boundary conditions for the mold’s thermal analysis. Temperature field results were then imported as thermal loads into a linear static structural analysis. Fluid–solid coupling interfaces were defined on the inner surfaces of the upper heating plate, guide ring and lower heating plate. Molding force was applied to the upper surface of the mounting ring, while fixed supports were assigned to the lower surface of the lower heating plate (Figure 3). The material properties of key components are listed in

Table 1. The material selection and parameters of key mold components.

Component	Material	Density (kg/m3)	Thermal Expansion Coefficient (/K)	Elastic Modulus (GPa)	Poisson’s Ratio
Guide Ring/Upper Side Plate/Lower Side Plate	35# Steel	7850	1.2 × 10−5	203	0.3
Mounting Ring/Lower Base/Upper Cover	45# Steel	7850	1.2 × 10−5	210	0.27
Guide Strip/Slide Block/Upper Slide Block	40Cr Steel	7850	1.2 × 10−5	195	0.3
Tread Segment	A514 Steel	7850	1.2 × 10−5	60	0.32

.

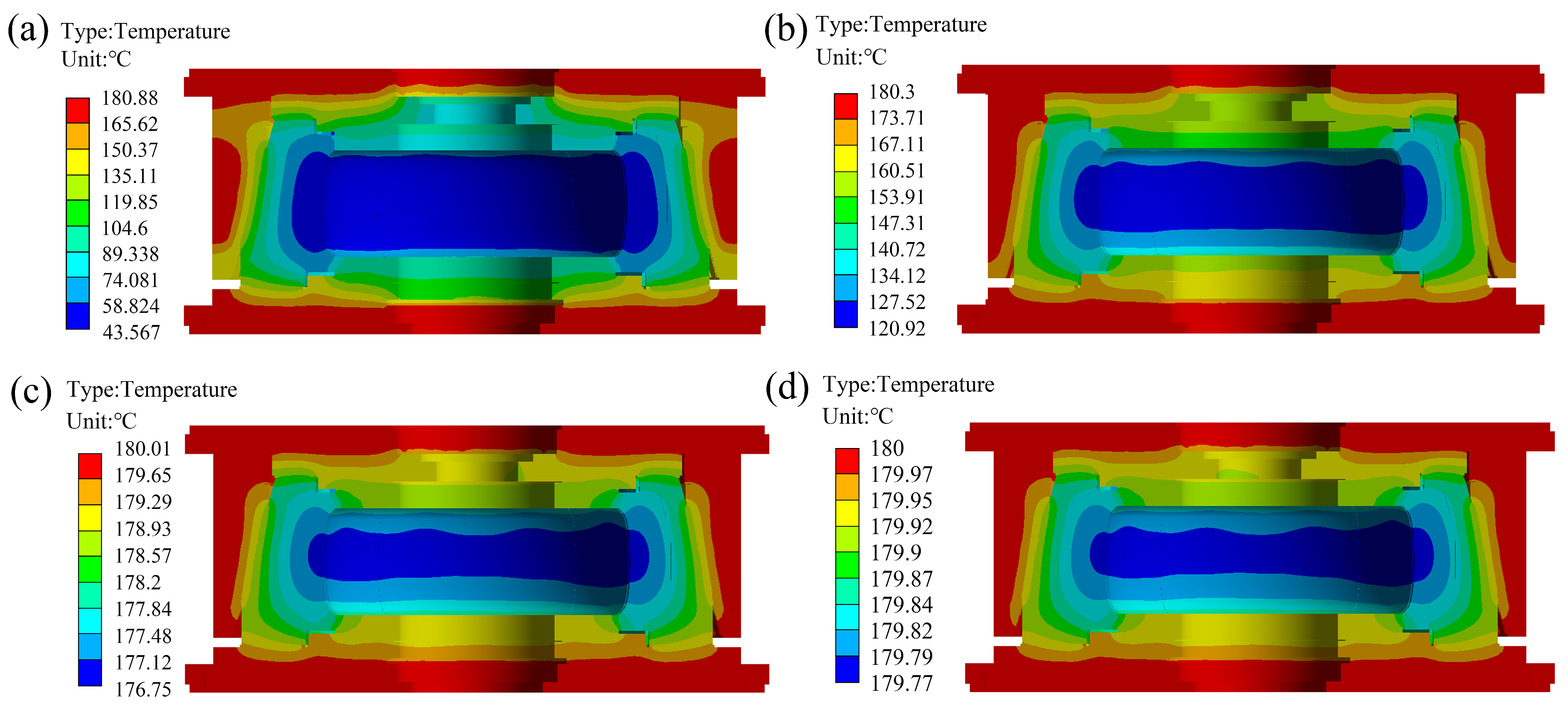
3.2. Multi-Field Coupled Temperature Field Analysis

Figure 4 illustrates the temperature distribution cloud maps of the fluid domain within the internal cavities of the upper heating plate, guide ring and lower heating plate filled with 180 °C steam. The figure reveals minor temperature fluctuations in localized regions of the upper and lower heating plate, attributed to irregular cavity geometries (non-uniform cross-sectional flow channels) that induce small-scale reflux in specific areas. From an overall trend perspective, the temperature reduction across the three fluid domains from the inlet to the outlet is extremely minor, with the entire fluid domain remaining above 179.99 °C. This uniformity ensures favorable thermal conditions for efficient heat transfer from the fluid to the mold [16]. Incorporating fluid temperature field analysis enhances the fidelity to actual production processes, thereby improving the accuracy of subsequent mold-wide temperature field evaluations.

The three heat sources (heating plates and guide ring) transfer heat inward from the external components of the mold, and the final temperature distribution is reflected in the upper side plate, tread segment and lower side plate. Figure 5 presents the internal temperature distribution cloud maps, showing heat propagation from the upper heating plate, guide ring and lower heating plate through the upper cover slide block, slide block and lower base to the upper side plate, tread segment and lower side plate. Seven measurement points on the forming components were selected to visualize their heating trends (locations shown in Figure 6). Figure 7 displays the heating curves of these seven internal measurement points. Notably, the lower side plate exhibits the fastest temperature rise, followed by the upper side plate, while the tread segment, particularly measurement point #6 at its center, shows the slowest heating rate. This discrepancy arises from variations in component thickness between the measurement points and heat sources, leading to differences in heat transfer rates.

During the mold heating process (raising the mold temperature to the level required for tire production), a significant temperature increase is observed within the first 4000 s, followed by a gradual slowdown in heating. After 9000 s, the temperatures of all components stabilize above 178 °C. Once the mold is fully heated, the local minimum temperature reaches 179.77 °C, meeting the requirements for rubber tire formation. The global temperature difference is controlled within 0.13%, demonstrating excellent temperature uniformity and providing optimal thermal conditions for rubber tire molding. The temperature values at each measurement point corresponding to the time points are listed in

Table 2. The temperature values at each measurement point corresponding to the aforementioned time points. (Unit: °C).

	1#	2#	3#	4#	5#	6#	7#
4000 s	164.1	158.8	168.8	164.3	150.6	144.9	153.4
9000 s	179.1	178.9	179.4	179.1	178.3	178.0	178.5
14,400 s	179.9	179.8	179.9	179.9	179.8	179.8	179.8

.

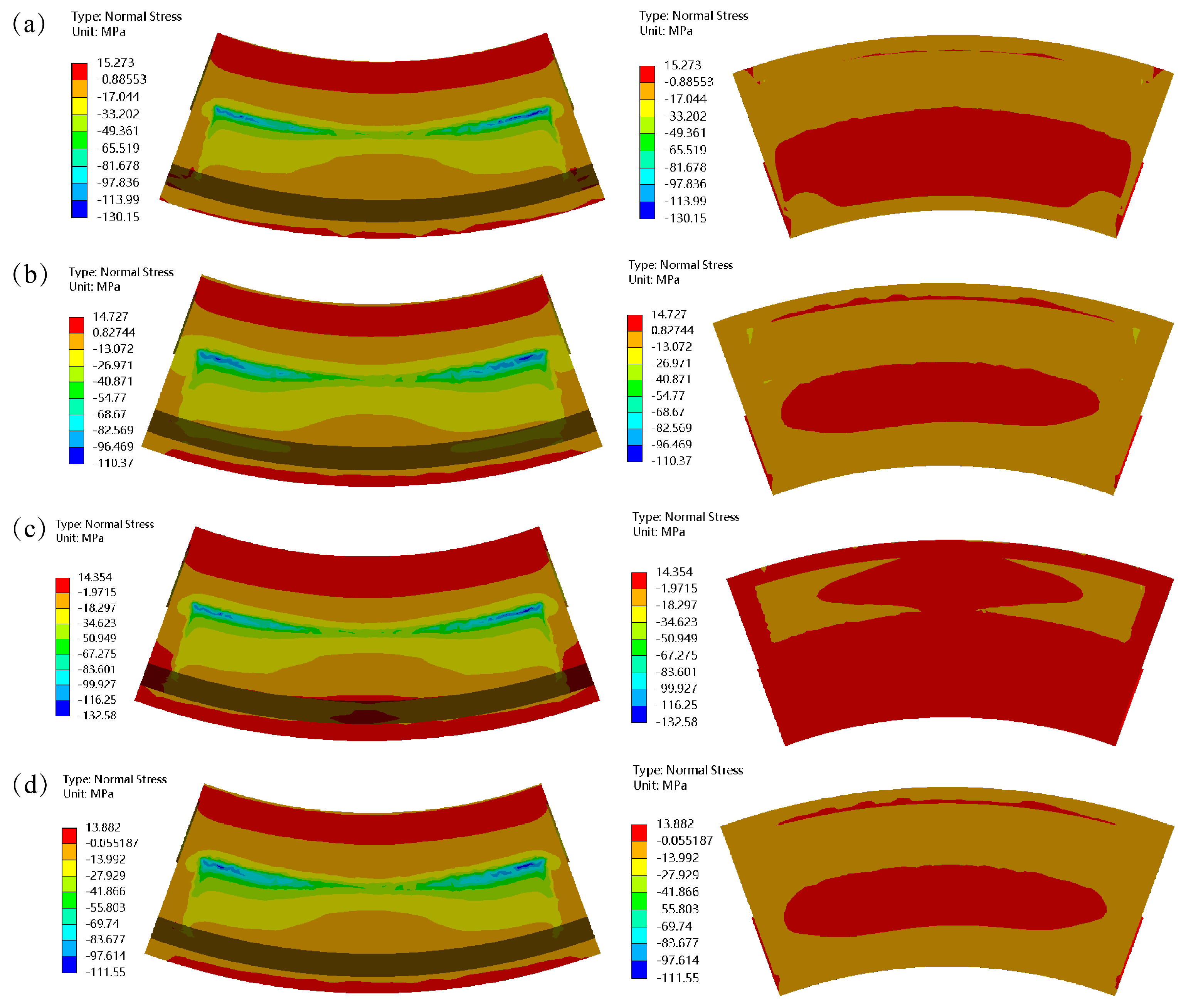
3.3. Stress Analysis Based on Multi-Field Coupling

In actual production processes, the components in contact with rubber tires are the upper side plate, tread segment and lower side plate. Particularly, as the primary forming component, the deformation behavior of the tread segment directly affects the molding quality of rubber tires. Therefore, this section focuses on analyzing the stress distribution of the tread segment under the coupled effects of temperature fields (based on fluid temperature) and force fields. The locations of stress measurement points are illustrated in Figure 8.

When the mold with its base constrained is subjected solely to the temperature field, thermal stress comprises thermal expansion stress and temperature gradient-induced stress. Upon applying molding forces, the total stress acting on the mold comprises both thermally induced stress (from the temperature field) and mechanically induced stress (from external molding forces). These stresses superimpose, and the total stress ${\sigma }_{total}$ can be expressed as their summation [4]:

$${\sigma }_{total}={\sigma }_{thermal}+{\sigma }_{mechanical}$$

(11)

The combined effect of thermal stress and mechanical stress exerts a more significant influence on the tread segment [17,18]. Figure 9 illustrates the stress cloud maps of the upper and lower surfaces of the tread segment under identical temperature loading but varying molding forces. Due to the constrained base of the mold, thermal stress is generated under temperature loading, typically manifesting as compressive stress. However, since the constraint is not entirely rigid, a coexistence of tensile and compressive stresses occurs. When molding forces are applied, the total stress gradually decreases as the molding force increases. Within the range of 70 T to 100 T, each 10 T increase in molding force reduces the total stress by approximately 0.5 MPa. However, this effect diminishes as the force increases, as shown in the figure. Based on the stress analysis results across the four working conditions, it is evident that temperature loading has a greater impact on the mold’s stress distribution than mechanical stress.

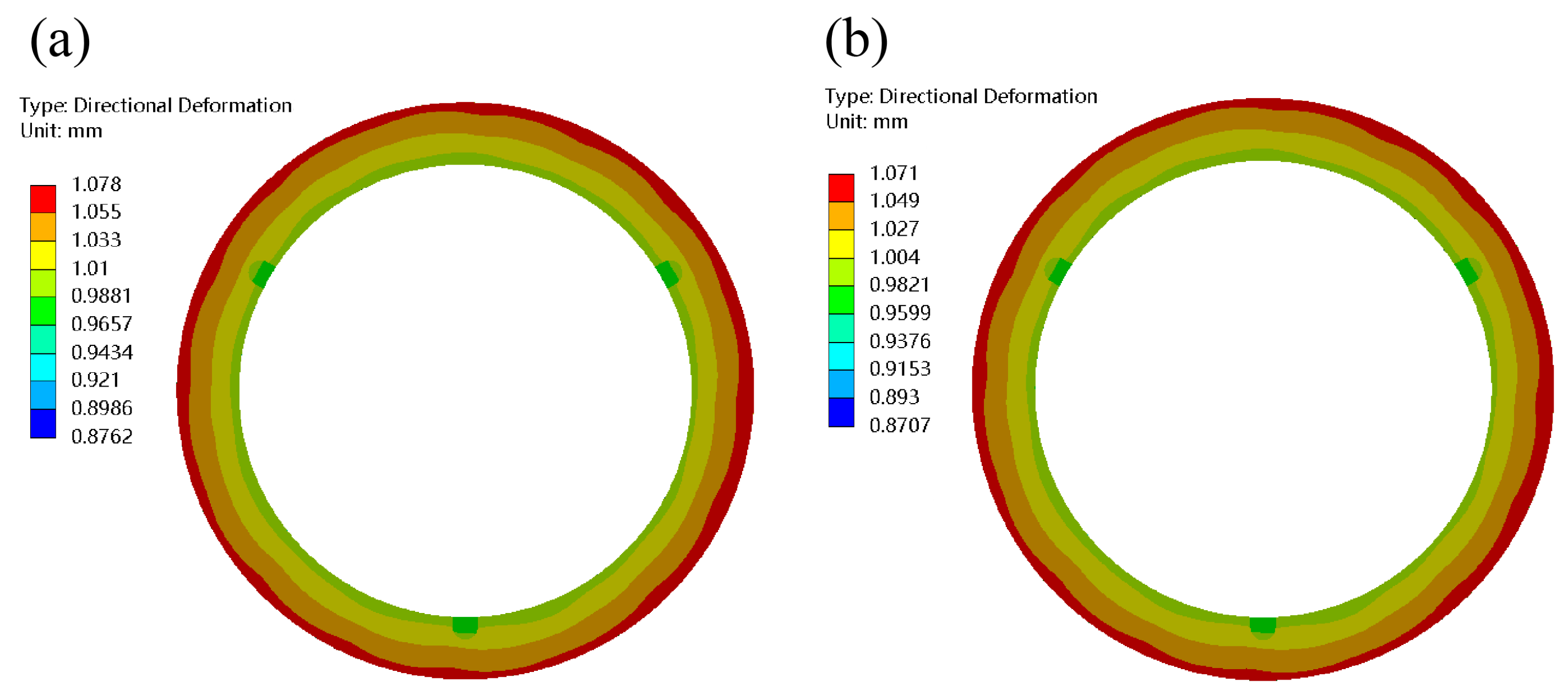
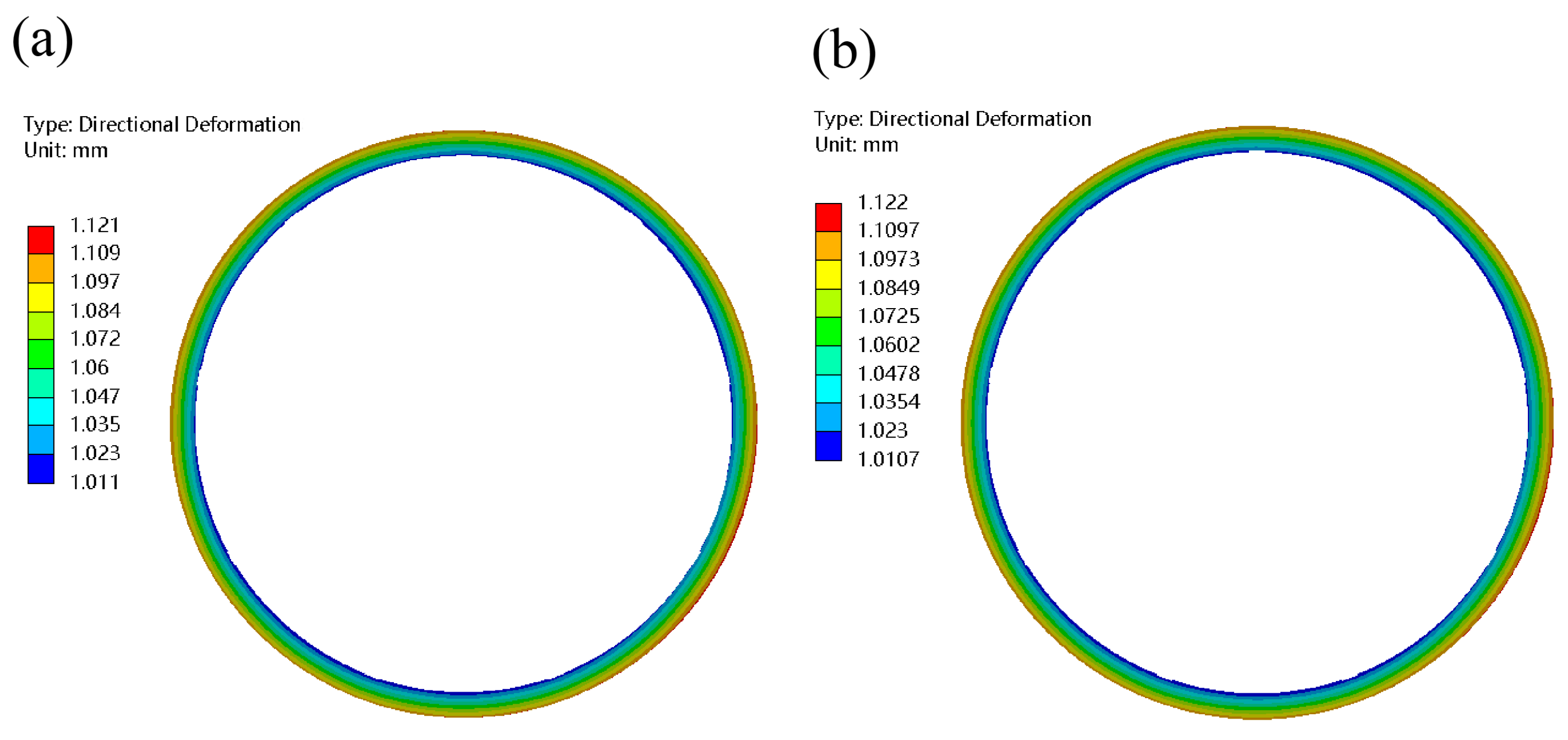
3.4. Deformation Analysis Based on Multi-Field Coupling

The mounting ring is the direct load-bearing component of molding forces, while the guide ring, bound to the mounting ring, serves as an indirect load-bearing component. Under the combined effects of temperature loading and pressure loading, both components undergo certain deformations [19]. When subjected solely to temperature loading, the mounting ring and guide ring exhibit expansion deformation [20,21]. Figure 10 shows the axial deformation cloud maps of the mounting ring under identical temperature loading but varying molding forces. As illustrated, the expansion deformation of the mounting ring decreases upon applying molding forces, with the deformation magnitude further decreasing as the force increases. It can be inferred that molding forces induce compressive deformation in the axial direction of the mounting ring. Figure 11 presents the radial deformation cloud maps of the guide ring under identical temperature loading but different molding forces under the same working conditions (with identical molding forces); the deformation magnitude of the guide ring gradually decreases from the outer circumference inward. When the molding force increases from 70 T to 80 T, the radial deformation of the guide ring slightly increases, with the outer circumference expanding by only 0.001 mm. The simulation process effectively replicates the actual working conditions of the mold.

To facilitate comparison with subsequent experiments and further validate the feasibility and accuracy of the simulation model and method, four uniformly distributed measurement points were selected on the upper surface of the mounting ring, as shown in Figure 12, and three uniformly distributed measurement points were taken at a position 20 mm below the outer surface of the guide ring, as illustrated in Figure 13.

4. Experimental Section

To validate the accuracy of the numerical simulations, this study designed a corresponding experimental system, which primarily includes heat transfer testing, stress testing and deformation testing of the mold.

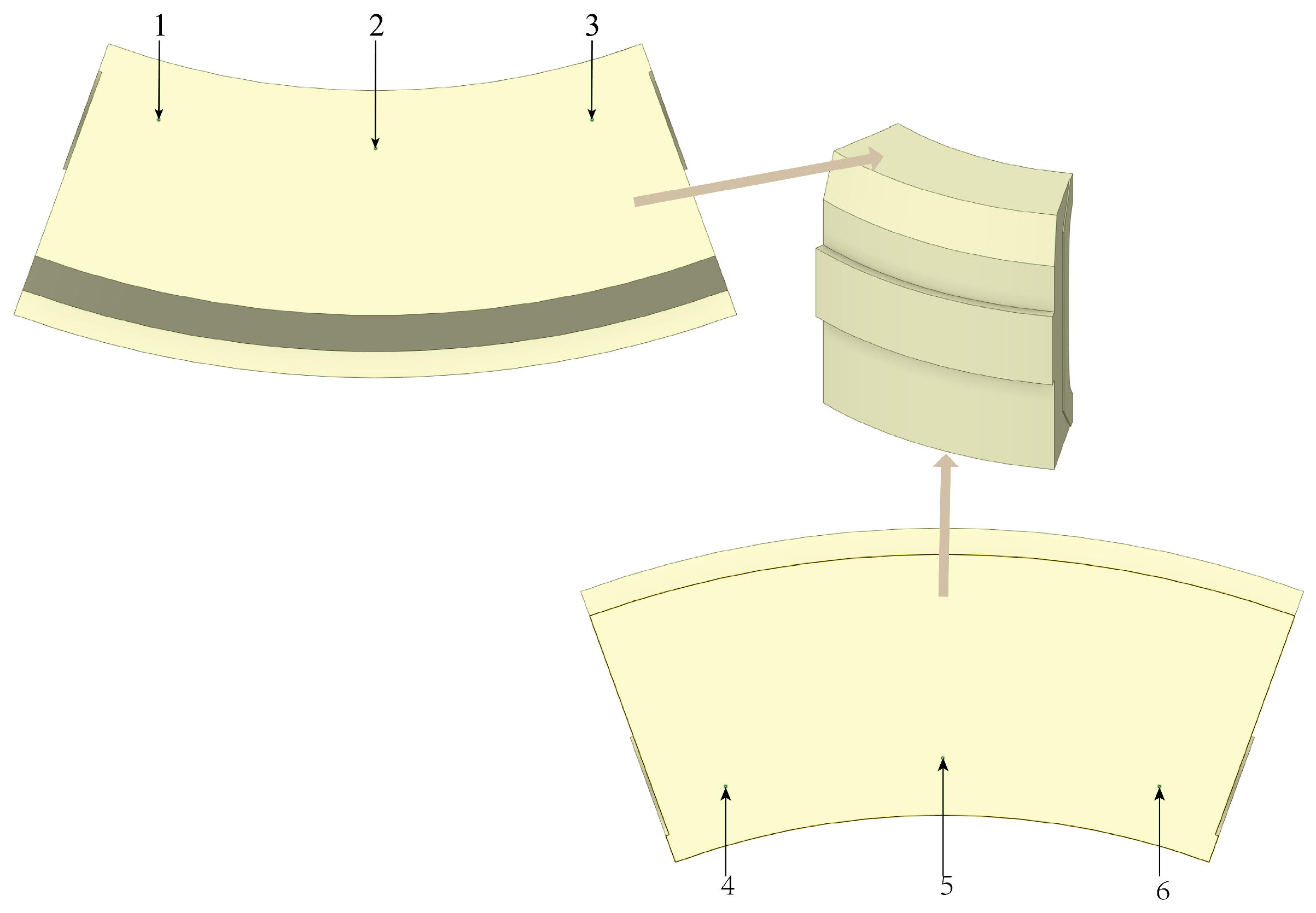
4.1. Testing System

High-temperature steam (180 °C) was employed as the heat source, uniformly heating the mold through the steam chambers of the upper heating plate, guide ring and lower heating plate. High-precision thermocouples were installed on the upper side plate, tread segment and lower side plate to monitor the temperature in real time, with dynamic changes recorded by a DAS (data acquisition system). The testing setup is shown in Figure 14. Strain gauges were mounted on the upper and lower surfaces of the tread segment, and their stress responses under molding forces were synchronously captured using strain meters and the data acquisition system. Dial indicators were positioned at critical locations on the mounting ring and guide ring to quantify deformation behavior under the coupled effects of molding forces and temperature loading. The testing setup is shown in Figure 15.

4.2. Experimental Conditions

The steam inlet gauge pressure was set to 1.15 MPa, with the temperature strictly controlled at 180 °C to simulate the heating environment of actual vulcanization processes. Molding forces (70 T, 80 T, 90 T and 100 T) were applied instantaneously, covering the typical operational range. Due to the instability of dial indicators under high-temperature conditions, deformation testing was conducted at room temperature (23 °C). High-temperature deformation data were indirectly validated through multi-field coupled simulations.

4.3. Uncertainty Assessment of Experimental and Simulation Results

Uncertainty in Experimental Data:

(1)

Measurement Errors

Thermocouple accuracy: ±0.5 °C (Manufacturer’s calibration value), DAS (Data Acquisition System) error: ±0.1% FS (Full Scale).

(2)

Repeatability Verification

Three tests were conducted on the mold under identical operating conditions, revealing fluctuation ranges of ±1.3 °C for temperature measurement points and ±0.2 MPa for stress measurement points.

(3)

Combined Uncertainty

Temperature uncertainty range: ±1.5 °C, Stress uncertainty range: ±0.3 MPa.

Uncertainty in Simulation Data:

(1)

Fluctuation ranges of key parameters are listed in the

Table 3. Key simulation parameters and their uncertainties.

Parameter	Standard Value	Fluctuation Range	Basis
Steam Temperature	180 °C	±2 °C	Vulcanizer control accuracy
Thermal Conductivity	50 W/m·K	±5%	Material handbook tolerance
Molding forces	80 T	±3%	Hydraulic system error

below.

(2)

Simulation of key parameters

Temperature uncertainty range: ±1.6 °C, Stress uncertainty range: ±0.2 MPa.

Reliability of Results Comparison:

(1)

Temperature Field Validation

For all seven temperature measurement points, the errors between simulation and experimental results were less than 8%. Under thermally stabilized conditions, the simulation uncertainty range (±1.6 °C) fully encompassed the experimental uncertainty range (±1.5 °C).

(2)

Stress Validation

The errors were below 6% at six stress measurement points. The simulation uncertainty range (±0.2 MPa) was narrower than the experimental uncertainty range (±0.3 MPa).

5. Simulation and Experimental Results Verification

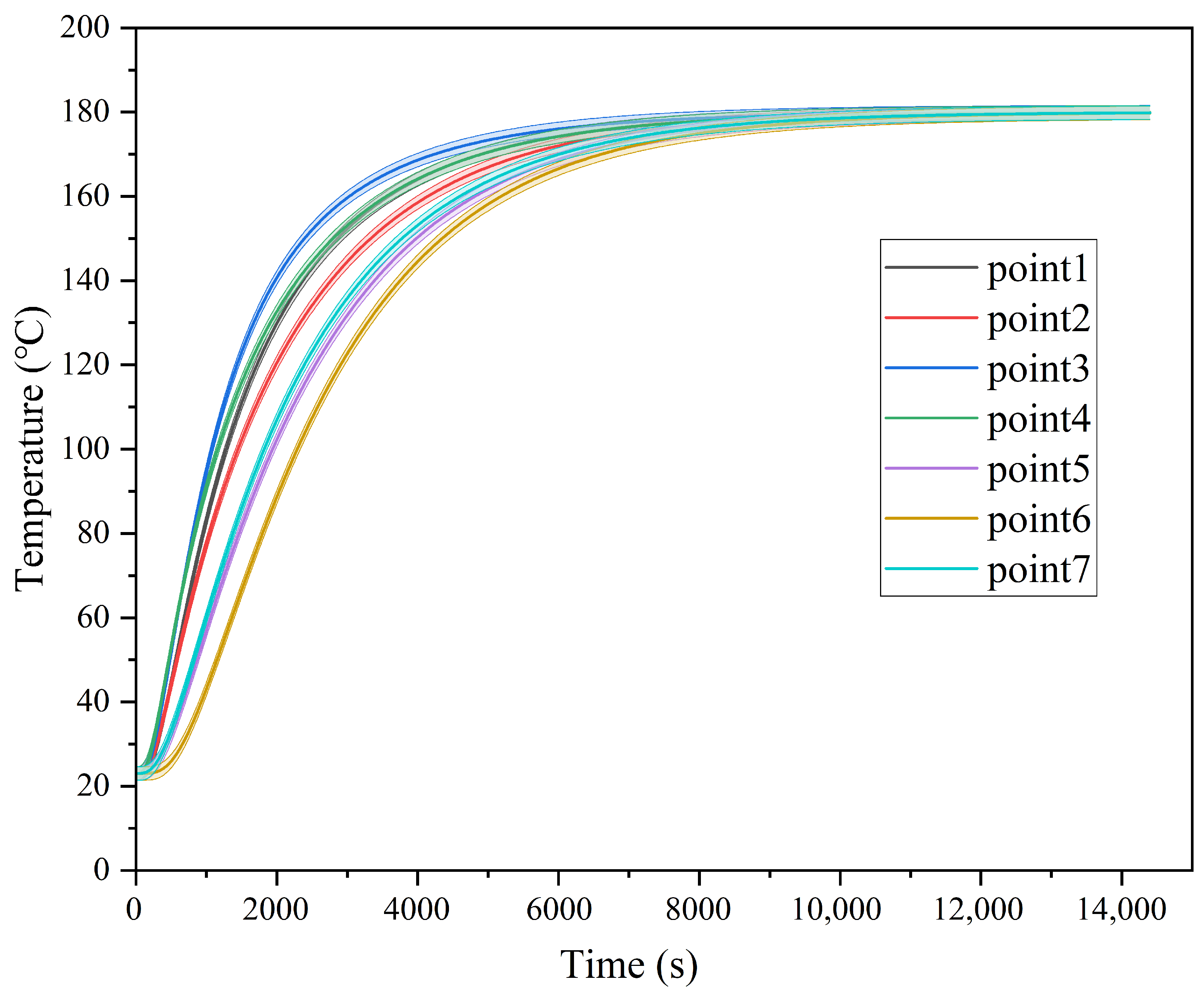
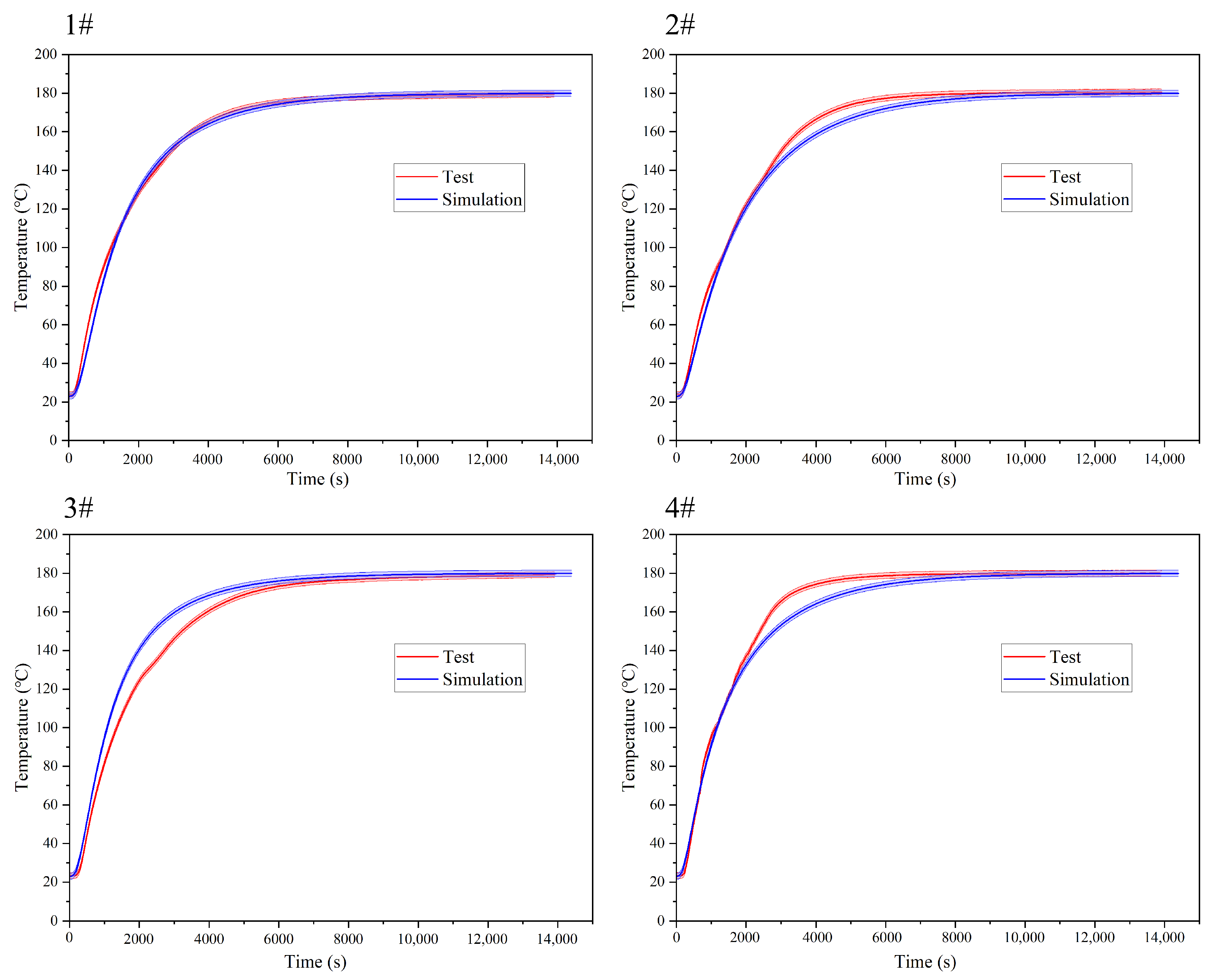
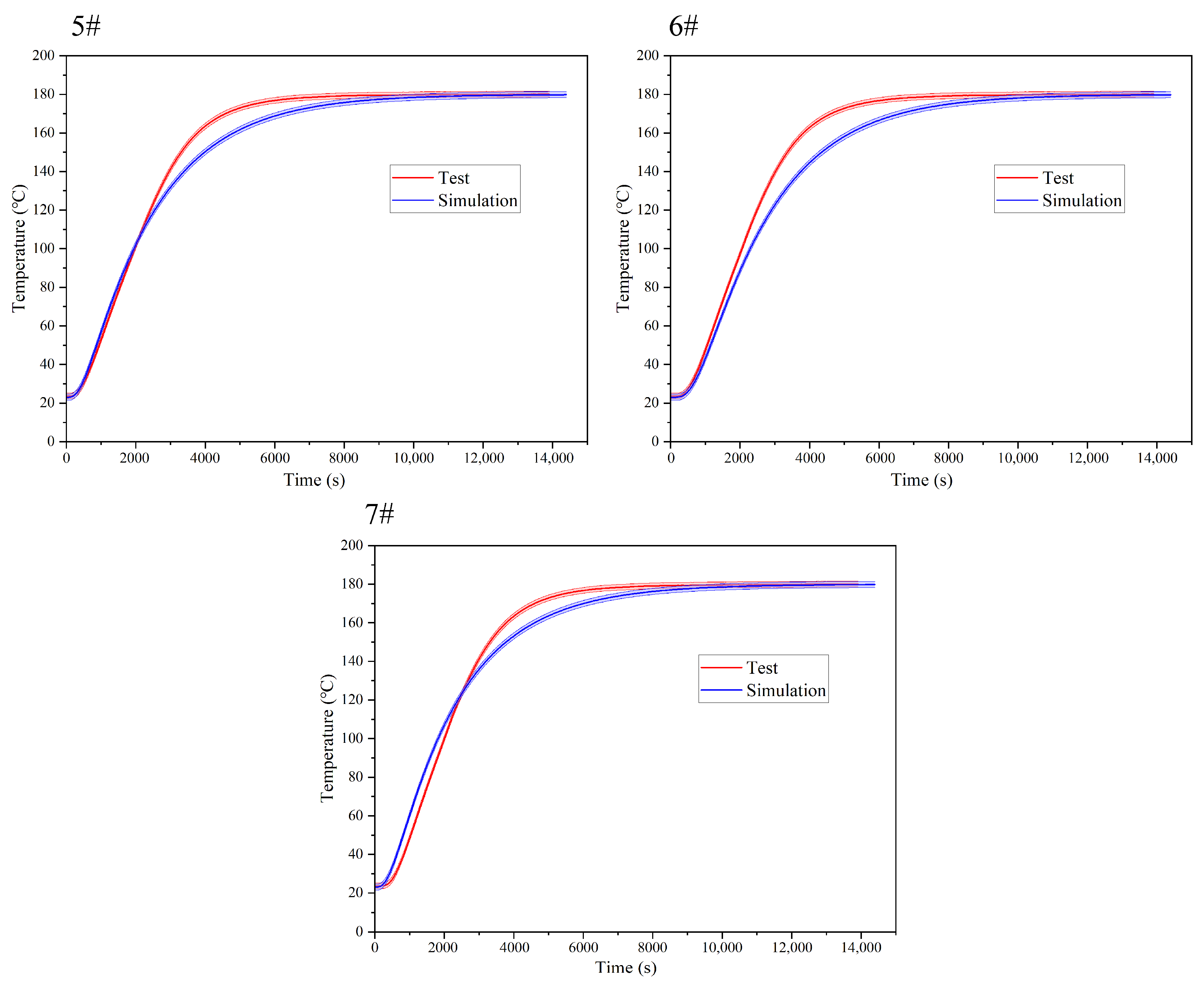
5.1. Temperature Rise Process Comparison and Verification

The temperature measurement experiment was conducted under the actual working conditions of the mold, where a 4 h preheating process was implemented to achieve stable operational temperatures. Figure 16 presents comparative temperature curves between experimental measurements and numerical simulations across seven monitoring points. Comparative analysis between the simulation results from Section 2 and experimental data from Section 3 revealed that the temperature rise rates at measurement points on the upper and lower side plates (1# to 4#) are faster than those at points on the tread segment (5# to 7#). This phenomenon can be attributed to the shorter heat transfer distances between the side plates and heating plates, coupled with smaller component thicknesses along the thermal pathways, which collectively enhanced heat transfer efficiency. The simulation and experimental data demonstrated exceptional agreement at monitoring points 1# and 2# on the upper side plate, with maximum consistency observed in these locations. However, monitoring point 6# on the tread segment showed a relatively lower correlation between simulated and experimental temperature profiles, though all measurement discrepancies remained within 8%.

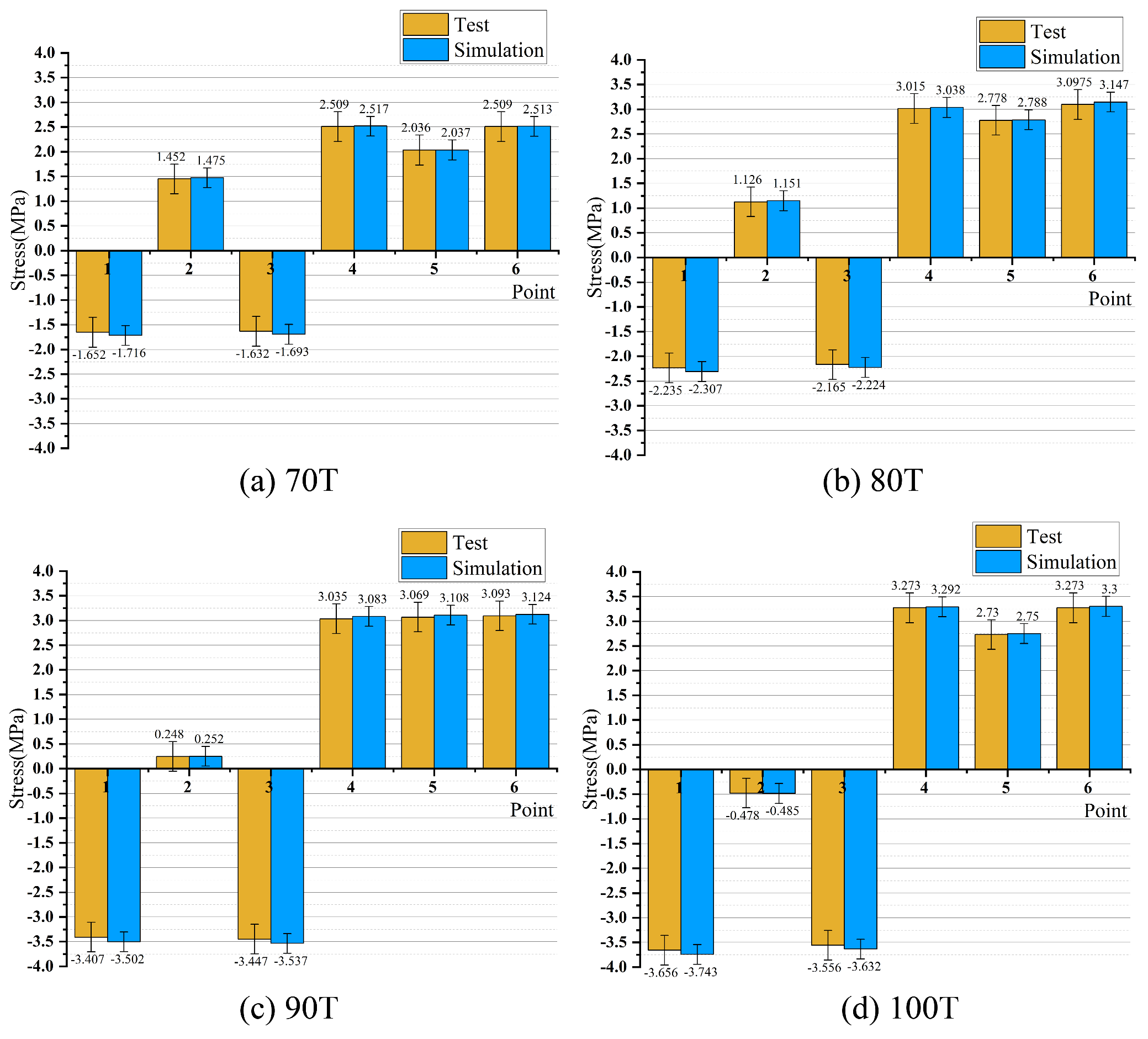
5.2. Stress Value Comparison and Verification

Figure 17 presents a comparison of experimental and simulated values at six measurement points on the upper and lower surfaces of the tread segment under four molding force conditions (70 T, 80 T, 90 T and 100 T) at 180 °C. It is evident that the stress values at all measurement points exhibit a positive correlation with the molding force, and the errors between simulated and experimental values under each condition are controlled within 6%, thereby validating the feasibility and accuracy of the numerical simulation method.

5.3. Deformation Comparison and Verification

Table 4. Experimental and simulated deformation values at four measurement points on the mounting ring under ambient temperature (Unit: mm).

	70 T			80 T
	Test	Simulation	Error	Test	Simulation	Error
1	−0.17	−0.18	6%	−0.21	−0.21	0%
2	−0.21	−0.22	5%	−0.24	−0.24	4%
3	−0.16	−0.17	6%	−0.19	−0.19	5%
4	−0.20	−0.21	5%	−0.23	−0.24	4%

presents the experimental and simulated deformation values at four measurement points on the mounting ring under ambient temperature. As shown in the table, the mounting ring exhibits compressive deformation when subjected solely to molding force, and the magnitude of deformation increases proportionally with the applied molding force.

Table 5. Deformation values at four measurement points on the mounting ring under actual working conditions (Unit: mm).

	70 T	80 T
1	1.04	1.04
2	1.03	1.04
3	1.04	1.04
4	1.03	1.04

provides the deformation values at four measurement points on the mounting ring under actual working conditions, where both molding force and thermal load are applied. By comparing Table 3 and Table 4, it is evident that the mounting ring exhibits expansion deformation under the coupled effects of molding force and thermal load. In this scenario, the influence of thermal load on the deformation of the mounting ring is approximately 5 to 7 times greater than that of the molding force.

Table 6. Experimental and simulated deformation values at three measurement points on the guide ring under ambient temperature (Unit: mm).

	70 T			80 T
	Test	Simulation	Error	Test	Simulation	Error
1	0.020	0.021	5%	0.021	0.022	4.8%
2	0.018	0.019	6%	0.020	0.021	5%
3	0.019	0.020	5%	0.019	0.020	5.3%
4	0.020	0.021	5%	0.021	0.022	4.8%

presents the experimental and simulated deformation values at three measurement points on the guide ring under ambient temperature. As shown in the table, the deformation of the guide ring is minimal when subjected solely to molding force. Additionally, the deformation change is not significant when the molding force increases from 70 T to 80 T. This is attributed to the large structure of the guide ring and the fact that the measurement points are located on the lower part of its outer surface.

Table 7. Deformation values at three measurement points on the guide ring under actual working conditions. (Unit: mm).

	70 T	80 T
1	1.104	1.104
2	1.103	1.103
3	1.102	1.102
4	1.104	1.104

provides the deformation values at three measurement points on the guide ring under actual working conditions, where both molding force and thermal load are applied. By comparing Table 5 and Table 6, it is evident that the guide ring exhibits significant expansion deformation under the coupled effects of molding force and thermal load, reaching 1.1 mm, which is approximately 50 times greater than the deformation observed under ambient temperature conditions.

The comprehensive analysis of the above data indicates that the errors between simulated and experimental values under ambient temperature are controlled within 6%. This demonstrates that the simulation model established in this study aligns with the actual working conditions of the mold. Furthermore, thermal loads have a more substantial impact on mold deformation than external mechanical loads, underscoring the critical influence of temperature factors in mold design and operational processes.

6. Conclusions

This study established a multi-physics coupling model for tire mold vulcanization, integrating fluid-thermal-structural interaction analysis while accounting for heat transfer effects in fluid domains. Using the ANSYS platform, sequential simulations were conducted along with clamping force simulation, leading to stress and deformation analysis of critical components. Experimental validation confirmed the model’s accuracy. The main conclusions are as follows:

(1)

This investigation establishes a multi-physics coupling framework integrating steam heat transfer, mold thermodynamics and fluid-structure coupling boundary conditions. It achieves the research on complex segmented tire molds based on multi-physics field coupling, overcoming the limitations of traditional single-field analysis. Compared to the simplified method of assigning heat source values directly, the model incorporates heat transfer analysis of the fluid domain, reducing the temperature field prediction error to 0.13%. The results are approximately 2% lower than those obtained in previous studies by other researchers [9], significantly enhancing the predictive capability of heat transfer and mechanical behavior in complex molds.

(2)

The study reveals that the influence of thermal loads on mold deformation far exceeds that of mechanical loads. The expansive deformation of the guide ring under high temperatures reaches 1.1 mm, which is 50 times greater than that under ambient molding forces. This phenomenon highlights the central role of temperature factors in the vulcanization process: the impact of the temperature field must be prioritized in mold design to mitigate thermal stress accumulation and extend mold lifespan.

By integrating multi-physics coupling theory with experimental validation, this study not only provides a theoretical foundation for high-precision simulation of tire molds but also establishes a new paradigm for the efficient design and manufacturing of tire molds. Furthermore, it lays a methodological groundwork for the multidisciplinary optimization of complex industrial equipment.