A Health Status Identification Method for Rotating Machinery Based on Multimodal Joint Representation Learning and a Residual Neural Network
Abstract
:1. Introduction
- (1)
- Construction of a multimodal feature set: to address the heterogeneity of different modal data, we integrated multiple source signals (e.g., vibration signals, temperature signals) to construct a comprehensive and representative multimodal feature set for equipment condition characterization.
- (2)
- Design of a joint representation learning layer: Considering the complementarity and consistency among modalities, we designed a joint representation learning layer that combines orthogonal projection with a Transformer-based architecture. This enables the joint learning of multimodal features within a shared subspace, resulting in more generalizable and discriminative feature representations.
- (3)
- Development of a health state assessment model: we proposed a health state assessment model based on a ResNet, which effectively utilizes deep feature information to achieve the efficient and accurate recognition of equipment health states.
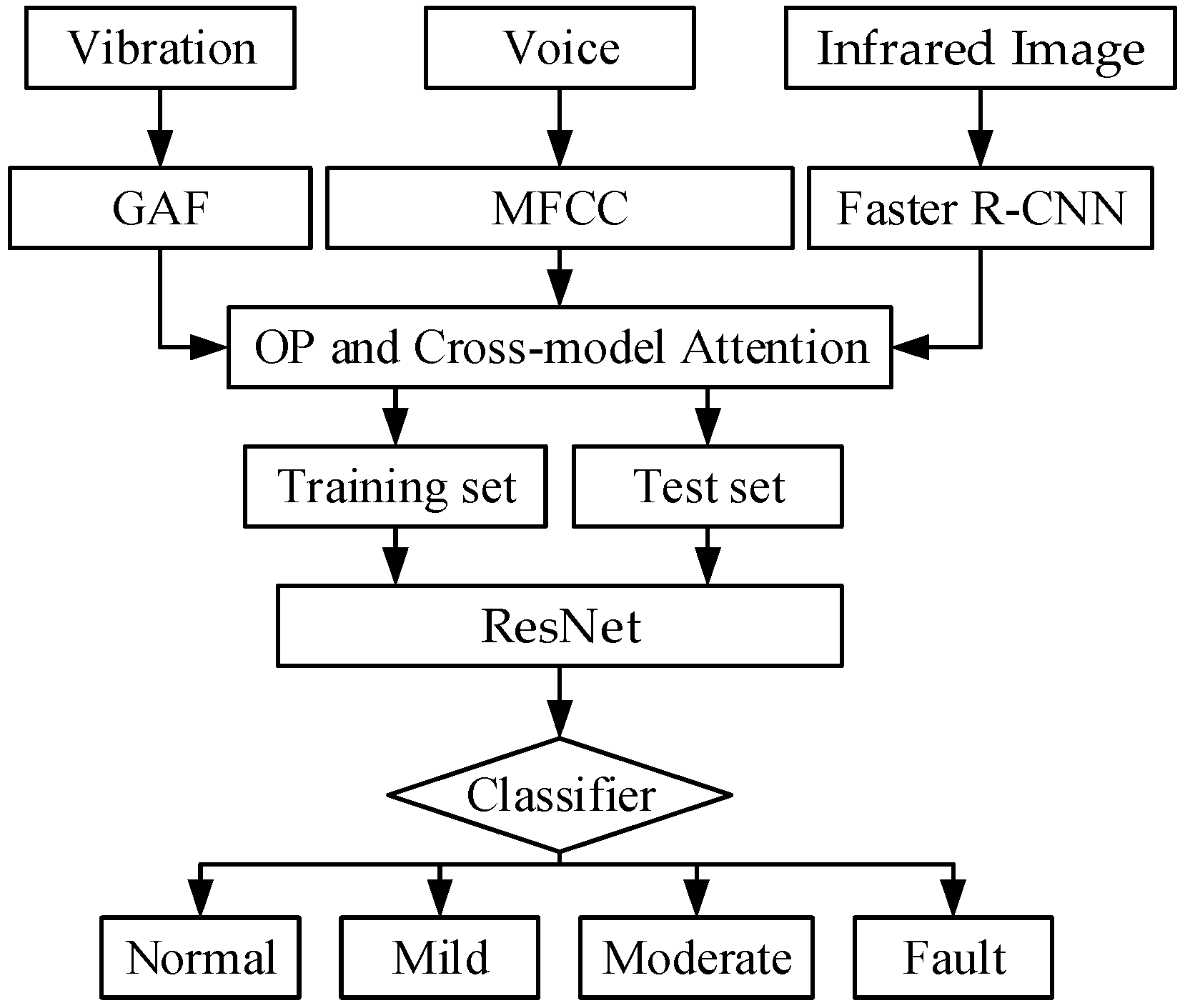
2. Multimodal Joint Representation Learning and Residual Neural Network-Based Health Status Recognition Method
2.1. Single Modal Feature Construction Method
2.1.1. Vibration Signal Feature Extraction Based on GAF
- Data Normalization: since there is no significant disparity within the latent feature sequences, mean normalization is applied to map the data in the range of [−1, 1] without altering their inherent distribution characteristics.
- Encoding Mapping in Polar Coordinates: after normalization, the latent feature sequence is re-encoded from Cartesian coordinates to polar coordinates using coordinate transformation formulas.
- Gram Matrix Computation and Feature Map Construction: once converted to the polar coordinate system, the normalized latent feature sequence is used to compute a Gram matrix, where the correlations over different time intervals are represented using trigonometric sum or difference relationships between points.
2.1.2. Voice Signal Feature Extraction Based on MFCCs
2.1.3. Image Signal Feature Extraction Based on Faster R-CNN
2.2. Multimodal Joint Representation Learning
2.2.1. Orthogonal Projection
- First, L2 normalization is applied to encode each sequence, obtaining , , and , as well as , , and . Then, we measure the correlation between the corresponding positions of two modality vectors by computing the dot product, as follows:
- Second, we use the SoftMax operation to approximate the correlation between modality v and modality a (or i) at corresponding positions, as well as the correlation between each element in (or ) and modality v (or i).
- Third, we perform a 1 − x operation on the correlation values (for each input x), returning 1 − x, performing subtraction at each position to obtain a dissimilarity vector. This vector measures the degree of difference between the two modality representations at corresponding positions. Then, we multiply the original representations ( and ) with these dissimilarity vectors to obtain the information components that are orthogonal to the target modality. These components eliminate redundant information between other modalities and the target modality, thereby preserving only the parts that are orthogonal to the target modality vector for further processing.
- Then, these orthogonal components are added to the target modality, obtaining the fused latent adaptation from modality a and i to v. In this process, the original representation of modality v is preserved while incorporating complementary information from other modalities.
- After this, can participate in the cross-attention process of the t-th encoder of modality v (serving as the source for K and V).
2.2.2. Joint Representation Learning Layer
2.2.3. Modality-Specific Representation
2.2.4. Decoding
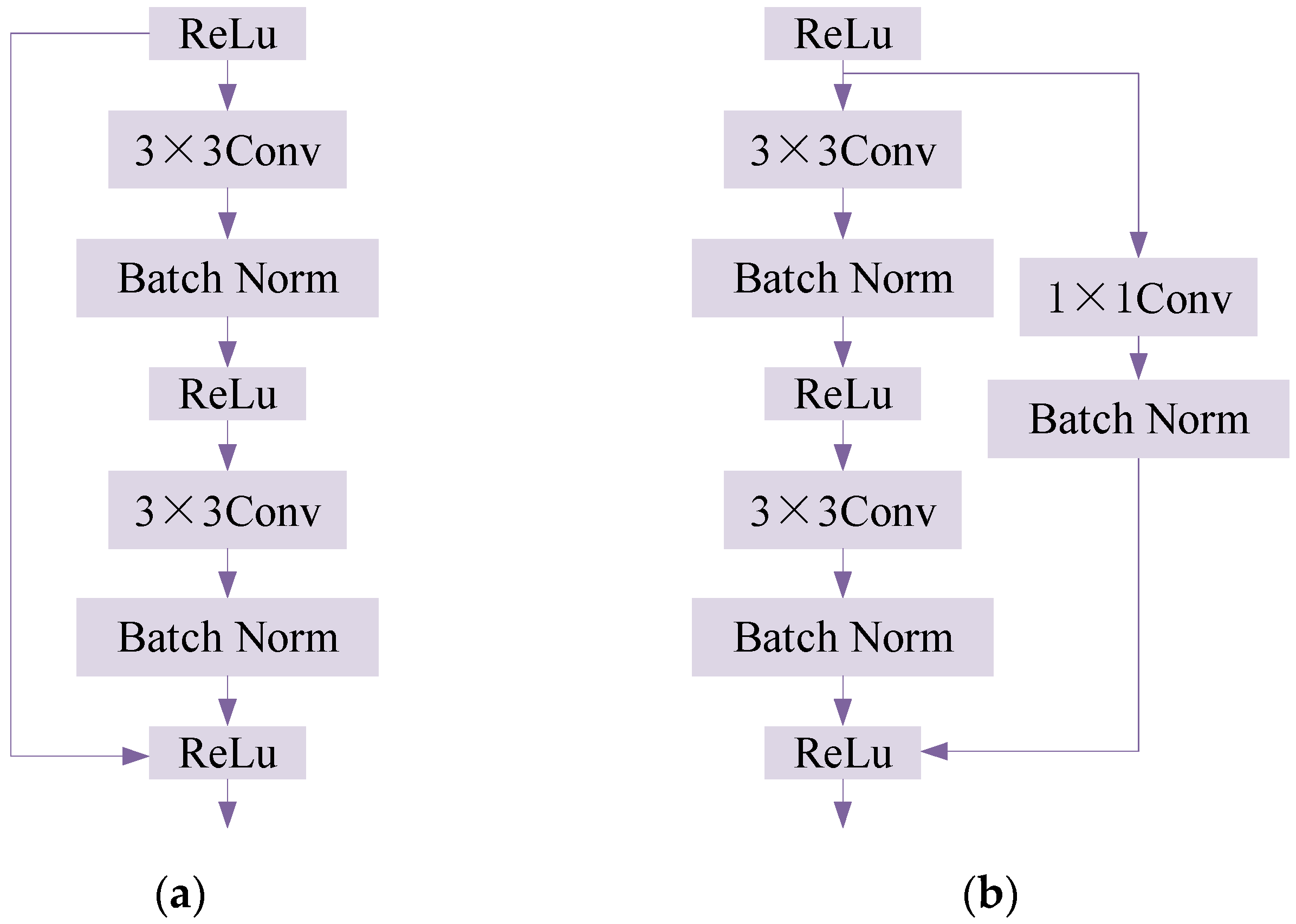
2.3. Health Condition Assessment Model Based on Residual Neural Network
2.4. Model Evaluation Metrics
3. Example Analysis and Experiment
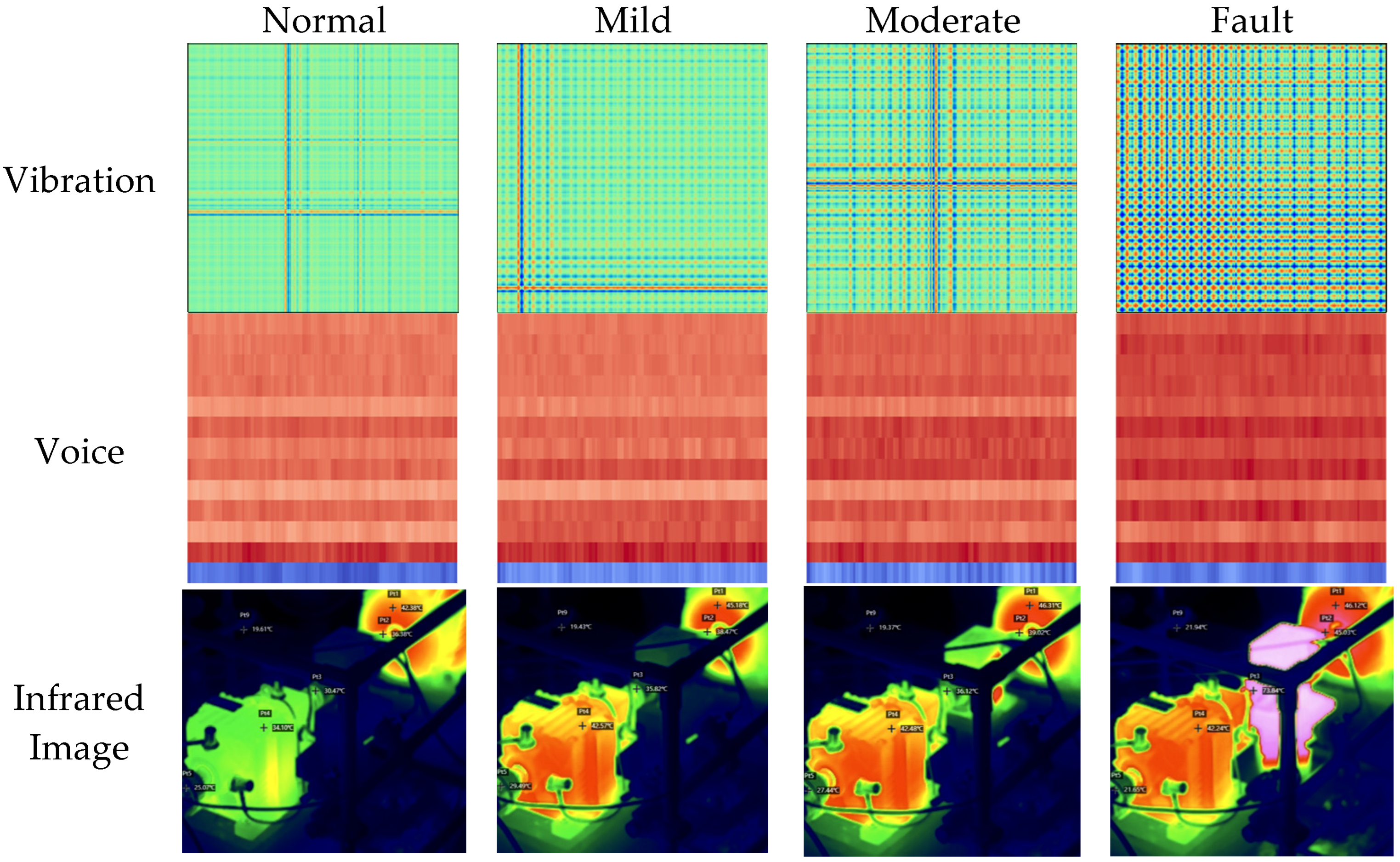
3.1. Platform Introduction
3.2. Feature Set Construction
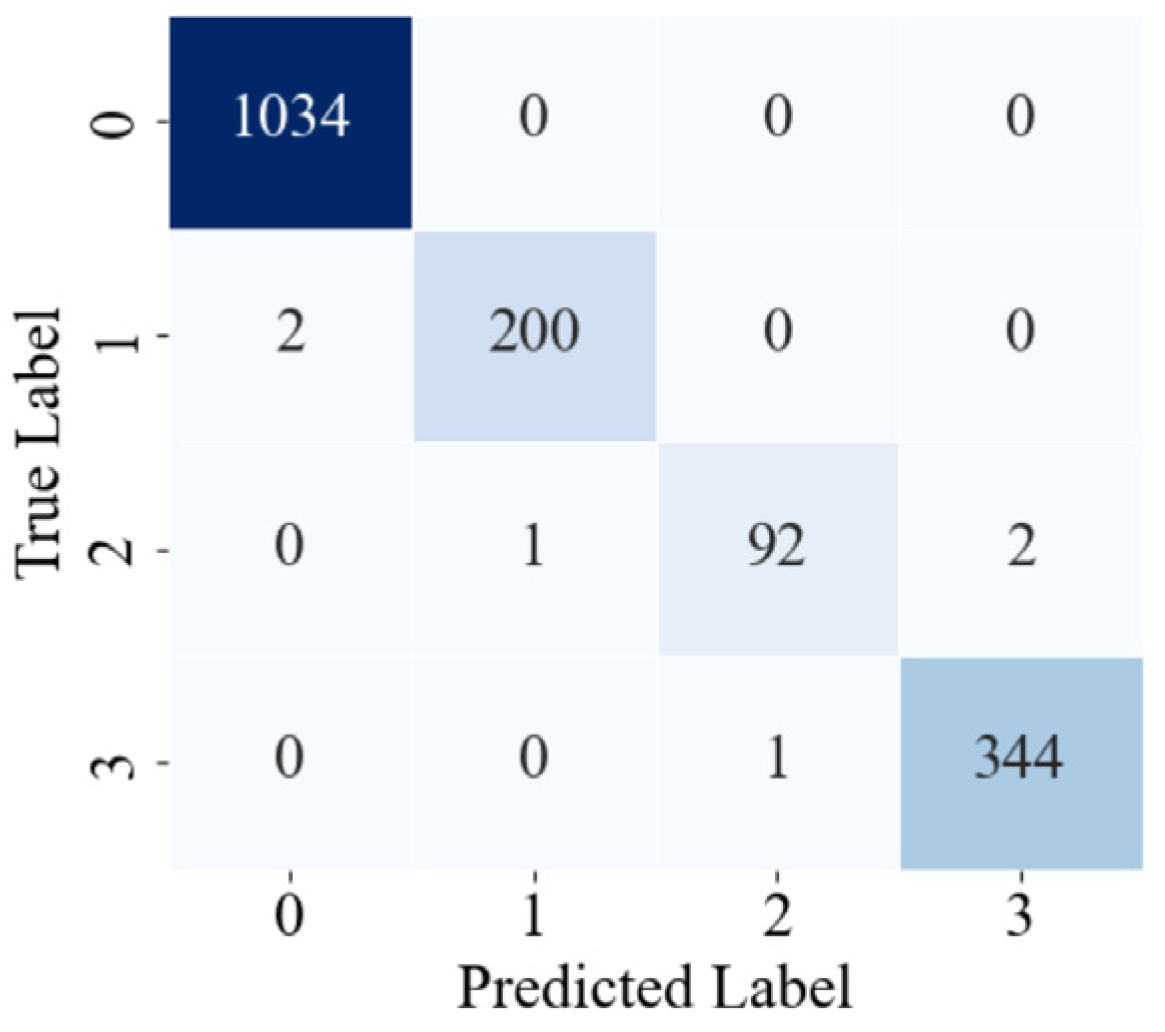
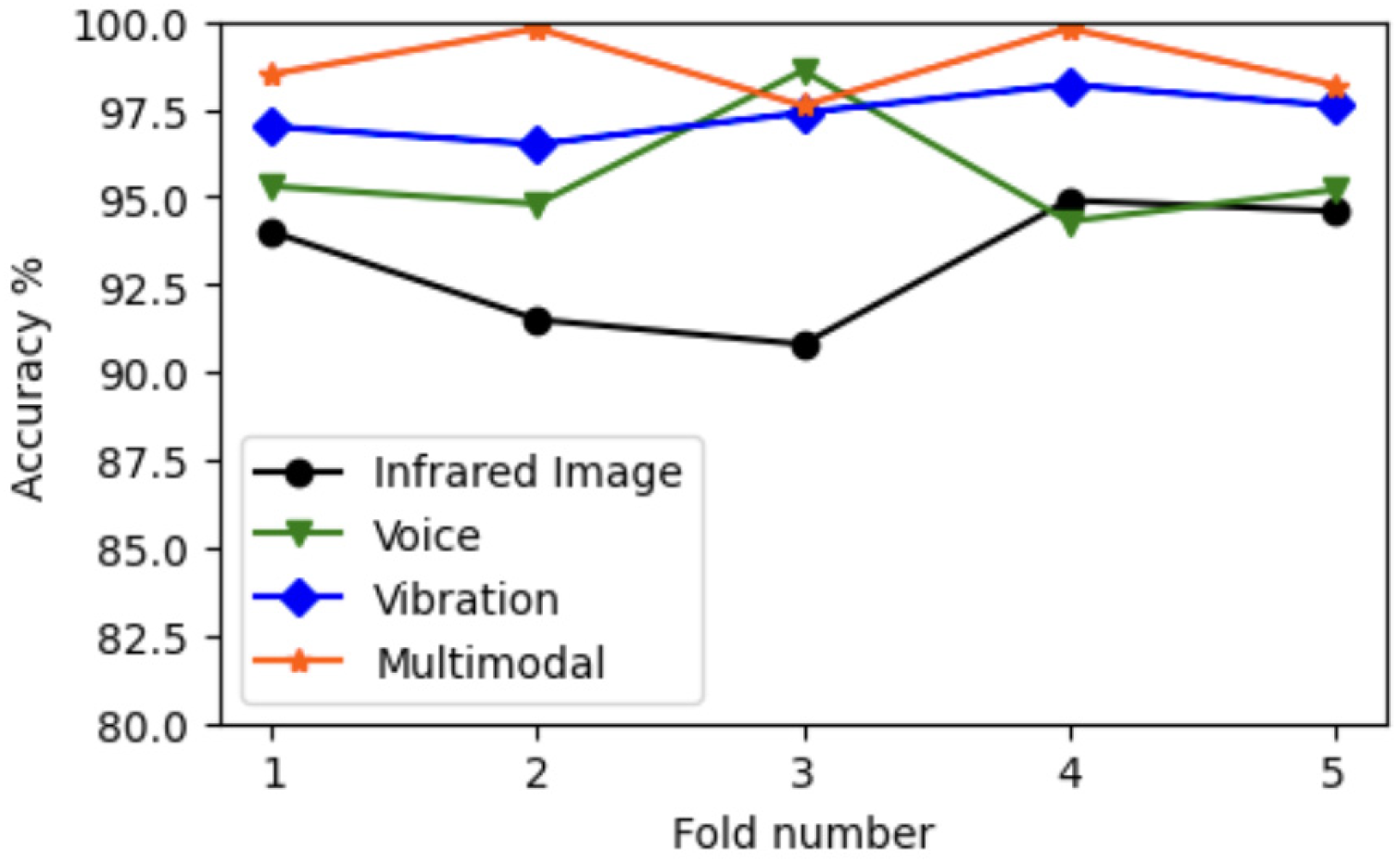
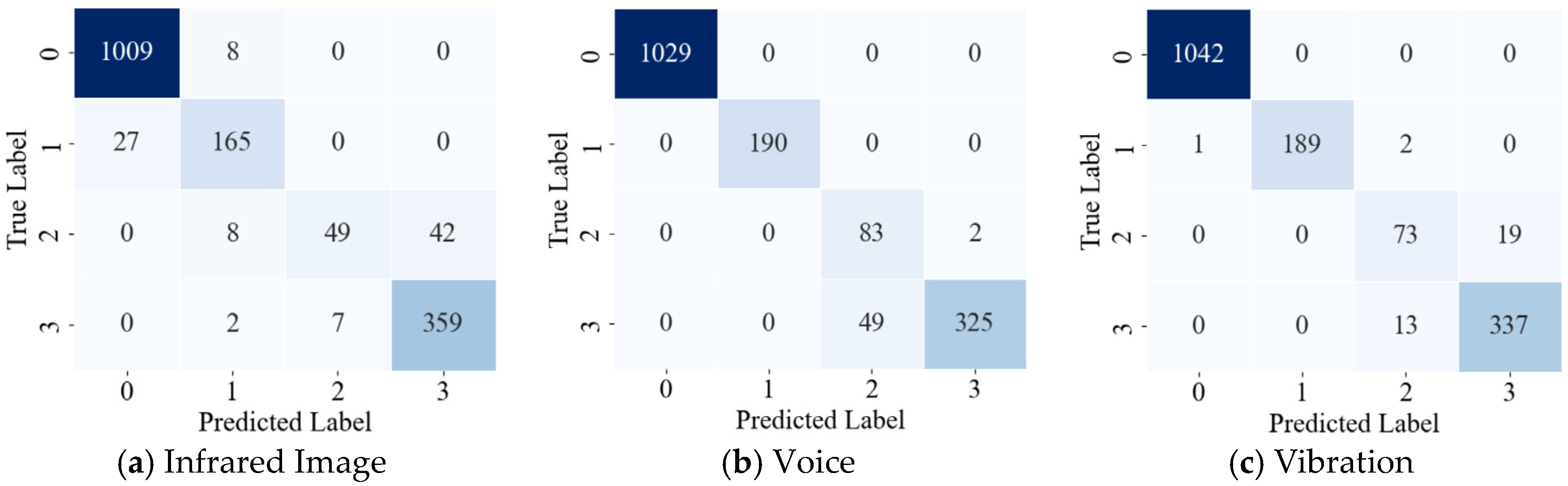
3.3. Experimental Validation
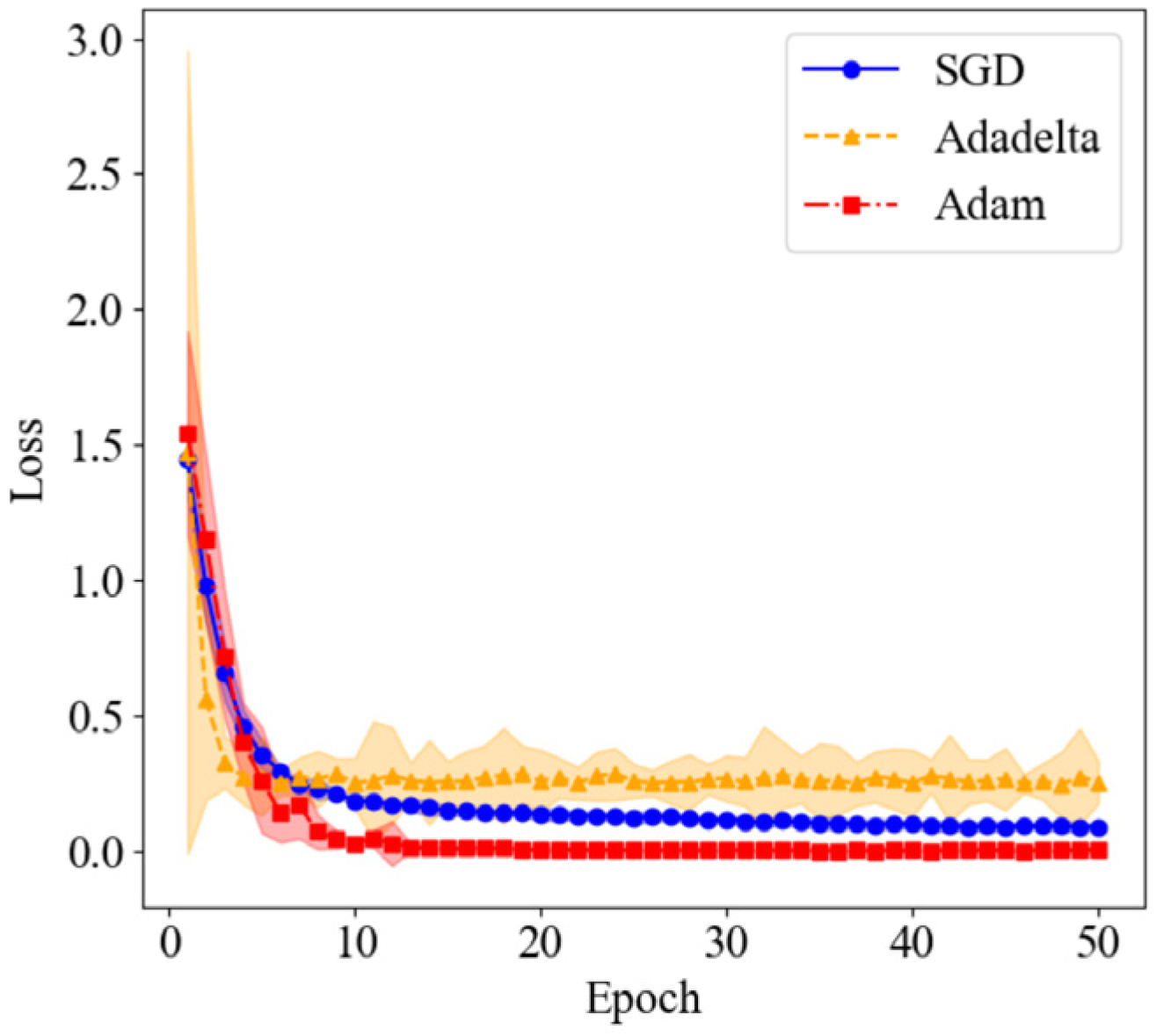
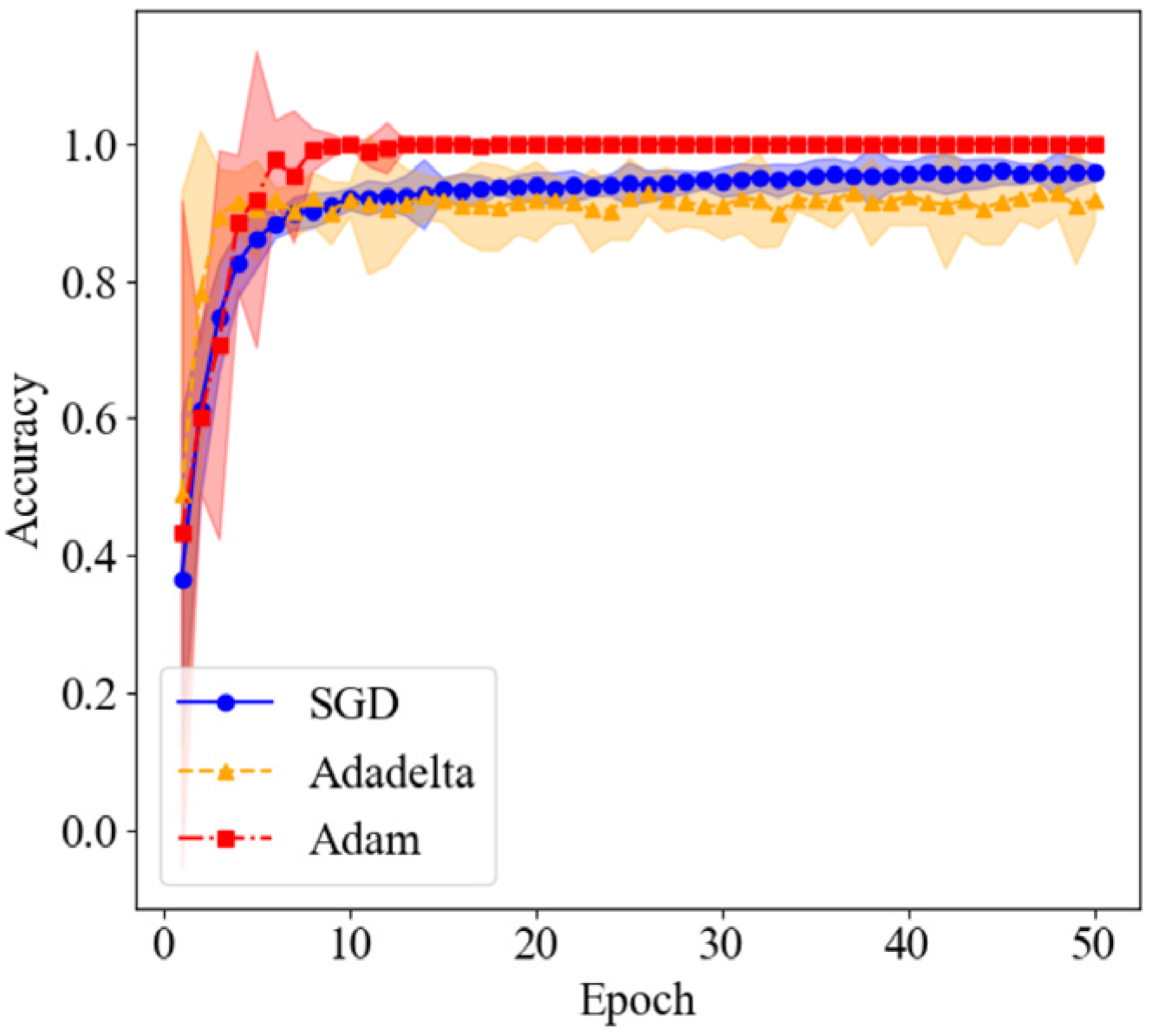
3.4. Method Comparison
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GAF | Gramian Angular Field |
| MFCCs | Mel-Frequency Cepstral Coefficients |
| RCNN | Region-based Convolutional Neural Network |
| ES | Expert System |
| AHP | Analytic Hierarchy Process |
| AdaBN | Adaptive Batch Normalization |
| M2FN | Multimodal to Fusion Network |
| GASF | Gramian Angular Summation Field |
| GADF | Gramian Angular Difference Field |
| ResNet | Residual Neural Network |
| TP | True Positive |
| FP | False Positive |
| FN | False Negative |
| TN | True Negative |
| DCT | Discrete Cosine Transform |
| RPN | Region Proposal Network |
| RoI | Region of Interest |
| MSE | Mean Squared Error |
| FCM | Fuzzy C-Means |
| SD | Standard Deviation |
References
- Zhou, F.; Shen, J.; Yang, X.; Liu, X.; Liu, W. Modified hierarchical multiscale dispersion entropy and its application to fault identification of rotating machinery. IEEE Access 2020, 8, 161361–161376. [Google Scholar] [CrossRef]
- Luo, P.; Hu, N.; Zhang, L.; Shen, J.; Cheng, Z. Improved phase space warping method for degradation tracking of rotating machinery under variable working conditions. Mech. Syst. Signal Process. 2021, 157, 107696. [Google Scholar] [CrossRef]
- Sotnik, S.; Deineko, Z.; Lyashenko, V. Key Directions for Development of Modern Expert Systems. Int. J. Eng. Inf. Syst. 2022, 6, 4–10. [Google Scholar]
- Kafeel, A.; Aziz, S.; Awais, M.; Khan, M.A.; Afaq, K.; Idris, S.A. An expert system for rotating machine fault detection using vibration signal analysis. Sensors 2021, 21, 7587. [Google Scholar] [CrossRef]
- Degroff, J.; Hou, G.J.W. Fault Tree Analysis for Robust Design. Designs 2025, 9, 19. [Google Scholar] [CrossRef]
- Chen, K.; Chen, H.; Bisantz, A.; Shen, S.; Sahin, E. Where failures may occur in automated driving: A fault tree analysis approach. J. Cogn. Eng. Decis. Mak. 2023, 17, 147–165. [Google Scholar] [CrossRef]
- Abdulhamid, A.; Rahman, M.M.; Kabir, S.; Ghafir, I. Enhancing safety in iot systems: A model-based assessment of a smart irrigation system using fault tree analysis. Electronics 2024, 13, 1156. [Google Scholar] [CrossRef]
- Chorol, L.; Gupta, S.K. Evaluation of groundwater heavy metal pollution index through analytical hierarchy process and its health risk assessment via Monte Carlo simulation. Process Saf. Environ. Prot. 2023, 170, 855–864. [Google Scholar] [CrossRef]
- Ma, L.; Li, N.; Zhu, P.; Tang, K.; Khan, A.; Wang, F.; Yu, G. A novel fuzzy neural network architecture search framework for defect recognition with uncertainties. IEEE Trans. Fuzzy Syst. 2024, 32, 3274–3285. [Google Scholar] [CrossRef]
- Wei, F.F.; Chi, T.; Chen, X. A multi-feature fusion and situation awareness-based method for fatigue driving level determination. Electronics 2023, 12, 2884. [Google Scholar] [CrossRef]
- Guo, L.; Wang, T.; Dong, X.; Zhang, P.; Zeng, H.; Zhang, J. A Dynamic Cloud Center of Gravity Model for Real-Time System-Level Health Status Assessment of Intelligent Ship. J. Mar. Sci. Eng. 2025, 13, 384. [Google Scholar] [CrossRef]
- Ren, L.; Ma, H.; Zhou, W.; Huang, S.; Wu, X. A Condition Monitoring Method of Hydraulic Gear Pumps Based on Multilevel Mechanism-Data Fusion. Int. J. Aerosp. Eng. 2024, 2024, 5587168. [Google Scholar]
- Yang, L.; He, X.; Zhang, C.; Lai, X.; Li, J.; Song, X. Crack identification driven by the fusion of mechanism and data for the variable-cross-section cantilever beam. Mech. Syst. Signal Process. 2023, 196, 110320. [Google Scholar]
- Liu, W.; Xu, J.; Dong, J. A state estimation method for multisensor uncertain systems based on sequential fusion and zonotope. IEEE Sens. J. 2023, 23, 13301–13310. [Google Scholar]
- Wu, D.; Zhong, X.; Peng, X.; Hu, H.; Liu, Q. Multimodal information fusion for high-robustness and low-drift state estimation of UGVs in diverse scenes. IEEE Trans. Instrum. Meas. 2022, 71, 8505115. [Google Scholar]
- Nisha, A.S.; Manohar, C.S. Dynamic state estimation in nonlinear stiff systems using implicit state space models. Struct. Control. Health Monit. 2022, 29, e2959. [Google Scholar]
- Duan, Y.; Cao, X.; Zhao, J.; Li, M.; Yang, X. A Spatiotemporal Fusion Autoencoder-Based Health Indicator Automatic Construction Method for Rotating Machinery Considering Vibration Signal Expression. IEEE Sens. J. 2023, 23, 24822–24838. [Google Scholar]
- Ong, P.; Tan, Y.K.; Lai, K.H.; Sia, C.K. A deep convolutional neural network for vibration-based health-monitoring of rotating machinery. Decis. Anal. J. 2023, 7, 100219. [Google Scholar] [CrossRef]
- Singh, M.; Kumar, S.; Nandan, D. Faulty voice diagnosis of automotive gearbox based on acoustic feature extraction and classification technique. J. Eng. Res. 2023, 11, 100051. [Google Scholar]
- Park, J.; Kim, Y.; Na, K.; Youn, B.D.; Chen, Y.; Zuo, M.J.; Bae, Y.C. An image-based feature extraction method for fault diagnosis of variable-speed rotating machinery. Mech. Syst. Signal Process. 2022, 167, 108524. [Google Scholar]
- Kong, Y.; Han, Q.; Chu, F. Sparsity assisted intelligent recognition method for vibration-based machinery health diagnostics. J. Vib. Control 2022, 29, 4230–4241. [Google Scholar]
- Storti, G.; Martini, V.; Okabe, E.P.; Machado, T.H.; Cavalca, K.L. Enhancing Structural Health Monitoring Through Automatic Modal Parameter Identification for Rotating Machinery on Flexible Foundation Structures. Lect. Notes Civ. Eng. 2024, 514, 196–208. [Google Scholar]
- Fan, H.; Ren, Z.; Zhang, X.; Cao, X.; Ma, H.; Huang, J. A gray texture image data-driven intelligent fault diagnosis method of induction motor rotor-bearing system under variable load conditions. Measurement 2024, 233, 114742. [Google Scholar]
- Fan, H.; Ren, Z.; Cao, X.; Zhang, X.; Huang, J. A GTI&Ada-act LMCNN method for intelligent fault diagnosis of motor rotor-bearing unit under variable conditions. IEEE Trans. Instrum. Meas. 2024, 73, 3508314. [Google Scholar]
- Babak, V.; Babak, S.; Zaporozhets, A. Stochastic Models of Diagnostic Signals Arising During the Operation of Electrical Equipment. In Statistical Diagnostics of Electric Power Equipment; Springer Nature: Cham, Switzerland, 2024; Volume 571, pp. 75–122. [Google Scholar]
- Ma, Y.; Wen, G.; Cheng, S.; He, X.; Mei, S. Multimodal convolutional neural network model with information fusion for intelligent fault diagnosis in rotating machinery. Meas. Sci. Technol. 2022, 33, 125109. [Google Scholar]
- Babak, V.; Zaporozhets, A.; Kuts, Y.; Fryz, M.; Scherbak, L. Identification of Vibration Noise Signals of Electric Power Facilities. In Noise signals: Modelling and Analyses; Springer Nature: Cham, Switzerland, 2024; Volume 567, pp. 143–170. [Google Scholar]
- Wu, Z.; Xu, R. A Modal Fusion Deep Clustering Method for Multi-sensor Fault Diagnosis of Rotating Machinery. J. Electron. Inf. Technol. 2025, 47, 244–259. [Google Scholar]
- Cao, X.; Li, Y.; Yu, K.; Zhang, Y. Integrated Multimodal Fault Diagnosis of Industrial Gearboxes Using Vibration Signals and Infrared Thermal Imaging. In Proceedings of the 2024 Global Reliability and Prognostics and Health Management Conference, Beijing, China, 11–13 October 2024; pp. 1–5. [Google Scholar]
- Tong, J.; Liu, C.; Zheng, J.; Pan, H. Multi-sensor information fusion and coordinate attention-based fault diagnosis method and its interpretability research. Eng. Appl. Artif. Intell. 2023, 124, 106614. [Google Scholar]
- Cui, J.; Xie, P.; Wang, X.; Wang, J.; He, Q.; Jiang, G. M2FN: An end-to-end multi-task and multi-sensor fusion network for intelligent fault diagnosis. Measurement 2022, 204, 112085. [Google Scholar]
- Xu, Y.; Feng, K.; Yan, X.; Yan, R.; Ni, Q.; Sun, B.; Lei, Z.; Zhang, Y.; Liu, Z. CFCNN: A novel convolutional fusion framework for collaborative fault identification of rotating machinery. Inf. Fusion 2023, 95, 1–16. [Google Scholar]
- Chen, J.; Duan, N.; Zhou, X.; Wang, Z. Diagnostic Model for Transformer Core Loosening Faults Based on the Gram Angle Field and Multi-Head Attention Mechanism. Appl. Sci. 2024, 14, 10906. [Google Scholar] [CrossRef]
- Song, N.; Du, S.; Wu, Z.; Zhong, L.; Yang, L.T.; Yang, J.; Wang, S. GAF-Net: Graph attention fusion network for multi-view semi-supervised classification. Expert Syst. Appl. 2024, 238, 122151. [Google Scholar]
- Cabrera, D.; Medina, R.; Cerrada, M.; Sánchez, R.V.; Estupiñan, E.; Li, C. Improved Mel Frequency Cepstral Coefficients for Compressors and Pumps Fault Diagnosis with Deep Learning Models. Appl. Sci. 2024, 14, 1710. [Google Scholar] [CrossRef]
- Yan, S.; Chen, P.; Liang, S.; Zhang, L.; Li, X. Target Detection in Infrared Image of Transmission Line Based on Faster-RCNN. In International Conference on Advanced Data Mining and Applications; Springer International Publishing: Cham, Switzerland, 2022; pp. 276–287. [Google Scholar]
- Jia, Y.; Dong, L.; Qi, J.; Li, Q. Research on Improving ResNet18 for Classifying Complex Images Based on Attention Mechanism. In China Intelligent Networked Things Conference; Springer Nature: Singapore, 2024; pp. 123–139. [Google Scholar]
- Cao, X.; Xu, X.; Duan, Y.; Yang, X. Health Status Recognition of Rotating Machinery Based on Deep Residual Shrinkage Network under Time-varying Conditions. IEEE Sens. J. 2022, 22, 18332–18348. [Google Scholar]
- Blake, M.P.; Mitchel, W.S. Vibration and Acoustic Measurement; Spartan Books: New York, NY, USA, 1972. [Google Scholar]
- Rai, A.; Upadhyay, S.H. An integrated approach to bearing prognostics based on EEMD-multi feature extraction, Gaussian mixture models and Jensen-Rényi divergence. Appl. Soft Comput. 2018, 71, 36–50. [Google Scholar]






| Actual Positive | Actual Negative | |
|---|---|---|
| Predict positive | True Positive (TP) | False Positive (FP) |
| Predict negative | False Negative (FN) | True Negative (TN) |
| Number | Parameter Name | Unit |
|---|---|---|
| 1 | Vertical Output Vibration | |
| 2 | Vertical Input Vibration | |
| 3 | Horizontal Output Vibration | |
| 4 | Horizontal Input Vibration | |
| 5 | Voice Output | |
| 6 | Voice Input | |
| 7 | Infrared Image |
| Sensor Type | Model | Sensitivity | Measurement Range |
|---|---|---|---|
| Vibration Sensor | CT1020LC | 200 mV/g | |
| Voice Sensor | AWA14423 | 50 mV/Pa | 3.15–20 k/Hz |
| Infrared Image Sensor | K16E19 | 6500 V/W | −50~+125 °C |
| Health Level | Operating Condition | Level Label |
|---|---|---|
| Normal | Operating normally, no maintenance needed | 0 |
| Mild | Stable operating condition, scheduled maintenance | 1 |
| Moderate | Signs of deterioration in operating condition, timely maintenance required | 2 |
| Fault | Cannot operate normally, requires shutdown for repair | 3 |
| Modality | Average Recognition Accuracy | Average Precision | Average Recall | Average F1-Score |
|---|---|---|---|---|
| Infrared Image | 93.27 | 91.61 | 93.18 | 91.71 |
| Voice | 96.32 | 97.75 | 96.33 | 93.48 |
| Vibration | 98.02 | 98.17 | 98.02 | 98.05 |
| Multimodal | 99.18 | 99.25 | 99.18 | 99.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, X.; Shi, K. A Health Status Identification Method for Rotating Machinery Based on Multimodal Joint Representation Learning and a Residual Neural Network. Appl. Sci. 2025, 15, 4049. https://doi.org/10.3390/app15074049
Cao X, Shi K. A Health Status Identification Method for Rotating Machinery Based on Multimodal Joint Representation Learning and a Residual Neural Network. Applied Sciences. 2025; 15(7):4049. https://doi.org/10.3390/app15074049
Chicago/Turabian StyleCao, Xiangang, and Kexin Shi. 2025. "A Health Status Identification Method for Rotating Machinery Based on Multimodal Joint Representation Learning and a Residual Neural Network" Applied Sciences 15, no. 7: 4049. https://doi.org/10.3390/app15074049
APA StyleCao, X., & Shi, K. (2025). A Health Status Identification Method for Rotating Machinery Based on Multimodal Joint Representation Learning and a Residual Neural Network. Applied Sciences, 15(7), 4049. https://doi.org/10.3390/app15074049




