Federated Learning-Based Framework to Improve the Operational Efficiency of an Articulated Robot Manufacturing Environment
Abstract
:1. Introduction
2. Materials and Methods
2.1. Federated Learning
2.2. Industrial Articulated Robot Control in Smart Factories
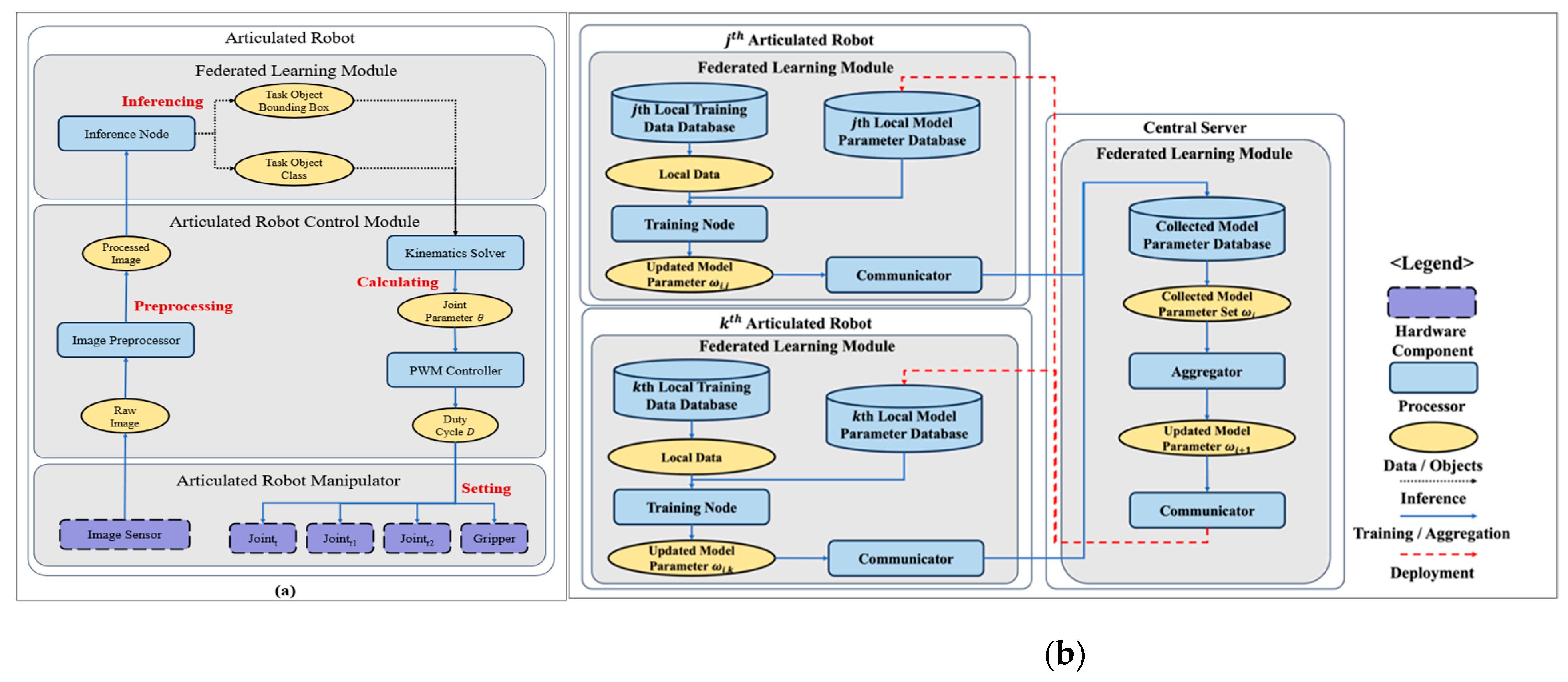
2.3. Federated Learning for Articulated Robot Control
2.3.1. FL Module
| Algorithm 1 Pseudo Code of Train/Aggregate and Deploy modes that occur in the FL Module of the Articulated Robot and Central Server |
| 1 Initialize initial global model parameter 2 Deploy model parameter across overall clients 3 while global model performance does not achieve the set performance 4 for round 5 Sample clients set 6 for client in set 7 Train local model of client 8 Send updated model parameter to server 9 Aggregate process with received model parameter set 10 Deploy global model parameter 11 end for 12 end for |
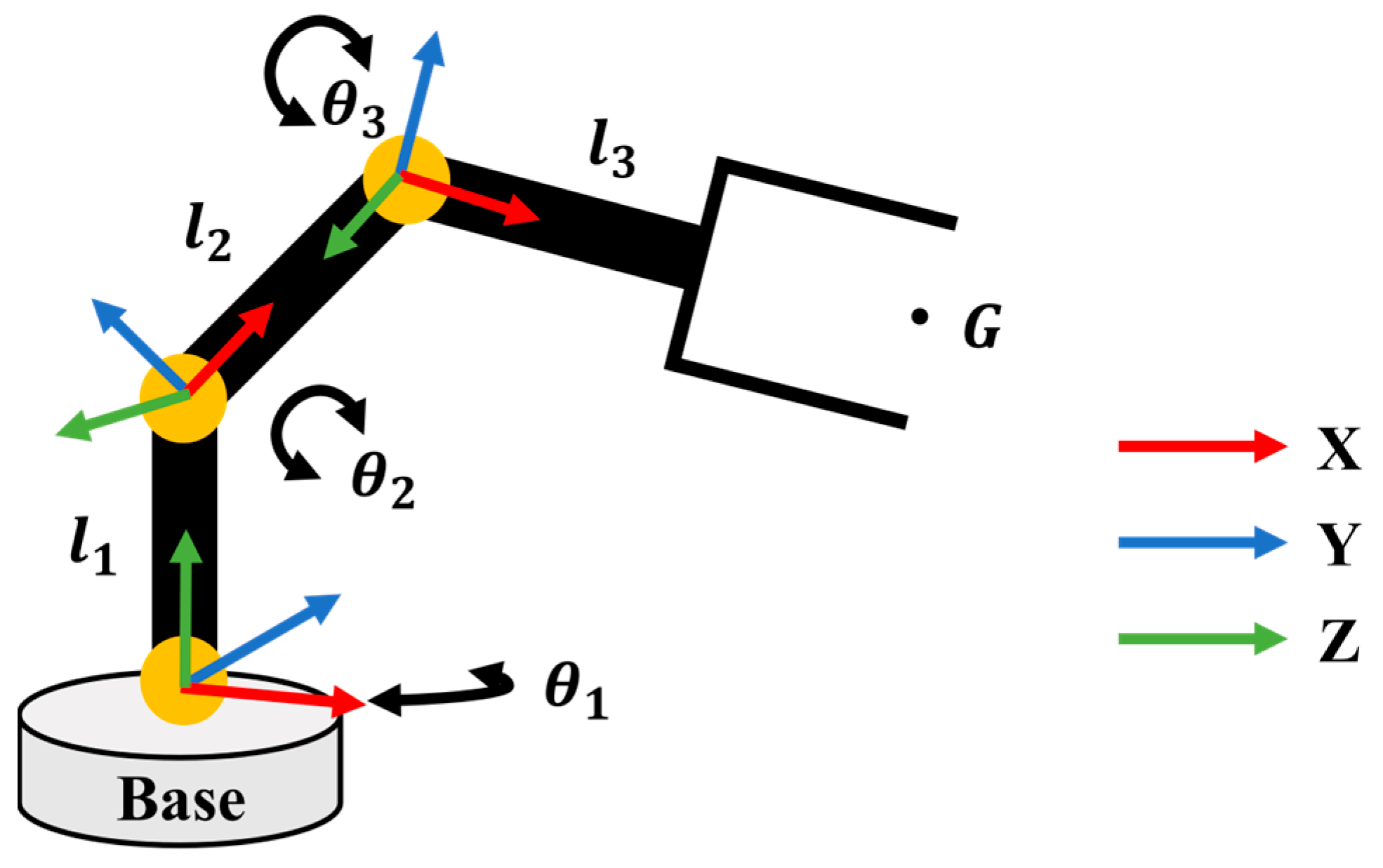
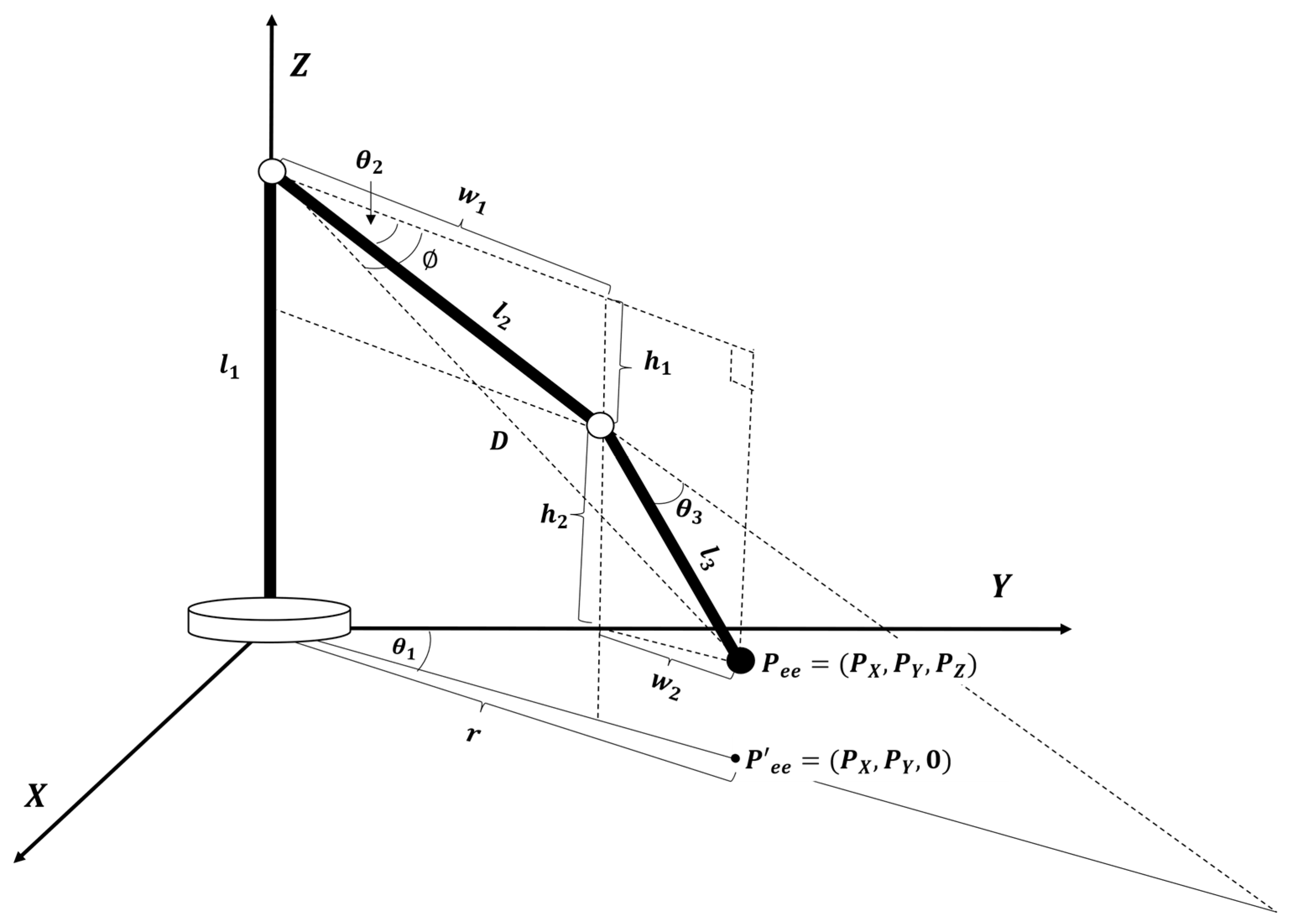
2.3.2. Articulated Robot Control Module
| Algorithm 2 Pseudo code of the articulated robot control module of a client |
| 1 Capture of a picking object using a camera sensor 2 Initialize coordinates of task plan and 3 Initialize actuator angles , , and 4 Perform image preprocessing process 5 Return the preprocessed image 6 Update and from inference node 7 Update , , and from the kinematics solver 8 Set duty cycle to each actuator with the derived , , and |
| Algorithm 3 Pseudo code of the adaptive threshold method with Gaussian filter |
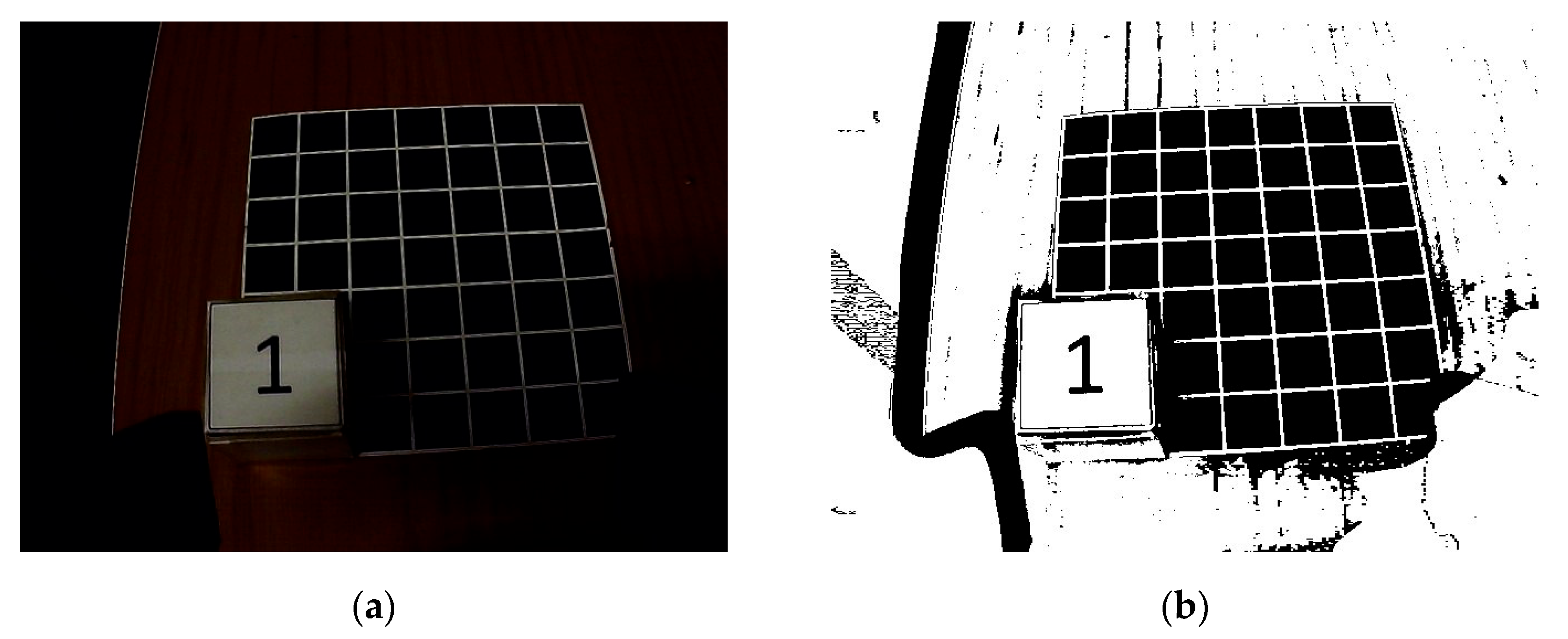
| 1 Set which is constant for adjusting threshold 2 Set which is resolution (number of pixels) of sub-area 3 Initialize and which are central coordinates of sub-area 4 For in 5 Compute which is gaussian weighted average of pixels 6 Compute threshold with and of 7 Binarize pixels 8 End for 9 Return processed image |
3. Results
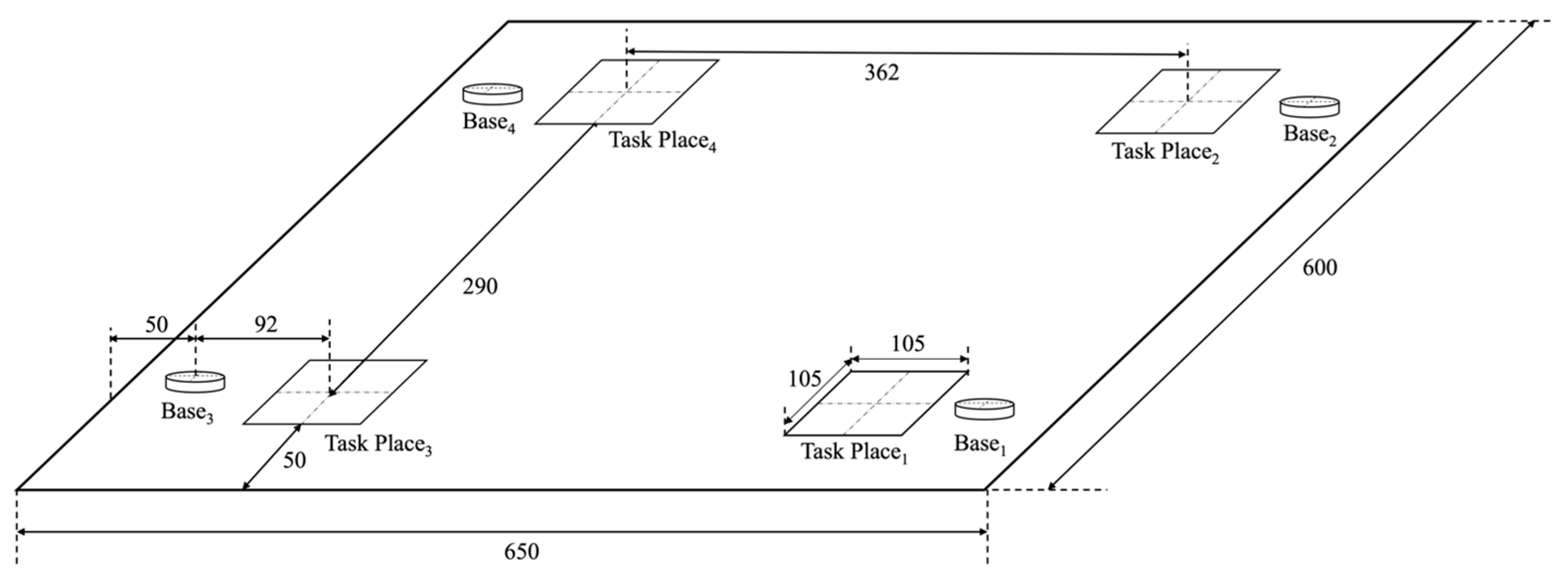
3.1. Scenario
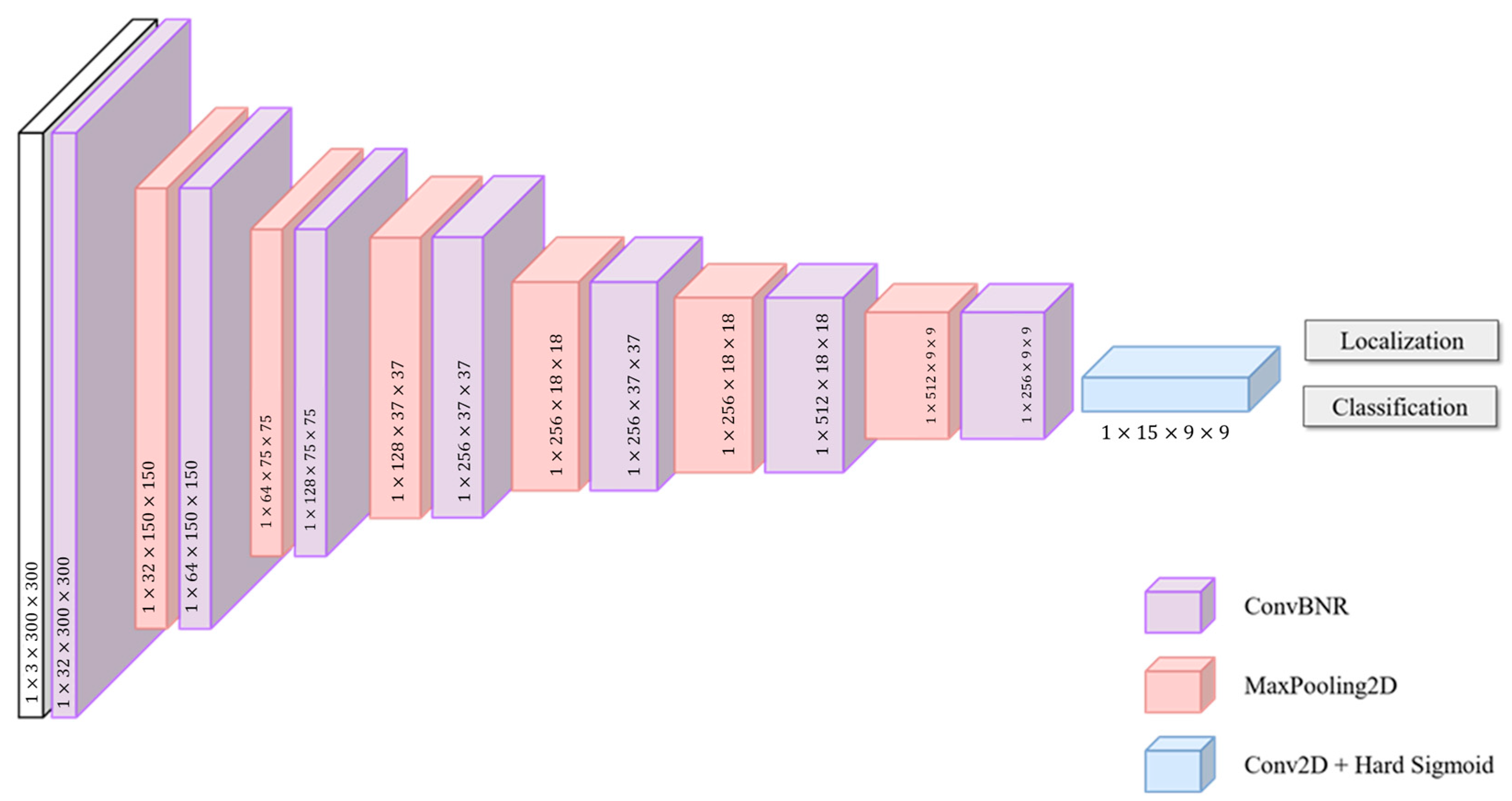
3.2. Object Detection Model Performance
3.3. Robot Control Performance
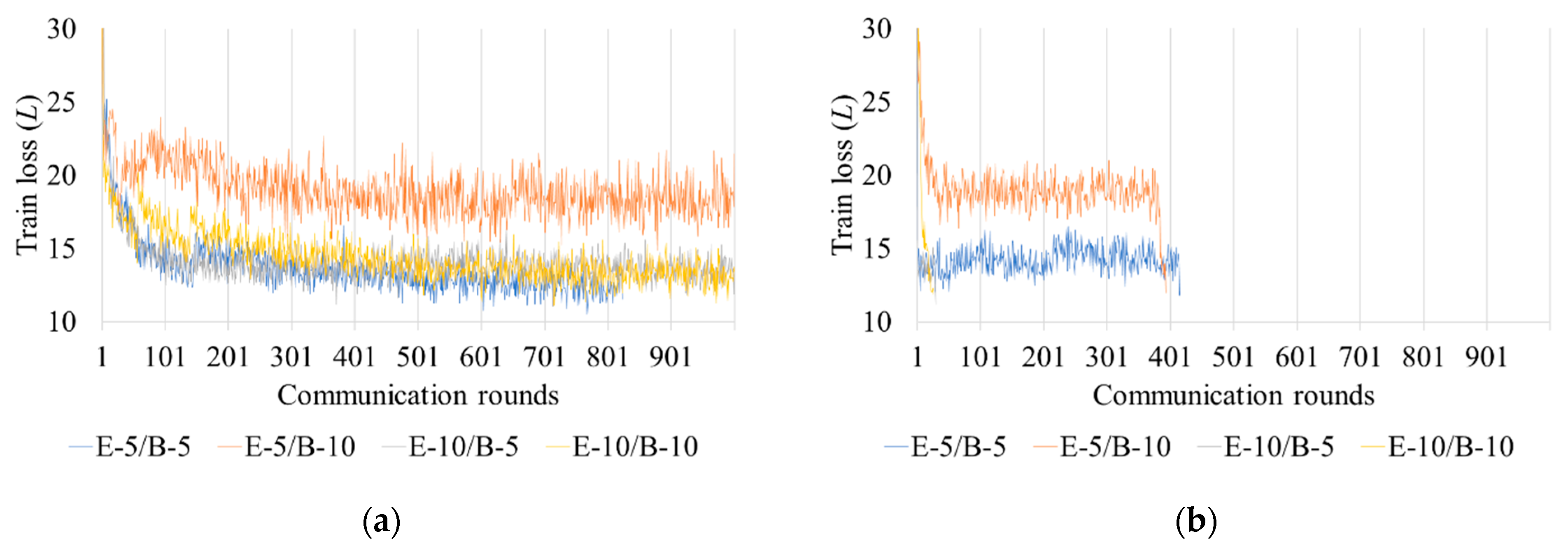
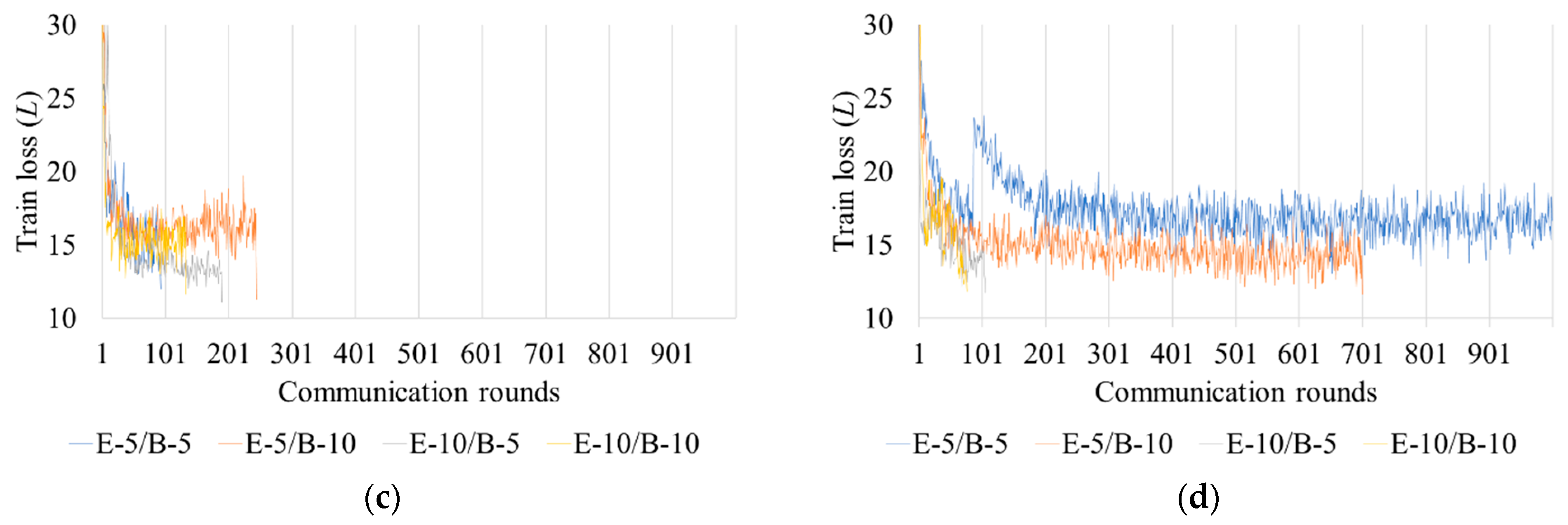
3.4. Federated Learning Performance
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lasi, H.; Fettke, P.; Kemper, H.G.; Feld, T.; Hoffmann, M. Industry 4.0. Bus. Inf. Syst. Eng. 2014, 6, 239–242. [Google Scholar]
- Prashar, G.; Vasudev, H.; Bhuddhi, D. Additive manufacturing: Expanding 3D printing horizon in industry 4.0. Int. J. Interact. Des. Manuf. 2023, 17, 2221–2235. [Google Scholar]
- Al-Alimi, S.; Yusuf, N.K.; Ghaleb, A.M.; Lajis, M.A.; Shamsudin, S.; Zhou, W.; Altharan, Y.M.; Abdulwahab, H.S.; Saif, Y.; Didane, D.H.; et al. Recycling aluminium for sustainable development: A review of different processing technologies in green manufacturing. Results Eng. 2024, 23, 102566. [Google Scholar]
- Krishnan, R. Challenges and benefits for small and medium enterprises in the transformation to smart manufacturing: A systematic literature review and framework. J. Manuf. Technol. Manag. 2024, 35, 918–938. [Google Scholar]
- Mattila, J.; Ala-Laurinaho, R.; Autiosalo, J.; Salminen, P.; Tammi, K. Using digital twin documents to control a smart factory: Simulation approach with ROS, gazebo, and Twinbase. Machines 2022, 10, 225. [Google Scholar] [CrossRef]
- Groover, M.P. Automation, Production Systems, and Computer-Integrated Manufacturing, 5th ed.; Pearson Education: London, UK, 2019. [Google Scholar]
- Bahrin, M.A.K.; Othman, M.F.; Azli, N.H.N.; Talib, M.F. Industry 4.0: A review on industrial automation and robotic. J. Teknol. 2016, 78, 137–143. [Google Scholar]
- ISO 8373:2021; Robotics-Vocabulary. International Organization for Standardization: Geneva, Switzerland, 2021. Available online: https://www.iso.org/standard/75539.html (accessed on 11 March 2025).
- Sun, Y.; Bai, L.; Dong, D. Lighter and more efficient robotic joints in prostheses and exoskeletons: Design, actuation and control. Front. Robot. AI 2023, 10, 1063712. [Google Scholar]
- Wada, K.; Okada, K.; Inaba, M. Joint learning of instance and semantic segmentation for robotic pick-and-place with heavy occlusions in clutter. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019. [Google Scholar]
- Mohammed, M.Q.; Chung, K.L.; Chyi, C.S. Pick and place objects in a cluttered scene using deep reinforcement learning. Int. J. Mech. Eng. Mechatron. 2020, 20, 50–57. [Google Scholar]
- Zeng, A.; Song, S.; Yu, K.T.; Donlon, E.; Hogan, F.R.; Bauza, M.; Ma, D.; Taylor, O.; Liu, M.; Romo, E.; et al. Robotic pick-and-place of novel objects in clutter with multi-affordance grasping and cross-domain image matching. Int. J. Robot. Res. 2022, 41, 690–705. [Google Scholar]
- Matenga, A.; Murena, E.; Kanyemba, G.; Mhlanga, S. A novel approach for developing a flexible automation system for rewinding an induction motor stator using robotic arm. Procedia Manuf. 2019, 33, 296–303. [Google Scholar]
- Rauch, E.; Dallasega, P.; Unterhofer, M. Requirements and barriers for introducing smart manufacturing in small and medium-sized enterprises. IEEE Eng. Manag. Rev. 2019, 47, 87–94. [Google Scholar]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated optimization in heterogeneous networks. Proc. Mach. Learn. Syst. 2020, 2, 429–450. [Google Scholar]
- Wen, J.; Zhang, Z.; Lan, Y.; Cui, Z.; Cai, J.; Zhang, W. A survey on federated learning: Challenges and applications. Int. J. Mach. Learn. Cybern. 2023, 14, 513–535. [Google Scholar]
- Qi, P.; Chiaro, D.; Guzzo, A.; Ianni, M.; Fortino, G.; Piccialli, F. Model aggregation techniques in federated learning: A comprehensive survey. Future Gener. Comput. Syst. 2024, 150, 272–293. [Google Scholar]
- Jiang, X.; Zhang, J.; Zhang, L. Fedradar: Federated multi-task transfer learning for radar-based internet of medical things. IEEE Trans. Netw. Serv. Manag. 2023, 20, 1459–1469. [Google Scholar]
- Zinkevich, M.; Weimer, M.; Li, L.; Smola, A. Parallelized stochastic gradient descent. Adv. Neural Inf. Process. Syst. 2010, 23, 1–9. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar]
- Dean, J.; Corrado, G.; Monga, R.; Chen, K.; Devin, M.; Mao, M.; Ranzato, M.; Senior, A.; Tucker, P.; Yang, K.; et al. Large scale distributed deep networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1–9. [Google Scholar]
- Kang, J.; Xiong, Z.; Niyato, D.; Zou, Y.; Zhang, Y.; Guizani, M. Reliable federated learning for mobile networks. IEEE Wirel. Commun. 2020, 27, 72–80. [Google Scholar]
- So, J.; Güler, B.; Avestimehr, A.S. CodedPrivateML: A fast and privacy-preserving framework for distributed machine learning. IEEE J. Sel. Areas Inf. Theory 2021, 2, 441–451. [Google Scholar]
- Van Steen, M.; Tanenbaum, A.S. A brief introduction to distributed systems. Computing 2016, 98, 967–1009. [Google Scholar]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; Agüera y Arcas, B. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, Ft. Lauderdale, FL, USA, 20–22 April 2017. [Google Scholar]
- Kundroo, M.; Kim, T. Demystifying impact of key hyper-parameters in federated learning: A case study on CIFAR-10 and Fashion MNIST. IEEE Access 2024, 12, 120570–120583. [Google Scholar]
- Zhao, Y.; Zhao, J.; Jiang, L.; Tan, R.; Niyato, D.; Li, Z.; Lyu, L.; Liu, Y. Privacy-preserving blockchain-based federated learning for IoT devices. IEEE Internet Things J. 2020, 8, 1817–1829. [Google Scholar]
- Feng, J.; Rong, C.; Sun, F.; Guo, D.; Li, Y. PMF: A privacy-preserving human mobility prediction framework via federated learning. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2020, 4, 1–21. [Google Scholar]
- Lee, J.; Sun, J.; Wang, F.; Wang, S.; Jun, C.H.; Jiang, X. Privacy-preserving patient similarity learning in a federated environment: Development and analysis. JMIR Med. Inform. 2018, 6, e7744. [Google Scholar]
- Szegedi, G.; Kiss, P.; Horváth, T. Evolutionary Federated Learning on EEG-data. In Proceedings of the Information Technologies—Applications and Theory (ITAT), Donovaly, Slovakia, 20–24 September 2019. [Google Scholar]
- Ryalat, M.; ElMoaqet, H.; AlFaouri, M. Design of a Smart Factory Based on Cyber-Physical Systems and Internet of Things towards Industry 4.0. Appl. Sci. 2023, 13, 2156. [Google Scholar] [CrossRef]
- Steiber, A.; Alänge, S.; Ghosh, S.; Goncalves, D. Digital transformation of industrial firms: An innovation diffusion perspective. Eur. J. Innov. Manag. 2021, 24, 799–819. [Google Scholar]
- Evjemo, L.D.; Gjerstad, T.; Grøtli, E.I.; Sziebig, G. Trends in smart manufacturing: Role of humans and industrial robots in smart factories. Curr. Robot. Rep. 2020, 1, 35–41. [Google Scholar]
- Ray, P.P. Internet of robotic things: Concept, technologies, and challenges. IEEE Access 2016, 4, 9489–9500. [Google Scholar]
- Mick, S.; Lapeyre, M.; Rouanet, P.; Halgand, C.; Benois-Pineau, J.; Paclet, F.; Cattaert, D.; Oudeyer, P.; de Rugy, A. Reachy, a 3D-printed human-like robotic arm as a testbed for human-robot control strategies. Front. Neurorobotics 2019, 13, 65. [Google Scholar]
- Xie, F.; Chen, L.; Li, Z.; Tang, K. Path smoothing and feed rate planning for robotic curved layer additive manufacturing. Robot. Comput. Integr. Manuf. 2020, 65, 101967. [Google Scholar] [CrossRef]
- Paul, R.P. Robot Manipulators: Mathematics, Programming, and Control: The Computer Control of Robot Manipulators; MIT Press: Cambridge, MA, USA, 1981. [Google Scholar]
- Luenberger, D.G. Linear and Nonlinear Programming; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Aristidou, A.; Lasenby, J. FABRIK: A fast, iterative solver for the Inverse Kinematics problem. Graph. Models 2011, 73, 243–260. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLO9000: Better, faster, stronger. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. Ssd: Single shot multibox detector. In Proceedings of the 14th European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Convolutional Deep Belief Networks on Cifar-10. 2010. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=bea5780d621e669e8069f05d0f2fc0db9df4b50f (accessed on 6 April 2025).
- Yu, Z.; Mohammed, A.; Panahi, I. A review of three PWM techniques. In Proceedings of the American Control Conference, Albuquerque, NM, USA, 4–6 June 1997. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. Adv. Neural Inf. Process. Syst. 2015, 28, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Huang, R.; Pedoeem, J.; Chen, C. YOLO-LITE: A real-time object detection algorithm optimized for non-GPU computers. In Proceedings of the 2018 IEEE International Conference on Big Data (big Data), Seattle, WA, USA, 10–13 December 2018. [Google Scholar]
- Kampa, T.; Müller, C.K.; Großmann, D. Interlocking IT/OT security for edge cloud-enabled manufacturing. Ad Hoc Netw. 2024, 154, 103384. [Google Scholar]
- Lin, C.C.; Tsai, C.T.; Liu, Y.L.; Chang, T.T.; Chang, Y.S. Security and privacy in 5g-iiot smart factories: Novel approaches, trends, and challenges. Mob. Netw. Appl. 2023, 28, 1043–1058. [Google Scholar] [CrossRef]
- Cubuk, E.D.; Zoph, B.; Mane, D.; Vasudevan, V.; Le, Q.V. Autoaugment: Learning augmentation strategies from data. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Snell, J.; Swersky, K.; Zemel, R. Prototypical networks for few-shot learning. Adv. Neural Inf. Process. Syst. 2017, 30, 1–11. [Google Scholar]
- Doshi, K.; Yilmaz, Y. Federated learning-based driver activity recognition for edge devices. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 3338–3346. [Google Scholar]



| Metric | Description |
|---|---|
| Training completion time (s) for participating clients in FL module at each round. | |
| Average hardware resource share percentage (%) of memory and CPU in FL module at each round. | |
| Total network traffic (download and upload; Mb) per client in FL module at each round. | |
| Average picking task completion time (s) for ith articulated robot over 30 iterations. | |
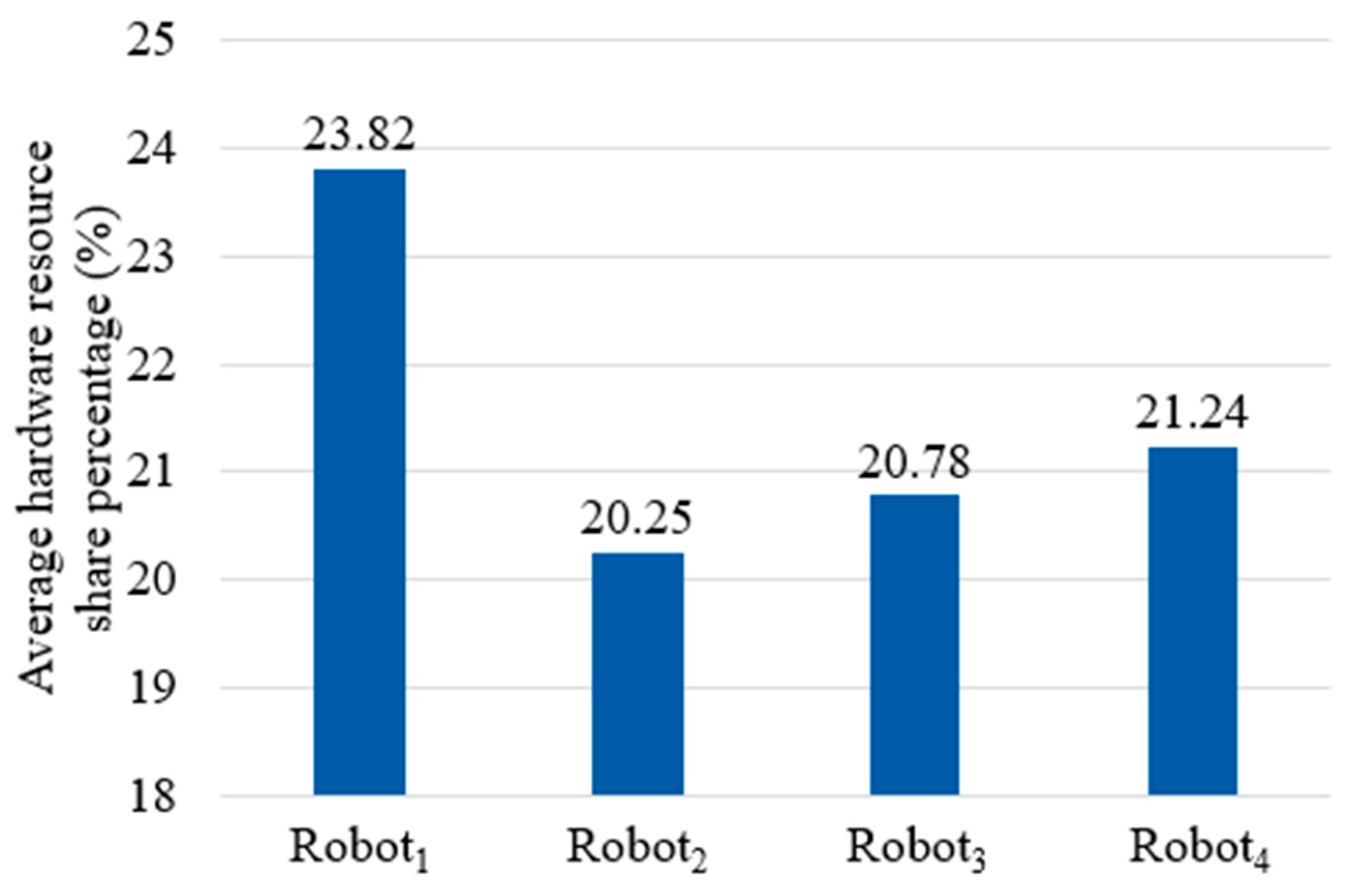
| Average hardware resource share percentage (%) of memory and CPU of ith articulated robot control module performing picking task over 30 iterations. |
| Category | Specification |
|---|---|
| SoC | Broadcom BCM2711 SoC |
| CPU | 1.5 GHz ARM Cortex-A72 MP4 |
| GPU | Broadcom VideoCore VI MP2 500 MHz |
| Memory | 8 GB LPDDR4 with 2 GB swap memory |
| Network | 802.11b/g/n/ac Dual-Band |
| Power | 5 V, 3 A |
| Category | Specification | |
|---|---|---|
| Actuator | Small torque | 9.4 kg/cm (4.8 V) |
| Operating speed | 0.17 s per 60° | |
| Dead bandwidth | ||
| Frequency | 50 Hz | |
| Power | 5 V, 3 A | |
| Model | Epochs | FLOPs | #Param | GPU Usage (%) |
|---|---|---|---|---|
| Proposed model | 36 | 1.8 B | 3.5 M | 18.2% |
| Faster R-CNN 1 | 15 | 33.2 B | 42.5 M | 87.5% |
| SSD 2 | 11 | 34.9 B | 35.6 M | 78.3% |
| YOLO-LITE | 47 | 1.6 B | 2.2 M | 14.7% |
| Type | C | B | E | Rounds 1 | (s) | (%) | (Mb) |
|---|---|---|---|---|---|---|---|
| FedSGD | 1.0 | ∞ | 1 | NA | 82,980 | 45.8 | 14,125.62 |
| FedAVG | 0.25 | 5 | 5 | 823 | 199,140 | 32.5 | 14,625.37 |
| 10 | NA | 493,140 | 33.7 | 14,255.37 | |||
| 10 | 5 | NA | 265,560 | 35.7 | 14,154.28 | ||
| 10 | NA | 503,940 | 38.6 | 15,053.75 | |||
| 0.5 | 5 | 5 | NA | 323,940 | 31.7 | 29,046.56 | |
| 10 | 106 | 581,220 | 33.1 | 3000.76 | |||
| 10 | 5 | 700 | 228,780 | 36.2 | 19,828.44 | ||
| 10 | 76 | 570,480 | 37.5 | 2303.5 | |||
| 0.75 | 5 | 5 | 415 | 368,452 | 32.6 | 17,622.48 | |
| 10 | 30 | 235,325 | 32.8 | 1363.89 | |||
| 10 | 5 | 393 | 364,380 | 38.3 | 17,864.67 | ||
| 10 | 26 | 423,423 | 38.2 | 1259.88 | |||
| 1.0 | 5 | 5 | 93 | 46,324 | 32.3 | 6008.68 | |
| 10 | 190 | 203,285 | 32.8 | 10,983.64 | |||
| 10 | 5 | 244 | 86,325 | 37.3 | 15,764.74 | ||
| 10 | 133 | 232,152 | 37.2 | 8593.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
So, J.; Lee, I.-B.; Kim, S. Federated Learning-Based Framework to Improve the Operational Efficiency of an Articulated Robot Manufacturing Environment. Appl. Sci. 2025, 15, 4108. https://doi.org/10.3390/app15084108
So J, Lee I-B, Kim S. Federated Learning-Based Framework to Improve the Operational Efficiency of an Articulated Robot Manufacturing Environment. Applied Sciences. 2025; 15(8):4108. https://doi.org/10.3390/app15084108
Chicago/Turabian StyleSo, Junyong, In-Bae Lee, and Sojung Kim. 2025. "Federated Learning-Based Framework to Improve the Operational Efficiency of an Articulated Robot Manufacturing Environment" Applied Sciences 15, no. 8: 4108. https://doi.org/10.3390/app15084108
APA StyleSo, J., Lee, I.-B., & Kim, S. (2025). Federated Learning-Based Framework to Improve the Operational Efficiency of an Articulated Robot Manufacturing Environment. Applied Sciences, 15(8), 4108. https://doi.org/10.3390/app15084108







