Coordinated Optimization of Feeder Flex-Route Transit Scheduling for Urban Rail Systems

Abstract

Given the distinct operational features of flex-route transit (FRT) compared to conventional fixed-route systems, this study integrates FRT with urban rail transit and proposes a collaborative optimization approach for feeder flex-route operations and scheduling. The model incorporates path planning, timetable design, and vehicle scheduling to minimize travel costs, enhance operational efficiency, and improve service quality. A mixed-integer nonlinear programming method is applied to optimize scheduling while aligning with rail timetables and passenger transfer behavior. Simulation experiments based on realistic urban transit scenarios are conducted to validate the model, optimizing key operational parameters such as departure intervals, vehicle deployment, and stop selection. The results demonstrate that the proposed approach effectively adjusts schedules and vehicle assignments to accommodate fluctuating passenger demand. This study offers both a theoretical foundation and a practical framework for integrated scheduling of feeder flex-route services, with potential applications for improving coordination and performance in multimodal public transit systems.

1. Introduction

With the continuous rise in travel demand and the increasing preference for speed and comfort, the proliferation of private cars and online ride-hailing services has led to severe traffic congestion and a steady decline in public transit usage, particularly buses. The reduction or suspension of bus services disproportionately affects low-income groups and the elderly. As frequent bus users, these populations are left with limited alternatives and must endure the inconvenience of disrupted transit services. Thus, optimizing bus services to enhance urban travel efficiency and accommodate diverse mobility needs remains an urgent research priority.

Public transit systems are essential for ensuring efficient urban mobility, yet conventional fixed-route transit services often fail to accommodate fluctuating passenger demand, leading to inefficiencies in scheduling, resource allocation, and service coverage. To address these limitations, flex-route transit has emerged as a hybrid model combining the reliability of fixed-route services with the adaptability of demand-responsive transit [1,2]. FRT has been widely implemented in various metropolitan areas to enhance first-mile and last-mile connectivity, optimize vehicle deployment, and reduce overall operational costs. However, despite its growing adoption, the optimization of FRT scheduling and operation planning remains underexplored. Existing research primarily focuses on fixed-route timetabling or fully demand-responsive transit, overlooking the unique challenges posed by FRT, such as balancing operational efficiency with passenger convenience and integrating FRT with existing urban transit networks. Addressing these challenges is critical for improving public transit accessibility, service reliability, and network efficiency. This study aims to bridge this gap by proposing a collaborative optimization approach for FRT operation and timetable scheduling, integrating passenger demand dynamics, urban rail connectivity, and real-time scheduling constraints. By developing a comprehensive optimization framework, this research provides theoretical insights and practical solutions to enhance FRT’s role in modern urban transport systems.

In the absence of flexible travel demand, FRT operates like a conventional bus, adhering to a fixed route and station stops. Upon reaching the interchange station area, FRT can dynamically pick up or drop off passengers from the base route, effectively completing the “first/last mile” segment of their journey. As shown in Figure 1, there are two types of passengers in the L × W service area. Type I passengers: transfer from the subway station (Origin) to the flex-route transit and then reach the demand point (Destination); Type II passengers: from the demand point (Origin), board the flex-route transit to the subway station (Destination) and then enter the subway station.

Therefore, optimizing the coordinated scheduling and route planning of feeder flex-route transit is essential to enhancing operational efficiency, improving service quality, minimizing costs for both the system and passengers, and increasing public transit attractiveness and ridership.

To address the limitations of conventional bus–rail coordination in meeting last-mile travel needs, this research introduces a collaborative optimization framework that integrates feeder flex-route transit with urban rail systems. A mixed-integer nonlinear programming model is formulated to jointly optimize routing, scheduling, and vehicle allocation, incorporating passenger transfer behavior and spatiotemporal constraints. The proposed approach contributes both theoretically and practically to the advancement of flexible feeder service scheduling in multimodal urban transport systems.

The remainder of this paper is organized as follows: In Section 2, the relevant literature is reviewed and key research gaps are identified. In Section 3, the flex-route transit operation organization model is proposed. The corresponding algorithms for the proposed model are designed in Section 4. Case studies are presented in Section 5 to illustrate the performance of collaborative optimization methods, and a summary of findings is presented in Section 6.

2. Literature Review

When optimizing transit operations, while some studies focus solely on headway adjustments, a greater number explore the combined optimization of headway alongside other factors such as load factor, vehicle type, stop selection, and fare policies [3,4,5,6,7]. The urgent need for flexibility and personalization of travel has prompted continuous research and innovation related to the bus bridging service. Wang and Yuan proposed a non-uniform departure timetable optimization model based on the bus connecting high-speed rail stations as the research object. The results show that, compared to a uniform departure schedule, a non-uniform departure interval can effectively reduce passenger transfer waiting times [8]. Dou and Meng [9] developed an optimization model to determine the optimal vehicle departure times and type ratios, focusing on railway station–bus connectivity. Their approach reduced operating costs by adjusting the vehicle types used in feeder bus services. Xiong et al. [10] examined the collaborative optimization of community shuttle bus and subway services and employed a hybrid approach integrating genetic and Frank–Wolfe algorithms to derive an optimal synchronous scheduling scheme. Liu and Wu [11] addressed the issue of large numbers of passengers stranded due to rail transit network interruptions. They developed a timetable optimization model for bus–rail connections and proposed corresponding strategies to enhance connectivity. To address rail transit interruptions, Chen and An [12] proposed a comprehensive optimization framework for bus bridging routes and timetables under time-varying demand, incorporating a merging strategy for fast and short-distance routes to improve service efficiency. Jin et al. [13] introduced a column-generation algorithm within a two-step framework to generate candidate bus bridge routes. A multi-network flow model was established, and a detailed headway design was implemented. Accounting for bus travel time uncertainties, Liang et al. [14] proposed a robust optimization method to determine bus crossing routes and frequencies.

Michaelis and Schöbel [15] proposed an integrated model for segmenting bus routes and scheduling periodic timetables. Kaspi and Raviv [16] introduced a comprehensive route planning and cyclic timetable model, incorporating a cross-entropy heuristic algorithm for optimization. Evelien et al. [17] optimized bus route frequencies by adjusting route structures to minimize passenger delays. Cao and Ceder [18] proposed a nonlinear model and genetic algorithm integrating shuttle bus timetables with vehicle scheduling while accounting for skip–stop operations.

While existing studies have explored timetable optimization, headway adjustments, and bus–rail coordination, limited research has focused on the integrated optimization of flex-route transit operation planning and timetable synchronization with urban rail systems. Prior research primarily addresses either fixed-route bus connections or fully demand-responsive transit models, yet a significant gap remains in optimizing the hybrid characteristics of flex-route transit, particularly in balancing cost efficiency with service quality and ensuring seamless connectivity between flex-route services and urban rail networks. Furthermore, most studies focus on static scheduling models, whereas real-world transit operations require dynamic and adaptable scheduling frameworks that respond to fluctuating passenger demand and transit network conditions.

Passengers take urban rail transit schedules into account when planning their short-distance travel to optimize their overall trip efficiency. To ensure seamless connectivity, it is essential to align the operational strategies of flex-route transit with urban rail transit services. Bus schedule formulation comprises two critical aspects: vehicle scheduling design and timetable preparation, both of which are fundamental to enhancing the efficiency and service quality of the bus system. Currently, bus operation planning in most cities still relies on manual scheduling [19]. Therefore, an intelligent bus operation planning method must be developed, considering operational demand constraints. This approach integrates vehicle scheduling design with timetable optimization to determine the optimal departure intervals, departure frequency, and fleet size for flex-route transit, culminating in a comprehensive operational plan.

This paper aims to address these gaps by introducing an integrated optimization approach that aligns flex-route transit scheduling with urban rail timetables, leveraging demand-driven adjustments and dynamic scheduling mechanisms to improve transit network performance. The key elements of this approach include:

(1)

Joint Optimization of Path and Timetable—Unlike prior studies that optimize these components separately, this research integrates them to enhance coordination between flex-route transit and urban rail.

(2)

Passenger Demand and Transfer Behavior Analysis—The proposed model incorporates real-time demand data and passenger transfer patterns to enhance service reliability and efficiency.

(3)

A Dynamic Scheduling Framework—By developing a mixed-integer nonlinear programming (MINLP) model, this study introduces a more flexible and adaptive scheduling mechanism, allowing for real-time adjustments to improve system resilience.

(4)

Cost-Efficiency and Service Quality Trade-Off—The model considers both operator costs and passenger-centric factors (waiting times, transfer failures, travel delays) to find an optimal balance.

3. Mathematical Model

To address the “last mile” travel demand for connecting urban rail transit stations, this study develops an operational model for feeder flex-route transit to coordinate with urban rail transit schedules. The model applies to a multi-vehicle flex-route transit service system. Considering factors such as bus operation time, fleet configuration, service standards, and policies, this study determines the optimal departure interval, departure frequency, departure time, and fleet size for flex-route transit. This enables the formulation of a collaborative optimization scheme for scheduling variable-route buses, enhancing connectivity and improving public transit service levels.

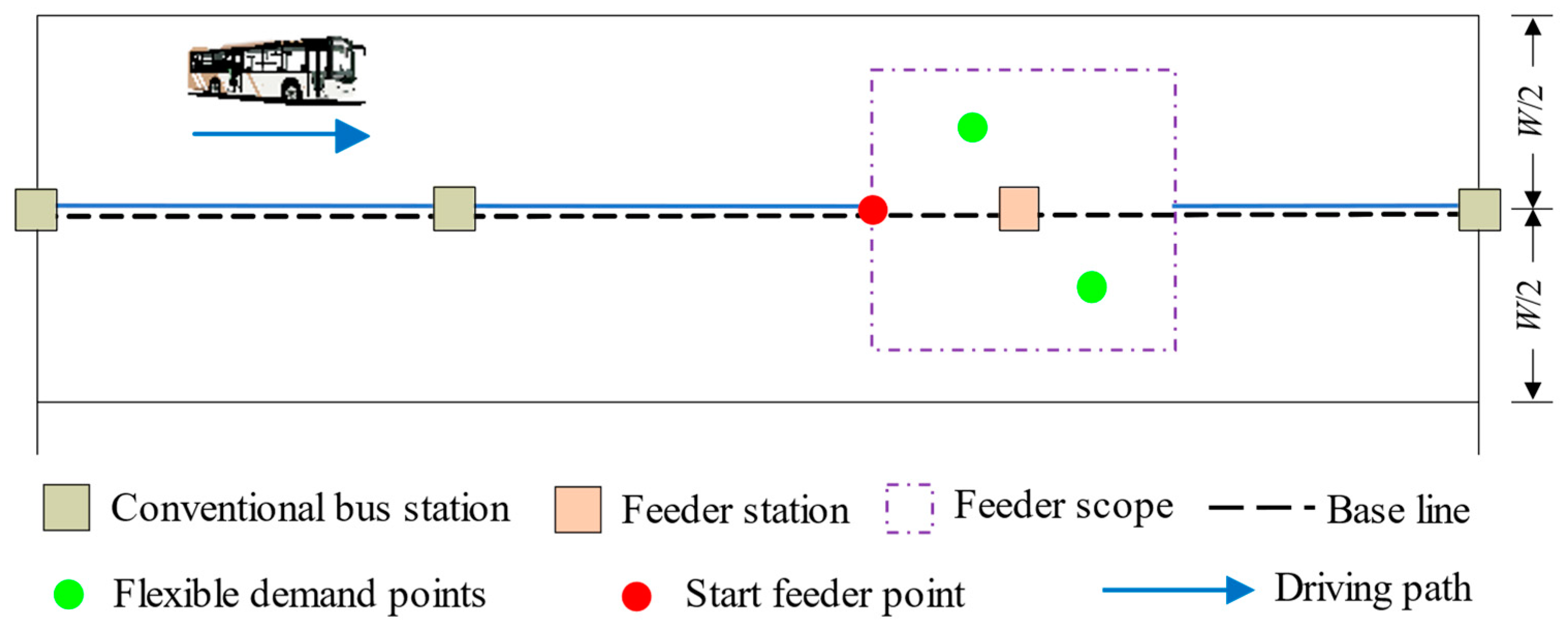
3.1. Model Assumptions

Reducing transfer waiting time is typically achieved by increasing bus departure frequency through shorter intervals. However, excessively increasing bus departure frequency raises operational costs, and deploying larger-capacity vehicles requires consideration of road conditions for feeder flex-route transit. These approaches may not effectively address capacity shortages at specific stations during peak periods. The operation of urban rail and feeder flex-route transit is affected by multiple factors, and their surrounding environments are relatively complex. Therefore, before constructing the model, appropriate simplifications and assumptions should be applied based on real-world conditions.

(1) The capacities of urban rail and flex-route transit are assumed to meet demand, and each passenger boards the nearest arriving vehicle, irrespective of congestion levels. This assumption is realistic for commuters during peak hours; (2) Urban rail transit operates strictly according to a predetermined schedule, while flex-route transit consistently departs on time, with any station departure delays effectively managed. This assumption serves as a reasonable approximation commonly applied in transfer optimization research [20,21]; (3) Flex-route transit vehicles are assumed to operate at a uniform speed; (4) the required transfer time is considered constant.

3.2. Notation

A directed graph G = (S, A, T) was defined to represent the route planning network of vehicles, where S represents the set of all optional stops (including interchange station and flexible demand points), A = S² represents the edge set formed by all optional stops, and T = (t_ij) is the set of vehicles driving time corresponding to each edge. The following symbols are used in this paper:

Q_I—set of type I passengers

Q_II—set of type II passengers

Q—Q_I ∪ Q_II, set of all passengers (demand), quantity q_m, q ∈ Q

K—set of feeder flex-route transit vehicle departure shift, k ∈ K

R_n—set of non-interchange stations (demand points outside the base line) that need to be passed by feeder flex-route transit

ψ—proper subset of S other than empty set

RT_a—urban rail transit arrival time

RT_d—urban rail transit departure time

ε—time required for passengers to get in and out of the urban rail transit station for transfer

t_p,q—time when passenger q transfers from urban rail transit to flex-route transit to reach the bus station

t_d,q—scheduled bus station arrival time of passenger q who transfer from flex-route transit to urban rail transit

θ_W—unit value of waiting time cost of transfer passengers/flex-route transit waiting at interchange station

θ_L—unit value of time cost for passengers transferring from flex-route transit to urban rail transit to arrive late at interchange station

θ_F—unit conversion value (number of people converted to cost) of the cost of transfer failure (passengers are not served by flex-route transit service)

θ_O—unit value of vehicle/enterprise operation costs

q_k—actual number of passengers taking feeder flex-route transit shift k

d_ij,k—Manhattan distance from stop i to stop j for feeder flex-route transit shift k

v—vehicle running speed of feeder flex-route transit

H—departure interval during operation cycle of feeder flex-route transit

h—operation cycle of feeder flex-route transit

k_m—number of departures within the operating period

τ—maximum tolerable waiting or late arrival time for passengers

P_p,q,k—time when feeder flex-route transit shift k picks up passenger q

P_d,q,k—time when feeder flex-route transit shift k drops off passenger q

t_a,i,k—arrival time of feeder flex-route transit shift k at station i

t_b,i,k—departure time of feeder flex-route transit shift k at station i

t_rn—service time of feeder flex-route transit at flexible demand points

x_ij,k = {0,1}—indicates if an arc (i, j) is chosen by feeder flex-route transit shift k (x_ij,k = 1) or not (x_ij,k = 0)

y_q,k = {0,1}—indicates if passenger q taking feeder flex-route transit shift k (y_q,k = 1) or not (y_q,k = 0)

z_q,k = {0,1}—indicates if waiting time or late arrival time of transfer passenger q taking feeder flex-route transit shift k is greater than the acceptable maximum waiting time τ (z_q,k = 1) or not (z_q,k = 0)

3.3. Flex-Route Transit Operation Organization Model

The conventional fixed-route public transport timetable compilation method is not suitable for feeder flex-route transit, because flex-route transit has the characteristics of sharing and the uncertainty of vehicle operation, which makes it difficult to provide accurate arrival time for passengers [22,23]. The commonly used calculation methods for determining departure frequency [24], including two methods based on maximum passenger flow (station survey) and two methods based on cross-sectional passenger flow (following survey data), are not fully applicable to this study. Therefore, this section proposes a method for calculating the departure time interval of flex-route transit based on the urban rail transit timetable, passenger reservation requirements, and departure time window constraints.

For the two cases of urban rail transit transfer feeder flex-route transit and feeder flex-route transit transfer urban rail transit, the optimal transfer conditions are as follows: When passengers transferring from urban rail transit to feeder flex-route transit arrive at the bus station, the feeder vehicle is already at the station, allowing passengers to transfer without waiting. Similarly, when passengers arrive at the urban rail platform, the train is already at the station, and they can board without delay. This transfer process can be illustrated in a time–space diagram, as shown in Figure 2.

When the left passenger transfers from the urban rail transit to the feeder flex-route transit, he needs to get off at the time of RT_a, and after the transfer time ε, he reaches the interchange bus station at the time of t_p (before t_b,k) and successfully gets on the bus. Similarly, the right side of the passenger from the feeder flex-route transit transfer urban rail transit success condition is at or before td time to interchange bus station, through the transfer time ε at or before RT_d time to reach the urban rail transit station for transfer. According to the above analysis, the conditions of transfer coordination between the two can be obtained, which can be calculated by the following formula:

$$t_p=R{T}_a+\epsilon$$

(1)

$$t_d=R{T}_d-\epsilon$$

(2)

If passengers arrive too early at the bus station when transferring from urban rail transit to flex-route transit, they must wait for a certain period before being served; if the passenger arrives late and the previous vehicle is scheduled to serve them, the vehicle must wait for the passenger to arrive at the station before picking them up for the next departure. This delay is considered part of the waiting time cost. When passengers transfer from flex-route transit to urban rail transit, arriving early at either the bus or urban rail station does not result in a delay; if the actual arrival time exceeds the expected arrival time, the passenger must wait for the next urban rail transit, and the delay is recorded as a late arrival time cost.

In compiling the flex-route transit timetable for urban rail transit transfers, the focus shifts from a single-vehicle system to a multi-vehicle system. Therefore, the objective function of the timetable compilation model not only considers the passenger perspective but also incorporates the broader interests of both passengers and enterprises, as well as the public welfare aspect of public transit. The primary constraints of the model include the running time and departure interval constraints.

3.3.1. Objective Function

The Objective Function (3) of the feeder flex-route transit timetable formulation model is to minimize the system cost U. The system cost U includes the waiting time cost U_W for passengers/flex-route transit, the late arrival time cost U_L for passengers taking flex-route transit, the transfer failure cost U_F, and the enterprise operating cost U_O.

$$\min U=U_W+U_L+U_F+U_O$$

(3)

Due to the involvement of multiple vehicle systems and vehicle departure intervals, the waiting time is defined as Formula (4); The cost of late arrival time is defined as Formula (5) according to the above rules; The cost of transfer failure during the transfer process is related to the number of failed passengers, as shown in Formula (6); The operating cost of a company depends on the cost of multiple vehicle travel time, which is the total distance traveled by multiple vehicles divided by the operating speed of the vehicles, as shown in Formula (7).

$$U_W={\theta }_W{{\displaystyle \sum }}_{q\in Q_{\mathrm{I}}}{{\displaystyle \sum }}_{k\in K}{y}_{q,k}\left|P_{p,q,k}-t_{p,q}\right|$$

(4)

$$U_L=\{\begin{array}{c}0,P_{d,q,k}\le t_{d,q}\\ {\theta }_L{{\displaystyle \sum }}_{q\in Q_{\mathrm{II}}}{{\displaystyle \sum }}_{k\in K}{y}_{q,k}\left(P_{d,q,k}-t_{d,q}\right),P_{d,q,k}>t_{d,q}\end{array}$$

(5)

$$U_F={\theta }_F\left(q_m-{{\displaystyle \sum }}_{k\in K}{q}_k\right)$$

(6)

$$U_O={\theta }_O{{\displaystyle \sum }}_{i\in S}{{\displaystyle \sum }}_{j\in S}{{\displaystyle \sum }}_{k\in K}{x}_{ij,k}{d}_{ij,k}/v$$

(7)

3.3.2. Constraint Condition

The model constraints mainly include vehicle operation constraints, departure interval constraints and passenger transfer constraints. The details are as follows:

(1)

Vehicle operation constraints

Constraints (8) means that when x_ij,k = 1, the arrival time of shift k at point j will not be earlier than the departure time from point i plus the travel time between two points. When x_ij,k = 0, this constraint is invalid, where M is a sufficiently large number.

$$t_{a,j,k}\ge t_{b,i,k}+x_{ij,k}{d}_{ij,k}/v-M\left(1-x_{ij,k}\right),\forall \left(i,j\right)\in S,k\in K$$

(8)

Constraints (9) ensure that the departure time of shift k at the demand point is equal to the time when the vehicle reaches the demand point plus the parking service time.

$$t_{b,i,k}=t_{a,i,k}+t_{rn},\forall i\in R_n, k\in K$$

(9)

By eliminating all cycles that make other points disjoint, it is ensured that the optimal solution does not contain meaningless subcycles.

$${{\displaystyle \sum }}_{i\in \psi }{{\displaystyle \sum }}_{j\in \psi }{x}_{ij,k}\le \left|\psi \right|-1,\forall \psi \subseteq S,\psi \ne \varnothing ,k\in K$$

(10)

(2)

Departure interval constraints

The flex-route transit departure interval is calculated when the vehicle arrives at the feeder service area along the base line, as shown in Figure 3. During the operation of the flex-route transit, the departure interval is constrained by the time interval [H_min, H_max] (the lower and upper limits of the vehicle departure interval). The determination of the departure interval in different periods can be calculated according to the model.

$$H_{\min }\le H\le H_{\max },\forall H\in {\mathbb{N}}^{+}$$

(11)

The value of the optimal departure interval calculated by the model is not fixed. To facilitate the preparation, the initial departure time interval is processed as follows:

$$k_m=h/H,\forall h\in {\mathbb{N}}^{+},H|h$$

(12)

(3)

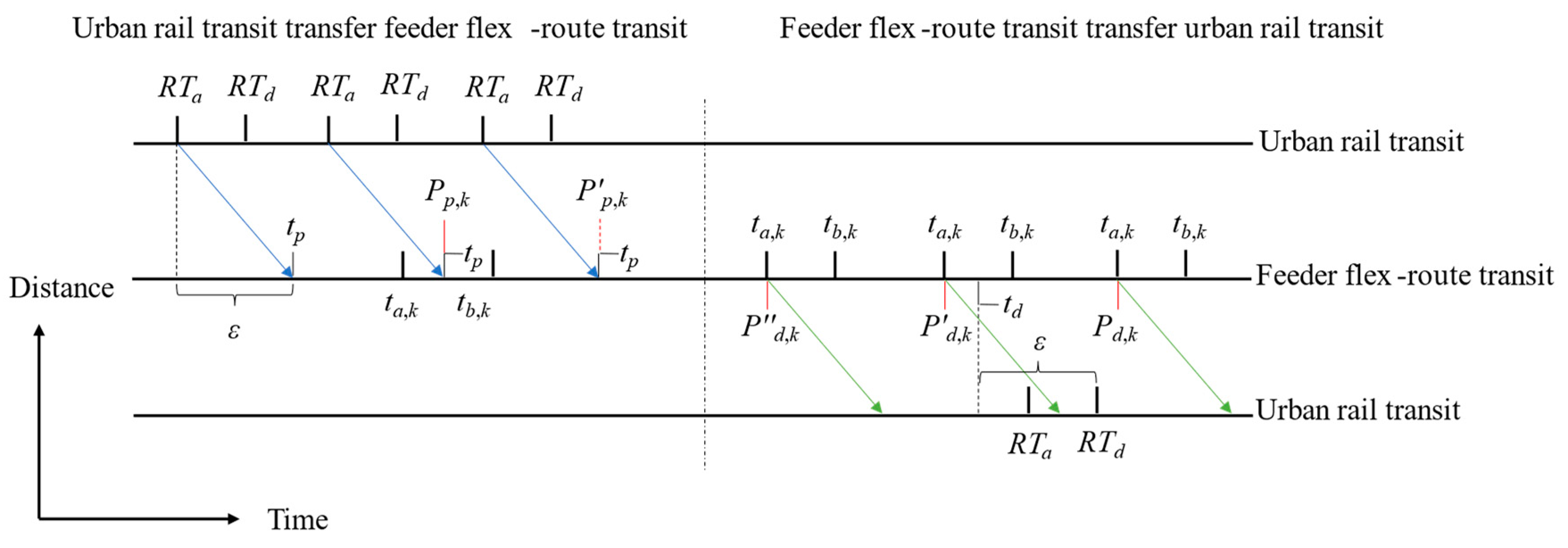
Passenger transfer constraints

For passengers, each passenger can only be served once at most, either served or rejected.

$${{\displaystyle \sum }}_{k\in K}{y}_{q,k}\le 1,\forall q\in Q$$

(13)

The Constraints (14), (15) are used to judge whether the transfer passengers can successfully complete the transfer. If the transfer is successful (using the flex-route transit), y_q,k is 1, otherwise is 0.

$$M\left(y_{q,k}-1\right)\le \left|P_{p,q,k}-t_{p,q}\right|<M{y}_{q,k},\forall q\in Q_{\mathrm{I}},k\in K$$

(14)

$$M\left(y_{q,k}-1\right)\le \left|P_{d,q,k}-t_{d,q}\right|<M{y}_{q,k},\forall q\in Q_{\mathrm{II}},k\in K$$

(15)

z_q,k is {0, 1}. When the waiting time or late arrival time of transfer passengers on the flex-route transit is greater than the acceptable maximum delay time τ, it is 1; otherwise, it is 0, as shown in Constraints (16), (17).

$$M\left(z_{q,k}-1\right)\le \left|P_{p,q,k}-t_{p,q}\right|-\tau <M{z}_{q,k},\forall q\in Q_{\mathrm{I}},k\in K$$

(16)

$$M\left(z_{q,k}-1\right)\le \left|P_{d,q,k}-t_{d,q}\right|-\tau <M{z}_{q,k},\forall q\in Q_{\mathrm{II}},k\in K$$

(17)

4. Solution Approach

When designing the operation organization scheme of feeder flex-route transit, the problem can be subdivided into two sub-problems: “departure interval setting algorithm design” and “shift setting algorithm design”.

4.1. Departure Interval Setting Stage

When determining the departure interval, it is essential to account for the characteristics of the bus schedule and develop a practical and well-structured plan. Although the departure interval is derived from the model, it does not directly represent the optimal solution. Since the departure interval is relatively fixed for buses, the system cost must be evaluated iteratively to determine the most suitable interval. Based on relevant standards and empirical data, the upper and lower limits of the departure interval are established. The system cost associated with each possible departure interval is then calculated and compared to identify the optimal departure interval for the vehicle. The pseudo-code for the specific solution algorithm is shown in Algorithm 1.

Algorithm 1 Departure interval setting algorithm
Input:	Lower limit of departure interval Hmin, upper limit of departure interval Hmax, departure interval Hν, where: Hν = Hmin, …, Hmax, ν = 1, 2, …, n
Output:	Optimal departure interval H*, Optimal system cost U*(H*)
Step 0		Take the initial departure interval H1 = Hmin, let the optimal departure interval H* = H1, calculate the current system cost U(H1), let the optimal system cost U*(H*) = U(H1);
Loop:		While ν < n
Step 1			Based on the current departure interval, obtain a new vehicle departure interval Hν + 1,and judge the constraint condition, if Hν+1 does not satisfy the constraint condition, repeat Step 1;
Step 2			Calculate the system cost U(Hν+1) under departure interval Hν+1, if U(Hν+1) < U*(H*), accept Hν+1 as the new optimal departure interval, H* = Hν+1, Otherwise, retain the original optimal departure interval H*;
Step 3			If termination condition Hn = Hmax is satisfied, then output optimal departure interval H* and optimal system cost U*(H*), termination routine, Otherwise, repeat Step 1.

4.2. Shift Setting Stage

Each departure interval corresponds to a unique passenger allocation and flex-route transit shift configuration. The system cost is determined by analyzing the specific connection conditions and shift arrangements following passenger allocation and scheduling. Therefore, corresponding algorithms must be developed to address this aspect. Passenger assignment and shift scheduling determine which passengers are served in each shift, a problem that can be addressed using a genetic algorithm. However, due to constraints related to passenger time windows and the operational cycle of feeder flex-route transit, the genetic algorithm generates a large number of invalid chromosomes. To enhance the overall efficiency of the algorithm, appropriate methods must be developed to convert invalid chromosomes into valid ones. If the design method is inadequate, the genetic algorithm may converge prematurely and become trapped in a local optimum. To address this issue, this section introduces a feedback mechanism that attempts to reassign rejected passengers to flex-route transit shifts during passenger allocation and vehicle scheduling. This improves solution quality and enhances algorithmic efficiency in exploring the target search space. The specific pseudo-code of the algorithm is shown in Algorithm 2.

Algorithm 2 Shift setting algorithm
Input:	Population size, crossover probability, mutation probability, maximum number of iterations Imax
Output:	Optimal solution u, Optimal system cost U
Step 0		Input feeder flex-route transit operation parameters, set population size, crossover probability, mutation probability, maximum number of iterations Imax, initialize the number of population iterations In = 0;
Loop:		While In < Imax
Step 1			Encoding: chromosome adopts a matrix composed of 0–1 variables to reflect the two-dimensional relationship between passenger allocation and shift setting. Due to the phenomenon of rejection of passengers in flex-route transit, not all passengers can be served, so it is necessary to assume that there is a new virtual shift on the basis of all feeder shifts to store rejected passengers;
Step 2			Fitness function: when the feeder flex-route transit completes a complete shift setting in the operation cycle, the fitness corresponding to the chromosome is calculated;
Step 3			Chromosome update: (1) after the assignment and setting of each passenger and shift are completed, the system will reject the travel requirements of some passengers due to relevant constraints, feed back the information of the rejected passengers to the chromosome, and change the corresponding genes to achieve chromosome update; (2) if the current chromosome meets the constraints, but the quality is not high, it is easy to cause premature convergence. It is necessary to try to rearrange the rejected passengers back to the flex-route transit to improve the quality of the chromosome and jump out of the local optimum;
Step 4			Selection: elite retention strategy and tournament method;
Step 5			Crossing: select a single-point crossing method, arbitrarily select the position of the crossing point, use the crossing point as the boundary point, and recombine the two chromosomes;
Step 6			Mutation: using a single point mutation method, when a chromosome undergoes mutation, randomly select the location where the gene will mutate, and passengers at that location will switch to the corresponding service shift;
Step 7			Update population fitness, calculate the objective function values of offspring, update and record the optimal solution of the population;
Step 8			Iteration count update, In = In + 1;
Step 9			Algorithm termination conditions: In ≥ Imax.

5. Result Analysis

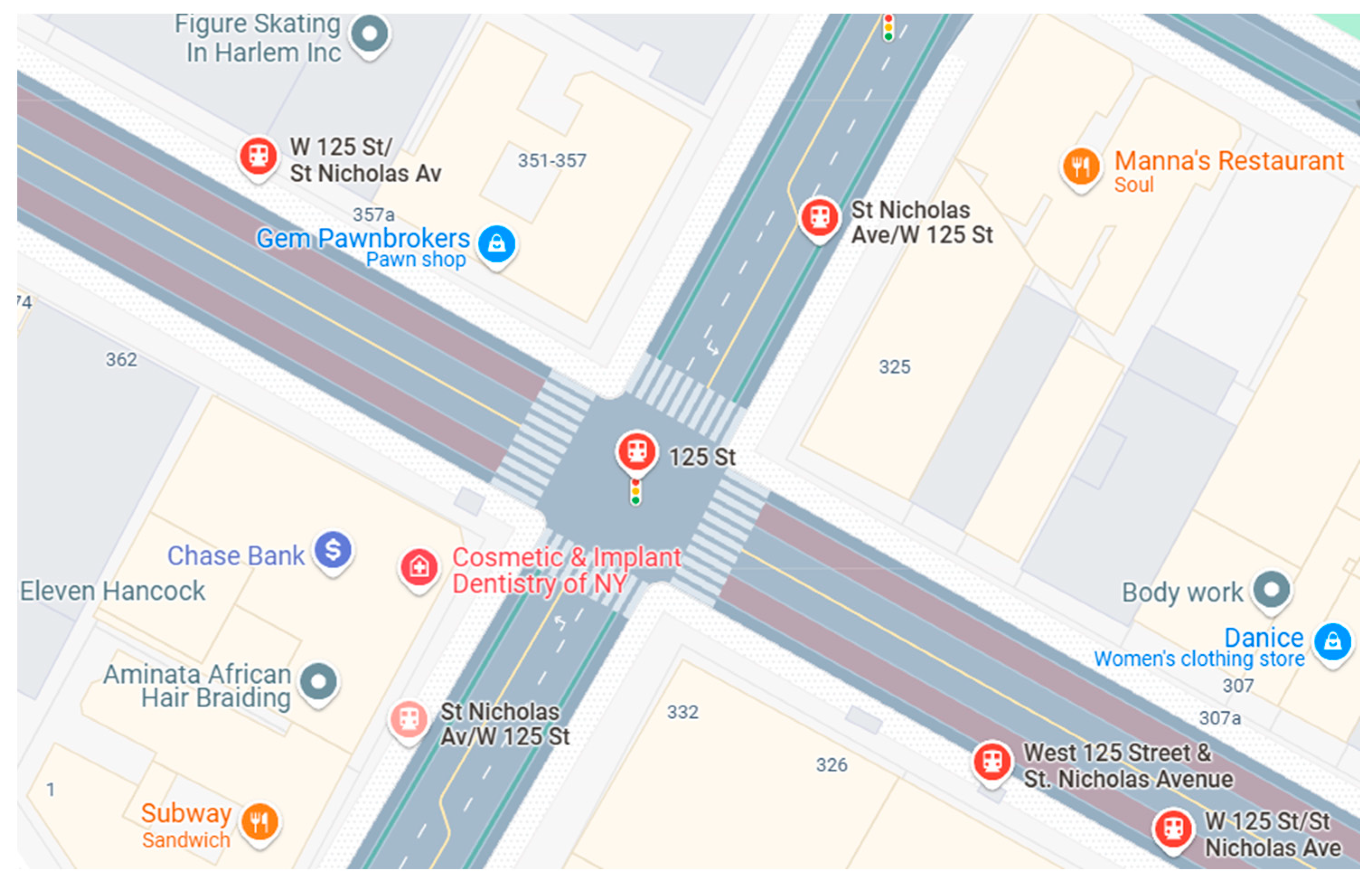
5.1. Case Description

This section selects the St Nicholas Av/W 125 St station of the M3 bus line and the 125 St station of the subway A/B line in Manhattan, New York as examples to verify the model and algorithm based on operational data such as traffic flow, lines, and timetables, as shown in Figure 4. In the feeder service area, the M3 route is converted into a flex-route transit system, enabling vehicles to deviate from the baseline to accommodate passengers with flexible travel demands.

Numerous points of interest (POIs) surround the interchange station, attracting a significant number of passengers traveling between destinations. Passengers are likely to arrive at a specific POI after taking the subway and depart from a POI before boarding the subway. This study primarily addresses the “last mile” travel problem for subway passengers, selecting POIs near the transit line and station. A set of travel demands is randomly generated within the selected POIs.

For simulation analysis, the complexity of the road network is not the focus of this study; therefore, the system is abstracted as an L × W service area, where flex-route transit facilitates passenger connections. Given the focus on “last mile” short-distance travel, L and W are set to 2 miles, indicating that the distance from the central interchange station to the feeder service boundary is 1 mile.

To ensure efficient transfer service, synchronization between the subway schedule and feeder flex-route transit operations is required. The actual departure interval of the subway line typically ranges from 8 to 15 min. For this study, the subway departure interval is set to 10 min. The flex-route transit system schedules operations based on the temporal and spatial distribution of travel demand, formulating a feasible departure and operation plan.

Refer to [9,25,26,27,28,29,30] for relevant parameters in the research system. θ_W, θ_L, and θ_O are 1 USD/min, 1 USD/min, and 1 USD/min, respectively. Considering the public welfare of public transit, as far as possible to meet travel demand, and reduce the rejection rate, and θ_F is set to 5 USD/passenger. H_min is 3 min, H_max is 60 min, v is 25 miles/h, ε is 3 min, τ is 10 min, and t_rn is 0.3 min. Similar to related research [27,28], linear motion is used to reproduce the real road network.

This section is based on the Matlab R2021a platform, on the computer of Intel(R) Core(TM) i7-8750H CPU @ 2.20 GHz, 8 GB RAM, windows 11 system, the model is solved by the programming. For each simulation experiment, the parameters of the genetic algorithm are uniformly set as follows: the chromosome population size is 80, the probability of crossover behavior is 0.9, the probability of mutation behavior is 0.1, and the maximum number of iterations is 500.

5.2. Case Analysis

Based on the system’s relevant parameter values and the spatio-temporal characteristics of passenger demand, the optimal departure interval for different demand levels can be determined. The departure interval discussed here specifically applies to feeder flex-route transit within the feeder service area and does not imply that all M3 bus services operate at this frequency.

In system cost calculations, the default weight coefficient assigned to each time-related cost is set to 1. If greater emphasis is placed on passenger waiting time and late arrival costs, their corresponding weight coefficients are increased while maintaining all other conditions constant. For instance, when the weight coefficient ratio for waiting time cost, late arrival time cost, transfer failure cost, and enterprise operation cost is set to 2:2:1:1, the optimal departure interval is adjusted accordingly, as shown in

Table 1. Optimal departure intervals corresponding to different demand levels.

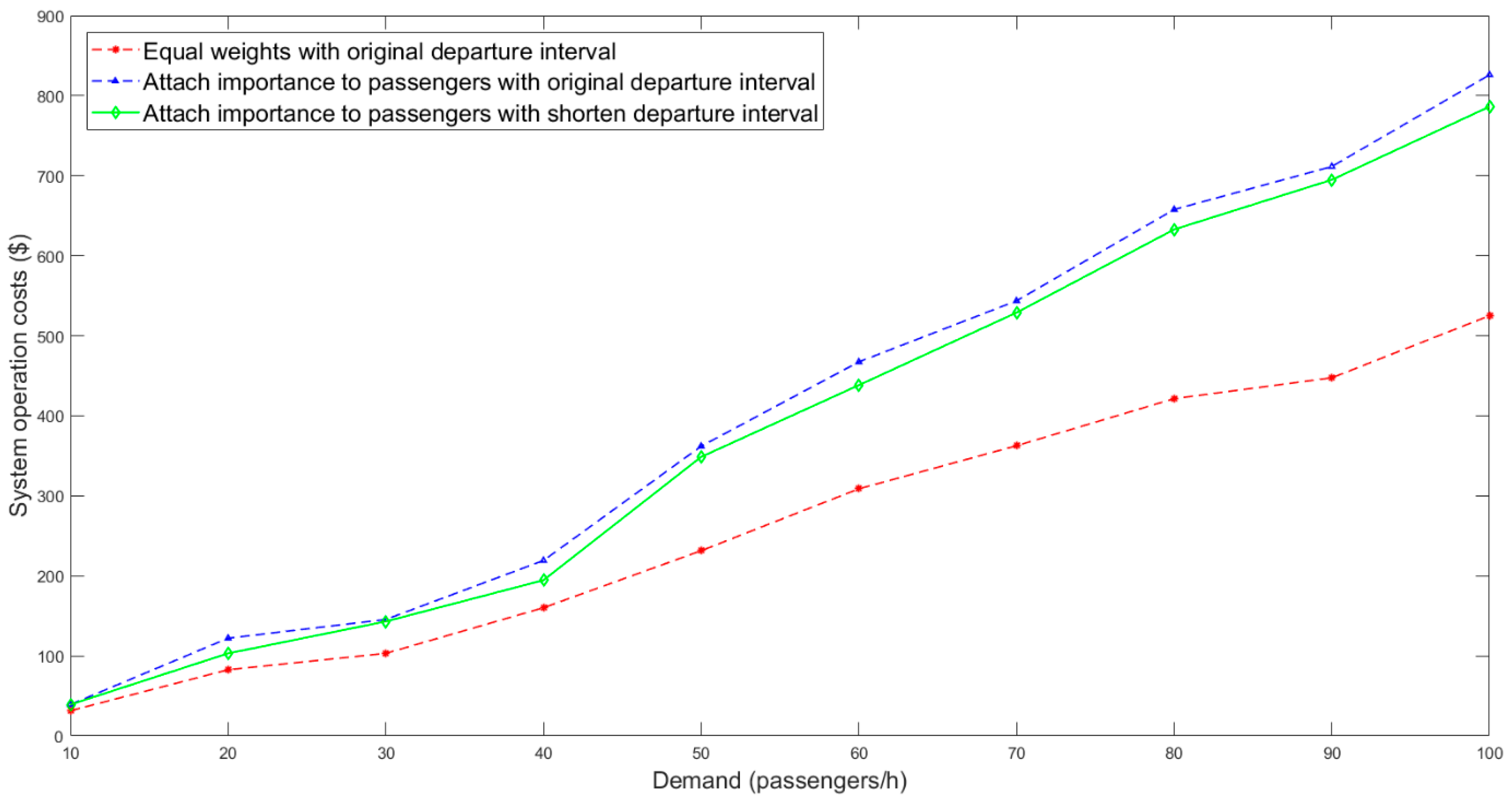
H (min)	Demand Levels (Passengers/h)
	10	20	30	40	50	60	70	80	90	100
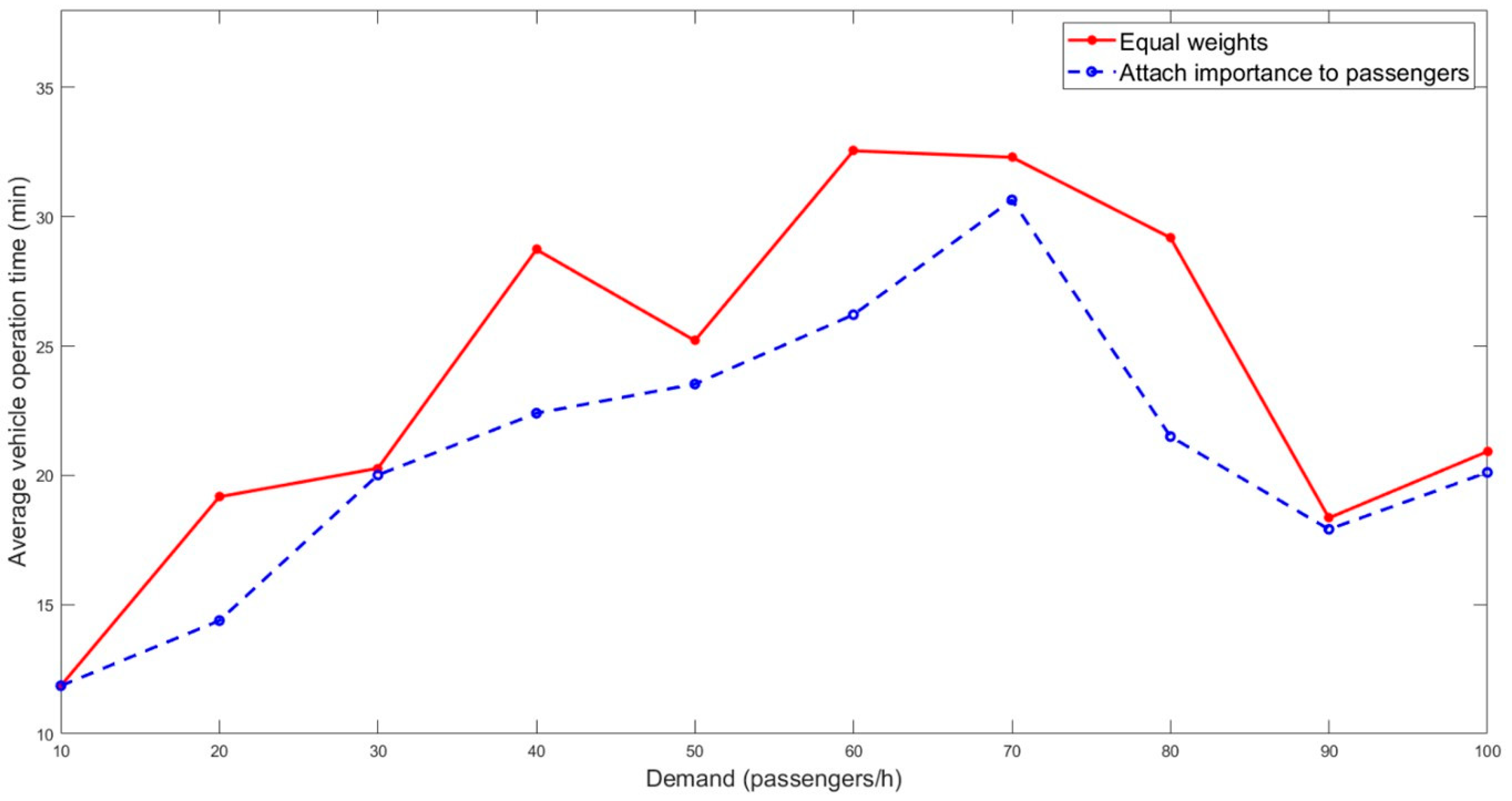
Equal weights	30	30	20	20	15	15	12	10	6	6
Attach importance to passengers	30	20	20	15	12	10	10	6	5	5

.

As shown in Table 1, when greater emphasis is placed on passenger waiting costs and late arrival time, the optimal departure interval adjusts accordingly as the corresponding weight coefficient increases. This requires reducing the departure interval, increasing the departure frequency, minimizing passenger-related travel time costs, and optimizing overall system operation costs.

Using the departure interval under the same weight as an example, the system operation cost U, average vehicle running time, number of departures, and rejection rate (percentage of passengers not served due to constraints) at each demand level are calculated, as shown in

Table 2. System simulation results corresponding to different demand levels.

Demand Levels (Passengers/h)	H (min)	U (USD)	Average Vehicle Running Time (min)	Number of Departure Shifts	Rejection Rate (%)
10	30	31.46	11.86	2	0
20	30	82.71	19.17	2	5
30	20	103.16	20.27	3	0
40	20	160.18	28.73	3	7.5
50	15	231.41	25.21	4	0
60	15	308.76	32.55	4	6.67
70	12	362.57	32.30	5	5.71
80	10	421.44	29.19	6	2.5
90	6	447.48	18.35	10	0
100	6	525.12	20.92	10	3

.

Table 2 shows that when passenger demand is high and service frequency is relatively low, the average vehicle running time increases. However, since increasing service frequency raises operating costs, this scheme represents the optimal solution under these conditions. If greater emphasis is placed on passenger waiting costs and late arrival time, the average vehicle running time and system running cost under different demand levels will also change, as shown in Figure 5 and Figure 6.

As shown in Figure 5, as the departure frequency increases, the number of vehicles operating per cycle rises, the average number of passengers per shift declines, and the corresponding average running distance shortens, leading to a reduction in the average vehicle running time per cycle.

In Figure 6, “Equal weights with original departure interval” represents the total operating cost of the system under the default weight values, which aligns with the data presented in Table 2. “Attach importance to passengers with original departure interval” refers to the system operating cost at the original departure interval under adjusted weight values. “Attach importance to passengers with short departure interval” represents the system operating cost when the departure interval and average vehicle running time are reduced accordingly.

As the passenger weight coefficient increases, the system operating cost under normal conditions also rises. At this stage, decreasing the departure interval, increasing the departure frequency, and expanding the number of operating vehicles significantly reduce passenger waiting and late arrival times, leading to a corresponding decrease in total system cost. However, as the number of vehicle departures increases, the corresponding operating costs also rise, limiting the extent of overall system cost reductions.

Specifically, the routine simulation verification is based on a passenger demand level of 50 people per hour, as shown in Figure 7. In the figure, red dots represent origins where passengers transfer from flex-route transit to the subway, while green dots indicate destinations where passengers transfer from the subway to flex-route transit. The subway arrives and departs from the interchange station every 10 min between 7:00 and 7:59, while flex-route transit departs from the feeder area boundary at 7:00. The departure interval and corresponding system operating parameters are computed by prioritizing passenger-related considerations.

Based on passenger reservation data and relevant parameters, demand allocation is performed to derive the collaborative optimization scheme for vehicle running path and timetable scheduling, as presented in

Table 3. Operation path, service time, and service demand of feeder flex-route transit.

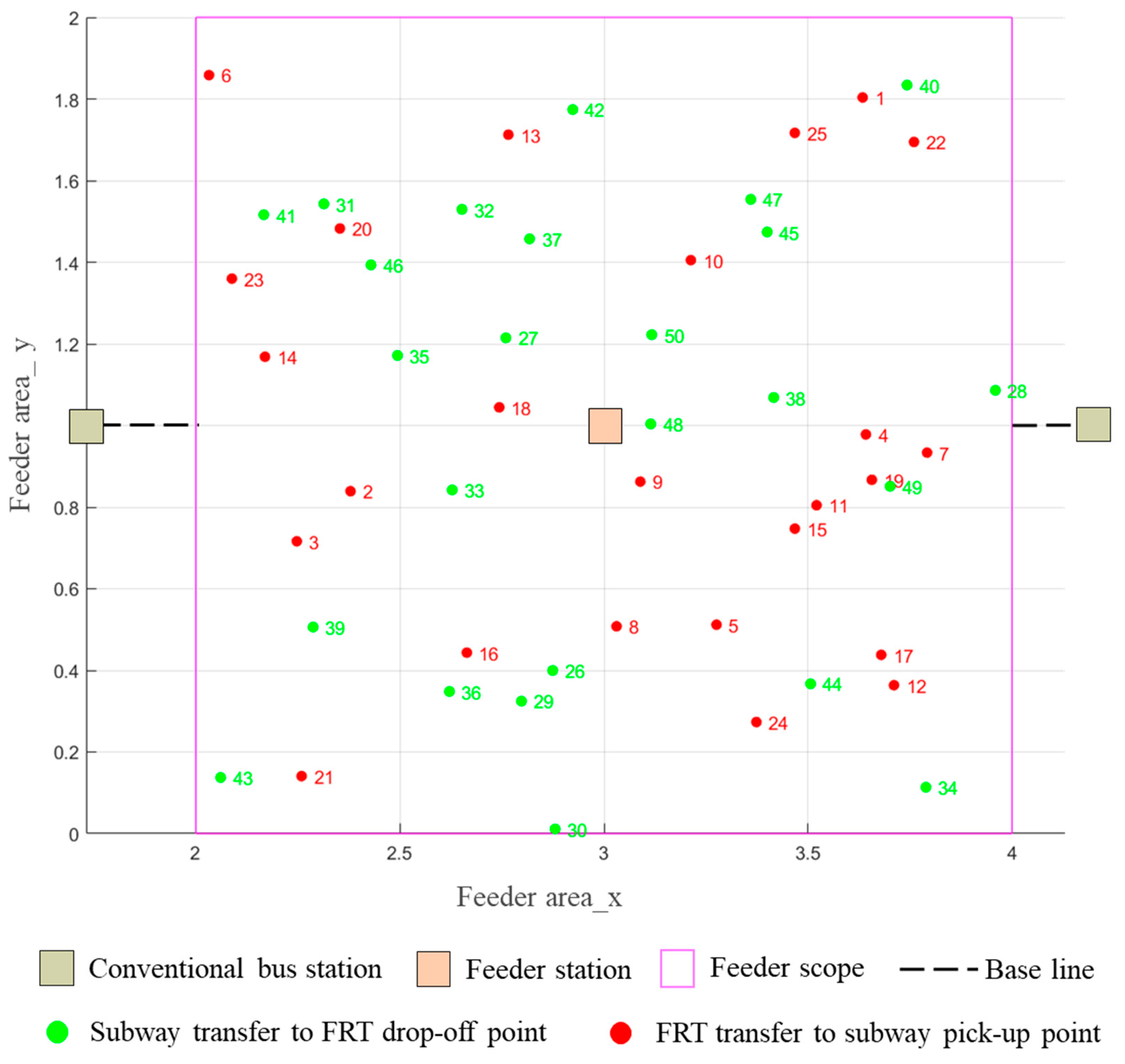
Vehicle Shifts	Departure Time of Interchange Station	Vehicle Running Path	Cumulative Number of Passengers
1	7:13	14-2-13-10-9-0-50-32-35-26-38-49	11
2	7:23	6-3-12-25-0-41-29-44-40	8
3	7:33	23-16-5-11-1-0-42-33-36-28	9
4	7:43	18-4-7-19-15-17-0-27-46-43-30-48-47	12
5	7:53	20-21-24-8-0-37-31-39-34-45	9

.

6. Conclusions

This paper examines the “last mile” travel demand characteristics and transfer behaviors of passengers using urban rail transit, explores the operational organization and connectivity between buses and urban rail transit, and proposes a strategy to convert conventional buses into flex-route transit for improved connectivity. Without requiring the introduction of a new feeder line, this approach simultaneously meets existing bus travel demand and accommodates urban rail transit passengers with short-distance travel needs.

Drawing from conventional fixed-point and fixed-line bus timetable preparation methods, this study summarizes the process of flex-route transit path planning and station timetable development for urban rail transit connectivity. For a multi-vehicle flex-route transit service system, a collaborative optimization scheme for transit operations is developed. By examining passenger transfer behaviors and the operational characteristics of both transit systems, this research introduces a collaborative optimization method for feeder FRT scheduling and route planning. The methodology employs a mixed integer nonlinear programming approach to optimize departure intervals, vehicle deployment, and scheduling strategies.

Simulation experiments based on real-world urban transit scenarios are conducted to validate the proposed model. Considering relevant operational characteristics and applicability, the optimal departure interval, departure frequency, number of operating vehicles, and station departure times for flex-route transit are determined. The findings suggest that optimizing departure intervals and vehicle scheduling reduces passenger waiting times and operational costs while ensuring high service reliability.

This study establishes a theoretical foundation and a practical framework for automated scheduling in feeder transit systems. Future research could expand upon this work by investigating larger-scale collaborative networks, integrating diverse vehicle types, and implementing dynamic pricing and subsidy strategies to enhance system efficiency and promote equity in public transportation.