Experimental Investigation on the Effects of Cutting Direction and Joint Spacing on the Cuttability Behaviour of a Conical Pick in Jointed Rock Mass
Abstract
:1. Introduction
2. Experimental Methodology
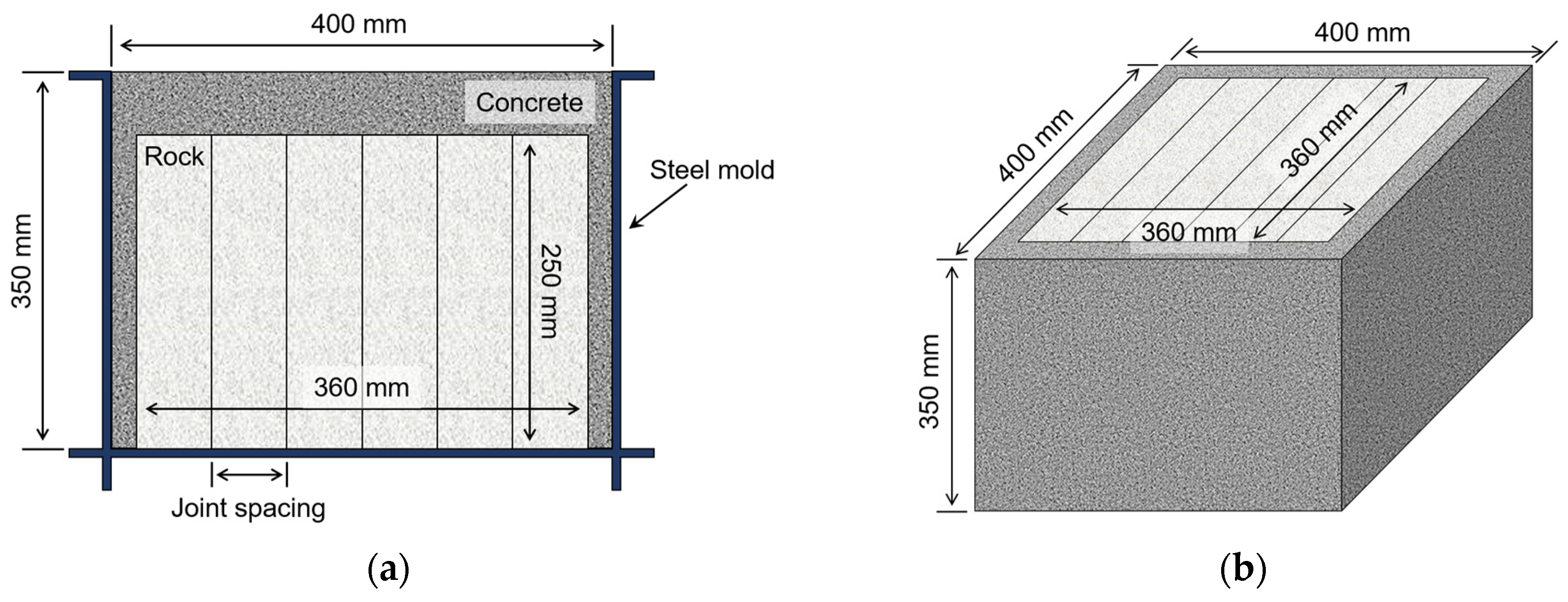
2.1. Preparation of Jointed Rock Mass Specimens
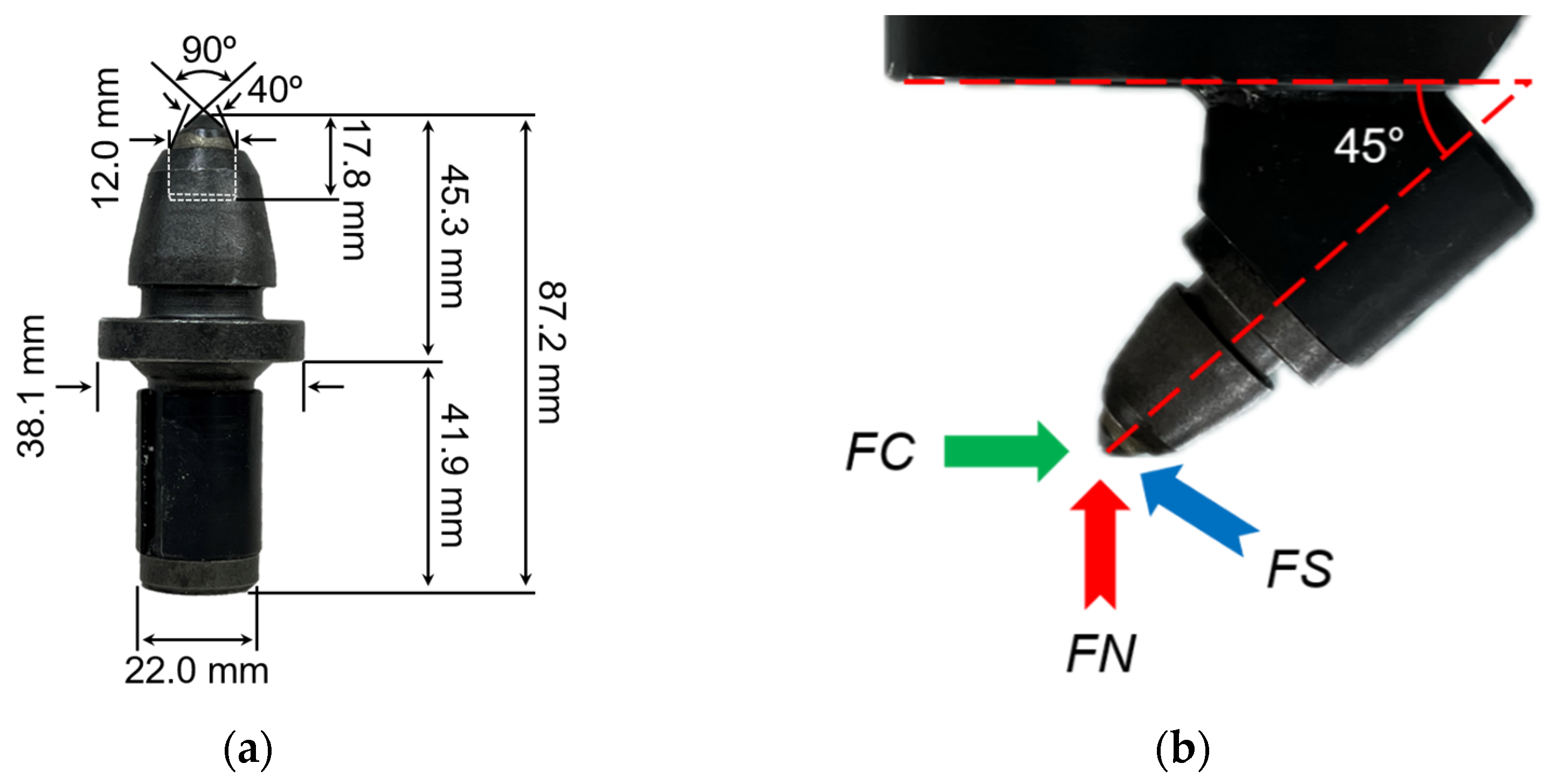
2.2. Laboratory-Scale Linear Cutting Machine and Cutting Tool
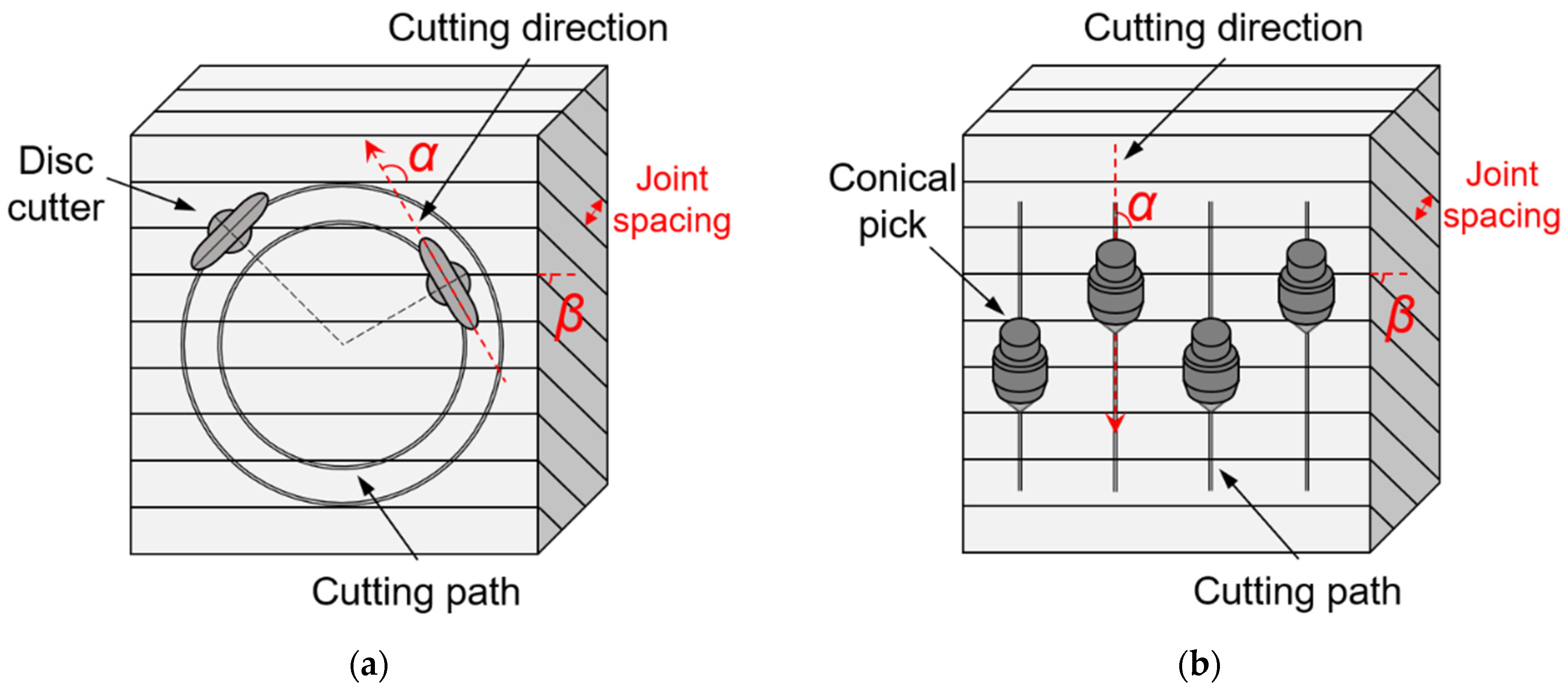
2.3. Experimental Procedure
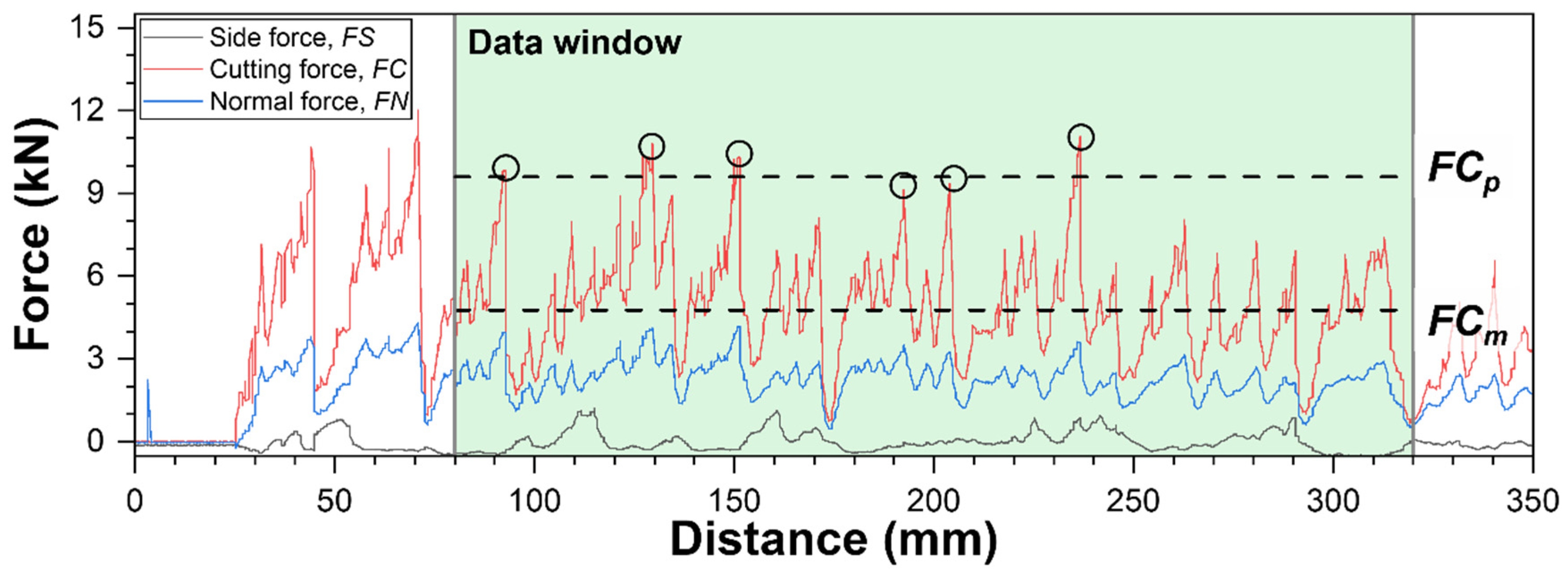
2.4. Data Processing
3. Experimental Results and Discussion
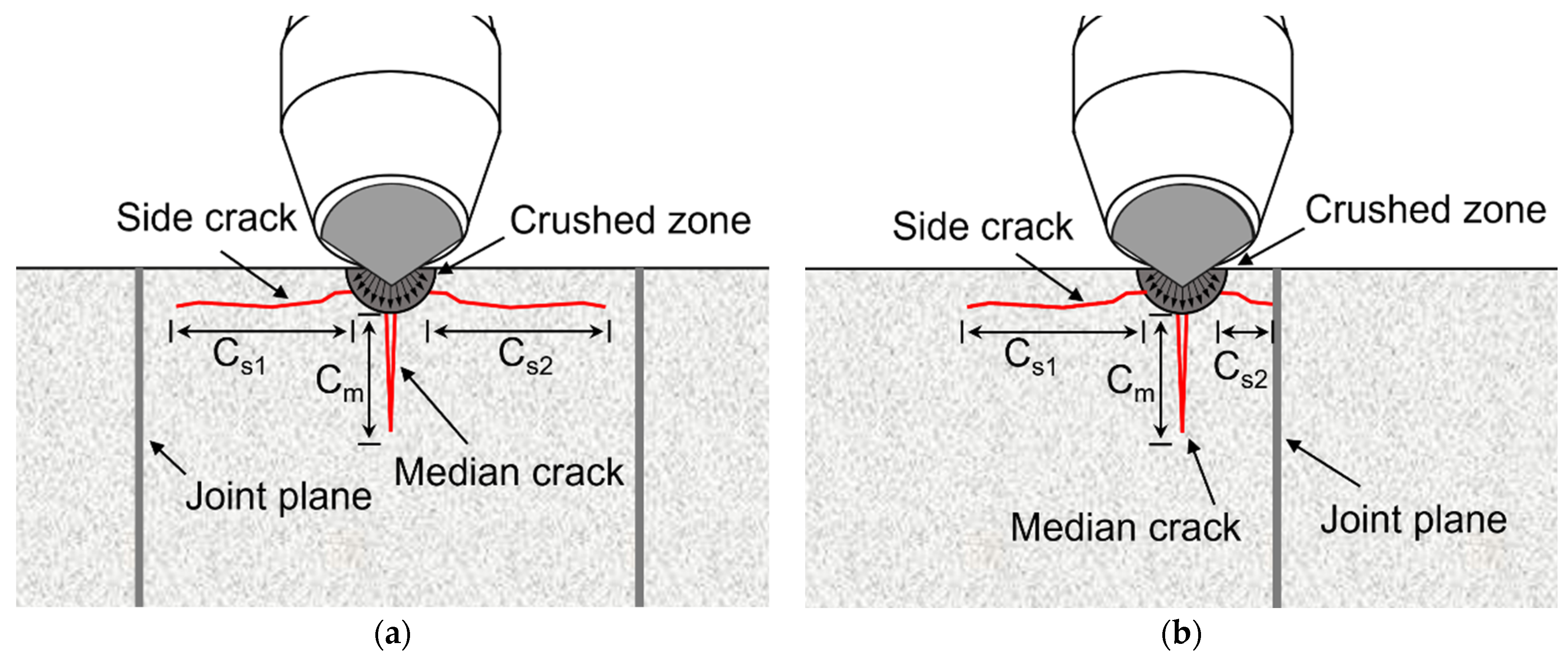
3.1. Characteristics of Cutting Force in Jointed Rock Mass
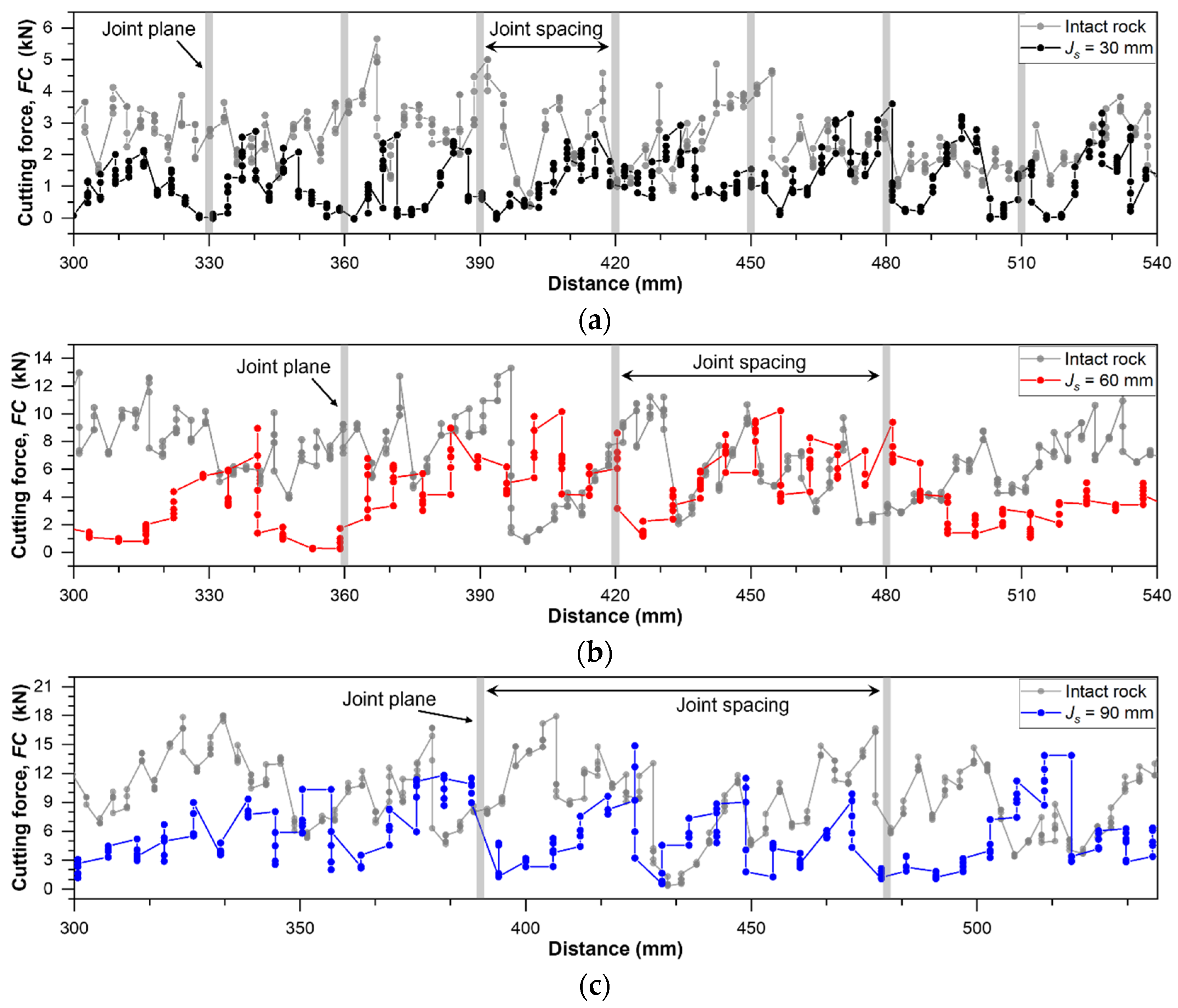
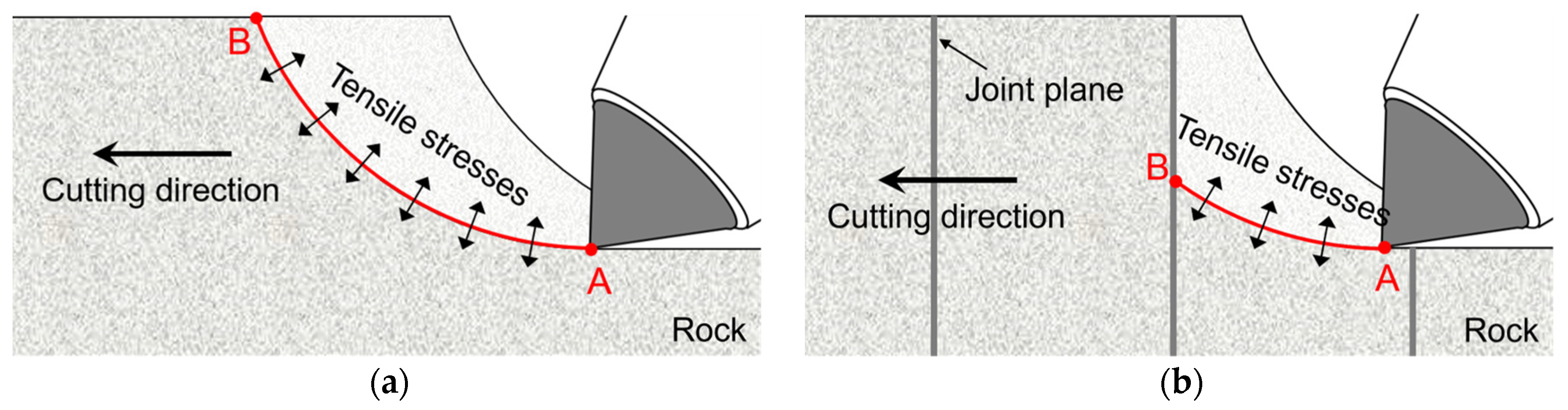
3.1.1. Cutting Force in the Direction Perpendicular to the Joint Plane
3.1.2. Cutting Force in the Direction Parallel to the Joint Plane
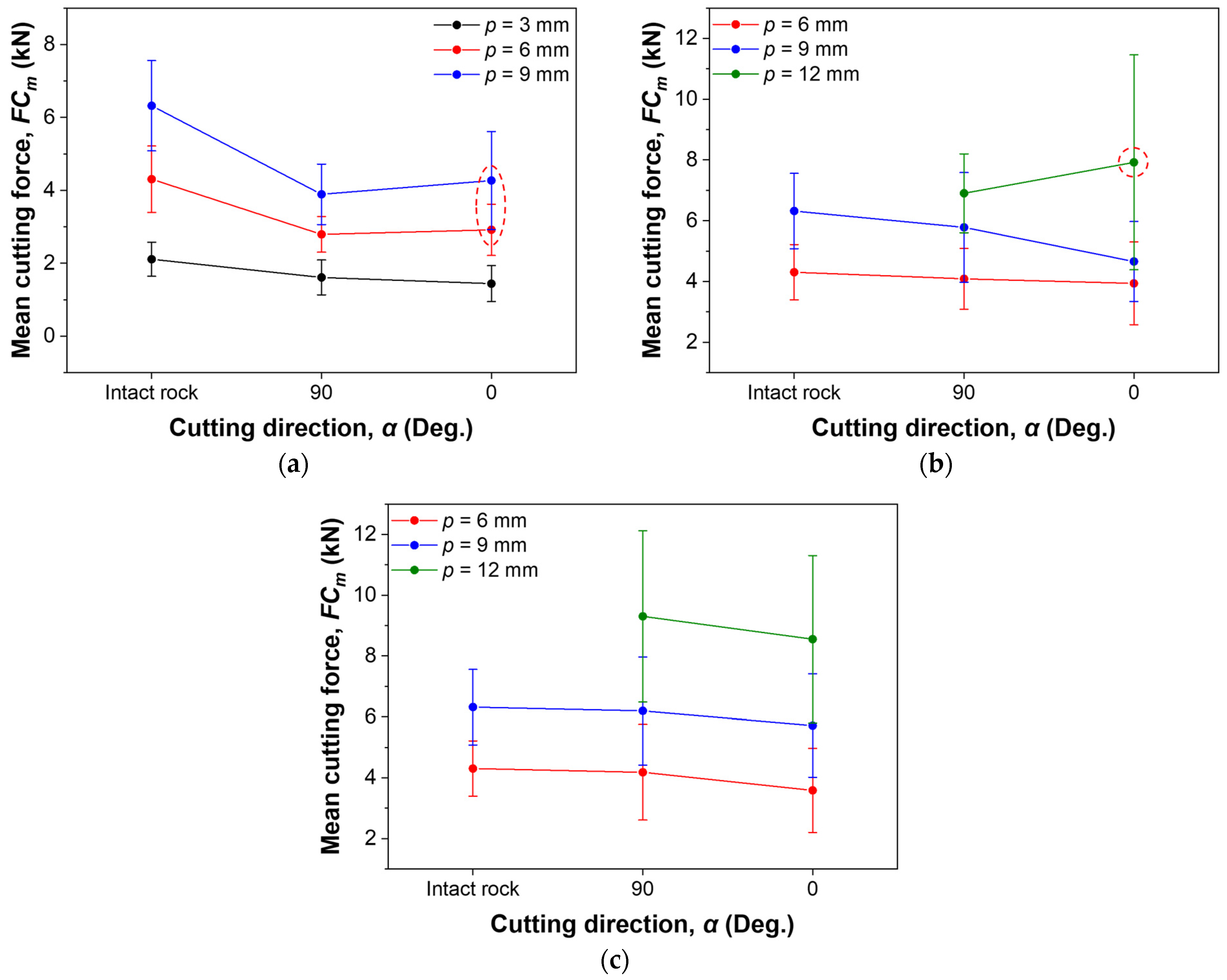
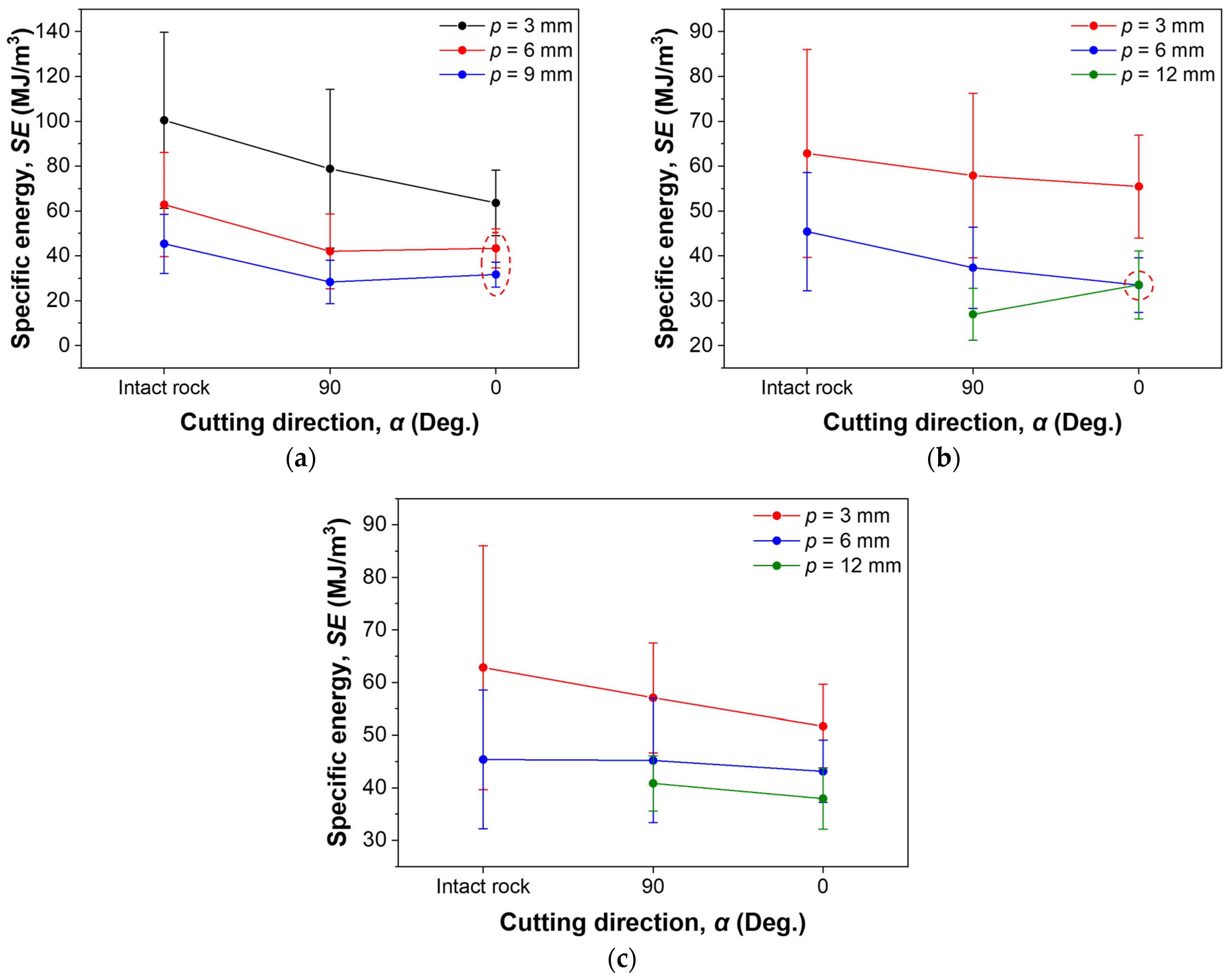
3.2. Effect of Cutting Direction and Joint Spacing on Cutting Performance
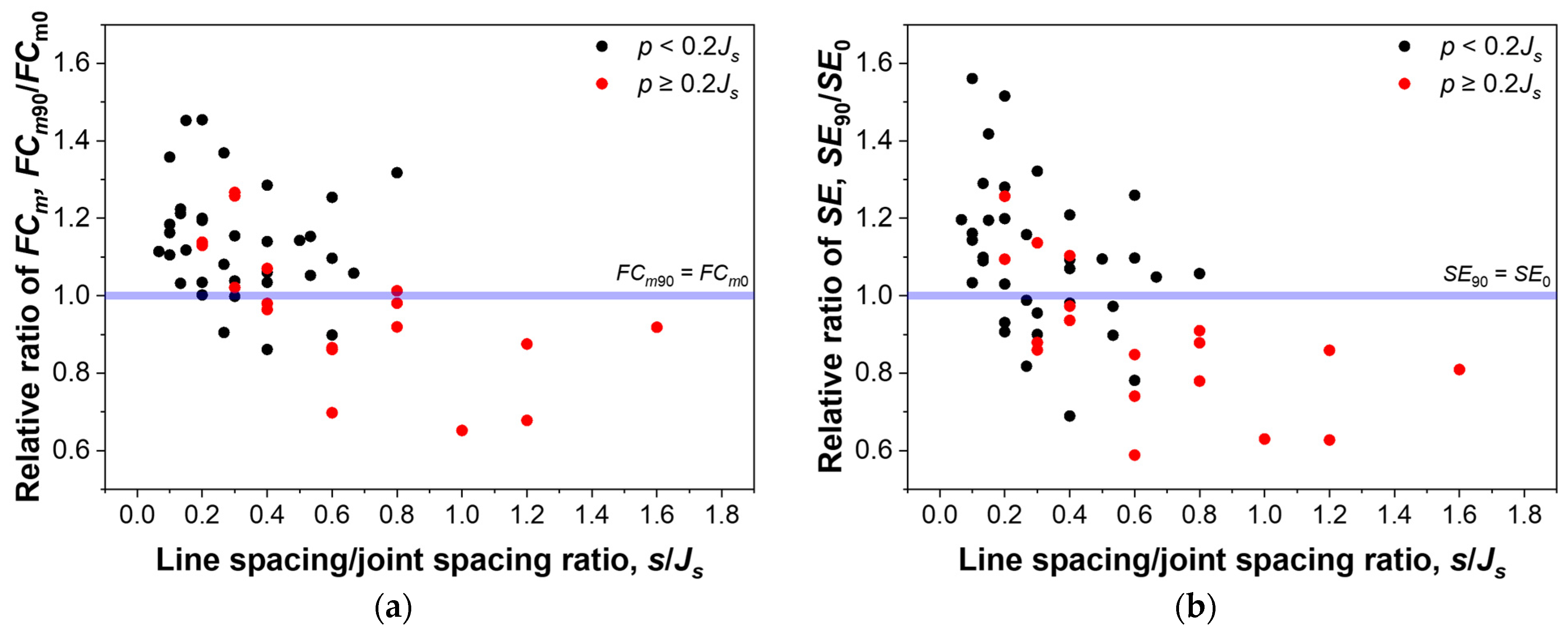
3.2.1. Effect of Cutting Direction
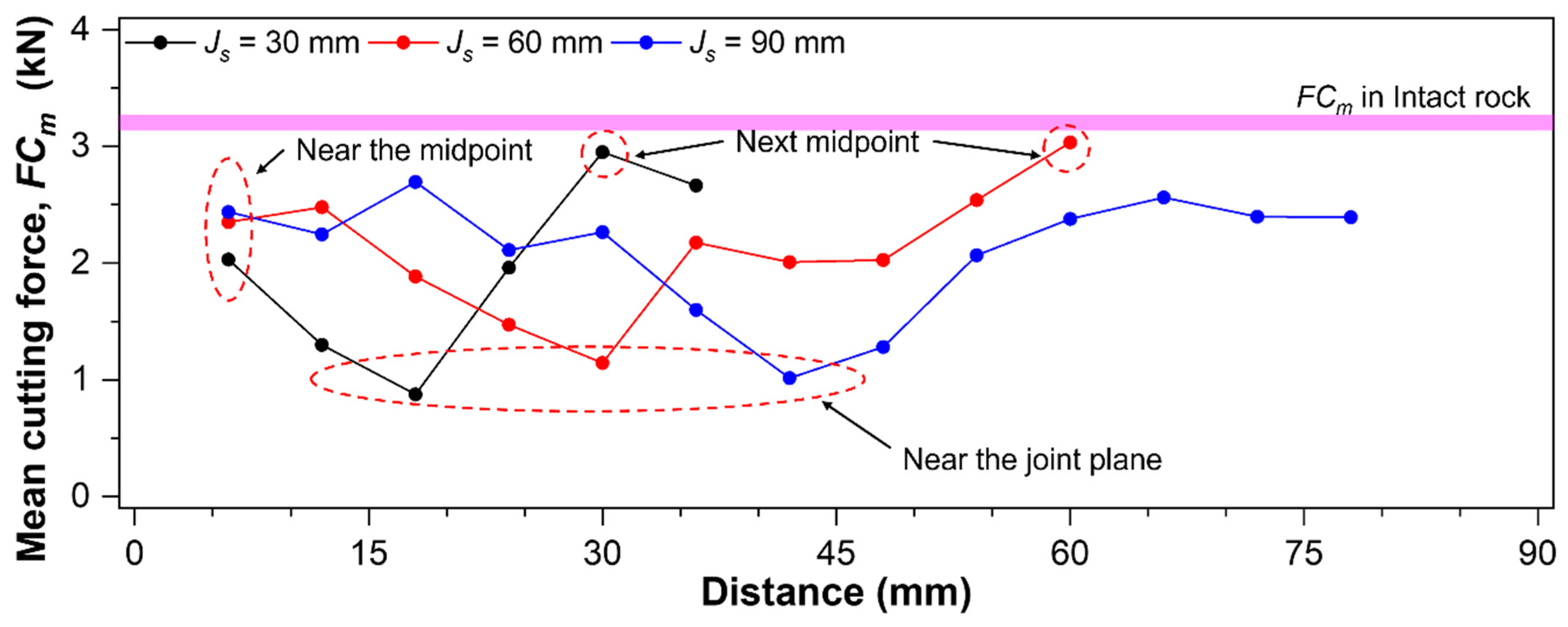
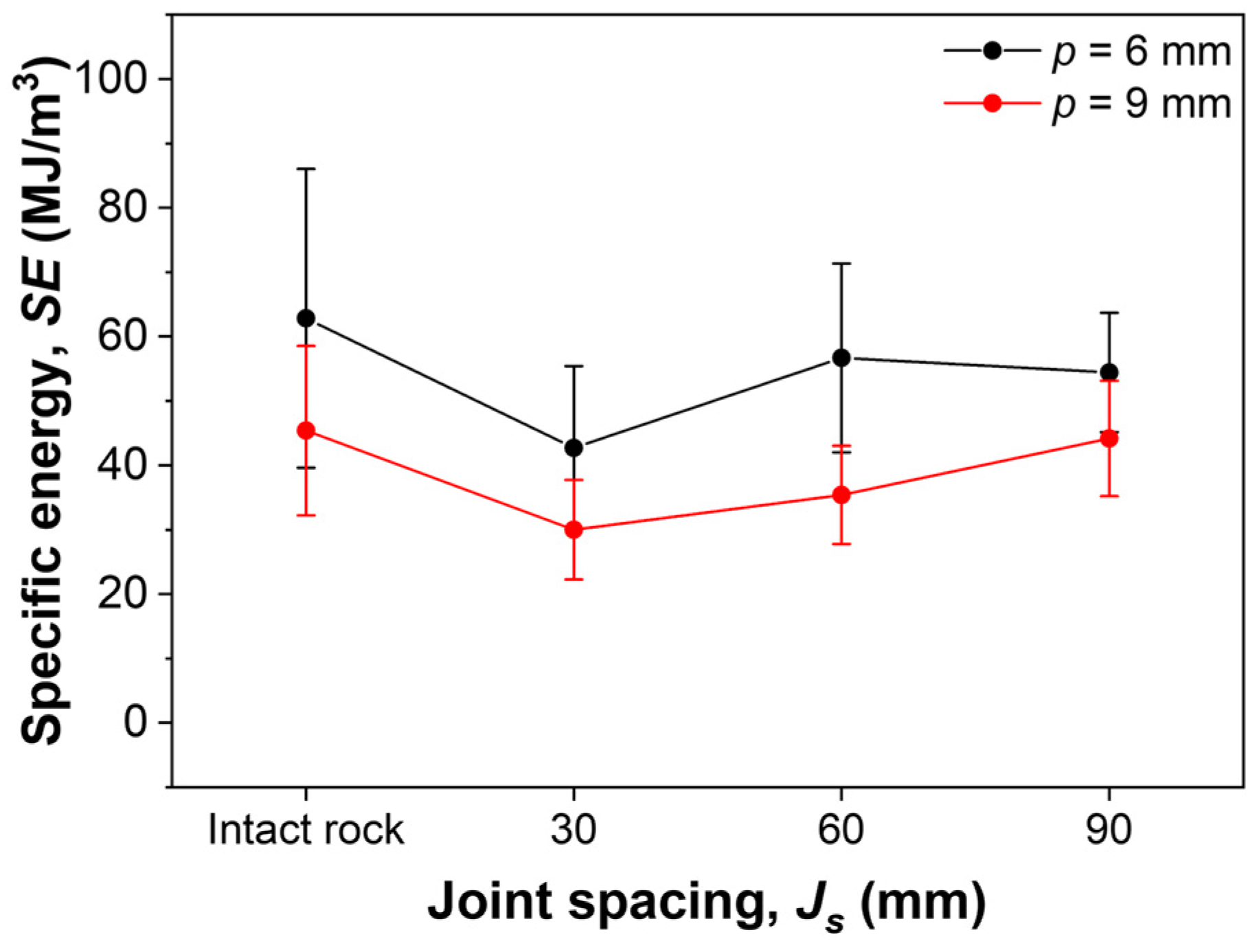
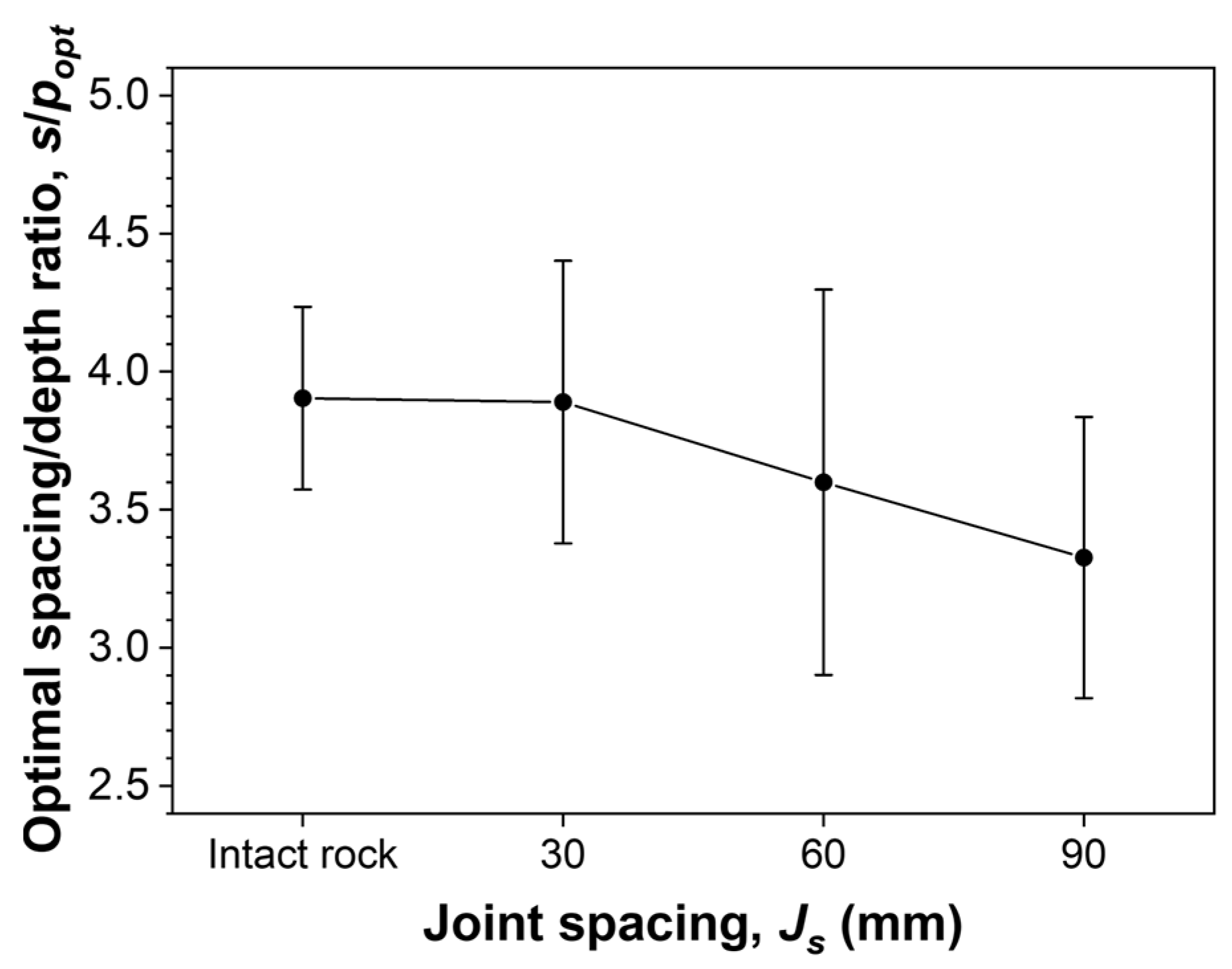
3.2.2. Effect of Joint Spacing
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sapigni, M.; Berti, M.; Bethaz, E.; Busillo, A.; Cardone, G. TBM performance estimation using rock mass classifications. Int. J. Rock Mech. Min. Sci. 2002, 39, 771–788. [Google Scholar] [CrossRef]
- Hassanpour, J.; Rostami, J.; Zhao, J. A new hard rock TBM performance prediction model for project planning. Tunn. Undergr. Space Technol. 2011, 26, 595–603. [Google Scholar] [CrossRef]
- Rasouli Maleki, M. Rock Joint Rate (RJR); a new method for performance prediction of tunnel boring machines (TBMs) in hard rocks. Tunn. Undergr. Space Technol. 2018, 73, 261–286. [Google Scholar] [CrossRef]
- Salimi, A.; Rostami, J.; Moormann, C. Application of rock mass classification systems for performance estimation of rock TBMs using regression tree and artificial intelligence algorithms. Tunn. Undergr. Space Technol. 2019, 92, 103046. [Google Scholar] [CrossRef]
- Farrokh, E. A study of various models used in the estimation of advance rates for hard rock TBMs. Tunn. Undergr. Space Technol. 2020, 97, 103219. [Google Scholar] [CrossRef]
- Xu, H.; Gong, Q.; Lu, J.; Yin, L.; Yang, F. Setting up simple estimating equations of TBM penetration rate using rock mass classification parameters. Tunn. Undergr. Space Technol. 2021, 115, 104065. [Google Scholar] [CrossRef]
- Bilgin, N.; Seyrek, T.; Erding, E.; Shahriar, K. Roadheaders glean valuable tips for Istanbul Metro. Tunn. Tunn. Int. 1990, 22, 29–32. [Google Scholar]
- Ebrahimabadi, A.; Goshtasbi, K.; Shahriar, K.; Cheraghi Seifabad, M. A model to predict the performance of roadheaders based on the Rock Mass Brittleness Index. J. S. Afr. Inst. Min. Metall. 2011, 111, 355–364. [Google Scholar]
- Abdolreza, Y.C.; Siamak, H.Y. A new model to predict roadheader performance using rock mass properties. J. Coal Sci. Eng. 2013, 19, 51–56. [Google Scholar] [CrossRef]
- Dibavar, B.; Kahraman, S.; Rostami, M.; Fener, M. A New Rock Mass Cuttability Classification for Roadheaders Used in Coal Mining. Min. Metall. Explor. 2023, 40, 1141–1152. [Google Scholar] [CrossRef]
- Gong, Q.M.; Zhao, J.; Jiao, Y.Y. Numerical modeling of the effects of joint orientation on rock fragmentation by TBM cutters. Tunn. Undergr. Space Technol. 2005, 20, 183–191. [Google Scholar] [CrossRef]
- Gong, Q.M.; Jiao, Y.Y.; Zhao, J. Numerical modelling of the effects of joint spacing on rock fragmentation by TBM cutters. Tunn. Undergr. Space Technol. 2006, 21, 46–55. [Google Scholar] [CrossRef]
- Bejari, H.; Khademi Hamidi, J. Simultaneous effects of joint spacing and orientation on TBM cutting efficiency in jointed rock masses. Rock Mech. Rock Eng. 2013, 46, 897–907. [Google Scholar] [CrossRef]
- Choi, S.O.; Lee, S.J. Numerical study to estimate the cutting power on a disc cutter in jointed rock mass. KSCE J. Civ. Eng. 2016, 20, 440–451. [Google Scholar] [CrossRef]
- Xue, Y.; Zhou, J.; Liu, C.; Shadabfar, M.; Zhang, J. Rock fragmentation induced by a TBM disc-cutter considering the effects of joints: A numerical simulation by DEM. Comput. Geotech. 2021, 136, 104230. [Google Scholar] [CrossRef]
- Afrasiabi, N.; Rafiee, R.; Noroozi, M. Investigating the effect of discontinuity geometrical parameters on the TBM performance in hard rock. Tunn. Undergr. Space Technol. 2019, 84, 326–333. [Google Scholar] [CrossRef]
- Yin, L.; Miao, C.; He, G.; Dai, F.; Gong, Q. Study on the influence of joint spacing on rock fragmentation under TBM cutter by linear cutting test. Tunn. Undergr. Space Technol. 2016, 57, 137–144. [Google Scholar] [CrossRef]
- Yang, H.Q.; Li, Z.; Jie, T.Q.; Zhang, Z.Q. Effects of joints on the cutting behavior of disc cutter running on the jointed rock mass. Tunn. Undergr. Space Technol. 2018, 81, 112–120. [Google Scholar] [CrossRef]
- Yang, H.; Liu, J.; Liu, B. Investigation on the Cracking Character of Jointed Rock Mass Beneath TBM Disc Cutter. Rock Mech. Rock Eng. 2018, 51, 1263–1277. [Google Scholar] [CrossRef]
- Liu, B.; Yang, H.; Haque, E.; Wang, G. Effect of Joint Orientation on the Breakage Behavior of Jointed Rock Mass Loaded by Disc Cutters. Rock Mech. Rock Eng. 2021, 54, 2087–2108. [Google Scholar] [CrossRef]
- Song, K.; Yang, H.; Xie, J.; Karekal, S. An Optimization Methodology of Cutter-Spacing for Efficient Mechanical Breaking of Jointed Rock Mass. Rock Mech. Rock Eng. 2022, 55, 3301–3316. [Google Scholar] [CrossRef]
- Liu, B.; Li, B.; Zhang, L.; Huang, R.; Gao, H.; Luo, S.; Wang, T. Disc-cutter induced rock breakage mechanism for TBM excavation in rock masses with different joint shear strengths. Undergr. Space 2024, 19, 119–137. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, W.; Lv, Y. The investigation of rock cutting simulation based on discrete element method. Geomech. Eng. 2017, 13, 977–995. [Google Scholar]
- Wang, M. Study conical pick cutting performance and fatigue life in breaking rock plate process with numerical simulation. Sci. Rep. 2024, 14, 857. [Google Scholar] [CrossRef]
- ASTM D7012-14; Standard Test Methods for Compressive Strength and Elastic Moduli of Intact Rock Core Specimens Under Varying States of Stress and Temperatures. ASTM International: West Conshohocken, PA, USA, 2014.
- ASTM D3967-08; Standard Test Method for Splitting Tensile Strength of Intact Rock Core Specimens with Flat Loading Platens. ASTM International: West Conshohocken, PA, USA, 2008.
- ASTM C97/C97M-15; Standard Test Methods for Absorption and Bulk Specific Gravity of Dimension Stone. ASTM International: West Conshohocken, PA, USA, 2015.
- Khosravi, M.; Ramezanzadeh, A.; Zare, S. Effect of Rock Joint on Boreability of TBM at Northern Section of Kerman Water Conveyance Tunnel. Int. J. Min. Geo-Eng. 2021, 55, 145–150. [Google Scholar]
- Howarth, D.F. The effect of jointed and fissured rock on the performance of tunnel boring machines. In Proceedings of the ISRM International Symposium, Tokyo, Japan, 21–24 September 1981. [Google Scholar]
- Sanio, H.P. Prediction of the performance of disc cutters in anisotropic rock. Int. J. Rock Mech. Min. Sci. 1985, 22, 153–161. [Google Scholar] [CrossRef]
- Wang, X.; Su, O.; Wang, Q.F.; Liang, Y.P. Effect of cutting depth and line spacing on the cuttability behavior of sandstones by conical picks. Arab. J. Geosci. 2017, 10, 525. [Google Scholar] [CrossRef]
- Yasar, S.; Yilmaz, A.O. Drag pick cutting tests: A comparison between experimental and theoretical results. J. Rock Mech. Geotech. Eng. 2018, 10, 893–906. [Google Scholar] [CrossRef]
- Evans, I. Theoretical aspects of coal ploughing. In Mechanical Properties of Non-Metallic Brittle Materials; Watton, W.H., Ed.; Butterworths: London, UK, 1958; pp. 451–468. [Google Scholar]
- Lin, Q.B.; Cao, P.; Li, K.H.; Cao, R.H.; Zhou, K.P.; Deng, H.W. Experimental study on acoustic emission characteristics of jointed rock mass by double disc cutter. J. Cent. South Univ. 2018, 25, 357–367. [Google Scholar] [CrossRef]
- Jiang, M.; Liao, Y.; Wang, H.; Sun, Y. Distinct element method analysis of jointed rock fragmentation induced by TBM cutting. Eur. J. Environ. Civ. Eng. 2018, 22, s79–s98. [Google Scholar] [CrossRef]
- Naghadehi, M.Z.; Mikaeil, R. Optimization of tunnel boring machine (TBM) disc cutter spacing in jointed hard rock using a distinct element numerical simulation. Period. Polytech. Civ. Eng. 2017, 61, 56–65. [Google Scholar] [CrossRef]







| Material | ρ (g/cm3) | E (GPa) | ν | σc (MPa) | σt (MPa) |
|---|---|---|---|---|---|
| Finike limestone | 2.22 | 21.1 | 0.13 | 49.0 | 5.00 |
| Concrete | 2.38 | 38.9 | 0.30 | 42.0 | 2.51 |
| Cement mortar | 2.11 | 8.7 | 0.20 | 6.0 | 0.90 |
| Specimen | Cutting Depth, p (mm) | Line Spacing, s (mm) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| I | J30 | 3 | 3 | 6 | 9 | 12 | 15 | 18 | ||
| I | J30 | J60 | J90 | 6 | 6 | 9 | 12 | 18 | 24 | 36 |
| I | J30 | J60 | J90 | 9 | 9 | 12 | 18 | 24 | 36 | 48 |
| J60 | J90 | 12 | 12 | 18 | 24 | 36 | 48 | 60 | ||
| p (mm) | s (mm) | s/p | FCm (kN) | FCp (kN) | SE (MJ/m3) | s/popt |
|---|---|---|---|---|---|---|
| 3 | 3 | 1 | 1.57 | 3.18 | 178.0 | 4.13 |
| 6 | 2 | 1.65 | 4.14 | 96.9 | ||
| 9 | 3 | 1.99 | 5.20 | 78.2 | ||
| 12 | 4 | 2.19 | 5.29 | 72.9 | ||
| 15 | 5 | 2.53 | 6.14 | 80.8 | ||
| 18 | 6 | 2.73 | 6.75 | 95.8 | ||
| 6 | 6 | 1 | 3.32 | 6.93 | 108.3 | 4.05 |
| 9 | 1.5 | 3.51 | 7.72 | 63.0 | ||
| 12 | 2 | 3.82 | 8.83 | 54.6 | ||
| 18 | 3 | 4.59 | 11.05 | 47.4 | ||
| 24 | 4 | 4.94 | 13.62 | 46.0 | ||
| 36 | 6 | 5.66 | 13.35 | 57.7 | ||
| 9 | 9 | 1 | 4.87 | 11.34 | 66.6 | 3.52 |
| 12 | 1.33 | 5.12 | 12.14 | 54.3 | ||
| 18 | 2 | 6.07 | 14.12 | 39.2 | ||
| 24 | 2.67 | 6.57 | 16.48 | 32.9 | ||
| 36 | 4 | 7.16 | 18.14 | 33.5 | ||
| 48 | 5.33 | 8.13 | 19.65 | 45.9 |
| α (Deg.) | p (mm) | s (mm) | s/p | s/Js | FCm (kN) | FCp (kN) | SE (MJ/m3) | s/popt |
|---|---|---|---|---|---|---|---|---|
| 0 | 3 | 3 | 1 | 0.1 | 0.76 | 1.86 | 93.1 | 4.33 |
| 6 | 2 | 0.2 | 1.02 | 2.66 | 54.3 | |||
| 9 | 3 | 0.3 | 1.33 | 3.61 | 55.7 | |||
| 12 | 4 | 0.4 | 1.62 | 4.16 | 59.1 | |||
| 15 | 5 | 0.5 | 2.00 | 5.24 | 57.9 | |||
| 18 | 6 | 0.6 | 1.91 | 4.66 | 61.4 | |||
| 6 | 6 | 1 | 0.2 | 2.09 | 5.16 | 60.1 | 4.23 | |
| 9 | 1.5 | 0.3 | 2.15 | 5.85 | 44.6 | |||
| 12 | 2 | 0.4 | 2.78 | 6.84 | 41.3 | |||
| 18 | 3 | 0.6 | 3.21 | 8.21 | 35.9 | |||
| 24 | 4 | 0.8 | 3.44 | 9.08 | 38.8 | |||
| 36 | 6 | 1.2 | 3.83 | 9.92 | 39.6 | |||
| 9 | 9 | 1 | 0.3 | 2.56 | 7.51 | 39.1 | 3.45 | |
| 12 | 1.33 | 0.4 | 3.06 | 9.34 | 28.9 | |||
| 18 | 2 | 0.6 | 4.07 | 10.23 | 29.2 | |||
| 24 | 2.67 | 0.8 | 4.36 | 11.30 | 26.8 | |||
| 36 | 4 | 1.2 | 5.90 | 15.28 | 27.6 | |||
| 48 | 5.33 | 1.6 | 5.67 | 15.43 | 38.4 | |||
| 90 | 3 | 3 | 1 | 0.1 | 1.03 | 3.01 | 145.2 | 4.07 |
| 6 | 2 | 0.2 | 1.49 | 3.83 | 82.3 | |||
| 9 | 3 | 0.3 | 1.38 | 3.96 | 73.6 | |||
| 12 | 4 | 0.4 | 1.39 | 4.91 | 40.8 | |||
| 15 | 5 | 0.5 | 2.28 | 6.14 | 63.4 | |||
| 18 | 6 | 0.6 | 2.10 | 6.19 | 67.4 | |||
| 6 | 6 | 1 | 0.2 | 2.36 | 7.82 | 75.5 | 4.18 | |
| 9 | 1.5 | 0.3 | 2.20 | 7.46 | 38.4 | |||
| 12 | 2 | 0.4 | 2.68 | 7.43 | 38.7 | |||
| 18 | 3 | 0.6 | 2.78 | 7.54 | 30.4 | |||
| 24 | 4 | 0.8 | 3.37 | 8.68 | 35.3 | |||
| 36 | 6 | 1.2 | 3.36 | 10.57 | 34.0 | |||
| 9 | 9 | 1 | 0.3 | 3.22 | 9.23 | 44.5 | 3.07 | |
| 12 | 1.33 | 0.4 | 3.00 | 8.97 | 31.9 | |||
| 18 | 2 | 0.6 | 3.50 | 10.88 | 21.6 | |||
| 24 | 2.67 | 0.8 | 4.41 | 12.18 | 23.5 | |||
| 36 | 4 | 1.2 | 4.00 | 15.02 | 17.3 | |||
| 48 | 5.33 | 1.6 | 5.21 | 15.76 | 31.1 |
| α (Deg.) | p (mm) | s (mm) | s/p | s/Js | FCm (kN) | FCp (kN) | SE (MJ/m3) | s/popt |
|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 6 | 1 | 0.1 | 2.39 | 6.33 | 73.5 | 4.54 |
| 9 | 1.5 | 0.15 | 3.01 | 7.75 | 64.4 | |||
| 12 | 2 | 0.2 | 3.12 | 7.82 | 46.8 | |||
| 18 | 3 | 0.3 | 4.26 | 10.70 | 45.6 | |||
| 24 | 4 | 0.4 | 4.84 | 12.63 | 46.2 | |||
| 36 | 6 | 0.6 | 6.03 | 14.47 | 56.2 | |||
| 9 | 9 | 1 | 0.15 | 2.71 | 9.06 | 38.2 | 3.66 | |
| 12 | 1.33 | 0.2 | 4.14 | 11.38 | 43.3 | |||
| 18 | 2 | 0.3 | 4.08 | 12.20 | 31.1 | |||
| 24 | 2.67 | 0.4 | 4.81 | 15.74 | 28.4 | |||
| 36 | 4 | 0.6 | 5.94 | 16.56 | 28.0 | |||
| 48 | 5.33 | 0.8 | 6.27 | 15.23 | 31.7 | |||
| 12 | 12 | 1 | 0.2 | 4.49 | 13.96 | 33.4 | 3.31 | |
| 18 | 1.5 | 0.3 | 4.84 | 14.93 | 30.7 | |||
| 24 | 2 | 0.4 | 6.32 | 17.23 | 27.4 | |||
| 36 | 3 | 0.6 | 10.04 | 20.47 | 37.8 | |||
| 48 | 4 | 0.8 | 8.08 | 19.65 | 25.7 | |||
| 60 | 5 | 1 | 13.77 | 24.39 | 46.3 | |||
| 90 | 6 | 6 | 1 | 0.1 | 2.77 | 7.27 | 84.0 | 3.90 |
| 9 | 1.5 | 0.15 | 3.36 | 8.51 | 77.0 | |||
| 12 | 2 | 0.2 | 3.72 | 9.45 | 56.2 | |||
| 18 | 3 | 0.3 | 4.25 | 10.99 | 41.0 | |||
| 24 | 4 | 0.4 | 5.01 | 12.39 | 45.4 | |||
| 36 | 6 | 0.6 | 5.42 | 13.07 | 43.9 | |||
| 9 | 9 | 1 | 0.15 | 3.94 | 10.41 | 54.2 | 3.75 | |
| 12 | 1.33 | 0.2 | 4.15 | 11.18 | 40.3 | |||
| 18 | 2 | 0.3 | 4.71 | 14.38 | 29.8 | |||
| 24 | 2.67 | 0.4 | 6.18 | 17.01 | 31.0 | |||
| 36 | 4 | 0.6 | 7.45 | 17.50 | 35.3 | |||
| 48 | 5.33 | 0.8 | 8.27 | 21.55 | 33.5 | |||
| 12 | 12 | 1 | 0.2 | 5.11 | 14.66 | 36.5 | 2.44 | |
| 18 | 1.5 | 0.3 | 6.13 | 18.55 | 27.0 | |||
| 24 | 2 | 0.4 | 6.76 | 19.85 | 26.6 | |||
| 36 | 3 | 0.6 | 7.01 | 21.79 | 22.3 | |||
| 48 | 4 | 0.8 | 7.43 | 20.59 | 20.1 | |||
| 60 | 5 | 1 | 8.98 | 23.60 | 29.1 |
| α (Deg.) | p (mm) | s (mm) | s/p | s/Js | FCm (kN) | FCp (kN) | SE (MJ/m3) | s/popt |
|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 6 | 1 | 0.07 | 2.07 | 5.87 | 63.4 | 3.88 |
| 9 | 1.5 | 0.1 | 2.64 | 6.81 | 58.7 | |||
| 12 | 2 | 0.13 | 2.83 | 7.38 | 43.8 | |||
| 18 | 3 | 0.2 | 3.97 | 9.53 | 47.6 | |||
| 24 | 4 | 0.27 | 4.10 | 10.55 | 44.8 | |||
| 36 | 6 | 0.4 | 5.90 | 12.69 | 52.0 | |||
| 9 | 9 | 1 | 0.1 | 3.73 | 10.12 | 52.2 | 3.38 | |
| 12 | 1.33 | 0.13 | 4.53 | 12.03 | 42.8 | |||
| 18 | 2 | 0.2 | 4.91 | 12.79 | 37.9 | |||
| 24 | 2.67 | 0.27 | 5.90 | 15.85 | 36.3 | |||
| 36 | 4 | 0.4 | 8.38 | 16.22 | 42.3 | |||
| 48 | 5.33 | 0.53 | 6.85 | 16.10 | 47.3 | |||
| 12 | 12 | 1 | 0.13 | 5.60 | 14.49 | 43.7 | 2.99 | |
| 18 | 1.5 | 0.2 | 5.69 | 16.05 | 31.9 | |||
| 24 | 2 | 0.27 | 7.75 | 18.39 | 34.0 | |||
| 36 | 3 | 0.4 | 9.15 | 20.72 | 32.2 | |||
| 48 | 4 | 0.53 | 10.61 | 28.98 | 42.4 | |||
| 60 | 5 | 0.67 | 12.52 | 25.46 | 43.5 | |||
| 90 | 6 | 6 | 1 | 0.07 | 2.31 | 6.52 | 75.9 | 3.92 |
| 9 | 1.5 | 0.1 | 2.92 | 6.47 | 60.7 | |||
| 12 | 2 | 0.13 | 3.43 | 7.91 | 47.8 | |||
| 18 | 3 | 0.2 | 4.50 | 11.61 | 49.0 | |||
| 24 | 4 | 0.27 | 5.62 | 12.62 | 51.9 | |||
| 36 | 6 | 0.4 | 6.32 | 12.47 | 57.4 | |||
| 9 | 9 | 1 | 0.1 | 4.42 | 10.49 | 60.6 | 3.16 | |
| 12 | 1.33 | 0.13 | 5.55 | 11.63 | 55.2 | |||
| 18 | 2 | 0.2 | 5.08 | 13.79 | 34.3 | |||
| 24 | 2.67 | 0.27 | 5.34 | 14.62 | 29.7 | |||
| 36 | 4 | 0.4 | 8.89 | 17.98 | 45.3 | |||
| 48 | 5.33 | 0.53 | 7.90 | 16.13 | 46.0 | |||
| 12 | 12 | 1 | 0.13 | 5.78 | 17.72 | 48.1 | 2.62 | |
| 18 | 1.5 | 0.2 | 6.83 | 21.01 | 40.9 | |||
| 24 | 2 | 0.27 | 8.37 | 22.46 | 33.6 | |||
| 36 | 3 | 0.4 | 10.43 | 22.91 | 38.9 | |||
| 48 | 4 | 0.53 | 11.16 | 25.80 | 38.1 | |||
| 60 | 5 | 0.67 | 13.25 | 24.75 | 45.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.-E.; Kim, M.-S.; Yoo, W.-K.; Kim, C.-Y. Experimental Investigation on the Effects of Cutting Direction and Joint Spacing on the Cuttability Behaviour of a Conical Pick in Jointed Rock Mass. Appl. Sci. 2025, 15, 4347. https://doi.org/10.3390/app15084347
Kim H-E, Kim M-S, Yoo W-K, Kim C-Y. Experimental Investigation on the Effects of Cutting Direction and Joint Spacing on the Cuttability Behaviour of a Conical Pick in Jointed Rock Mass. Applied Sciences. 2025; 15(8):4347. https://doi.org/10.3390/app15084347
Chicago/Turabian StyleKim, Han-Eol, Min-Seong Kim, Wan-Kyu Yoo, and Chang-Yong Kim. 2025. "Experimental Investigation on the Effects of Cutting Direction and Joint Spacing on the Cuttability Behaviour of a Conical Pick in Jointed Rock Mass" Applied Sciences 15, no. 8: 4347. https://doi.org/10.3390/app15084347
APA StyleKim, H.-E., Kim, M.-S., Yoo, W.-K., & Kim, C.-Y. (2025). Experimental Investigation on the Effects of Cutting Direction and Joint Spacing on the Cuttability Behaviour of a Conical Pick in Jointed Rock Mass. Applied Sciences, 15(8), 4347. https://doi.org/10.3390/app15084347






