Tensile Properties of Granite Under Cyclic Thermal Shock and Loading

Abstract

This study investigates the tensile properties of granite subjected to cyclic thermal treatment under cyclic loading-unloading conditions, which is of great significance for the modification of hot dry rock reservoirs. Brazilian splitting tests under cyclic loading-unloading were conducted on granite samples exposed to 400 °C cyclic water-cooling shock (applied for 1, 3, 5, and 7 cycles) at different preset load upper limits (65%, 70%, 75%, and 80% of the peak load). The experimental results reveal the evolution of the tensile properties of granite under the combined effects of 400 °C cyclic water-cooling shock and cyclic loading-unloading. The findings indicate that the tensile strength of granite decreases with an increasing number of cyclic water-cooling shocks and further declines as the preset load upper limit decreases. Under typical conditions, the peak displacement of granite exhibits three distinct stages with increasing loading-unloading cycles: rapid increase, slow increase, and eventual failure. During the slow increase stage, peak displacement decreases due to an increase in elastic stiffness. Initially, elastic stiffness increases with the number of cycles, followed by a stabilization phase, and subsequently declines. After granite failure, macroscopic failure cracks gradually deviate from the center as additional cyclic water-cooling shocks are applied. In contrast, cyclic loading-unloading has a minimal effect on macroscopic cracks. Furthermore, as the number of cycles increases, microcrack evolution transitions from intergranular to transgranular cracking. Under cyclic loading-unloading conditions, these cracks continue to propagate, ultimately forming a fracture network. The findings of this study provide a theoretical foundation for the fracturing and modification of hot dry rock reservoirs.

1. Introduction

Hot dry rock (HDR) is a clean and renewable energy source with temperatures ranging from 150 °C to 650 °C. It is widely distributed across the globe and has abundant reserves, gradually emerging as a promising alternative to traditional fossil fuels [1,2]. Enhanced geothermal systems (EGS) are the primary technological approach for exploiting hot dry rock. This process involves hydraulic fracturing to modify the geothermal reservoir, followed by the injection of heat transfer fluid to exchange heat with the rock. The heated fluid is then pumped to the surface for thermal energy extraction [3]. However, during cyclic injection and production processes, the thermal shock induced by the heat transfer fluid interacting with the geothermal reservoir tends to weaken the tensile strength of the rock, and may even trigger seismic events, leading to geological hazards and public concern [4,5]. Moreover, at 400 °C, the mechanical properties of hot dry rock deteriorate significantly, with a marked reduction in tensile strength [6]. In enhanced geothermal systems (EGS), the reservoir rocks are subjected to repeated heating and cooling cycles, coupled with cyclic mechanical loading, which induces substantial changes in their physical and mechanical properties, severely affecting the stability of underground engineering structures [7,8,9]. Therefore, investigating the tensile behavior of granite under the combined effects of cyclic water-cooling shock at 400 °C and cyclic loading and unloading is of great significance for hydraulic fracturing and stability assessment of hot dry rock geothermal reservoirs.

In the process of geothermal reservoir reconstruction, extensive rock damage is predominantly initiated by tensile failure in specific localized regions [10]. A substantial number of experimental studies have been conducted both domestically and internationally to investigate the effects of high temperatures on the tensile mechanical properties and physical characteristics of rocks. Zhang et al. [11] found that the deterioration of the tensile mechanical properties of granite after 400 °C cyclic water-cooling shock is attributable to the non-uniform expansion of mineral grains. Ref. [12] conducted Brazilian splitting tests on granite after 300 °C cyclic water-cooling shock and observed a gradual decrease in tensile strength with increasing numbers of water-cooling shocks, accompanied by a continuous reduction in the tensile modulus. Zhu et al. [13] performed physical property tests and Brazilian splitting tests on granite subjected to 1 and 30 cycles of 500 °C water-cooling shock. Their results indicated that as the number of cooling shocks increases, the tensile strength of granite decreases, while its volume expands, mass decreases, and density is reduced. Furthermore, Zhu et al. [14,15] conducted uniaxial compression tests and Brazilian splitting tests on granite subjected to cyclic water-cooling shock within the temperature range of 250 °C to 650 °C. They reported that an increasing number of water-cooling shock cycles has a more pronounced effect on acoustic emission counts during uniaxial compression tests and significantly influences the extent of cracking in Brazilian splitting tests. In a separate study, Xu et al. [16] observed that after 650 °C cyclic water-cooling shock, both the tensile strength and longitudinal wave velocity of granite decrease with an increasing number of shocks. In a comparative analysis of water-cooling shock and furnace natural cooling on the tensile mechanical properties of granite, Kahraman [17,18] found that water-cooling shock leads to more severe deterioration of mechanical properties and induces a greater number of microcracks. Zhou et al. [19] conducted Brazilian splitting tests on granite after water-cooling shock and liquid nitrogen cooling and found that when the temperature is below 200 °C, water-cooling shock causes greater damage to the granite, whereas above 200 °C, granite cooled with liquid nitrogen exhibits lower tensile strength.

In addition, considering that rocks in rock mass engineering are frequently subjected to cyclic loading, numerous studies have been conducted both domestically and internationally to address this issue. Erarslan et al. [20,21] performed Brazilian splitting tests on tuff under cyclic loading-unloading and found that rock failure initiates at the contact points between strong grains and a weak matrix. They also observed that when the preset load upper limit is below 65%, the rock is less prone to failure. Fan et al. [22] employed CT techniques to investigate the effects of cyclic loading-unloading on the pore structure of granite and observed that the increase in porosity is primarily concentrated within the first 20 loading cycles. Similarly, Lv et al. [23] conducted three-point bending tests on granite under cyclic loading-unloading at real-time high temperatures. Their results indicated that as the temperature increases, the fatigue failure threshold of granite gradually decreases. Ning et al. [24] conducted triaxial cyclic loading-unloading tests on granite under hydro-mechanical coupling and found that higher confining pressure results in reduced fatigue damage from cyclic loading-unloading while also exhibiting a compaction effect. Likewise, Ding et al. [25] performed triaxial cyclic loading-unloading tests on granite and reported that as the confining pressure and stress upper limit increase, the elastic modulus of granite increases while the damping ratio decreases. Zhao et al. [26] conducted uniaxial cyclic loading-unloading tests on granite at real-time high temperatures. Their findings indicated that at temperatures above 200 °C, both the elastic strain energy density and input energy density increase with rising temperature. The energy accumulation was predominantly observed during the loading phase.

In summary, with regard to the safety issues encountered during the fracturing and cyclic injection-production processes of hot dry rock reservoirs, the specific process is shown in Figure 1. Existing research mainly focuses on the impact of high temperatures on the physical and mechanical properties of rocks or solely considers the effects of cyclic loading and unloading. However, there is still a lack of systematic research on the evolution of rock tensile behavior under the combined effects of high temperatures and cyclic loading and unloading. To address this knowledge gap, the present study utilized Brazilian splitting tests on granite subjected to cyclic water-cooling shock at 400 °C (for 1, 3, 5, and 7 cycles) under varying preset load upper limits (65%, 70%, 75%, and 80% of the peak load). Furthermore, scanning electron microscope (SEM) analysis was performed to investigate the effects of the combined action of cyclic water-cooling shock and cyclic loading and unloading on the tensile properties of granite. The findings of this study provide a theoretical basis for the hydraulic fracturing modification of hot dry rock reservoirs.

2. Experimental Equipment and Scheme

2.1. Specimen Preparation

The granite specimens used in this study were collected from Nan an, Fujian Province. The granite has a density of 2.6 g/cm³, a porosity of 0.87%, and a longitudinal wave velocity of 5952 m/s. According to the recommended standard of the International Society for Rock Mechanics (ISRM) [27], the granite was processed into Brazilian discs with dimensions of ϕ50 mm × 25 mm, with an error of less than 0.2 mm (Figure 2). X-ray diffraction (XRD) analysis reveals that the mineral composition of the granite is primarily 6.94% muscovite, 24.21% quartz, 33.87% plagioclase, 32.42% sodium feldspar, and 2.57% other components. Furthermore, thin sections of the granite specimens were examined under a polarizing microscope (Figure 3), which shows that mica is mainly distributed between feldspar and quartz and that numerous primary microcracks exist within the mineral grains. The grain size ranges of quartz, feldspar, and mica in the granite are approximately 0.066–0.715 mm, 0.045–0.964 mm, and 0.052–0.437 mm, respectively. To ensure the reliability of the experimental results and the consistency of the sample composition, all samples in the experiment were taken from the same original rock.

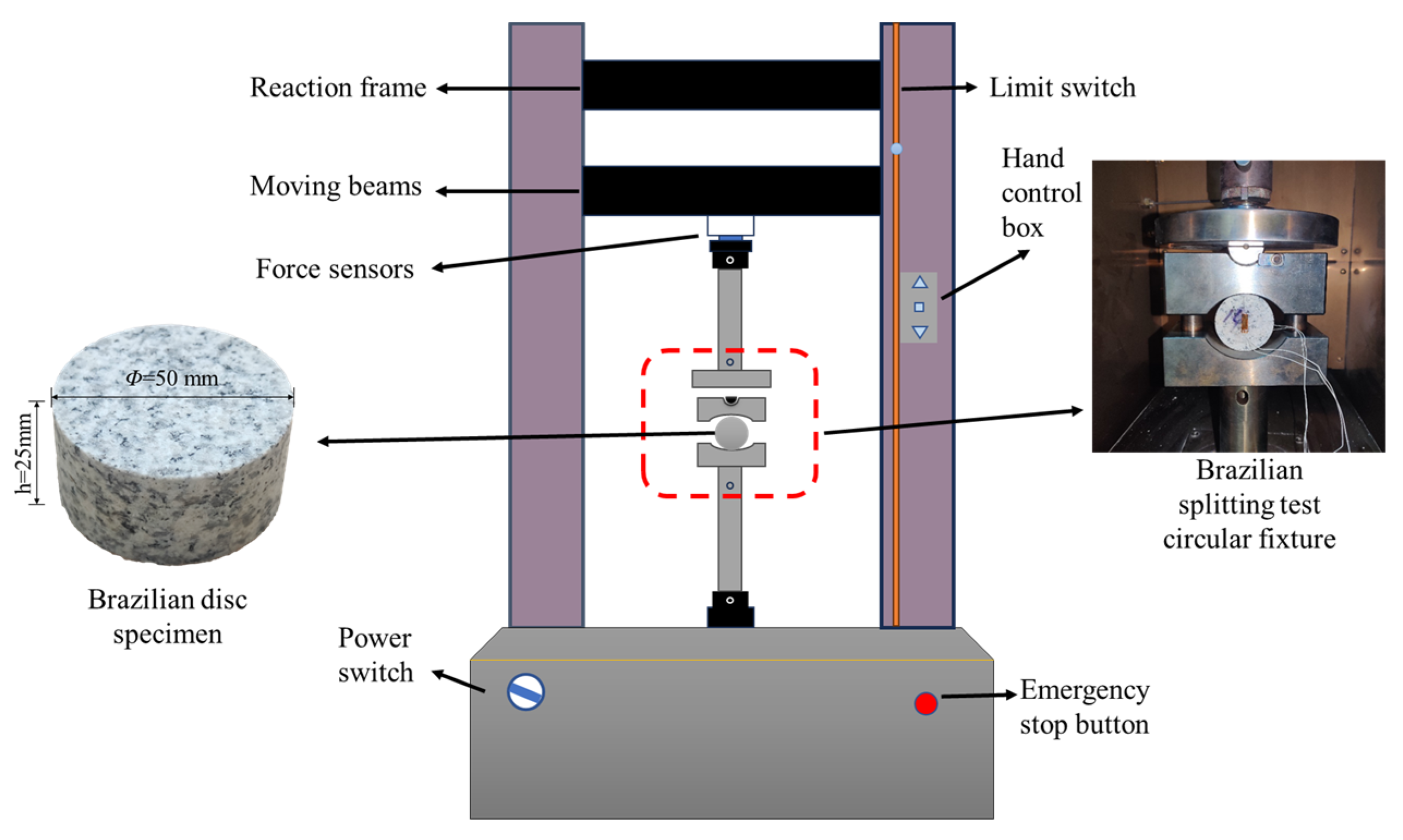
2.2. Experimental Equipment

In this experiment, an electronic universal testing machine (Figure 4) was used to perform Brazilian splitting tests on granite specimens subjected to high-temperature thermal treatment. The apparatus mainly consists of a reaction frame, a movable crossbeam, a force-displacement data acquisition system, a manual controller, and Brazilian splitting fixtures [23]. The equipment has a maximum loading capacity of 300 kN, and its force sensing system employs a Transcell load sensor with a measurement accuracy of 0.04% FS, capable of collecting load and deformation displacement data at a frequency of 30 Hz during the test. The use of curved fixtures in the Brazilian splitting test prevents displacement of the granite specimens during the experiment and minimizes the influence of stress concentration on the test results [6].

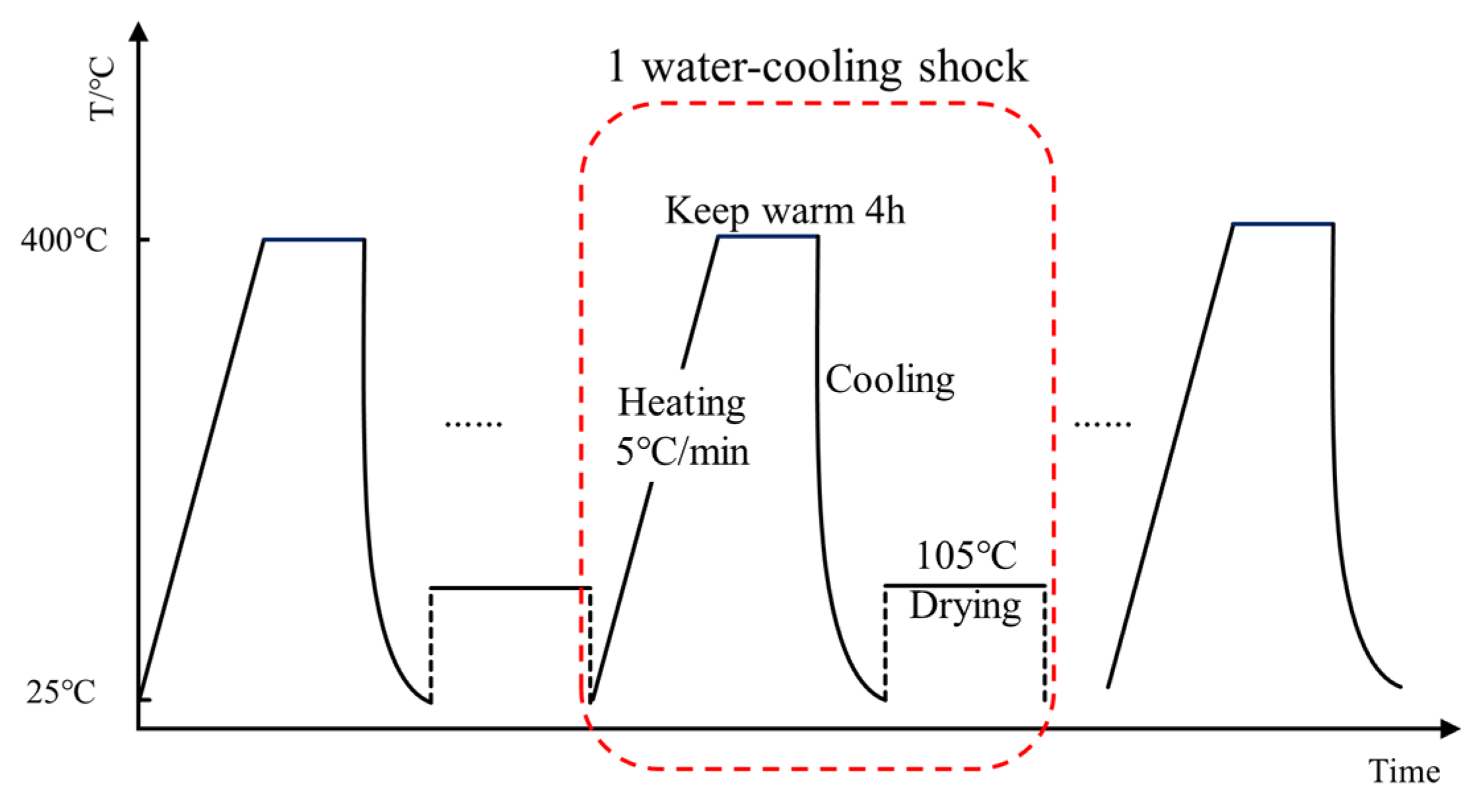
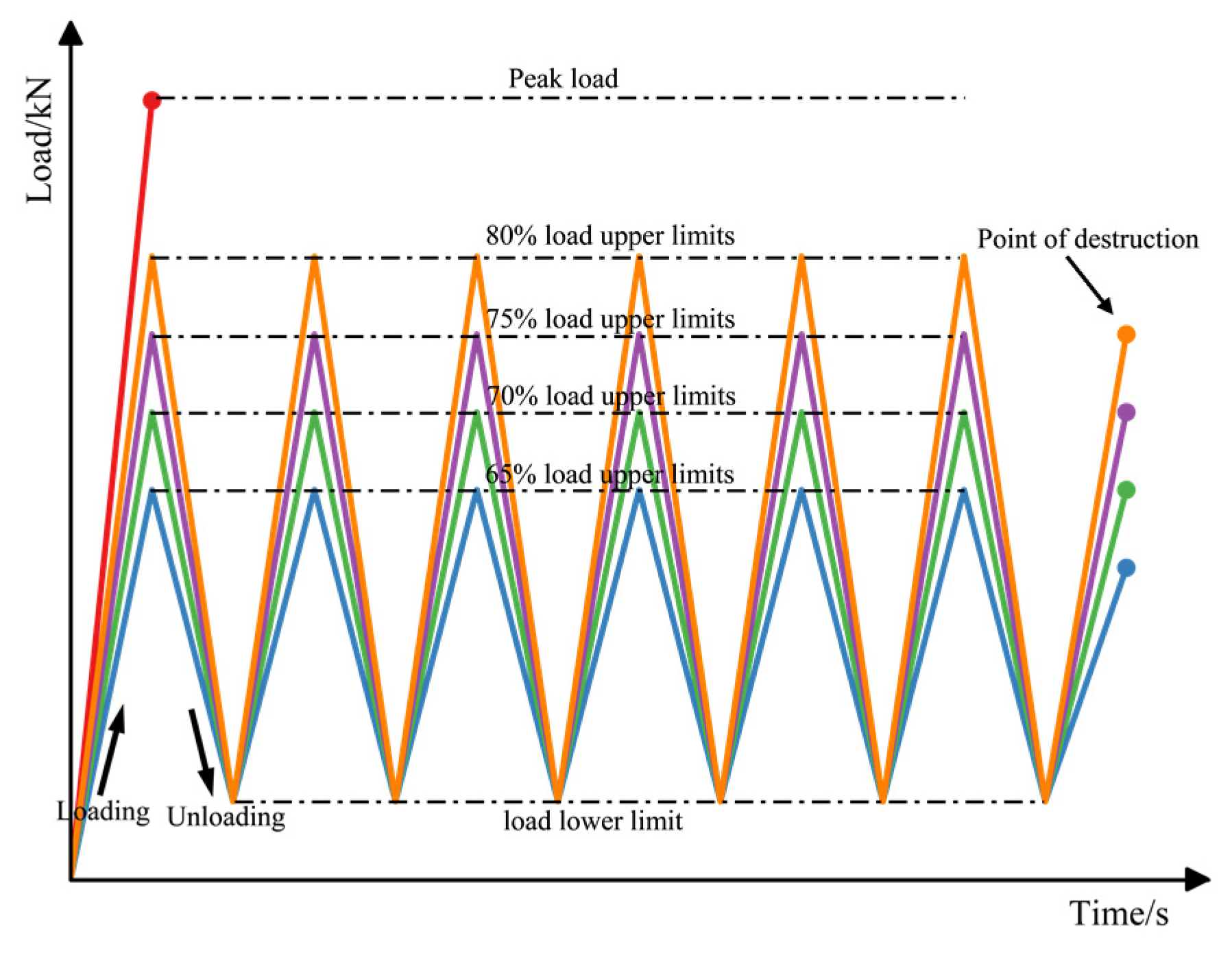
2.3. Experimental Steps

Heat Treatment Stage: The prepared specimens were placed in a muffle furnace and heated to 400 °C at a heating rate of 5 °C/min [14,28,29], then held at this temperature for 4 h to ensure uniform heating of the granite specimens. After heating, the specimens were transferred to a constant-temperature bath for cooling and soaking for 1 h. Once cooled, any excess moisture on the granite surfaces was wiped off, and the specimens were placed in a constant-temperature drying oven at 105 °C for 24 h. This entire process is considered one cycle of water-cooling shock. Granite specimens were subjected to 1, 3, 5, and 7 cycles of water-cooling shock, respectively, with a schematic diagram of the 400 °C cyclic water-cooling shock illustrated in Figure 5. Finally, the heat-treated granite specimens were stored in sealed bags for subsequent experiments.

Cyclic water-cooling shock has certain effects on the mass, volume, density, and longitudinal wave velocity of granite. For quantitative analysis, the granite mass loss rate, volume expansion rate, density attenuation rate, and longitudinal wave velocity reduction rate were used to describe the variation characteristics of the corresponding physical parameters. The calculation formulas [30] are as follows:

$$\omega ={\displaystyle \frac{\delta \left(T\right)-{\delta }_0}{{\delta }_0}}$$

(1)

where $\omega$ denotes the variation rate of each physical parameter, ${\mathsf{\delta }}_0$ represents the value of the corresponding physical parameter in the natural state of the granite, and $\delta \left(T\right)$ represents the value of the physical parameter after cyclic water-cooling shock.

Brazilian Splitting Test: In order to establish appropriate parameters for the cyclic loading-unloading Brazilian splitting tests, conventional Brazilian splitting tests were first conducted in order to measure the peak load of granite specimens subjected to water-cooling shock at different temperatures, as shown in Figure 6. It was established that when rocks undergo fatigue failure under cyclic loading-unloading conditions, a threshold exists for the preset load upper limit [23,31]. Consequently, the present study selected 65%, 70%, 75%, and 80% of the peak load as the preset load upper limits for cyclic loading-unloading, with the target number of cycles set at 500 for all tests. To ensure effective contact between the specimen and the test fixtures, 0.3 kN was selected as the load lower limit. The cyclic loading-unloading path for the Brazilian splitting test is illustrated in Figure 7, and the tests were conducted under displacement-controlled loading at a rate of 0.5 mm/min. To ensure the accuracy and reliability of the test results, three parallel tests were performed for each condition, and the mean value was calculated.

The Brazilian splitting method is the standard recommended by the International Society for Rock Mechanics for determining the tensile strength of rocks. The tensile strength (σₜ) is calculated using the following formula [32]:

$${\mathit{\sigma }}_t={\displaystyle \frac{2P}{\pi \mathit{DL}}}$$

(2)

where σₜ is the tensile strength of the rock (MPa), L is the thickness of the specimen (mm), D is the diameter of the specimen (mm), and P is the failure load of the specimen (kN).

3. Test Results and Analysis

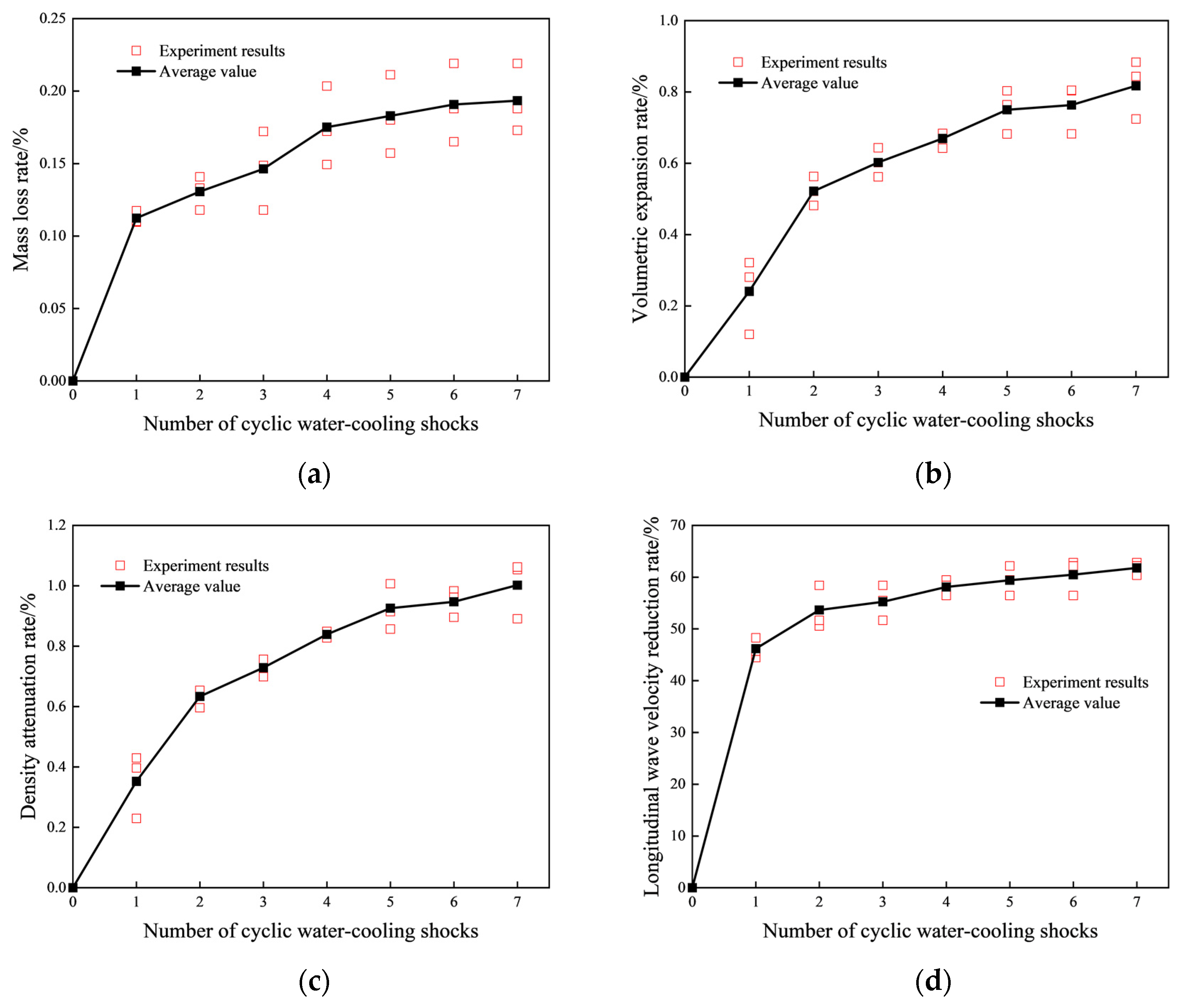
3.1. Physical Parameter Variations

Based on the calculations using Equation (1), the mass loss rate, volume expansion rate, density attenuation rate, and P-wave velocity reduction rate of granite after water-cooling shock at 400 °C were determined. Figure 8 shows the curve of the physical parameters of granite as a function of the number of cyclic water-cooling shocks. Under the 400 °C cyclic water-cooling shock condition, with an increasing number of quenching cycles, the mass loss rate, volumetric expansion rate, density attenuation rate, and longitudinal wave velocity reduction rate of granite gradually increase. For comparison, the natural state (25 °C) is taken as zero quenching cycles. After one quenching cycle, compared with the natural state, significant changes occur in the mass loss rate, volumetric expansion rate, density attenuation rate, and longitudinal wave velocity reduction rate of granite, although the magnitude of these changes gradually diminishes under subsequent cyclic water-cooling shocks. The mass loss rate of granite reaches 0.11% after one quenching cycle, with water loss remaining the primary reason for the reduction in mass. As internal moisture gradually evaporates, the impact of cyclic quenching on mass progressively diminishes [14]. The volumetric expansion rate of granite is mainly concentrated in the first two quenching cycles, increasing by 0.24% and 0.52%, respectively, and reaching 0.82% after the seventh quenching cycle. This is attributed to the fact that, with an increasing number of quenching cycles, thermal stresses cause the interactions among mineral grains within granite to gradually decrease, thereby reducing their influence on volumetric expansion [33]. The density attenuation rate is primarily caused by the combined effects of mass loss and volume expansion. After the first water-cooling shock, the density attenuation rate of granite was 0.35%. As the number of thermal shock cycles increases, the rate of density reduction gradually stabilizes, reaching approximately 1% after seven cycles. The longitudinal wave velocity reduction rate reaches 44.19% after one quenching cycle. With increasing quenching cycles, the sensitivity of the longitudinal wave velocity of granite to quenching gradually decreases, resulting in a reduction rate of 61.78% after the seventh quenching cycle.

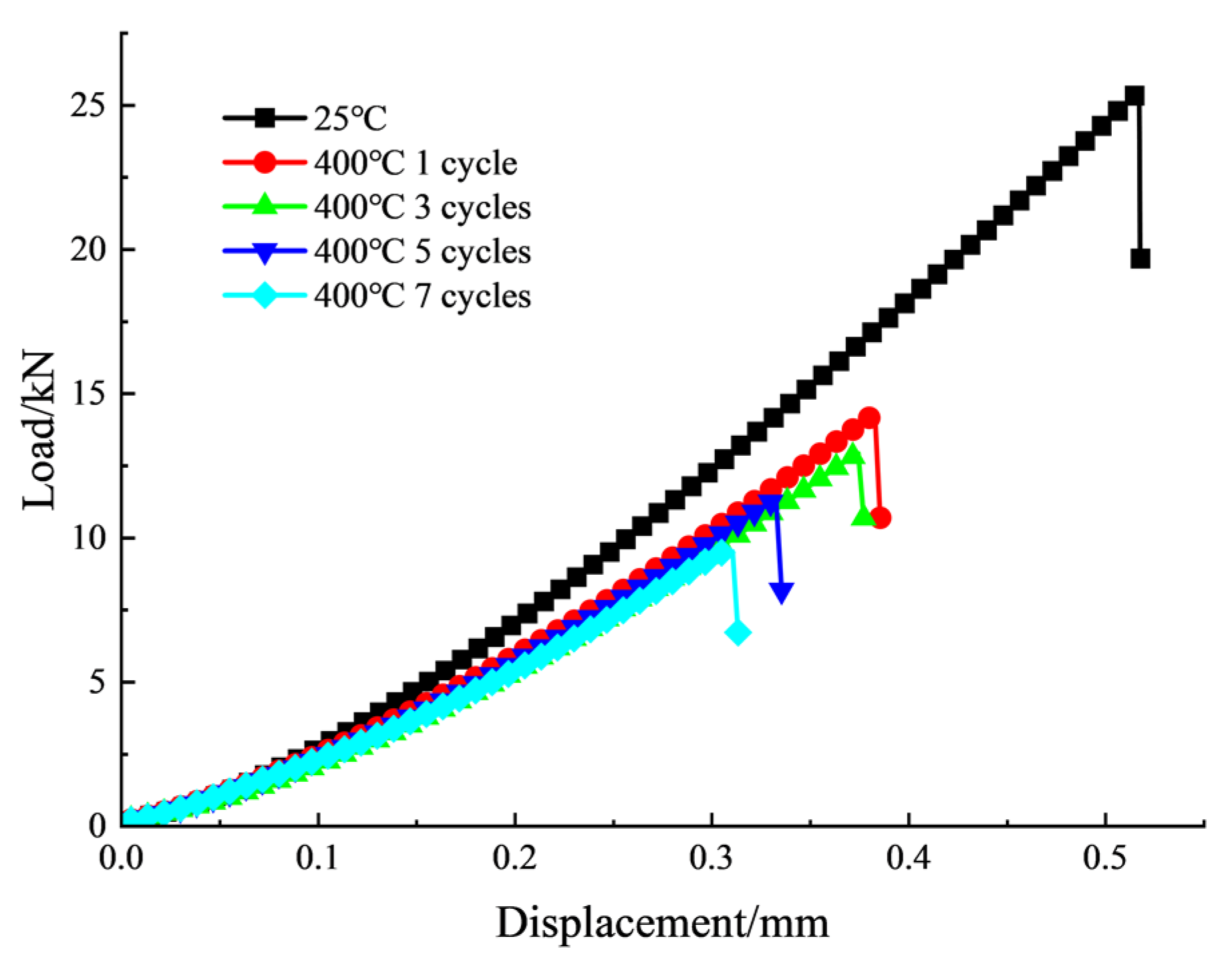
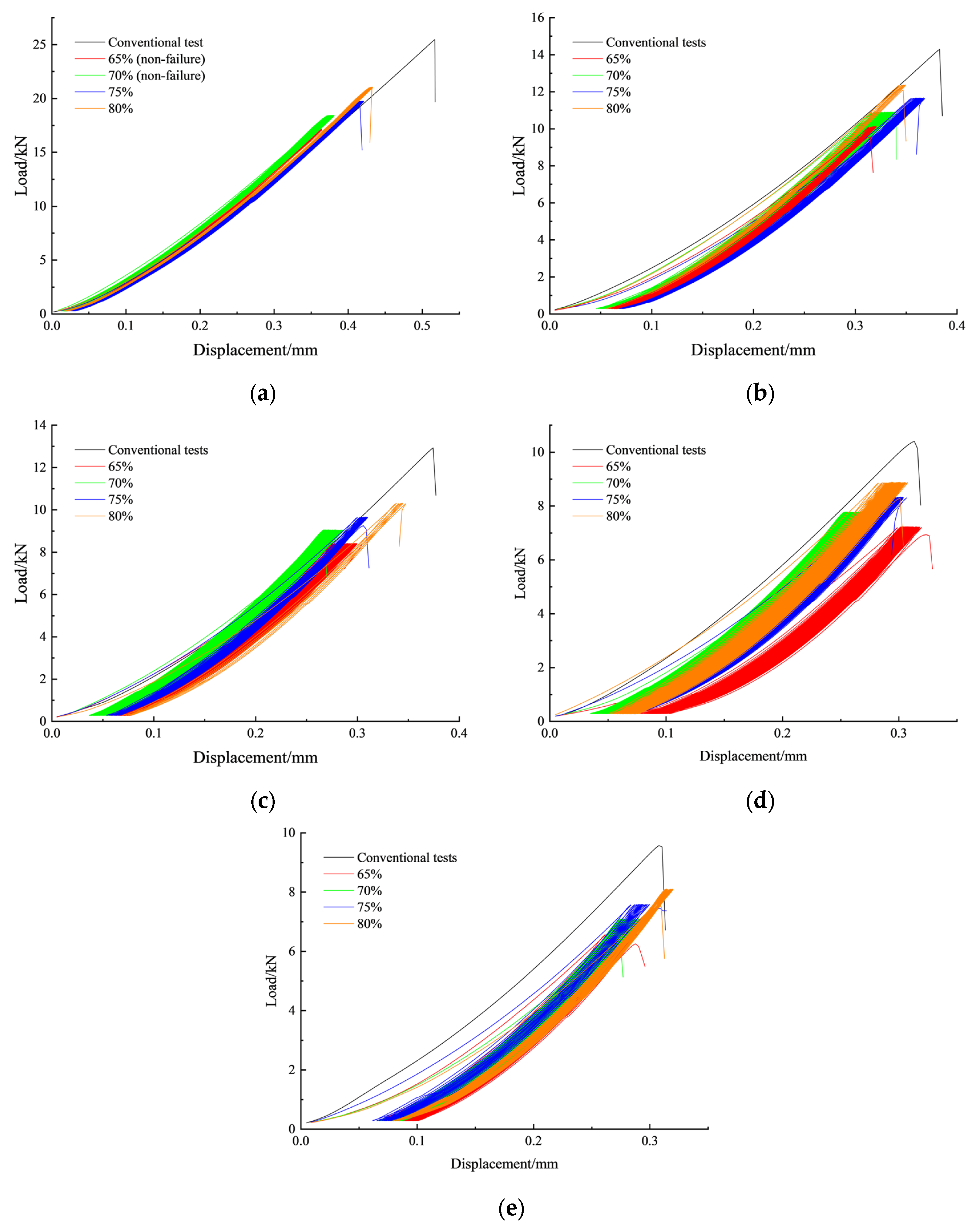
3.2. Load–Displacement Curve

Figure 9 presents the load–displacement curves obtained from the Brazilian splitting tests on granite after 400 °C cyclic water-cooling quenching. It can be observed that, following cyclic quenching, the load–displacement curves of granite exhibit a compaction stage, an elastic linear stage, a crack propagation stage, and an instability failure stage. With an increasing number of cyclic water-cooling shocks, the peak load shows a gradual decline. The peak loads of granite for 0, 1, 3, 5, and 7 quenching cycles are 26.37 kN, 14.29 kN, 12.82 kN, 11.31 kN, and 9.57 kN, respectively. This indicates that cyclic quenching imparts significant thermal damage to the granite, with thermal damage accumulating progressively as the number of quenching cycles increases; compared with the peak load of granite in its natural state, the peak load decreases by 45.81%, 51.38%, 57.11%, and 63.71% after 1, 3, 5, and 7 quenching cycles, respectively. Moreover, as observed in Figure 7, the deformation characteristics of granite are influenced by the 400 °C cyclic quenching, with the slope of the load–displacement curve gradually decreasing as the number of quenching cycles increases.

Figure 10 shows the load–displacement curves from the cyclic loading-unloading Brazilian splitting tests on granite after 400 °C cyclic water-cooling shock. It can be seen that the stages experienced by the load–displacement curves after a cyclic water-cooling shock are similar to those in conventional Brazilian splitting tests. After the first cyclic loading-unloading, the granite exhibits obvious plastic deformation, where the magnitude of plastic deformation is defined as the displacement from the starting point of the hysteresis loop during loading to the endpoint during unloading. For instance, under a 70% load upper limit, when cyclic water-cooling shocks are applied in 0, 1, 3, 5, and 7 cycles, the corresponding plastic deformation displacements after the first cyclic loading-unloading are 0.003 mm, 0.018 mm, 0.042 mm, 0.054 mm, and 0.071 mm, respectively. This indicates that, under the same preset load upper limit, the plastic deformation displacement of granite increases gradually with the number of cyclic water-cooling shocks. Moreover, after seven cyclic water-cooling shocks (Figure 10e), when the preset load upper limits are 65%, 70%, 75%, and 80%, the plastic deformation displacements are 0.056 mm, 0.071 mm, 0.057 mm, and 0.074 mm, respectively. This demonstrates that, under the same number of water-cooling shocks, the plastic deformation displacement of granite generally increases with the rise in the preset load upper limit.

As observed in Figure 10, following a 400 °C cyclic water-cooling shock, the slope of the hysteresis loop in the load–displacement curves of granite during cyclic loading-unloading progressively increases. This phenomenon is attributed to the gradual propagation of microcracks within the granite induced by the cyclic water-cooling shock, while the cyclic loading-unloading process compacts and closes these microcracks, thereby enhancing the resistance of granite to deformation [24]. When granite is subjected to a small number of water-cooling shocks, such as under one cycle (Figure 10b), the hysteresis loops in the load–displacement curves obtained from the cyclic loading-unloading Brazilian splitting test are relatively compact. However, when subjected to three and five cycles (Figure 10c,d), the hysteresis loop characteristics of the load–displacement curves evolve from “sparse” to “dense”, whereas, under seven cycles, the hysteresis loop characteristics exhibit a “sparse–dense–sparse” pattern.

In addition, by comparing the load–displacement curves from conventional Brazilian splitting tests with those from cyclic loading-unloading Brazilian splitting tests, it is found that even when the applied load is below the peak load observed in conventional tests, the granite specimen still fails in the cyclic loading-unloading tests. For example, after the granite is subjected to three water-cooling shocks when the preset load upper limits are 65%, 70%, 75%, and 80%, the failure loads of the granite specimens are 7.72 kN, 8.58 kN, 9.25 kN, and 10.23 kN, respectively. Compared with the peak loads from the conventional Brazilian splitting tests under the same conditions, the failure loads decreased by 40%, 33%, 28%, and 21%, respectively. This is attributed to the fact that the microcracks generated within the granite by the cyclic water-cooling shocks further propagate and coalesce under cyclic loading-unloading, ultimately leading to failure [34].

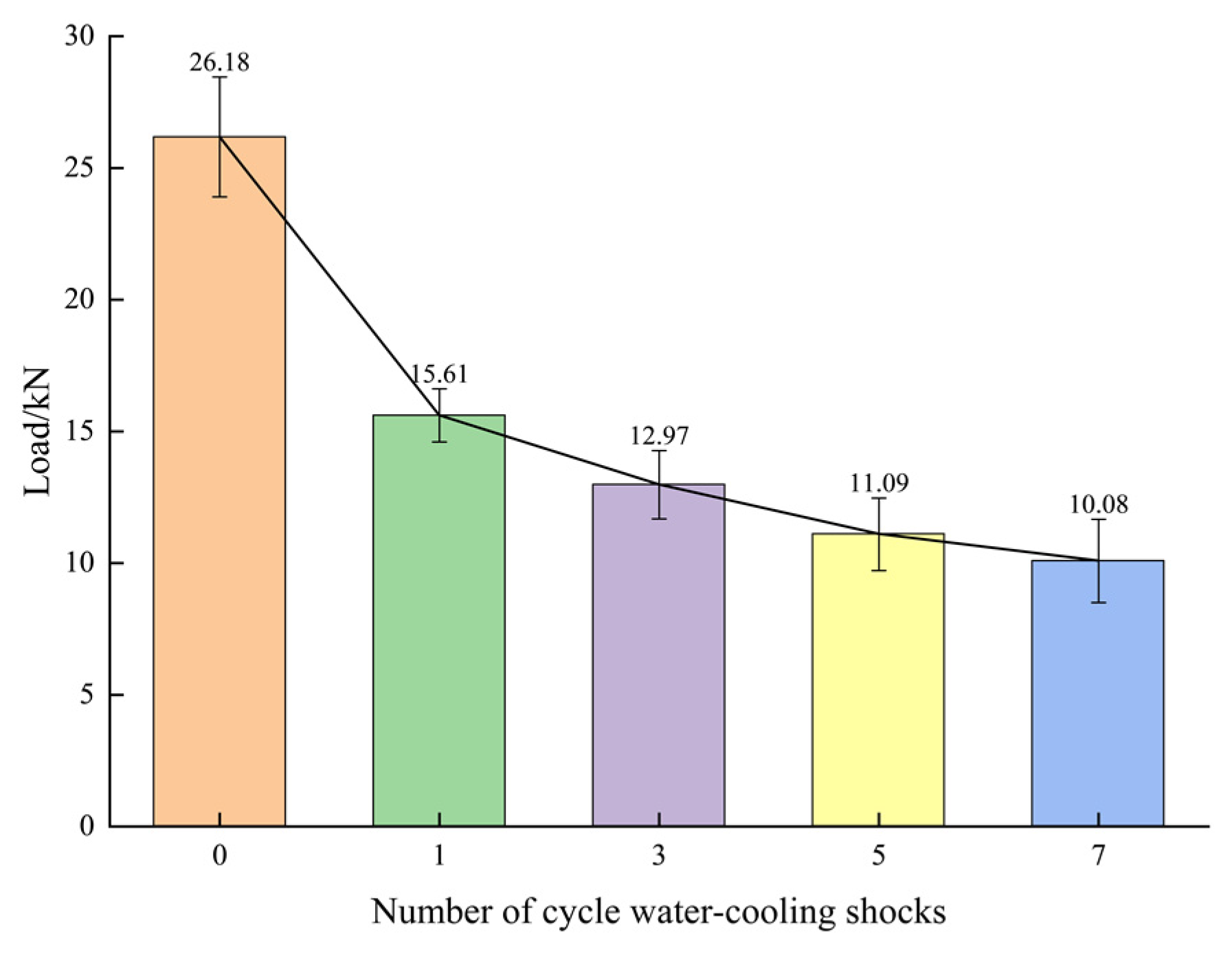
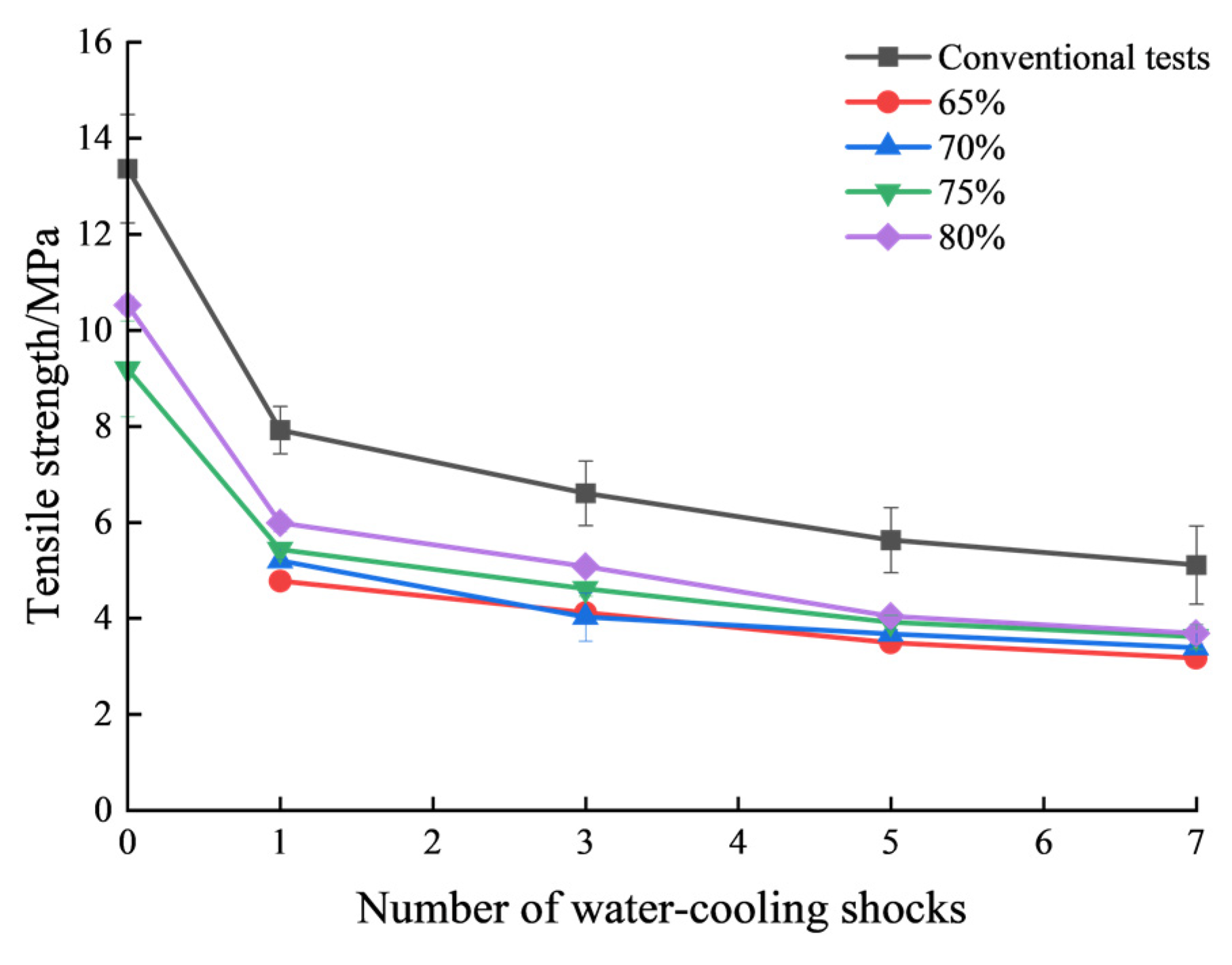
3.3. Tensile Strength

Figure 11 depicts the relationship between the tensile strength of granite and the number of cyclic water-cooling shocks under cyclic loading-unloading conditions. The tensile strength of granite gradually decreases with increasing water-cooling shock cycles. In the conventional Brazilian splitting test, under natural conditions (i.e., without water-cooling shocks), the tensile strength of granite is 13.37 MPa. However, after a single water-cooling shock, the tensile strength decreases to 7.92 MPa, representing a 41% reduction relative to the unshocked case. This reduction is attributed to significant thermal damage induced by the steep temperature gradient between the interior and exterior during the 400 °C water-cooling shock, generating numerous microcracks that reduce the tensile strength of the rock [28]. As the number of water-cooling shock cycles increases, the tensile strength continues to decline, although the rate of reduction becomes less pronounced. For three, five, and seven cycles, the tensile strengths are 6.61 MPa, 5.63 MPa, and 5.11 MPa, corresponding to reductions of 50%, 58%, and 62% relative to the natural condition, respectively. During the 400 °C water-cooling shock, partial local melting of quartz particles occurs; the molten quartz alters interparticle bonding within the rock, thereby reducing its overall strength [35]. In subsequent cycles, further quartz melting occurs, and due to the differing thermal expansion coefficients of quartz, mica, feldspar, and other minerals, the tensile strength of granite gradually decreases with additional cycles [11]. Some researchers have observed a thermal strengthening effect in granite after a 200 °C water-cooling shock [6]; however, under the 400 °C shock applied in this study, the tensile strength of granite decreases directly. This outcome is because the water-cooling shock simultaneously induces thermal strengthening and thermal damage in the granite, and at higher temperatures, the thermal strengthening effect is insufficient to compensate for the degradation of the mechanical properties of the rock caused by thermal damage [28].

In addition, Figure 11 also reveals that under the 400 °C cyclic water-cooling shock, the variation trend of tensile strength from the cyclic loading-unloading Brazilian splitting test is similar to that from the conventional Brazilian splitting test, both showing a gradual decrease in tensile strength with an increasing number of water-cooling shocks. However, compared with the tensile strength obtained from the conventional Brazilian splitting test, the tensile strength of granite under cyclic loading-unloading is significantly reduced. For instance, when the preset load upper limit is 75% after 0, 1, 3, 5, and 7 water-cooling shocks the tensile strengths of granite are 9.19 MPa, 5.43 MPa, 4.61 MPa, 3.91 MPa, and 3.61 MPa, respectively, which represents an overall decrease of approximately 30% compared to the conventional test. This phenomenon is primarily due to the continuous propagation and coalescence of microcracks under cyclic loading-unloading after the granite has been subjected to water-cooling shocks, eventually leading to a significant reduction in its tensile performance [13]. Similarly, it can be observed that under cyclic loading-unloading, the tensile strength of granite increases with the preset load upper limit. Taking the case of five water-cooling shocks as an example, when the preset load upper limits are 65%, 70%, 75%, and 80%, the corresponding tensile strengths from the cyclic loading-unloading Brazilian splitting test are 3.48 MPa, 3.67 MPa, 3.91 MPa, and 4.04 MPa, respectively, representing decreases of 38%, 35%, 30%, and 28% compared with the conventional Brazilian splitting test. This phenomenon is mainly because, during the cyclic loading-unloading process, as the load gradually approaches the preset load upper limit, the internal damage within the granite accumulates rapidly, and a higher preset load upper limit results in more accumulated damage, which in turn quickly reduces the number of cyclic loading-unloading cycles. However, the larger preset load upper limit leads to an increase in the tensile strength of granite under cyclic loading-unloading [36]. It is worth noting that, under the condition of zero water-cooling shocks (i.e., natural state), after 500 cycles of cyclic loading-unloading at preset load upper limits of 65% and 70%, the granite specimens did not fail. This is because the intact internal structure of granite in its natural state is not affected by thermal damage, and the strong cementation between the crystalline particles prevents failure [37]. The tensile strength values of granite under different conditions of cyclic loading-unloading are shown in

Table 1. Conventional and cyclic brazilian splitting test results of granite after 400 °C cyclic water-cooling shock.

Number of Water-Cooling Shock Cycles	Average Tensile Strength of Conventional Splitting/MPa	Preset Load Upper Limit/%	Number of Cyclic Loading and Unloading Cycles	Tensile Strength of Cyclic Brazilian Splitting /MPa	Reduction Amplitude/%
0	13.37	65	500	-	-
		70	500	-	-
		75	78	9.19	31
		80	39	10.52	21
1	7.92	65	128	4.78	40
		70	96	5.20	34
		75	25	5.43	31
		80	6	5.98	24
3	6.61	65	202	4.11	38
		70	87	4.03	39
		75	18	4.61	30
		80	4	5.08	23
5	5.63	65	452	3.49	38
		70	233	3.67	35
		75	94	3.91	31
		80	60	4.04	28
7	5.11	65	62	3.17	38
		70	58	3.38	34
		75	23	3.61	29
		80	12	3.68	28

.

To investigate the strength degradation behavior of granite under the coupled effects of cyclic loading-unloading and thermal shocks, this study proposes a semi-empirical model based on the 18 sets of experimental data listed in Table 1. By performing nonlinear regression analysis on the baseline tensile strength from conventional Brazilian splitting tests (σ_T), the predefined upper load limit (L), and the number of thermal shocks (N), the following expression is established:

$${\mathit{\sigma }}_T={\mathit{\sigma }}_{t0}\times L\times e^{-3\times 10^{-2}N},R^2=0.89$$

(3)

where σ_T is the tensile strength (MPa) under cyclic loading and unloading, σ_t0 is the tensile strength obtained from conventional tests (MPa), L is the predefined upper load limit (%), and N is the number of water-cooling shock cycles.

The model incorporates a linear proportional term L to represent the direct influence of cyclic loading amplitude and an exponential decay term ($e^{-3\times 10^{-2}N}$) to characterize thermal damage induced by cyclic water–thermal shocks. Model validation demonstrates a high degree of agreement between predicted and experimental values, with a coefficient of determination (R²) of 0.89. The mean absolute error (MAE) and mean absolute percentage error (MAPE) are 0.3 MPa and 7%, respectively, indicating strong reliability for engineering assessments. Under low-cycle thermal shocks (N ≤ 3), the model yields particularly accurate predictions (MAPE < 10%). For instance, when N = 3 and L = 75%, the prediction error is only 1.7%. By introducing an exponential decay term, the model overcomes the limitations of traditional linear assumptions and significantly enhances the characterization of thermal shock-induced damage. This model offers a concise and efficient theoretical tool for strength evaluation in the hydraulic fracturing of HDR reservoirs.

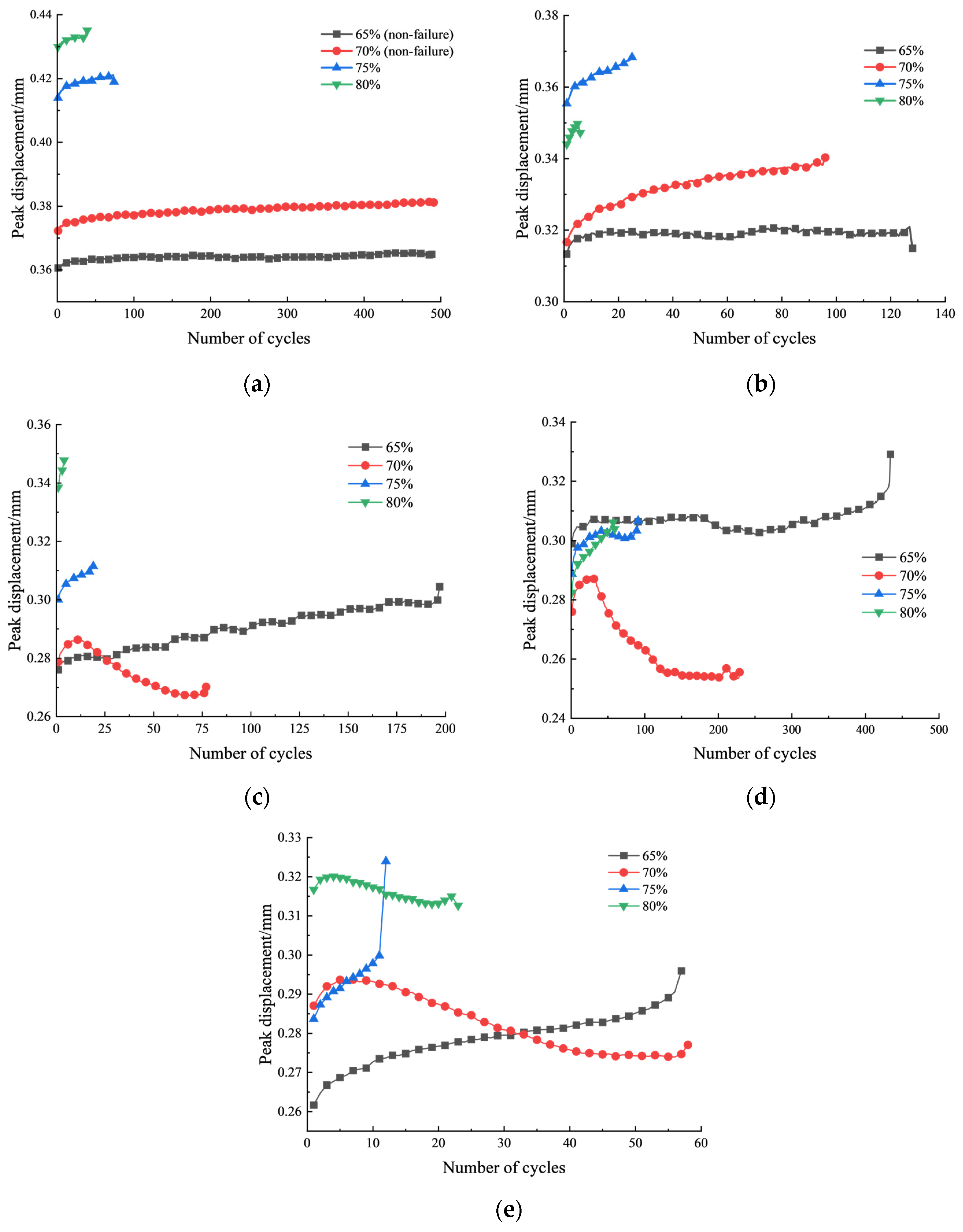
3.4. Cyclic Loading-Unloading Peak Displacement

Figure 12 shows the relationship between the peak displacement of the load–displacement curves from the cyclic loading-unloading Brazilian splitting tests on granite and the number of cyclic loading-unloading cycles. This curve intuitively reflects the ultimate deformation experienced by granite during each loading cycle. The curve can be divided into three stages: a rapid growth stage, a slow growth stage, and a failure stage. The rapid growth stage occurs in the early phase of cyclic loading-unloading, typically accounting for about one-third of the total cycles. In this stage, the peak displacement increases rapidly in each cycle—contributing to over 50% of the positive growth in peak displacement—because the water-cooling shock, together with the inherent primary fractures and pores in granite, is compacted under cyclic loading-unloading, resulting in significant plastic deformation [23]. After entering the slow growth stage, the deformation behavior of granite becomes more complex. Generally, as the number of cyclic loading-unloading cycles increases, although the internal pores of granite have become relatively compact, the gradual propagation of microcracks still causes a slight increase in peak displacement; however, some specimens even exhibit a decrease or negative growth in peak displacement, which will be analyzed further below. The failure stage occurs during the final few cycles of cyclic loading-unloading, where the peak displacement increases significantly until it reaches a critical value, leading to the sudden failure of the specimen. For instance, under the conditions of zero water-cooling shocks with preset load upper limits of 65% and 70% (Figure 12a), granite subjected to 500 cycles of cyclic loading-unloading did not fail, having only experienced the rapid and slow growth stages without reaching the failure stage.

In the cases of 0, 1, and 3 water-cooling shocks (Figure 12a–c), the peak displacement of the cyclic loading-unloading load–displacement curves shows a trend of gradual increase with the number of cycles. However, under the conditions of five and seven water-cooling shocks, the evolution of peak displacement with the number of cyclic loading-unloading cycles becomes increasingly complex. For example, after five water-cooling shocks with a 70% load upper limit (Figure 12d) and after seven water-cooling shocks with 70% and 80% load upper limits (Figure 12e), the peak displacement initially increases rapidly during the early cycles but then decreases—sometimes even falling below the initial peak displacement of the granite, exhibiting negative growth. This phenomenon is attributed to the closure of internal microcracks and micropores after the initial cycles of cyclic loading-unloading, as well as the melting and flow of low-melting-point particles such as quartz and mica [38]. Consequently, the interaction forces among particles with higher intrinsic strength are enhanced, thereby increasing the elastic stiffness of the granite and causing the specimen to gradually “harden” [39]. With continued cyclic loading-unloading, the internal cracks gradually enlarge, and the peak displacement increases again until the specimen ultimately fails. Moreover, this reflects the competitive relationship between damage accumulation induced by cyclic quenching and the compaction effect on the rock during the early stages of cyclic unloading.

Observation of Figure 11 reveals that the initial displacement of granite under cyclic loading-unloading generally increases with the preset load upper limit. For example, under a condition of three water-cooling shocks (Figure 12e), the initial peak displacements during the first cyclic loading-unloading are 0.27 mm, 0.28 mm, 0.30 mm, and 0.34 mm for preset load upper limits of 65%, 70%, 75%, and 80%, respectively. Similarly, under the same number of water-cooling shocks and cyclic loading-unloading cycles, the peak displacement of granite typically increases with the preset load upper limit. However, after five water-cooling shocks, the peak displacement does not consistently increase with the load upper limit. This is because, after five water-cooling shocks, the number of microcracks within granite increases, and the material enters a transitional phase from brittle to ductile behavior [40]. Due to the heterogeneous nature of granite, the distribution of internal microcracks is uneven, and the transition from ductile to brittle behavior varies among specimens, resulting in complex variations in peak displacement under different preset load upper limits [41]. In this study, analysis of the load–displacement curves and the variation in peak displacement reveals that the ductility of granite increases after five cycles of water-cooling shock. The assessment of ductile behavior can be further explored through experiments such as nano-indentation and fracture toughness testing.

In addition, Figure 11 shows that under the same number of water-cooling shocks, the number of cyclic loading-unloading cycles required to induce failure in granite decreases as the preset load upper limit increases. This is due to the fact that a higher load upper limit results in a larger peak displacement during loading, leading to more severe propagation of microcracks and greater damage accumulation per cycle [42], which makes granite more prone to failure.

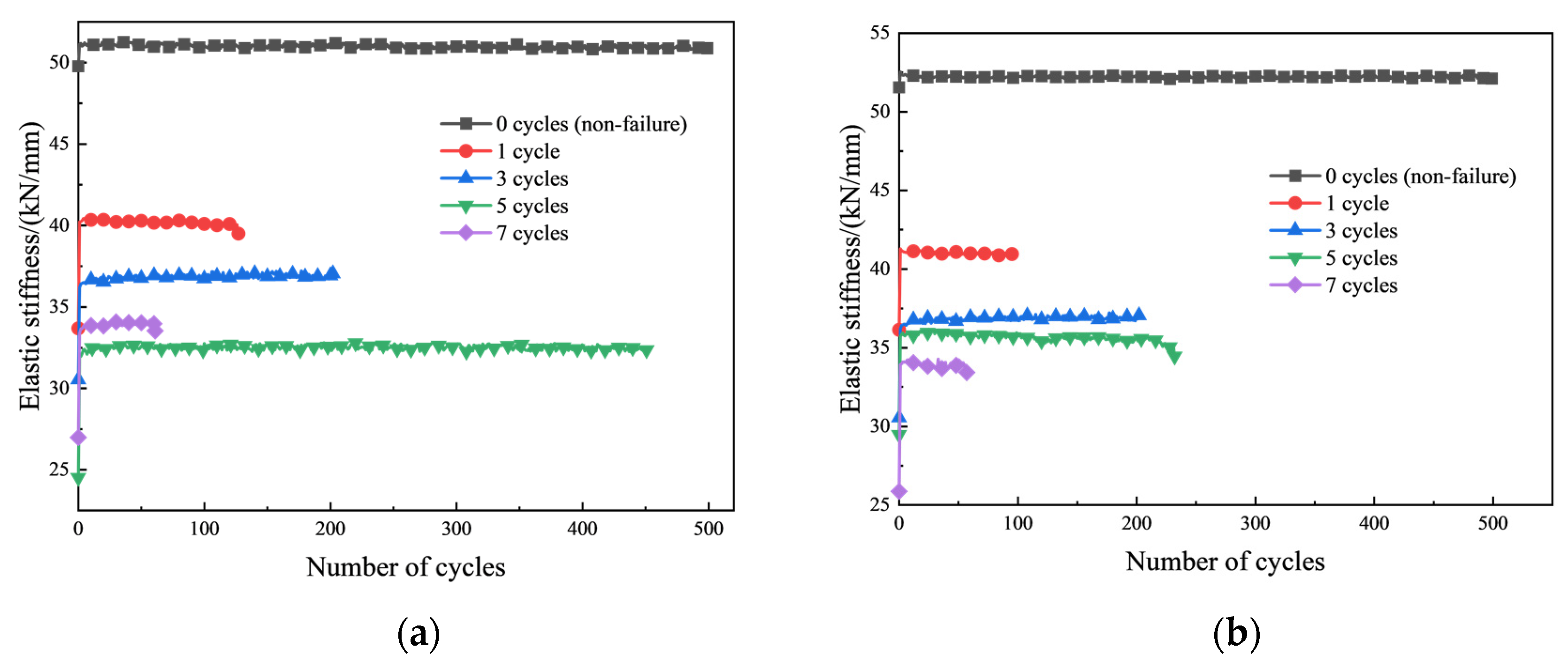
3.5. Elastic Stiffness

Elastic stiffness is a characteristic parameter that reflects the ability of granite to resist deformation. In order to ensure that both the starting and ending points of the approximate linear segment of elastic stiffness are within the loading curve, the elastic stiffness of the loading segment is defined as the slope between the two points corresponding to 30% and 70% of the load upper limit on the hysteresis loading segment of the load–displacement curve [43].

Figure 12 shows the variation of elastic stiffness of granite as a function of cyclic loading-unloading cycles in the Brazilian splitting test following different numbers of cyclic water-cooling shocks. The elastic stiffness initially increases markedly, then stabilizes, and ultimately decreases with additional loading-unloading cycles. The sharp initial increase in elastic stiffness is attributed to the compaction of internal pores during the first loading, which enhances granite density and its deformation resistance, accounting for approximately 80% of the total stiffness gain [38]. During the next few cycles, as the internal structure becomes progressively compacted, elastic stiffness increases slightly, corresponding to the rapid growth stage of peak displacement observed in Figure 13. Thereafter, although loading-unloading cycles continue, elastic stiffness remains nearly constant, corresponding to the slow growth stage of peak displacement. In the final cycles before failure, accumulation of internal damage due to continued cyclic loading causes elastic stiffness to decrease; at this stage, significant plastic deformation occurs in the granite, and peak displacement increases with cycle number until specimen failure, corresponding to the failure stage of peak displacement.

In addition, it is observed from Figure 13 that under the same preset load upper limit, the increase in elastic stiffness after the first loading shows a trend of gradually increasing with the number of water-cooling shocks. For instance, under a 70% load upper limit, the elastic stiffness of granite after the first cyclic loading is 51.55 kN/mm, 36.14 kN/mm, 30.54 kN/mm, 29.46 kN/mm, and 25.86 kN/mm after 0, 1, 3, 5, and 7 water-cooling shocks, respectively; after the first cyclic loading, the elastic stiffness increases to 52.53 kN/mm, 41.28 kN/mm, 36.18 kN/mm, 35.72 kN/mm, and 33.92 kN/mm, corresponding to an increase of 2%, 14%, 18%, 21%, and 31%, respectively. Similarly, under the same number of cyclic loading-unloading cycles, with the increase in the number of water-cooling shocks, the elastic stiffness of granite exhibits a decreasing trend. The aforementioned phenomena are attributed to the fact that the water-cooling shock exacerbates the generation and propagation of microcracks within the granite, and these microcracks continue to propagate during the cyclic water-cooling process. In particular, after multiple thermal cycles, the further expansion of microcracks reduces the integrity of the internal structure of the rock, thereby diminishing its elastic stiffness [44,45].

4. Failure Characteristics Analysis

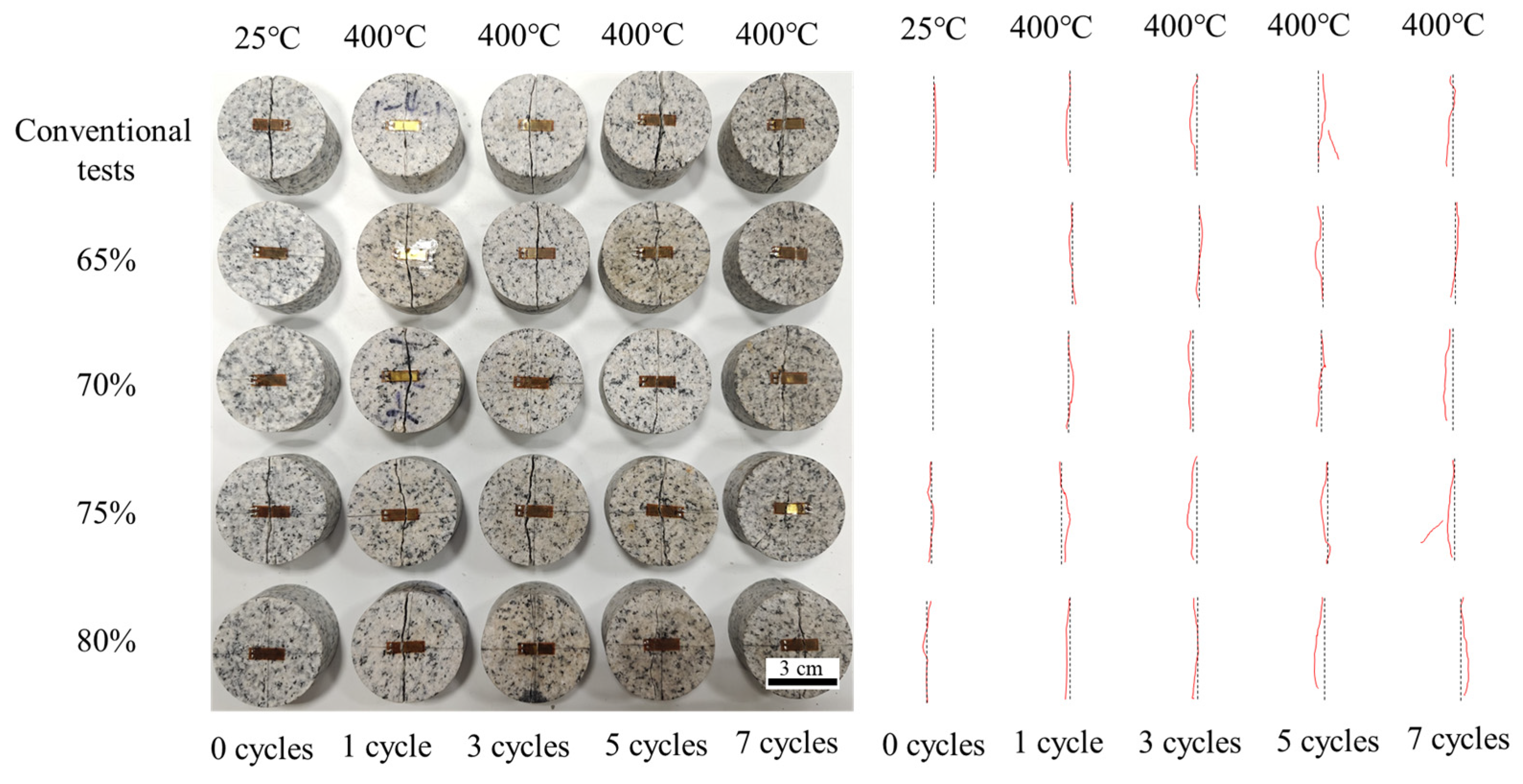
4.1. Macroscopic Failure Characteristics

Figure 14 shows the macroscopic failure morphology of granite specimens subjected to 400 °C cyclic water-cooling shocks and subsequent cyclic loading-unloading Brazilian splitting tests. It can be observed that all specimens exhibit the typical failure characteristics of Brazilian splitting tests, namely, failure occurs along the diameter of the granite specimen in the direction of the applied load. Compared with the conventional Brazilian splitting tests, changes in the load upper limit have almost no effect on the macroscopic failure characteristics in the cyclic loading-unloading tests. However, as the number of cyclic water-cooling shocks increases (beyond three cycles), the principal fracture in the granite changes from a straight line passing through the center to an arc that deviates from the center. In specimens subjected to five and seven water-cooling shocks, secondary fractures are also observed. This is attributed to the alteration in the ductility of granite caused by the cyclic water-cooling shocks, whereby the splitting failure mode transitions from tensile failure to a mixed tensile-shear failure [46].

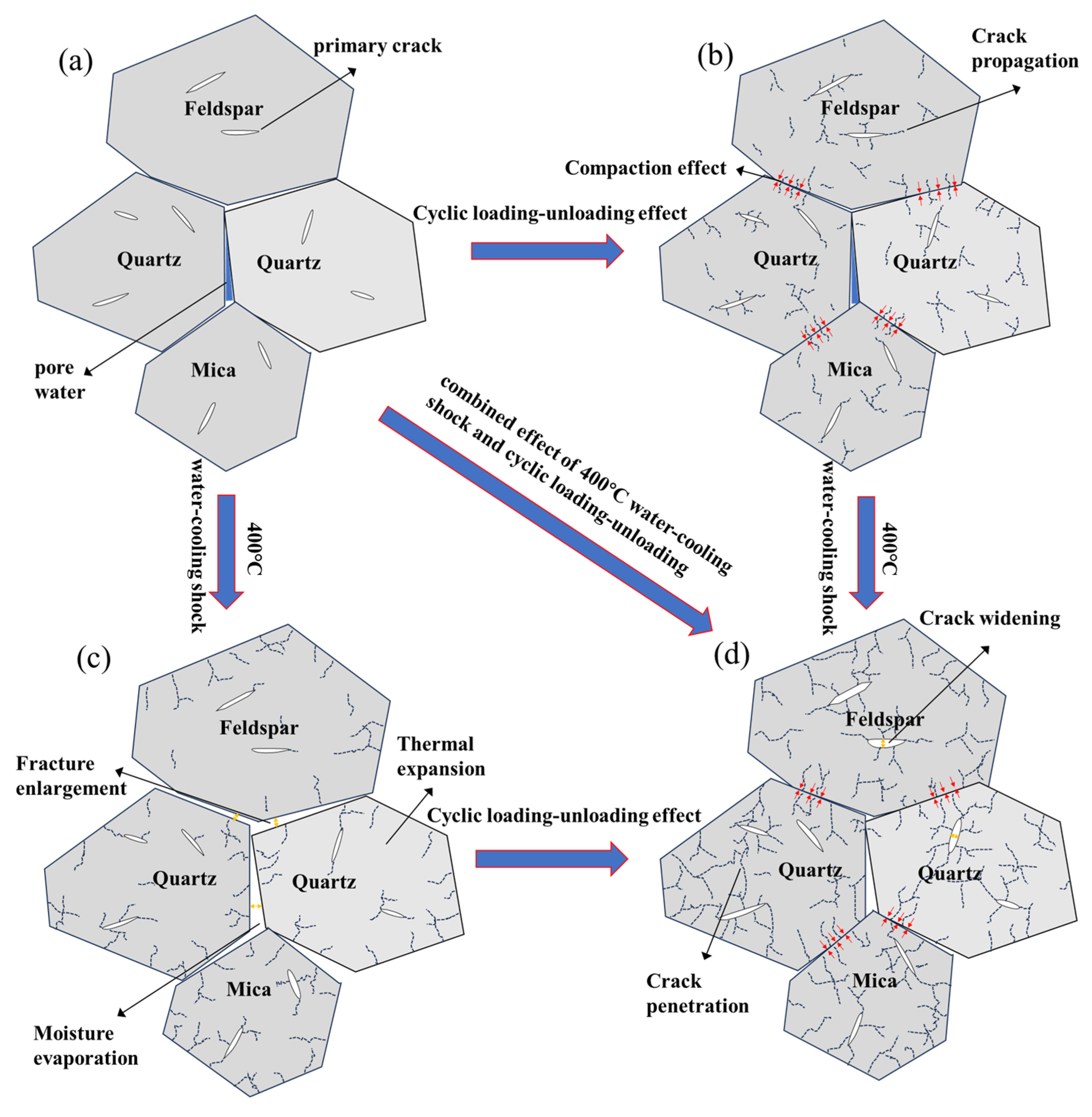
4.2. Microscopic Damage Mechanism Analysis

Figure 15 presents scanning electron microscope (SEM) images of granite specimens subjected to 400 °C cyclic water-cooling shocks, tested under both conventional Brazilian splitting and cyclic loading-unloading Brazilian splitting conditions. In the natural state (zero water-cooling shocks, Figure 15a), the microstructure of granite is relatively intact, and the fracture surfaces are fairly neat, with cracks predominantly following the intergranular paths. After undergoing cyclic loading-unloading (Figure 15b), the fracture surface of granite becomes progressively rougher, although its overall microstructure remains relatively sound; correspondingly, the tensile strength remains high and the increase in peak displacement is limited under cyclic loading-unloading. With the increase in the number of water-cooling shocks, after one and three shocks (Figure 15c,e), due to the evaporation of pore water and the effects of water-cooling shocks, the internal structure of granite becomes relatively loose. The microcrack morphology still is mainly intergranular, accompanied by a small number of intragranular cracks. The damage in the crystals primarily occurs in the peripheral regions of the mineral grains, which is attributed to the non-uniform thermal expansion of mineral particles at high temperatures that causes stress concentrations at the edges of intergranular cracks, leading to failure in those regions [47]. Following cyclic loading-unloading, the number of microcracks within the granite increases significantly (Figure 15b,d), with micro-fracture zones appearing at the grain boundaries, and the microcrack patterns becoming complex and tortuous. This is because cyclic loading-unloading promotes the gradual propagation and extension of microcracks until they eventually coalesce. At this stage, the increased crack density leads to a reduction in tensile strength and an increase in the increment of peak displacement. When the number of water-cooling shocks reaches five and seven (Figure 15g,i), the effect of thermal damage on the granite becomes markedly more significant, with the intergranular gaps enlarging once again. Under the electron microscope, the formation of micropores can be clearly observed. Moreover, compared with the conditions of fewer water-cooling shocks, the microcracks in granite are predominantly transgranular, with both their lengths and widths increasing significantly [44]. The cyclic loading-unloading process further promotes the propagation of cracks, and the intersection of cracks forms a complex network of fissures. This leads to the detachment of relatively large debris from the fracture surface, rendering the micro-fracture surface of the granite much rougher. At the same time, in the cyclic loading-unloading Brazilian splitting tests, the density of the hysteresis loops in the load–displacement curves of granite is significantly reduced, while the peak displacement required to induce failure increases considerably.

5. Discussion

Figure 16 illustrates the schematic diagram of the microscopic failure mechanism of granite subjected to cyclic water-cooling shock at 400 °C combined with cyclic loading and unloading. Under natural conditions, the mineral grains within granite remain relatively intact, containing only a small number of pre-existing microcracks (Figure 16a). The cyclic thermal shock at 400 °C significantly alters the physical properties of the granite. The evaporation of internal pore water and the intense thermal shock induce heterogeneous expansion among mineral grains, leading to the widening of intergranular cracks and the initiation of numerous intragranular microcracks (Figure 16c). After five cycles of water-cooling shock (Figure 15g), newly formed microcracks not only emerge within the crystals but also begin to interconnect, evolving into transgranular cracks. This process increases the porosity of granite [48]. As the number of thermal shock cycles increases, the number and width of cracks gradually reach a stable state [11]. Consequently, granite undergoes degradation in quality, expansion in volume, reduction in density, and a decrease in P-wave velocity, with the degradation rate gradually tapering off as the number of cycles increases. The corresponding mechanical properties also deteriorate. In conventional Brazilian splitting tests, the tensile strength of granite decreases progressively with more thermal shock cycles. Compared with the natural state, the tensile strength of granite after 1, 3, 5, and 7 cycles of water-cooling shock decreases by 41%, 51%, 58%, and 62%, respectively, with the rate of reduction gradually diminishing. These findings confirm a direct correlation between the number of microcracks and the degradation of tensile strength in rock. In addition, previous studies have proposed automated methods for measuring the water absorption of materials [49,50], which can be used to quantify microcrack density in granite and further explore the relationship between microcrack density and the deterioration of mechanical properties.

Under natural conditions, when granite is subjected to cyclic loading and unloading, as shown in Figure 16b, the original pores between mineral crystals are compacted, generating interaction forces between the grains. The applied load induces new microcracks in the contact zones between grains, and the pre-existing cracks within the crystals gradually propagate and extend under stress. However, the mineral grains remain largely intact, and the resultant failure predominantly occurs along grain boundaries where the particles are cemented (Figure 15b). Throughout the cyclic loading process, the load–displacement curves of granite under various preset upper load limits are densely clustered, and no significant variation in elastic stiffness is observed. Due to the strong cementation between mineral grains, granite specimens subjected to 65% and 70% of the preset peak load did not experience failure. This suggests that, under natural conditions, the tensile fatigue failure threshold of granite exceeds 70% of its peak strength, which aligns with the findings of Li and Erarslan regarding tensile failure thresholds in rock [21,31].

When granite is subjected to both cyclic water-cooling shock and cyclic loading, substantial thermal damage is already present prior to mechanical loading. Cyclic loading induces a compaction effect on the granite, enhancing its elastic stiffness (Figure 13), and this compaction effect becomes more pronounced with higher upper load limits [24], resulting in more significant increases in elastic stiffness under cyclic loading. A competitive mechanism exists between thermal damage induced by cyclic thermal shocks and the compaction effect during the early stages of cyclic loading [51,52]. Before the fifth cycle of water-cooling shock, damage accumulation dominates. Although some crack closure and self-healing effects occur under cyclic loading, plastic deformation continues to increase, leading to cumulative damage. After five and seven cycles of thermal shock, considerable thermal damage accumulates within the rock. At this stage, stress-driven local self-healing mechanisms begin to prevail, significantly enhancing the stiffness of the rock and resulting in a noticeable reduction in plastic displacement (Figure 12d,e). In both cases, final failure initiates from the cracks formed by thermal shock. Under the effect of cyclic loading-unloading (Figure 16d), new cracks form within the granite crystals, and existing cracks propagate [53]. With continuous loading, crack widths expand, and cracks of varying lengths extend until they coalesce into macroscopic fractures (Figure 15j).

6. Conclusions

This study investigates the effects of cyclic water-cooling shock at 400 °C and cyclic loading-unloading on the tensile properties of granite through Brazilian splitting tests and scanning electron microscopy (SEM) analysis. The main conclusions are as follows:

• For granite subjected to cyclic water-cooling shock at 400 °C, an increase in shock cycles leads to mass loss, volume expansion, density reduction, and a decrease in P-wave velocity. The most significant changes occur after the first quenching, after which the variation trends gradually stabilize. With the increasing number of water-cooling shock cycles, the tensile strength gradually decreases, while the rate of decrease diminishes progressively.
• The tensile strength of granite in cyclic loading-unloading Brazilian splitting tests decreases progressively with increasing water-cooling shock cycles. Additionally, the tensile strength under cyclic loading-unloading conditions is significantly lower than that in conventional Brazilian splitting tests. As the preset load upper limit decreases, the tensile strength also exhibits a declining trend.
• Under cyclic loading-unloading, the initial peak displacement increases with the preset load upper limit. However, at five shock cycles, no clear trend is observed due to the transition of granite from brittle to ductile behavior. As the preset load upper limit increases, the number of cycles required for failure decreases. The elastic stiffness of granite initially increases with the number of loading-unloading cycles, then stabilizes before eventually decreasing. Moreover, with increasing water-cooling shock cycles, the overall elastic stiffness shows a decreasing trend. In the early stages of cyclic loading and unloading during the Brazilian splitting test, a competitive mechanism exists between damage accumulation and compaction effects in granite. When the number of water-cooling shock cycles is low, damage accumulation dominates; however, after five cycles, the compaction effect becomes the prevailing mechanism.
• With an increasing number of cyclic water-cooling shocks, macro-fracture patterns in granite transition from straight to curved cracks. SEM observations reveal that microcracks become more numerous and wider with additional shock cycles. Under cyclic loading-unloading, the microcrack width further increases, and the fracture surface becomes rougher.