Abstract
Steganography, a technique for concealing information, often faces challenges such as low decoding accuracy and inadequate extraction of edge and global features. To overcome these limitations, we propose a dual-stream U-Net framework with integrated edge enhancement for image steganography. Our main contributions include the adoption of a dual-stream U-Net structure in the encoder, integrating an edge-enhancement stream with the InceptionDMK module for multi-scale edge detail extraction, and incorporating a multi-scale median attention (MSMA) module into the original input stream to enhance feature representation. This dual-stream design promotes deep feature fusion, thereby improving the edge details and embedding capacity of stego images. Moreover, an iterative optimization strategy is employed to progressively refine the selection of cover images and the embedding process, achieving enhanced stego quality and decoding performance. Experiments show that our method produces high-quality stego images across multiple public datasets, achieving near-100% decoding accuracy. It also surpasses existing methods in visual quality metrics like PSNR and SSIM. This framework offers a promising approach for enhancing steganographic security in real-world applications such as secure communication and data protection.
1. Introduction
With the proliferation of social networking platforms, privacy protection has become an urgent challenge. Image steganography, as an information-hiding technique, achieves covert transmission by embedding sensitive information into multimedia content (such as images and videos). Unlike traditional encryption techniques, steganography utilizes the redundant space in digital media to embed information while avoiding third-party attention. This technology plays a crucial role not only in secure data transmission [1] but also finds widespread application in digital copyright identification and privacy protection, making it a key tool in information security [2].
Traditional image steganography techniques can be categorized into spatial domain and transform domain methods. Spatial domain-based methods, such as Least Significant Bit (LSB) replacement [3] and Pixel Value Differencing (PVD) [4], conceal information by directly modifying image pixel values, which are simple to implement but vulnerable to statistical analysis detection. Transform domain-based methods include Discrete Fourier Transform (DFT) [5], Discrete Cosine Transform (DCT) [6], and Discrete Wavelet Transform (DWT) [7] algorithms, which embed information by mapping images to the transform domain, demonstrating superior detection resistance and robustness compared to spatial domain methods.
The aforementioned methods are non-adaptive steganographic algorithms that overlook the impact of image texture complexity. Adaptive steganographic algorithms embed information in areas with complex textures and rich features, including Syndrome-Trellis Codes (STC) [8], which are linear code-based embedding techniques generating efficient and secure changes; Highly Undetectable steGanOgraphy (HUGO) [9], which uses prediction-error expansion to embed information in a hard-to-detect way; Wavelet Obtained Weights (WOW) [10] uses wavelet transform to obtain weights for embedding information, balancing embedding capacity and security; Spatial Universal Wavelet Relative Distortion (S-UNIWARD) [11] is a wavelet-domain distortion function measuring cover-stego relative distortion to reduce embedded information detectability. However, despite their advantages, traditional steganographic techniques face inherent limitations. Most methods rely on hand-crafted heuristics to determine embedding locations, which can lead to suboptimal performance when dealing with complex textures or adversarial detection models. Furthermore, as steganalysis techniques advance, traditional approaches struggle to maintain their security guarantees. To address these challenges, researchers have turned to deep learning-based methods, which enable adaptive and more robust information embedding strategies.
Deep learning-based approaches have demonstrated significant potential in overcoming these limitations by automatically learning optimal embedding locations and feature representations. With the rapid development of deep learning technology, breakthrough progress has been made in image steganography. Baluja [12] proposed an end-to-end training steganographic network architecture, achieving effective information hiding in natural images. HiDDeN [13] can embed up to 0.2 bpp of information through training encoder and decoder networks. Duan et al. [14] performed image embedding based on the U-Net [15] architecture, using convolutional neural networks to extract hidden information, though its generalization ability and robustness still require further validation. The emergence of Generative Adversarial Networks (GAN) [16] has further advanced steganographic technology. SteganoGAN [17] employed different encoder-decoder structures with a critic network but achieved decoding error rates of 5–30%. CHAT-GAN [18] enhanced steganographic image quality and information extraction accuracy through channel attention mechanisms, utilized stegananalysis networks as discriminators to improve security, and increased information recovery precision through error correction codes. Although error correction codes can improve information extraction accuracy, their application increases computational burden and may reduce steganographic capacity. Chen et al. proposed LISO [19] in their research, a neural network-based iterative optimization approach for image steganography. LISO achieves zero error rates up to 3 bits per pixel without using error correction codes by learning optimization steps while maintaining proximity to the natural image manifold, though the visual quality of its steganographic images is relatively low.
The existing deep learning-based steganography methods have made remarkable progress in information hiding, yet they still face several challenges. First, many approaches struggle with high error rates when recovering large volumes of embedded information, which is critical for practical applications. Second, the visual quality of stego images often remains suboptimal, especially when dealing with complex images, potentially raising suspicion and reducing security. Third, the limited ability to capture image edges and texture details restricts the effective extraction of high-level features, impacting both the quality and security of the stego image. Motivated by these challenges, this paper proposes a novel image steganography method based on LISO, aimed at addressing these critical issues. The primary contributions of this paper are as follows:
- We propose an innovative dual-stream U-Net architecture that enhances the model’s ability to learn from the intricate edges and contours of the cover image. An edge-enhanced image is introduced as an additional input stream, which effectively boosts the model’s capacity to capture edge and texture details. In the dual-stream structure, each input stream is connected via independent skip connections, ensuring the comprehensive fusion of multi-level features and addressing the objective of enhancing steganographic robustness and visual quality.
- We propose a multi-scale median attention (MSMA) module. This module comprises three key components: median-enhanced pooling, channel blending, and hierarchical deep convolution. First, median-enhanced pooling combines average, max, and median pooling to preserve edge and structural details. Then, channel blending improves inter-channel information exchange. Finally, hierarchical deep convolution enables multi-scale feature extraction, enhancing feature representation and improving steganography quality and decoding accuracy. In subsequent experiments, it was shown that the module improves the quality of steganography, with a 2.5 dB increase in average PSNR and a reduction in Error Rate to 0.
- We introduce the InceptionDMK module (Inception-style Depthwise Multi-Kernel Convolution), which extracts global features while maintaining the capture of local details. This module significantly improves the network’s ability to extract multi-scale features and its computational efficiency. By leveraging the detailed features from the edge-enhanced image, the module facilitates efficient embedding and reliable decoding of steganographic information, even in complex image scenarios, thus providing robust technical support for information-hiding applications.
The remainder of this paper is organized as follows. Section 2 introduces some related work on image steganography techniques. Section 3 provides a detailed explanation of the technical principles and implementation process of our proposed method. Section 4 explains the metrics for evaluating the model and conducts an extensive experimental analysis and assessment of the method. Section 5 summarizes our work.
2. Relate Work
2.1. Traditional Steganography Methods
Classical steganographic methods operate directly in the spatial domain to encode data. Least Significant Bit (LSB) [3] steganography conceals information by replacing the least significant bits of an image’s pixel RGB color components. Westfeld et al. [20] proposed the Jsteg algorithm based on LSB technology, primarily replacing the least significant bits in the AC coefficients of the original image with secret information. However, as the amount of information increases, this method gradually reveals statistical characteristics, leading to the “paired values” phenomena between pixel values, making it difficult to resist RS [21] (Regular and Singular) analysis. To address this issue, Westfeld et al. [22] proposed the F5 algorithm, which combines Hamming code with minimal image modification to embed information, effectively enhancing steganographic security and detection resistance. Additionally, the Pixel Value Differencing (PVD) technique utilizes brightness differences between adjacent pixels to hide information, reducing the “paired values” phenomenon and increasing information hiding capacity, though this method is vulnerable to histogram analysis attacks. Subsequently, scholars proposed many PVD-based steganographic algorithms [23,24,25], effectively improving the limitations of the PVD algorithm.
Compared to spatial domain methods, transform domain methods typically demonstrate higher robustness and security by utilizing image characteristics in the transform domain. The DFT algorithm [5] employs frequency domain characteristics to embed information into image frequency components, enhancing information concealment. The DCT algorithm [6], as a core technology in JPEG compression, utilizes image energy concentration characteristics to embed information in transform coefficients, offering good steganographic performance and compression resistance. The DWT algorithm [7] leverages multi-scale characteristics based on wavelet decomposition to embed information by analyzing local image features. These methods significantly improve steganographic concealment and security by fully utilizing image characteristics in the transform domain.
In recent years, distortion function-based steganographic methods have further advanced technological development. Peveny et al. [9] proposed Highly Undetectable steGanOgraphy (HUGO), which achieves highly undetectable steganography by designing distortion functions that minimize differences between stego and cover images in SPAM second-order feature space. Holub et al. [10] introduced Wavelet Obtained Weights (WOW), which uses directional filters to evaluate pixel modification impacts on high-frequency image information and defines a new distortion measurement method. Li et al. proposed the HILL algorithm [26], innovating on WOW by combining high-pass and low-pass filters to optimize distortion function design, fully utilizing carrier image texture features. Spatial Universal Wavelet Relative Distortion (S-UNIWARD) [11] achieves efficient information embedding in any domain by introducing the UNIWARD distortion function. This method uses wavelet transforms to extract high-frequency subband features, embedding information in hard-to-model regions, significantly enhancing steganographic analysis resistance and concealment.
2.2. Deep Learning Based Steganography
In 2017, Hayes et al. [27] proposed the HayesGAN model, which adopts an adversarial architecture including embedding, extraction, and steganalysis networks. The embedding network is responsible for embedding secret information into images, the extraction network recovers hidden information, and the steganalysis network detects whether images contain secret information, providing a novel generative adversarial approach to steganographic technology. In 2018, Zhu et al. [13] proposed an end-to-end steganographic model HiDDeN, implementing data hiding through encoder and decoder networks and enhancing model robustness by adding noise layers to simulate transmission attacks. To further increase hiding capacity, in 2019, Zhang et al. [17] proposed the SteganoGAN model, whose encoding-decoding network design includes three structures: basic network, residual network, and dense network. The evaluator determines whether images are carrier or stego images, and the model incorporates Reed–Solomon code, with its DenseNet-based encoder achieving a hiding capacity of 4.4 bpp.
Li et al. [28] proposed the HCISNet model based on SteganoGAN, combining the ASPP spatial pyramid pooling module with DenseNet to build an encoder, further increasing hiding capacity to 5.68 bpp. Tan et al. [18] also improved SteganoGAN by introducing channel attention modules to identify beneficial channels in feature maps and error correction codes for hiding information bits. Zhang et al. proposed the Adaptive Frequency Domain Channel Attention Network (AFcaNet) [29], enhancing frequency feature utilization through fine-grained weight allocation, though it improved feature extraction capability without significantly enhancing steganographic capacity. Jing et al. [30] proposed a reversible image-hiding network HiNet, significantly improving image-hiding security and recovery accuracy through shared network parameters and frequency domain hiding techniques. Kishore et al. proposed Fixed Neural Network Steganography (FNNS) [31], which utilizes neural networks’ sensitivity to minor perturbations by optimizing subtle modifications to input images for information hiding. It can reliably hide information without compromising image visual quality, achieving nearly 0% error rate in information recovery (supporting up to 3 bpp). However, this method relies on fixed decoder networks, limiting further enhancement of steganographic capabilities. Bui et al. [32] proposed an innovative method for robust steganography using autoencoder latent space. The core of this method is training a simple lightweight network while freezing the pre-trained encoder.
3. The Proposed Method
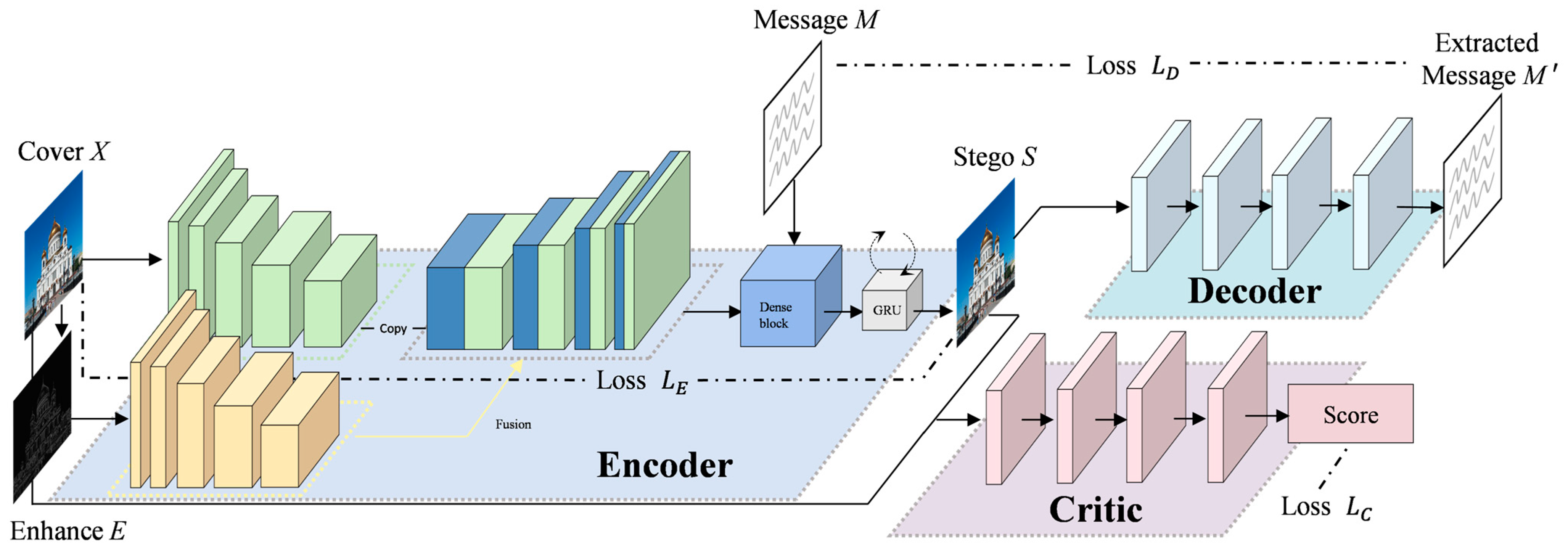
The edge regions of an image typically exhibit higher local entropy and more complex texture features, which not only provide a greater capacity for information embedding but also contribute to stronger pixel disturbance masking effects. Building on this idea, we design an edge-aware dual-stream U-Net architecture in the encoder to optimize the steganography performance through edge enhancement. The method first applies the Sobel operator to the cover image for edge detection and enhancement, creating an edge-enhanced image E that strengthens structural information and provides additional texture details for subsequent feature extraction. The original cover image and the enhanced image are fed into the network as dual inputs, where each undergoes independent feature extraction via separate contracting paths. These features are then fused in the shared expanding path, integrating both edge and global information. To further enhance feature extraction, a multi-scale median attention (MSMA) mechanism is applied after each layer in the contracting path, improving the representation of steganography-related features while reducing redundant information. Additionally, the enhanced channel includes the InceptionDMK module, which utilizes multi-scale convolutions to capture multi-dimensional features. The combined features, along with the secret information , are iteratively optimized using dense convolutional blocks and Gated Recurrent Unit (GRU) units to generate a high-quality stego image . The decoder, a relatively simple feedforward convolutional neural network, is responsible for accurately extracting the hidden information prime from the stego image . The discriminator, similar in structure to the decoder, is trained as a neural classifier to distinguish between the cover and stego images. It is adversarially trained with the encoder and decoder, thereby improving the quality of the generated stego images.
The overall framework of the proposed method depicts an overview of the proposed framework (Figure 1).
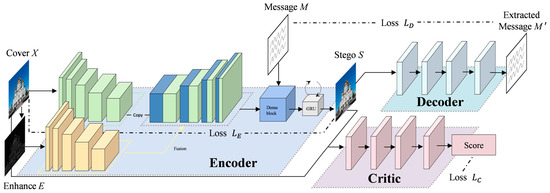
Figure 1.
The overall framework of the proposed method.
3.1. Encoder Architecture
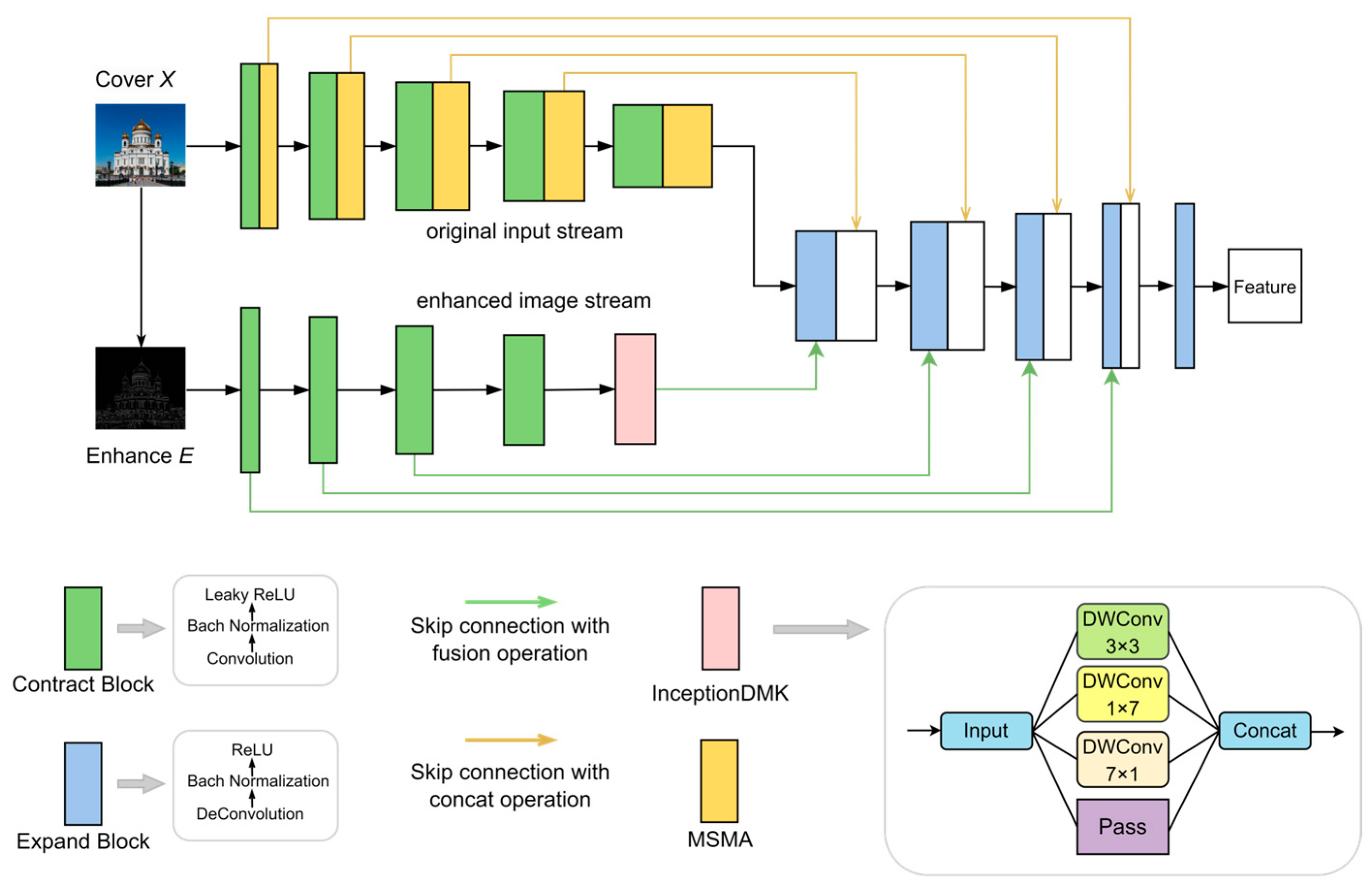
The dual-stream U-Net module in our encoder is depicted in Figure 2. The module receives the cover image and the enhanced edge image as input. The features of the shrinking and expanding paths are fused through a specific jump-joining strategy. The original input stream introduces multi-scale median attention (MSMA) in the contraction path, while the edge enhancement stream introduces the InceptionDMK module combining depth-separable convolution with multi-scale filtering, as detailed in the following structure:
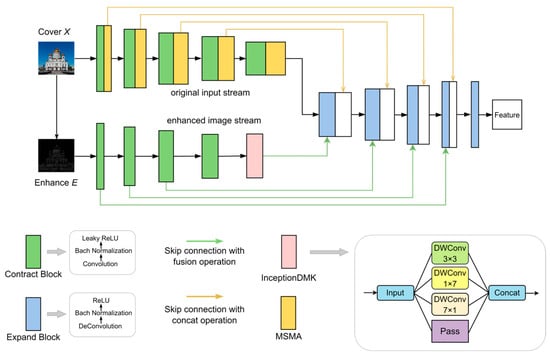
Figure 2.
General structure of dual-stream U-Net and InceptionDMK.
Dual-stream Input: The edges and contours of an image are critical areas for steganography. To better learn these features, we design a dual-stream U-Net structure with both the cover image and the edge-enhanced image as inputs. The edge-enhanced image emphasizes edge features, assisting the network in learning the image’s texture and structural information more effectively.
Skip Connections: Different skip connection strategies are used to fuse feature maps between the contracting and expanding paths, ensuring that image details and structure are preserved, as shown in Table 1. Specific network structure of dual-stream U-Net. The feature flow from the contracting path’s enhanced image is fused with the feature flow from the expanding path, expressed as . The fused features are then concatenated with the feature flow from the contracting path’s cover image, expressed as .

Table 1.
Specific network structure of dual-stream U-Net.
Multi-scale median attention (MSMA): To further enhance performance, MSMA is applied after each layer of the contracting path for the original input stream, but not in the enhanced image stream. This decision is based on two considerations: (1) the original image typically contains more noise and redundant information, which MSMA can effectively suppress; and (2) the edge features of the enhanced image are already significantly highlighted, and applying MSMA could risk overfitting.
InceptionDMK Module: This module combines depthwise separable convolutions with multi-scale feature extraction to effectively capture multi-scale and multi-directional features of the image. It consists of four branches: a bypass branch retaining the original information, a 3 × 3 convolutional kernel branch, and 1 × 11 and 11 × 1 strip convolutional kernel branches for capturing edge information from different directions. The outputs from these branches are concatenated along the channel dimension, preserving tensor shapes and significantly improving edge detail extraction.
The following sections will provide a detailed explanation of the edge-enhanced image technique, the MSMA mechanism, and the InceptionDWK module.
3.1.1. Enhanced Images
Recent research by M. Hayat et al. [33] has demonstrated that edge-guided attention mechanisms can effectively preserve structural details and enhance edge features in images, providing a high-quality, texture-rich medium for secure steganographic embedding. Since edges and texture regions are information-rich while having minimal impact on human visual perception, they are ideal areas for information hiding [34]. Embedding information in these regions minimizes the effect on visual quality while improving the concealment of steganography. Changes in edges and textures help to mask distortions caused by embedding, making steganalysis significantly more difficult.
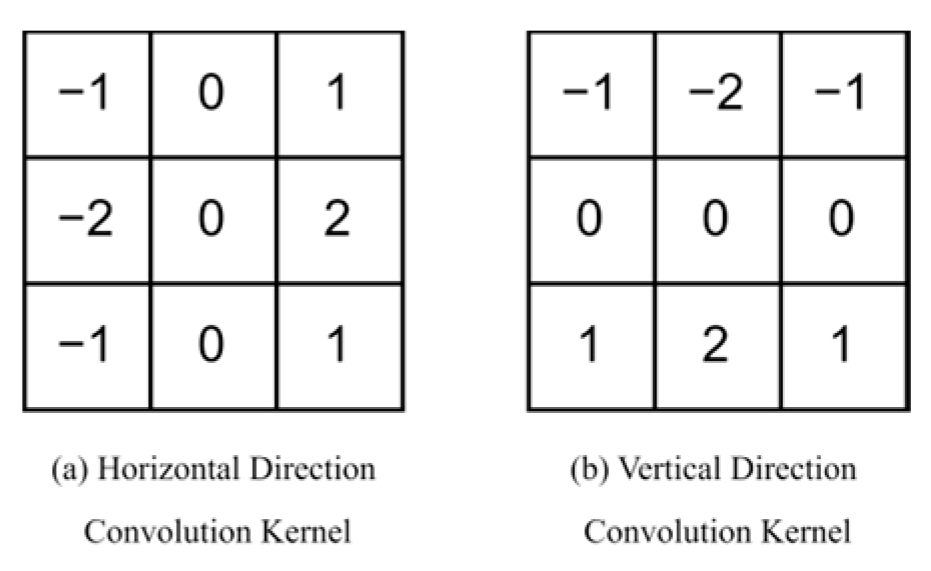
To better learn texture and structural features while preserving image quality, thereby enhancing the security and robustness of steganography, we introduce an additional input stream focused on image enhancement. This stream is designed to amplify texture and structural details, especially edge features. Common image enhancement operators include the Robert, Sobel, Laplacian, and Prewitt operators. In this study, we utilize the Sobel operator for image enhancement. Its convolution kernel is shown in Figure 3. Bidirectional Convolution Kernels. By computing the gradient magnitude, which combines horizontal and vertical gradients, the Sobel operator detects edge information and enhances edge features by adjusting the pixel values of the original image. The corresponding formula is provided below:
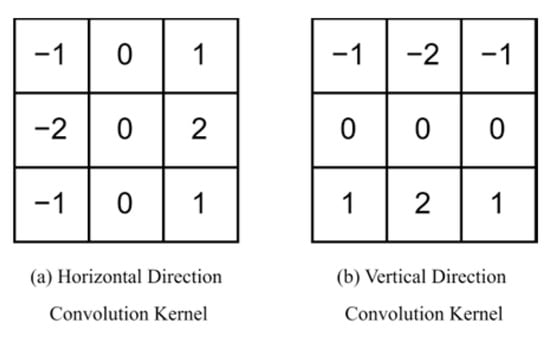
Figure 3.
Bidirectional Convolution Kernels.
represents the pixel value of the original image at the pixel position . denotes the gradient of the image in the horizontal direction, and denotes the gradient of the image in the vertical direction. is the coefficient of the enhancement intensity, and denotes the convolution operation.
3.1.2. Dense Block Structure
After the U-Net architecture, we introduce a dedicated Dense Block module [35]. Its core function is to deeply fuse the secret message M with image features. Unlike traditional convolutional blocks, Dense Block uses dense connectivity, enabling the network to better utilize feature information.
A Dense Block consists of three sequentially connected convolutional layers. Each layer receives not only the output of the previous layer but also the outputs of all preceding layers and the original input features. This dense connectivity offers two advantages: it enhances the model’s parameter efficiency through feature reuse. Moreover, each processing stage reintroduces the original features and the secret message M, effectively preventing the decay or loss of critical information during multi-layer transmission and providing a rich information foundation for subsequent processing.
3.2. Multi-Scale Median Attention
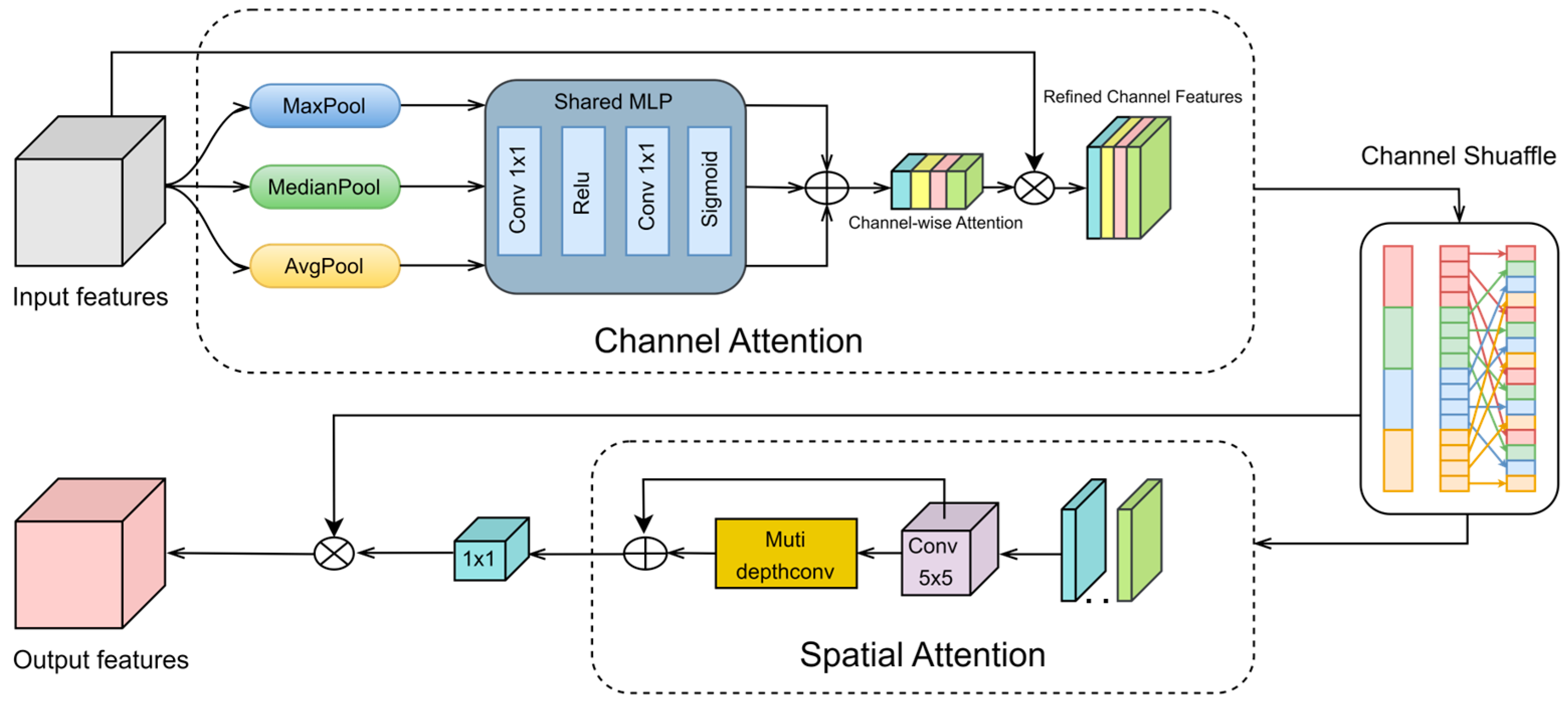
U-Net, as a widely used generator architecture, still encounters several limitations in feature learning. First, it lacks the capability to jointly model cross-region and cross-channel feature correlations, thereby limiting the expressiveness of feature representations. Second, although traditional skip connections preserve spatial details, they do not incorporate an explicit attention mechanism to selectively focus on key semantic regions. The SE-CCSA mechanism proposed by Hayat et al. [36] combines the squeeze excitation mechanism and the joint channel and spatial attention mechanism, which effectively preserves high-frequency details in the super-resolution task of pathology images, and verifies that a reasonable attentional mechanism can accurately focus on the critical regions, thus improving the quality of images. Based on this, we propose the multi-scale median attention (MSMA) module based on the CBAM framework [37]. This module integrates channel attention, spatial attention, and a channel shuffling mechanism to improve information exchange between channels, facilitating the adaptive extraction and integration of multi-scale features. By concentrating on key regions and features within the image, MSMA significantly enhances the model’s capability in feature extraction from images. The overall structure is shown in Figure 4.
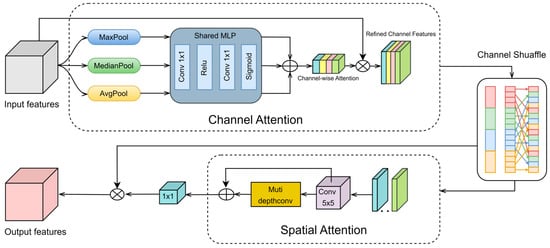
Figure 4.
The proposed structure of multi-scale median attention.
3.2.1. Channel Attention
Traditional channel attention mechanisms are primarily based on a combination of global average pooling and global max pooling. To enhance the model’s robustness to noise and better preserve edge and structural information, we adopt a median-enhanced triple-pooling strategy. By constructing a complementary feature representation framework integrating AvgPool, MaxPool, and MedianPool, we obtain three complementary feature representations. The dimensions of the resulting pooled features are given by the following:
where represents the number of channels. These pooled features are then processed by a shared multilayer perceptron (MLP) comprising two 1 × 1 convolutional layers with a ReLU activation function. Specifically, the first convolutional layer reduces the feature dimension from to (where r denotes the reduction ratio), while the second convolutional layer restores it to C. A Sigmoid activation function is applied to constrain the output values within the range [0, 1], generating three attention maps. By summing these three attention maps element-wise, we obtain a fused channel attention map. The final channel attention map is then element-wise multiplied with the original input feature map to obtain the weighted feature map.
3.2.2. Channel Shuffle
After enhancing channel attention, there may still be insufficient mixing of information across channels. Insufficient integration of inter-channel information may restrict feature expressiveness, hindering the full effectiveness of the channel attention mechanism. To address this issue, we introduce the concept of [38], utilizing a channel shuffle operation to facilitate cross-channel information exchange. The input feature map is divided into four groups, each containing C/4 of the total channels. A transposition operation is applied to shuffle the channel order within each group. The shuffled feature maps are then restored to their original shape. This approach promotes better information mixing across different channels, enhancing feature representation and ultimately boosting model performance.
3.2.3. Spatial Attention
Traditional single-scale convolutional kernels are inherently limited in capturing multi-scale feature representations, which substantially impacts the model’s capability to handle features of different scales and complexities. In contrast, multi-scale feature extraction methods effectively capture cross-scale and multi-directional information from feature maps, thereby enhancing model performance in complex scenes and diverse object recognition tasks. To model multi-scale spatial relationships, we adopt a hierarchical deep convolutional structure. First, the channel attention-optimized features F′ are passed through a 5 × 5 depthwise convolution layer to extract basic features.
Then, the output feature map Fb from the initial convolution layer is further processed through multiple depthwise convolution layers with different kernel sizes, including 1 × 11 and 1 × 7 convolutions, to facilitate multi-scale feature extraction. The extracted multi-scale features are summed element-wise and passed through a 1 × 1 convolution layer to obtain a spatial attention map. Finally, the spatial attention map is element-wise multiplied by the weighted feature map to generate the final feature representation.
3.3. InceptionDMK Module
Edge images primarily contain contour and structural information. Inspired by the Inception [39] architecture, our InceptionDMK module effectively captures fine directional features, such as horizontal and vertical edges, through depthwise separable convolutions with square and strip-shaped kernels. This design is particularly suited for enhancing edge-detail channels. The module integrates the strengths of depthwise separable convolutions and multi-scale feature extraction through four parallel branches, as shown in Figure 2.
- Bypass branch (): This branch directly bypasses convolution operations, preserving the original input features.
- Local spatial feature branch (): Employs a 3 × 3 square kernel depthwise separable convolution to extract local spatial features from the image.
- Horizontal feature branch (): Utilizes a 1 × 7 horizontal strip-shaped kernel to capture directional features along the horizontal axis.
- Vertical feature branch (): Uses a 7 × 1 vertical strip-shaped kernel to extract vertical directional features.
The outputs of these branches are concatenated along the channel dimension, ensuring that the output tensor matches the input tensor in channel count and spatial dimensions. This design efficiently combines multi-scale and multi-directional features. The enhanced InceptionDMK module retains computational efficiency while significantly improving the extraction of multi-scale and multi-directional features. This allows the network to enhance edge details more effectively while achieving stronger feature representation capabilities.
3.4. Iterative Optimisation
To enhance the quality and effectiveness of the stego image, we adopt the iterative learning optimization method proposed by Chen et al. [19]. This method incrementally adjusts the perturbation vector to ensure that the stego image remains stable on the natural image manifold. Unlike traditional one-shot optimization methods, this approach leverages GRU units to iteratively optimize the perturbation by integrating feedback from the loss function. This approach quickly reduces errors, improves hidden data accuracy, and enhances the stego image’s natural appearance.
The input for each iteration xt includes three components:
Current perturbation : Represents the modification applied to the original image in the previous iteration.
Gradient of the loss function : the gradient of the current perturbation on the total loss. Guides the adjustment of the perturbation to minimize the loss.
Original image features : Features extracted from carrier images after dual stream U-Net results.
GRU-based hidden state updates: The GRU (Gated Recurrent Unit) updates the hidden state ht based on the previous hidden state ht−1 and the current input xt. The update equations are as follows:
Here, represents the activation function, is the update gate controlling how much of the new state is retained, and is the reset gate determining how much of the past state is forgotten. The hidden state serves as the basis for generating the update direction.
Generating the update direction : The hidden state ht is processed through a fully convolutional network to produce the update direction. This update direction indicates how to adjust the perturbation to further reduce the loss.
Updating the perturbation: Using the generated update update the current perturbation to obtain the new perturbation .
is the learning rate, is the gradient with respect to the perturbation, and the function is used to process these inputs and update the perturbation with respect to the GRU. Finally, the steganographic image is generated after several iterations, where denotes the total number of iterative optimizations.
3.5. Decoder Architecture
The decoder module is designed to extract hidden information from stego images with a focus on simplicity and efficient feature extraction, meeting the data recovery requirements of steganography. The module consists of three convolutional blocks, each containing a convolutional layer (with a kernel size of 3 and a stride of 1), followed by a LeakyReLU activation function and Batch Normalization layers. After these three blocks, a final convolutional layer transforms the feature maps into the required data depth to generate the decoded output. This architecture ensures accurate decoding while maintaining high computational efficiency.
3.6. Critic Architecture
The discriminator is designed similarly to the discriminator in generative adversarial networks (GAN). Its primary function is to assess the authenticity of input images, determining whether they are original cover images or stego images. The architecture mirrors the decoder, comprising three convolutional blocks that include a convolutional layer, a LeakyReLU activation function, and Batch Normalization layers. However, the discriminator differs in its final layers: the last convolutional layer reduces the channel count of the feature map to one, followed by a global average pooling (GAP) layer that aggregates the feature map into a scalar score. This score represents the probability that the input is either a cover or stego image. This design choice strikes an effective balance between computational efficiency and adversarial learning performance. By adopting an architecture similar to the decoder, the discriminator reduces computational costs and parameter complexity, avoiding the introduction of excessive hyperparameters that could increase resource consumption during training and inference. At the same time, this streamlined design ensures that the discriminator can effectively distinguish between cover and stego images without succumbing to issues such as overfitting or gradient instability. This balance is critical for maintaining both robust adversarial evaluation and practical computational efficiency. By providing precise and reliable decisions, the discriminator plays a crucial role in supporting adversarial training, ensuring robust evaluation of the steganographic process.
3.7. Loss Function
We have developed a combined loss function aimed at ensuring the stego image both effectively embeds secret information and visually maintains high similarity to the original image. This loss function consists of three components: decoding information loss (), image quality loss (), and critic loss (). These components are optimized together to improve the embedding effectiveness and visual quality of the stego image while minimizing information recovery errors and image distortions.
Decoding Information Loss (): The purpose of the information recovery loss is to ensure accurate recovery of the hidden information from the stego image. We use Binary Cross-Entropy Loss (BCE Loss) to measure the degree of match between the decoded message from the stego image and the original secret message . The formula for this loss is as follows:
where represents the dot product. Minimizing this loss ensures efficient recovery of accurate secret information from the stego image.
Image Quality Loss : To ensure that the stego image visually resembles the original cover image, we introduce the image quality loss , which measures the pixel-wise differences between the stego image and the original cover image using Mean Squared Error (MSE):
where is the original cover image, is the stego image, and is the total number of pixels. By minimizing , we ensure that the generated stego image retains a high visual similarity to the original image, avoiding noticeable artifacts or distortions.
Critic Loss : To enhance the concealment of the stego image and make it harder for detectors or the human eye to differentiate it, we design the critic loss . Similar to the discriminator in Generative Adversarial Networks (GANs), the critic network’s objective is to determine if the generated stego image is indistinguishable from the original image . This loss is defined as follows:
where and represent the critic’s output scores for the stego image and the original cover image, respectively. Minimizing this loss ensures that the generated stego image appears more natural and less detectable.
Total Loss Function: The final loss function is a weighted combination of the three losses, considering the accuracy of information recovery, image quality, and concealment:
where and are the weights that regulate the image quality loss and the commenter loss, and is a decay factor that controls the effect of the loss during the iteration. is at each step of iteration , and the model uses the decoder to recover the message from the steganographic image at that step . is the steganographic image at step .
4. Experiments
4.1. Experimental Settings
This study utilizes the PyTorch 1.7.1 deep learning framework to construct the model and implements the complete training and inference pipeline in Python 3.9.7. To enhance the model’s generalization ability and training performance, we preprocess the images before training, applying random cropping, rotation, and normalization. The images are resized to 360 × 360 × 3. The network is trained and evaluated on an NVIDIA GRID V100 GPU, with a batch size of 2 and a total of 100 training epochs.
To validate the effectiveness of our method, we conduct evaluations on three different datasets: Div2k [40], MS-COCO [41], and CelebA [42]. Div2k, commonly used for super-resolution image reconstruction tasks, consists of 1000 high-resolution images. We randomly select 800 images for training, 100 for validation, and 100 for testing. For MS-COCO and CelebA, we randomly select 1000 images for training, 1000 for validation, and 200 for testing for each dataset.
The secret information is represented by randomly generated binary vectors. In practical applications, these vectors can be replaced with encoded text or binary images. By tuning the hyperparameters of the loss function, we can effectively control the contribution of different loss components to the total loss, thereby accelerating model convergence.
In order to analyze the impact of the loss function hyperparameters α and β and the number of iterations T on the model performance, we performed a sensitivity analysis, as shown in Table 2. The experimental results indicate that the larger the value of α (e.g., 100), the better the image quality, but the decoding error rate increases. In addition, although increasing the number of iterations T helps to reduce the decoding error rate, too many iterations have a limited effect on improving the image quality instead of increasing the computational cost and affecting the efficiency of the model. In order to strike a balance between image quality, decoding accuracy, and computational efficiency, the model achieves the best performance with T = 10, step size η = 1, attenuation coefficient γ = 0.8, and loss weight α = β = 1.

Table 2.
Performance with different settings of the relative weights of each item in the loss function.
4.2. Evaluation Metrics
In this study, we utilized several evaluation metrics to quantitatively assess the performance of the steganography algorithm and the quality of the stego images. These metrics include the error rate, peak signal-to-noise ratio (PSNR) [43], structural similarity index (SSIM) [44], and feature similarity indexing method (FSIM) [45].
The error rate measures the difference between the original message and the message recovered from the stego image. A lower error rate indicates higher accuracy in message recovery by the steganography algorithm. It is defined as follows:
where represents the original message, is the recovered message, and denotes the total number of bits in the message. The error rate (ϵ) is inversely equivalent to decoding accuracy, where . For example, an error rate of 0.02 (2%) indicates a decoding accuracy of 98%.
The peak signal-to-noise ratio (PSNR) [43] is used to objectively evaluate the quality of an image after steganography, compression, or other processing, by calculating the pixel differences at corresponding positions in two images. A higher PSNR value indicates less image degradation, suggesting that the image has undergone minimal distortion.
where is the maximum possible value of image pixels, and represents the mean squared error, defined as follows:
where is the total number of pixels in the image, and and are the pixel values of the stego image and the cover image, respectively.
The structural similarity index (SSIM) [44] is a critical metric for assessing the similarity between two images. Unlike PSNR, SSIM focuses not only on pixel-level differences but also on capturing structural changes within the image. It is defined as follows:
where and represent the means of the original and stego images, respectively; and are their respective variances; and is their covariance. Constants and are used for computational stability, where is the dynamic range of the image, typically set to 255, and , .
The Feature Similarity Index (FSIM) is a novel image quality assessment metric designed to measure the similarity between two images. Unlike traditional metrics such as Peak Signal-to-Noise Ratio (PSNR) or Structural Similarity Index (SSIM), FSIM assesses perceptual image quality by analyzing two complementary low-level features—Phase Congruency (PC) and Gradient Magnitude (GM). Since our method integrates both edge and global information within the shared expansion path of the dual-stream U-Net, we also consider FSIM as an evaluation metric. FSIM is defined as follows:
where are the reference and distorted images, respectively. is the local similarity at pixel x, computed as the product of the similarities of PC and GM features:
Here, are the similarity measures for PC and GM features, respectively. is the maximum PC value at pixel x between the two images, used as a weighting function to reflect the importance of each pixel in the overall similarity. The similarity measures for PC and GM are defined as follows:
where are the PC values of at pixel x. are the GM values of at pixel x. and are positive constants used to stabilize the similarity measures. Their values depend on the dynamic range of PC and GM values, respectively. By integrating the error rate, PSNR, SSIM, and FSIM we can comprehensively evaluate the performance of the steganography algorithm in terms of message recovery accuracy and the quality of the stego images.
4.3. Experimental Results
The performance of our method on the Div2k, MS-COCO, and CelebA datasets is presented in Table 3, Table 4, Table 5 and Table 6. Comparing our method with other widely used steganographic techniques clearly highlights its significant advantages. Across different embedding payloads (ranging from 1 bit to 3 bits), our method consistently achieves a 0% error rate, significantly outperforming the SteganoGAN and FNNS series methods, which exhibit a rapid increase in error rates under higher payloads (for instance, SteganoGAN’s error rate rises to 13.74% at a 3-bit payload), a result that is unacceptable in image steganography. While the PSNR and SSIM values decline as the amount of embedded data increases, our method continues to demonstrate exceptional robustness in error rate control compared to other advanced techniques. This is especially evident under high payload conditions (e.g., 4 bits), where it still maintains excellent decoding accuracy and visual quality.

Table 3.
Comparison with other state-of-the-art steganography algorithms with different payloads on Div2k dataset.

Table 4.
Comparison with other state-of-the-art steganography algorithms with different payloads on MS-COCO dataset.

Table 5.
Comparison with other state-of-the-art steganography algorithms with different payloads on CelebA dataset.

Table 6.
Comparison of FSIM performance of different steganographic methods under multi-load conditions.
It is worth noting that, in terms of the FSIM metric, our method has achieved optimal performance across all test datasets. On the Div2k dataset, our method attains FSIM values of 0.9949 and 0.9947 for 1-bit and 2-bit payloads, respectively, significantly outperforming LISO (0.9925 and 0.9836) and other comparison methods. On the MS-COCO dataset, our method is even more outstanding, maintaining a high FSIM value of 0.9892 at a 4-bit payload, compared to LISO’s 0.8815 under the same conditions. Similarly, on the CelebA dataset, our method consistently achieves superior FSIM values across all payload conditions. These results indicate that our method effectively preserves edge and global information during the steganography process.
4.4. Model Complexity Analysis
In terms of model complexity analysis, we compared the proposed method with other steganographic algorithms, as summarized in Table 7. Regarding computational complexity, our method requires 330.353 FLOPs, which is significantly higher than SteganoGAN and FNNS but 19% lower than LISO (408.770 GFLOPs). For parameter count, our model utilizes 2.502M parameters, exceeding those of comparative methods, primarily due to the adoption of a more complex network architecture to enhance steganography performance. In processing speed, our method achieves an average of 0.4594 s per image, outperforming LISO (0.5993 s/img) but lagging behind SteganoGAN and FNNS. Overall, while our approach demands relatively higher computational resources, it achieves superior steganographic performance through moderate computational overhead, demonstrating a favorable performance trade-off in practical applications.

Table 7.
Comparison of computational complexity with other steganographic algorithms.
4.5. Robustness Analysis
In the robustness analysis, we comprehensively evaluated the anti-interference capability of our method for hiding 1-bit information on the Div2k dataset. As shown in Table 8, our method demonstrates excellent performance under various common noise conditions. The results show that under three interference conditions—JPEG compression (quality factor of 80), additive Gaussian noise, and multiplicative Gaussian noise—our method maintains a low decoding error rate (3 × 10−3, 7 × 10−4, and 2 × 10−4, respectively). Additionally, the structural similarity index (SSIM) and peak signal-to-noise ratio (PSNR) show good values across all three conditions, indicating that our method effectively preserves image quality.

Table 8.
Robustness performance 1bit on Div2k.
However, it is worth noting that under JPEG compression, the SSIM and PSNR values are relatively lower (0.883 and 33.57, respectively), suggesting that our method has slightly inferior image quality preservation under JPEG compression. This may be due to the significant loss of high-frequency information caused by JPEG compression, which affects both information hiding and image quality.
Overall, the proposed method in this study exhibits good anti-interference capabilities for practical applications, efficiently recovering hidden information under various noise conditions while maintaining satisfactory image quality. Future research can further optimize the algorithm to enhance its robustness under conditions such as JPEG compression.
4.6. Ablation Study
To comprehensively evaluate the effectiveness of our proposed edge-enhanced dual-stream U-Net architecture, multi-scale median attention (MSMA) module, and InceptionDWK module in steganographic models, we conducted a systematic ablation study on the Div2k dataset. The primary goal of this study is to assess the impact of these modules on model performance. By progressively removing each module and observing the resulting performance changes, we quantitatively analyze the contribution of each module.
In the ablation experiments on the edge-enhanced dual-stream U-Net structure (EDSU), we replace the dual-stream structure with the original U-Net structure with the edge-enhanced input stream removed in order to analyze the contribution of the edge-enhancement feature to the quality of the steganographic image and the decoding performance. When the dual-stream structure was replaced with the single-stream U-Net, the experimental results revealed a marked decline in both PSNR and SSIM values (PSNR dropped from 38.92 to 32.51), indicating that the edge-enhanced input stream significantly enhanced the model’s ability to capture detailed information. The dual-stream architecture, by combining color information and edge features, improved both the visual quality and the information integrity of the stego image. Table 9 summarizes the experimental results for different ablation configurations. As shown in the table, the removal of these modules led to varying degrees of performance degradation across metrics such as peak signal-to-noise ratio (PSNR), structural similarity index (SSIM), and error rate, further underscoring the essential role these modules play in the model.

Table 9.
Ablation experiments results on the Div2k dataset.
To evaluate the effectiveness of the multi-scale median attention (MSMA) module, we conducted a controlled ablation experiment. First, we constructed a dual-stream baseline model, excluding the influence of the InceptionDWK module. Based on this baseline, we replaced the attention module in turn with the CBAM [37] and ECA [46] attention mechanisms. Using the same training strategy, we performed comparative validation on a standard dataset. As shown in Table 10, quantitative results demonstrate that MSMA achieves significant improvements in PSNR, SSIM, and reconstruction error.

Table 10.
Ablation experiments results of MSMA attention mechanism on the Div2k dataset.
4.7. Visualisation and Analysis of Results
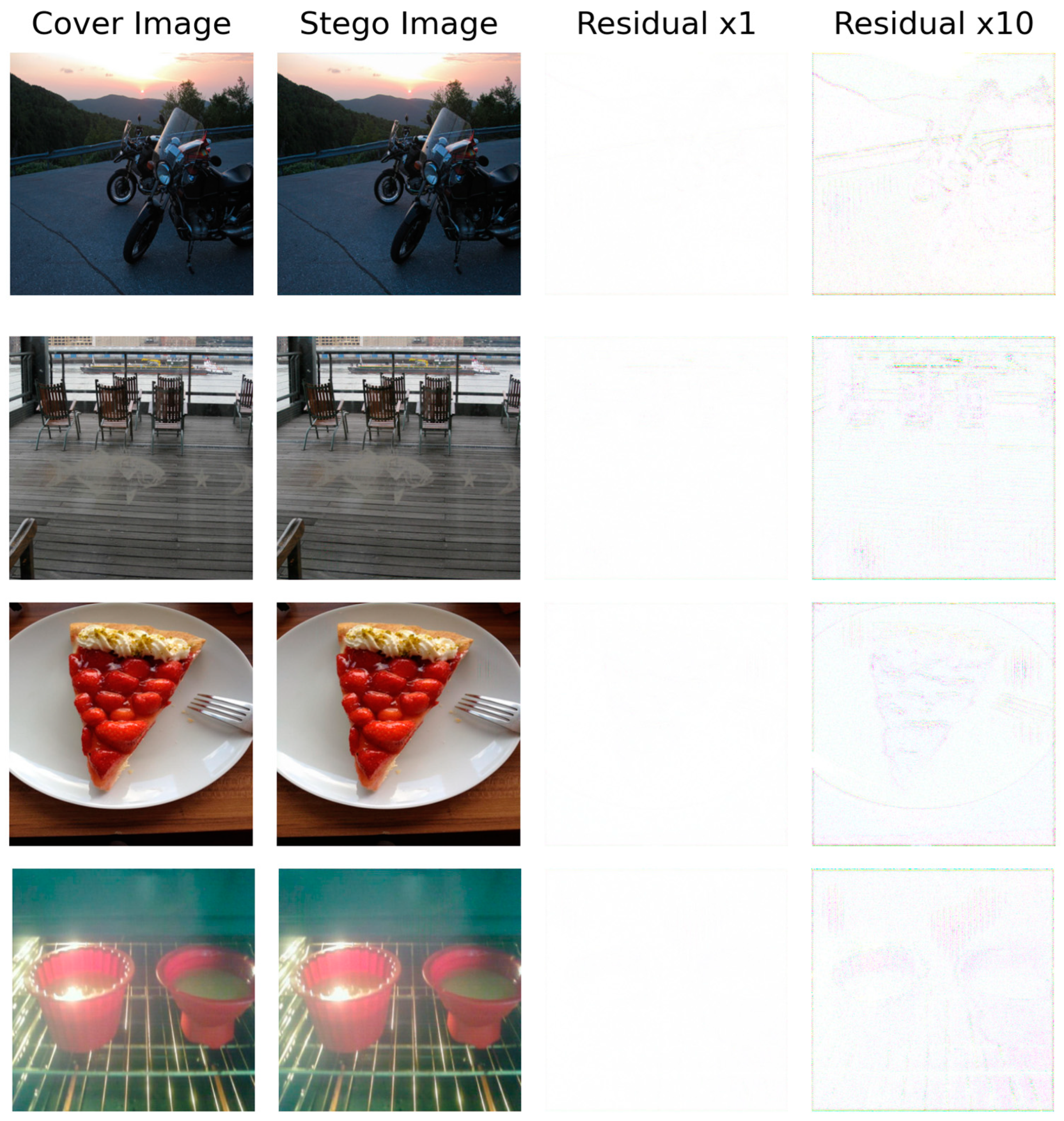
Image-hiding technology must ensure imperceptibility in a subjective sense. During subjective visual evaluations, we observed that the generated stego images are nearly indistinguishable from the cover images when viewed with the naked eye. To further verify the security of the stego images, we conducted residual analysis, which calculates the difference between the stego and cover images to produce a residual map that visually highlights their differences. Four image sets were randomly selected for this analysis, and residual maps were generated for both the cover and stego images. As illustrated in Figure 5, under a Residual ×1 scale, the residual maps are almost entirely black, indicating that the hidden information is imperceptible and the differences between the images are negligible. When scaled to Residual ×10, only faint contours are visible, with no secret information revealed. These findings demonstrate the high security and imperceptibility of our method, as the embedding process minimally alters the original cover image, enabling the secure concealment and transmission of information.
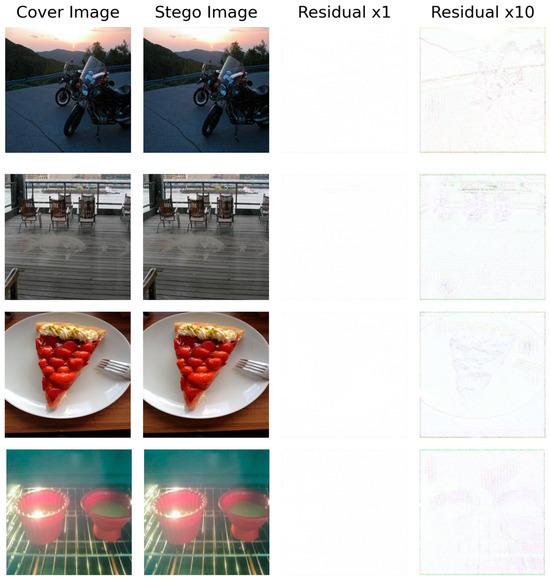
Figure 5.
Visualization of cover, steganography, and corresponding residual images.
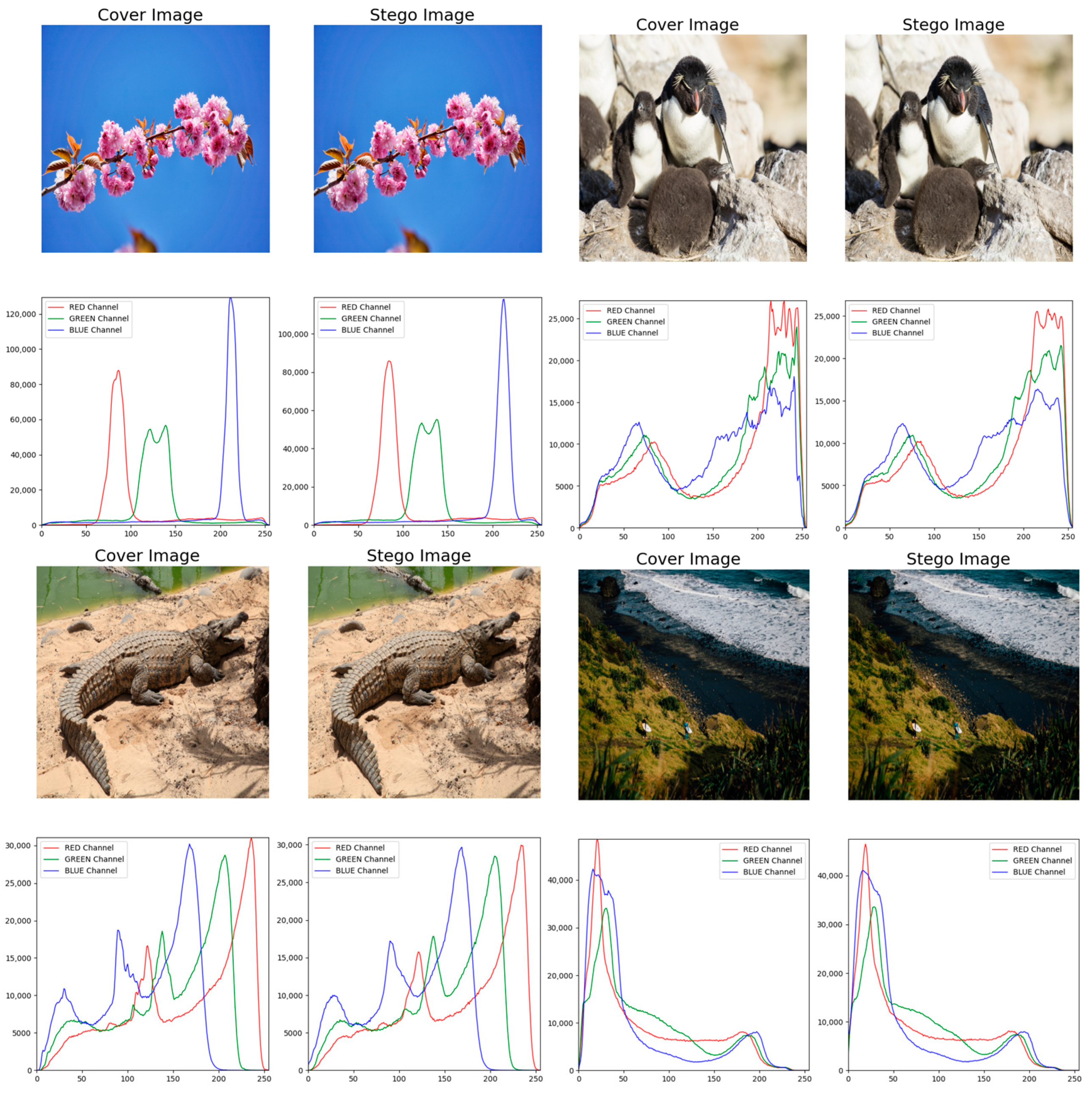
In addition to residual analysis, we also evaluated the statistical consistency between the stego and cover images using pixel histograms, a tool that visualizes pixel value distributions by dividing the range into intervals and counting pixel frequencies within each. As shown in Figure 6, the first and third columns display the Cover images, while the second and fourth columns show the Stego images. The histograms reveal the distributions of the red, green, and blue channels (R, G, and B values), represented by red, green, and blue lines, respectively. The results indicate minimal differences in pixel value distribution between the Cover and Stego images. Notably, closer examination reveals that the pixel value distributions of the cover images become smoother after embedding the steganographic information. This observation suggests that our method not only effectively embeds secret information but also enhances the statistical properties of the stego images, making their distribution more similar to that of natural images. This improvement bolsters the resistance of stego images to detection, further enhancing the concealment and security of the method.
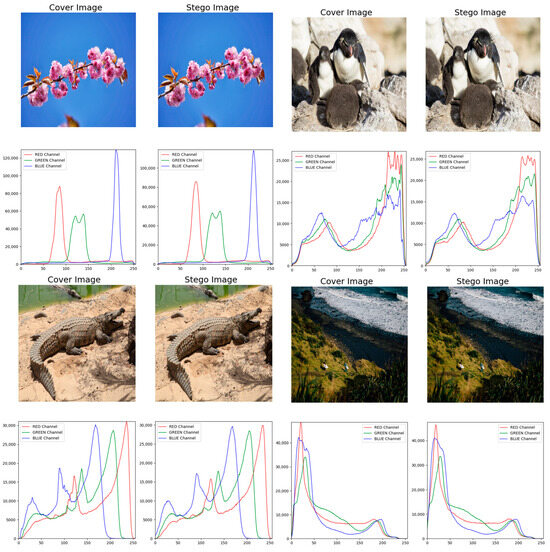
Figure 6.
Model security analysis with histograms. The horizontal axis of a pixel histogram represents pixel intensity values, while the vertical axis indicates the number of pixels at each corresponding intensity value.
4.8. Steganalysis
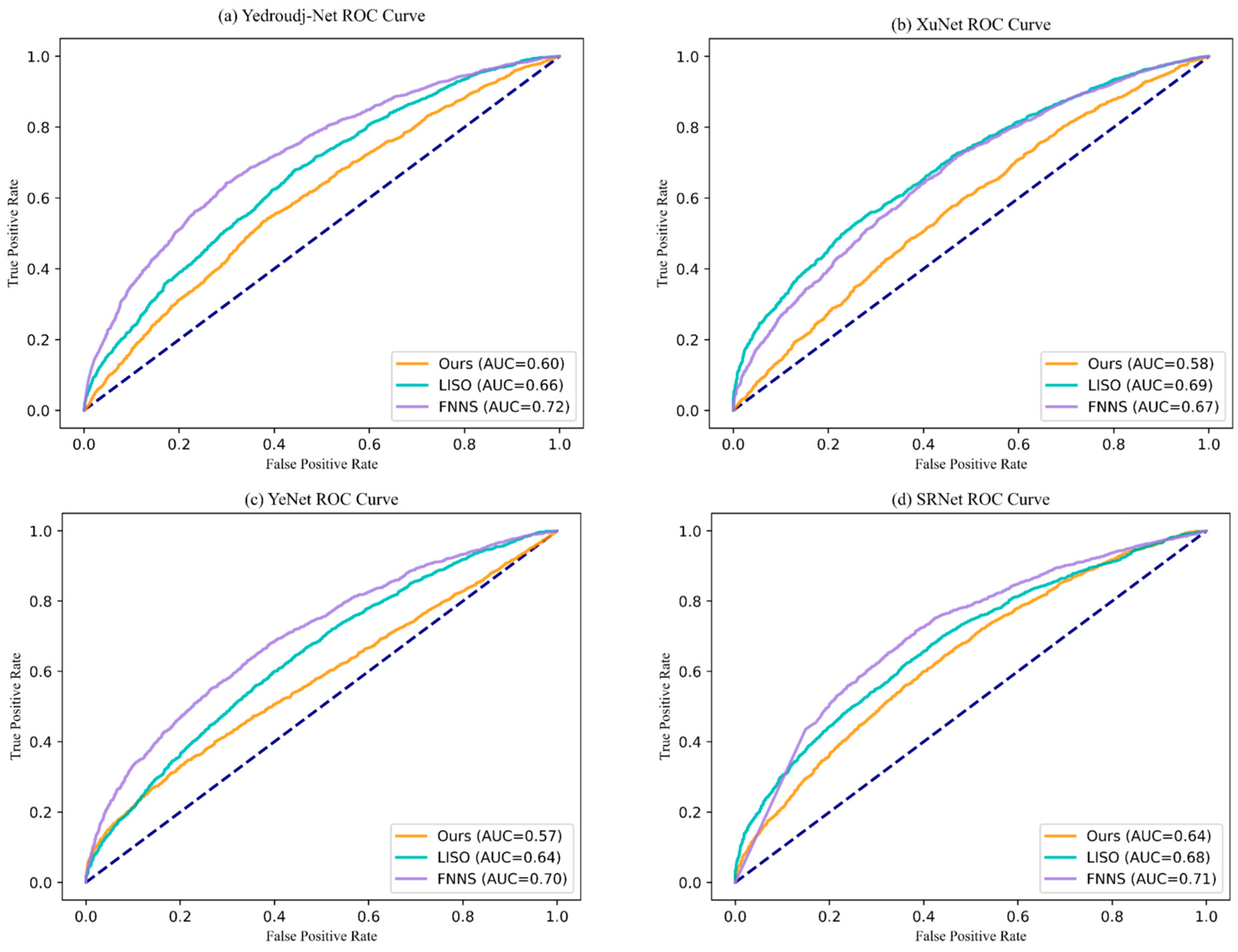
To thoroughly assess the security and detectability of the proposed steganographic method, this study employs four state-of-the-art deep learning-based steganalysis networks for validation: XuNet [47], YeNet [48], SRNet [49], and Yedroudj-Net [50]. Steganalysis aims to distinguish stego images from cover images, thereby evaluating both the imperceptibility and resistance to detection of the steganographic algorithm. Based on the results obtained from these four steganalysis tools, we plotted the Receiver Operating Characteristic (ROC) curve (see Figure 7) to analyze the trade-off between the false positive rate (i.e., misclassifying cover images as stego images) and the true positive rate (i.e., correctly identifying stego images). In Figure 7, the blue diagonal line represents the baseline of random guessing, which serves as a reference for comparing actual model performance. Generally, the closer the ROC curve is to this diagonal, the more the detection results approximate random guessing, indicating a higher level of imperceptibility for the steganographic scheme.
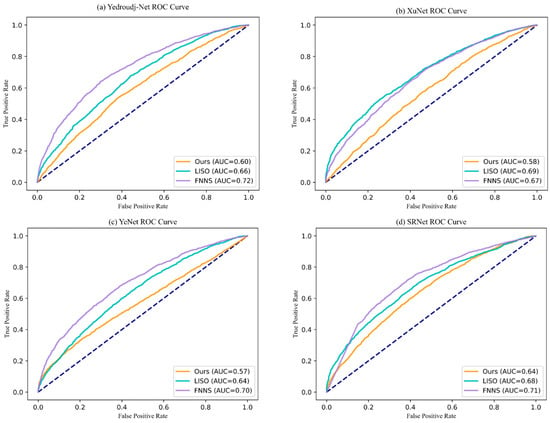
Figure 7.
ROC curve for hidden message detection.
To further validate the security of our method, we conducted comparative experiments with two advanced steganographic methods, LISO and FNNS. We employed the above four deep learning-based steganalysis networks to evaluate the steganographic security of different methods under an embedding payload of 1 bpp. For each steganographic method, we generated 7000 pairs of cover and stego images to retrain the steganalysis networks. As shown in the figure, our method demonstrates significantly stronger robustness against detection compared to LISO and FNNS across all four steganalysis networks.
5. Conclusions
In this paper, we propose a dual-stream U-Net-based image steganography network with edge enhancement to overcome the limitations of existing steganographic techniques in edge feature extraction and global feature fusion while improving the quality of stego images and decoding accuracy. Our dual-stream U-Net architecture integrates edge-enhanced images with multi-scale median attention, significantly enhancing the model’s feature representation capability and information embedding efficiency. Furthermore, the proposed InceptionDMK module strengthens the network’s multi-scale feature extraction, enabling steganographic information to be embedded more effectively in complex visual environments. These contributions collectively enhance the network’s capability to balance high embedding capacity with minimal visual distortion and decoding errors. Experimental results demonstrate that our method generates high-quality stego images across multiple public datasets, achieving a decoding accuracy close to 100% and significantly outperforming existing approaches in terms of PSNR and SSIM. Compared to current techniques, our method maintains a high steganographic capacity while achieving lower error rates and superior visual quality, which is of great significance in the field of information security.
Nevertheless, our study has some limitations. First, when handling high payload information, further improvements in steganographic capacity may be constrained. Additionally, the computational complexity of the model and parameter tuning require further optimization. Moreover, while the Sobel operator offers advantages in computational efficiency, stability, and adaptability, we acknowledge the significant potential of deep learning-based methods for complex edge detection tasks. In particular, approaches such as HED, DexiNed, RCN, and BDCN enable more precise edge extraction. In future work, we plan to refine the network architecture to reduce computational overhead while exploring the application of steganographic techniques to other multimedia formats, such as video and audio. Additionally, future work will involve evaluating the model on security-sensitive datasets to validate its robustness in real-world applications while exploring the integration of advanced deep learning-based edge detection methods to further enhance edge feature extraction and steganographic performance. We believe that with continued advancements, our approach will introduce new possibilities and challenges for steganography in the field of information security.
Author Contributions
Conceptualization, Y.Z. and Z.L.; methodology, P.J. and Y.Z.; formal analysis, Y.Z.; investigation, Y.Z. and Z.L.; resources, P.J.; data curation, Y.Z.; writing—original draft preparation, Y.Z.; writing—review and editing, P.J.; visualization, Y.Z.; supervision, P.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to express their gratitude to the Graduate School and the College of Computer and Information Engineering at Nanjing Tech University for this research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Denis, R.; Madhubala, P. Hybrid data encryption model integrating multi-objective adaptive genetic algorithm for secure medical data communication over cloud-based healthcare systems. Multimed. Tools Appl. 2021, 80, 21165–21202. [Google Scholar] [CrossRef]
- Yang, L.; Deng, H.; Dang, X. A novel coverless information hiding method based on the most significant bit of the cover image. IEEE Access 2020, 8, 108579–108591. [Google Scholar] [CrossRef]
- Johnson, N.F.; Jajodia, S. Exploring steganography: Seeing the unseen. Computer 1998, 31, 26–34. [Google Scholar] [CrossRef]
- Wu, D.C.; Tsai, W.H. A steganographic method for images by pixel-value differencing. Pattern Recognit. Lett. 2003, 24, 1613–1626. [Google Scholar] [CrossRef]
- Ramkumar, M.; Akansu, A.N.; Alatan, A. A robust data hiding scheme for images using DFT. In Proceedings of the International Conference on Image Processing, Kobe, Japan, 24–28 October 1999; pp. 211–215. [Google Scholar]
- Kaur, B.; Kaur, A.; Singh, J. Steganographic approach for hiding image in DCT domain. Int. J. Adv. Eng. Technol. 2011, 1, 72–78. [Google Scholar]
- Chen, P.Y.; Lin, H.J. A DWT based approach for image steganography. Int. J. Appl. Sci. Eng. 2006, 4, 275–290. [Google Scholar]
- Filler, T.; Judas, J.; Fridrich, J. Minimizing additive distortion in steganography using syndrometrellis codes. IEEE Trans. Inf. Forensics Secur. 2011, 6, 920–935. [Google Scholar] [CrossRef]
- Pevný, T.; Filler, T.; Bas, P. Using high-dimensional image models to perform highly undetectable steganography. In Proceedings of the International Workshop on Information Hiding, Calgary, AB, Canada, 28–30 June 2010; Springer: Calgary, AB, Canada, 2010; p. 161177. [Google Scholar]
- Holub, V.; Fridrich, J. Designing steganographic distortion using directional filters. In Proceedings of the 2012 IEEE International Workshop on Information Forensics and Security (WIFS), Costa, Adeje, Spain, 2–5 December 2012; IEEE Computer Society: Washington, DC, USA, 2013; pp. 234–239. [Google Scholar]
- Holub, V.; Fridrich, J. Digital image steganography using universal distortion. In Proceedings of the First ACM Workshop on Information Hiding and Multimedia Security, Montpellier, France, 17–19 June 2013; ACM: Montpellier, France; p. 5968. [Google Scholar]
- Baluja, S. Hiding images in plain sight: Deep steganography. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; The MIT Press: Cambridge, MA, USA, 2017; Volume 30, pp. 2069–2079. [Google Scholar]
- Zhu, J.; Kaplan, R.; Johnson, J.; Fei-Fei, L. HiDDeN: Hiding data with deep networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Duan, X.; Jia, K.; Li, B.; Guo, D.; Zhang, E.; Qin, C. Reversible image steganography scheme based on a U-Net structure. IEEE Access 2019, 7, 9314–9323. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; MIT Press: Cambridge, MA, USA, 2014; Volume 27. [Google Scholar]
- Zhang, K.A.; Cuesta-Infante, A.; Xu, L.; Veeramachaneni, K. Steganogan High capacity image steganography with gans. arXiv 2019, arXiv:1901.03892. [Google Scholar]
- Tan, J.; Liao, X.; Liu, J.; Cao, Y.; Jiang, H. Channel attention image steganography with generative adversarial networks. IEEE Trans. Netw. Sci. Eng. 2021, 9, 888–903. [Google Scholar] [CrossRef]
- Chen, X.; Kishore, V.; Weinberger, K.Q. Learning iterative neural optimizers for image steganography. In Proceedings of the Eleventh International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2022. [Google Scholar]
- Westfeld, A.; Pfitzmann, A. Attacks on Steganographic Systems International Work·50·Shop on Information Hiding; Springer: Berlin/Heidelberg, Germany, 1999; pp. 61–76. [Google Scholar]
- Jessica, F.; Goljan, M.; Du, R. Reliable detection of LSB steganography in color and grayscale images. In Proceedings of the 2001 Workshop on Multimedia and Security: New Challenges, Ottawa, ON, Canada, 5 October 2001; pp. 27–30. [Google Scholar]
- Westfeldt, A. F5–a steganographic algorithm. In Proceedings of the International Workshop on Information Hiding, Pittsburgh, PA, USA, 25–27 April 2001; Springer: Berlin/Heidelberg, Germany; pp. 289–302. [Google Scholar]
- Wu, H.C.; Wu, N.I.; Tsai, C.S.; Hwang, M.S. Image steganographic scheme based on pixel-value differencing and LSB replacement methods. IEE Proc.-Vis. Image Signal Process. 2005, 152, 611–6157. [Google Scholar] [CrossRef]
- Wang, C.M.; Wu, N.I.; Tsai, C.S.; Hwang, M.S. A high quality steganographic method with pixel-value differencing and modulus function. J. Syst. Softw. 2008, 81, 150–158. [Google Scholar] [CrossRef]
- Hong, W.; Chen, T.S.; Luo, C.W. Data embedding using pixel value differencing and diamond encoding with multiple-base notational system. J. Syst. Softw. 2012, 85, 1166–1175. [Google Scholar] [CrossRef]
- Li, B.; Tan, S.; Wang, M.; Huang, J. Investigation on cost assignment in spatial image steganography. IEEE Trans. Inf. Forensics Secur. 2014, 9, 1264–1277. [Google Scholar] [CrossRef]
- Hayes, J.; Danezis, G. Generating steganographic images via adversarial training. In Proceedings of the NIPS, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Li, Y.; Liu, J.; Liu, X.; Wang, X.; Gao, X.; Zhang, Y. HCISNet: Higher capacity invisible image steganographic network. IET Image Process. 2021, 15, 3332–3346. [Google Scholar] [CrossRef]
- Zhang, S.; Li, H.; Lim, L.; Lu, J.; Zuo, Z. A high-capacity steganography algorithm based on adaptive frequency channel attention networks. Sensors 2022, 22, 7844. [Google Scholar] [CrossRef] [PubMed]
- Jing, J.; Deng, X.; Xu, M.; Wang, J.; Guan, Z. Hinet: Deep image hiding by invertible network. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021; pp. 4733–4742. [Google Scholar]
- Kishore, V.; Chen, X.; Wang, Y.; Li, B.; Weinberger, K.Q. Fixed Neural Network Steganography: Train the Images, Not the Network. In Proceedings of the International Conference on Learning Representations (ICLR), Virtual, 25–29 April 2022. [Google Scholar]
- Bui, T.; Agarwal, S.; Yu, N.; Collomosse, J. RoSteALS: Robust Steganography using Autoencoder Latent Space. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Vancouver, BC, Canada, 18–22 June 2023; pp. 933–942. [Google Scholar]
- Hayat, M.; Aramvith, S. E-SEVSR—Edge Guided Stereo Endoscopic Video Super-Resolution. IEEE Access 2024, 12, 30893–30906. [Google Scholar] [CrossRef]
- Song, B.; Wei, P.; Wu, S.; Lin, Y.; Zhou, W. A survey on Deep-Learning-based image steganography. Expert Syst. Appl. 2024, 254, 124390. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar] [CrossRef]
- Hayat, M. Squeeze & Excitation joint with Combined Channel and Spatial Attention for Pathology Image Super-Resolution. Frankl. Open 2024, 8, 100170. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. Shufflenet: An extremely efficient convolutional neural network for mobile devices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 8–22 June 2018; pp. 6848–6856. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Agustsson, E.; Timofte, R. NTIRE 2017 challenge on single image superresolution: Dataset and study. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 1122–1131. [Google Scholar]
- Lin, T.-Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Doll, P.; Zitnick, C.L. Microsoft coco: Common objects in context. In Proceedings of the European Conference on Computer Vision, Zürich, Switzerland, 6–12 September 2014; Springer: Berlin/Heidelberg, Germany; pp. 740–755. [Google Scholar]
- Liu, Z.; Luo, P.; Wang, X.; Tang, X. Large-scale celebfaces attributes (celeba) dataset. Retrieved August 2018, 15, 11. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Ponomarenko, N.; Ieremeiev, O.; Lukin, V.; Egiazarian, K.; Jin, L.; Astola, J.; Vozel, B.; Chehdi, K.; Carli, M.; Battisti, F.; et al. Color image database TID2013: Peculiarities and preliminary results. In Proceedings of the European Workshop on Visual Information Processing (EUVIP), Paris, France, 10–12 June 2013; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A Feature Similarity Index for Image Quality Assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Wu, B.; Zhu, P.; Li, P.; Zuo, W.; Hu, Q. ECA-Net: Efficient channel attention for deep convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11534–11542. [Google Scholar]
- Xu, G.; Wu, H.Z.; Shi, Y.Q. Structural design of convolutional neural networks for steganalysis. IEEE Signal Process. Lett. 2016, 23, 708–712. [Google Scholar] [CrossRef]
- Ye, J.; Ni, J.; Yi, Y. Deep learning hierarchical representations for image steganalysis. IEEE Trans. Inf. Forensics Secur. 2017, 12, 2545–2557. [Google Scholar] [CrossRef]
- Boroumand, M.; Chen, M.; Fridrich, J. Deep residual network for steganalysis of digital images. IEEE Trans. Inf. Forensics Secur. 2018, 14, 1181–1193. [Google Scholar] [CrossRef]
- Yedroudj, M.; Comby, F.; Chaumont, M. Yedroudj-Net: An Efficient CNN for Spatial Steganalysis. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 2092–2096. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).