Power Harvested Maximization for Solar Photovoltaic Energy System Under Static and Dynamic Conditions
Abstract
1. Introduction
- ▪
- Model and design the power and control circuits of the photovoltaic energy conversion system under static and dynamic environments.
- ▪
- Apply and compare two advanced metaheuristics-based MPPT techniques, Cuckoo Search Optimizer and Particle Swarm Optimization, to optimize, simulate, and follow the global maximum power output of the PV energy system in both static and dynamic environments. These algorithms are selected for their proven efficiency and robustness in handling the challenges of non-linear and multi-modal optimization problems such as those arising under partial shading in PV energy systems. CSO is known for its superior convergence speed and ability to escape local optima, while PSO excels in simplicity, adaptability, and achieving high accuracy. By leveraging the strengths of these methods, this study aims to provide a detailed comparative analysis of their performance in maximizing PV system efficiency.
- ▪
- Investigate the performance of the proposed photovoltaic energy conversion system under both time-variant and -invariant PSCs.
- ▪
- Analyze and compare the effectiveness of the selected metaheuristic-based MPPT techniques in terms of global power tracking, convergence time, and oscillations around the steady state.
2. Solar Photovoltaic Power System Description Under Study
3. Maximum Power Point Tracking Algorithms
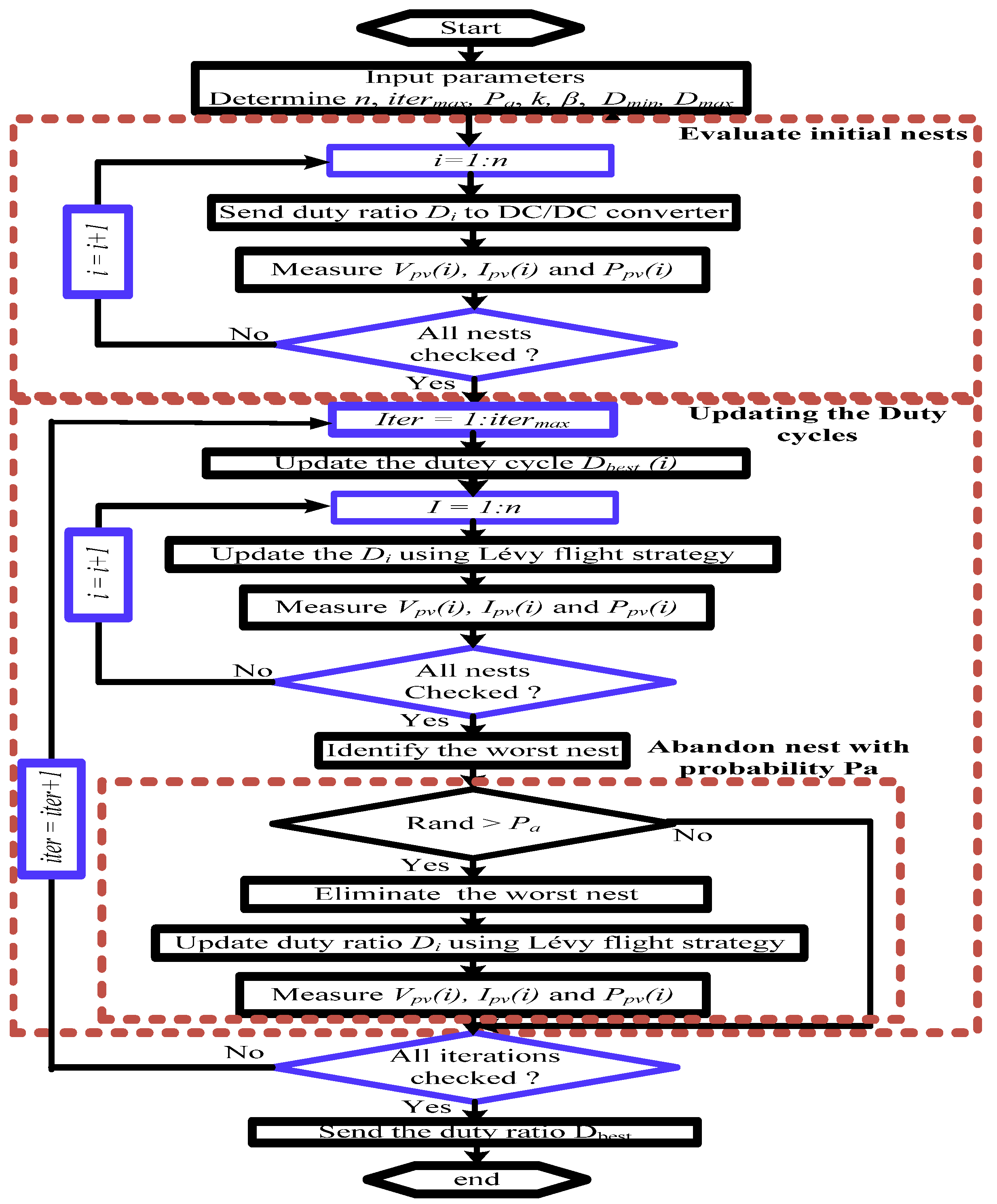
3.1. The Cuckoo Search Optimizer (CSO)
- ▪
- The cuckoo introduces eggs sequentially, placing one egg at a time in a nest chosen at random.
- ▪
- Nests containing superior-quality eggs are retained and may be passed on to subsequent generations.
- ▪
- To enhance the chances of the hatchlings receiving more nourishment, the cuckoo may eliminate some of the host bird’s eggs.
- ▪
- Upon detecting an unfamiliar egg, the host bird faces a decision point. It may either eliminate the cuckoo’s eggs or abandon the nest entirely, opting to construct a new one elsewhere, with a probability denoted as Pa.
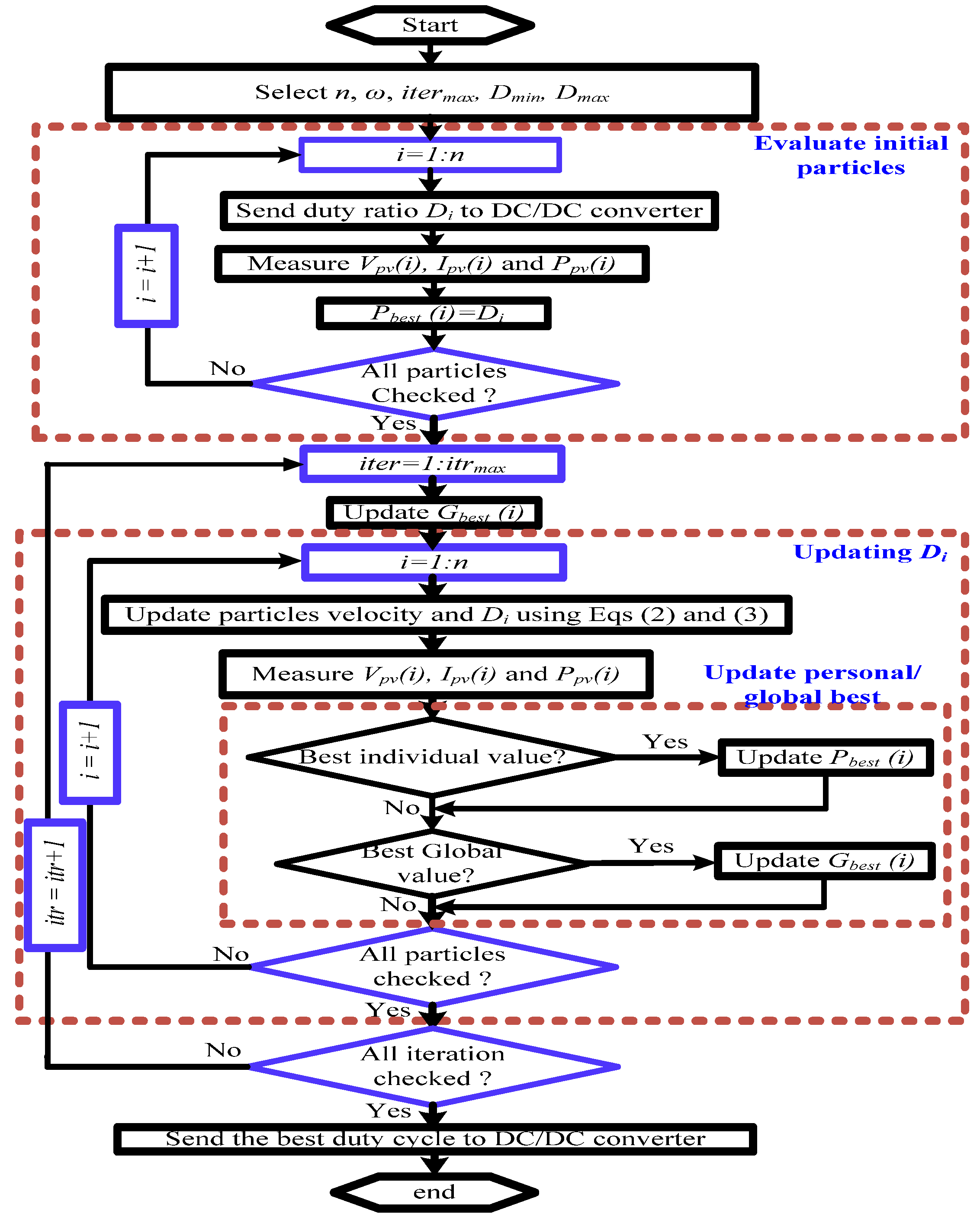
3.2. Particle Swarm Optimization (PSO)
4. Simulation Results and Discussion
5. Conclusions
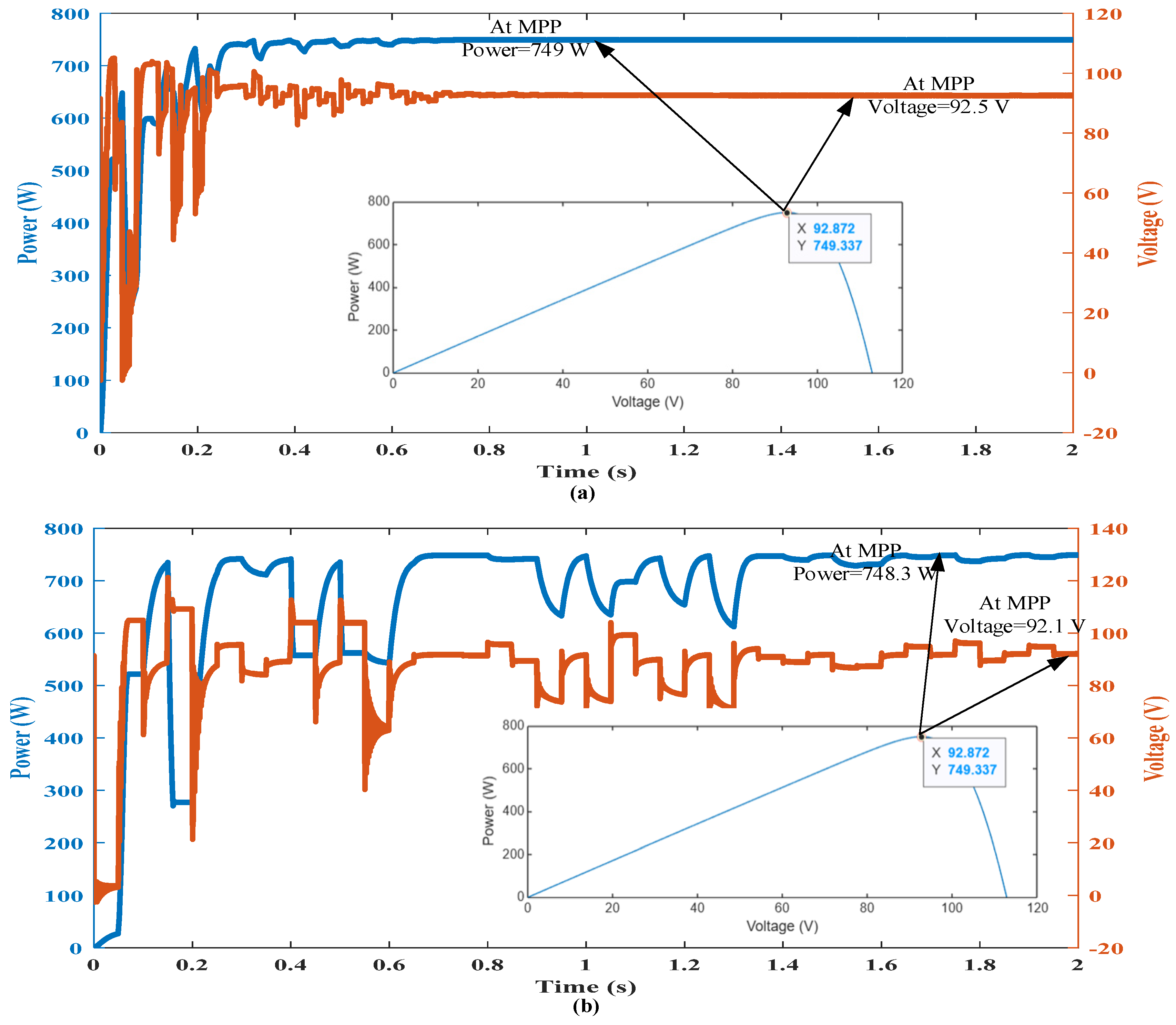
- In static uniform conditions, both CSO and PSO effectively tracked the single peak, with CSO demonstrating faster tracking than PSO. For example, CSO attained a PPV of 743.66 W (99.55% efficiency), outperforming PSO’s 738.5 W (98.8% efficiency). Moreover, PSO showed greater oscillations around the GPP compared with CSO, indicating CSO’s superior stability during steady-state operation.
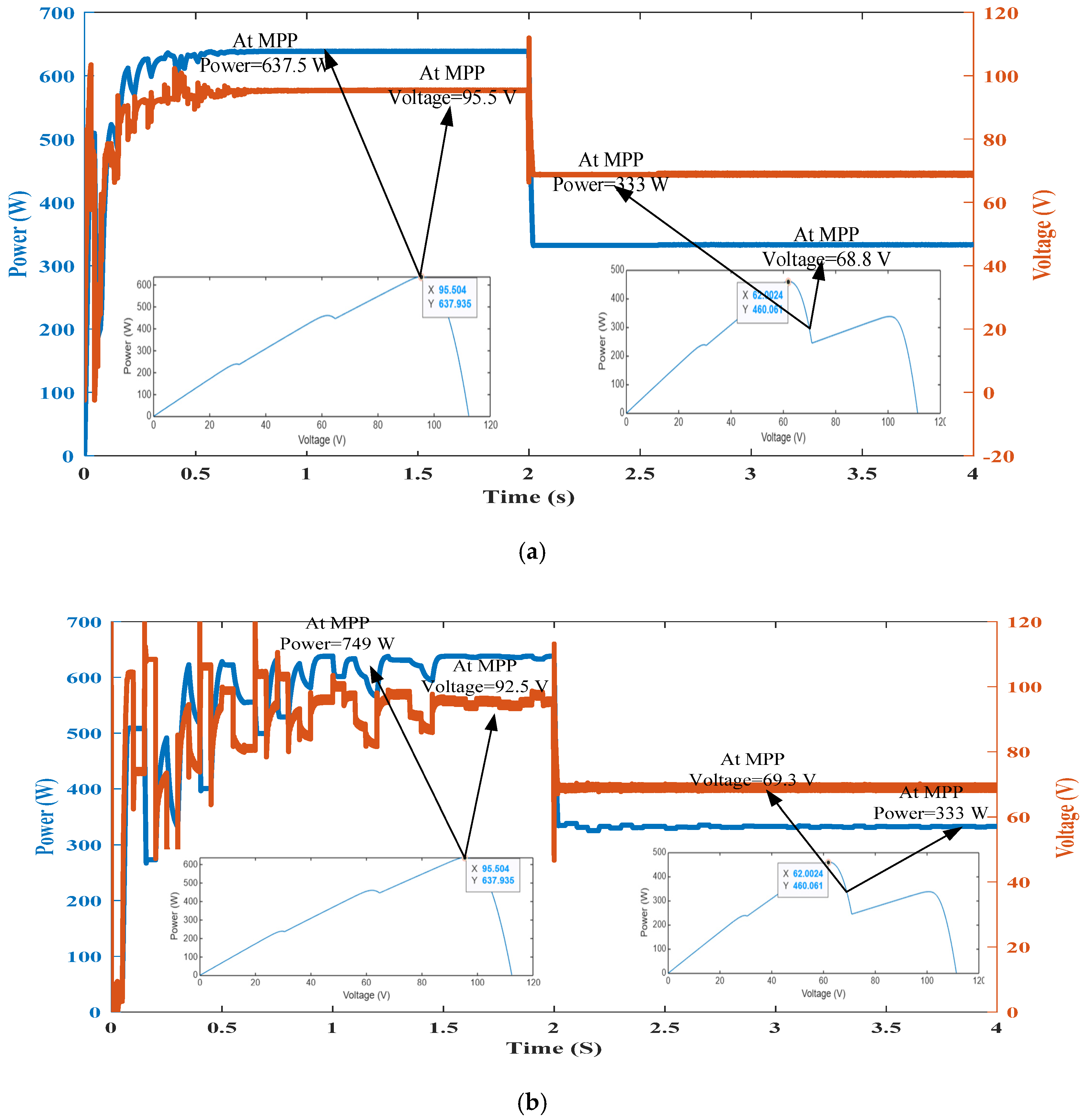
- Under static PSCs, the power–voltage curve displayed a single GPP alongside multiple local peaks. Both algorithms successfully tracked the GPP, but CSO surpassed PSO with quicker tracking and reduced oscillations. In this scenario, both achieved 636.9 W (99.9% efficiency), though CSO’s faster convergence and lower oscillation profile were notable.
- In dynamic uniform conditions, CSO and PSO initially tracked the GPP effectively, but they could not adjust after subsequent irradiance shifts.
- In dynamic PSCs, both algorithms tracked the GPP at first, but they were unable to follow the new GPP following changes in irradiance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Full Form |
| ANN | Artificial neural network |
| CSO | Cuckoo Search Optimization |
| DC | Direct current |
| FLC | Fuzzy logic control |
| GA | Genetic algorithm |
| GPP | Global peak power |
| IBC | Interleaved boost converter |
| IC | Incremental conductance |
| MPP | Maximum power point |
| MPPT | Maximum power point tracking |
| P&O | Perturb and observe |
| PSC | Partial shading condition |
| PSO | Particle Swarm Optimization |
| PV | Photovoltaic |
| SSA-PSO | Salp swarm algorithm–Particle Swarm Optimization |
References
- Kannan, N.; Vakeesan, D. Solar energy for future world: A review. Renew. Sustain. Energy Rev. 2016, 62, 1092–1105. [Google Scholar] [CrossRef]
- Smara, Z.; Aissat, A.; Deboucha, H.; Rezk, H.; Mekhilef, S. An enhanced global MPPT method to mitigate overheating in PV systems under partial shading conditions. Renew. Energy 2024, 234, 121187. [Google Scholar] [CrossRef]
- Li, P.; Silverman, M.; Bazzi, A. Fault-Tolerant Power-Sharing Strategy with A Novel MPPT Method for Parallel PV Converters in Electric Airplanes. In Proceedings of the 2023 IEEE Transportation Electrification Conference & Expo (ITEC), Chiang Mai, Thailand, 28 November–1 December 2023; pp. 1–6. [Google Scholar]
- Khan, M.Y.A.; Liu, H.; Hashemzadeh, S.M.; Yuan, X. A novel high step-up DC–DC converter with improved P&O MPPT for photovoltaic applications. Electr. Power Compon. Syst. 2021, 49, 884–900. [Google Scholar]
- Jabbar, R.I.; Mekhilef, S.; Mubin, M.; Mohammed, K.K. A modified perturb and observe MPPT for a fast and accurate tracking of MPP under varying weather conditions. IEEE Access 2023, 11, 76166–76176. [Google Scholar] [CrossRef]
- Ibrahim, M.H.; Ang, S.P.; Dani, M.N.; Rahman, M.I.; Petra, R.; Sulthan, S.M. Optimizing step-size of perturb & observe and incremental conductance MPPT techniques using PSO for grid-tied PV system. IEEE Access 2023, 11, 13079–13090. [Google Scholar]
- Mahmod Mohammad, A.N.; Mohd Radzi, M.A.; Azis, N.; Shafie, S.; Atiqi Mohd Zainuri, M.A. An Enhanced Adaptive Perturb and Observe Technique for Efficient Maximum Power Point Tracking Under Partial Shading Conditions. Appl. Sci. 2020, 10, 3912. [Google Scholar] [CrossRef]
- Worku, M.Y.; Hassan, M.A.; Maraaba, L.S.; Shafiullah, M.; Elkadeem, M.R.; Hossain, M.I.; Abido, M.A. A comprehensive review of recent maximum power point tracking techniques for photovoltaic systems under partial shading. Sustainability 2023, 15, 11132. [Google Scholar] [CrossRef]
- Ibrahim, A.W.; Zhijian, F.; Farh, H.M.H.; Zhiguo, W.; Ameur, K.; Al-Shamma’a, A.A.; Al-Shaalan, A.M. Dynamic global power extraction of partially shaded PV system using a hybrid MPSO-PID with anti-windup strategy. Eng. Appl. Artif. Intell. 2020, 126, 106965. [Google Scholar]
- Kumar, N.; Nema, S.; Nema, R.K.; Verma, D. A state-of-the-art review on conventional, soft computing, and hybrid techniques for shading mitigation in photovoltaic applications. Int. Trans. Electr. Energy Syst. 2020, 30, e12420. [Google Scholar] [CrossRef]
- Farh, H.M.; Othman, M.F.; Eltamaly, A.M.; Al-Saud, M.S. Maximum power extraction from a partially shaded PV system using an interleaved boost converter. Energies 2018, 11, 2543. [Google Scholar] [CrossRef]
- Ibrahim, A.W.; Zhijian, F.; Farh, H.M.H.; Dagal, I.; Al-Shamma’a, A.A.; Al-Shaalan, A.M. Hybrid SSA-PSO based intelligent direct sliding-mode control for extracting maximum photovoltaic output power and regulating the DC-bus voltage. Int. J. Hydrogen Energy 2024, 51, 348–370. [Google Scholar]
- Farh, H.M.H.; Fathy, A.; Al-Shamma’a, A.A.; Mekhilef, S.; Al-Shaalan, A.M. Global research trends on photovoltaic maximum power extraction: Systematic and scientometric analysis. Sustain. Energy Technol. Assess. 2024, 61, 103585. [Google Scholar] [CrossRef]
- Obeidi, N.; Kermadi, M.; Belmadani, B.; Allag, A.; Achour, L.; Mesbahi, N.; Mekhilef, S. A modified current sensorless approach for maximum power point tracking of partially shaded photovoltaic systems. Energy 2023, 263, 125618. [Google Scholar] [CrossRef]
- Bingöl, O.; Özkaya, B. A comprehensive overview of soft computing based MPPT techniques for partial shading conditions in PV systems. Mühendislik Bilim. Ve Tasarım Derg. 2019, 7, 926–939. [Google Scholar] [CrossRef]
- Ali, M.N.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M. Promising MPPT methods combining metaheuristic, fuzzy-logic and ANN techniques for grid-connected photovoltaic. Sensors 2021, 21, 1244. [Google Scholar] [CrossRef]
- Mehedi, I.M.; Salam, Z.; Ramli, M.Z.; Chin, V.J.; Bassi, H.; Rawa, M.J.H.; Abdullah, M.P. Critical evaluation and review of partial shading mitigation methods for grid-connected PV system using hardware solutions: The module-level and array-level approaches. Renew. Sustain. Energy Rev. 2021, 146, 111138. [Google Scholar] [CrossRef]
- Kushwaha, N.; Yadav, V.K.; Saha, R. Effect of partial shading on photovoltaic systems performance and its mitigation techniques—A review. Energy Sources Part A Recovery Util. Environ. Eff. 2023, 45, 11155–11180. [Google Scholar] [CrossRef]
- Khadidja, S.; Mountassar, M.; M’hamed, B. Comparative study of incremental conductance and perturb & observe MPPT methods for photovoltaic system. In Proceedings of the 2017 International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; pp. 1–6. [Google Scholar]
- Yang, X.S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Rezk, H.; Fathy, A.; Abdelaziz, A.Y. A comparison of different global MPPT techniques based on meta-heuristic algorithms for photovoltaic system subjected to partial shading conditions. Renew. Sustain. Energy Rev. 2017, 74, 377–386. [Google Scholar] [CrossRef]
- Farh, H.M.; Eltamaly, A.M. Maximum power extraction from the photovoltaic system under partial shading conditions. In Modern Maximum Power Point Tracking Techniques for Photovoltaic Energy Systems; Springer International Publishing: Cham, Switzerland, 2019; pp. 107–129. [Google Scholar]
- Farh, H.M.; Eltamaly, A.M.; Ibrahim, A.B.; Othman, M.F.; Al-Saud, M.S. Dynamic global power extraction from partially shaded photovoltaic using deep recurrent neural network and improved PSO techniques. Int. Trans. Electr. Energy Syst. 2019, 29, e12061. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; MHFarh, H.; SAl Saud, M. Impact of PSO reinitialization on the accuracy of dynamic global maximum power detection of variant partially shaded PV systems. Sustainability 2019, 11, 2091. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Farh, H.M.; Al-Saud, M.S. Grade point average assessment for metaheuristic GMPP techniques of partial shaded PV systems. IET Renew. Power Gener. 2019, 13, 1215–1231. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z. A review of maximum power point tracking techniques of PV system for uniform insolation and partial shading condition. Renew. Sustain. Energy Rev. 2013, 19, 475–488. [Google Scholar] [CrossRef]
- Al-Obeidat, F.; Belacel, N.; Carretero, J.A.; Mahanti, P. Automatic parameter settings for the PROAFTN classifier using hybrid particle swarm optimization. In Canadian Conference on Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2010; pp. 184–195. [Google Scholar]
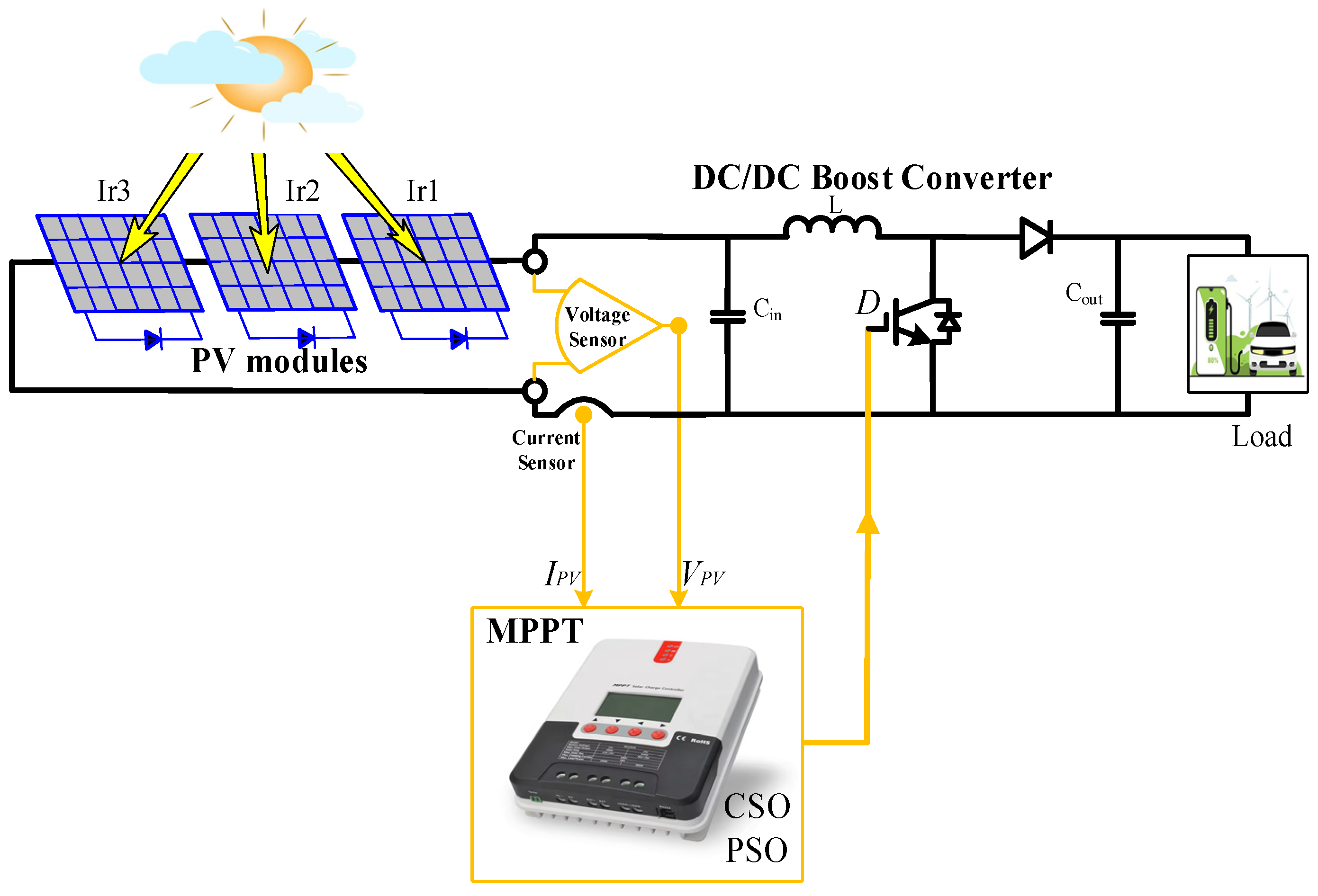
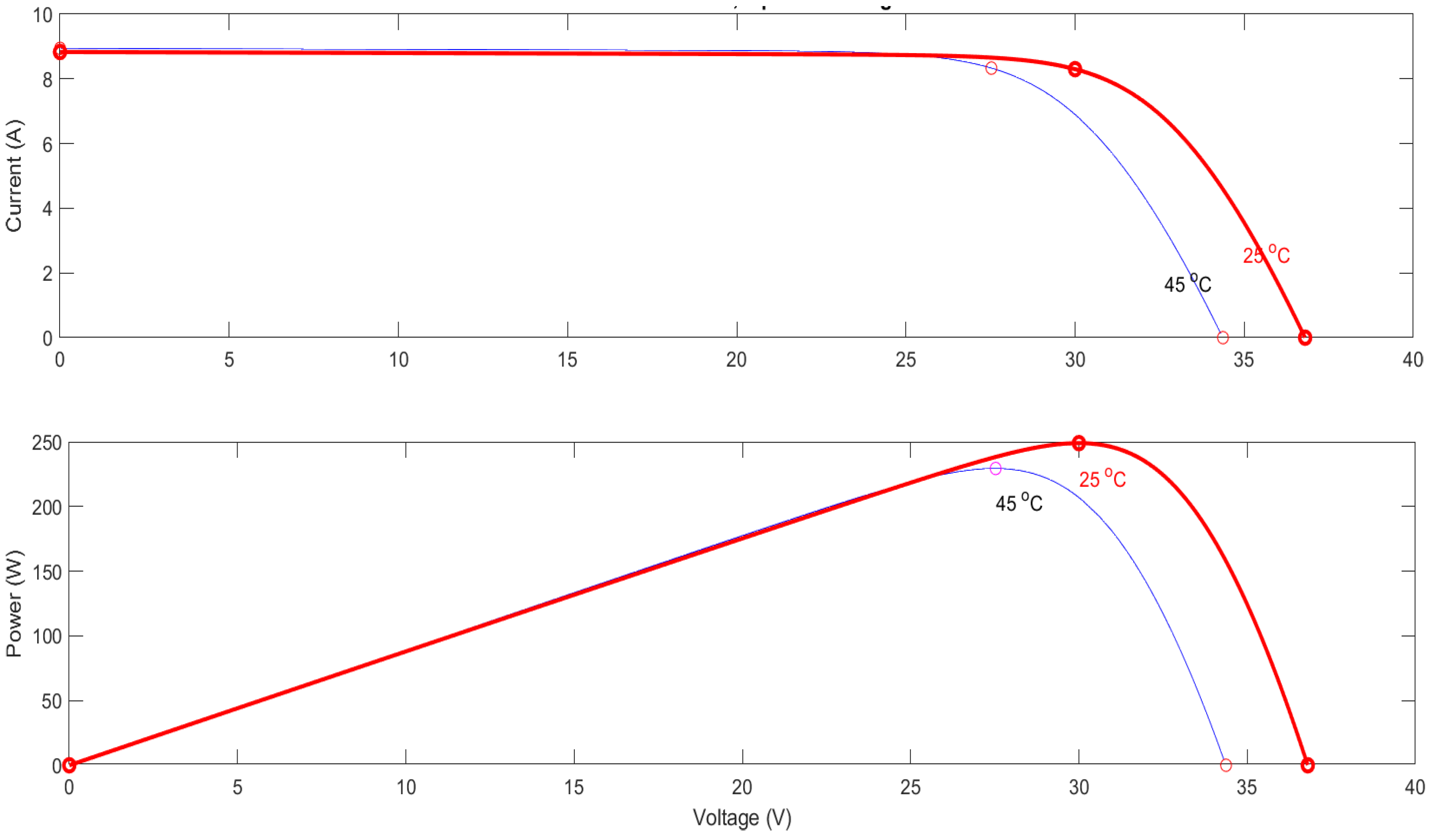


| Parameter | Value |
|---|---|
| Module Type | Polycrystalline |
| Configuration | Single-sided |
| Pmax (W) | 249 W |
| VOpen.circuit (V) | 36.5 V |
| Cells (number of each module) | 60 |
| IShort.circuit (A) | 8.83 A |
| Vmax (V) | 30.2 V |
| Imax (A) | 8.30 A |
| ILight.generated (A) | 8.83 A |
| IDiode saturation (A) | 1.0132 × 10−10 |
| Diode factor of ideality | 0.94812 |
| Parameter | Value |
|---|---|
| fSwitching | f |
| Inductor | L |
| Output capacitor | Co |
| Input capacitor | Cin |
| Load | R |
| Imax (A) | 8.30 A |
| ILight.generated (A) | 8.83 A |
| IDiode saturation (A) | 1.0132 × 10−10 |
| Diode factor of ideality | 0.94812 |
| 1 | Initialize the population of host nests (solutions) within the search space (n, β, Pa, k, itermax, Dmin, Dmax). |
| 2 | Assess the fitness of each nest using the objective function, which in this case is the PV energy system’s power output under varying environmental circumstances. |
| 3 | Update the best solution: Identify the best solution (nest) based on the fitness evaluation. |
| 4 | Generate new solutions: Employ the cuckoo’s random walk behavior to generate new candidate solutions using the following equation: |
| 5 | Evaluate new solutions: Evaluate the fitness of the new candidate solutions. |
| 6 | Replace solutions: Replace the host nests with the new solutions based on a predefined selection criterion. If rand > pa, apply step 7; otherwise, apply step 4. |
| 7 | Destroy nests: With a probability of Pa, certain nests are destroyed, and new random nests are generated to replace them. Evaluate the fitness of all new nests. |
| 8 | Update the best solution: Identify the best solution (nest) based on the fitness evaluation. |
| 9 | Check for the termination criteria: If the stopping condition are met, stop the algorithm and output the GPP. Otherwise, go to step 4. |
| Initialize the population of host nests within the search space (CSO parameters: n, β, Pa, k, itermax, Dmin, Dmax). |
| 1 | Initialize the population of particles within the search space, each with a position and velocity; i.e., define PSO coefficients ω, c1, and c2 for the global peak search, sequentially send duty ratios, and ascertain the corresponding power. |
| 2 | Evaluate the fitness of each particle using the objective function representing the PV system’s power output under varying environmental conditions. |
| 3 | Update the best solution for each particle and the global best solution based on the fitness evaluation. |
| 4 | Update the velocity and position of each particle using the following: For particle i: |
| 5 | Check for the termination criteria: If the stopping criteria are met, stop the algorithm and output the GPP. Otherwise, go to step 3. |
| Cases | Scenario #1 | |
|---|---|---|
| Theoretical values | Irradiance (W/m2) | [1000,1000,1000] |
| PMPP (W) | 749.34 | |
| VMPP (V) | 92.9 | |
| PSO results | PPV (W) | 748 |
| VPV (V) | 92.1 | |
| Tracking time (s) | 1.6 | |
| PSO Efficiency | 99.59% | |
| CSO results | PPV (W) | 749 |
| VPV (V) | 92.5 | |
| Tracking time (s) | 0.6 | |
| PSO Efficiency | 99.73% | |
| Cases | Scenario #3 | ||
|---|---|---|---|
| Theoretical values | Time | (0–2.0 s) | (2.0–4 s) |
| Irradiance (W/m2) | [1000,1000,1000] | [850,850,850] | |
| PMPP (W) | 749.3 | 638.4 | |
| VMPP (V) | 92.9 | 92.8 | |
| PSO results | PPV (W) | 746 | 525 |
| VPV (V) | 92.5 | 76.4 | |
| PSO Efficiency | 98.8% | 91.6% | |
| CSO results | PPV (W) | 749 | 593 |
| VPV (V) | 92.5 | 82.4 | |
| PSO Efficiency | 99.55% | 93.3% | |
| Cases | Scenario #4 | ||
|---|---|---|---|
| Theoretical values | Time | (0–2.0 s) | (2.0–4 s) |
| Irradiance (W/m2) | [1000,900,800] | [1000,400,900] | |
| PMPP (W) | 637.9 | 460.1 | |
| VMPP (V) | 95.5 | 62 | |
| PSO results | PPV (W) | 637.7 | 332 |
| VPV (V) | 95.5 | 69.3 | |
| PSO Efficiency | 99.9% | 72.2% | |
| CSO results | PPV (W) | 637.5 | 333 |
| VPV (V) | 95.5 | 68.8 | |
| PSO Efficiency | 99.9% | 72.2% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Shamma’a, A.A.; Hussein Farh, H.M. Power Harvested Maximization for Solar Photovoltaic Energy System Under Static and Dynamic Conditions. Appl. Sci. 2025, 15, 4486. https://doi.org/10.3390/app15084486
Al-Shamma’a AA, Hussein Farh HM. Power Harvested Maximization for Solar Photovoltaic Energy System Under Static and Dynamic Conditions. Applied Sciences. 2025; 15(8):4486. https://doi.org/10.3390/app15084486
Chicago/Turabian StyleAl-Shamma’a, Abdullrahman A., and Hassan M. Hussein Farh. 2025. "Power Harvested Maximization for Solar Photovoltaic Energy System Under Static and Dynamic Conditions" Applied Sciences 15, no. 8: 4486. https://doi.org/10.3390/app15084486
APA StyleAl-Shamma’a, A. A., & Hussein Farh, H. M. (2025). Power Harvested Maximization for Solar Photovoltaic Energy System Under Static and Dynamic Conditions. Applied Sciences, 15(8), 4486. https://doi.org/10.3390/app15084486








