Modified Grey Wolf Optimizer and Application in Parameter Optimization of PI Controller
Abstract
Featured Application
Abstract
1. Introduction
2. Related Works
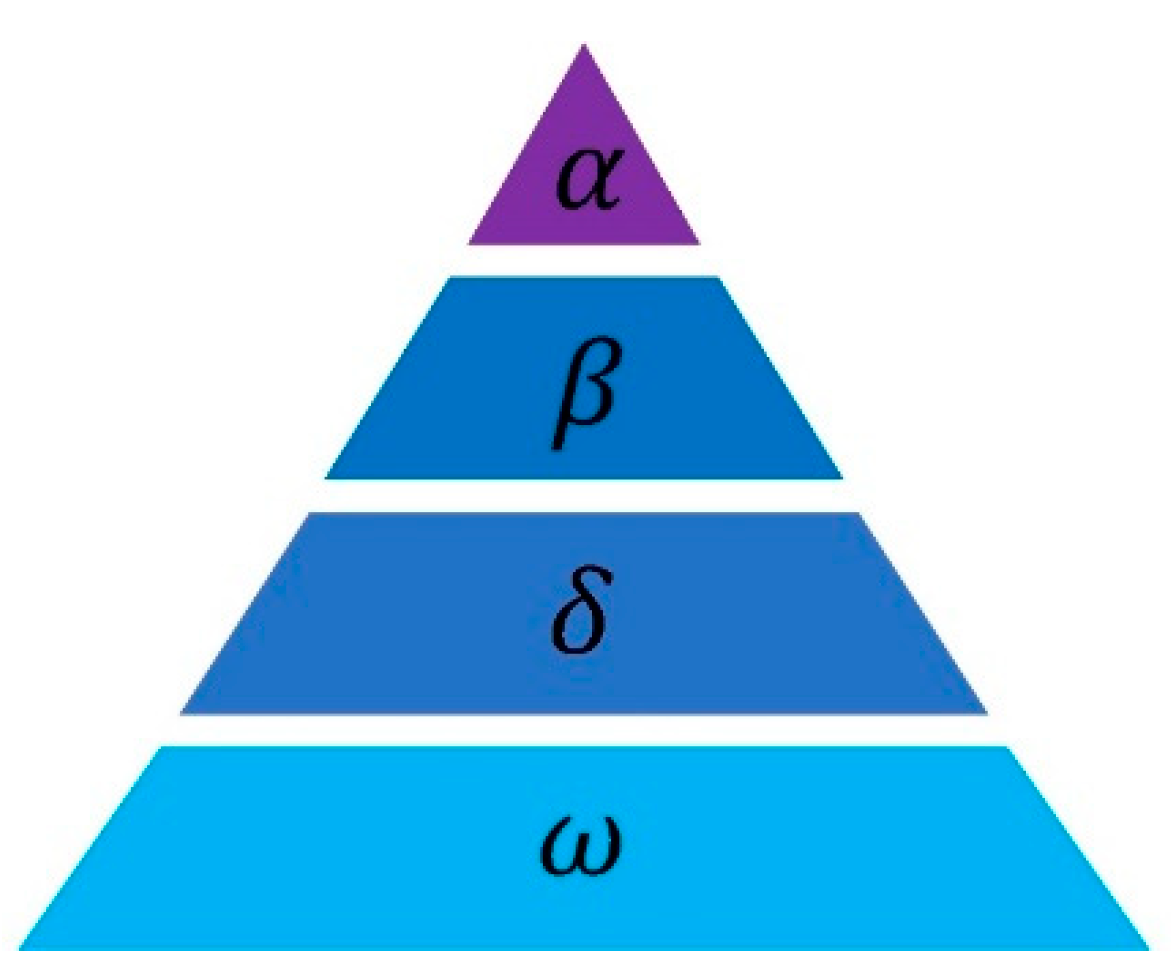
2.1. Grey Wolf Optimizer
2.2. Gaussian Mutation
2.3. Cauchy Mutation
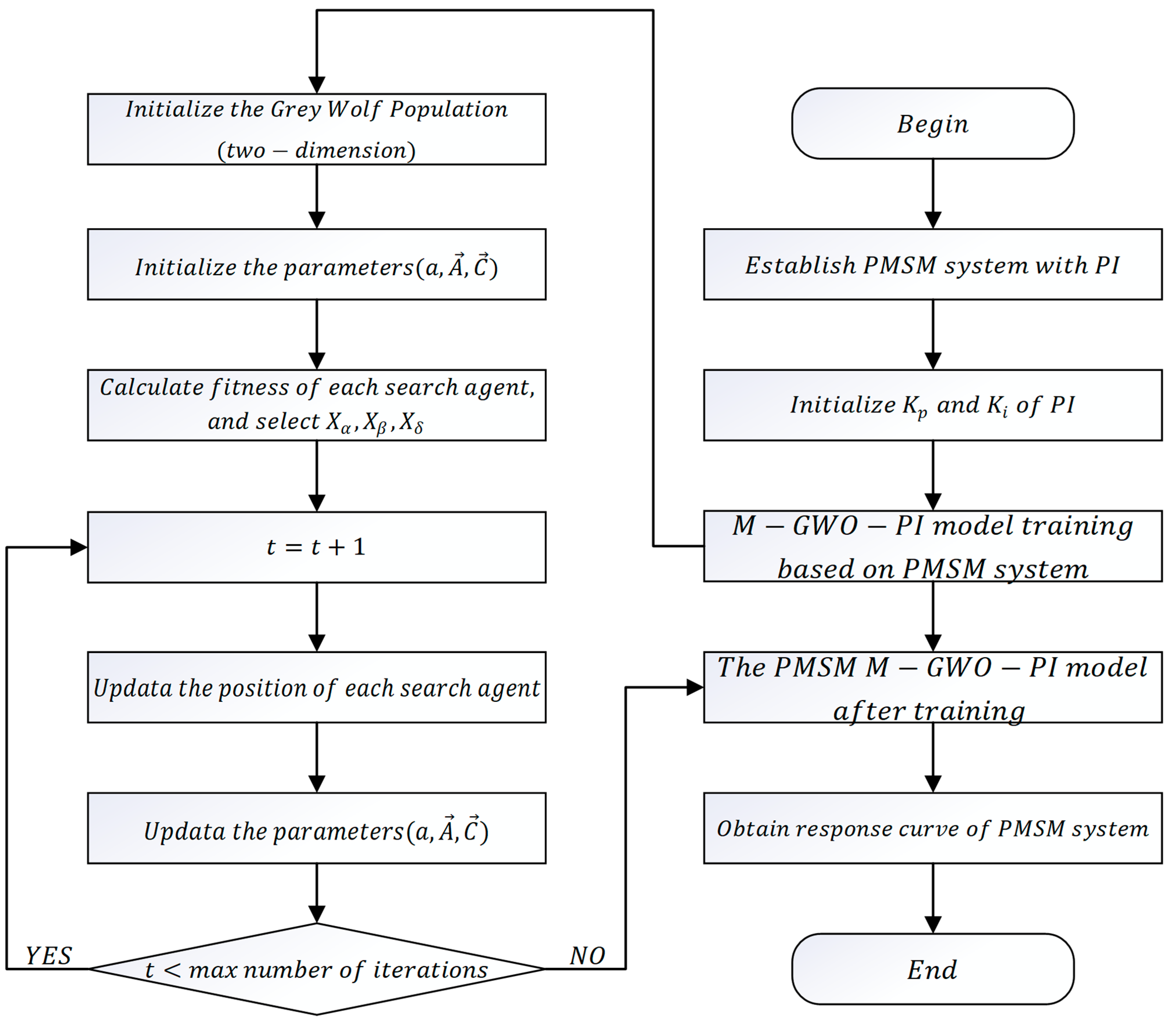
3. Modified Grey Wolf Optimizer
| Algorithm 1 The pseudo code of M-GWO—Modified Based Grey Wolf Optimizer |
| ) |
| 2: Calculate the fitness of each search agent |
| is the best search agent |
| is the second search agent |
| is the third search agent |
| 6: number of iterations) |
| 7: For each search agent |
| 8: |
| by Equation (14) |
| 10: else |
| by Equation (15) |
| 12: end If |
| by Equation (7) |
| by Equation (8) |
| by Equation (17) |
| 16: end For |
| 17: |
| 18: |
| 19: end While |
| 20: |
4. Experimental Evaluation and Results
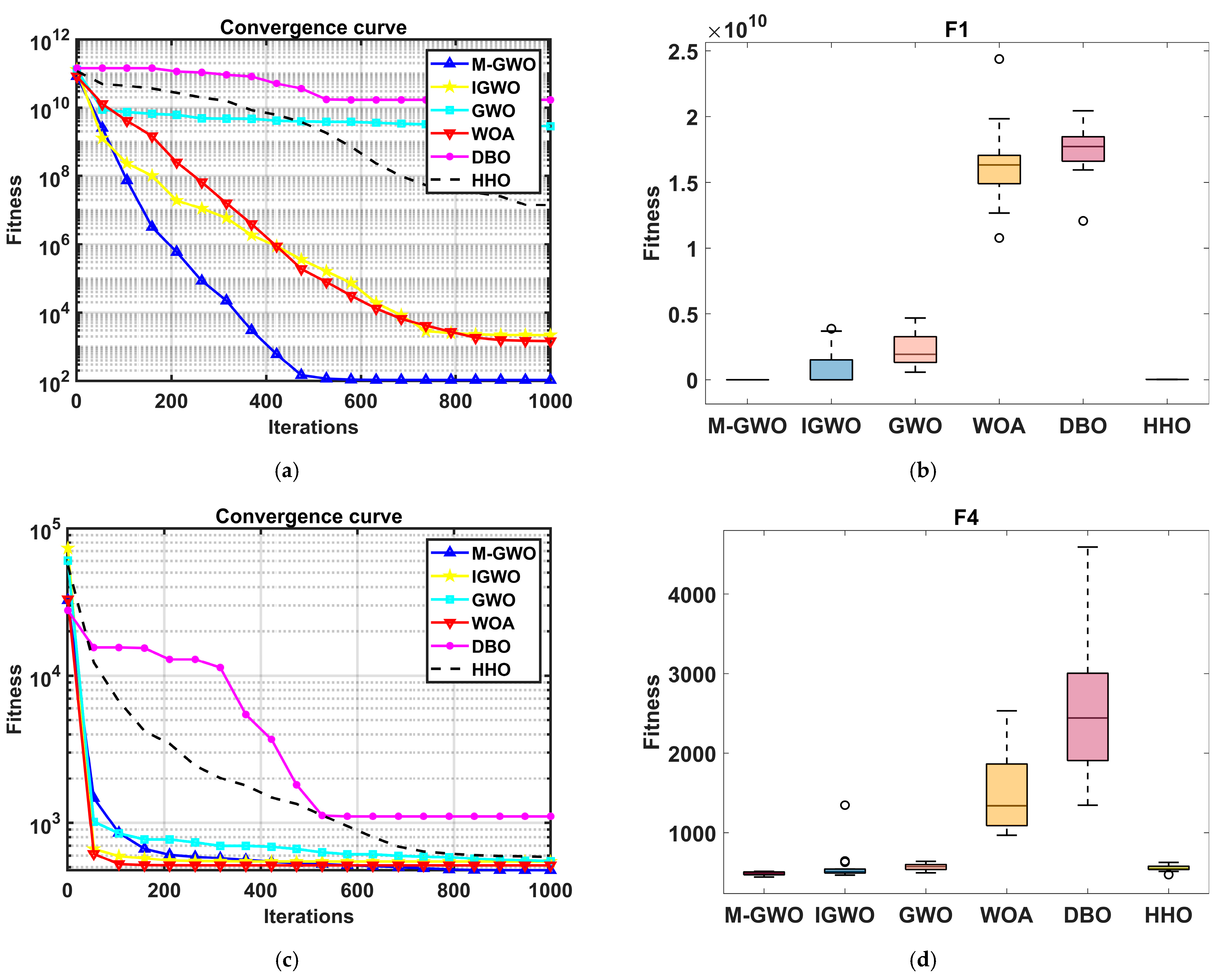
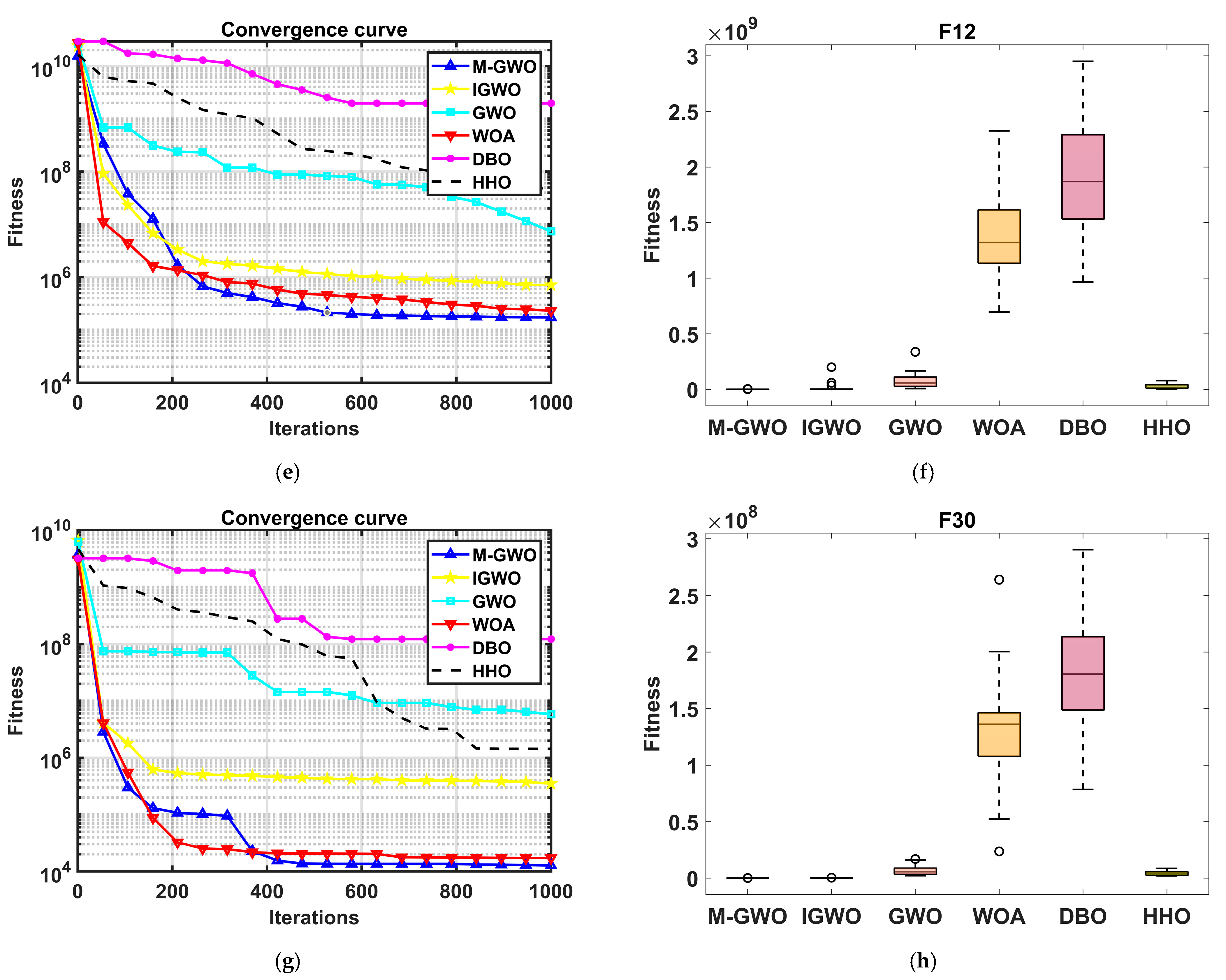
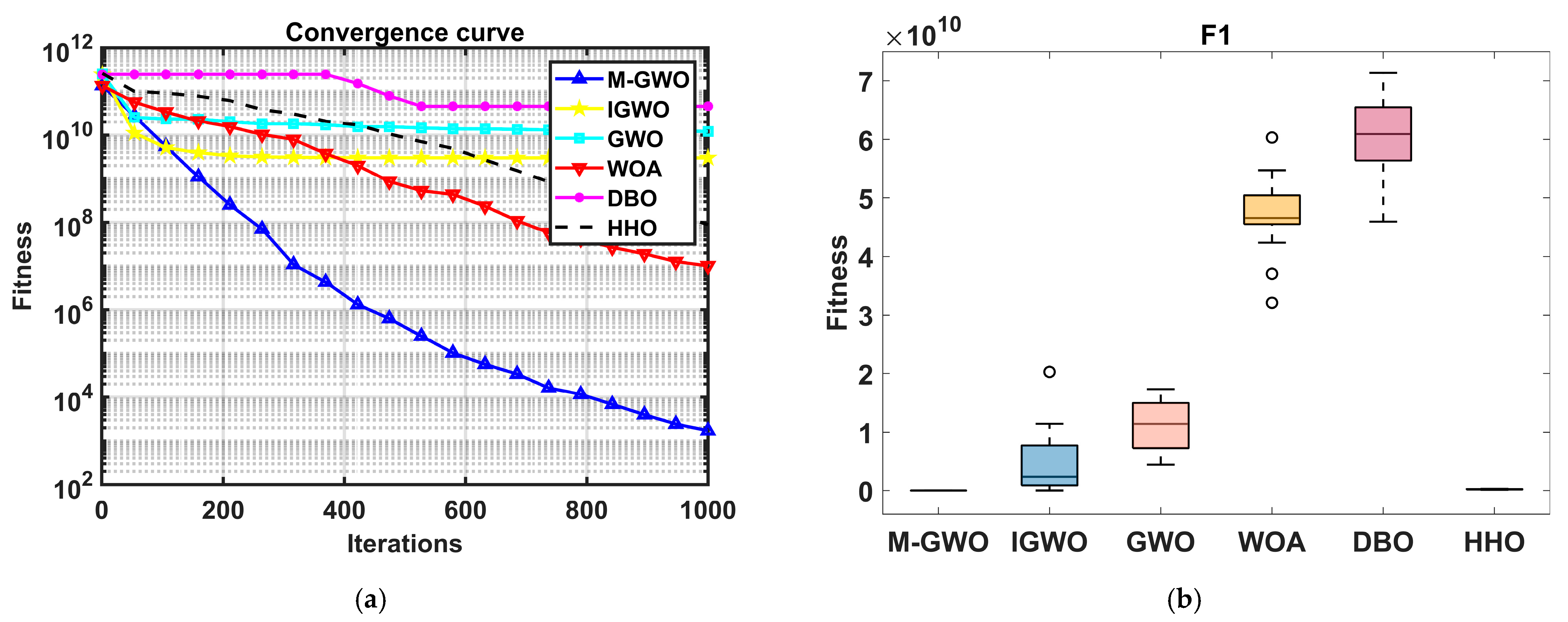
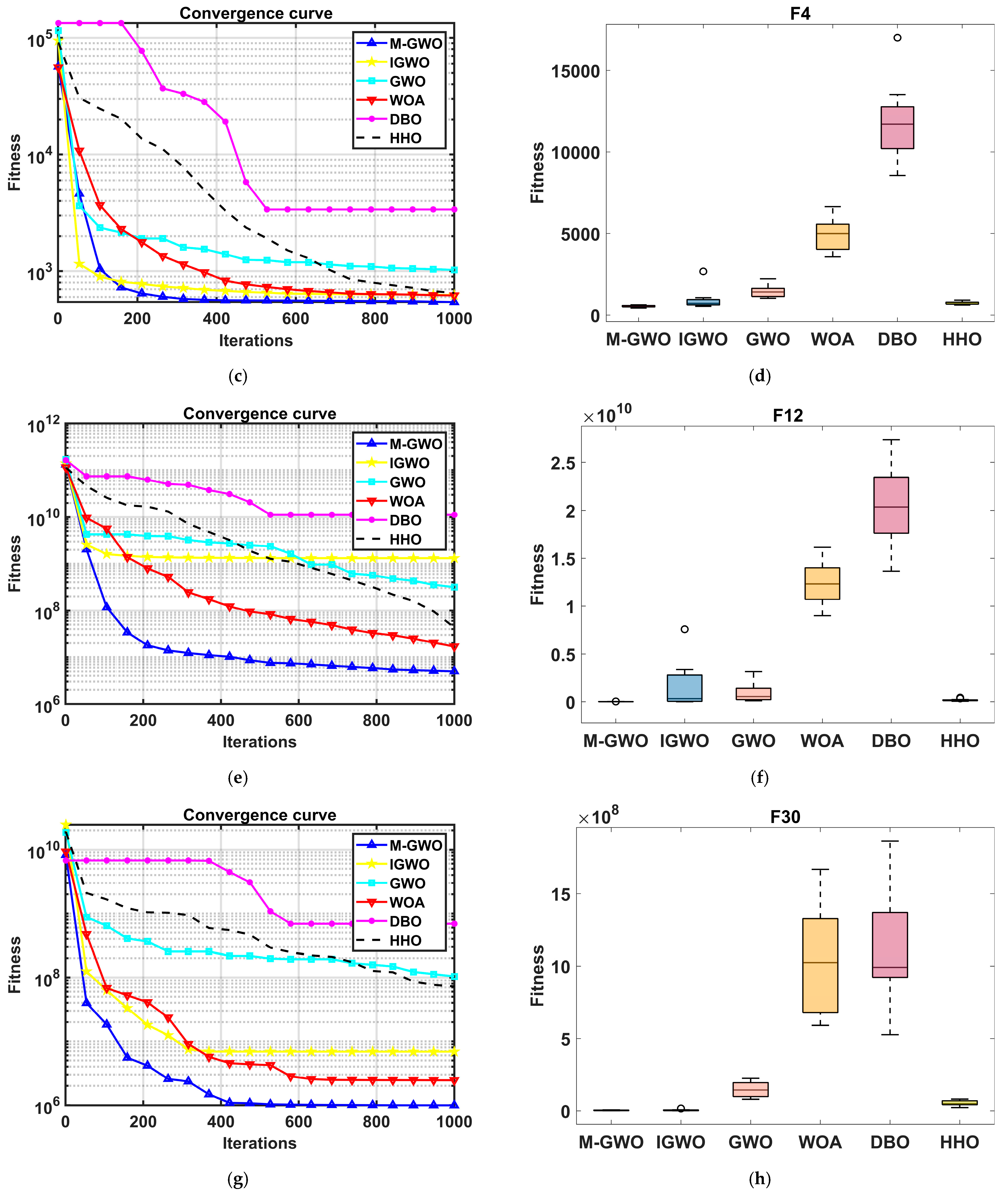
4.1. The Test Results of Benchmark Function
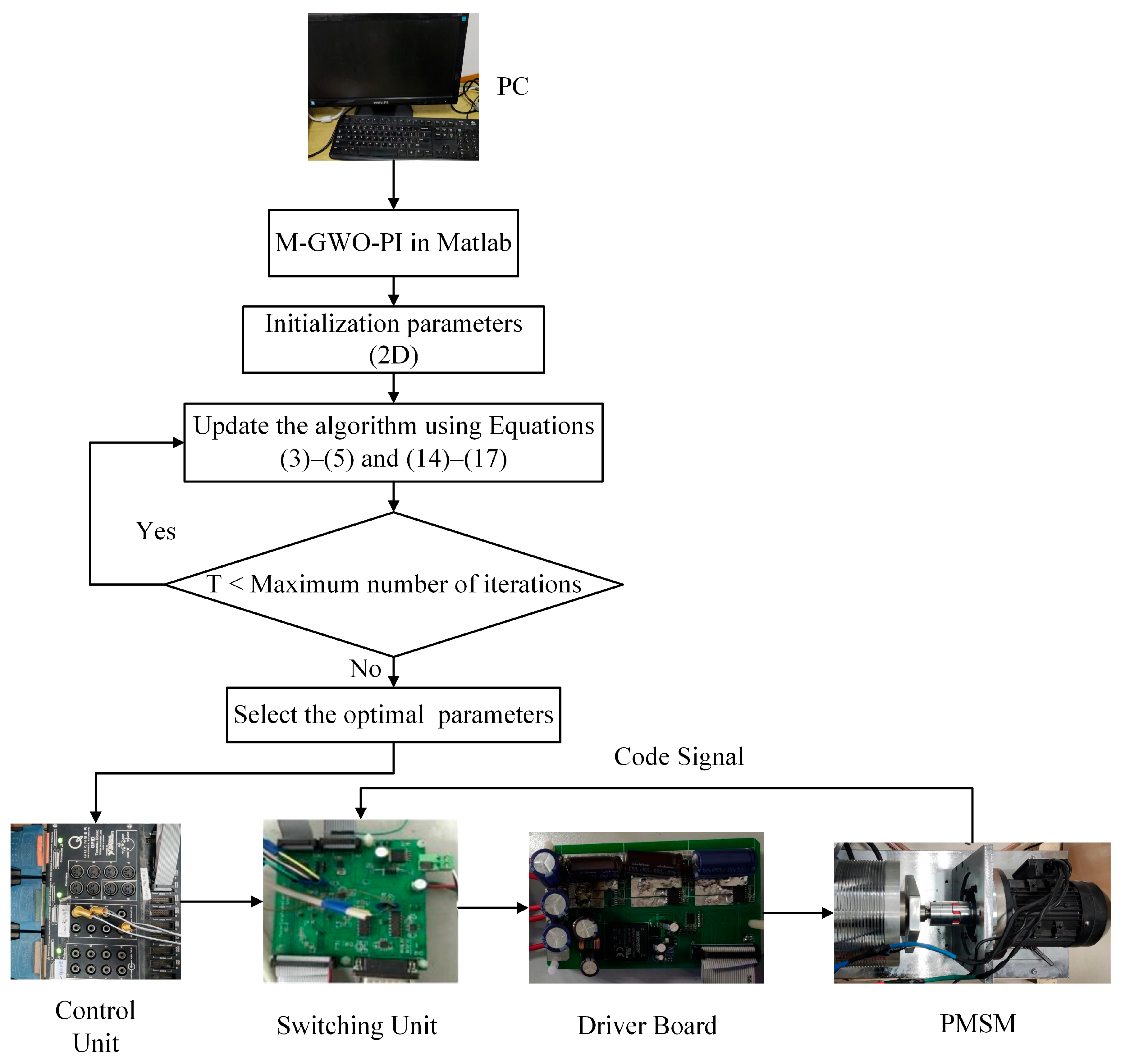
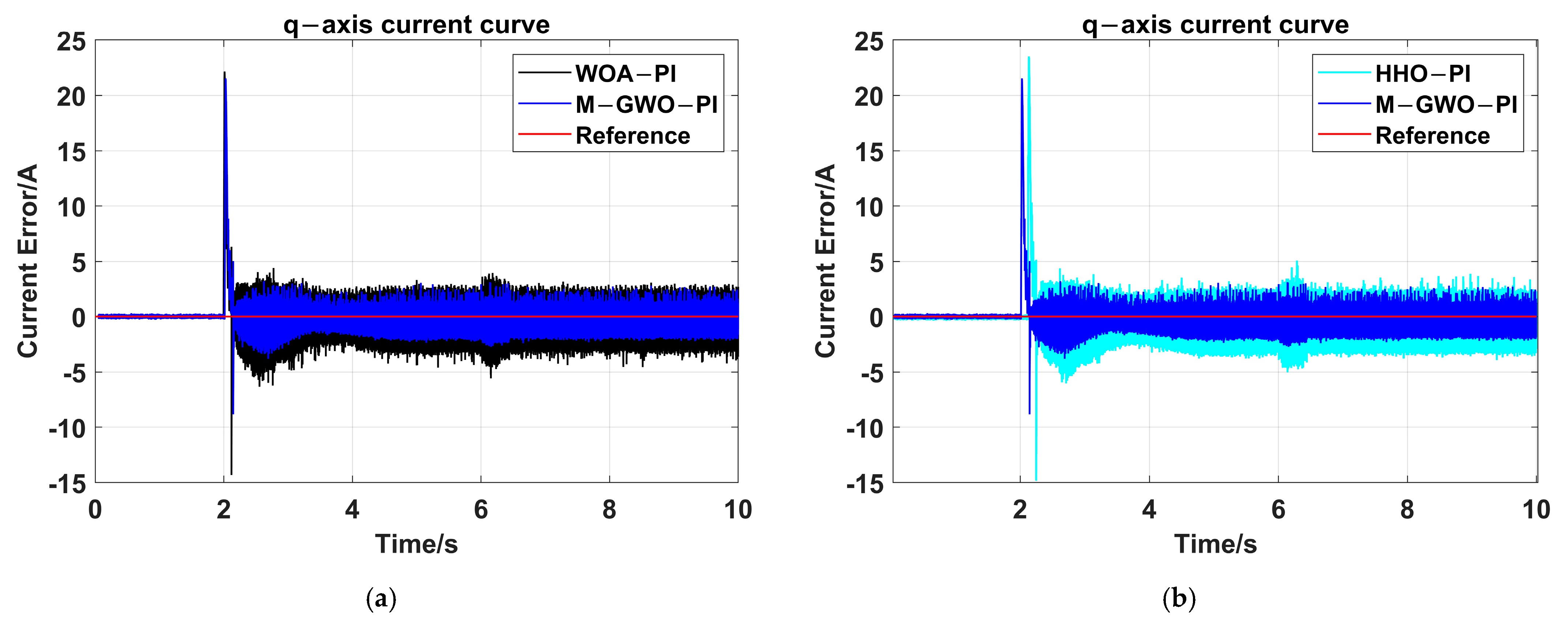
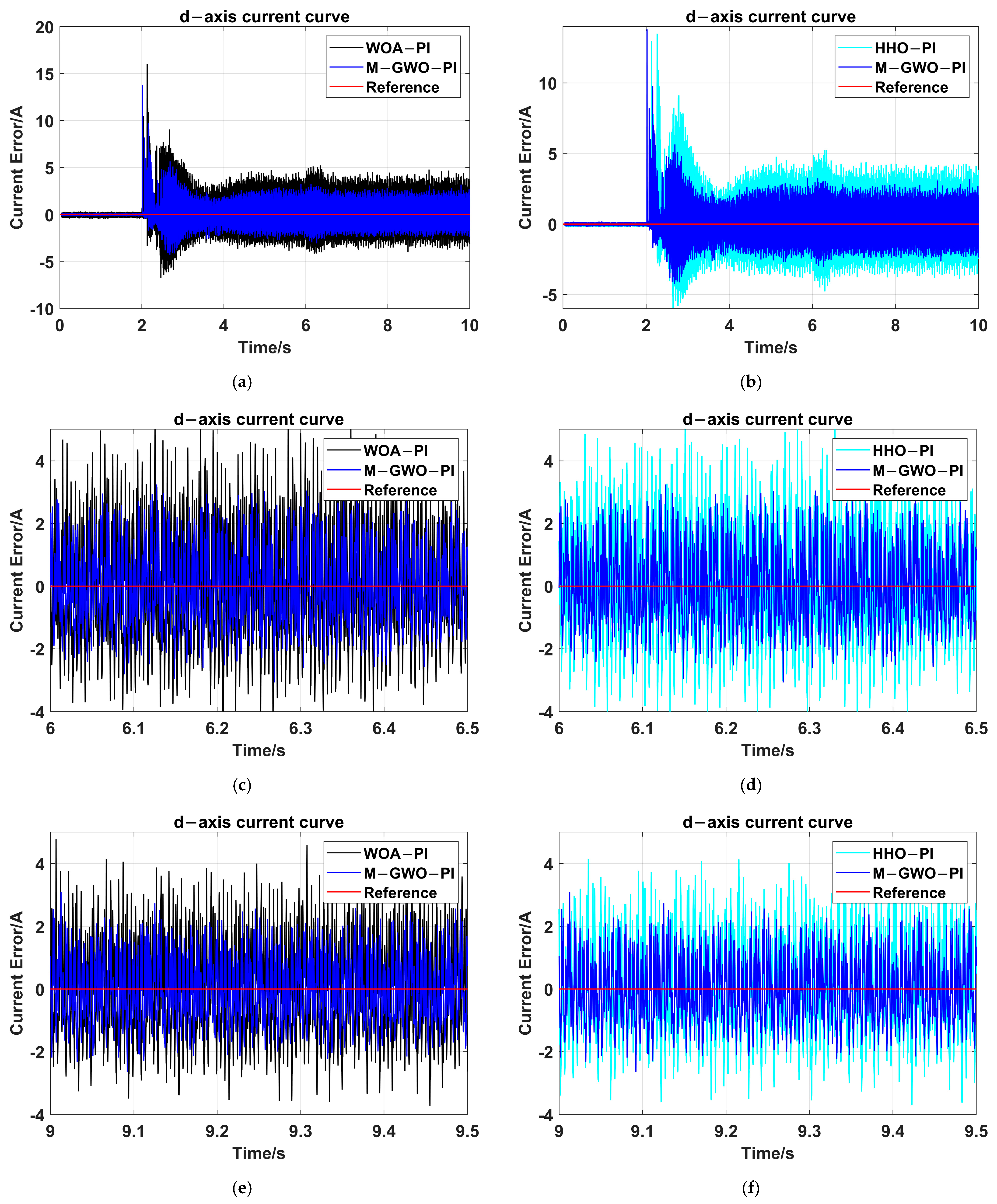
4.2. Application of M-GWO to PI Controller Parameters
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- (1)
- Bent Cigar Function
- (2)
- Sum of Different Power Function
- (3)
- Zakharov Function
- (4)
- Rosenbrock’s Function
- (5)
- Rastrigin’s Function
- (6)
- Expanded Schaffer’s F6 Functionwhere .
- (7)
- Lunacek bi-Rastrgin Functionwhere , , ,, , for ,
- (8)
- Non-continuous Rotated Rastrigin’s Functionwhere, for ,
- (9)
- Levy Functionwhere .
- (10)
- Modified Schwefel’s Functionwhere × 102and,
- (11)
- High Conditioned Elliptic Function
- (12)
- Discuss Function
- (13)
- Ackley’s Function
- (14)
- Weierstrass Functionwhere , and .
- (15)
- Griewank’s Function
- (16)
- Katsuura Function
- (17)
- HappyCat Function
- (18)
- HGBat Function
- (19)
- Expanded Griewank’s plus Rosenbrock’s Function
- (20)
- Schaffer’s F7 Functionwhere
- Unimodal Functions
- B.
- Hybrid Functions
- C.
- Composite Functions
Appendix B
| Function | Dim | Index | M-GWO | IGWO | GWO | WOA | DBO | HHO |
|---|---|---|---|---|---|---|---|---|
| F1 | 30 | Min | 1.07 × 102 | 1.18 × 102 | 5.19 × 109 | 2.06 × 102 | 8.21 × 1010 | 1.29 × 108 |
| Mean | 4.41 × 103 | 9.34 × 103 | 2.87 × 1010 | 1.12 × 1010 | 2.28 × 1011 | 2.58 × 108 | ||
| SD | 6.16 × 103 | 8.32 × 103 | 2.38 × 1010 | 1.97 × 1010 | 3.15 × 1010 | 5.42 × 107 | ||
| 50 | Min | 2.69 × 102 | 3.21 × 104 | 1.51 × 106 | 4.17 × 109 | 2.96 × 1010 | 1.22 × 108 | |
| Mean | 3.67 × 103 | 8.43 × 105 | 4.04 × 109 | 1.15 × 1010 | 4.21 × 1010 | 1.93 × 108 | ||
| SD | 3.02 × 103 | 1.01 × 106 | 4.45 × 109 | 5.19 × 109 | 3.96 × 109 | 4.61 × 107 | ||
| F3 | 30 | Min | 1.99 × 105 | 2.47 × 105 | 3.35 × 105 | 2.46 × 105 | 2.28 × 105 | 2.58 × 105 |
| Mean | 2.96 × 105 | 3.84 × 105 | 5.02 × 105 | 3.84 × 105 | 4.02 × 105 | 3.62 × 105 | ||
| SD | 5.38 × 103 | 7.68 × 103 | 1.07 × 105 | 5.39 × 103 | 2.01 × 105 | 7.46 × 103 | ||
| 50 | Min | 7.22 × 104 | 8.23 × 104 | 2.42 × 105 | 1.72 × 105 | 1.02 × 105 | 1.01 × 105 | |
| Mean | 1.28 × 105 | 1.38 × 105 | 1.59 × 105 | 1.36 × 105 | 1.51 × 105 | 1.34 × 105 | ||
| SD | 2.21 × 104 | 3.75 × 104 | 5.02 × 104 | 1.69 × 104 | 2.85 × 104 | 2.01 × 104 |
| Function | Dim | Index | M-GWO | IGWO | GWO | WOA | DBO | HHO |
|---|---|---|---|---|---|---|---|---|
| F4 | 30 | Min | 4.04 × 102 | 4.75 × 102 | 5.06 × 102 | 4.71 × 102 | 8.21 × 102 | 4.95 × 102 |
| Mean | 4.90 × 102 | 6.00 × 102 | 6.72 × 102 | 4.98 × 102 | 1.26 × 103 | 5.44 × 102 | ||
| SD | 3.45 × 101 | 2.24 × 102 | 3.60 × 102 | 2.80 × 101 | 3.92 × 102 | 2.79 × 101 | ||
| 50 | Min | 4.34 × 102 | 4.59 × 102 | 6.08 × 102 | 4.81 × 102 | 1.05 × 103 | 6.36 × 102 | |
| Mean | 5.50 × 102 | 1.06 × 103 | 1.36 × 103 | 5.63 × 102 | 1.62 × 103 | 7.63 × 102 | ||
| SD | 6.97 × 101 | 6.49 × 102 | 3.91 × 102 | 7.58 × 101 | 1.16 × 103 | 7.51 × 101 | ||
| F5 | 30 | Min | 5.62 × 102 | 5.71 × 102 | 6.21 × 102 | 6.29 × 102 | 6.82 × 102 | 6.42 × 102 |
| Mean | 6.16 × 102 | 6.26 × 102 | 7.23 × 102 | 7.37 × 102 | 6.99 × 102 | 7.59 × 102 | ||
| SD | 4.19 × 101 | 4.19 × 101 | 5.62 × 101 | 5.12 × 101 | 4.23 × 101 | 4.17 × 101 | ||
| 50 | Min | 6.32 × 102 | 6.76 × 102 | 7.58 × 102 | 8.19 × 102 | 8.22 × 102 | 8.67 × 102 | |
| Mean | 7.45 × 102 | 7.62 × 102 | 8.49 × 102 | 8.76 × 102 | 1.17 × 103 | 9.17 × 102 | ||
| SD | 3.66 × 101 | 4.89 × 101 | 3.12 × 101 | 2.87 × 101 | 4.49 × 101 | 2.86 × 101 | ||
| F6 | 30 | Min | 6.00 × 102 | 6.03 × 102 | 6.16 × 102 | 6.29 × 102 | 6.25 × 102 | 6.49 × 102 |
| Mean | 6.10 × 102 | 6.12 × 102 | 6.41 × 102 | 6.48 × 102 | 6.36 × 100 | 6.63 × 102 | ||
| SD | 4.25 × 100 | 8.45 × 100 | 1.44 × 101 | 1.05 × 101 | 5.29 × 100 | 5.67 × 100 | ||
| 50 | Min | 6.10 × 102 | 6.13 × 102 | 6.30 × 102 | 6.47 × 102 | 6.52 × 102 | 6.68 × 102 | |
| Mean | 6.22 × 102 | 6.31 × 102 | 6.55 × 102 | 6.61 × 102 | 6.72 × 102 | 6.78 × 102 | ||
| SD | 5.31 × 100 | 1.19 × 101 | 8.97 × 100 | 7.61 × 100 | 8.81 × 100 | 5.07 × 100 | ||
| F7 | 30 | Min | 7.87 × 102 | 8.17 × 102 | 8.57 × 102 | 9.91 × 102 | 1.12 × 103 | 1.13 × 103 |
| Mean | 8.42 × 102 | 8.95 × 102 | 1.05 × 103 | 1.21 × 103 | 1.22 × 103 | 1.31 × 103 | ||
| SD | 3.45 × 101 | 5.12 × 101 | 1.29 × 102 | 9.66 × 101 | 5.02 × 101 | 6.73 × 101 | ||
| 50 | Min | 8.79 × 102 | 9.38 × 102 | 1.16 × 103 | 1.38 × 103 | 1.22 × 103 | 1.64 × 103 | |
| Mean | 1.04 × 103 | 1.10 × 103 | 1.52 × 103 | 1.72 × 103 | 1.66 × 103 | 1.86 × 103 | ||
| SD | 1.02 × 102 | 6.98 × 101 | 2.03 × 102 | 1.01 × 102 | 4.49 × 101 | 1.03 × 102 | ||
| F8 | 30 | Min | 8.55 × 102 | 8.74 × 102 | 8.82 × 102 | 9.19 × 102 | 1.01 × 103 | 9.07 × 102 |
| Mean | 9.02 × 102 | 9.13 × 102 | 9.57 × 102 | 9.79 × 102 | 1.06 × 103 | 9.82 × 102 | ||
| SD | 3.37 × 101 | 2.46 × 101 | 3.32 × 101 | 3.28 × 101 | 2.33 × 101 | 3.06 × 101 | ||
| 50 | Min | 9.38 × 102 | 1.04 × 103 | 1.14 × 103 | 9.61 × 102 | 1.35 × 103 | 1.15 × 103 | |
| Mean | 1.04 × 103 | 1.18 × 103 | 1.19 × 103 | 1.05 × 103 | 1.49 × 103 | 1.21 × 103 | ||
| SD | 6.40 × 101 | 4.34 × 101 | 2.41 × 101 | 3.64 × 101 | 4.31 × 101 | 3.29 × 101 | ||
| F9 | 30 | Min | 9.25 × 102 | 1.12 × 103 | 2.41 × 103 | 3.03 × 103 | 3.32 × 103 | 5.62 × 103 |
| Mean | 2.37 × 103 | 2.56 × 103 | 4.95 × 103 | 5.14 × 104 | 6.69 × 103 | 8.34 × 103 | ||
| SD | 9.08 × 102 | 2.04 × 103 | 8.26 × 102 | 4.90 × 102 | 4.15 × 103 | 9.37 × 102 | ||
| 50 | Min | 2.71 × 103 | 1.18 × 104 | 4.33 × 103 | 1.13 × 104 | 1.08 × 104 | 2.01 × 104 | |
| Mean | 9.84 × 103 | 1.39 × 104 | 7.62 × 103 | 1.31 × 104 | 2.88 × 104 | 2.83 × 104 | ||
| SD | 4.97 × 103 | 4.16 × 103 | 1.54 × 104 | 8.26 × 102 | 4.53 × 103 | 3.35 × 103 | ||
| F10 | 30 | Min | 2.84 × 103 | 3.26 × 103 | 3.59 × 103 | 3.82 × 103 | 5.22 × 103 | 4.60 × 103 |
| Mean | 4.51 × 103 | 4.86 × 103 | 4.98 × 103 | 5.37 × 103 | 6.61 × 103 | 5.99 × 103 | ||
| SD | 7.98 × 102 | 1.30 × 103 | 5.10 × 102 | 6.68 × 102 | 4.71 × 102 | 7.60 × 102 | ||
| 50 | Min | 4.93 × 103 | 6.09 × 103 | 6.59 × 103 | 6.64 × 103 | 1.05 × 104 | 7.40 × 103 | |
| Mean | 6.97 × 103 | 7.89 × 103 | 7.96 × 103 | 8.83 × 103 | 1.46 × 104 | 9.78 × 103 | ||
| SD | 1.00 × 103 | 1.57 × 103 | 9.17 × 102 | 9.02 × 102 | 6.92 × 102 | 1.31 × 103 |
| Function | Dim | Index | M-GWO | IGWO | GWO | WOA | DBO | HHO |
|---|---|---|---|---|---|---|---|---|
| F11 | 30 | Min | 1.14 × 103 | 1.17 × 103 | 1.36 × 103 | 1.21 × 103 | 2.15 × 103 | 1.21 × 103 |
| Mean | 1.27 × 103 | 1.34 × 103 | 2.15 × 103 | 1.33 × 103 | 2.28 × 103 | 1.29 × 103 | ||
| SD | 7.11 × 101 | 8.19 × 101 | 9.27 × 102 | 8.20 × 101 | 2.47 × 102 | 5.21 × 101 | ||
| 50 | Min | 1.30 × 103 | 1.26 × 103 | 2.05 × 103 | 1.22 × 103 | 2.15 × 103 | 1.41 × 103 | |
| Mean | 1.47 × 103 | 1.49 × 103 | 5.88 × 103 | 1.36 × 103 | 4.55 × 103 | 1.69 × 103 | ||
| SD | 8.20 × 101 | 2.86 × 102 | 1.87 × 103 | 7.35 × 101 | 3.52 × 103 | 1.07 × 102 | ||
| F12 | 30 | Min | 6.79 × 104 | 4.16 × 104 | 1.67 × 105 | 6.79 × 104 | 6.18 × 107 | 4.78 × 106 |
| Mean | 4.93 × 105 | 1.29 × 106 | 1.07 × 108 | 4.93 × 105 | 3.11 × 108 | 2.40 × 107 | ||
| SD | 4.61 × 105 | 1.07 × 106 | 4.42 × 108 | 4.61 × 105 | 4.18 × 107 | 1.85 × 107 | ||
| 50 | Min | 1.46 × 106 | 5.32 × 106 | 7.42 × 106 | 3.96 × 107 | 6.85 × 107 | 4.71 × 107 | |
| Mean | 5.45 × 106 | 1.66 × 107 | 1.72 × 109 | 1.43 × 109 | 2.28 × 108 | 1.75 × 108 | ||
| SD | 2.88 × 106 | 1.19 × 107 | 2.61 × 109 | 1.91 × 109 | 5.29 × 107 | 1.09 × 108 | ||
| F13 | 30 | Min | 3.07 × 103 | 5.89 × 103 | 1.92 × 103 | 2.36 × 107 | 3.32 × 106 | 2.64 × 105 |
| Mean | 2.29 × 104 | 3.68 × 104 | 3.83 × 107 | 1.50 × 107 | 8.13 × 106 | 5.36 × 105 | ||
| SD | 2.53 × 104 | 2.57 × 104 | 1.93 × 108 | 3.68 × 107 | 4.52 × 106 | 1.79 × 105 | ||
| 50 | Min | 8.62 × 103 | 1.44 × 104 | 4.61 × 104 | 8.17 × 105 | 3.32 × 106 | 2.31 × 106 | |
| Mean | 2.98 × 104 | 7.10 × 104 | 1.48 × 108 | 5.15 × 108 | 4.81 × 106 | 5.42 × 106 | ||
| SD | 1.76 × 104 | 4.21 × 104 | 1.32 × 108 | 9.07 × 108 | 2.29 × 106 | 3.58 × 106 | ||
| F14 | 30 | Min | 3.53 × 104 | 3.64 × 103 | 6.39 × 103 | 9.77 × 103 | 2.45 × 105 | 1.05 × 104 |
| Mean | 2.88 × 103 | 5.67 × 104 | 6.95 × 104 | 5.05 × 105 | 1.62 × 106 | 5.67 × 105 | ||
| SD | 3.16 × 104 | 6.43 × 104 | 5.17 × 104 | 6.20 × 105 | 1.39 × 106 | 8.48 × 105 | ||
| 50 | Min | 2.36 × 104 | 6.32 × 104 | 4.07 × 104 | 2.13 × 105 | 2.41 × 106 | 1.39 × 105 | |
| Mean | 1.69 × 105 | 3.77 × 105 | 1.26 × 106 | 1.33 × 106 | 7.19 × 106 | 2.45 × 106 | ||
| SD | 1.09 × 105 | 2.99 × 105 | 2.62 × 106 | 1.51 × 106 | 3.96 × 106 | 1.99 × 106 | ||
| F15 | 30 | Min | 1.95 × 103 | 2.03 × 103 | 2.24 × 103 | 2.01 × 104 | 2.07 × 106 | 3.30 × 104 |
| Mean | 1.04 × 104 | 1.40 × 104 | 1.46 × 104 | 2.41 × 106 | 7.37 × 106 | 8.71 × 104 | ||
| SD | 1.33 × 104 | 1.39 × 104 | 1.43 × 104 | 6.36 × 106 | 5.53 × 106 | 4.82 × 104 | ||
| 50 | Min | 2.36 × 104 | 6.32 × 104 | 4.07 × 104 | 2.13 × 105 | 9.85 × 106 | 1.39 × 105 | |
| Mean | 1.69 × 105 | 3.77 × 105 | 1.26 × 106 | 1.33 × 106 | 1.93 × 107 | 2.45 × 106 | ||
| SD | 1.09 × 105 | 2.99 × 105 | 2.62 × 106 | 1.51 × 106 | 9.96 × 106 | 1.99 × 106 | ||
| F16 | 30 | Min | 1.76 × 103 | 2.15 × 103 | 2.36 × 103 | 2.34 × 103 | 2.58 × 103 | 2.38 × 103 |
| Mean | 2.49 × 103 | 2.63 × 103 | 2.86 × 103 | 2.98 × 103 | 3.64 × 103 | 3.51 × 103 | ||
| SD | 3.22 × 102 | 3.09 × 102 | 3.86 × 102 | 3.71 × 102 | 2.69 × 102 | 4.93 × 102 | ||
| 50 | Min | 2.63 × 103 | 4.28 × 103 | 4.09 × 104 | 1.62 × 108 | 3.61 × 105 | 3.21 × 103 | |
| Mean | 1.59 × 104 | 3.18 × 104 | 1.43 × 107 | 6.98 × 108 | 7.11 × 105 | 2.19 × 104 | ||
| SD | 1.11 × 104 | 2.26 × 104 | 1.85 × 107 | 2.19 × 108 | 3.42 × 105 | 1.91 × 104 | ||
| F17 | 30 | Min | 1.81 × 103 | 1.89 × 103 | 2.06 × 103 | 2.10 × 103 | 2.21 × 103 | 2.05 × 103 |
| Mean | 2.04 × 103 | 2.23 × 103 | 2.42 × 103 | 2.29 × 103 | 2.42 × 103 | 2.62 × 103 | ||
| SD | 1.67 × 102 | 1.98 × 102 | 2.10 × 102 | 2.57 × 102 | 2.01 × 102 | 2.92 × 102 | ||
| 50 | Min | 2.37 × 103 | 2.39 × 103 | 2.69 × 103 | 2.81 × 103 | 3.52 × 103 | 2.73 × 103 | |
| Mean | 2.85 × 103 | 3.18 × 103 | 3.26 × 103 | 3.61 × 103 | 4.71 × 103 | 3.79 × 103 | ||
| SD | 2.77 × 102 | 3.32 × 102 | 3.89 × 102 | 3.85 × 102 | 4.13 × 102 | 5.01 × 102 | ||
| F18 | 30 | Min | 2.12 × 104 | 6.77 × 104 | 9.68 × 104 | 9.78 × 104 | 3.28 × 105 | 1.23 × 105 |
| Mean | 3.01 × 105 | 5.91 × 105 | 7.13 × 105 | 2.11 × 106 | 1.02 × 106 | 1.64 × 106 | ||
| SD | 2.92 × 105 | 4.69 × 105 | 1.39 × 106 | 4.81 × 106 | 7.79 × 105 | 2.29 × 106 | ||
| 50 | Min | 2.52 × 105 | 6.13 × 105 | 5.28 × 105 | 1.03 × 106 | 2.23 × 107 | 1.12 × 106 | |
| Mean | 1.53 × 106 | 2.79 × 106 | 3.55 × 106 | 1.21 × 107 | 4.51 × 107 | 4.94 × 106 | ||
| SD | 1.31 × 106 | 2.11 × 106 | 2.87 × 106 | 1.67 × 107 | 2.36 × 107 | 4.09 × 106 | ||
| F19 | 30 | Min | 2.29 × 103 | 2.09 × 103 | 1.63 × 104 | 2.06 × 103 | 3.32 × 104 | 7.39 × 104 |
| Mean | 9.51 × 103 | 2.19 × 104 | 3.16 × 106 | 1.34 × 104 | 6.21 × 104 | 8.47 × 105 | ||
| SD | 1.13 × 104 | 3.94 × 104 | 8.83 × 106 | 1.36 × 104 | 4.52 × 104 | 7.52 × 105 | ||
| 50 | Min | 2.34 × 103 | 4.51 × 103 | 3.35 × 104 | 3.73 × 103 | 2.19 × 105 | 2.25 × 105 | |
| Mean | 1.86 × 104 | 3.56 × 105 | 1.38 × 107 | 2.53 × 104 | 5.31 × 105 | 1.54 × 106 | ||
| SD | 1.64 × 104 | 1.66 × 106 | 2.82 × 107 | 1.27 × 104 | 2.08 × 105 | 1.07 × 106 | ||
| F20 | 30 | Min | 2.13 × 103 | 2.25 × 103 | 2.27 × 103 | 2.29 × 103 | 2.52 × 103 | 2.41 × 103 |
| Mean | 2.43 × 103 | 4.46 × 103 | 2.67 × 103 | 2.75 × 103 | 2.71 × 103 | 2.72 × 103 | ||
| SD | 2.10 × 102 | 1.81 × 102 | 2.21 × 102 | 2.40 × 102 | 1.36 × 102 | 2.07 × 102 | ||
| 50 | Min | 2.42 × 103 | 2.56 × 103 | 2.76 × 103 | 3.02 × 103 | 3.04 × 103 | 3.03 × 103 | |
| Mean | 2.91 × 103 | 3.01 × 103 | 3.56 × 103 | 3.57 × 103 | 3.41 × 103 | 3.55 × 103 | ||
| SD | 2.83 × 102 | 3.18 × 102 | 4.12 × 102 | 2.33 × 102 | 2.37 × 102 | 2.77 × 102 |
| Function | Dim | Index | M-GWO | IGWO | GWO | WOA | DBO | HHO |
|---|---|---|---|---|---|---|---|---|
| F21 | 30 | Min | 2.35 × 103 | 2.37 × 103 | 2.41 × 103 | 2.41 × 101 | 2.42 × 103 | 2.23 × 103 |
| Mean | 2.40 × 103 | 2.43 × 103 | 2.47 × 103 | 2.51 × 103 | 2.48 × 103 | 2.57 × 103 | ||
| SD | 2.88 × 101 | 3.23 × 101 | 3.81 × 101 | 6.71 × 101 | 2.92 × 101 | 8.64 × 101 | ||
| 50 | Min | 2.47 × 103 | 2.53 × 103 | 2.46 × 103 | 2.57 × 103 | 2.71 × 103 | 2.73 × 103 | |
| Mean | 2.54 × 103 | 2.64 × 101 | 2.57 × 103 | 2.77 × 103 | 2.82 × 103 | 2.87 × 103 | ||
| SD | 5.61 × 101 | 6.02 × 101 | 7.51 × 101 | 1.08 × 102 | 3.41 × 101 | 7.49 × 101 | ||
| F22 | 30 | Min | 2.30 × 103 | 2.30 × 103 | 2.39 × 103 | 2.30 × 103 | 3.28 × 103 | 2.33 × 103 |
| Mean | 3.83 × 103 | 4.40 × 103 | 4.56 × 103 | 5.55 × 103 | 4.12 × 103 | 6.76 × 103 | ||
| SD | 2.08 × 103 | 1.89 × 103 | 1.84 × 103 | 2.22 × 103 | 2.78 × 102 | 1.77 × 103 | ||
| 50 | Min | 7.53 × 103 | 8.53 × 103 | 7.45 × 103 | 8.18 × 103 | 1.03 × 104 | 9.96 × 103 | |
| Mean | 9.24 × 103 | 9.76 × 103 | 9.81 × 103 | 1.02 × 104 | 1.51 × 104 | 1.19 × 104 | ||
| SD | 1.05 × 103 | 8.78 × 102 | 2.05 × 103 | 9.64 × 102 | 6.33 × 102 | 1.01 × 103 | ||
| F23 | 30 | Min | 2.71 × 103 | 2.77 × 103 | 2.78 × 103 | 2.78 × 103 | 2.87 × 103 | 3.08 × 103 |
| Mean | 2.78 × 103 | 2.86 × 103 | 2.93 × 103 | 2.92 × 103 | 2.96 × 103 | 3.21 × 103 | ||
| SD | 4.87 × 101 | 6.20 × 101 | 8.75 × 101 | 9.08 × 101 | 2.63 × 101 | 1.21 × 102 | ||
| 50 | Min | 2.94 × 103 | 2.92 × 103 | 2.96 × 103 | 3.08 × 103 | 3.32 × 103 | 3.51 × 103 | |
| Mean | 3.03 × 103 | 3.25 × 103 | 3.31 × 103 | 3.38 × 103 | 3.40 × 103 | 3.79 × 103 | ||
| SD | 8.21 × 101 | 1.52 × 102 | 1.49 × 102 | 1.62 × 102 | 3.22 × 101 | 1.52 × 102 | ||
| F24 | 30 | Min | 2.89 × 103 | 2.89 × 103 | 2.97 × 103 | 2.94 × 103 | 3.09 × 103 | 3.09 × 103 |
| Mean | 2.93 × 103 | 3.03 × 103 | 3.09 × 103 | 3.07 × 103 | 3.15 × 103 | 3.42 × 103 | ||
| SD | 6.67 × 101 | 6.97 × 101 | 9.56 × 101 | 8.28 × 101 | 2.22 × 101 | 1.56 × 102 | ||
| 50 | Min | 3.06 × 103 | 3.20 × 103 | 3.27 × 103 | 3.34 × 103 | 3.46 × 103 | 3.75 × 103 | |
| Mean | 3.22 × 103 | 3.36 × 103 | 3.56 × 103 | 3.54 × 103 | 3.59 × 103 | 4.27 × 103 | ||
| SD | 9.50 × 101 | 1.25 × 102 | 1.66 × 102 | 1.10 × 102 | 2.31 × 101 | 2.15 × 102 | ||
| F25 | 30 | Min | 2.88 × 103 | 2.89 × 103 | 2.95 × 103 | 2.88 × 103 | 3.01 × 103 | 2.89 × 103 |
| Mean | 2.89 × 103 | 2.91 × 103 | 3.04 × 103 | 2.90 × 103 | 3.23 × 103 | 2.93 × 103 | ||
| SD | 1.26 × 101 | 4.57 × 101 | 8.55 × 101 | 1.61 × 101 | 1.87 × 102 | 1.91 × 101 | ||
| 50 | Min | 3.00 × 103 | 3.01 × 103 | 3.31 × 103 | 3.03 × 103 | 3.22 × 103 | 3.14 × 103 | |
| Mean | 3.04 × 103 | 3.08 × 103 | 3.83 × 103 | 3.14 × 103 | 3.61 × 103 | 3.25 × 103 | ||
| SD | 2.11 × 101 | 3.52 × 101 | 3.64 × 102 | 9.22 × 101 | 1.26 × 102 | 8.79 × 101 | ||
| F26 | 30 | Min | 2.90 × 103 | 3.28 × 103 | 3.65 × 103 | 2.80 × 103 | 3.12 × 103 | 3.20 × 103 |
| Mean | 5.57 × 103 | 4.84 × 103 | 4.91 × 103 | 5.97 × 103 | 3.34 × 103 | 7.30 × 103 | ||
| SD | 1.23 × 103 | 1.05 × 103 | 4.81 × 102 | 1.35 × 103 | 1.41 × 102 | 1.47 × 103 | ||
| 50 | Min | 2.92 × 103 | 5.64 × 103 | 3.53 × 103 | 2.90 × 103 | 3.15 × 103 | 4.05 × 103 | |
| Mean | 5.76 × 103 | 6.99 × 103 | 7.46 × 103 | 6.93 × 103 | 5.28 × 103 | 1.08 × 104 | ||
| SD | 3.61 × 103 | 7.46 × 102 | 1.45 × 103 | 3.72 × 103 | 3.75 × 103 | 1.93 × 103 | ||
| F27 | 30 | Min | 3.20 × 103 | 3.20 × 103 | 3.21 × 103 | 3.22 × 103 | 2.26 × 103 | 3.26 × 103 |
| Mean | 3.25 × 103 | 3.29 × 103 | 3.26 × 103 | 3.26 × 103 | 3.31 × 103 | 3.53 × 103 | ||
| SD | 2.77 × 101 | 5.08 × 102 | 3.18 × 101 | 3.19 × 101 | 4.42 × 101 | 1.68 × 102 | ||
| 50 | Min | 3.34 × 103 | 3.36 × 103 | 3.44 × 103 | 3.59 × 103 | 3.46 × 103 | 3.80 × 103 | |
| Mean | 3.49 × 103 | 3.70 × 103 | 3.65 × 103 | 3.75 × 103 | 3.71 × 103 | 4.52 × 103 | ||
| SD | 1.33 × 102 | 2.93 × 102 | 9.89 × 101 | 1.02 × 102 | 2.22 × 102 | 4.03 × 102 | ||
| F28 | 30 | Min | 3.02 × 103 | 3.21 × 103 | 3.32 × 103 | 3.20 × 103 | 3.20 × 103 | 3.27 × 103 |
| Mean | 3.10 × 103 | 3.29 × 103 | 3.45 × 103 | 3.24 × 103 | 3.31 × 103 | 3.33 × 103 | ||
| SD | 2.77 × 101 | 1.50 × 102 | 7.63 × 101 | 2.79 × 101 | 3.36 × 102 | 4.71 × 101 | ||
| 50 | Min | 3.30 × 103 | 3.33 × 103 | 3.73 × 103 | 3.27 × 103 | 3.44 × 103 | 3.53 × 103 | |
| Mean | 3.34 × 103 | 3.92 × 103 | 4.45 × 103 | 3.32 × 103 | 3.71 × 103 | 3.76 × 103 | ||
| SD | 3.65 × 101 | 6.94 × 102 | 3.83 × 102 | 2.28 × 101 | 5.27 × 102 | 1.29 × 102 | ||
| F29 | 30 | Min | 3.45 × 103 | 3.86 × 103 | 4.45 × 103 | 3.69 × 103 | 3.46 × 103 | 3.66 × 103 |
| Mean | 3.78 × 103 | 3.89 × 103 | 5.02 × 103 | 4.08 × 103 | 3.81 × 103 | 4.68 × 103 | ||
| SD | 1.01 × 102 | 2.08 × 102 | 2.60 × 102 | 2.61 × 102 | 1.25 × 102 | 4.59 × 102 | ||
| 50 | Min | 3.94 × 103 | 4.28 × 103 | 4.17 × 103 | 4.34 × 103 | 4.21 × 103 | 4.82 × 103 | |
| Mean | 4.69 × 103 | 4.75 × 103 | 4.94 × 103 | 5.14 × 103 | 4.98 × 103 | 6.20 × 103 | ||
| SD | 4.54 × 102 | 2.88 × 102 | 4.05 × 102 | 4.62 × 102 | 4.69 × 102 | 7.31 × 102 | ||
| F30 | 30 | Min | 5.30 × 103 | 6.41 × 103 | 1.07 × 106 | 5.42 × 103 | 3.28 × 107 | 5.68 × 105 |
| Mean | 1.73 × 104 | 1.79 × 105 | 1.10 × 107 | 1.96 × 104 | 8.27 × 107 | 4.33 × 106 | ||
| SD | 1.25 × 104 | 5.22 × 105 | 8.19 × 106 | 1.99 × 104 | 4.22 × 107 | 2.71 × 106 | ||
| 50 | Min | 9.48 × 105 | 1.25 × 106 | 8.13 × 105 | 4.85 × 107 | 4.29 × 108 | 3.12 × 107 | |
| Mean | 1.86 × 106 | 3.53 × 106 | 4.71 × 106 | 1.45 × 108 | 1.05 × 109 | 5.73 × 107 | ||
| SD | 7.16 × 105 | 2.17 × 106 | 7.35 × 106 | 9.78 × 107 | 3.39 × 108 | 1.71 × 107 |
| Function | Dim | M-GWO | IGWO | GWO | WOA | DBO | HHO |
|---|---|---|---|---|---|---|---|
| F1 | 30 | 1.207 s | 1.337 s | 1.115 s | 1.357 s | 1.088 s | 1.447 s |
| 50 | 1.886 s | 2.016 s | 1.769 s | 2.224 s | 1.629 s | 2.301 s | |
| F3 | 30 | 1.124 s | 1.284 s | 1.054 s | 1.292 s | 1.044 s | 1.331 s |
| 50 | 1.771 s | 1.904 s | 1.692 s | 1.885 s | 1.706 s | 1.928 s | |
| F4 | 30 | 1.224 s | 1.314 s | 1.088 s | 1.295 s | 1.118 s | 1.323 s |
| 50 | 1.639 s | 1.715 s | 1.407 s | 1.699 s | 1.517 s | 1.903 s | |
| F5 | 30 | 1.391 s | 1.507 s | 1.216 s | 1.517 s | 1.336 s | 1.492 s |
| 50 | 1.873 s | 2.224 s | 1.743 s | 2.007 s | 1.721 s | 2.109 s | |
| F6 | 30 | 1.287 s | 1.134 s | 1.478 s | 1.056 s | 1.392 s | 1.219 s |
| 50 | 1.532 s | 1.671 s | 1.557 s | 1.645 s | 1.592 s | 1.613 s | |
| F7 | 30 | 1.167 s | 1.423 s | 1.098 s | 1.356 s | 1.274 s | 1.489 s |
| 50 | 1.507 s | 1.629 s | 1.548 s | 1.663 s | 1.581 s | 1.694 s | |
| F8 | 30 | 1.321 s | 1.045 s | 1.487 s | 1.132 s | 1.269 s | 1.403 s |
| 50 | 1.523 s | 1.654 s | 1.576 s | 1.689 s | 1.512 s | 1.637 s | |
| F9 | 30 | 1.153 s | 1.437 s | 1.082 s | 1.364 s | 1.298 s | 1.426 s |
| 50 | 1.545 s | 1.612 s | 1.587 s | 1.673 s | 1.539 s | 1.691 s | |
| F10 | 30 | 1.283 s | 1.147 s | 1.462 s | 1.095 s | 1.371 s | 1.524 s |
| 50 | 1.518 s | 1.642 s | 1.569 s | 1.685 s | 1.533 s | 1.627 s | |
| F11 | 30 | 1.218 s | 1.473 s | 1.056 s | 1.392 s | 1.127 s | 1.489 s |
| 50 | 1.524 s | 1.678 s | 1.732 s | 1.596 s | 1.614 s | 1.765 s | |
| F12 | 30 | 1.263 s | 1.417 s | 1.089 s | 1.352 s | 1.194 s | 1.476 s |
| 50 | 1.537 s | 1.792 s | 1.645 s | 1.583 s | 1.721 s | 1.668 s | |
| F13 | 30 | 1.237 s | 1.498 s | 1.073 s | 1.326 s | 1.185 s | 1.459 s |
| 50 | 1.576 s | 1.749 s | 1.512 s | 1.637 s | 1.784 s | 1.695 s | |
| F14 | 30 | 1.254 s | 1.437 s | 1.092 s | 1.368 s | 1.213 s | 1.481 s |
| 50 | 1.642 s | 1.537 s | 1.789 s | 1.594 s | 1.673 s | 1.721 s | |
| F15 | 30 | 1.123 s | 1.287 s | 1.056 s | 1.342 s | 1.098 s | 1.312 s |
| 50 | 1.732 s | 1.548 s | 1.695 s | 1.517 s | 1.764 s | 1.623 s | |
| F16 | 30 | 1.134 s | 1.279 s | 1.067 s | 1.328 s | 1.115 s | 1.349 s |
| 50 | 1.756 s | 1.589 s | 1.647 s | 1.792 s | 1.534 s | 1.678 s | |
| F17 | 30 | 1.142 s | 1.263 s | 1.089 s | 1.317 s | 1.128 s | 1.336 s |
| 50 | 1.637 s | 1.482 s | 1.594 s | 1.671 s | 1.468 s | 1.523 s | |
| F18 | 30 | 1.287 s | 1.123 s | 1.349 s | 1.078 s | 1.312 s | 1.156 s |
| 50 | 1.655 s | 1.497 s | 1.572 s | 1.689 s | 1.473 s | 1.536 s | |
| F19 | 30 | 1.267 s | 1.122 s | 1.349 s | 1.078 s | 1.312 s | 1.156 s |
| 50 | 1.519 s | 1.628 s | 1.453 s | 1.674 s | 1.581 s | 1.692 s | |
| F20 | 30 | 1.214 s | 1.098 s | 1.316 s | 1.167 s | 1.289 s | 1.144 s |
| 50 | 1.467 s | 1.643 s | 1.529 s | 1.685 s | 1.491 s | 1.576 s | |
| F21 | 30 | 1.317 s | 1.089 s | 1.254 s | 1.432 s | 1.173 s | 1.298 s |
| 50 | 1.542 s | 1.478 s | 1.613 s | 1.597 s | 1.459 s | 1.634 s | |
| F22 | 30 | 1.285 s | 1.117 s | 1.341 s | 0.956 s | 1.312 s | 1.122 s |
| 50 | 1.531 s | 1.679 s | 1.484 s | 1.592 s | 1.656 s | 1.463 s | |
| F23 | 30 | 0.956 s | 1.298 s | 1.056 s | 1.312 s | 1.091 s | 1.005 s |
| 50 | 1.507 s | 1.623 s | 1.498 s | 1.645 s | 1.576 s | 1.472 s | |
| F24 | 30 | 1.045 s | 0.987 s | 1.056 s | 1.192 s | 0.941 s | 1.017 s |
| 50 | 1.324 s | 1.476 s | 1.359 s | 1.412 s | 1.387 s | 1.435 s | |
| F25 | 30 | 1.023 s | 1.156 s | 0.978 s | 1.102 s | 1.200 s | 0.945 s |
| 50 | 1.368 s | 1.492 s | 1.317 s | 1.454 s | 1.343 s | 1.429 s | |
| F26 | 30 | 1.087 s | 0.923 s | 1.159 s | 1.046 s | 1.191 s | 0.965 s |
| 50 | 1.372 s | 1.481 s | 1.334 s | 1.467 s | 1.395 s | 1.443 s | |
| F27 | 30 | 1.132 s | 0.976 s | 1.054 s | 1.189 s | 0.997 s | 1.023 s |
| 50 | 1.356 s | 1.428 s | 1.389 s | 1.473 s | 1.319 s | 1.497 s | |
| F28 | 30 | 1.164 s | 0.928 s | 1.073 s | 1.197 s | 0.956 s | 1.032 s |
| 50 | 1.342 s | 1.416 s | 1.367 s | 1.434 s | 1.391 s | 1.489 s | |
| F29 | 30 | 1.112 s | 0.984 s | 1.067 s | 1.143 s | 0.939 s | 1.015 s |
| 50 | 1.327 s | 1.419 s | 1.378 s | 1.463 s | 1.354 s | 1.445 s | |
| F30 | 30 | 0.921 s | 1.058 s | 1.173 s | 0.964 s | 1.136 s | 1.092 s |
| 50 | 1.336 s | 1.472 s | 1.383 s | 1.429 s | 1.398 s | 1.451 s |
References
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Mirjalili, S. The Ant Lion Optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Duan, Y.; Yu, X. A collaboration-based hybrid GWO-SCA optimizer for engineering optimization problems. Expert Syst. Appl. 2023, 213 Pt B, 119017.1–119017.16. [Google Scholar] [CrossRef]
- Uzlu, E. Estimates of greenhouse gas emission in Turkey with grey wolf optimizer algorithm-optimized artificial neural networks. Neural Comput. Appl. 2021, 33, 13567–13585. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, J.; Cui, F.; Wang, Y.; Xu, Y.; Zhu, Y. Configuration and Robust Optimization Method of Energy Storage Capacity on the User Side of Power Grid Based on Improved Grey Wolf Algorithm. J. Phys. Conf. Ser. 2023, 2655, 012005. [Google Scholar] [CrossRef]
- Wang, S.; Zhu, D.; Zhou, C.; Sun, G. Improved grey wolf algorithm based on dynamic weight and logistic mapping for safe path planning of UAV low-altitude penetration. J. Supercomput. 2024, 80, 25818–25852. [Google Scholar] [CrossRef]
- Rajesh, B. Landslides Identification Through Conglomerate Grey Wolf Optimization and Whale Optimization Algorithm; BASE University Working Papers; BASE University: Bengaluru, India, 2021. [Google Scholar]
- Wang, Z.; Dai, D.; Zeng, Z.; He, D.; Chan, S. Multi-strategy enhanced Grey Wolf Optimizer for global optimization and real world problems. Clust. Comput. 2024, 27, 10671–10715. [Google Scholar] [CrossRef]
- Jiang, J.H.; Zhao, Z.Y.; Liu, Y.T.; Li, W.H.; Wang, H. DSGWO: An improved grey wolf optimizer with diversity enhanced strategy based on group-stage competition and balance mechanisms. Knowl.-Based Syst. 2022, 250, 109100. [Google Scholar] [CrossRef]
- Xue, H.; Liu, Z.; Ren, K.; Huang, J.; Meng, L.; Zhang, H. Distribution loss reduction strategy based on improved Grey Wolf algorithm. In Proceedings of the 2023 8th Asia Conference on Power and Electrical Engineering (ACPEE), Tianjin, China, 14–16 April 2023; pp. 1936–1941. [Google Scholar] [CrossRef]
- Kannan, K.; Yamini, B.; Fernandez, F.M.H.; Priyadarsini, P.U. A novel method for spectrum sensing in cognitive radio networks using fractional GWO-CS optimization. Ad Hoc Netw. 2023, 144, 103135. [Google Scholar] [CrossRef]
- Li, L.; He, Y.; Zhang, H.; Fung, J.C.; Lau, A.K. Enhancing IAQ, thermal comfort, and energy efficiency through an adaptive multi-objective particle swarm optimizer-grey wolf optimization algorithm for smart environmental control. Build. Environ. 2023, 235, 110235. [Google Scholar] [CrossRef]
- Wang, Q.; Yue, C.; Li, X.; Liao, P.; Li, X. Enhancing robustness of monthly streamflow forecasting model using embedded-feature selection algorithm based on improved gray wolf optimizer. J. Hydrol. 2023, 617, 128995. [Google Scholar] [CrossRef]
- Xia, Z. Control of Pivot Steering for Bilateral Independent Electrically Driven Tracked Vehicles Based on GWO-PID. World Electr. Veh. J. 2024, 15, 231. [Google Scholar] [CrossRef]
- Roy, S.P.; Shubham; Singh, A.K.; Mehta, R.K.; Roy, O.P. Application of GWO and TLBO Algorithms for PID Tuning in Hybrid Renewable Energy System. In Computer Vision and Robotics. Algorithms for Intelligent Systems; Springer: Singapore, 2022. [Google Scholar] [CrossRef]
- Yildirim, Ş.; Çabuk, N.; Bakircioğlu, V. Optimal PID Controller Design For Trajectory Tracking Of A Dodecarotor Uav Based On Grey Wolf Optimizer. Konya J. Eng. Sci. 2023, 11, 10–20. [Google Scholar] [CrossRef]
- Hocaoğlu, G.S.; Çavli, N.; Kılıç, E.; Danayiyen, Y. Nonlinear Convergence Factor Based Grey Wolf Optimization Algorithm and Load Frequency Control. In Proceedings of the 2023 5th Global Power, Energy and Communication Conference (GPECOM), Nevsehir, Turkiye, 14–16 June 2023; pp. 282–287. [Google Scholar] [CrossRef]
- Dey, S.; Banerjee, S.; Dey, J. Implementation of Optimized PID Controllers in Real Time for Magnetic Levitation System. In Computational Intelligence in Machine Learning; Lecture Notes in Electrical Engineering; Springer: Singapore, 2022. [Google Scholar] [CrossRef]
- Kommadath, R.; Kotecha, P. Teaching Learning Based Optimization with focused learning and its performance on CEC2017 functions. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 5–8 June 2017; pp. 2397–2403. [Google Scholar] [CrossRef]
- Jing, N. IGWO-LSTM based power prediction for wind power generation. In Proceedings of the 2023 IEEE 5th International Conference on Civil Aviation Safety and Information Technology (ICCASIT), Dali, China, 11–13 October 2023; pp. 1141–1146. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]

| Algorithms | Parameters Used in the Algorithm |
|---|---|
| M-GWO | |
| IGWO | |
| GWO | |
| WOA | |
| DBO | |
| HHO |
| Parameter | Meaning of Parameter | Value |
|---|---|---|
| Inverter amplification actor | 1 | |
| Stator q-axis inductance | ||
| Stator d-axis inductance | ||
| Inverter switching cycle | ||
| Stator resistance per phase | ||
| Number of poles | 5 | |
| Back electromotive force constant | 0.004 V/rpm |
| Methods | PI Parameters | |
|---|---|---|
| M-GWO-PI | 0.317 | 71.6756 |
| WOA-PI | 0.216 | 100.4651 |
| HHO-PI | 0.3 | 93.2684 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheng, L.; Wu, S.; Lv, Z. Modified Grey Wolf Optimizer and Application in Parameter Optimization of PI Controller. Appl. Sci. 2025, 15, 4530. https://doi.org/10.3390/app15084530
Sheng L, Wu S, Lv Z. Modified Grey Wolf Optimizer and Application in Parameter Optimization of PI Controller. Applied Sciences. 2025; 15(8):4530. https://doi.org/10.3390/app15084530
Chicago/Turabian StyleSheng, Long, Sen Wu, and Zongyu Lv. 2025. "Modified Grey Wolf Optimizer and Application in Parameter Optimization of PI Controller" Applied Sciences 15, no. 8: 4530. https://doi.org/10.3390/app15084530
APA StyleSheng, L., Wu, S., & Lv, Z. (2025). Modified Grey Wolf Optimizer and Application in Parameter Optimization of PI Controller. Applied Sciences, 15(8), 4530. https://doi.org/10.3390/app15084530





