Using Bootstrapping to Determine Artificial Neural Network Confidence Intervals—Case Study of Particleboard Internal Bond Determined from Production Data
Abstract
:1. Introduction
2. Materials and Methods
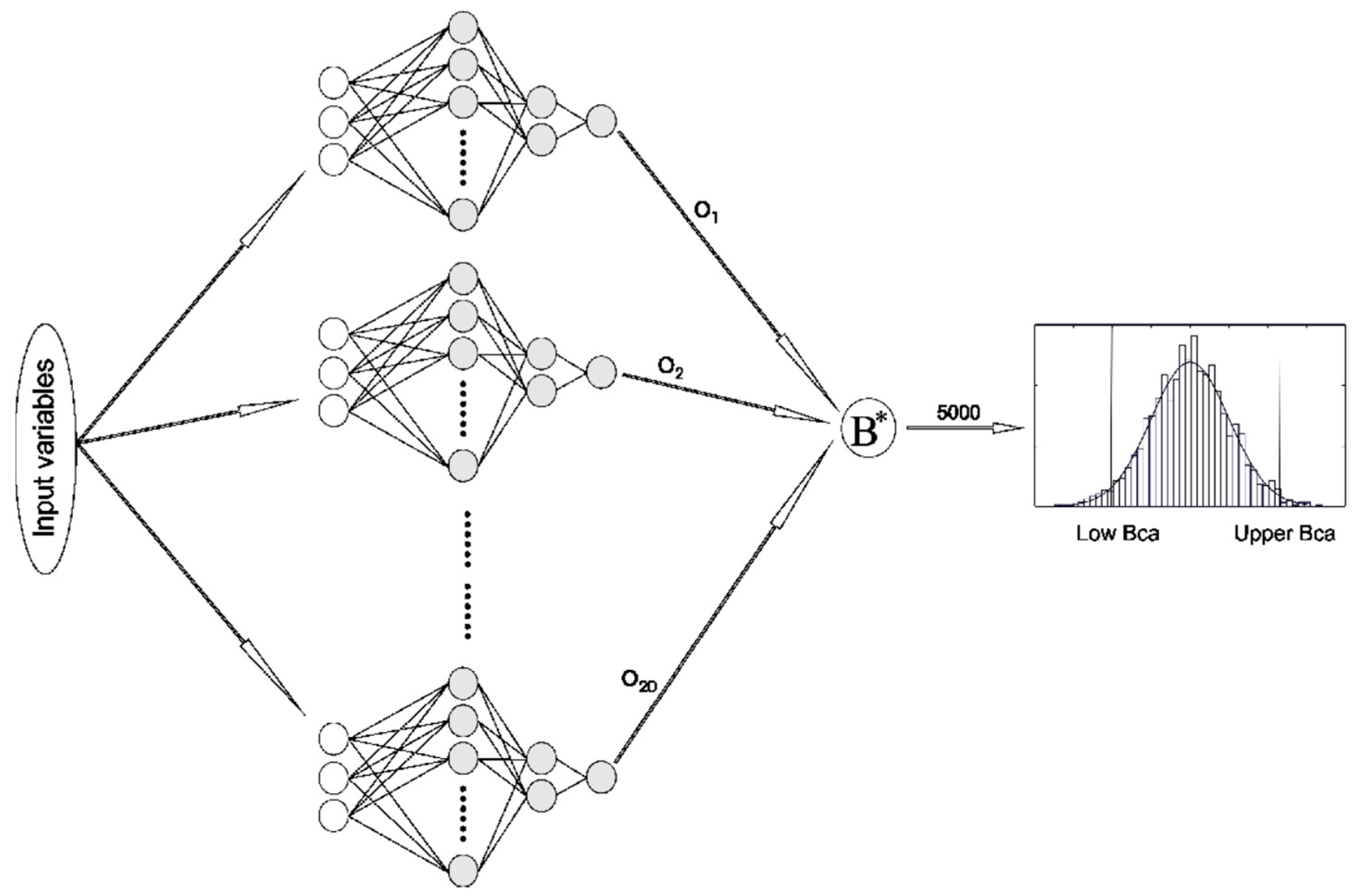
2.1. Bootstrap Methodology
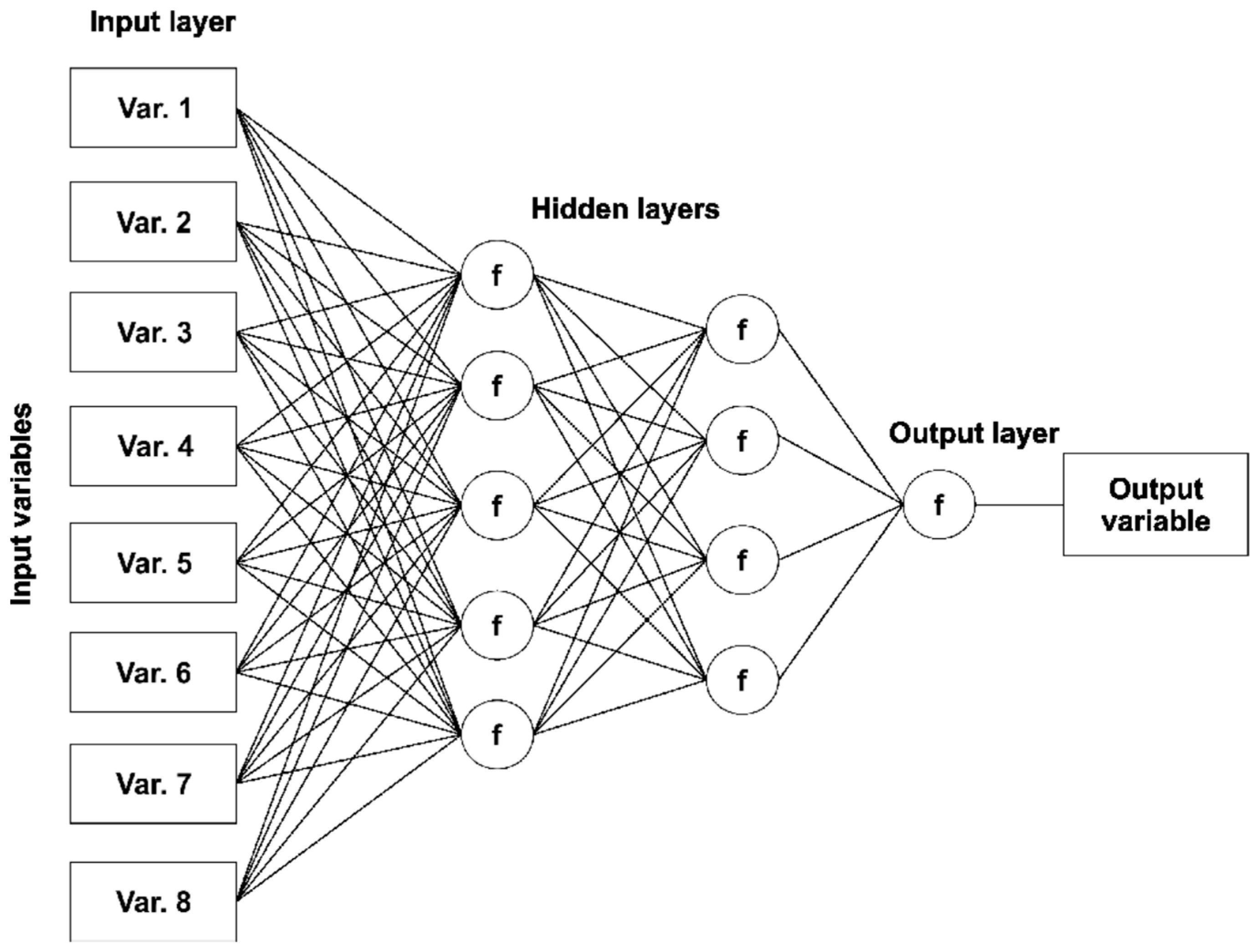
2.2. Artificial Neural Networks (ANN)
3. Results
3.1. Artificial Neural Network (ANN) Results
3.2. Bootstrap Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- EN 309; Particleboards. Definition and Classification. European Committee of Standardization (CEN): Brussels, Belgium, 2005.
- Food and Agriculture Organization of the United Nations (FAO). ForesSTAT. 2025. Available online: https://www.fao.org/faostat/en/#data/FO (accessed on 10 January 2025).
- EN 319; Particleboards and Fibreboards. Determination of Tensile Strength Perpendicular to the Plane of the Board. European Committee of Standardization (CEN): Brussels, Belgium, 1993.
- Kelly, M.W. Critical Literature Review of Relationships Between Processing Parameters and Physical Properties of Particleboard; Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 1977; p. 65.
- Esteban, L.G.; Guindeo Casasús, A.; Peraza Oramas, C.; de Palacios, P. La Madera y su Tecnología; Fundación Conde del Valle de Salazar, Mundiprensa and AITIM: Madrid, Spain, 2002; p. 332. [Google Scholar]
- Nemli, G.; Aydin, I.; Zekoviç, E. Evaluation of some of the properties of particleboard as function of manufacturing parameters. Mater. Des. 2007, 28, 1169–1176. [Google Scholar] [CrossRef]
- Young, T.M.L.B.; Winistorfer, P.M.; Wang, S. Multivariate control charts of MDF and OSB vertical density profiles attributes. For. Prod. J. 1999, 49, 79–86. [Google Scholar]
- Montgomery, D. Introduction to Statistical Quality Control, 6th ed.; John Wiley and Sons: New York, NY, USA, 2008; p. 754. [Google Scholar]
- Cook, D.F.; Chiu, C.C. Predicting the internal bond strength of particleboard, utilizing a radial basis function neural network. Eng. Appl. Artif. Intell. 1997, 10, 171–177. [Google Scholar] [CrossRef]
- Cai, Z.; Wu, Q.; Lee, J.; Hiziroglu, S. Influence of board density, mat construction, and chip type on performance of particleboard made from eastern red cedar. For. Prod. J. 2004, 54, 226–232. [Google Scholar]
- Clapp, N.E., Jr.; Young, T.M.; Guess, F.M. Predictive modeling the internal bond of medium density fiberboard using a modified principal component analysis. For. Prod. J. 2008, 58, 49–55. [Google Scholar]
- García Fernández, F.; Esteban, L.G.; de Palacios, P.; Navarro, N.; Conde, M. Prediction of standard particleboard mechanical properties utilizing an artificial neural network and subsequent comparison with a multivariate regression model. Investig. Agrar. Sist. Recur. For. 2008, 17, 178–187. [Google Scholar] [CrossRef]
- Esteban, L.G.; García Fernández, F.; de Palacios, P.; González Rodrigo, B. Use of artificial neural networks as a predictive method to determine moisture resistance of particle and fiber boards under cyclic testing conditions (UNE-EN 321). Wood Fiber Sci. 2010, 42, 335–345. [Google Scholar]
- Ozsahin, S. Optimization of process parameters in oriented strand board manufacturing with artificial neural network analysis. Eur. J. Wood Wood Prod. 2013, 71, 769–777. [Google Scholar] [CrossRef]
- Shao, Y.E.; Hou, C.D. Hybrid Artificial Neural Networks Modeling for Faults Identification of a Stochastic Multivariate Process. Abstr. Appl. Anal. 2013, 2013, 386757. [Google Scholar] [CrossRef]
- Tiryaki, S.; Bardak, S.; Bardak, T. Experimental investigation and prediction of bonding strength of Oriental beech (Fagus orientalis Lipsky) bonded with polyvinyl acetate adhesive. J. Adhes. Sci. Technol. 2015, 29, 2521–2536. [Google Scholar] [CrossRef]
- Chen, C.; Li, J.; Yin, J.; Zhang, F.; Yao, J. Quality Prediction Based on ANN in Tobacco Redrying Process. Adv. Mater. Res. 2011, 211–212, 1046–1050. [Google Scholar] [CrossRef]
- Cheng, C.S.; Cheng, H.P. Identifying the source of variance shifts in the multivariate process using neural networks and support vector machines. Expert Syst. Appl. 2008, 35, 198–206. [Google Scholar] [CrossRef]
- Abbasi, B. A neural network applied to estimate process capability of non-normal processes. Expert Syst. Appl. 2019, 36, 3093–3100. [Google Scholar] [CrossRef]
- Esteban, L.G.; García Fernández, F.; de Palacios, P.; Conde, M. Artificial neural networks in variable process control: Application in particleboard manufacture. For. Syst. 2009, 18, 92–100. [Google Scholar] [CrossRef]
- Hosseinifard, S.Z.; Abdollahian, M.; Zeephongsekul, P. Application of artificial neural networks in linear profile monitoring. Expert Syst. Appl. 2011, 38, 4920–4928. [Google Scholar] [CrossRef]
- Cook, D.F.; Whittaker, A.D. Neural network models for prediction of process parameters in wood products manufacturing. In Proceedings of the 1st Industrial Engineering Research Conference, Chicago, IL, USA, 20–21 May 1992. [Google Scholar]
- Cabaneros, S.M.; Huges, B. Methods used for handling and quantifying model uncertainty of artificial neural network models for air pollution forecasting. Environ. Modell. Softw. 2022, 158, 105529. [Google Scholar] [CrossRef]
- Cao, R. An overview of bootstrap methods for estimating and predicting in time series. Test 1999, 8, 95–116. [Google Scholar] [CrossRef]
- Khosravi, A.; Nahavandi, S.; Creighton, D. Quantifying uncertainties of neural network-based electricity price forecast. Appl. Energy 2013, 112, 120–129. [Google Scholar] [CrossRef]
- Hadjicharalambous, M.; Polycarpou, M.M.; Panayiotou, C.G. Online Approximation of Prediction Intervals Using Artificial Neural Networks. In Artificial Neural Networks and Machine Learning—ICANN 2018: 27th International Conference on Artificial Neural Networks, Rhodes, Greece, 4–7 October 2018; Kůrková, V., Manolopoulos, Y., Hammer, B., Iliadis, L., Maglogiannis, I., Eds.; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Young, T.M.; Perhac, D.G.; Guess, F.; León, R.V. Bootstrap confidence intervals for percentiles of reliability data for wood-plastic composites. For. Prod. J. 2008, 58, 106–114. [Google Scholar]
- International Laboratory Accreditation Cooperation (ILAC). Guidelines on the Reporting of Compliance with Specification; ILAC-G8:03; ILAC: Silverwater, Australia, 2009. [Google Scholar]
- Shahanaghi, K.; Nakhjiri, P. A new optimized uncertainty evaluation applied to Monte-Carlo simulation in platinum resistance thermometer calibration. Measurement 2010, 43, 901–911. [Google Scholar] [CrossRef]
- Young, T.M.; Leon, R.V.; Chen, C.H.; Chen, W.W.; Guess, F.M. Robustly Estimating Lower Percentiles When Observations Are Costly. Qual. Eng. 2015, 27, 361–373. [Google Scholar] [CrossRef]
- Edwards, D.J.; Guess, F.M.; Young, T.M. Improved estimation of the lower percentiles of material properties. Wood Sci. Technol. 2011, 45, 533–546. [Google Scholar] [CrossRef]
- Khosravi, A.; Nahavandi, S.; Creigton, D.; Atiya, A.F. Lower upper bound estimation method for construction of neural network-based prediction intervals. IEEE Trans. Neural Netw. 2011, 22, 337–346. [Google Scholar] [CrossRef] [PubMed]
- Khosravi, A.; Nahavandi, S.; Creigton, D.; Atiya, A.F. Comprehensive review of neural network-based prediction intervals and new advances. IEEE Trans. Neural Netw. 2011, 22, 1341–1356. [Google Scholar] [CrossRef]
- Khosravi, A.; Nahavandi, S.; Srinivasan, D.; Khosravi, R. Constructing Optimal Prediction Intervals by Using Neural Networks and Bootstrap Method. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1810–1815. [Google Scholar] [CrossRef] [PubMed]
- García Fernández, F.; Esteban, L.G.; de Palacios, P.; García-Iruela, A.; Cabedo Gallén, R. Estimating the Uncertainty of a Multilayer Perceptron Using the Monte Carlo Method. Adv. Mater. Res. 2013, 628, 324–329. [Google Scholar] [CrossRef]
- Hosen, M.A.; Khosravi, A.; Nahavandi, S.; Creighton, D. Aggregation of PI-based Forecast to Enhance Prediction Accuracy. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN) IEEE International Joint Conference on Neural Networks, Beijing, China, 6–11 July 2014. [Google Scholar]
- Hosen, M.A.; Khosravi, A.; Nahavandi, S.; Creighton, D. Improving the Quality of Prediction Intervals Through Optimal Aggregation. IEEE Trans. Ind. Electron. 2015, 62, 4420–4429. [Google Scholar] [CrossRef]
- Nerea Portillo, J.; Matutano, C.; Negro Valdecantos, V. Uncertainties in the application of artificial neural networks in ocean engineering. Ocean Eng. 2023, 284, 115193. [Google Scholar] [CrossRef]
- Stoma, P.; Stoma, M.; Dudziak, A.; Caban, J. Bootstrap Analysis of the Production Processes Capability Assessment. Appl. Sci. 2019, 9, 5360. [Google Scholar] [CrossRef]
- Chryssolouris, G.; Lee, M.; Ramsey, A. Confidence interval prediction for neural network models. IEEE Trans. Neural Netw. 1996, 7, 229–232. [Google Scholar] [CrossRef]
- MacKay, K.J.C. A practical Bayesian framework for backpropagation networks. Neural Comput. 1992, 4, 448–472. [Google Scholar] [CrossRef]
- EN 312; Particleboards. Specifications. European Committee of Standardization (CEN): Brussels, Belgium, 2010.
- EN 326-1; Wood-Based Panels. Sampling, Cutting and Inspection. Part 1: Sampling and Cutting of Test Pieces and Expression of Test Results. European Committee of Standardization (CEN): Brussels, Belgium, 1994.
- EN 322; Wood-Based Panels. Determination of the Moisture Content. European Committee of Standardization (CEN): Brussels, Belgium, 1993.
- EN 323; Wood-Based Panels. Determination of Density. European Committee of Standardization (CEN): Brussels, Belgium, 1993.
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman & Hall: New York, NY, USA, 1993; p. 436. [Google Scholar]
- Mazloumi, E.; Rose, G.; Currie, G.; Moridpour, S. Prediction intervals to account for uncertainties in neural network predictions: Methodology and application in bus travel time prediction. Eng. Appl. Artif. Intell. 2011, 24, 534–542. [Google Scholar] [CrossRef]
- Zhang, C.; Fu, Y. Probalilistic electricity price forecast with optimal prediction intervals. IEEE Trans. Power Syst. 2024, 39, 442–452. [Google Scholar] [CrossRef]
- Su, D.; Ting, Y.Y.; Ansel, J. Tight prediction intervals using expanded internal minimization. arXiv 2018, arXiv:1806.11222. [Google Scholar] [CrossRef]
- Lai, Y.; Shi, Y.; Han, Y.; Shao, Y.; Qi, M.; Li, B. Exploring uncertainty in regression neural networks for construction of prediction intervals. IEEE Trans. Knowl. Data Eng. 2022, 481, 249–257. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Z.; Chen, T. Interval prediction of ultra-short-term photovoltaic power based on a hybrid model. Electr. Power Syst. Res. 2023, 216, 109035. [Google Scholar] [CrossRef]
- Kasiviswanathan, K.S.; Cibin, R.; Sudheer, K.P.; Chaubey, I. Constructing prediction interval for artificial neural network rainfall runoff models based on ensemble simulations. J. Hidrol. 2013, 499, 275–288. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- De Veaux, R.; Ungar, L.H. Neural networks in applied statistics—Discussion. Technometrics 1996, 38, 215–218. [Google Scholar] [CrossRef]
- Cook, D.F.; Ragsdale, C.T.; Major, R.L. Combining a neural network with a genetic algorithm for process parameter optimization. Eng. Appl. Artif. Intell. 2000, 13, 391–396. [Google Scholar] [CrossRef]
- Ozsahin, S. The use of an artificial neural network for modeling the moisture absorption and thickness swelling of oriented strand board. BioResources 2012, 7, 1053–1067. [Google Scholar] [CrossRef]
- Iliadis, L.; Tachos, S.; Avramidis, S.; Mansfield, S. Hybrid e-regression and validation soft computing techniques: The case of wood dielectric loss factor. Neurocomputing 2013, 107, 33–39. [Google Scholar] [CrossRef]
- Buratti, C.; Barelli, L.; Moretti, E. Application of artificial neural network to predict thermal transmittance of wooden windows. Appl. Energy 2012, 98, 425–432. [Google Scholar] [CrossRef]
- Buratti, C.; Barelli, L.; Moretti, E. Wooden windows: Sound insulation evaluation by means of artificial neural networks. Appl. Acoust. 2013, 74, 740–745. [Google Scholar] [CrossRef]
- De Palacios, P.; Fernández, F.G.; García-Iruela, A.; González-Rodrigo, B.; Esteban, L.G. Study of the influence of physical properties on internal bond of particleboard type P2 using artificial neural networks. Comput. Electron. Agric. 2018, 155, 142–149. [Google Scholar] [CrossRef]
- Demuth, H.; Beale, M.; Hagan, M. Neural Network Toolbox User’s Guide Release 13, 4th ed.; The MathWorks Inc.: Natick, MA, USA, 2002; p. 808. [Google Scholar]
- Sarle, W.S. Neural Network FAQ, Part 1 of 7: Introduction, Periodic Posting to the Usenet Newsgroup comp.ai.neural-nets. 2022. Available online: https://gbif.es/wp-content/uploads/2010/05/NeuralNetworkFAQ.pdf (accessed on 10 January 2025).
- Sha, W. Comment on the issues of statistical modelling with particular reference to the use of artificial neural networks. Appl. Catal. A-Gen. 2007, 324, 87–89. [Google Scholar] [CrossRef]
- EN 326-2; Wood-Based Panels. Sampling, Cutting and Inspection. Part 2: Initial Type Testing and Factory Production Control. European Committee of Standardization (CEN): Brussels, Belgium, 2014.
- EN 326-2; Sampling, Cutting and Inspection. Part 2: Quality Control in the Factory. European Committee of Standardization (CEN): Brussels, Belgium, 2000.
- Papadopoulus, G.; Edwards, P.; Murray, A.F. Confidence estimation methods for neural networks: A practical comparison. IEEE Trans. Neural Netw. 2001, 12, 1278–1287. [Google Scholar] [CrossRef]
- Secchi, P.; Zoi, E.; di Maio, F. Quantifying uncertainties in the estimation of safety parameters by using bootstrapped artificial neural networks. Ann. Nucl. Energy 2008, 35, 2338–2350. [Google Scholar] [CrossRef]
- Demirkir, C.; Özsahin, S.; Aydin, I.; Colakoglu, G. Optimization of some panel manufacturing parameters for the best bonding strength of plywood. Int. J. Adhes. Adhes. 2013, 46, 14–20. [Google Scholar] [CrossRef]
- Bardak, S.; Tiryaki, S.; Nemli, G.; Aydin, A. Investigation and neural network prediction of wood bonding quality based on pressing conditions. Int. J. Adhes. Adhes. 2016, 68, 115–123. [Google Scholar] [CrossRef]
- García Fernández, F.; de Palacios, P.; Esteban, L.G.; García-Iruela, A.; Gonzalez Rodrigo, B.; Menasalvas, E. Prediction of MOR and MOE of structural plywood board using an artificial neural network and comparison with a multivariate regression model. Compos. Part B Eng. 2012, 43, 3528–3533. [Google Scholar] [CrossRef]
- André, N.; Cho, H.W.; Baek, S.H.; Jeong, M.K.; Young, T.M. Prediction of internal bond strength in a medium density fiberboard process using multivariate statistical methods and variable selection. Wood Sci. Technol. 2008, 42, 521–534. [Google Scholar] [CrossRef]
- Khosravi, A.; Nahavandi, S.; Creigton, D. Construction of optimal prediction intervals for load forecasting problems. IEEE Trans. Power Syst. 2010, 25, 1496–1503. [Google Scholar] [CrossRef]
- Khosravi, A.; Nahavandi, S. An optimized mean variance estimation method for uncertainty quantification of wind power forecasts. Int. J. Electr. Power Energy Syst. 2014, 61, 446–454. [Google Scholar] [CrossRef]
- Shrivastava, N.A.; Panigrahi, B.K. Point and prediction interval estimation for electricity markets with machine learning techniques and wavelet transforms. Neurocomputing 2013, 118, 301–310. [Google Scholar] [CrossRef]
- Wan, C.; Xu, Z.; Pinson, P.; Dong, Z.Y.; Wong, K.P. Optimal prediction of wind power generation. IEEE Trans. Power Syst. 2014, 29, 1166–1174. [Google Scholar] [CrossRef]
- Kasiviswanathan, K.S.; Sudheer, K.P. Comparison of methods used for quantifying prediction interval in artificial neural network hydrologic models. Model. Earth Syst. Environ. 2016, 2, 22. [Google Scholar] [CrossRef]
- Nourani, V.; Paknezhad, N.J.; Sharghi, E.; Khosravi, A. Estimation of prediction intervals in ANN-based multi-GCMs downscaling of hydro-climatologic parameters. J. Hydrol. 2019, 579, 124226. [Google Scholar] [CrossRef]
- Nourani, V.; Sayyah-Fard, M.; Kantoush, S.A.; Bharambe, K.P.; Sumi, T.; Saber, M. Optimization-based prediction uncertainty qualification of climatic parameters. J. Hydrometeorol. 2023, 24, 1679–1697. [Google Scholar] [CrossRef]
- Al-Dahidi, S.; Ayadi, O.; Alrbai, M.; Adeeb, J. Ensemble approach of optimized artificial neural networks for solar photovoltaic power prediction. IEEE Access 2019, 7, 81741–81758. [Google Scholar] [CrossRef]
- Seyedian, S.M.; Kisi, O.; Parsaie, A.; Kashani, M. Improving the reliability of compound chanel discharge prediction using machine learning techniques and resampling methods. Water Resour. Manag. 2024, 38, 4685–4709. [Google Scholar] [CrossRef]
- Chen, H.; Zheng, Y.; Huang, H.; Wang, Z.; Yang, B. A point-interval prediction framework for minimum miscibility pressure of CO2-crude oil systems. Fuel 2025, 381, 133573. [Google Scholar] [CrossRef]

| Property | Mean | Std. Deviation | Min. | Max. |
|---|---|---|---|---|
| Thickness (mm) | 19.80 | 7.38 | 7.82 | 40.14 |
| Density (kg/m3) | 668.81 | 37.09 | 562.41 | 782.78 |
| MC (%) | 9.48 | 0.73 | 7.68 | 14.30 |
| Variable | Mean | Std. Deviation | Min | Max |
|---|---|---|---|---|
| Particle temperature (°C) | 43.76 | 6.21 | 30 | 57 |
| Resin temperature (°C) | 27.9 | 10.3 | 7.5 | 40.4 |
| Mat moisture content (%) | 4.7 | 0.6 | 6.6 | 3.6 |
| Resin percentage (%) | 8.90 | 0.27 | 8.15 | 9.75 |
| Additive percentage (%) | 0.30 | 0.03 | 0.16 | 0.48 |
| Mat velocity (mm/s) | 455.8 | 119.7 | 185 | 755 |
| Press temperature (°C) | 230.4 | 9.8 | 184.4 | 268.4 |
| Internal bond (N/mm2) | 0.56 | 0.11 | 0.30 | 0.98 |
| Network | Phase | Structure | R2 | R | p-Value |
|---|---|---|---|---|---|
| 1 | Training | [7 3 3] | 0.82 | 0.91 | 0.96 |
| Validation | 0.80 | 0.89 | 0.82 | ||
| Testing | 0.57 | 0.75 | 0.72 | ||
| Total | 0.76 | 0.87 | 0.76 | ||
| 2 | Training | [8 1] | 0.81 | 0.90 | 0.95 |
| Validation | 0.73 | 0.85 | 0.29 | ||
| Testing | 0.55 | 0.73 | 0.97 | ||
| Total | 0.71 | 0.84 | 0.70 | ||
| 3 | Training | [8 2] | 0.71 | 0.84 | 0.87 |
| Validation | 0.69 | 0.83 | 0.24 | ||
| Testing | 0.60 | 0.77 | 0.93 | ||
| Total | 0.66 | 0.81 | 0.72 | ||
| 4 | Training | [7 1 1] | 0.82 | 0.91 | 0.59 |
| Validation | 0.69 | 0.83 | 0.72 | ||
| Testing | 0.63 | 0.79 | 0.39 | ||
| Total | 0.74 | 0.86 | 0.50 | ||
| 5 | Training | [7 1 1] | 0.78 | 0.88 | 0.92 |
| Validation | 0.69 | 0.83 | 0.41 | ||
| Testing | 0.50 | 0.71 | 0.72 | ||
| Total | 0.69 | 0.83 | 0.61 | ||
| 6 | Training | [5 2 2] | 0.68 | 0.83 | 0.76 |
| Validation | 0.67 | 0.82 | 0.24 | ||
| Testing | 0.63 | 0.79 | 0.47 | ||
| Total | 0.62 | 0.79 | 0.61 | ||
| 7 | Training | [8 1] | 0.69 | 0.83 | 0.20 |
| Validation | 0.66 | 0.81 | 0.67 | ||
| Testing | 0.64 | 0.80 | 0.99 | ||
| Total | 0.64 | 0.80 | 0.46 | ||
| 8 | Training | [7 2 1] | 0.86 | 0.93 | 0.65 |
| Validation | 0.66 | 0.81 | 0.51 | ||
| Testing | 0.56 | 0.75 | 0.21 | ||
| Total | 0.73 | 0.85 | 0.25 | ||
| 9 | Training | [8 2] | 0.82 | 0.90 | 0.95 |
| Validation | 0.64 | 0.80 | 0.51 | ||
| Testing | 0.51 | 0.72 | 0.92 | ||
| Total | 0.72 | 0.85 | 0.89 | ||
| 10 | Training | [5 1 1] | 0.80 | 0.89 | 0.95 |
| Validation | 0.63 | 0.80 | 0.14 | ||
| Testing | 0.63 | 0.79 | 0.85 | ||
| Total | 0.69 | 0.83 | 0.51 | ||
| 11 | Training | [5 1] | 0.70 | 0.84 | 0.95 |
| Validation | 0.64 | 0.80 | 0.35 | ||
| Testing | 0.66 | 0.81 | 0.60 | ||
| Total | 0.66 | 0.81 | 0.67 | ||
| 12 | Training | [7 2 1] | 0.90 | 0.95 | 0.98 |
| Validation | 0.62 | 0.79 | 0.18 | ||
| Testing | 0.59 | 0.77 | 0.40 | ||
| Total | 0.73 | 0.86 | 0.34 | ||
| 13 | Training | [5 1 1] | 0.79 | 0.89 | 0.98 |
| Validation | 0.62 | 0.79 | 0.22 | ||
| Testing | 0.51 | 0.71 | 0.65 | ||
| Total | 0.67 | 0.82 | 0.74 | ||
| 14 | Training | [4 3 3] | 0.85 | 0.92 | 0.99 |
| Validation | 0.63 | 0.79 | 0.71 | ||
| Testing | 0.54 | 0.73 | 0.64 | ||
| Total | 0.74 | 0.86 | 0.72 | ||
| 15 | Training | [7 2 2] | 0.71 | 0.84 | 0.98 |
| Validation | 0.61 | 0.78 | 0.43 | ||
| Testing | 0.62 | 0.79 | 0.21 | ||
| Total | 0.66 | 0.81 | 0.42 | ||
| 16 | Training | [7 2] | 0.78 | 0.89 | 0.93 |
| Validation | 0.60 | 0.78 | 0.19 | ||
| Testing | 0.60 | 0.78 | 0.90 | ||
| Total | 0.68 | 0.82 | 0.61 | ||
| 17 | Training | [5 3 3] | 0.83 | 0.91 | 0.99 |
| Validation | 0.60 | 0.78 | 0.23 | ||
| Testing | 0.58 | 0.76 | 0.89 | ||
| Total | 0.71 | 0.84 | 0.58 | ||
| 18 | Training | [5 2 2] | 0.76 | 0.87 | 0.98 |
| Validation | 0.61 | 0.78 | 0.29 | ||
| Testing | 0.57 | 0.75 | 0.35 | ||
| Total | 0.66 | 0.82 | 0.39 | ||
| 19 | Training | [5 1] | 0.75 | 0.87 | 0.95 |
| Validation | 0.59 | 0.77 | 0.27 | ||
| Testing | 0.50 | 0.71 | 0.97 | ||
| Total | 0.65 | 0.80 | 0.68 | ||
| 20 | Training | [7 1] | 0.63 | 0.80 | 0.89 |
| Validation | 0.58 | 0.76 | 0.68 | ||
| Testing | 0.60 | 0.77 | 0.21 | ||
| Total | 0.61 | 0.78 | 0.44 |
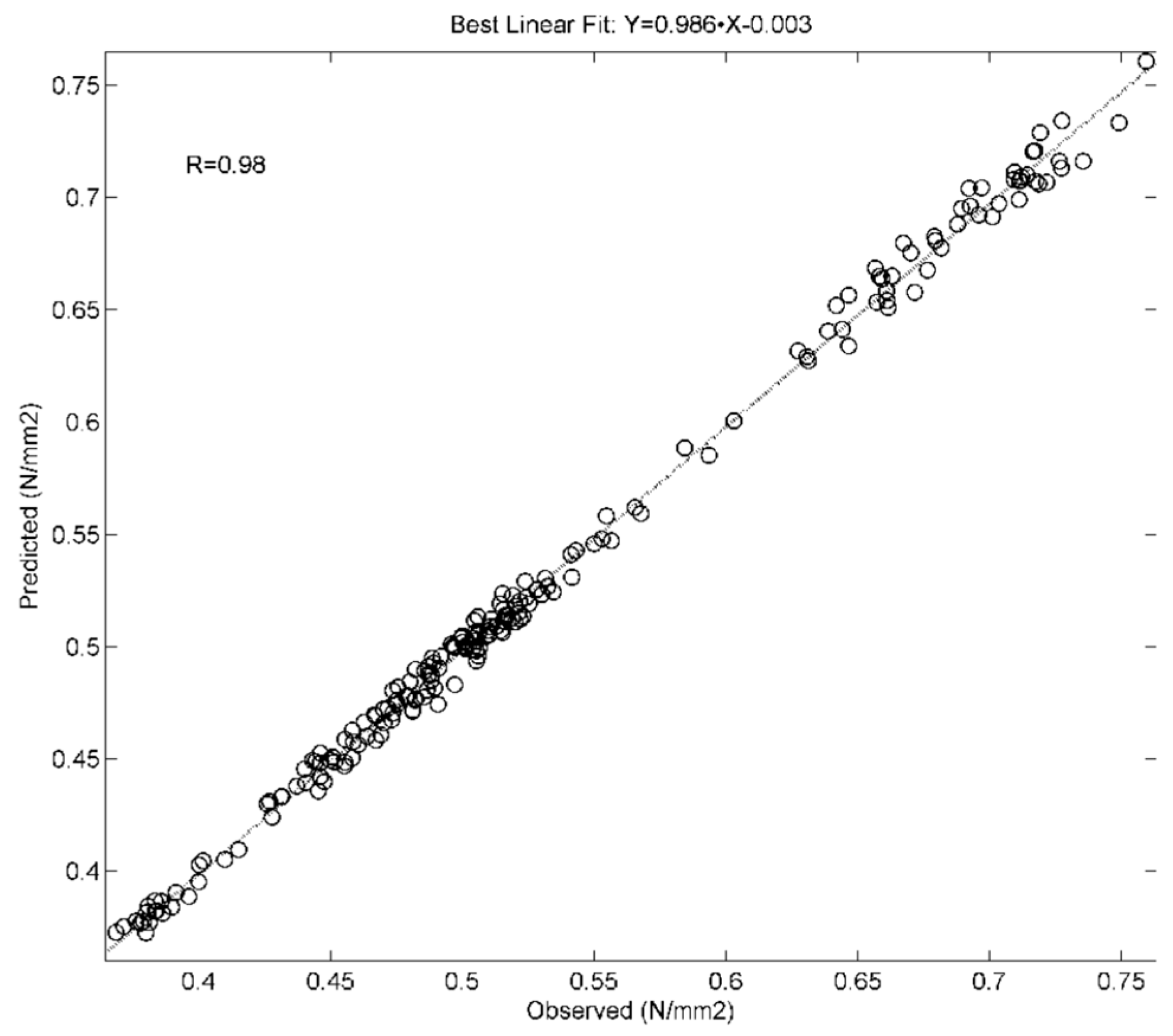
| Property | Equation | R2 | R | RMSE | p-Value | PICP (%) |
|---|---|---|---|---|---|---|
| Internal bond | 0.986·X − 0.003 | 0.96 | 0.98 | 0.06 | 0.97 | 93.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García Fernández, F.; de Palacios, P.; García-Iruela, A.; Esteban, L.G. Using Bootstrapping to Determine Artificial Neural Network Confidence Intervals—Case Study of Particleboard Internal Bond Determined from Production Data. Appl. Sci. 2025, 15, 4554. https://doi.org/10.3390/app15084554
García Fernández F, de Palacios P, García-Iruela A, Esteban LG. Using Bootstrapping to Determine Artificial Neural Network Confidence Intervals—Case Study of Particleboard Internal Bond Determined from Production Data. Applied Sciences. 2025; 15(8):4554. https://doi.org/10.3390/app15084554
Chicago/Turabian StyleGarcía Fernández, Francisco, Paloma de Palacios, Alberto García-Iruela, and Luis García Esteban. 2025. "Using Bootstrapping to Determine Artificial Neural Network Confidence Intervals—Case Study of Particleboard Internal Bond Determined from Production Data" Applied Sciences 15, no. 8: 4554. https://doi.org/10.3390/app15084554
APA StyleGarcía Fernández, F., de Palacios, P., García-Iruela, A., & Esteban, L. G. (2025). Using Bootstrapping to Determine Artificial Neural Network Confidence Intervals—Case Study of Particleboard Internal Bond Determined from Production Data. Applied Sciences, 15(8), 4554. https://doi.org/10.3390/app15084554









