Ion Beam Formation and Modification of Cobalt Nanoparticles
Abstract
:1. Introduction
2. Experimental Section
3. Formation of Cobalt Nanoparticles by Ion Implantation
3.1. Introduction
3.2. Results
3.3. Summary
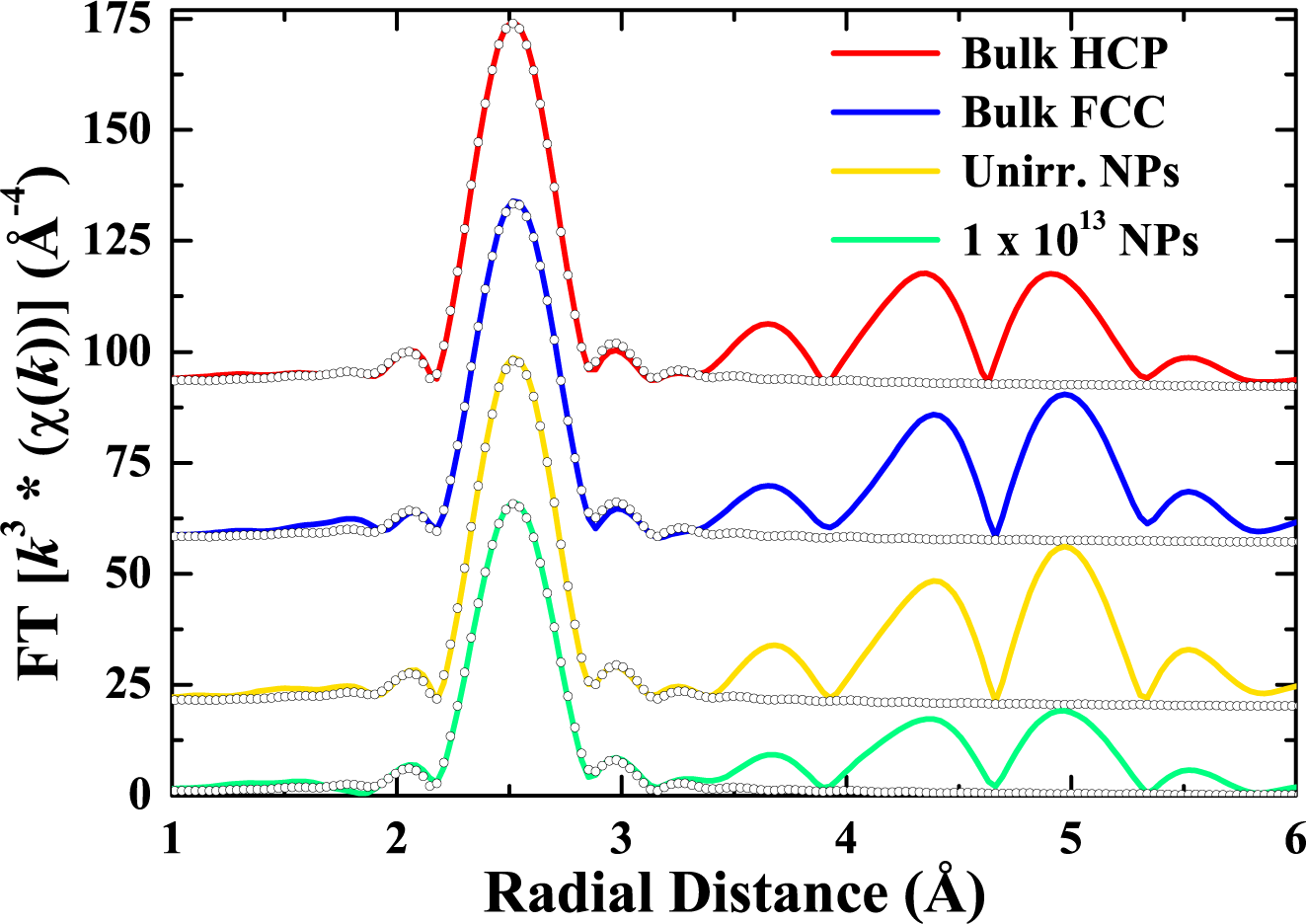
4. Ion Irradiation-Induced Amorphisation of Cobalt Nanoparticles
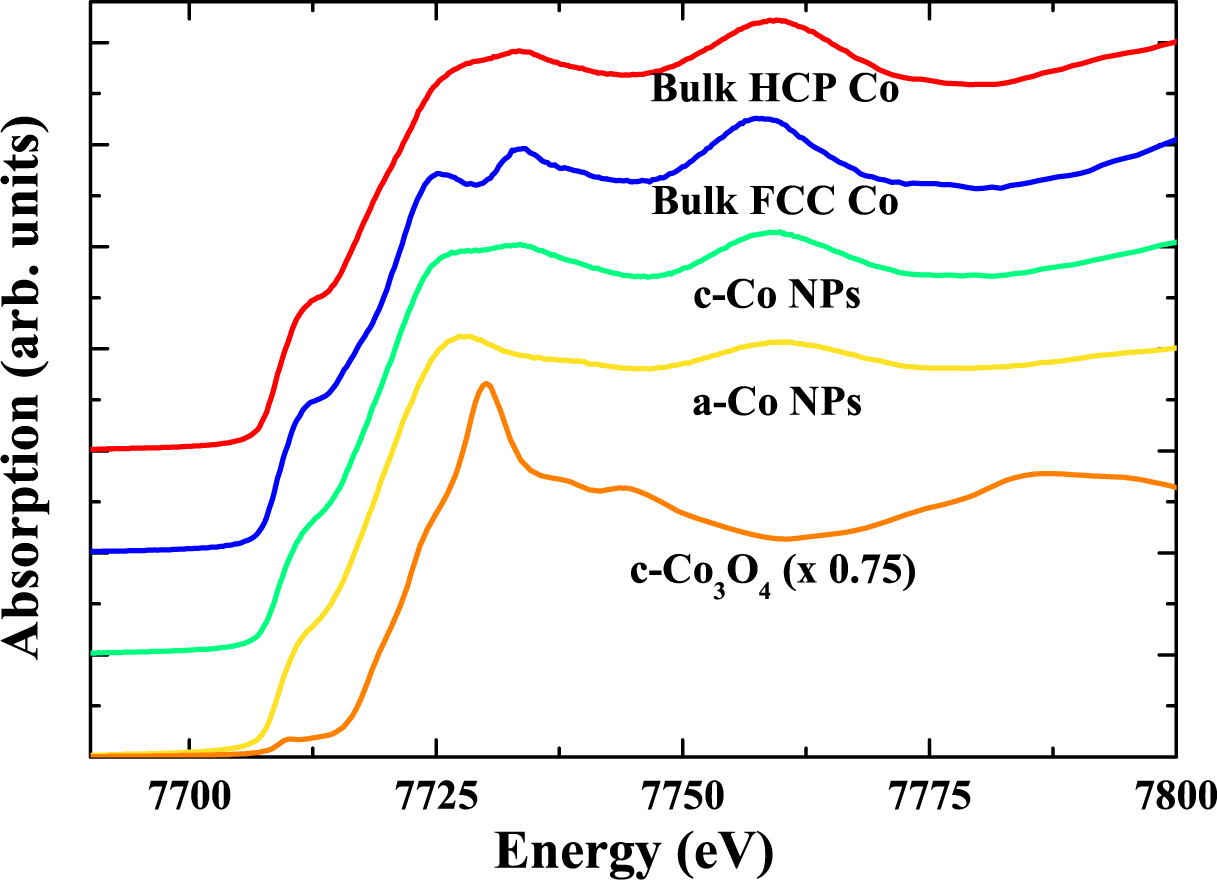
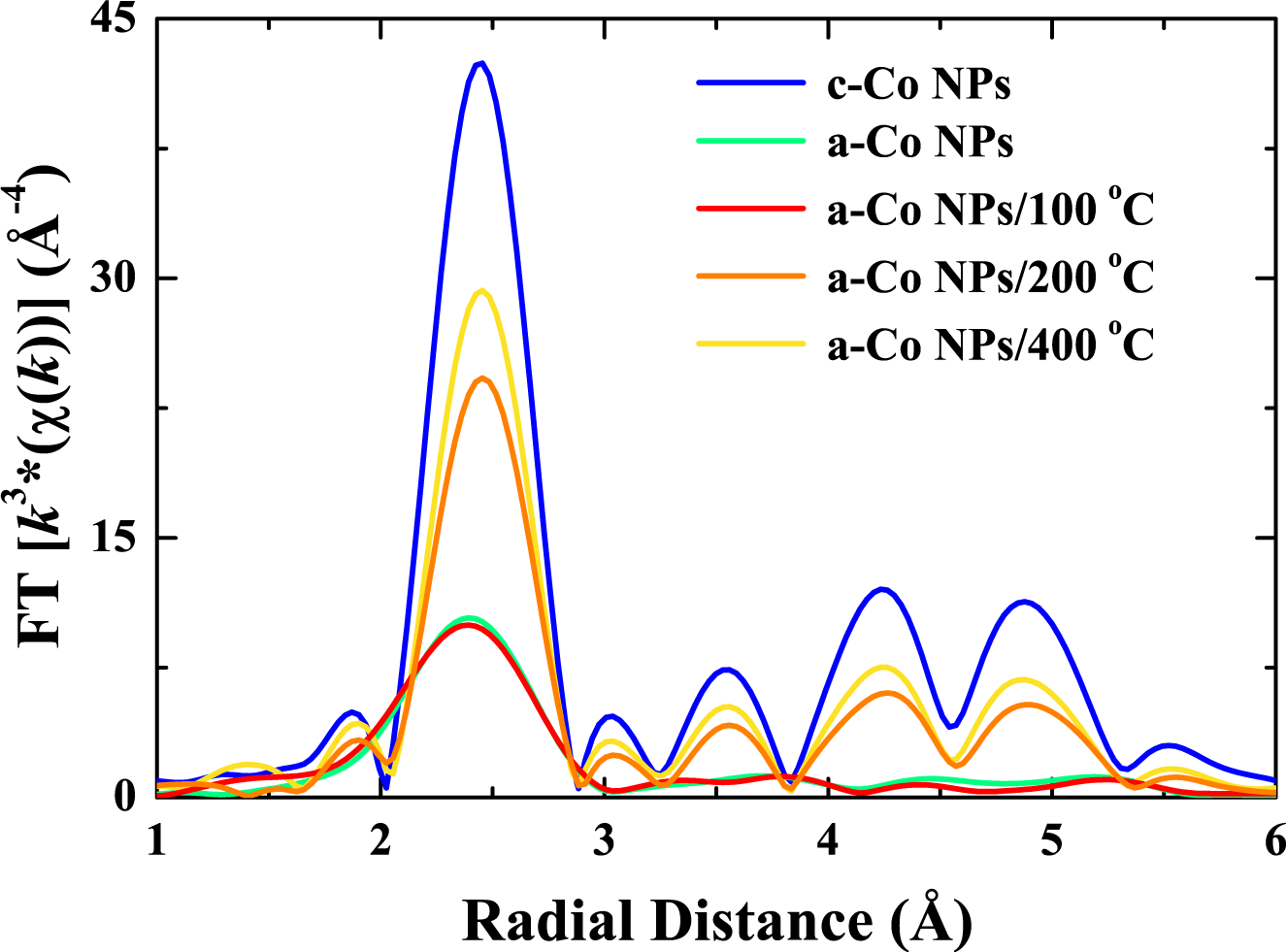
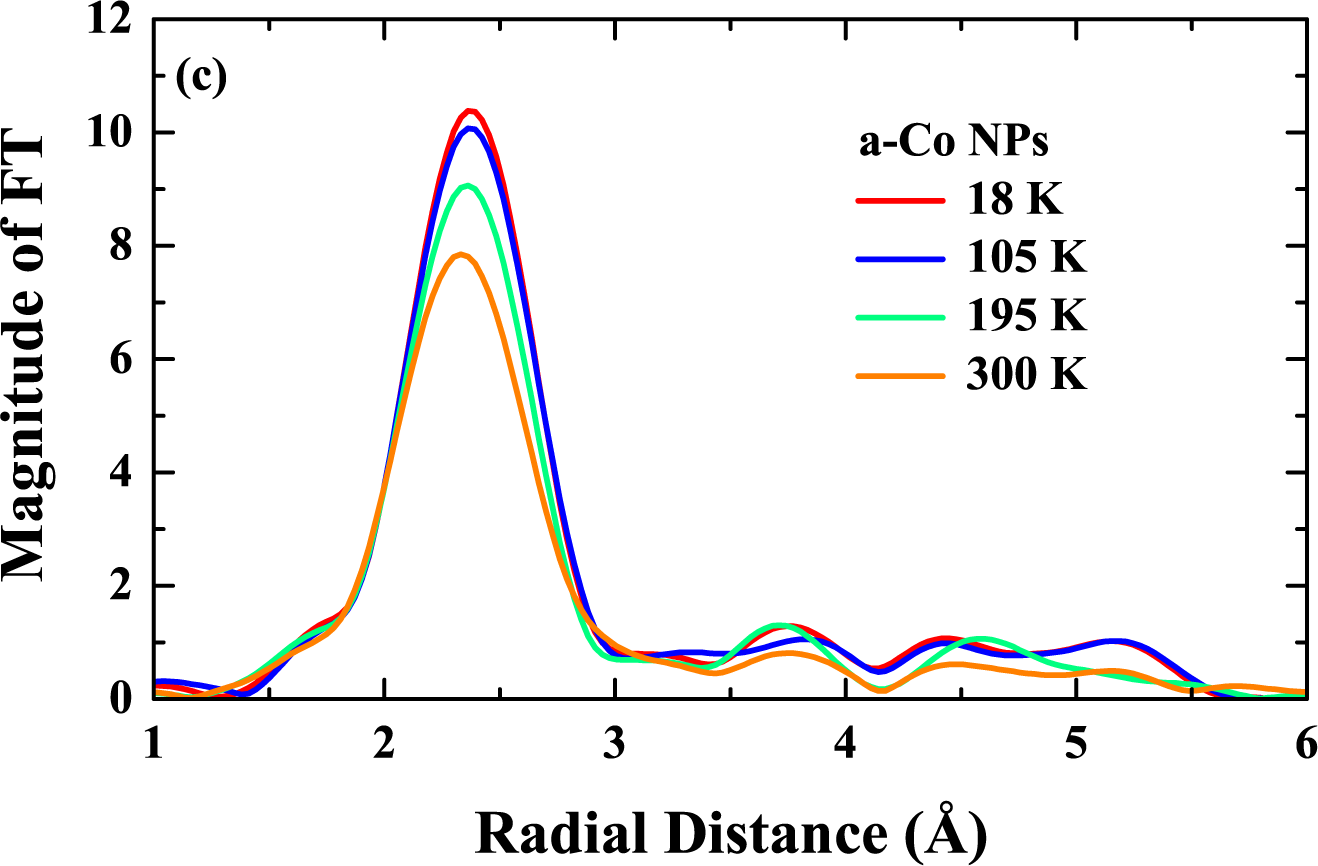
4.1. Introduction
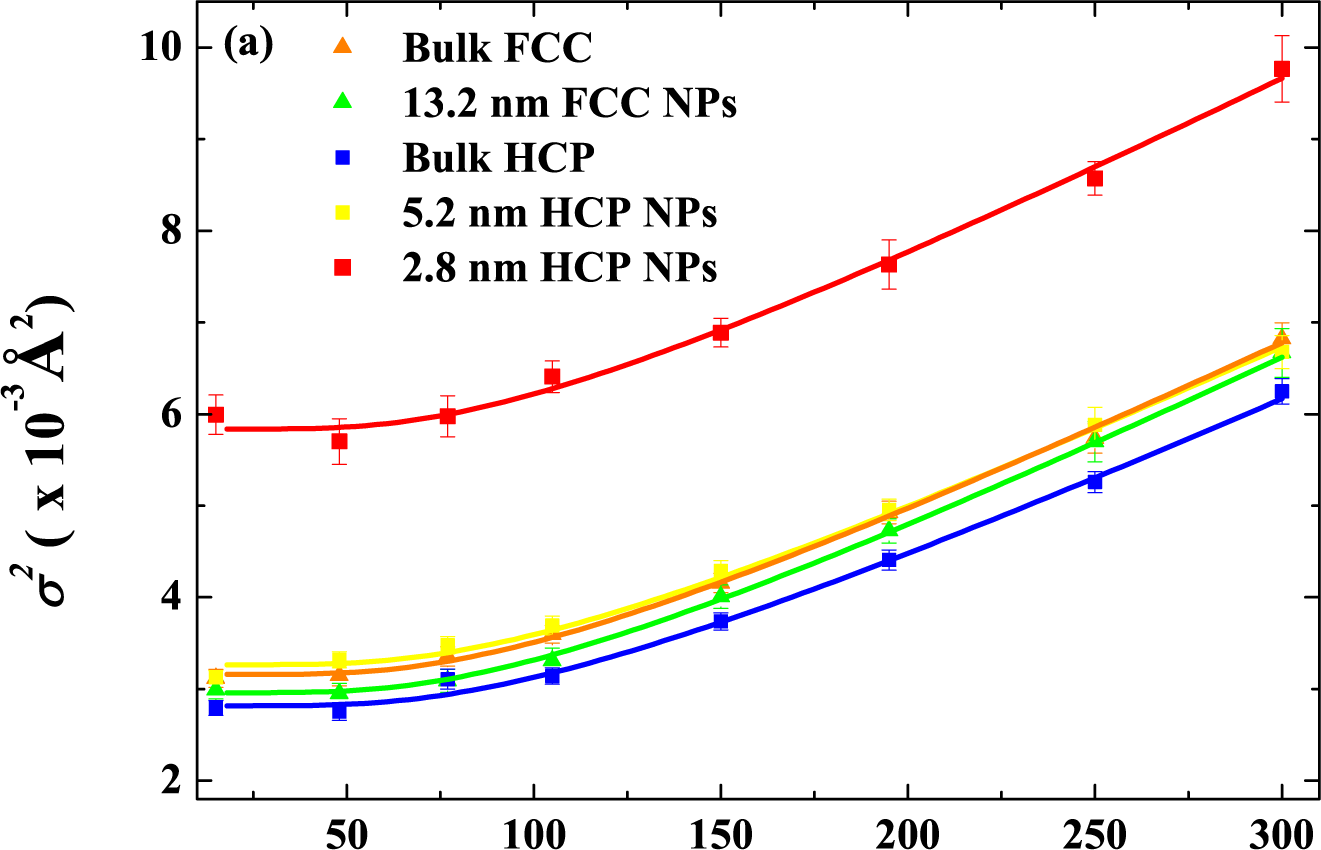
4.2. Results
4.3. Summary
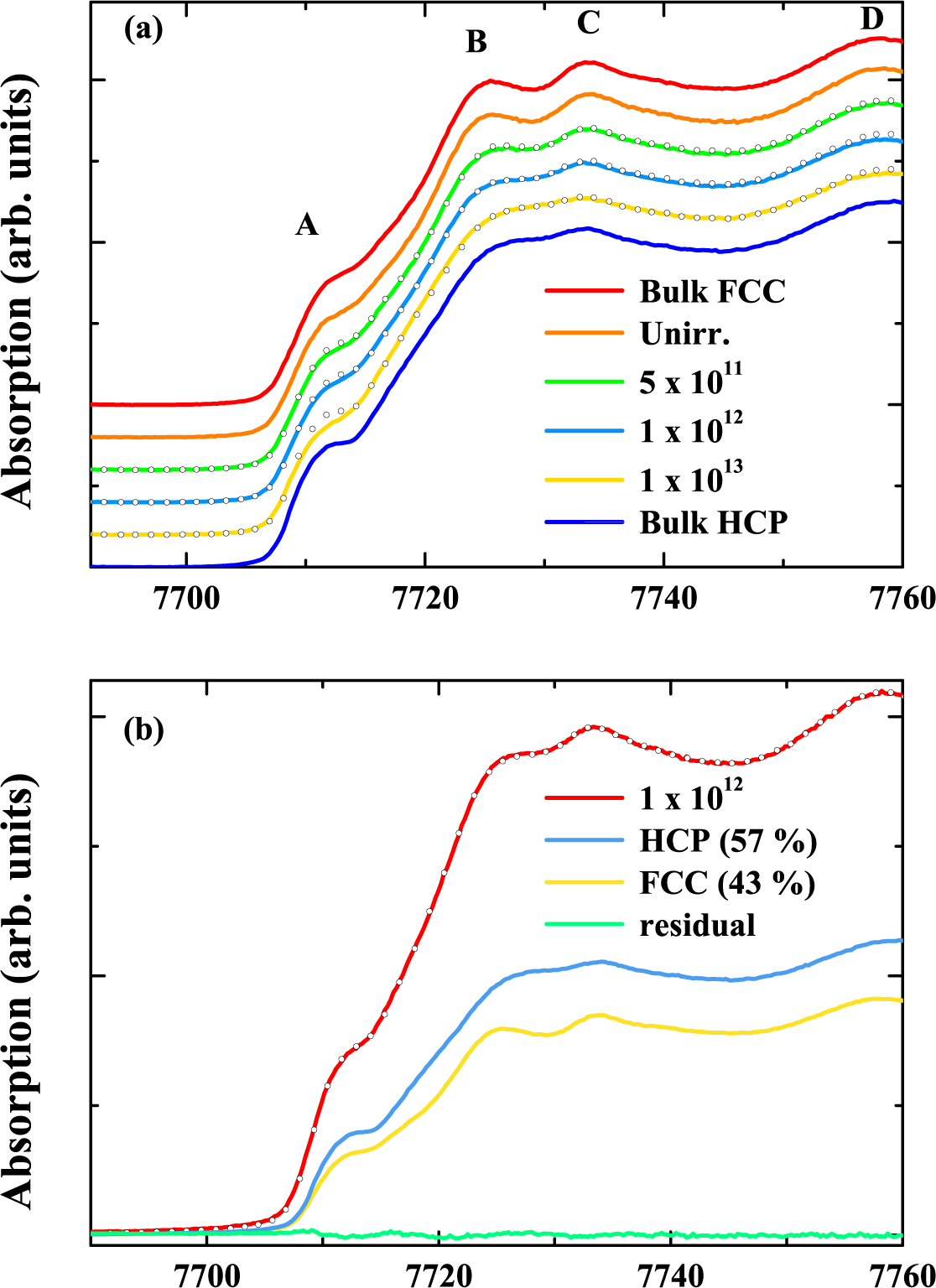
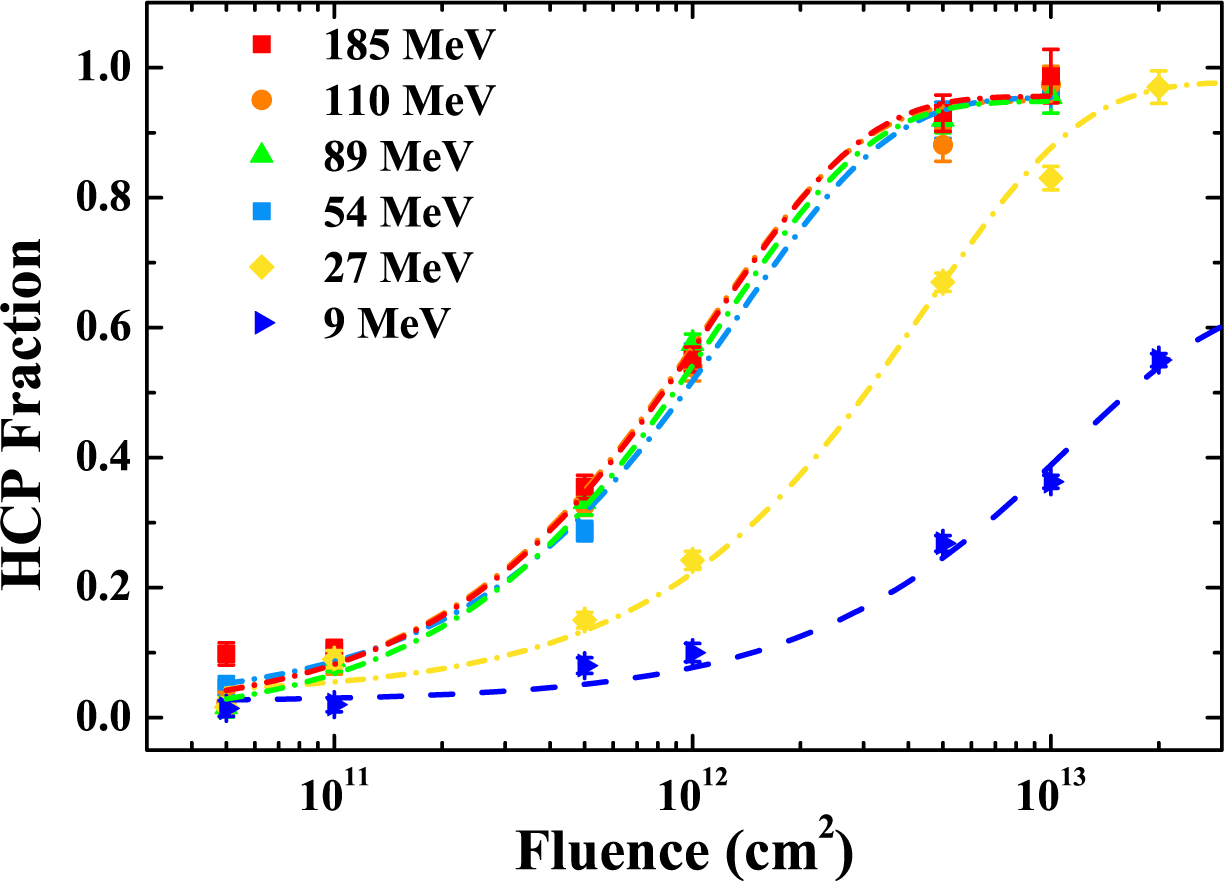
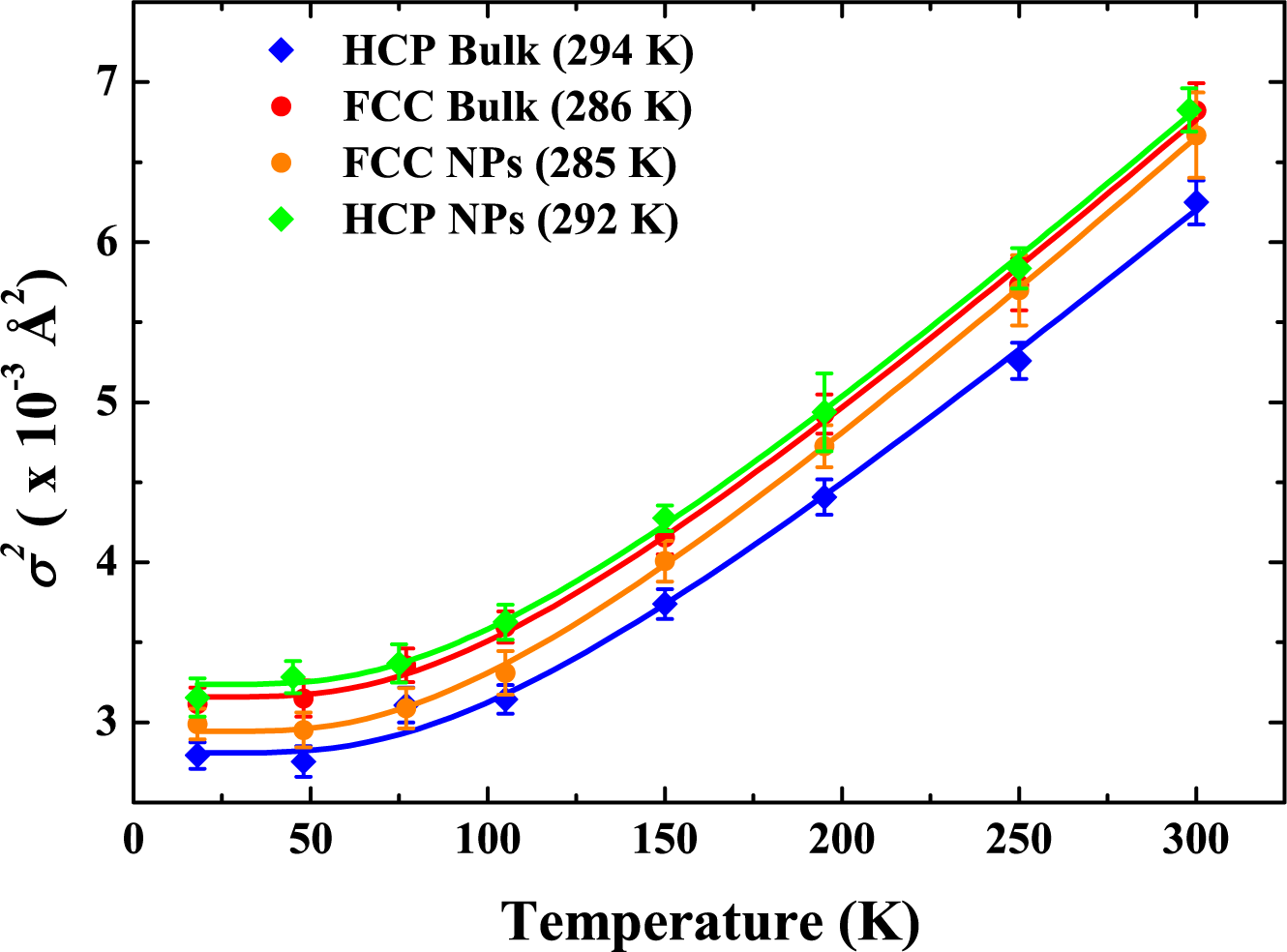
5. Swift Heavy Ion Irradiation-Induced FCC-to-HCP Phase Transformation in Cobalt Nanoparticles
5.1. Introduction
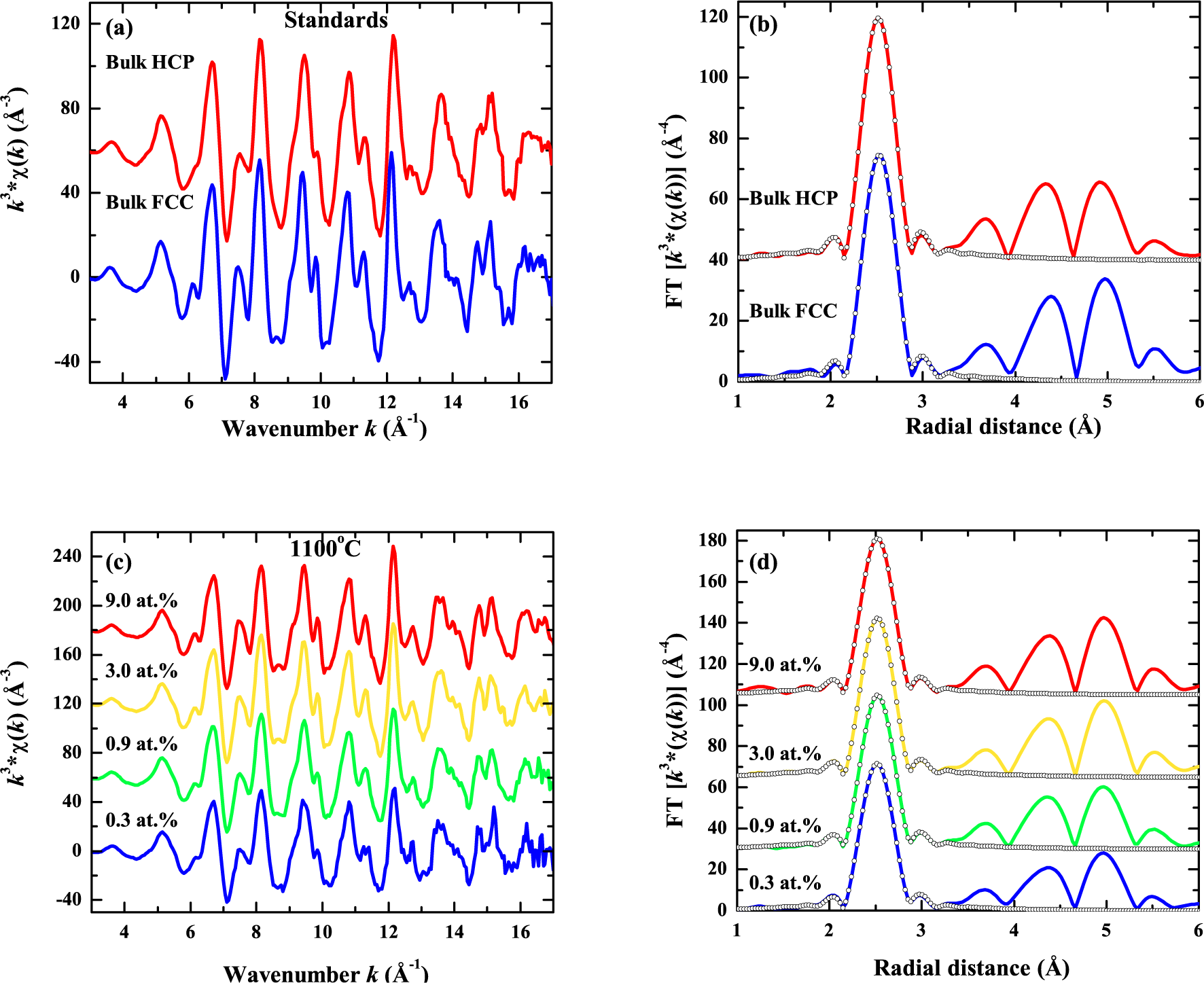
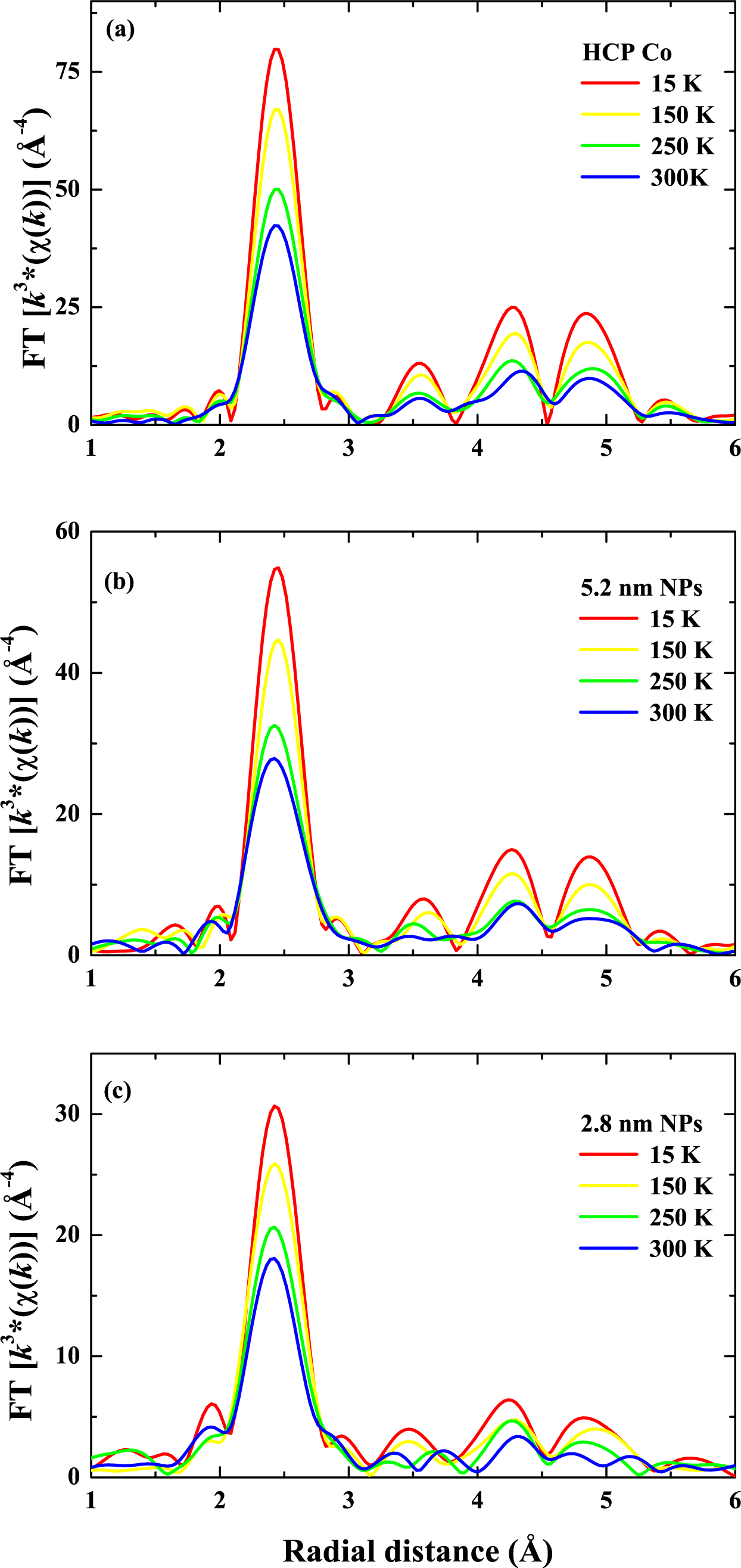
5.2. Results
5.3. Summary
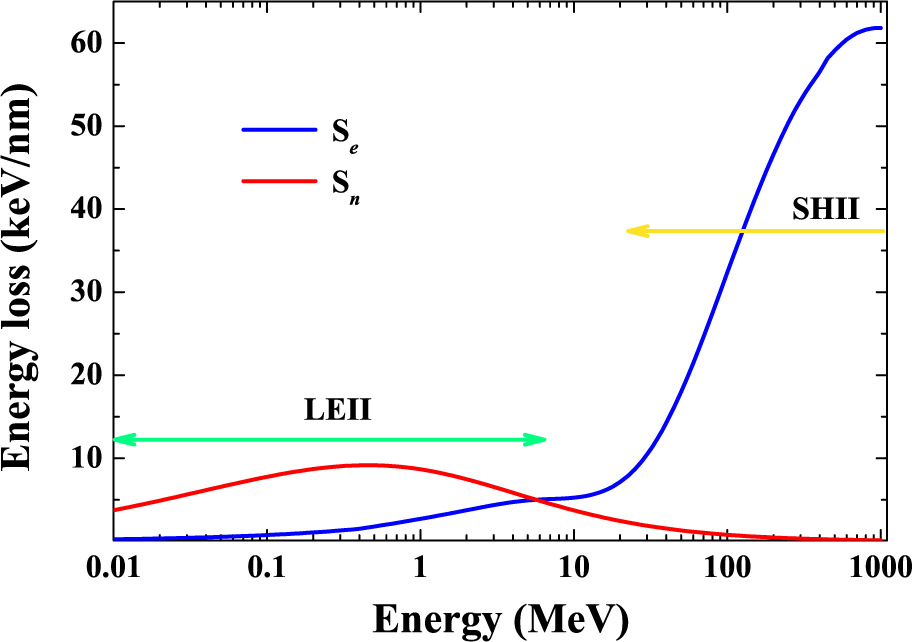
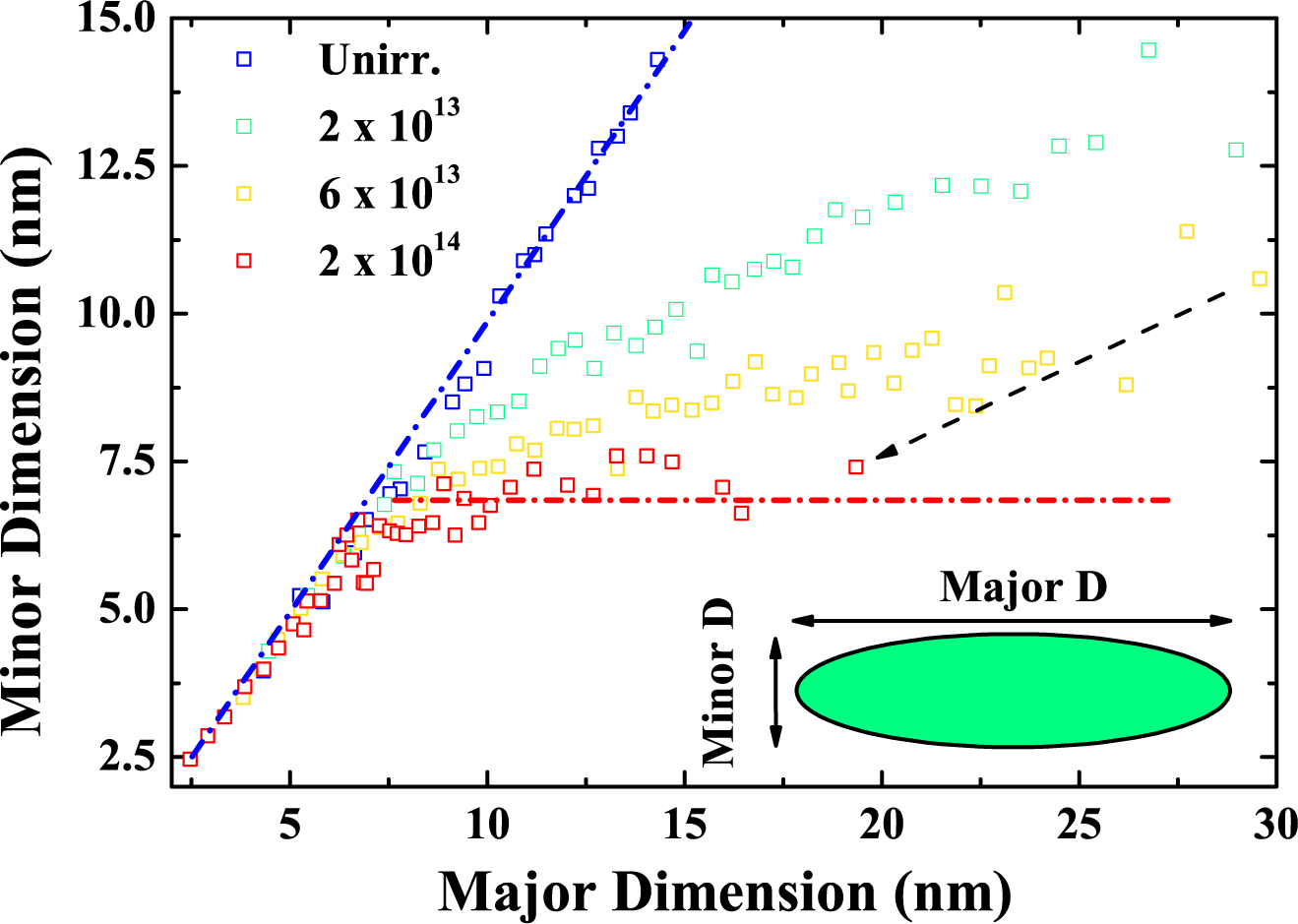
6. Swift Heavy Ion Irradiation-Induced Shape and Structural Changes in Cobalt Nanoparticles
6.1. Introduction
6.2. Results
6.3. Summary
7. Conclusions
Acknowledgments
References
- Kelly, K.L.; Coronado, E.; Zhao, L.L.; Schatz, G.C. The optical properties of metal nanoparticles: The influence of size, shape, and dielectric environment. J. Phys. Chem. B. 2003, 107, 668–677. [Google Scholar]
- Kreibig, U.; Vollmer, M. Optical Properties of Metal Clusters; Springer-Verlag: New York, NY, USA, 2010. [Google Scholar]
- Jensen, T.; Kelly, L.; Lazarides, A.; Schatz, G.C. Electrodynamics of noble metal nanoparticles and nanoparticle clusters. J. Clust. Sci. 1999, 10, 295–317. [Google Scholar]
- Daniel, M.C.; Astruc, D. Gold nanoparticles: Assembly, supramolecular chemistry, quantum-size-related properties, and applications toward biology, catalysis, and nanotechnology. Chem. Rev. 2004, 104, 293–346. [Google Scholar]
- Mulvaney, P. Surface plasmon spectroscopy of nanosized metal particles. Langmuir 1996, 12, 788–800. [Google Scholar]
- Murphy, C.J.; San, T.K.; Gole, A.M.; Orendorff, C.J.; Gao, J.X.; Gou, L.; Hunyadi, S.E.; Li, T. Anisotropic metal nanoparticles: Synthesis, assembly, and optical applications. J. Phys. Chem. B. 2005, 109, 13857–13870. [Google Scholar]
- Burda, C.; Chen, X.B.; Narayanan, R.; El-Sayed, M.A. Chemistry and properties of nanocrystals of different shapes. Chem. Rev. 2005, 105, 1025–1102. [Google Scholar]
- Meldrum, A.; Haglund, R.F.; Boatner, L.A.; White, C.W. Nanocomposite materials formed by ion implantation. Adv. Mater. 2001, 13, 1431–1444. [Google Scholar]
- Ercolessi, F.; Andreoni, W.; Tosatti, E. Melting of small gold particles: Mechanism and size effects. Phys. Rev. Lett. 1991, 66, 911–914. [Google Scholar]
- Lai, S.L.; Guo, J.Y.; Petrova, V.; Ramanath, G.; Allen, L.H. Size-dependent melting properties of small tin particles: Nanocalorimetric measurements. Phys. Rev. Lett. 1996, 77, 99–102. [Google Scholar]
- Olson, E.A.; Efremov, M.Y.; Zhang, M.; Zhang, Z.; Allen, L.H. Size-dependent melting of Bi nanoparticles. J. Appl. Phys. 2005, 97, 034304–034309. [Google Scholar]
- Frenkel, A.I.; Hills, C.W.; Nuzzo, R.G. A. View from the inside: Complexity in the atomic scale ordering of supported metal nanoparticles. J. Phys. Chem. B. 2001, 105, 12689–12703. [Google Scholar]
- Sun, S.; Murray, C.B. Synthesis of monodisperse cobalt nanocrystals and their assembly into magnetic superlattices. J. Appl. Phys. 1999, 85, 4325–4330. [Google Scholar]
- Puntes, V.F.; Krishnan, K.M.; Alivisatos, A.P. Colloidal nanocrystal shape and size control: The case of cobalt. Science 2001, 291, 2115–2117. [Google Scholar]
- Pankhurst, Q.A.; Connolly, J.; Jones, S.K.; Dobson, J. Applications of magnetic nanoparticles in biomedicine. J. Phys. D-Appl. Phys. 2003, 36, R167–R181. [Google Scholar]
- Ross, C. Patterned magnetic recording media. Ann. Rev. Mater. Res. 2001, 31, 203–235. [Google Scholar]
- Kitakami, O.; Sato, H.; Shimada, Y.; Sato, F.; Tanaka, M. Size effect on the crystal phase of cobalt fine particles. Phys. Rev. B. 1997, 56, 13849–13854. [Google Scholar]
- Mattei, G.; Maurizio, C.; Fernandez, C.D.; Mazzoldi, P.; Battaglin, G.; Canton, P.; Cattaruzza, E.; Scian, C. Nucl. Instrum. Methods Phys. Res. B. 2006, 250, 206–209.
- Sato, H.; Kitakami, O.; Sakurai, T.; Shimada, Y.; Otani, Y.; Fukamichi, K. Structure and magnetism of hcp-Co fine particles. J. Appl. Phys. 1997, 81, 1858–1862. [Google Scholar]
- Zhang, G.L.; Wu, Z.Y.; Li, A.G.; Wang, Y.S.; Zhang, J.; Abbas, M.I.; Hu, R.; Ni, X.B.; Tong, Y.P.; Hwu, Y.K. XANES investigation of the local structure of Co nanoclusters embedded in Ag. Phys. Rev. B. 2004, 69, 115405. [Google Scholar]
- Cezar, J.C.; Tolentino, H.C.N.; Knobel, M. Structural, magnetic, and transport properties of Co nanoparticles within a Cu matrix. Phys. Rev. B. 2003, 68, 054404. [Google Scholar]
- Meldrum, A.; Boatner, L.A.; Sorge, K. Microstructure and magnetic properties of Co nanoparticles in ion-implanted Al2O3. Nucl. Instrum. Methods Phys. Res. B. 2003, 207, 36–44. [Google Scholar]
- Jacobsohn, L.G.; Hawley, M.E.; Cooke, D.W.; Hundley, M.F.; Thompson, J.D.; Schulze, R.K.; Nastasi, M. Synthesis of cobalt nanoparticles by ion implantation and effects of postimplantation annealing. J. Appl. Phys. 2004, 96, 4444–4450. [Google Scholar]
- Zhao, X.Q.; Veintemillas-Verdaguer, S.; Bomati-Miguel, O.; Morales, M.P.; Xu, H.B. Thermal history dependence of the crystal structure of Co fine particles. Phys. Rev. B. 2005, 71, 024106. [Google Scholar]
- Song, Y.J.; Modrow, H.; Henry, L.L.; Saw, C.K.; Doomes, E.E.; Palshin, V.; Hormes, J.; Kumar, C.S.S.R. Microfluidic synthesis of cobalt nanoparticles. Chem. Mater. 2006, 18, 2817–2827. [Google Scholar]
- Zeng, H.; Zheng, M.; Skomski, R.; Sellmyer, D.J.; Liu, Y.; Menon, L.; Bandyopadhyay, S. Magnetic properties of self-assembled Co nanowires of varying length and diameter. J. Appl. Phys. 2000, 87, 4718–4720. [Google Scholar]
- Nordlund, K.; Ghaly, M.; Averback, R.S.; Caturla, M.; Diaz de la Rubia, T.; Tarus, J. Defect production in collision cascades in elemental semiconductors and fcc metals. Phys. Rev. B. 1998, 57, 7556–7570. [Google Scholar]
- Lesueur, D.; Dunlop, A. Damage creation via electronic excitations in metallic targets. 2. A theoretical model. Radiat. Eff. Defect. Solids. 1993, 126, 163–172. [Google Scholar]
- Fleischer, R.L.; Price, P.B.; Walker, R.M. Ion explosion spike mechanism for formation of charged-particle tracks in solids. J. Appl. Phys. 1965, 36, 3645–3652. [Google Scholar]
- Volkov, A.E.; Borodin, V.A. Heating of metals in swift heavy ion tracks by electron-ion energy exchange. Nucl. Instrum. Methods Phys. Res. B. 1998, 146, 137–141. [Google Scholar]
- Wang, Z.G.; Dufour, C.; Paumier, E.; Toulemonde, M. The Se sensitivity of metals under swift-heavy-ion irradiation: A transient thermal-process. J. Phys. Condens. Matter. 1994, 6, 6733–6750. [Google Scholar]
- Toulemonde, M.; Dufour, C.; Paumier, E. Transient thermal-process after a high-energy heavy-ion irradiation of amorphous metals and semiconductors. Phys. Rev. B. 1992, 46, 14362–14369. [Google Scholar]
- Ziegler, J.; Beirsack, J.P.; Littmark, U. The Stopping and Range of Ions in Matter; Pergamon Press: New York, NY, USA, 1985. [Google Scholar]
- Cheung, A.; Azevedo, G.D.; Glover, C.J.; Llewellyn, D.J.; Elliman, R.G.; Foran, G.J.; Ridgway, M.C. Structural perturbations within Ge nanocrystals in silica. Appl. Phys. Lett. 2004, 84, 278–280. [Google Scholar]
- Giulian, R.; Kluth, P.; Araujo, L.L.; Sprouster, D.J.; Byrne, A.P.; Cookson, D.J.; Ridgway, M.C. Shape transformation of Pt nanoparticles induced by swift heavy-ion irradiation. Phys. Rev. B. 2008, 78, 125413. [Google Scholar]
- Ravel, B.; Newville, M; Athena, Artemis. Hephaestus: Data analysis for X-ray absorption spectroscopy using IFEFFIT. J. Synchrotron Radiat 2005, 12, 537–541. [Google Scholar]
- Newville, M. IFEFFIT: Interactive XAFS analysis and FEFF fitting. J. Synchrotron Radiat 2001, 8, 322–324. [Google Scholar]
- Rehr, J.J.; Albers, R.C. Theoretical approaches to X-ray absorption fine structure. Rev. Mod. Phys. 2000, 72, 621–654. [Google Scholar]
- Tsao, C.S.; Lin, T.L. Analysis of small-angle scattering data from spherical particles by both the indirect transform method and the maximum-entropy method. J. Appl. Crystallogr. 1997, 30, 353–361. [Google Scholar]
- Ilavsky, J.; Jemian, P.R. Irena: Tool suite for modeling and analysis of small-angle scattering. J. Appl. Crystallogr. 2009, 42, 347–353. [Google Scholar]
- Sprouster, D.J.; Giulian, R.; Araujo, L.L.; Kluth, P.; Johannessen, B.; Cookson, D.J.; Foran, G.J.; Ridgway, M.C. Structural and vibrational properties of Co nanoparticles formed by ion implantation. J. Appl. Phys. 2010, 107, 014313. [Google Scholar]
- Dalba, G.; Fornasini, P. EXAFS Debye-Waller factor and thermal vibrations of crystals. J. Synchrotron Radiat 1997, 4, 243–255. [Google Scholar]
- Johannessen, B.; Kluth, P.; Llewellyn, D.J.; Foran, G.J.; Cookson, D.J.; Ridgway, M.C. Amorphization of embedded Cu nanocrystals by ion irradiation. Appl. Phys. Lett. 2007, 90, 073119. [Google Scholar]
- Djurabekova, F.; Nordlund, K. Atomistic simulation of the interface structure of Si nanocrystals embedded in amorphous silica. Phys. Rev. B. 2008, 77, 115325. [Google Scholar]
- Araujo, L.L.; Giulian, R.; Sprouster, D.J.; Schnohr, C.S.; Llewellyn, D.J.; Kluth, P.; Cookson, D.J.; Foran, G.J.; Ridgway, M.C. Size-dependent characterization of embedded Ge nanocrystals Structural and thermal properties. Phys. Rev. B. 2008, 78, 094112. [Google Scholar]
- Johannessen, B.; Kluth, P.; Glover, C.J.; Azevedo, G.D.; Llewellyn, D.J.; Foran, G.J.; Ridgway, M.C. Structural characterization of Cu nanocrystals formed in SiO2 by high-energy ion-beam synthesis. J. Appl. Phys. 2005, 98, 024307. [Google Scholar]
- Kluth, P.; Johannessen, B.; Giraud, V.; Cheung, A.; Glover, C.J.; Azevedo, G.D.; Foran, G.J.; Ridgway, M.C. Bond length contraction in Au nanocrystals formed by ion implantation into thin SiO2. Appl. Phys. Lett. 2004, 85, 3561–3563. [Google Scholar]
- Giulian, R.; Araujo, L.L.; Kluth, P.; Sprouster, D.J.; Schnohr, C.S.; Johannessen, B.; Foran, G.J.; Ridgway, M.C. The influence of annealing conditions on the growth and structure of embedded Pt nanocrystals. J. Appl. Phys. 2009, 105, 044303. [Google Scholar]
- Sprouster, D.J.; Giulian, R.; Araujo, L.L.; Kluth, P.; Johannessen, B.; Kirby, N.; Ridgway, M.C. Formation and structural characterization of Ni nanoparticles embedded in SiO2. J. Appl. Phys. 2011, 109, 113517. [Google Scholar]
- Frenkel, A.I.; Rehr, J.J. Thermal expansion and X-ray-absorption fine-structure cumulants. Phys. Rev. B. 1993, 48, 585–588. [Google Scholar]
- Sevillano, E.; Meuth, H.; Rehr, J.J. Extended X-ray absorption fine structure Debye-Waller factors. I. Monatomic crystals. Phys. Rev. B. 1979, 20, 4908–4911. [Google Scholar]
- Dalba, G.; Fornasini, P.; Grisenti, R.; Pasqualini, D.; Diop, D.; Monti, F. Anharmonicity effects on the extended X-ray-absorption fine structure: The case of cadmium selenide. Phys. Rev. B. 1998, 58, 4793–4802. [Google Scholar]
- Knapp, G.S.; Pan, H.K.; Tranquada, J.M. Extended X-ray-absorption fine-structure Einstein frequency and moments of the phonon spectrum: An experimental and theoretical study. Phys. Rev. B. 1985, 32, 2006–2009. [Google Scholar]
- Tröger, L.; Yokoyama, T.; Arvanitis, D.; Lederer, T.; Tischer, M.; Baberschke, K. Determination of bond lengths, atomic mean-square relative displacements, and local thermal expansion by means of soft-X-ray photoabsorption. Phys. Rev. B. 1994, 49, 888–903. [Google Scholar]
- Meyer, R.; Lewis, L.J.; Prakash, S.; Entel, P. Vibrational properties of nanoscale materials: From nanoparticles to nanocrystalline materials. Phys. Rev. B. 2003, 68, 104303. [Google Scholar]
- Kluth, P.; Johannessen, B.; Araujo, L.L.; Ridgway, M.C. Vibrational properties of Au and Cu nanocrystals formed by ion implantation. AIP Conf. Proc. 2006, 882, 731–733. [Google Scholar]
- Dalba, G.; Fornasini, P.; Grisenti, R.; Purans, J. Sensitivity of extended X-ray-absorption fine structure to thermal expansion. Phys. Rev. Lett. 1999, 82, 4240–4243. [Google Scholar]
- Giulian, R.; Araujo, L.L.; Kluth, P.; Sprouster, D.J.; Schnohr, C.S.; Foran, G.J.; Ridgway, M.C. Temperature-dependent EXAFS analysis of embedded Pt nanocrystals. J. Phys. Condens. Matter. 2009, 21, 155302. [Google Scholar]
- Gaskell, P.H. Thermal properties of silica. 2. Thermal expansion coefficient of vitreous silica. Trans. Faraday Soc. 1966, 62, 1505–1510. [Google Scholar]
- White, G.K. Thermal-expansion of reference materials—Copper, silica and silicon. J. Phys. D-Appl. Phys. 1973, 6, 2070–2078. [Google Scholar]
- Sprouster, D.J.; Giulian, R.; Araujo, L.L.; Kluth, P.; Johannessen, B.; Nordlund, K.; Kirby, N.; Ridgway, M.C. Ion irradiation induced amorphisation of cobalt nanoparticles. Phys. Rev. B. 2010, 81, 155414. [Google Scholar]
- Moller, W.; Eckstein, W. Tridyn—A TRIM simulation code including dynamic composition changes. Nucl. Instrum. Methods Phys. Res. B. 1984, 2, 814–818. [Google Scholar]
- Diaz, J.; Morales, R.; Valvidares, S.M.; Alameda, J.M. Phase separation in Fe-Si and Co-Si sputtered ferromagnetic alloys and the origin of their magnetic anisotropy. Phys. Rev. B. 2005, 72, 144413. [Google Scholar]
- Li, P.; Chen, I.W.; Pennerhahn, J.E. X-ray absorption studies of zirconia polymorphs. I. Characteristic local structures. Phys. Rev. B. 1993, 48, 10063–10073. [Google Scholar]
- Long, G.J.; Hautot, D.; Pankhurst, Q.A.; Vandormael, D.; Grandjean, F.; Gaspard, J.P.; Briois, V.; Hyeon, T.; Suslick, K.S. Mössbauer-effect and X-ray-absorption spectral study of sonochemically prepared amorphous iron. Phys. Rev. B. 1998, 57, 10716–10722. [Google Scholar]
- Magnan, H.; Chandesris, D.; Rossi, G.; Jezequel, G.; Hricovini, K.; Lecante, J. Determination of the local order in amorphous Cobalt films. Phys. Rev. B. 1989, 40, 9989–9992. [Google Scholar]
- Johannessen, B.; Kluth, P.; Llewellyn, D.J.; Foran, G.J.; Cookson, D.J.; Ridgway, M.C. Ion-irradiation-induced amorphization of Cu nanoparticles embedded in SiO2. Phys. Rev. B. 2007, 76, 184203. [Google Scholar]
- Ridgway, M.C.; Azevedo, G.D.; Glover, C.J.; Yu, K.M.; Foran, G.J. Common structure in amorphised compound semiconductors. Nucl. Instrum. Methods Phys. Res. B. 2002, 199, 235–239. [Google Scholar]
- Ridgway, M.C.; Glover, C.J.; Yu, K.M.; Foran, G.J.; Clerc, C.; Hansen, J.L.; Larsen, A.N. Ion-dose-dependent microstructure in amorphous Ge. Phys. Rev. B. 2000, 61, 12586–12589. [Google Scholar]
- Schnohr, C.S.; Kluth, P.; Araujo, L.L.; Sprouster, D.J.; Byrne, A.P.; Foran, G.J.; Ridgway, M.C. Anisotropic vibrations in crystalline and amorphous InP. Phys. Rev. B. 2009, 79, 195203. [Google Scholar]
- Heimendahl, L.V. Metallic glasses as relaxed bernal structures. J. Phys. F. 1975, 5, L141–L145. [Google Scholar]
- Kluth, P.; Johannessen, B.; Foran, G.J.; Cookson, D.J.; Kluth, S.M.; Ridgway, M.C. Disorder and cluster formation during ion irradiation of Au nanoparticles in SiO2. Phys. Rev. B. 2006, 74, 014202. [Google Scholar]
- Ridgway, M.C.; Glover, C.J.; Foran, G.J.; Yu, K.M. Characterization of the local structure of amorphous GaAs produced by ion implantation. J. Appl. Phys. 1998, 83, 4610–4614. [Google Scholar]
- Johannessen, B. Ion beam formation and modification of metallic nanoparticles Ph.D. Thesis, Australian National University, Canberra, Australia, 2008.
- Kara, A.; Rahman, T.S. Vibrational properties of metallic nanocrystals. Phys. Rev. Lett. 1998, 81, 1453–1456. [Google Scholar]
- Gilbert, B.; Huang, F.; Zhang, H.Z.; Waychunas, G.A.; Banfield, J.F. Nanoparticles: Strained and stiff. Science 2004, 305, 651–654. [Google Scholar]
- The validity of this suggestion can be tested by chemically dissolving the SiO2 matrix subsequent to irradiation to produce free-standing a-Co NPs.
- D’Orleans, C.; Stoquert, J.P.; Estournes, C.; Cerruti, C.; Grob, J.J.; Guille, J.L.; Haas, F.; Muller, D.; Richard-Plouet, M. Anisotropy of Co nanoparticles induced by swift heavy ions. Phys. Rev. B. 2003, 67, 220101. [Google Scholar]
- Fukumi, K.; Chayahara, A.; Kadono, K.; Kageyama, H.; Akai, T.; Mizoguchi, H.; Kitamura, N.; Makihara, M.; Horino, Y.; Fujii, K. Coordination structures of implanted Fe, Co, and Ni ions in silica glass by X-ray absorption fine structure spectroscopy. J. Mater. Res. 2001, 16, 155–162. [Google Scholar]
- Shirakawa, J.; Nakayama, M.; Uchimoto, Y.; Wakihara, M. Multiple scattering calculation for Co K-edge XANES spectra of nanometer-scale metal deposited during Li insertion into LiCoVO4. Electrochem. Solid State Lett 2006, 9, A200–A202. [Google Scholar]
- Song, C.; Zeng, F.; Shen, Y.X.; Geng, K.W.; Xie, Y.N.; Wu, Z.Y.; Pan, F. Local Co structure and ferromagnetism in ion-implanted Co-doped LiNbO3. Phys. Rev. B. 2006, 73, 172412. [Google Scholar]
- Watanabe, N.; Morais, J.; Accione, S.B.B.; Morrone, A.; Schmidt, J.E.; Alves, M.C.M. Electronic, structural, and magnetic properties of cobalt aggregates embedded in polypyrrole. J. Phys. Chem. B. 2004, 108, 4013–4017. [Google Scholar]
- Hormes, J.; Modrow, H.; Bonnemann, H.; Kumar, C. The influence of various coatings on the electronic, magnetic, and geometric properties of cobalt nanoparticles. J. Appl. Phys. 2005, 97, 10R102. [Google Scholar]
- Torchio, R.; Kvashnin, Y.O.; Pascarelli, S.; Mathon, O.; Marini, C.; Genovese, L.; Bruno, P.; Garbarino, G.; Dewaele, A.; Occelli, F.; Loubeyre, P. X-Ray magnetic circular dichroism measurements in Ni up to 200 GPa: Resistant ferromagnetism. Phys. Rev. Lett. 2011, 107, 237202. [Google Scholar]
- Lefevre, P.; Magnan, H.; Heckmann, O.; Briois, V.; Chandesris, D. Adsorpttion site, growth, and structure of Co on Cu(111) determined by multiple-scattering analysis of X-ray-absorption spectra. Phys. Rev. B. 1995, 52, 11462–11466. [Google Scholar]
- Sprouster, D.J. Ion beam formation and modification of Cobalt nanoparticles Ph.D. thesis; Australian National University: Canberra, Australia, 2010. [Google Scholar]
- Gibbons, J.F. Ion Implantation in semiconductors .2. Damage production and annealing. Proc. IEEE. 1972, 60, 1062–1096. [Google Scholar]
- Heckmann, O.; Magnan, H.; Lefevre, P.; Chandesris, D.; Rehr, J.J. Crystallographic structure of cobalt films on Cu(001)— Elastic-deformation to a tetragonal structure. Surf. Sci. 1994, 312, 62–72. [Google Scholar]
- Kemner, K.M.; Elam, W.T.; Idzerda, Y.U.; Wolf, J.A.; Prinz, G.A. Polarization-dependent extended X-ray absorption fine structure measurements of metastable fcc Co on (100) diamond. Appl. Phys. Lett. 1996, 68, 3389–3391. [Google Scholar]
- Kemner, K.M.; Elam, W.T.; Harris, V.G.; Idzerda, Y.U.; Wolf, J.A. Distinguishing the close-packed hexagonal and face centered cubic phases of the metallization of diamond by polarization-dependent extended X-ray absorption fine structure. J. Vac. Sci. Technol. B. 1996, 14, 3207–3209. [Google Scholar]
- Dammak, H.; Dunlop, A.; Lesueur, D. Phase transformation induced by swift heavy ion irradiation of pure metals. Nucl. Instrum. Methods Phys. Res. B. 1996, 107, 204–211. [Google Scholar]
- Benyagoub, A.; Levesque, F.; Couvreur, F.; Gibert-Mougel, C.; Dufour, C.; Paumier, E. Evidence of a phase transition induced in zirconia by high energy heavy ions. Appl. Phys. Lett. 2000, 77, 3197–3199. [Google Scholar]
- Benyagoub, A. Mechanism of the monoclinic-to-tetragonal phase transition induced in zirconia and hafnia by swift heavy ions. Phys. Rev. B. 2005, 72, 094114. [Google Scholar]
- Benyagoub, A.; Klaumünzer, S.; Toulemonde, M. Radiation-induced compaction and plastic flow of vitreous silica. Nucl. Instrum. Methods Phys. Res. B. 1998, 146, 449–454. [Google Scholar]
- Klaumünzer, S. Ion tracks in quartz and vitreous silica. Nucl. Instrum. Methods Phys. Res. B. 2004, 225, 136–153. [Google Scholar]
- van Dillen, T.; Polman, A.; Onck, P.R.; van der Giessen, E. Anisotropic plastic deformation by viscous flow in ion tracks. Phys. Rev. B. 2005, 71, 024103. [Google Scholar]
- van Dillen, T.; Siem, M.Y.S.; Polman, A. Stress map for ion irradiation: Depth-resolved dynamic competition between radiation-induced viscoelastic phenomena in SiO2. Appl. Phys. Lett. 2004, 85, 389–391. [Google Scholar]
- Snoeks, E.; Polman, A.; Volkert, C.A. Densification, anisotropic deformation, and plastic flow of SiO2 during MeV heavy ion irradiation. Appl. Phys. Lett. 1994, 65, 2487–2489. [Google Scholar]
- Brongersma, M.L.; Snoeks, E.; van Dillen, T.; Polman, A. Origin of MeV ion irradiation-induced stress changes in SiO2. J. Appl. Phys. 2000, 88, 59–64. [Google Scholar]
- Kluth, P.; Schnohr, C.S.; Pakarinen, O.H.; Djurabekova, F.; Sprouster, D.J.; Giulian, R.; Ridgway, M.C.; Byrne, A.P.; Trautmann, C.; Cookson, D.J.; Nordlund, K.; Toulemonde, M. Fine structure in swift heavy ion tracks in amorphous SiO2. Phys. Rev. Lett. 2008, 101, 175503. [Google Scholar]
- Dallanora, A.; Marcondes, T.L.; Bermudez, G.G.; Fichtner, P.F.P.; Trautmann, C.; Toulemonde, M.; Papaleo, R.M. Nanoporous SiO2/Si thin layers produced by ion track etching: Dependence on the ion energy and criterion for etchability. J. Appl. Phys. 2008, 104, 024307. [Google Scholar]
- Jensen, J.; Razpet, A.; Skupinski, M.; Possnert, G. Ion track formation below 1 MeV/u in thin films of amorphous SiO2. Nucl. Instrum. Methods Phys. Res. B. 2006, 243, 119–126. [Google Scholar]
- D’Orleans, C.; Cerruti, C.; Estournes, C.; Grob, J.J.; Guille, J.L.; Haas, F.; Muller, D.; Richard-Plouet, M.; Stoquert, J.P. Irradiations of implanted cobalt nanoparticles in silica layers. Nucl. Instrum. Methods Phys. Res. B. 2003, 209, 316–322. [Google Scholar]
- D’Orleans, C.; Stoquert, J.P.; Estournes, C.; Grob, J.J.; Muller, D.; Cerruti, C.; Haas, F. Deformation yield of Co nanoparticles in SiO2 irradiated with 200 MeV 127I ions. Nucl. Instrum. Methods Phys. Res. B. 2004, 225, 154–159. [Google Scholar]
- D’Orleans, C.; Stoquert, J.P.; Estournes, C.; Grob, J.J.; Muller, D.; Guille, J.L.; Richard-Plouet, M.; Cerruti, C.; Haas, F. Elongated Co nanoparticles induced by swift heavy ion irradiations. Nucl. Instrum. Methods Phys. Res. B. 2004, 216, 372–378. [Google Scholar]
- Sprouster, D.J.; Giulian, R.; Araujo, L.L.; Kluth, P.; Johannessen, B.; Cookson, D.J.; Ridgway, M.C. Swift heavy-ion irradiation-induced shape and structural transformation in cobalt nanoparticles. J. Appl. Phys. 2011, 109, 113504. [Google Scholar]
- Roorda, S.; van Dillen, T.; Polman, A.; Graf, C.; van Blaaderen, A.; Kooi, B.J. Aligned gold nanorods in silica made by ion irradiation of core-shell colloidal particles. Adv. Mater. 2004, 16, 235–127. [Google Scholar]
- Klaumünzer, S.; Hou, M.D.; Schumacher, G. Coulomb explosions in a metallic glass due to the passage of fast heavy ions? Phys. Rev. Lett. 1986, 57, 850–853. [Google Scholar]
- Hou, M.d.; Klaumünzer, S.; Schumacher, G. Dimensional changes of metallic glasses during bombardment with fast heavy ions. Phys. Rev. B. 1990, 41, 1144–1157. [Google Scholar]
- Benyagoub, A.; Löffler, S.; Rammensee, M.; Klaumünzer, S.; Saemann-Ischenko, G. Plastic deformation in SiO2 induced by heavy-ion irradiation. Nucl. Instrum. Methods Phys. Res. B. 1992, 65, 228–231. [Google Scholar]
- van Dillen, T.; Polman, A.; Fukarek, W.; van Blaaderen, A. Energy-dependent anisotropic deformation of colloidal silica particles under MeV Au irradiation. Appl. Phys. Lett. 2001, 78, 910–912. [Google Scholar]
- Van Dillen, T.; van der Giessen, E.; Onck, P.R.; Polman, A. Size-dependent ion-beam-induced anisotropic plastic deformation at the nanoscale by nonhydrostatic capillary stresses. Phys. Rev. B. 2006, 74, 132103. [Google Scholar]
- Penninkhof, J.J.; van Dillen, T.; Roorda, S.; Graf, C.; van Blaaderen, A.; Vredenberg, A.M.; Polman, A. Anisotropic deformation of metallo-dielectric core-shell colloids under MeV ion irradiation. Nucl. Instrum. Methods Phys. Res. B. 2006, 242, 523–529. [Google Scholar]
- Klaumü nzer, S. Modification of nanostructures by high-energy ion beams. Nucl. Instrum. Methods Phys. Res. B. 2006, 244, 1–7. [Google Scholar]
- Ridgway, M.C.; Giulian, R.; Sprouster, D.J.; Kluth, P.; Araujo, L.L.; Llewellyn, D.J.; Byrne, A.P.; Kremer, F.; Fichtner, P.F.P.; Rizza, G.; Amekura, H.; Toulemonde, M. Role of thermodynamics in the shape transformation of embedded metal nanoparticles induced by swift heavy-ion irradiation. Phys. Rev. Lett. 2011, 106, 095505. [Google Scholar]
- Awazu, K.; Wang, X.; Fujimaki, M.; Tominaga, J.; Aiba, H.; Ohki, Y.; Komatsubara, T. Elongation of gold nanoparticles in silica glass by irradiation with swift heavy ions. Phys. Rev. B. 2008, 78, 054102. [Google Scholar]
- Dufour, C.; Khomenkov, V.; Rizza, G.; Toulemonde, M. Ion-matter interaction: The three-dimensional version of the thermal spike model. Application to nanoparticle irradiation with swift heavy ions. J. Phys. D-Appl. Phys. 2012, 45, 065302. [Google Scholar]
- Kluth, P.; Giulian, R.; Sprouster, D.J.; Schnohr, C.S.; Byrne, A.P.; Cookson, D.J.; Ridgway, M.C. Energy dependent saturation width of swift heavy ion shaped embedded Au nanoparticles. Appl. Phys. Lett. 2009, 94, 113107. [Google Scholar]
- Jiang, T.; Ellis, D.E. X-ray absorption near edge structures in cobalt oxides. J. Mat. Res. 1996, 11, 2242–2256. [Google Scholar]
- Kraft, S.; Schattat, B.; Bolse, W.; Klaumünzer, S.; Harbsmeier, F.; Kulinska, A.; Loffl, A. Ion beam mixing of ZnO/SiO2 and Sb/Ni/Si interfaces under swift heavy ion irradiation. J. Appl. Phys. 2002, 91, 1129–1134. [Google Scholar]
- Schattat, B.; Bolse, W.; Klaumünzer, S.; Harbsmeier, F.; Jasenek, A. Atomic mixing of Ni2O3/SiO2, NiO/SiO2, and Ni/SiO2 interfaces induced by swift heavy ion irradiation. Appl. Phys. A-Mater. Sci. Process. 2003, 76, 165–169. [Google Scholar]
- Som, T.; Satpati, B.; Satyam, P.V.; Kabiraj, D.; Gupta, A.; Mishra, N.C. Interface modification in Co/Ge bilayer using swift heavy ions. J. Appl. Phys. 2004, 96, 7141–7146. [Google Scholar]
- Kumar, R.; Khan, M.W.; Srivastava, J.P.; Arora, S.K.; Sofin, R.G.S.; Choudhary, R.J.; Shvets, I.V. Swift heavy ion irradiation-induced modifications in structural, magnetic and electrical transport properties of epitaxial magnetite thin films. J. Appl. Phys. 2006, 100, 033703. [Google Scholar]
- Spiga, S.; Mantovan, R.; Fanciulli, M.; Ferretti, N.; Boscherini, F.; d’Acapito, F.; Schmidt, B.; Grotzschel, R.; Mucklich, A. Local structure of Sn implanted in thin SiO2 films. Phys. Rev. B. 2003, 68, 205419. [Google Scholar]
- d’Acapito, F.; Mobilio, S.; Battaglin, G.; Cattaruzza, E.; Gonella, F.; Caccavale, F.; Mazzoldi, P.; Regnard, J.R. Valence state and local atomic structure of copper in Cu-implanted silica glass. J. Appl. Phys. 2000, 87, 1819–1824. [Google Scholar]






















| Energy (MeV) | Range (μm) | Se SiO2 (keV/nm) | Se Co (keV/nm) | Sn SiO2 (keV/nm) | Sn Co (keV/nm) |
|---|---|---|---|---|---|
| 9 | 2 | 2.6 | 5.2 | 1.4 | 3.9 |
| 27 | 6.3 | 4.8 | 9.4 | 0.7 | 2 |
| 54 | 9.9 | 9 | 19.4 | 0.4 | 1.2 |
| 89 | 13 | 12.7 | 29.8 | 0.3 | 0.9 |
| 110 | 14.6 | 14.2 | 34.5 | 0.2 | 0.7 |
| 185 | 19.2 | 17.6 | 45.1 | 0.2 | 0.5 |
| Sample | Annealing temp(°C) | Δ BL (Å) | σ2 (10−3 Å) | CN (atoms) | C3 (10−5 Å) | size (nm) |
|---|---|---|---|---|---|---|
| Bulk FCC | – | 2.491(0.003) | 2.98(0.12) | 12(fixed) | −3.9(3.3) | – |
| Bulk HCP | – | 2.481(0.002) | 2.73(0.09) | 12(fixed) | −2.2(2.4) | – |
| 9.0 at.% | 1, 100 | 2.488(0.004) | 2.64(0.14) | 11.2(0.3) | −4.0(3.7) | 17.4 |
| 800 | 2.469(0.005) | 3.74(0.17) | 9.7(0.3) | −9.3(2.3) | 4.0(0.9) | |
| 4.5 at.% | 400a | 2.479(0.004) | 3.20(0.14) | 11.0(0.3) | −5.2(1.2) | 5.2(1.2) |
| 4.0 at.% | 400a | 2.473(0.006) | 3.61(0.20) | 10.6(0.3) | −5.8(1.9) | 4.9(1.0) |
| 3.0 at.% | 1, 100 | 2.485(0.004) | 2.75(0.12) | 11.7(0.3) | −6.0(1.3) | 13.2(3.7) |
| 800 | 2.464(0.006) | 4.43(0.21) | 9.2(0.3) | −11.6(2.8) | 3.2(0.7) | |
| 0.9 at.% | 1, 100 | 2.483(0.004) | 2.96(0.13) | 11.7(0.3) | −7.7(1.7) | 11.5(2.8) |
| 800 | 2.456(0.009) | 5.59(0.34) | 8.1(0.4) | −15.8(4.6) | 2.8(0.5) | |
| 0.3 at.% | 1, 100 | 2.485(0.004) | 3.04(0.12) | 11.4(0.2) | −3.4(1.6) | 11.4(2.5) |
| 800 | 2.453(0.01) | 5.78(0.36) | 7.6(0.4) | −18.3(5.0) | 2.1(0.5) |
| Sample | ΘE (K) | (10−3 Å) | keff (N/m) | β (eVÅ−3) | C3S (10−5Å3) |
|---|---|---|---|---|---|
| Bulk HCP | 295(1) | 0.03(0.01) | 72(1) | 1.08(0.15) | −3.8(0.7) |
| Bulk FCC | 286(2) | 0.28(0.05) | 68(1) | 0.80(0.13) | −5.8(0.6) |
| 13.2 nm FCC NPs | 285(3) | 0.04(0.01) | 68(1) | 0.83(0.17) | −7.0(0.7) |
| 5.2 nm HCP NPs | 291(3) | 0.46(0.06) | 72(1) | 1.30(0.13) | −10.0(0.3) |
| 2.8 nm HCP NPs | 280(3) | 2.76(0.10) | 66(2) | 3.2(0.47) | −15.8(2.6) |
| HCP (hkl) | d (Å) | FCC (hkl) | d (Å) | Peak | d (Å) |
|---|---|---|---|---|---|
| (100) | 2.17 | (111) | 2.05 | A | 2.15(0.02) |
| (002) | 2.03 | (200) | 1.77 | B | 2.02(0.03) |
| (101) | 1.92 | (220) | 1.25 | C | 1.92(0.02) |
| (110) | 1.25 | (311) | 1.07 | D | 1.25(0.02) |
| (112) | 1.07 | (222) | 1.02 | E | 1.07(0.02) |
| Sample | BL (Å) | σ2 (10−3 Å2) | C3 (10−5 Å3) | CN (atoms) | Size (nm) |
|---|---|---|---|---|---|
| Bulk HCP | 2.481(0.002) | 2.63(0.13) | −3.2(3.9) | 12 | – |
| c-Co NPs | 2.469(0.003) | 4.08(0.16) | −13.3(4.8) | 10.0(0.2) | 3.7(1.0) |
| a-Co NPs | 2.491(0.004) | 12.45(0.72) | 78.9(13.3) | 7.8(0.9) | 3.6(1.0) |
| a-Co NPs/100 °C | 2.486(0.007) | 12.24(0.82) | 82.0(13.4) | 7.7(0.6) | 3.6(1.0) |
| a-Co NPs/400 °C | 2.466(0.004) | 7.41(0.23) | −22.1(7.8) | 9.0(0.7) | 3.6(1.0) |
| Sample | ΘE (K) | (10−3 Å2) | β (eV/Å) | C3S (10−5 Å3) |
|---|---|---|---|---|
| Bulk HCP | 294(1) | 0.02(0.01) | 1.06(0.09) | −4.0(0.6) |
| c-Co NPs | 283.5(1.2) | 1.23(0.2) | 1.78(0.10) | −13.7(0.8) |
| a-Co NPs | 320.8(4.5) | 9.84(0.3) | 11.69(0.97) | 74.5(3.0) |
| Peak | FCC (hkl) | d Å | Unirr d Å | HCP (hkl) | d Å | 2 × 1013 d Å |
|---|---|---|---|---|---|---|
| a | (111) | 2.05 | 2.05(0.01) | (100) | 2.17 | 2.17(0.01) |
| b | (200) | 1.77 | 1.78(0.01) | (002) | 2.03 | 2.03(0.01) |
| c | (220) | 1.25 | 1.26(0.01) | (101) | 1.92 | 1.91(0.01) |
| d | (311) | 1.07 | 1.07(0.02) | (110) | 1.25 | 1.25(0.02) |
| e | (222) | 1.02 | 1.02(0.02) | (103) | 1.15 | 1.16(0.02) |
| f | – | – | – | (112) | 1.07 | 1.07(0.02) |
| Sample | BL (Å) | σ2 (10−3 Å2) | C3 (10−5 Å3) | CN (atoms) | ΘE (K) | (10−3 Å |
|---|---|---|---|---|---|---|
| Bulk FCC | 2.492(0.002) | 3.00(0.1) | −3.2(2.1) | 12 | 286(1) | 0.16(0.05) |
| FCC NPs | 2.488(0.004) | 2.79(0.2) | −4.0(2.3) | 11.4(0.5) | 285(2) | 0.04(0.01) |
| Bulk HCP | 2.482(0.002) | 2.46(0.06) | −3.0(1.7) | 12 | 296(1) | 0.05(0.01) |
| HCP NPs | 2.476(0.004) | 3.31(0.3) | −3.3(2.7) | 10.8(0.5) | 292(2) | 0.35(0.05) |
© 2012 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sprouster, D.J.; Ridgway, M.C. Ion Beam Formation and Modification of Cobalt Nanoparticles. Appl. Sci. 2012, 2, 396-442. https://doi.org/10.3390/app2020396
Sprouster DJ, Ridgway MC. Ion Beam Formation and Modification of Cobalt Nanoparticles. Applied Sciences. 2012; 2(2):396-442. https://doi.org/10.3390/app2020396
Chicago/Turabian StyleSprouster, David J., and Mark C. Ridgway. 2012. "Ion Beam Formation and Modification of Cobalt Nanoparticles" Applied Sciences 2, no. 2: 396-442. https://doi.org/10.3390/app2020396
APA StyleSprouster, D. J., & Ridgway, M. C. (2012). Ion Beam Formation and Modification of Cobalt Nanoparticles. Applied Sciences, 2(2), 396-442. https://doi.org/10.3390/app2020396





