Next Article in Journal
Fluorinated and Non-Fluorinated Electro-Optic Copolymers: Determination of the Time and Temperature Stability of the Induced Electro-Optic Coefficient
Previous Article in Journal / Special Issue
Ab Initio Study of Lattice Site Occupancies in Binary Sigma Phases Using a Single-Site Mean Field Model
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 2
Issue 3
10.3390/app2030669
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Non-Stoichiometry and Calphad Modeling of Frank-Kasper Phases

by
Jean-Marc Joubert
* and
Jean-Claude Crivello
Chimie Métallurgique des Terres Rares, Institut de Chimie et des Matériaux Paris-Est, 2-8 rue Henri Dunant, Thiais Cedex 94320, France
*
Author to whom correspondence should be addressed.
Appl. Sci. 2012, 2(3), 669-681; https://doi.org/10.3390/app2030669
Submission received: 24 July 2012 / Revised: 28 August 2012 / Accepted: 28 August 2012 / Published: 10 September 2012
(This article belongs to the Special Issue Frank-Kasper Phases)
Browse Figures
Versions Notes

Abstract

:
One of the many singularities of Frank-Kasper phases is their ability to accommodate extremely large composition ranges by atom mixing on the different sites of the crystal structures. This phenomenon will be reviewed in the present paper with special emphasis on the experimental demonstration of this phenomenon, the theoretical calculation of disordered structures and the modeling of these phases.

Graphical Abstract

1. Introduction

Frank-Kasper (FK) phases are fascinating compounds. They not only represent one of the largest group of intermetallics, but they are also characterized by the richness of their structural and physical properties. Their application as high temperature structural materials (see e.g., Laves, σ, χ and A15 phases in [1]) and superconducting materials (A15 Nb3Sn) is also worth mentioning. One of their most original features is the structural ability of several phases of this group to accommodate extremely wide ranges of non-stoichiometry. The measurement, the analysis, the calculation and the modeling of this non-stoichiometry represent challenges from both the experimental and theoretical point of views and are the subject of the present paper.

2. Generalities and Particular Features of FK Phases

FK phases are generally characterized by the association of (at least) two elements of different size and different electronic properties (for a review see [2,3,4]). They are defined from the structural point of view by the sole presence of tetrahedral interstices. This consequently results in a limited number of possible coordination polyhedra, classified following their coordination number (CN) into low coordination site CN12 (icosahedron), and high coordination sites CN14, CN15, CN16. The CN13 polyhedron, for example, present in the χ phase, is strictly speaking not a FK polyhedron, but this phase has properties so close to those of other FK phases that it may be classified in this group.
Single elements may also crystallize in one of the FK structures. For example, this is the case for β-U (structure of the σ phase), α-Mn (structure of the χ phase) and β-Mn. This is also the case for different metastable structures of Ta (A15 [5], σ [6]).
While the size ratio between the two elements may be quite flexible in certain phases (Laves phases), it is restricted to a very small range for other phases (σ). It seems to play a key role for the site preference, with the general rule being that the larger element prefers the sites with higher coordination numbers. Very often the more electropositive atom corresponds also to the atom with larger atomic radius, so it may be difficult to deconvoluate the electronic effect from the size effect. In the following, the larger radius element will be designated A as opposed to the smaller element which will be designated B.
Figure 1 presents the homogeneity ranges of different FK phases. It can be seen that, while several phases depart only slightly from their ordered composition (e.g., AB2 for C14 and C15 Laves phases), other phases appear at very distinct A/B ratios depending on the A-B system (σ and χ phases, and to a lesser extent the µ phase). Additionally, in a given system, the homogeneity range may be quite large (e.g., the σ phase in W-Re system extends from 29 to 57 at.% W).
Applsci 02 00669 g001 1024
Figure 1. Homogeneity ranges of various Frank-Kasper (FK) phases in the combined systems in which they crystallize represented as a function of the composition of the larger (A) element. The ordered or ideal composition(s) for each phase is indicated.
Figure 1. Homogeneity ranges of various Frank-Kasper (FK) phases in the combined systems in which they crystallize represented as a function of the composition of the larger (A) element. The ordered or ideal composition(s) for each phase is indicated.
Applsci 02 00669 g001
From what is known experimentally, the major structural defect responsible for the stoichiometry deviation from the ideal, ordered crystal structure is substitution. In the case where the deviation is very limited, this can be called an anti-site defect since the major element at each given site is clearly identified (e.g., Laves phases). For other systems for which the non-stoichiometry is much larger, it may not be easy to identify the stoichiometric ordered composition, and some sites may completely switch as a function of composition from the occupation by one atom to the occupation by the other atom (see e.g., the case of the µ phase in Section 3.2).
A common idea concerning the site occupancies of A atoms within the homogeneity domain (i.e., as a function of A composition) originates from Kasper [7,8], though it is not expressed as clearly in their original papers. Considering the tendency of A atom to prefer the occupancy of high CN sites (with larger atom volume to fit it), it is supposed that A would occupy sequentially the sites from high to low coordination as a function of A composition. Different sites of equal CN would be occupied simultaneously. This scheme will be called Kasper rules in the following paragraphs. An example of this ideal behavior is represented in the case of the σ phase in Figure 2.
Applsci 02 00669 g002 1024
Figure 2. Ideal site occupancies following Kasper rules for the σ phase. As a function of A composition, sites of decreasing CN are occupied sequentially. Sites with equal coordinations are occupied simultaneously. It should be understood that the B atom completes each site to full occupancy when A occupancy is not equal to unity.
Figure 2. Ideal site occupancies following Kasper rules for the σ phase. As a function of A composition, sites of decreasing CN are occupied sequentially. Sites with equal coordinations are occupied simultaneously. It should be understood that the B atom completes each site to full occupancy when A occupancy is not equal to unity.
Applsci 02 00669 g002

3. Studying Non-Stoichiometry Experimentally

3.1. Experimental Techniques

Among the different experimental techniques that can be used to study the non-stoichiometry, we can cite the Mössbauer spectroscopy. It has proved to be useful in order to study the magnetic properties of the σ phase [9,10,11] or even to show phase transitions [12,13].
However, most interesting systems (like σ phase for example) are too complex for this technique to be used by itself to determine with certainty quantitative values for the site occupancies. However, it may be used in combination with crystallographic studies with success [14]. Other techniques like positron annihilation seem to be quite useful in studying structural defects like the measurement of vacancies, but again, with qualitative results. Nuclear magnetic resonance has also recently been used in the case of the σ phase [15].
In the case of FK phases, the most suited technique is the Rietveld refinement of powder diffraction data. This method is in general very useful to determine site occupancies when atoms mix on different sites [16,17]. Provided that the diffraction contrast between the different elements is sufficient, X-ray diffraction is the most effective technique. This is the case, for example, in the refinement of site occupancies of transition metals pertaining to different series. Conversely, for elements close in the periodic table, the neutron diffraction contrast may be larger, though this is not always the case.
In the case of ternary compounds, in which three elements may mix on some sites, more sophisticated techniques have to be used since there are two site occupancies per site to be determined and single diffraction data can only yield one average scattering per site. Therefore, combined analysis of different diffraction data sets in which the contrast is different has to be used. Two techniques are in this case available: resonant diffraction [18,19] and combined X-ray and neutron analysis [20].

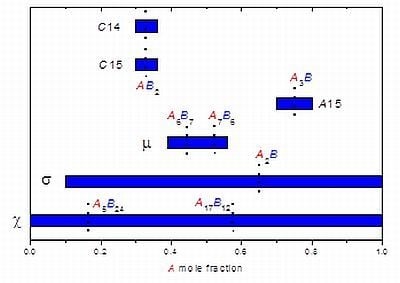
3.2. Results on Different FK Phases

A systematic study of the site occupancies for different FK phases has been conducted as a function of composition. The existing data has been reviewed in the following papers: µ [21], σ [22], χ [23]. The comparison between these different phases indicates that these three phases behave differently as far as the Kasper rules are concerned.
The µ phase presents two sites of equal coordination numbers (3a and 18h with CN12) that have very different behaviors. Site 3a may be occupied by either A or B. Two stoichiometric (ordered) compositions can therefore be defined A6B7 in which site 3a is occupied by B and A7B6 in which site 3a is occupied by A. Even more interesting is the fact that in certain system (e.g., Mo-Co) site 3a may undergo a reversal of its occupancy within the homogeneity domain of the phase [21]. The non-stoichiometry in this phase is therefore mainly accommodated by the site exchange in this particular site. Site 18h with the same coordination has a completely different behavior, since it is found to be mainly occupied by B in all the studied systems, independently of the composition, except at very high A content.
On the other hand, the σ phase presents sites of distinct coordination (CN14 and CN15) that behave rather similarly as shown in Figure 3. For this phase, it has been shown that a single ordered composition A2B exists. The ideal scheme for atom replacement drawn in the same figure is therefore significantly different from that assumed by applying the Kasper rules (Figure 2).
Applsci 02 00669 g003 1024
Figure 3. Experimental site occupancies for the σ phase in all the studied systems (redrawn from [22]). The ideal scheme to describe the experimental data is drawn with lines.
Figure 3. Experimental site occupancies for the σ phase in all the studied systems (redrawn from [22]). The ideal scheme to describe the experimental data is drawn with lines.
Applsci 02 00669 g003
Finally, the χ phase, contrary to the other phases, obeys in a rather strict manner the Kasper rule with sequential A occupancy of site CN16, CN13 and CN12 as a function of A composition. Two ordered compositions may therefore be defined A5B24 and A17B12 and are indeed observed experimentally in certain systems (Zr-Re for the first, Mg-Al for the latter).

4. Non-Stoichiometry Studied by First Principle Calculations

First principle calculations are generally limited to the calculation of perfectly ordered periodic structures which seems, at first, not to be very useful to study the non-stoichiometry and disorder related to atomic mixing. However, several solutions to this problem have been found which are summarized in the following.
One of the first attempts to compute thermodynamically properties of FK phases from first principle techniques has been made by Turchi et al. [24]. They proposed to study ordering effects in the A15 structure with Tight-Binding (TB) calculation in the context of the Generalized Perturbation Method (GPM [25]), by coupling with a statistical thermodynamic method like the Monte Carlo simulation or the Cluster Variation Method (CVM [26,27]). For other FK phases in which local order is known to be less important, such as the σ phase, other approaches have been tested.
The first significant work done on the σ phase has been performed on the two systems Cr-Fe [28] and Re-W [29]. The energies associated to the change of local atomic configurations have been parameterized by a set of Effective Cluster Interactions (ECI). 42 configurations have been considered, issued from the 25 = 32 ordered binary compounds generated by the ordered distribution of the two atoms on the 5 sites, with an additional set of 10 super-structures which allows to determine pair interactions between sites of the same type. The total energy of each configuration was obtained by Density Functional Theory (DFT) using Local Density Approximation (LDA) with the Linear Muffin-Tin Orbital method (LMTO) [30]. Then, the Connolly-Williams Method (CWM [31]) was used to extract the ECI interactions. The ECI was employed to compute the site occupancies and energy terms of the σ phase as a function of temperature and composition, within the tetrahedron approximation of the CVM. Computed site occupancies were in pretty good agreement with the experimental ones, however, they exhibited curious composition dependence at low temperature (see Figure 4). Indeed, Ising-type hamiltonian favors several non-existing single pairs, and affects the preference of single-site and multi-site interactions.
In [32], results on Re-W obtained with CWM-CVM has been compared by a simple random distribution of the Bragg-Williams Approximation (BWA [33]), and concluded that the BWA is sufficient to describe the Re-W σ phase without occupancy reversal phenomena at low temperature (see Figure 4). Moreover, the advantages of using only BWA are several: (i) it is well compatible with the Compound Energy Formalism (CEF) used widely in the Calphad method [34]; (ii) it requires only the total energy of each end-member (32 configurations for a binary σ phase) which can be easily obtained by DFT calculations; (iii) no heavy analytic treatment is needed; and (iv) extrapolations to higher-order system are conceivable. Another comparative study of the finite temperature thermodynamic properties was performed on the µ Nb-Ni phase [35]. Compared to Cluster Expansion (CE) with CVM, it was shown that BWA used in the CEF was sufficient to describe experimental site occupancies of the µ phase (see Figure 5, left). A very good agreement of the Generalized Gradient Approximation (GGA) DFT-BWA results [36] with experimental site occupancies was also obtain for another FK phase: the χ phase in Mo-Re (Figure 5, right), with also a relative agreement obtained between the computed and experimental phase diagrams of Mo-Re and W-Re systems.
Applsci 02 00669 g004 1024
Figure 4. W site fraction in σ Re-W, obtained by CWM-CVM at 500K (left) [29], and obtained by BWA at 300K (right) [32]. Experimental points from [29].
Figure 4. W site fraction in σ Re-W, obtained by CWM-CVM at 500K (left) [29], and obtained by BWA at 300K (right) [32]. Experimental points from [29].
Applsci 02 00669 g004
Applsci 02 00669 g005 1024
Figure 5. (left) Nb site fraction in µ Nb-Ni obtained by both CWM-CVM and DFT-BWA at 1,273K [35], experimental data from [17]. (right) Mo site fraction in χ Mo-Re obtained by DFT-BWA at 1,873K [36], experimental points from [37].
Figure 5. (left) Nb site fraction in µ Nb-Ni obtained by both CWM-CVM and DFT-BWA at 1,273K [35], experimental data from [17]. (right) Mo site fraction in χ Mo-Re obtained by DFT-BWA at 1,873K [36], experimental points from [37].
Applsci 02 00669 g005
Prototype σ Cr-Fe has been by far the most investigated system by many different first-principles calculations. 10 years after the first CWM-CVM study [28], Korzhavyi et al. [38] were able to better reproduce the experimental data by adopting the BWA in the CEF formalism with the 25 = 32 end-members calculation in the Korringa-Kohn-Rostoker (KKR) method (see Figure 6). The influence of magnetism on the stability was investigated with disordered local moments, based on the Coherent Potential Approximation (CPA) of the spin orientation. Magnetic order in the same system was also studied in [39], who used 3 different DFT approaches: LMTO-ASA, Full-Potential Linear Augmented Plane Wave (FLAPW) and pseudopotential methods [40] (VASP package was used for this latter [41,42]). Instead of using BWA-CEF, Cieslak et al. [43] used a combined KKR-CPA method for modeling the chemical disorder. Finally, a new calculation has been done by using Ising-type configurational Hamiltonian and a single-site mean-field approach for two different σ-Cr-Fe compositions [44].
Applsci 02 00669 g006 1024
Figure 6. Fe site fraction in σ Cr-Fe, obtained by CWM-CVM at 500K (left) [28], and obtained by BWA at 1,000K (right) [38]. Experimental points from [45].
Figure 6. Fe site fraction in σ Cr-Fe, obtained by CWM-CVM at 500K (left) [28], and obtained by BWA at 1,000K (right) [38]. Experimental points from [45].
Applsci 02 00669 g006
Increased computer performance has allowed researchers to investigate more complex problems. For the first time, the total energies of every ordered configuration of a ternary σ phase, i.e., 35 = 243 configurations in the Cr-Mo-Re were calculated in [46], followed by studies of σ Cr-Ni-Re [47] and σ Mo-Ni-Re [20]. For the latter, the use of BWA showed a very good agreement with the experimental ternary site occupations. This result has confirmed that ignoring the Short-Range-Order (SRO) contribution is possible for the σ phase, because of the small amount of neighbor atoms sharing the same site. The vibrational contribution has also been subject of discussion. It is now admitted that configurational entropy well taken into account by the BWA represents the main contribution. Phonon calculation with the direct method [48] and experimental phonon dispersion on a σ-Fe-Cr compound has shown a vibrational entropy of about 0.03 kJ·K−1·mol−1[49] almost negligible compared to values of the configurational entropy.

5. Calphad Modeling of FK Phases

5.1. Basics of Calphad Modeling

The aim of the Calphad modeling is to describe the Gibbs energies of each phase of a given system. This yields the possibility of combining these phases and systems in a database allowing to make predictions of the phase equilibria in a multi-component system. In the Calphad approach, generally, phases are described not only in their stable ranges of stability, but also outside in metastable states. The most convenient way of describing the Gibbs energy of a non-stoichiometric ordered phase is to use the so-called compound energy formalism, also called sublattice model [50]. It consists in dividing the phase into different sub-lattices in which atom mixing may or may not occur. The Gibbs energy is then defined by applying the thermodynamics of solution on each sublattice on which disorder is present. The reference term for the Gibbs energy is given by a linear combination of the Gibbs energies of so-called end-members which are the ordered compounds defined by the model.
Let’s take the example of a phase of stoichiometric composition AB2 with A on one site and B on another site, and having a homogeneity range extending on both side of the stoichiometric composition. If the mechanism is an anti-site defect for both hypo- and hyper-stoichiometric compositions, then the two sublattices may be used and the sublattice model would be written (A,B)(A,B)2 in which the bold element designates the major element on each sublattice. This model generates four end-members of compositions AA2, AB2, BA2 and BB2, among which only one corresponds to a stable composition. One of the tasks of Calphad assessors is to assign values to the Gibbs energies of these compounds.
One should be able, with this method, to describe both the composition range of the phase (in the preceding example, one may note that the phase is defined from pure A to pure B) and the configurational entropy in a correct manner (which would not be the case if the phase was treated with a single sublattice (A,B)).
However, this approach requires the knowledge of the mechanism for non-stoichiometry (number of sites on which disorder is present and type of disorder). Let’s imagine that the non-stoichiometry on the B rich side of the preceding compound is due to A vacancies, then the model should be written (A,vac)B2 which gives rise to different end-members AB2 and pure B with a totally vacant A site, a different range of described composition (from AB2 to pure B), and different configurational entropy for the same composition.
On the other hand, for crystal structures containing more than two crystallographic sites on which disorder occurs, the number of end-members to be evaluated varies exponentially with the number of sublattices. This yields the necessity to simplify the description and reduce the number of sublattices by (i) combining different sites in single sublattices and (ii) not allowing all the elements on the different sublattices.

5.2. Simple Models

Note that a review on this subject is given in [51]. Since, it is commonly accepted that the mechanism for non-stoichiometry is substitutional in FK phases, it is easy to derive sublattice models for the most simple FK phases which contain only two crystallographic sites. The sublattice models for phases such as A15 or C15 may be described as follows (A,B)3(A,B) and (A,B)(A,B)2.
The case of Laves phase C14 is more complex since three sites are present. It has been suggested that the two sites occupied preferentially by B could be joined in order to get the same model as for the C15 phase [52]. Other authors suggest, on the contrary, based on some experimental measurements, that the site occupancy may be significantly different between these two sites and that three sublattices should be used [53].
On the other hand, phases like the δ phase are so complex (14 sites) that they have to be simplified. A common model for this phase is A12(A,B)20B24 [54,55].
Between these extreme examples, phases with a moderately high number of crystal sites (four to five) may be discussed.
The µ phase has been commonly described by grouping the two sites of CN12 in a single sublattice [56,57] in models such as (A,B)21A18 or (A,B)21(A,B)18. However, the recent detailed crystallographic study presented in Section 3.2 showed that, contrary to the expectation, the two sites of CN12 have strongly different site occupancies and should be dissociated. Resulting model can be (A)12(A,B)6(A,B)3(A,B)18. This proposed new model was applied to Nb-Ni system in [58].
Over the years, many different models have been used for the σ phase (for a review see [22]). Some of them use grouping of the sites based on convenience and should be avoided (e.g., A4(A,B)18B8). More recent ones are based, as in the case of the µ phase, on the expectation that Kasper rules are valid (e.g., (A4(A,B)16(A,B)10). Again, it has been shown that it was not the case and that, contrary to the expectation, sites of CN15 and CN14 have no particular reasons to be dissociated [22]. This yields to the proposal of a new model simpler that the previously used one: (A,B)2(A,B). This recent model has been used to describe the systems Mo-Re [37] and Cr-Fe [59].
For the χ phase, since the observed site occupancies are well accounted for by the Kasper rules, the issued proposal was (A,B)5(A,B)12(A,B)12. [23]. A discussion was made in this article on the need to allow or not all the elements on the different sublattices in order to reduce the number of end-members generated by the model.
A summary of these recommendations can be found in Table 1. These examples emphasize the need for accurate experimental crystallographic data for each phase to reveal how deviations from stoichiometry are accommodated in order to help define the model. In addition, it has been proved that the use of measured experimental site occupancies was quite useful in the Calphad approach to help define the relative stability of the different end-members generated by the model.
Table
Table 1. Proposed Calphad sublattice models for selected FK phases issued from crystallographic analysis. Bold characters indicate the major element, if any.
Table 1. Proposed Calphad sublattice models for selected FK phases issued from crystallographic analysis. Bold characters indicate the major element, if any.
PhaseSite coordination and multiplicity per cellIdeal composition(s)Sublattice model
A15(CN14)6(CN12)2A3B (A,B)3(A,B)
C15(CN16)8(CN12)16AB2 (A,B)(A,B)2
C14(CN16)4(CN12)2(CN12)6AB2 (A,B)(A,B)2 or
(A,B)(A,B)0.5(A,B)1.5
µ(CN16)6(CN15)6(CN14)6(CN12)3(CN12)18A6B7 or A7B6(A)12(A,B)6(A,B)3(A,B)18
σ(CN15)4(CN14)8(CN14)8(CN12)8(CN12)2A2B (A,B)2(A,B)
χ(CN16)2(CN16)8(CN13)24(CN12)24A5B24 or A17B12(A,B)5(A,B)12(A,B)12

5.3. More Complex Models

Due to the development of both thermodynamic calculation softwares and DFT calculations, models can now be defined using one sublattice per site. Of course this necessitates the use of the DFT calculated enthalpies of formation in order to be able to assign values for the stability of each end-member. Examples of such calculations for the σ and the µ phase, each with 5 sublattices have been presented in Section 4 [32,35].

6. Conclusions

We have shown that non-stoichiometry in FK phases could be described and analyzed from experimental measurements. We have shown that the simple application of CN rules for the prediction of site occupancy is misleading and experimental measurement should support any proposed scheme. Nowadays, with the increase of computation facilities, these complex phases can not only be calculated by DFT but also their non-stoichiometry predicted. Finally, Calphad models help in describing these phases in comparison with the other phases in the same systems, allowing the description of the complete phase diagram. Multi-component databases may then be built that succeed in predicting the precipitation of these phases in complex alloys. Modern approaches such as those described in the present paper may be used in the future in new thermodynamic databases for increased accuracy in their predictions.

Acknowledgments

The contribution of Pierre Joubert to the proof reading of the manuscript is greatly appreciated. Financial support from the Agence Nationale de la Recherche (Project Armide 2010 BLAN 912 01) is also acknowledged.

Conflict of Interest

The authors declare no conflict of interest.

References

  1. Fleischer, R.L. Miscellaneous novel intermetallics. In Intermetallic Compounds; Westbrook, J.H., Fleischer, R.L., Eds.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 1994; Volume 2, pp. 237–256. [Google Scholar]
  2. Frank, F.C.; Kasper, J.S. Complex alloy structures regarded as sphere packings. I. Definitions and basic principles. Acta Crystallogr. 1958, 11, 184–190. [Google Scholar] [CrossRef]
  3. Frank, F.C.; Kasper, J.S. Complex alloy structures regarded as sphere packings. II. Analysis and classification of representative structures. Acta Crystallogr. 1959, 12, 483–499. [Google Scholar] [CrossRef]
  4. Sinha, A.K. Topologically close-packed structures of transition metal alloys. Prog. Mater. Sci. 1972, 15, 79–185. [Google Scholar]
  5. Cortella, L.; Vinet, B.; Desré, P.J.; Pasturel, A.; Paxton, A.T.; van Schilfgaarde, M. Evidences of transitory metastable phases in refractory metals solidified from highly undercooled liquids in a drop tube. Phys. Rev. Lett. 1993, 70, 1469–1472. [Google Scholar] [CrossRef]
  6. Moseley, P.T.; Seabrook, C.J. The crystal structure of β-tantalum. Acta Crystallogr. 1973, B29, 1170–1171. [Google Scholar]
  7. Kasper, J.S. Atomic and Magnetic Ordering in Transition Metal Structures. In Proceedings of the Theory of Alloy PhasesNational Metal Congress and Exposition, Philadelphia, PA, USA, 15–21 October 1955; American Society for Metals: Materials Park, OH, USA, 1956; pp. 264–278. [Google Scholar]
  8. Kasper, J.S.; Waterstrat, R.M. Ordering of atoms in the σ phase. Acta Crystallogr. 1956, 9, 289–295. [Google Scholar] [CrossRef]
  9. Van der Kraan, A.M.; de Mooij, D.B.; Buschow, K.H.J. Magnetic properties and 57Fe Mössbauer effect in V1-xFex alloys. Phys. Status Solidi (a) 1985, 88, 231–237. [Google Scholar] [CrossRef]
  10. Cieslak, J.; Reissner, M.; Steiner, W.; Dubiel, S.M. Magnetic moments and Curie temperatures of σ-FeCr alloys. J. Magn. Magn. Mater. 2004, 272–276, 534–535. [Google Scholar] [CrossRef]
  11. Cieslak, J.; Costa, B.F.O.; Dubiel, S.M.; Reissner, M.; Steiner, W. Magnetic ordering above room temperature in the sigma-phase of Fe66V34. J. Magn. Magn. Mater. 2009, 321, 2160–2165. [Google Scholar] [CrossRef]
  12. Vilar, R.; Cizeron, G. Evolutions structurales développées au sein de la phase σ Fe-Cr. Acta Metall. 1987, 35, 1229–1236. [Google Scholar] [CrossRef]
  13. Petrov, Y.I.; Shafranovsky, E.A.; Krupyanskii, Y.F.; Essine, S.V. Structure and Mössbauer spectra for the Fe-Cr system: From bulk alloy to nanoparticules. J. Appl. Phys. 2002, 91, 352–361. [Google Scholar]
  14. Cieslak, J.; Reissner, M.; Steiner, W.; Dubiel, S.M. Site occupation and local hyperfine fields in σ Fe-Cr alloys. J. Magn. Magn. Mater. 2007, 310, e613–e615. [Google Scholar] [CrossRef]
  15. Dubiel, S.M.; Tozoni, J.R.; Cieslak, J.; Braz, D.C.; Vidoto, E.L.G.; Bonagamba, T.J. Sublattice magnetism in σ-phase Fe100-xVx (x = 34.4, 39.9, and 47.9) studied via zero-field 51V NMR. Phys. Rev. 2010, B81, 184407:1–184407:5. [Google Scholar]
  16. Joubert, J.-M. Contribution of the Rietveld method to non-stoichiometric phase modeling. Part I: Generalities. Calphad 2002, 26, 419–425. [Google Scholar] [CrossRef]
  17. Joubert, J.-M.; Feutelais, Y. Contribution of the Rietveld method to non-stoichiometric phase modeling. Part II: Experimental examples. Calphad 2002, 26, 427–438. [Google Scholar] [CrossRef]
  18. Joubert, J.-M.; Cerný, R.; Emerich, H. Mixed site occupancies in µ-Zr-Nb-Al by resonant powder diffraction. Z. Krist. Suppl. 2007, 26, 311–316. [Google Scholar]
  19. Tobola, J.; François, M.; Elkaim, E.; Joubert, J.-M.; Vilasi, M. Resonant X-ray diffraction study and electronic structure calculations of three Mo-Ru-Si ternary phases. Intermetallics 2009, 18, 781–790. [Google Scholar]
  20. Yaqoob, K.; Crivello, J.-C.; Joubert, J.-M. Comparison of the site occupancies determined by combined Rietveld refinement and by DFT calculations: The example of the ternary Mo-Ni-Re σ phase. Inorg. Chem. 2012, 51, 3071–3078. [Google Scholar] [CrossRef]
  21. Joubert, J.-M.; Dupin, N. Mixed site occupancies in the μ phase. Intermetallics 2004, 12, 1373–1380. [Google Scholar] [CrossRef]
  22. Joubert, J.-M. Crystal chemistry and Calphad modelling of the σ phase. Prog. Mater. Sci. 2008, 53, 528–583. [Google Scholar] [CrossRef]
  23. Joubert, J.-M.; Phejar, M. The crystal chemistry of the χ phase. Prog. Mater. Sci. 2009, 54, 945–980. [Google Scholar] [CrossRef]
  24. Turchi, P.E.A.; Finel, A. Ordering phenomena in A15-based alloys. Phys. Rev. B 1992, 46, 702–725. [Google Scholar]
  25. Ducastelle, F.; Gautier, F. Generalized perturbation theory in disordered transitional alloys: Applications to the calculation of ordering energies. J. Phys. F Metal Phys. 1976, 6, 2039–2062. [Google Scholar] [CrossRef]
  26. Kikuchi, R. A theory of cooperative phenomena. Phys. Rev. 1951, 81, 988–1003. [Google Scholar] [CrossRef]
  27. Sanchez, J.; Ducastelle, F.; Gratias, D. Generalized cluster description of multicomponent systems. Physica 1984, A128, 334–350. [Google Scholar]
  28. Sluiter, M.H.F.; Esfarjani, K.; Kawazoe, Y. Site occupation reversal in the Fe-Cr σ·phase. Phys. Rev. Lett. 1995, 75, 3142–3146. [Google Scholar] [CrossRef]
  29. Berne, C.; Sluiter, M.; Kawazoe, Y.; Hansen, T.; Pasturel, A. Site occupancies in the Re-W sigma phase. Phys. Rev. B 2001, 64, 144103:1–144103:8. [Google Scholar]
  30. Andersen, O.K. Linear methods in band theory. Phys. Rev. 1975, B12, 3060–3083. [Google Scholar]
  31. Connolly, J.W.D.; Williams, A.R. Density-functional theory applied to phase transformations in transition-metal alloys. Phys. Rev. 1983, B27, 5169–5172. [Google Scholar]
  32. Fries, S.G.; Sundman, B. Using Re-W sigma phase first-principles results in the Bragg-Williams approximation. Phys. Rev. B 2002, 66, 012203:1–012203:4. [Google Scholar]
  33. Bragg, W.L.; Williams, E.J. The effect of thermal agitation on atomic arrangement in alloys. Proc. R. Soc. (London) 1934, A145, 699–730. [Google Scholar]
  34. Ansara, I.; Dupin, N.; Sundman, B. Reply to the paper: “When is a compound energy not a compound energy? A critique of the 2-sublattice order/disorder model” of Nigel Saunders, Calphad 20 (1996) 491-499. Calphad 1997, 21, 535–542. [Google Scholar] [CrossRef]
  35. Dupin, N.; Fries, S.G.; Joubert, J.-M.; Sundman, B.; Sluiter, M.; Kawazoe, Y.; Pasturel, A. Using Nb-Ni μ phase first principles results in the Bragg-Williams approximation to calculate finite temperature thermodynamic properties. Philos. Mag. 2006, 86, 1631–1641. [Google Scholar] [CrossRef]
  36. Crivello, J.-C.; Joubert, J.-M. First principles calculations of the σ and χ phases in the Mo-Re and W-Re systems. J. Phys. Condens. Matter 2010, 22, 035402. [Google Scholar] [CrossRef]
  37. Farzadfar, S.-A.; Levesque, M.; Phejar, M.; Joubert, J.-M. Thermodynamic assessment of the Molybdenum-Rhenium System. Calphad Comput. Coupling Phase Diagr. Thermochem. 2009, 33, 502–510. [Google Scholar] [CrossRef]
  38. Korzhavyi, P.A.; Sundman, B.; Selleby, M.; Johansson, B. Atomic, electronic, and magnetic structure of iron-based sigma-phases. Mater. Res. Soc. Symp. Proc. 2005, 842, 517–522. [Google Scholar]
  39. Pavlu, J.; Vrestal, J.; Sob, M. Ab initio study of formation energy and magnetism of sigma phase in Cr-Fe and Cr-Co systems. Intermetallics 2010, 18, 212–220. [Google Scholar] [CrossRef]
  40. Singh, D.J.; Nordström, L. Planewaves, Pseudopotentials and the LAPW Method; Springer: Berlin, Germany, 2006. [Google Scholar]
  41. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
  42. Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
  43. Cieslak, J.; Tobola, J.; Dubiel, S.M.; Sikora, W. Magnetic properties of σ-FeCr alloys as calculated with the charge- and spin-self-consistent KKR(CPA) method. Phys. Rev. 2010, B82, 224407:1–224407:9. [Google Scholar]
  44. Kabliman, E.; Blaha, P.; Schwarz, K.; Ruban, A.V.; Johansson, B. Ab initio-based mean-field theory of the site occupation in the Fe-Cr σ-phase. Phys. Rev. 2011, B83, 092201:1–092201:4. [Google Scholar]
  45. Yakel, H.L. Atom distribution in sigma phases. I. Fe and Cr atom distribution in a binary sigma phase equilibrated at 1063, 1013 and 923 K. Acta Crystallogr. 1983, B39, 20–28. [Google Scholar]
  46. Crivello, J.-C.; Palumbo, M.; Abe, T.; Joubert, J.-M. Ab initio ternary s-phase diagram: The Cr-Mo-Re system. Calphad Comput. Coupling Phase Diagr. Thermochem. 2010, 34, 487–494. [Google Scholar]
  47. Palumbo, M.; Abe, T.; Fries, S.G.; Pasturel, A. First-principles approach to phase stability for a ternary σ phase: Application to Cr-Ni-Re. Phys. Rev. 2011, B83, 144109:1–144109:7. [Google Scholar]
  48. Parlinski, K.; Li, Z.Q.; Kawazoe, Y. First-principles determination of the soft mode in cubic ZrO2. Phys. Rev. Lett. 1997, 78, 4063–4066. [Google Scholar] [CrossRef]
  49. Dubiel, S.M.; Cieslak, J.; Sturhahn, W.; Sternik, M.; Piekarz, P.; Stankov, S.; Parlinski, K. Vibrational properties of α- and σ-phase Fe-Cr alloy. Phys. Rev. Lett. 2010, 104, 155503:1–15503:4. [Google Scholar]
  50. Sundman, B.; Ågren, J. A regular solution model for phases with several components and sublattices, suitable for computer applications. J. Phys. Chem. Solids 1981, 42, 297–301. [Google Scholar] [CrossRef]
  51. Ferro, R.; Cacciamani, G. Remarks on crystallochemical aspects in thermodynamic modelling. Calphad 2002, 26, 439–458. [Google Scholar] [CrossRef]
  52. Du, Y.; Liu, S.; Chang, Y.A.; Yang, Y. A thermodynamic modeling of the Cr-Nb-Ni system. Comput. Coupling Phase Diagr. Thermochem. 2005, 29, 140–148. [Google Scholar] [CrossRef]
  53. De Keyzer, J.; Cacciamani, G.; Dupin, N.; Wollants, P. Thermodynamic modelling and optimization of the Fe-Ni-Ti system. Calphad Comput. Coupling Phase Diagr. Thermochem. 2009, 33, 109–123. [Google Scholar] [CrossRef]
  54. Frisk, K. A thermodynamic evaluation of the Mo-Ni system. Calphad 1990, 14, 311–320. [Google Scholar] [CrossRef]
  55. Zhou, S.H.; Wang, Y.; Jiang, C.; Zhu, J.Z.; Chen, L.-Q.; Liu, Z.-K. First-principles calculations and thermodynamic modeling of the Ni-Mo system. Mater. Sci. Eng. A 2005, 397, 288–296. [Google Scholar] [CrossRef]
  56. Bolcavage, A.; Kattner, U.R. A reassessment of the calculated Ni-Nb phase diagram. J. Phase Equilibria 1996, 17, 92–100. [Google Scholar] [CrossRef]
  57. Davydov, A.; Kattner, U.R. Thermodynamic assessment of the Co-Mo system. J. Phase Equilibria 1999, 20, 5–16. [Google Scholar] [CrossRef]
  58. Joubert, J.-M.; Sundman, B.; Dupin, N. Assessment of the niobium-nickel system. Comput. Coupling Phase Diagr. Thermochem. 2004, 28, 299–306. [Google Scholar] [CrossRef]
  59. Xiong, W.; Hedström, P.; Selleby, M.; Odqvist, J.; Thuvander, M.; Chen, Q. An improved thermodynamic modeling of the Fe-Cr system down to zero kelvin coupled with key experiments. Calphad Comput. Coupling Phase Diagr. Thermochem. 2011, 35, 355–366. [Google Scholar] [CrossRef]

Share and Cite

MDPI and ACS Style

Joubert, J.-M.; Crivello, J.-C. Non-Stoichiometry and Calphad Modeling of Frank-Kasper Phases. Appl. Sci. 2012, 2, 669-681. https://doi.org/10.3390/app2030669

AMA Style

Joubert J-M, Crivello J-C. Non-Stoichiometry and Calphad Modeling of Frank-Kasper Phases. Applied Sciences. 2012; 2(3):669-681. https://doi.org/10.3390/app2030669

Chicago/Turabian Style

Joubert, Jean-Marc, and Jean-Claude Crivello. 2012. "Non-Stoichiometry and Calphad Modeling of Frank-Kasper Phases" Applied Sciences 2, no. 3: 669-681. https://doi.org/10.3390/app2030669

APA Style

Joubert, J.-M., & Crivello, J.-C. (2012). Non-Stoichiometry and Calphad Modeling of Frank-Kasper Phases. Applied Sciences, 2(3), 669-681. https://doi.org/10.3390/app2030669

Article Metrics

Back to TopTop