Electrohydrodynamic Nanofluid Hydrothermal Treatment in an Enclosure with Sinusoidal Upper Wall
Abstract
:1. Introduction
2. Problem Definition


3. Governing Equations
3.1. Mathematical Model
3.2. Numerical Method
4. Code Verification and Mesh Independency
| Mesh size | 31 × 61 | 41 × 81 | 51 × 101 | 61 × 121 | 71 × 141 | 81 × 161 |
|---|---|---|---|---|---|---|
| 6.180284 | 6.195644 | 6.211904 | 6.231994 | 6.235304 | 6.239816 |

5. Results and Discussion
| Material | ||||
|---|---|---|---|---|
| Ethylene glycol | 1110 | 2400 | 0.26 | 0.0162 |
| 5200 | 670 | 6 | - |




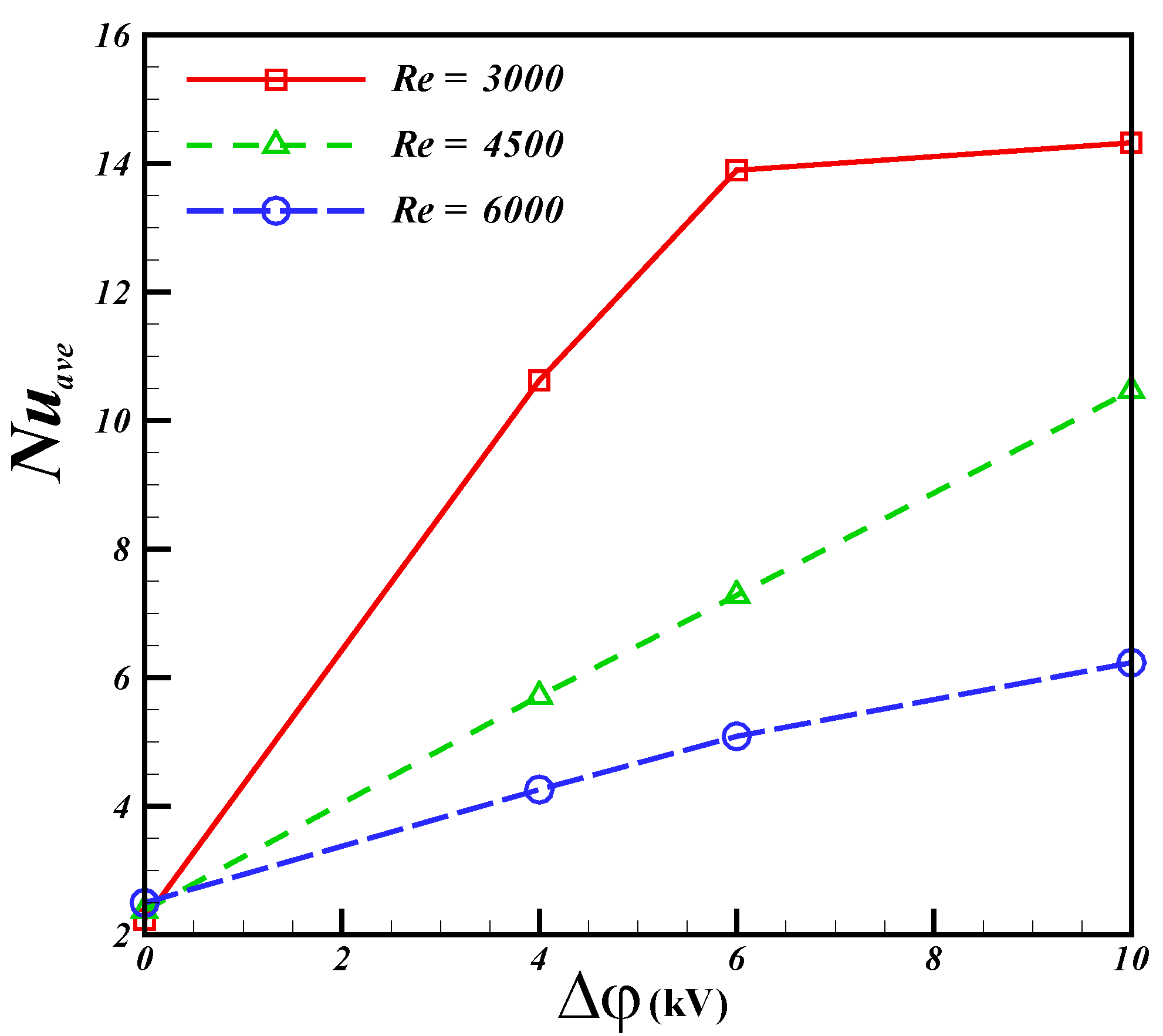
6. Conclusions
Author Contributions
Conflicts of Interest
Nomenclature
| ironic mobility | Temperature, | ||
| specific heat capacity | Cartesian components of velocity, , [m/s] | ||
| diffusion number , charge diffusion coefficient, | Greek symbols | ||
| Eckert number | dielectric permittivity | ||
| electric field, | Volume fraction | ||
| Coulomb force, | Dynamic viscosity | ||
| electric current density, | Density | ||
| characteristic length, | electric conductivity | ||
| electric field number | electric field potential | ||
| Pressure, | Subscripts | ||
| Prandtl number | Average | ||
| electric Prandtl number | Cold | ||
| electric charge density, | Solid particles | ||
| Reynolds number | Base fluid | ||
| Lorentz force number | Hot | ||
| Time, | Nanofluid | ||
References
- Shu, H.S.; Lai, F.C. Effect of Electrical Field on Buoyancy-Induced Flows in an Enclosure. In Proceedings of the Conference Record—IAS Annual Meeting (IEEE Industry Applications Society), Orlando, FL, USA, 8–12 October 1995; Volume 2, pp. 1465–1471.
- Kasayapanand, N.; Tiansuwan, J.; Asvapoositkul, W.; Vorayos, N.; Kiatsiriroat, T. Effect of the electrode arrangements in tube bank on the characteristic of electrohydrodynamic heat transfer enhancement: Low Reynolds number. J. Enhanc. Heat Transf. 2002, 9, 229–242. [Google Scholar] [CrossRef]
- Velkoff, H.R.; Godfrey, R. Low velocity heat transfer to a flat plate in the presence of a corona discharge in air. J. Heat Transf. 1979, 101, 157–163. [Google Scholar] [CrossRef]
- Lee, S.; Dulikravich, G.S.; Ahuja, V. Computations of Electro-thermo-convective Phenomena in Electro-rheological Fluids; American Society of Mechanical Engineers, Fluids Engineering Division FED: New York, NY, USA, 1993; Volume 164, pp. 29–42. [Google Scholar]
- Hsiao, K.-L. Heat and mass mixed convection for MHD visco-elastic fluid past a stretching sheet with ohmic dissipation. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1803–1812. [Google Scholar] [CrossRef]
- Khanafer, K.; Vafai, K.; Lightstone, M. Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids. Int. J. Heat Mass Transf. 2003, 46, 3639–3653. [Google Scholar] [CrossRef]
- Rahman, M.M.; Billah, M.M.; Rahman, A.T.M.M.; Kalam, M.A.; Ahsan, A. Numerical investigation of heat transfer enhancement of nanofluids in an inclined lid-driven triangular enclosure. Int. Commun. Heat Mass Transf. 2011, 38, 1360–1367. [Google Scholar] [CrossRef]
- Rahman, M.M.; Oztop, H.F.; Ahsan, A.; Saidur, R.; Al-Salem, K.; Rahim, N.A. Laminar Mixed Convection in Inclined Triangular Enclosures Filled with Water Based Cu Nanofluid. Ind. Eng. Chem. Res. 2012, 51, 4090–4100. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ellahi, R. Three dimensional mesoscopic simulation of magnetic field effect on natural convection of nanofluid. Int. J. Heat Mass Transf. 2015, 89, 799–808. [Google Scholar] [CrossRef]
- Hsiao, K.-L. Energy conversion conjugate conduction-convection and radiation over non-linearly extrusion stretching sheet with physical multimedia effects. Energy 2013, 59, 494–502. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D.; Javed, M.Y.; Ellahi, R. Effect of thermal radiation on magnetohydrodynamics nanofluid flow and heat transfer by means of two phase model. J. Magn. Magn. Mater. 2015, 374, 36–43. [Google Scholar] [CrossRef]
- Boutina, L.; Bessaïh, R. Numerical simulation of mixed convection air-cooling of electronic components mounted in an inclined channel. Appl. Therm. Eng. 2011, 31, 2052–2062. [Google Scholar] [CrossRef]
- Hatami, M.; Sheikholeslami, M.; Ganji, D.D. Laminar flow and heat transfer of nanofluid between contracting and rotating disks by least square method. Powder Technol. 2014, 253, 769–779. [Google Scholar] [CrossRef]
- Mansur, S.; Ishak, A.; Pop, I. Flow and heat transfer of nanofluid past stretching/shrinking sheet with partial slip boundary conditions. Appl. Math. Mech. 2014, 35, 1401–1410. [Google Scholar] [CrossRef]
- Ellahi, R. The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe: Analytical solutions. Appl. Math. Model. 2013, 37, 1451–1467. [Google Scholar] [CrossRef]
- Othman, M.I.A.; Zaki, S.A. The effect of thermal relaxation time on electrohydrodynamic viscoelastic fluid layer heated form below. Can. J. Phys. 2003, 81, 779–787. [Google Scholar] [CrossRef]
- Gawande, M.B.; Rathi, A.K.; Branco, P.S.; Varma, R.S. Sustainable Utility of Magnetically Recyclable Nano-Catalysts in Water: Applications in Organic Synthesis. Appl. Sci. 2013, 3, 656–674. [Google Scholar] [CrossRef]
- Kefayati, G.H.R. Lattice Boltzmann simulation of natural convection in nanofluid-filled 2D long enclosures at presence of magnetic field. Theor. Comput. Fluid Dyn. 2013, 27, 865–883. [Google Scholar] [CrossRef]
- Noreen, S.A.; Nadeem, S. Numerical and analytical simulation of the peristaltic flow of Jeffrey fluid with Reynold’s model of viscosity. Int. J. Numer. Methods Heat Fluid Flow 2012, 22, 458–472. [Google Scholar]
- Higashi, T.; Minegishi, H.; Nagaoka, Y.; Fukuda, T.; Echigo, A.; Usami, R.; Maekawa, T.; Hanajiri, T. Effects of Superparamagnetic Nanoparticle Clusters on the Polymerase Chain Reaction. Appl. Sci. 2012, 2, 303–314. [Google Scholar] [CrossRef]
- Ganapathirao, M.; Ravindran, R.; Pop, I. Non-uniform slot suction (injection) on an unsteady mixed convection flow over a wedge with chemical reaction and heat generation or absorption. Int. J. Heat Mass Transf. 2013, 67, 1054–1061. [Google Scholar] [CrossRef]
- Kefayati, G.H.R. Lattice Boltzmann simulation of MHD natural convection in a nanofluid-filled cavity with sinusoidal temperature distribution. Powder Technol. 2013, 243, 171–183. [Google Scholar] [CrossRef]
- Sakanova, A.; Keian, C.C.; Zhao, J. Performance Improvements of Microchannel Heat Sink Using Wavy Channel and Nanofluids. Int. J. Heat Mass Transf. 2015, 89, 59–74. [Google Scholar] [CrossRef]
- Wu, J.M.; Zhao, J. A Review of Nanofluids Heat Transfer and Critical heat Flux Enhancement-Research Gap to Engineering Application. Prog. Nucl. Energy 2013, 66, 13–24. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D. Hydrothermal Analysis in Engineering Using Control Volume Finite Element Method; Academic Press: London, UK, 2015. [Google Scholar]
- Sheikholeslami, M.; Bandpy, M.G.; Ellahi, R.; Hassan, M.; Soleimani, S. Effects of MHD on Cu-water nanofluid flow and heat transfer by means of CVFEM. J. Magn. Magn. Mater. 2014, 349, 188–200. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Rashidi, M.M. Ferrofluid heat transfer treatment in the presence of variable magnetic field. Eur. Phys. J. Plus 2015, 130, 115. [Google Scholar] [CrossRef]
- Bergles, A.E. Enhancement of Heat Transfer. In Proceedings of the 6th International Journal of Heat and Mass Transfer Conference, Toronto, Canada, 7–11 August 1978; pp. 89–108.
- Martin, P.J.; Richardson, A.T. Conductivity Models of Electrothermal Convection in Plane Layer of Dielectric Liquid. J. Heat Transf. 1984, 106, 131–136. [Google Scholar] [CrossRef]
- Worraker, W.J.; Richardson, A.T. The Effect of Temperature Variations in Charge Carrier Mobility on a Stationary Electrohydrodynamic Instability. J. Fluid Mech. 1979, 93, 29–45. [Google Scholar] [CrossRef]
- Fujino, T.; Yokoyama, Y.; Mori, Y.H. Augmentation of Laminar Forced-Convective Heat Transfer by the Application of a Transverse Electric Field. J. Heat Transf. 1989, 111, 345–351. [Google Scholar] [CrossRef]
- Moallemi, M.K.; Jang, K.S. Prandtl number effects on laminar mixed convection heat transfer in a lid-driven cavity. Int. J. Heat Mass Transf. 1992, 35, 1881–1892. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheikholeslami, M.; Ellahi, R. Electrohydrodynamic Nanofluid Hydrothermal Treatment in an Enclosure with Sinusoidal Upper Wall. Appl. Sci. 2015, 5, 294-306. https://doi.org/10.3390/app5030294
Sheikholeslami M, Ellahi R. Electrohydrodynamic Nanofluid Hydrothermal Treatment in an Enclosure with Sinusoidal Upper Wall. Applied Sciences. 2015; 5(3):294-306. https://doi.org/10.3390/app5030294
Chicago/Turabian StyleSheikholeslami, Mohsen, and Rahmat Ellahi. 2015. "Electrohydrodynamic Nanofluid Hydrothermal Treatment in an Enclosure with Sinusoidal Upper Wall" Applied Sciences 5, no. 3: 294-306. https://doi.org/10.3390/app5030294
APA StyleSheikholeslami, M., & Ellahi, R. (2015). Electrohydrodynamic Nanofluid Hydrothermal Treatment in an Enclosure with Sinusoidal Upper Wall. Applied Sciences, 5(3), 294-306. https://doi.org/10.3390/app5030294







