Abstract
We investigate the effect of chirped excitation and the excitation detuning on the coherent control of population transfer and vibrational states in a four-level system. Density matrix equations are studied for optimally enhanced processes by considering specific parameters typical of oxazine systems. Our simulations show a strong dependence on the interplay between chirp and excitation detuning and predict enhancement factors up to 3.2 for population transfer and up to 38.5 for vibrational coherences of electronic excited states. The study of the dynamics of the populations and vibrational coherences involved in the four-level system allows an interpretation of the different enhancement/suppression processes observed.
1. Introduction
Tailoring of the optical phase of femtosecond pulses has been used in several applications in photochemistry and time-resolved spectroscopy [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. In general, tailored pulses can be applied using two different approaches: Coherent Control (CC) or Quantum Control Spectroscopy (QCS). Closed-loop learning algorithms are exploited in CC to generate complex optical phases in order to optimize specific reaction pathways. CC has been used as a tool in the control of dynamic processes [17,18,19,20,21], and it explains how a specific state can be selectively populated, for example, to attain 100% population transfer [22,23,24,25], and recent studies have shown the possibility of having enhancements even higher than 100% [26,27,28,29,30,31,32,33,34,35]. QCS also exploits tailored excitation but differs from CC in its applications [30,36]. Its goal is to simplify complex molecular dynamics by tailoring excitation pulses to enhance or suppress specific molecular signal features. A central aspect in both approaches, CC and QCS, is the control of population transfer between the ground and excited states, as well as the generation of vibrational coherence in both potential surfaces. By controlling the population transfer or by suppressing specific molecular vibrational coherences, a photochemical reaction channel can be selectively chosen [27,29,32,37,38,39,40,41,42,43,44,45,46,47,48,49], or a certain mode in a multidimensional time-resolved signal can be suppressed [37,50,51,52,53,54,55].
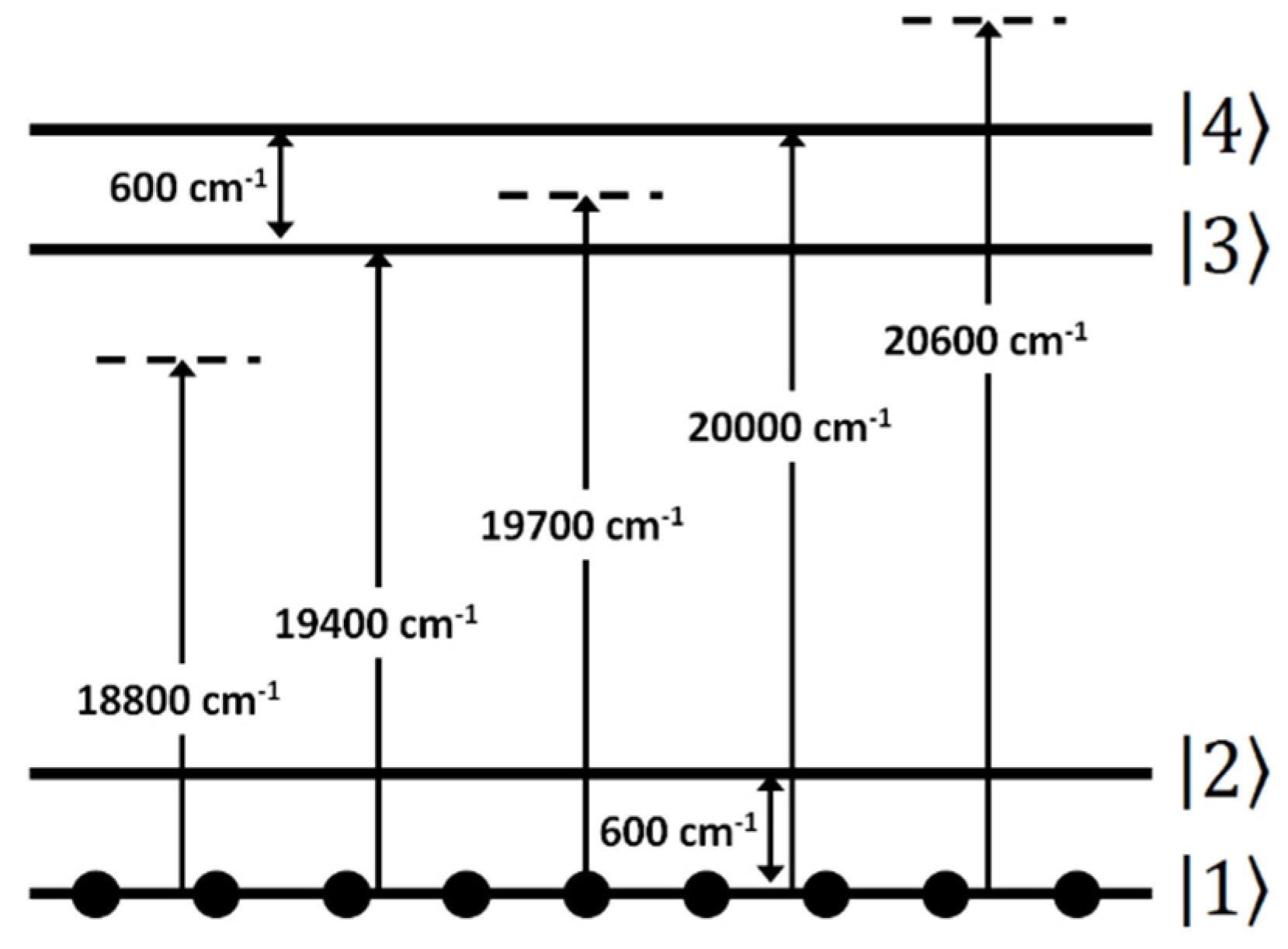
The control of population transfer and vibrational coherences in molecules in general is challenging since several molecular and optical parameters play a role. Indeed, the molecular system under study dictates the displacement of the addressed levels and the vibrational and electronic dephasing rates. While the electronic dephasing rates can in some cases be influenced by the choice of the solvent [56,57,58,59], the displacement between the ground and the excited states is generally fixed. Pulse characteristics can be more easily tailored than molecular properties. Crucial parameters are the spectral detuning of the excitation with respect to the molecular absorption region as well as the temporal shape of the excitation, which is tailored by using phase and/or amplitude shaping. In the present paper we address the coherent control of population transfer and vibrational states in laser dye oxazine systems. We have chosen oxazine systems since these systems are being extensively studied in spectrally and time-resolved transient absorption spectroscopy experiments, in the femtosecond time regime, to elucidate the fastest fundamental processes in photochemistry and photobiology, like isomerization and electron and photon transfer [60]. In particular, we analyze the response of a four-level system, consisting of two electronic states both including two vibrational sub-states (see Figure 1), to the excitation of chirped and detuned femtosecond laser pulses. We will show that the basic processes producing enhancement/suppression factors on the population transfer and vibrational coherences can be understood from this relatively simple molecular model by studying the dynamics of the density matrix elements, and will compare our results with previous theoretical studies and experimental measurements.
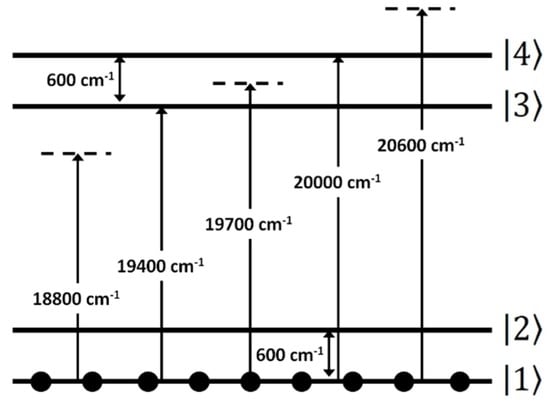
Figure 1.
Schematic of the four level system showing the transition wavenumbers considered and different excitation frequencies.
Indeed, an asymmetry in the molecular response to chirped pulses was first predicted theoretically by Ruhman and Kosloff [61] and observed experimentally by Bardeen et al. [62]. They explained how the excitation of a vibration in the ground state of a molecular system can be accomplished by negatively chirped pulses in an intrapulse pump-dump process. A similar scheme was implemented by Cao et al. [63] for quantum coherent control of population transfer. They demonstrated theoretically that electronic population inversion probabilities of up to 99% in molecular systems can be achieved by using intense positively chirped broadband laser pulses. Their results are robust with respect to thermal and condensed phase conditions and are supported by experimental evidence. For instance, solvent environment was recently shown to be sensitive to positively chirped pulses, and a dependence of the optimal chirp with respect to the displacement between excited and ground state’s molecular potentials was also found. On the way to find the optimal chirp for coherent manipulations, the electronic dephasing rate is theoretically studied to take both effects into account. It is found that for increasing dephasing times, the coherence is enhanced especially if negative chirp is added [64].
In this work we study in detail the influence of chirp, detuning and dephasing on the enhancement in population transfer and vibrational coherence in a four level system (Figure 1). We first describe the density matrix model and give the parameters used in Section 2. As mentioned above, the parameters used to solve our system are specific for the case of oxazine; however, due to the simplicity of the mathematical model that we consider, the physical mechanisms elucidated in our study are of a fundamental type and can therefore be extended to other systems. In Section 3 we show the main results obtained from the simulations. Maps showing the enhancement in the populations and the vibrational coherences have been produced by varying the incident spectral phase chirp from −103 fs2 to 103 fs2 and the excitation spectral detuning from −5 × 103 cm−1 to 5 × 103 cm−1. The most relevant regions in these maps are then studied in detail by plotting the evolution in time of the respective density matrix elements for the important specific cases (enhancement/suppression), and an interpretation of the observed effects is given. In Section 4 we present a study of the influence of the duration of the laser pulse on the observed enhancement effects. The influence of the laser peak intensity in some specific cases is shown in Section 5, and in Section 6 we investigate the important effect of electronic dephasing. A discussion and the conclusions are given in Section 7.
2. Density Matrix Simulations
A non-perturbative, time-dependent density matrix approach is used to simulate the interaction of a femtosecond laser pulse with a four level system consisting of 2 electronic states—ground and excited state, each containing two vibrational levels (Figure 1).
All simulations were carried out under the slowly-varying envelope (SVEA) and rotating-wave (RWA) approximations, by using a 4–5 order Runge-Kutta algorithm (see also [65]). The laser temporal pulse shape is a direct input to the code, and the system allows the laser pulse to interact with all electronic transitions. The model can be written as follows:
where are the populations of the levels, the off-diagonal elements represent the coherences between levels, and are the dipole coupling coefficients of the electronic transitions. are the angular frequencies of the transitions , with being the energies of the quantum states and (see Figure 1). represents the input slowly-varying complex amplitude of the electric field. E(t) is the slowly varying real field envelope, and is the slowly varying phase, which for transform limited pulses is chosen constant. The decay rates of the transitions are given by , and the relaxation times of the levels satisfy , and . The decay rates of the coherences are defined by , , , , and , which include the relaxation of the coherences and the purely dephasing rates . The parameters used are summarized in Table 1.

Table 1.
Parameters used in the simulations.
The non-diagonal terms ,, and define the electronic coherences and include dispersive and absorptive properties in the optical transitions, while and represent the vibrational coherences of the ground and excited states, respectively.
The enhancement factors are defined by the ratio between the values calculated using a chirped pulse (PS) and the ones calculated with a transform limited (TL) Gaussian pulse as: enhancement of population in the ground states , of vibrational coherence in the ground states , of population in the excited electronic state , and of vibrational coherence in the excited electronic state . The initial population is in level |1⟩ in all the simulations.
3. Main Results Obtained from the Simulations
In order to resolve the dependence on the central input pulse frequency and the amount of chirp on the transfer of population and the creation of vibrational coherences in the system, the central wavenumber of the input pulse is considered from 15,000 cm−1 to 25,000 cm−1 (see Figure 1), in steps of 100 cm−1, and the values of the spectral phase chirp have been taken from φʺ = −103 fs2 to 103 fs2, in steps of 10 fs2. The spectral chirp parameter φ'' has been implemented in the Fourier domain and is defined as φ(ω) = 0.5 φʺ ω2, with φ(ω) being the group delay dispersion (GDD) added to the spectral phase of the pulse. Therefore, since only the spectral phase of the laser pulse is varied in our study, the frequency content and the power remains as in the TL pulse for any value of the spectral chirp φʺ, as it is usually the case in the experiments. The rephasing of the spectral components produces a time broadening of the pulse given by , where is the full width at half maximun (FWHM) of the chirped pulse intensity profile and is the duration corresponding to the TL pulse [66].
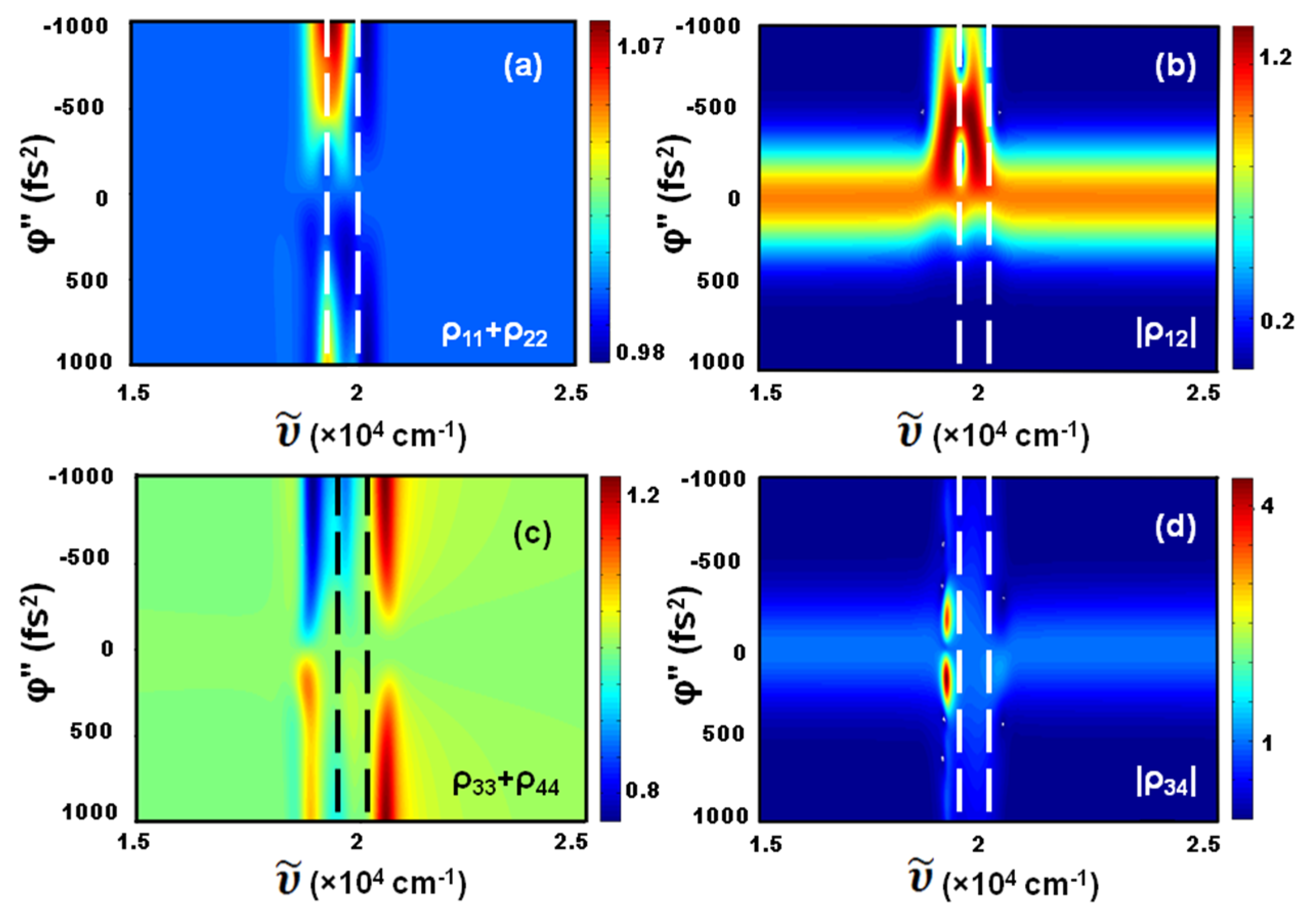
Figure 2 shows the results for the enhancement/suppression factor of the population in the ground state (Figure 2a), the vibrational coherence in the ground state (Figure 2b), the population in the upper state (Figure 2c) and the vibrational coherence in the upper state (Figure 2d), sufficiently long after the interaction of the system with the laser pulse.
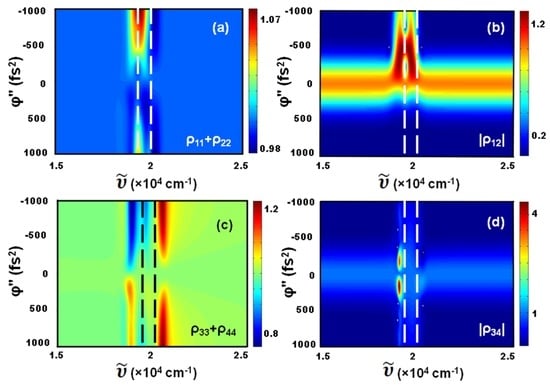
Figure 2.
Enhancement/suppression factor of (a) population in the ground state; (b) vibrational coherence in the ground state; (c) population in the upper state; and (d) vibrational coherence in the upper state. Dashed lines indicate the position of the excited states (see Figure 1).
As is clear from Figure 2, the interplay between chirp and excitation detuning is crucial for the coherent control of the population transfer and the enhancement or suppression of the vibrational coherences. We can observe regions with more than a 2% enhancement/suppression in the case of the population in the excited state (Figure 2c), and enhancement factors as high as 4 for the vibrations in this state (Figure 2d). In order to understand the origin of the processes involved in the calculations of Figure 2, the different time-scales involved in the interaction need to be considered. On the one hand, the period of the vibration both in the ground and the excited states, which in our simulations is Tvib = 1/(c) ≃ 60 fs. On the other hand, we note that the duration of the 30 fs laser pulse with φʺ = ±103 fs2 is ≃ 94 fs. For the values of the peak field amplitude and dipole coupling that we have considered, the period associated to the Rabi oscillations is TRabi = h/(μE) ≃ 180 fs. Also important is the spectral width of the 30 fs Gaussian laser pulse, which is 0.441/(ctp) ≃ 490 cm−1, which is to be compared with the 600 cm−1 of the vibrations considered in our simulations. The fastest dephasing rate in the simulations shown in Figure 2 is 100 fs, which therefore allows in this case for purely coherent processes, since all the interaction is basically finished before that time. We study the influence of the dephasing rates on the enhancement effects in the last part of the paper. We next describe in detail and provide an interpretation of the main results shown in Figure 2.
(1) Population in the ground state (ρ11 + ρ22):
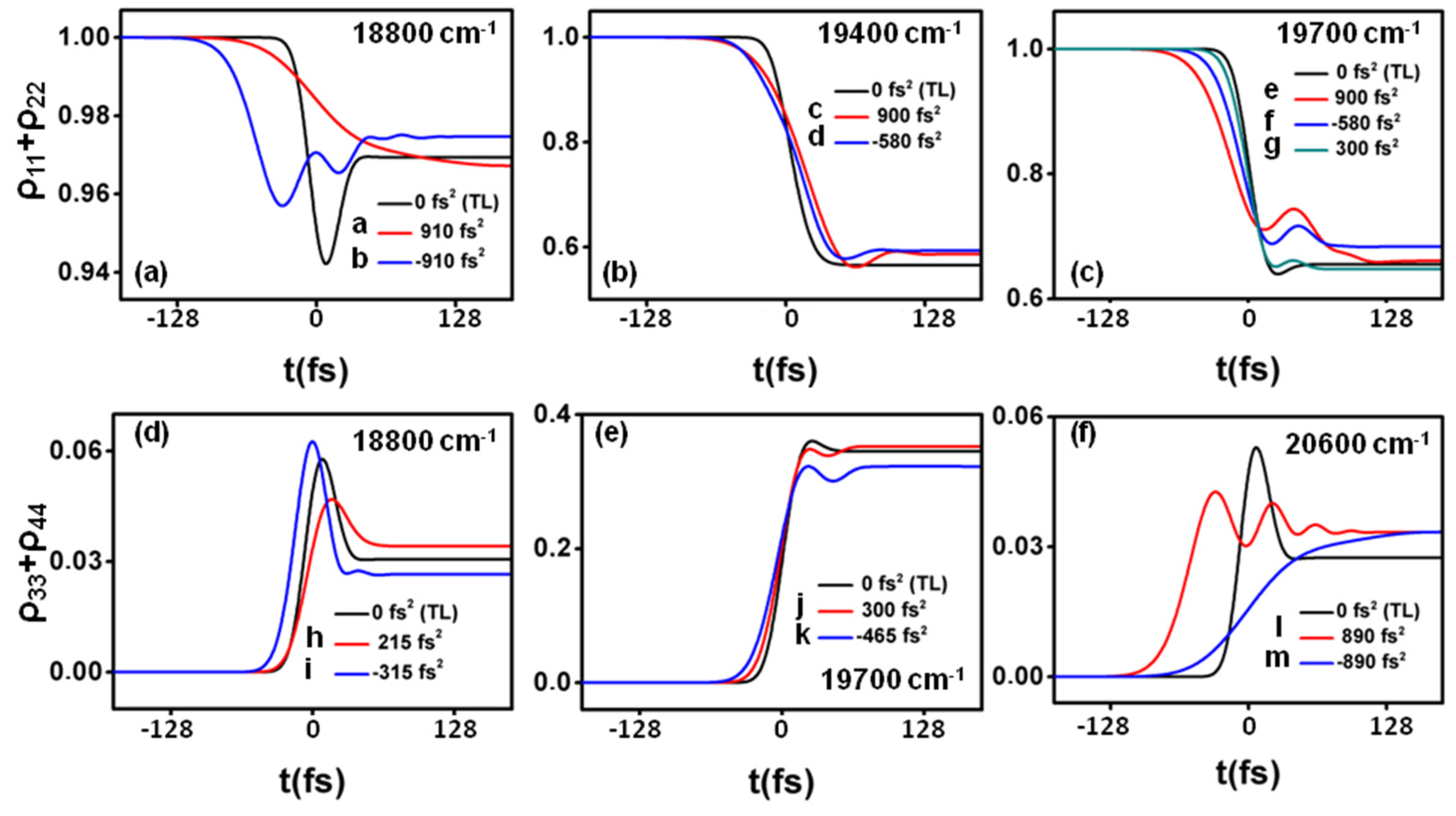
The peak enhancement of the population in the ground state (Figure 2a) is ≃ 1.073 at a chirp value of φʺ = −103 fs2 and for an excitation wave number of ≃ 19,520 cm−1, which is red-detuned and close to the resonance of the first upper vibrational state at = 19,400 cm−1. The highest suppression is obtained at a chirp of 103 fs2 with a laser central wavenumber of ≃ 20,320 cm−1, which is blue-detuned to the resonance of the second upper vibrational state at = 20,000 cm−1. The asymmetry of the enhancement with respect to the sign of the chirp can be understood as follows. The first half of the interacting laser pulse promotes population inversion, which can be available for stimulated emission depending on the shape of the laser pulse and its spectral components. In the case of the highest enhancement of the population ρ11 + ρ22, for instance, if we consider that the upper state is first excited at a wave number at ≃ 19,765 cm−1, which corresponds to the beginning of the laser pulse, a vibrational wave packet will be created in the upper state, which will initiate its oscillation between the upper state vibrational sublevels at this particular frequency. The round trip of the wave packet to the highest vibrational level at = 20,000 cm−1 and back to ≃ 19,765 cm−1 will take about 23.5 fs. From that time, the resonant transitions of the excited atom or molecule available for stimulated emission will be smaller than 19,765 cm−1, and therefore the red shifted frequencies of the negatively chirped laser pulse will meet them and stimulated transfer back to the ground state will be promoted. This is therefore an adiabatic intra-pulse pump-dump scenario that explains the enhancement observed for negatively chirped pulses. For a laser pulse positively chirped, e.g., at this same central pulse frequency of 19,520 cm−1, however, the later higher frequencies of the pulse cannot promote the system down and will instead continue exciting the system to the upper states. Consequently, the population of the ground state when the laser pulse is gone is not enhanced for positively chirped pulses, as it can be seen in Figure 2a. The results that we obtain with our simple four-level system are therefore fully corroborated by the previous theoretical studies and experimental measurements [61,62,63]. In Figure 3 we have plotted the evolution in time of the populations at some specific values of the central laser pulse wavenumber and chirp. Figure 3a shows how the maximum enhancement obtained for negatively chirped pulses at 18,800 cm−1 presents an oscillatory behavior of ρ11 + ρ22, while the TL pulse at this wavenumber induces a pump-dump scenario. Note that the transferred population is small at this detuning (≃5%). This behavior is qualitatively different from the more resonant cases in Figure 3b,c, where the pump-dump processes are not that clear and the population transfers become ≃40%.
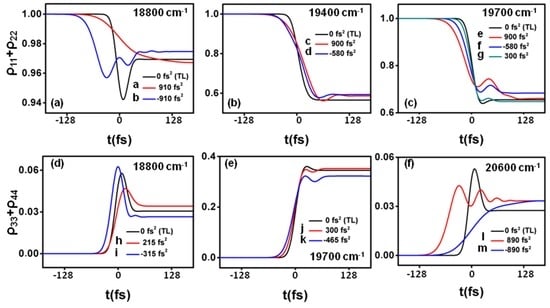
Figure 3.
Time evolution of the populations in the ground state (a–c); and in the upper states (d–f); for specific parameter values, as indicated. Note that the lines, which are named with letters, correspond to the parameter values detailed in Figure 5a,e.
(2) Coherence in the ground state |ρ12|:
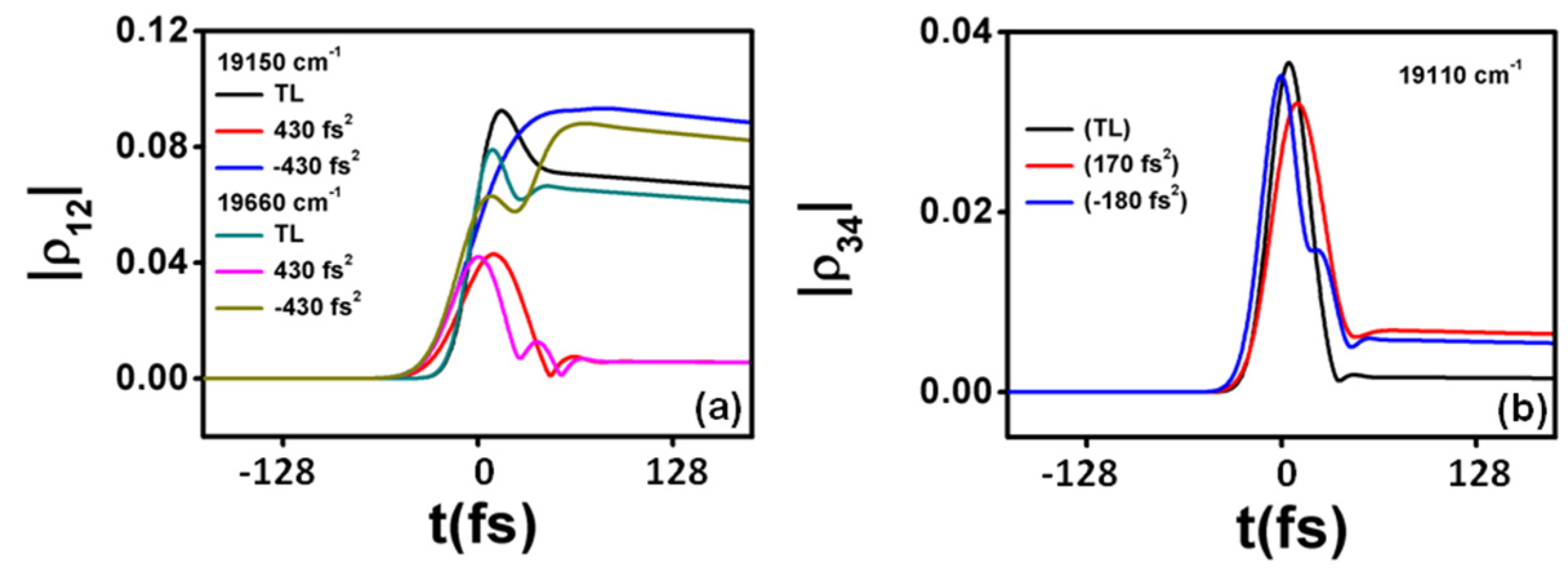
The highest enhancement of the coherence in the ground state is ≃1.35 and is obtained at a negative chirp of φʺ ≃ −430 fs2 and at the excitation wavenumbers of ≃ 19,660 cm−1 and ≃ 19,150 cm−1 (see Figure 2b). The enhancement of the vibrational coherence in the ground states therefore responds basically to the same phenomena that the one for the ground state population, i.e., the pump-dump intra-pulse mechanisms are promoted for negatively chirped pulses and suppressed for positive chirp. The details of the precise values of the two central laser pulse wavenumbers that produce the maximum enhancement are intriguing intra-pulse mechanisms which have not been clarified completely. Our result is in accordance with the studies made in [60], where it is observed for oxazine 1 systems in ethanol that ground-state vibrational coherences are enhanced predominantly by negatively chirped pulses. Figure 4 shows the evolution in time of the coherences at some specific values of the central laser pulse wavenumber and chirp. In Figure 4a the time evolution of the vibrational coherence in the ground states for the two different wave numbers that produce enhancement at negative chirp can be seen, and also the reduction of the coherence |ρ12| after the interaction of the first half of the pulse in the case of positively chirped pulses.
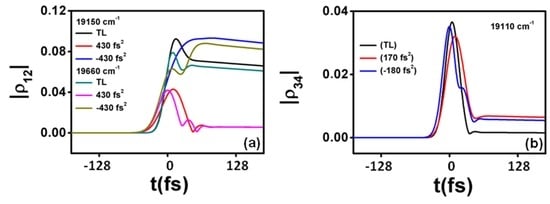
Figure 4.
Time evolution of the vibrational coherences in the ground state (a); and in the upper states (b), for the indicated parameter values.
(3) Population in the upper states (ρ33 + ρ44):
Figure 2c shows that the peak enhancement in population transfer to the upper states is ≃1.23 at the chirp values φʺ = ±103 fs2 and for an excitation wave number of ≃ 20,550 cm−1. A qualitatively different smaller enhancement of ≃1.1 is also obtained at the positive chirp φʺ = 260 fs2 and for an excitation wave number of ≃ 18,840 cm−1. The highest suppression is obtained at a close wave number of ≃ 18,920 cm−1 for a negative chirp of φʺ = −103 fs2. On the one hand, the symmetric enhancement with respect to chirp at ≃ 20,550 cm−1 can be understood by the evolution in time of the population in the upper states for the TL and the chirped pulses at this particular central laser pulse wavenumber, in Figure 3f. The behavior can be seen as the opposite to the effect in the ground state and for red detuned pulses (Figure 3a). In this case the oscillatory behavior corresponds to the positively chirped pulse. On the other hand, the enhancement obtained for red detuned pulses at ≃ 18,800 cm−1 is the consequence of an optimized pump-dump transition, as shown in Figure 3d, which as opposed to the enhancement of the population in the ground state, it is favored by positively chirped pulses, as was also observed in [57,58,59].
(4) Coherence in the upper states |ρ34|:
Figure 2d shows two narrow peaks of the upper vibrational coherence that are obtained at a pulse central frequency of ≃ 19,110 cm−1 and for spectral phase chirps as φʺ ≃ −180 fs2 and φʺ ≃ 170 fs2. The corresponding values are ≃3.56 and ≃4.34, respectively, and therefore a slightly higher enhancement is obtained with positively chirped pulses. Of relevance is the narrow parameters window observed in this case. The nearly symmetric values of the upper vibrational coherence observed in our simulations, however, shows that the vibrational states in the upper levels can be enhanced by relatively small positive or negative chirp values, with a central laser pulse wavenumber red shifted with respect to the resonance of the upper vibrational levels. This result is partially in accordance with the studies made in [60], where it is shown that excited state vibrational coherences are enhanced predominantly by positively chirped pulses. Figure 4b shows the evolution in time of the coherence |ρ34| at the relevant parameter values. It is clear that the two chirped pulses after the interaction of the first half of the pulse are able to retain the |ρ34| coherence as compared to the TL pulse.
4. Influence of the Duration of the Laser Pulse
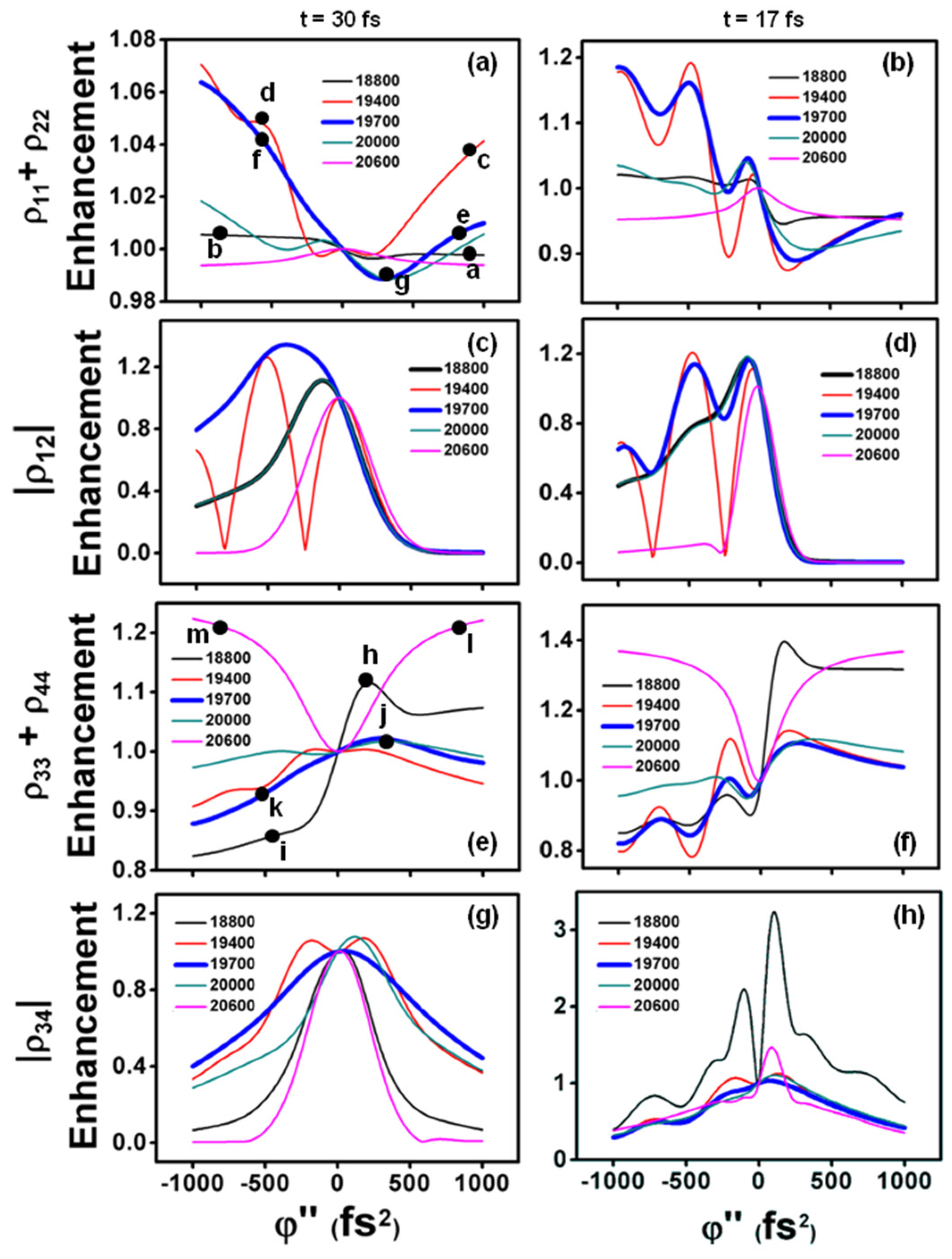
Although a systematic study of all the parameters involved is far from the scope of the present work, we have evaluated the effect of the TL laser pulse duration by repeating some of our simulations using a shorter laser pulse durations (17 fs), and then comparing the results to the ones obtained with the TL 30 fs pulse. Figure 5 shows the output obtained for five specific different laser pulse excitation wavenumbers (18,800 cm−1, 19,400 cm−1, 19,700 cm−1, 20,000 cm−1 and 20,600 cm−1). As it is indicated, in the left-hand part of the figure (Figure 5a,c,e,g) the simulations have been performed with a laser pulse of 30 fs, as in Figure 2. The right hand panels (Figure 5b,d,f,h) show the results obtained by keeping all the same parameters but using the shorter laser pulse.
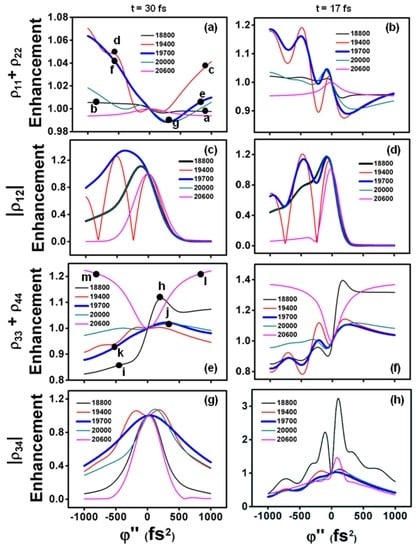
Figure 5.
Enhancement/suppression factors of (a,b) population in the ground state; (c,d) vibrational coherence in the ground state; (e,f) population in the upper state; and (g,h) vibrational coherence in the upper state. The right hand panels are for a laser pulse of 30 fs and the right hand panels for 17 fs, as indicated. The colored lines represent the different excitation frequencies: 18,800 cm−1 (black line), 19,400 cm−1 (red line), 19,700 cm−1 (blue line), 20,000 cm−1 (dark cyan line), and 20,600 cm−1 (magenta line). The electronic dephasing time is 100 fs for all cases. A bold (blue) line has been chosen for the excitation wavenumber of 19,700 cm−1, in order to clarify the comparisons with Figure 7.
The results in the left hand side of Figure 5 are cuts of the density maps shown in Figure 2 at specific excitation wavenumbers. The right hand side panels obtained for 17 fs show basically the same qualitative behavior as the ones obtained for 30 fs, except that we observe some undulations of the enhancement factors as the chirp is varied. An overall increase in the value of their maximum is also observed. The observed undulation may occur due to the larger effect of chirp on the shorter 17 fs pulse, since its duration for φʺ = ±103 fs2 results in ≃159 fs, i.e., it is longer than the 94 fs that correspond to the 30 fs pulse at these chirp values. The longer time broadening of the 17 fs pulse hence allows the upper state vibration to make several oscillations (Tvib ≃ 60 fs) during the intrapulse interaction, and can thus explain the observed enhancement undulations. The overall highest value of the enhancement factors obtained can be explained by the broader spectral wavelength of the 17 fs laser pulse (≃ 865 cm−1), which in this case covers all the resonant energies of the upper states, and therefore more resonant transitions become available. The maximum enhancement obtained with positively chirped pulses for the population in the upper state is in this case ≃1.4, at = 18,800 and with φʺ = 168.5 fs2 (Figure 5f). For the coherence in the upper state the maximum enhancement is ≃3.2 at = 18,800 and for φʺ = 168.5 fs2 (Figure 5h).
5. Influence of the Laser Peak Intensity
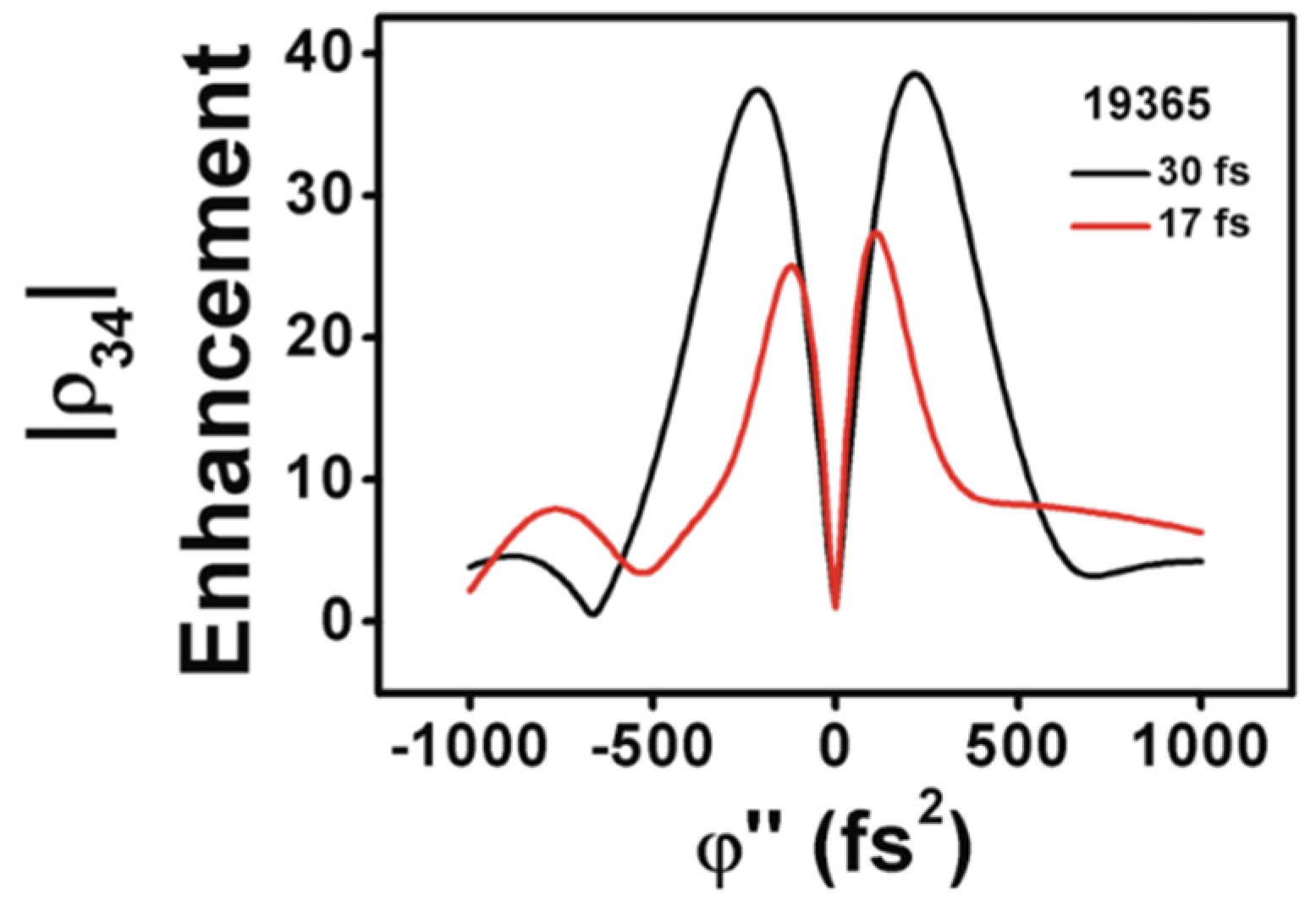
It is also worth noting that the Rabi period in the present simulations, as mentioned above, is ≃180 fs, which means that during the interaction times that we have considered (≲90 fs) the system is in the exciting half of the Rabi cycle. We have performed simulations by doubling the amplitude of the interacting pulse so that the Rabi period becomes of ≃90 fs. We would expect a response of the system to the fact that most of the interaction is produced during a whole Rabi cycle, but the results that we obtain are qualitatively the same as those described for a Rabi period of ≃180 fs. The only difference that we observe is quantitative. We obtain a higher enhancement factor of ≃3.2 for the population in ρ11 + ρ22. The maximum enhancement of |ρ12| results in ≃1.6, and for ρ33+ ρ44 is ≃2.1. Of relevance, however, is the maximum enhancement factor in |ρ34|, which becomes in this case ≃38.5. This large value is observed close to the resonance of the first vibrational upper state level, with ≃ 19,365 cm−1 and for two almost symmetric chirp values, namely φʺ ≃ −210 fs2 and φʺ ≃ 220 fs2 (see Figure 6).
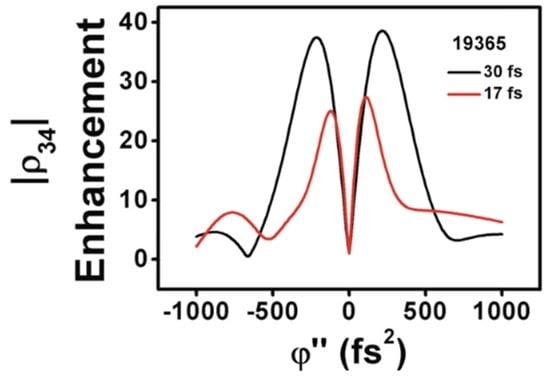
Figure 6.
Enhancement of in |ρ34| with ≃ 19,365 cm−1 and for pulse durations of 30 fs and 17 fs, as indicated.
6. Influence of the Electronic Dephasing
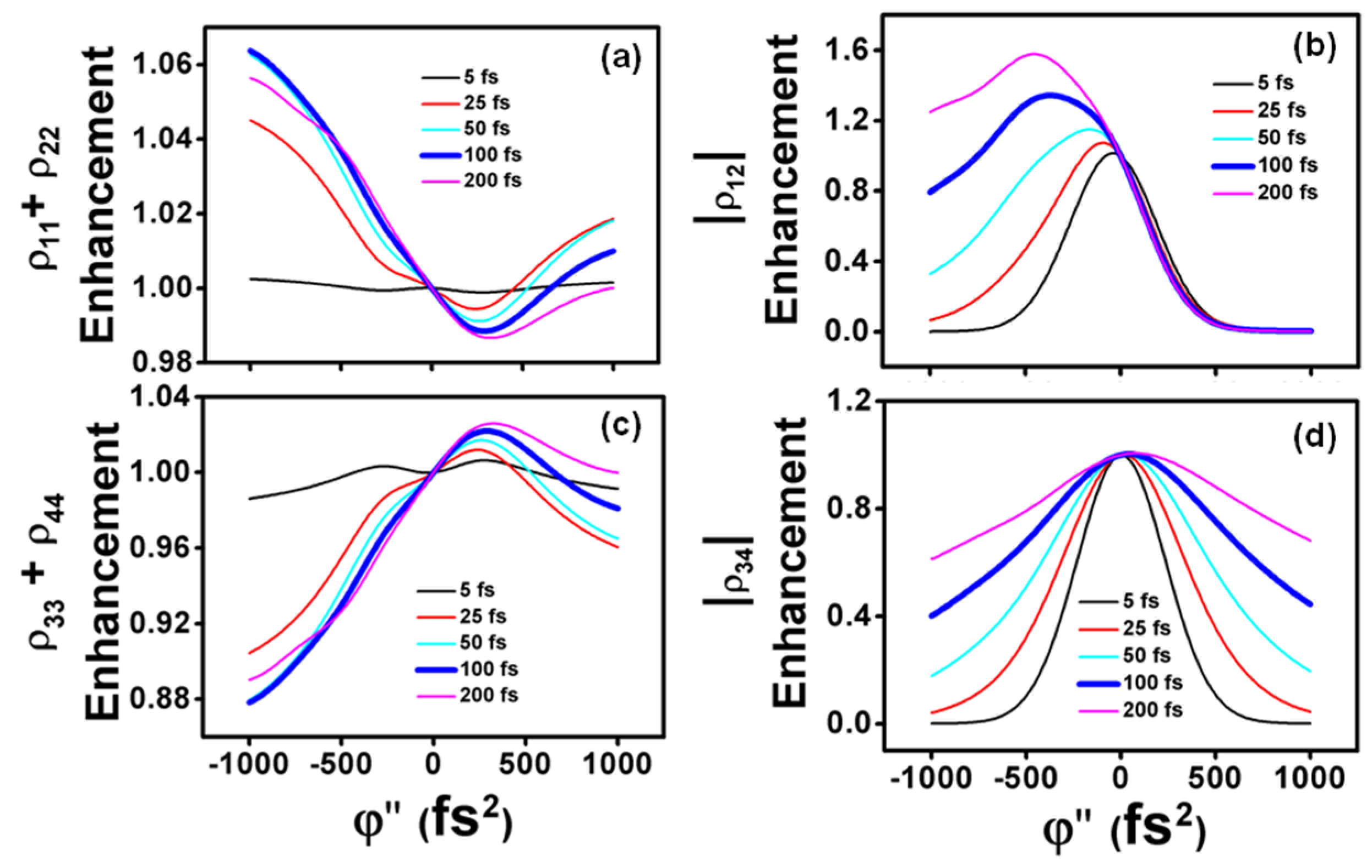
In all simulations above, the electronic dephasing (T2,elec ≡ ) was kept constant at 100 fs. The role of the electronic dephasing, however, has been already experimentally observed and theoretically discussed in several coherent control experiments of small and large molecular systems. In general, the magnitude of electronic dephasing of a given electronic transition determines how fast the induced dipole coherently oscillates after interacting with the laser electric field. In this regard, molecular systems with very fast electronic dephasing rates will be potentially less affected by, e.g., long tailored excitations than by shorter laser pulses, since the electronic coherence already dephases faster in the former case. We have considered the influence of electronic dephasing by studying the specific values T2,elec = 5 fs, 25 fs, 50 fs, 100 fs and 200 fs with a TL laser pulse of 30 fs centered at 19,700 cm−1. The case of T2,elec = 100 fs corresponds to the one considered in Figure 5 (left panels) and it is shown with thicker blue lines, both in Figure 5 and Figure 7, for a clearer comparison.
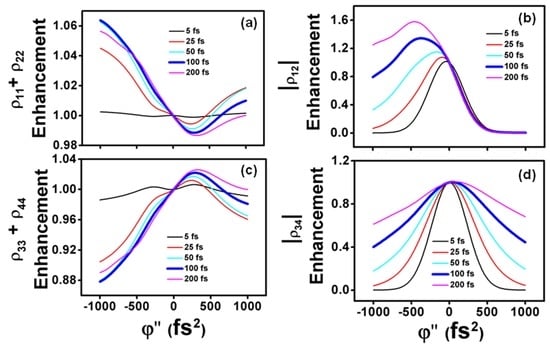
Figure 7.
Influence of electronic dephasing (T2,elec = 5 fs, 25 fs, 50 fs, 100 fs and 200 fs, as indicated) on the enhancement of (a) population in the ground state; (b) vibrational coherence in the ground state; (c) population in the upper state; and (d) vibrational coherence in the upper state, considering an excitation frequency of 19,700 cm−1. The bold blue lines show the electronic dephasing time T2,elec = 100 fs for a clearer comparison with Figure 5.
The results in Figure 7 are basically expected. They show how a faster electronic dephasing destroys the enhancement/suppression effect of the chirped pulses both in the populations of the ground and excited states (Figure 7a,c), so that for T2,elec = 5 fs no enhancement/suppression is obtained. This is clearly due to the lack of population transfer at this fast dephasing time. The vibrational coherences of the ground and upper states show a decrease in the enhancement in all cases as the dephasing times are reduced, and they also show a clear symmetric reduction for increasing positive and negative values of chirp as compared with the TL interaction (Figure 7b,d).
7. Discussion and Conclusions
The numerical calculations reported in this work produced two major results. The first one is the clear enhancement of population and vibrational coherence for near-resonant excitation obtained by using chirped laser pulses (Figure 5a,b,e,f). The enhancement of the population and the vibrational coherences in the upper and ground states differ, though, in the sign of the chirp and the direction of the detuning. While population transfer due to pump-dump processes from the ground and back to the ground states is maximized for negative chirp, when the laser is tuned near the lowest upper vibrational state (level ), enhancement of the population in the excited states is obtained both for positive and negative chirps, with a central laser wavelength slightly tuned above the upper vibrational states. The simulations show that the enhancement of the ground vibrational states is obtained by negatively chirped pulses slightly tuned above and below level , while the enhancement of the excited state vibrations is observed in a tiny region with both positive and negative small chirps and the laser slightly tuned below level .
The second major result is the absence of population enhancement in the upper states using chirped pulses, when their spectra are resonant with the transition (Figure 5e,f). Also important is the lack of any substantial change in the population enhancement with resonant chirped pulses when molecular electronic dephasing is increased to 200 fs (Figure 7c). This clearly indicates how robust this result is for a wide range of molecular systems. Perhaps even more importantly, our finding hints at why coherent control experiments of photochemical reactions in electronic excited states, which often use electronic resonant tailored excitations, have been challenging in many cases [67,68,69].
In conclusion, we have performed a numerical study on coherent control via chirped pulses in a four-level system by considering specific parameters typical of oxazine systems. We have studied in detail the influence of the detuning of the laser input pulse with respect to the electronic transitions. We have evaluated in some particular cases the effect of the duration of the laser pulse, its peak intensity, and also the influence of the electronic dephasing. We conclude that the time ordering of frequencies inside a pulse makes a fundamental difference in the population transfer and vibrational coherence generation, which can be computed with our four-level model. Intra-pulse adiabatic mechanisms explain most of the enhancement effects that we have observed. Although the results that we have presented are obtained for specific parameter values, the numerical model that we have studied is sufficiently simple to allow for an extension of our findings to other systems. An advance in the understanding of these light-matter interaction processes could open up new pathways and ideas in the field of nonlinear quantum control spectroscopy [70].
Acknowledgments
We are grateful to Tiago Buckup for careful reading of the manuscript. Support from the Spanish Ministry of Economy and Competitiveness through FIS2014-51997-R is acknowledged.
Author Contributions
Iduabo John Afa and Carles Serrat conceived and designed the simulations, and wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brixner, T.; Pfeifer, T.; Gerber, G.; Wollenhaupt, M.; Baumert, T. 2004 Progress in Lasers: Femtosecond Laser Spectroscopy; Kluwer: Dordecht, The Netherlands, 2004; Volume 9, pp. 229–271. [Google Scholar]
- Kohler, B.; Yakovlev, V.V.; Che, J.; Krause, J.L.; Messina, M.; Wilson, K.R.; Schwentner, N.; Whitnell, R.M.; Yan, Y. Quantum control of wave packet evolution with tailored femtosecond pulses. Phys. Rev. Lett. 1995. [Google Scholar] [CrossRef] [PubMed]
- Baumert, T.; Grosser, M.; Thalweiser, R.; Gerber, G. Femtosecond time-resolved molecular multiphoton ionization: The Na2 system. Phys. Rev. Lett. 1991, 67. [Google Scholar] [CrossRef] [PubMed]
- Vogt, G.; Nuernberger, P.; Brixner, T.; Gerber, G. Femtosecond pump-shaped-dump quantum control of retinal isomerization in bacteriorhodopsin. Chem. Phys. Lett. 2006, 433, 211–215. [Google Scholar] [CrossRef]
- Baumert, T.; Helbing, J.; Gerber, G. Advances in Chemical Physics-Photochemistry; Wiley: New York, NY, USA, 1997; pp. 47–77. [Google Scholar]
- Tannor, D.; Kazakov, V.; Orlov, V. Time Dependent Quantum Molecular Dynamics; Plenum: New York, NY, USA, 1992; pp. 347–360. [Google Scholar]
- Meshulach, D.; Silberberg, Y. Coherent quantum control of manipulation transitions by shaped ultrashort optical pulses. Phys. Rev. A 1999, 60. [Google Scholar] [CrossRef]
- Meshulach, D.; Silberberg, Y. Coherent quantum control of two-photon transitions by femtosecond laser pulse. Nature 1998, 396, 239–242. [Google Scholar]
- Hildner, R.; Brinks, D.; Van Hulst, N.F. Femtosecond coherence and quantum control of single molecules at room temperature. Nat. Phys. 2011, 7, 172–177. [Google Scholar] [CrossRef]
- Krüger, M.; Schenk, M.; Hommelhoff, P. Attosecond control of electrons emitted from a nanoscale metal tip. Nature 2011, 475, 78–81. [Google Scholar] [CrossRef] [PubMed]
- Herek, J.L.; Wohlleben, W.; Cogdell, R.J.; Zeidler, D.; Motzkus, M. Quantum control of energy flow in light harvesting. Nature 2002, 417, 533–535. [Google Scholar] [CrossRef] [PubMed]
- Prokhorenko, V.I.; Nagy, A.M.; Waschuk, S.A.; Brown, L.S.; Birge, R.R.; Miller, R.J.D. Coherent control of retinal isomerization in Bacteriorhodopsin. Science 2006, 313, 1257–1261. [Google Scholar] [CrossRef] [PubMed]
- Feurer, T.; Vaughan, J.C.; Nelson, K.A. Spatiotemporal coherent control of lattice vibrational waves. Science 2003, 299, 374–377. [Google Scholar] [CrossRef] [PubMed]
- Lüker, S.; Gawarecki, K.; Reiter, D.E.; Grodecka-Grad, A.; Axt, V.M.; Machnikowski, P.; Kuhn, T. Influence of acoustic phonons on the optical control of quantum dots driven by adiabatic passage. Phys. Rev. B 2012, 85. [Google Scholar] [CrossRef]
- Debnath, A.; Meier, C.; Chatel, B.; Amand, T. Chirped laser excitation of quantum dot excitons coupled to a phonon bath. Phys. Rev. B 2012, 86. [Google Scholar] [CrossRef]
- Renaud, N.; Grozema, F.C. Cooperative biexciton generation and destructive interference in coupled quantum dots uing adiabatic rapid passage. Phys. Rev. B 2014, 90. [Google Scholar] [CrossRef]
- Kuroda, D.G.; Singh, C.P.; Peng, Z.; Kleiman, V.D. Mapping excited-state dynamics by coherent control of a dendrimer’s photoemission efficiency. Science 2009, 326, 263–267. [Google Scholar] [CrossRef] [PubMed]
- Zewail, A.H. Femtochemistry: Ultrafast Dynamics of the Chemical Bond; World Sci.: New York, NJ, USA, 1994. [Google Scholar]
- Brumer, P.; Shapiro, M. Coherent Control of Molecular Dynamics; Springer: Heidelberg, Germany, 1999; pp. 191–213. [Google Scholar]
- Nuernberger, P.; Vogt, G.; Brixner, T.; Gerber, G. Femtosecond quantum control of molecular dynamics in the condensed phase. Phys. Chem. Chem. Phys. 2007, 9, 2470–2497. [Google Scholar] [CrossRef] [PubMed]
- Levine, R.D.; Jortner, J. Mode Selective Chemistry. In Proceedings of the 24th Jerusalem Symp. On Quantum Chemistry and Biochemistry, Jerusalem, Israel, 20–23 May 1991; pp. 535–571.
- Picón, A.; Biegert, J.; Jaron-Becker, A.; Becker, A. Coherent control of the vibrational state population in a nonpolar molecule. Phys. Rev. A 2011, 83. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, X.; Yan, X. Selective and efficient control of population transfer in the presence of an equally populated initial doublet. J. Opt. Soc. Am. B 2012, 29, 1551–1556. [Google Scholar] [CrossRef]
- Kumar, P.; Sarma, A.K. Ultrafast and selective coherent population transfer in four-level atoms by a single nonlinearly chirped femtosecond pulse. Phys. Rev. A 2013, 88. [Google Scholar] [CrossRef]
- Zhang, Z.; Tian, J.; Du, J. Selective population transfer and creation of an arbitrary superposition between quantum states in a Λ-type four-level system by a single linearly chirped pulse. Laser Phys. Lett. 2016, 13. [Google Scholar] [CrossRef]
- Weiner, A.M.; Leaird, D.E.; Wiederrecht, G.P.; Nelson, K.A. Femtosecond pulse sequences used for optical manipulation of molecular motion. Science 1990, 247, 1317–1319. [Google Scholar] [CrossRef] [PubMed]
- Hauer, J.; Skenderovic, H.; Kompa, K.L.; Motzkus, M. Enhancement of Raman modes by coherent control in β-carotene. Chem. Phys. Lett. 2006, 421, 523–528. [Google Scholar] [CrossRef]
- Buckup, T.; Hauer, J.; Motzkus, M. On the paradigm of coherent control: The phase-dependent light-matter interaction in the shaping window. New J. Phys. 2009, 11. [Google Scholar] [CrossRef]
- Hauer, J.; Buckup, T.; Motzkus, M. Quantum control spectroscopy of vibrational modes: Comparison of control scenarios for ground and excited states in β-carotene. Chem. Phys. 2008, 350, 220–229. [Google Scholar] [CrossRef]
- Wohllenben, W.; Buckup, T.; Herek, J.L.; Motzkus, M. Coherent control for spectroscopy and manipulation of biological dynamics. ChemPhysChem 2005, 6, 850–857. [Google Scholar] [CrossRef] [PubMed]
- Hauer, J.; Buckup, T.; Skenderovic, H.; Kompa, K.L.; Motzkus, M. Enhancement of Raman modes in complex molecules by coherent control. In Ultrafast Phenomena, X.V.; Springer: Berlin, Germany, 2007; p. 303. [Google Scholar]
- Hornung, T.; Skenderovic, H.; Motzkus, M. Observation of all-trans-β-carotene wavepacket motion on the electronic ground and excited state using degenerate four-wave mixing (DFWM) and pump-DFWM. Chem. Phys. Lett. 2005, 402, 283–288. [Google Scholar] [CrossRef]
- Kiefer, W.; Materny, A.; Schmitt, M. Femtosecond time-resolved spectroscopy of elementary molecular dynamics. Naturwissenschaften 2002, 89, 250–258. [Google Scholar] [CrossRef] [PubMed]
- Siebert, T.; Maksimenka, R.; Materny, A.; Engel, V.; Kiefer, W.; Schmitt, M. The role of specific normal modes during non-Born-Oppenheimer dynamics: The S1-S0 internal conversion of β-caroteneinterrogated on a femtosecond time-scale with coherent anti-Stokes Raman scattering. J. Ram. Spect. 2002, 33, 844–854. [Google Scholar] [CrossRef]
- Bitter, M.; Shapiro, E.A.; Milner, V. Enhancing strong-field-induced molecular vibration with femtosecond pulse shaping. Phys. Rev. A 2012, 86. [Google Scholar] [CrossRef]
- Buckup, T.; Hauer, J.; Voll, J.; Vivie-Riedle, R.; Motzkus, M. A general control mechanism of energy flow in the excited state of polyenic biochromophores. Faraday Discuss. 2011, 153, 213–225. [Google Scholar] [CrossRef] [PubMed]
- Amitay, Z.; Uberna, R.; Leone, S.R. Time-shifting the dynamics of Li2 multistate rovibrational wavepackets by state selective coherent phase control. In Proceedings of the US-Japan Workshop, Honolulu, HI, USA, 12–15 December 1999; Gordon, R.J., Fujimura, Y., Eds.; World Scientific: Singapore, Singapore, 2000; Volume 14, pp. 3–14. [Google Scholar]
- Yang, X.; Zhang, Z.; Yan, X.; Li, C. Enhanced selectivity and efficiency of coherent population transfer via train of pulse pairs. Phys. Rev. A 2010, 82. [Google Scholar] [CrossRef]
- Andrianov, I.V.; Paramonov, G.K. Selective excitation of the vibrational-rotational states and dissociation of diatomic molecules by picoseconds infrared laser pulses: Modeling for HF in the ground electronic state. Phys. Rev. A 1999, 59. [Google Scholar] [CrossRef]
- Korolkov, M.V.; Paramonov, G.K. Vibrationally state-selective electronic excitation of diatomic molecules by ultrashort laser pulses. Phys. Rev. A 1998, 57. [Google Scholar] [CrossRef]
- Savolainen, J.; Fanciulli, R.; Dijkhuizen, N.; Moore, A.L.; Hauer, J.; Buckup, T.; Motzkus, M.; Herek, J.L. Controlling the efficiency of an artificial light-harvesting complex. Proc. Natl. Acad. Sci. USA 2008, 105, 7641–7646. [Google Scholar] [CrossRef] [PubMed]
- Savolainen, J.; Buckup, T.; Hauer, J.; Jafarpour, A.; Serrat, C.; Motzkus, M.; Herek, J.L. Carotenoid deactivation in an artificial light-harvesting complex via a vibrationally hot ground state. Chem. Phys. 2009, 357, 181–187. [Google Scholar] [CrossRef]
- Buckup, T.; Lebold, T.; Weigel, A.; Wohlleben, W.; Motzkus, M. Singlet versus triplet dynamics of β-carotene studied by quantum control spectroscopy. J. Photochem. Photobiol. A 2006, 180, 314–321. [Google Scholar] [CrossRef]
- Buckup, T.; Hauer, J.; Möhring, J.; Motzkus, M. Multidimensional spectroscopy of β-carotene: Vibrational cooling in the excited state. Arch. Biochem. Biophys. 2009, 483, 219–223. [Google Scholar] [CrossRef] [PubMed]
- Buckup, T.; Lebold, T.; Weigel, A.; Wohlleben, W.; Motzkus, M. Multiphoton Quantum-control spectroscopy of β-carotene. In Ultrafast Phenomena, X.V.; Springer: Berlin, Germany, 2007; p. 483. [Google Scholar]
- Buckup, T.; Savolainen, J.; Wohlleben, W.; Herek, J.L.; Hashimoto, H.; Correia, R.R.B.; Motzkus, M. Pump-probe and pump-deplete-probe spectroscopies on carotenoids with N = 9–15 conjugated bonds. J. Chem. Phys. 2006, 125. [Google Scholar] [CrossRef] [PubMed]
- Buckup, T.; Wohlleben, W.; Heinz, B.; Savolainen, J.; Herek, J.L.; Hashimoto, H.; Cogdell, R.J.; Motzkus, M. Energy flow in carotenoids, studied with pump-deplete-probe, multiphoton- and coherent control spectroscopy. In Ultrafast Phenomena XIV; Springer: Berlin, Germany, 2005; p. 368. [Google Scholar]
- Consani, C.; Ruetzel, S.; Nuernberger, P.; Brixner, T. Quantum control spectroscopy of competing reaction pathways in a molecular switch. J. Phys. Chem. A 2014, 118, 11364–11372. [Google Scholar] [CrossRef] [PubMed]
- Wohlleben, W.; Buckup, T.; Hashimoto, H.; Cogdell, R.J.; Herek, J.L.; Motzkus, M. Pump-deplete-probe spectroscopy and the puzzle of carotenoid dark states. J. Phys. Chem. B 2004, 108, 3320–3325. [Google Scholar] [CrossRef]
- Kraack, J.P.; Motzkus, M.; Buckup, T. Selective nonlinear response preparation using femtosecond spectrally resolved four-wave-mixing. J. Chem. Phys. 2011, 135. [Google Scholar] [CrossRef]
- Nuernberger, P.; Ruetzel, S.; Brixner, T. Multidimensional electronic spectroscopy of photochemical reactions. Angew. Chem. Int. Ed. Engl. 2015, 54, 11368–11385. [Google Scholar] [CrossRef] [PubMed]
- Ruetzel, S.; Diekmann, M.; Nuernberger, P.; Walter, C.; Engels, B.; Brixner, T. Multidimensional spectroscopy of photoreactivity. Proc. Natl. Acad. Sci. USA 2014, 111, 4764–4769. [Google Scholar] [CrossRef] [PubMed]
- Meshulach, D.; Yelin, D.; Silberberg, Y. Adaptive real-time femtosecond pulse shaping. J. Opt. Soc. Am. B 1998, 15, 1615–1619. [Google Scholar] [CrossRef]
- Yelin, D.; Meshulach, D.; Silberberg, Y. Adaptive femtosecond pulse compression. Opt. Lett. 1997, 22, 1793–1795. [Google Scholar] [CrossRef] [PubMed]
- Feist, A.; Echternkamp, K.E.; Schauss, J.; Yalunin, S.V.; Schafer, S.; Ropers, C. Quantum coherent optical phase modulation in an ultrafast transmission electron microscope. Nature 2015, 521, 200–203. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.J.; Mukamel, S. Electronic dephasing, vibrational relaxation, and solvent friction in molecular nonlinear optical line shapes. J. Chem. Phys. 1988, 89. [Google Scholar] [CrossRef]
- Joo, T.; Albrecht, A.C. Electronic dephasing studies of molecules in solution at room temperature by femtosecond degenerate four wave mixing. Chem. Phys. 1993, 176, 233–247. [Google Scholar] [CrossRef]
- Nibbering, E.T.J.; Duppen, K.; Wiersma, D.A. Optical dephasing in solution: A line shape and resonance light scattering study of azulene in isopentane and cyclohexane. J. Chem. Phys. 1990, 93. [Google Scholar] [CrossRef]
- Wand, A.; Kallush, S.; Shoshanim, O.; Bismuth, O.; Kosloff, R.; Ruhman, S. Chirp effects on impulsive vibrational spectroscopy: A multimode perspective. Phys. Chem. Chem. Phys. 2010, 12, 2149–2163. [Google Scholar] [CrossRef] [PubMed]
- Malkmus, S.; Dürr, R.; Sobotta, C.; Pulvermacher, H.; Zinth, W.; Braun, M. Chirp dependence of wave packet motion in Oxazine 1. J. Phys. Chem. A 2005, 109, 10488–10492. [Google Scholar] [CrossRef] [PubMed]
- Ruhman, S.; Kosloff, R. Application of chirped ultrashort pulses for generating large-amplitude ground-state vibrational coherence: A computer simulation. J. Opt. Soc. Am. B 1990, 7, 1748–1752. [Google Scholar] [CrossRef]
- Bardeen, C.J.; Wang, Q.; Shank, C.V. Selective excitation of vibrational wave packet motion using chirped pulses. Phys. Rev. Lett. 1995, 75. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Bardeen, C.J.; Wilson, K.R. Molecular π-pulse for total inversion of electronic state population. Phys. Rev. Lett. 1998, 80. [Google Scholar] [CrossRef]
- Konar, A.; Lozovoy, V.V.; Dantus, M. Solvent environment revealed by positively chirped pulses. J. Phys. Chem. Lett. 2014, 5, 924–928. [Google Scholar] [CrossRef] [PubMed]
- Serrat, C.; Corbera, M.; Afa, J. Trichromatic π-Pulse for Ultrafast Total Inversion of a Four-Level Ladder System. Appl. Sci. 2015, 5, 1484–1493. [Google Scholar] [CrossRef]
- Diels, J.C.; Rudolph, W. Ultrashort Laser Pulse Phenomena, 2nd ed.; Academic Press: San Diego, CA, USA, 2006. [Google Scholar]
- Möhring, J.; Buckup, T.; Motzkus, M. A Quantum control spectroscopy approach by direct UV femtosecond pulse shaping. IEEE J. Sel. Top. Quant. Electron. 2012, 18, 449–459. [Google Scholar] [CrossRef]
- Florean, A.C.; Cardoza, D.; White, J.L.; Lanyi, J.K.; Sension, R.J.; Bucksbaum, P.H. Control of retinal isomerization in bacteriorhodopsin in the high-intensity regime. Proc. Natl. Acad. Sci. USA 2009, 106, 10896–10900. [Google Scholar] [CrossRef] [PubMed]
- Carroll, E.C.; Florean, A.C.; Bucksbaum, P.H.; Spears, K.G.; Sension, R.J. Phase control of the competition between electronic transitions in a solvated laser dye. Chem. Phys. 2008, 350, 75–86. [Google Scholar] [CrossRef]
- Buckup, T.; Hauer, J.; Serrat, C.; Motzkus, M. Control of excited-state population and vibrational coherence with shaped-resonant and near-resonant excitation. J. Phys. B At. Mol. Opt. Phys. 2008, 41. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).