A Simple Method for the Evaluation of the Pulse Width of an Ultraviolet Femtosecond Laser Used in Two-Photon Ionization Mass Spectrometry
Abstract
:1. Introduction
2. Theoretical Calculations
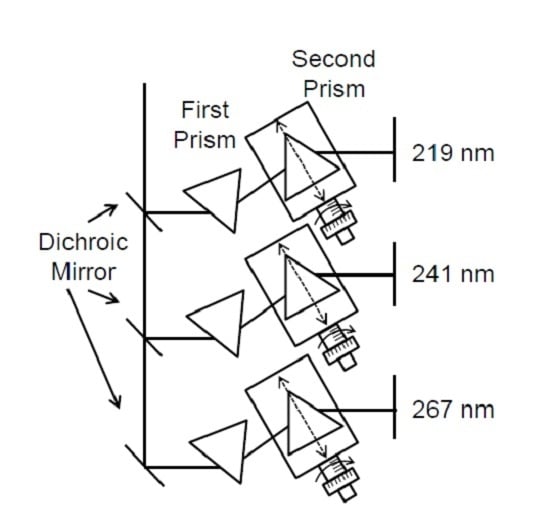
3. Experimental
4. Results and Discussion
4.1. Calculations
4.2. Puse Width Evaluation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Imasaka, T. Gas chromatography/multiphoton ionization/time-of-flight mass spectrometry using a femtosecond laser. Anal. Bioanal. Chem. 2013, 405, 6907–6912. [Google Scholar] [CrossRef] [PubMed]
- Trebino, R. Frequency-Resolved Optical Gating: The Measurement of Ultrashort Laser Pulses; Kluwer Academic Publishers: Boston, MA, USA, 2002. [Google Scholar]
- Chadwick, R.; Spahr, E.; Squier, J.A.; Durfee, C.G.; Walker, B.C.; Fittinghoff, D.R. Fringe-free, background-free, collinear third-harmonic generation frequency-resolved optical gating measurements for multiphoton microscopy. Opt. Lett. 2006, 31, 3366–3368. [Google Scholar] [CrossRef] [PubMed]
- Meshulach, D.; Barad, Y.; Silberberg, Y. Measurement of ultrashort optical pulses by third-harmonic generation. J. Opt. Soc. Am. B 1997, 14, 2122–2125. [Google Scholar] [CrossRef]
- Nomura, Y.; Shirai, H.; Ishii, K.; Tsurumachi, N.; Voronin, A.A.; Zheltikov, A.M.; Fuji, T. Phase-stable sub-cycle mid-infrared conical emission from filamentation in gases. Opt. Express 2012, 20, 24741–24747. [Google Scholar] [CrossRef] [PubMed]
- Shverdin, M.Y.; Walker, D.R.; Yavuz, D.D.; Yin, G.Y.; Harris, S.E. Generation of a single-cycle optical pulse. Phys. Rev. Lett. 2005, 94, 033904. [Google Scholar] [CrossRef] [PubMed]
- Tzankov, P.; Steinkellner, O.; Zheng, J.; Mero, M.; Freyer, W.; Husakou, A.; Babushkin, I.; Herrmann, J.; Noack, F. High-power fifth-harmonic generation of femtosecond pulses in the vacuum ultraviolet using a Ti:sapphire laser. Opt. Expess 2007, 15, 6389–6395. [Google Scholar] [CrossRef]
- Homann, C.; Lang, P.; Riedle, E. Generation of 30 fs pulses tunable from 189 to 240 nm with an all-solid-state setup. J. Opt. Soc. Am. B 2012, 29, 2765–2769. [Google Scholar] [CrossRef]
- Zuo, P.; Fuji, T.; Horio, T.; Adachi, S.; Suzuki, T. Simultaneous generation of ultrashort pulses at 158 and 198 nm in a single filamentation cell by cascaded four-wave mixing in Ar. Appl. Phys. B 2012, 108, 815–819. [Google Scholar] [CrossRef]
- Mero, M.; Zheng, J. Femtosecond optical parametric converter in the 168–182-nm range. Appl. Phys. B 2012, 106, 37–43. [Google Scholar] [CrossRef]
- Trushin, S.A.; Fuss, W.; Kosma, K.; Schmid, W.E. Widely tunable ultraviolet sub-30-fs pulses from supercontinuum for transient spectroscopy. Appl. Phys. B 2006, 85, 1–5. [Google Scholar] [CrossRef]
- Trushin, S.A.; Kosma, K.; Fuß, W.; Schmid, W.E. Sub- 10-fs supercontinuum radiation generated by filamentation of few-cycle 800 nm pulses in argon. Opt. Lett. 2007, 32, 2432–2434. [Google Scholar] [CrossRef] [PubMed]
- Kosma, K.; Trushin, S.A.; Schmid, W.E.; Fuß, W. Vacuum ultraviolet pulses of 11 fs from fifth-harmonic generation of a Ti:sapphire laser. Opt. Lett. 2008, 33, 723–725. [Google Scholar] [CrossRef] [PubMed]
- Beutler, M.; Ghotbi, M.; Noack, F. Generation of intense sub-20-fs vacuum ultraviolet pulses compressed by material dispersion. Opt. Lett. 2011, 36, 3726–3728. [Google Scholar] [CrossRef] [PubMed]
- Ghotbi, M.; Trabs, P.; Beutler, M.; Noack, F. Generation of tunable sub-45 femtosecond pulses by noncollinear four-wave mixing. Opt. Lett. 2013, 38, 486–488. [Google Scholar] [CrossRef] [PubMed]
- Wirth, A.; Hassan, M.T.; Grguraš, I.; Gagnon, J.; Moulet, A.; Luu, T.T.; Pabst, S.; Santra, R.; Alahmed, Z.A.; Azzeer, A.M.; et al. Synthesized light transients. Science 2011, 334, 195–200. [Google Scholar] [CrossRef] [PubMed]
- Mairesse, Y.; Quéré, F. Frequency-resolved optical gating for complete reconstruction of attosecond bursts. Phys. Rev. A 2005, 71, 011401. [Google Scholar] [CrossRef]
- Zaitsu, S.; Miyoshi, Y.; Kira, F.; Yamaguchi, S.; Uchimura, T.; Imasaka, T. Interferometric characterization of ultrashort deep ultraviolet pulses using a multiphoton ionization mass spectrometer. Opt. Lett. 2007, 32, 1716–1718. [Google Scholar] [CrossRef] [PubMed]
- Imasaka, T.; Imasaka, T. Searching for a molecule with a wide frequency domain for non-resonant two-photon ionization to measure the ultrashort optical pulse width. Opt. Commun. 2012, 285, 3514–3518. [Google Scholar] [CrossRef]
- Okuno, T.; Imasaka, T.; Kida, Y.; Imasaka, T. Autocorrelator for measuring an ultrashort optical pulse width in the ultraviolet region based on two-photon ionization of an organic compound. Opt. Commun. 2014, 310, 48–52. [Google Scholar] [CrossRef]
- Imasaka, T.; Okuno, T.; Imasaka, T. The search for a molecule to measure an autocorrelation trace of the second/third harmonic emission of a Ti:sapphire laser based on two-photon resonant excitation and subsequent one-photon ionization. Appl. Phys. B 2013, 113, 543–549. [Google Scholar] [CrossRef]
- Hamachi, A.; Okuno, T.; Imasaka, T.; Kida, Y.; Imasaka, T. Resonant and nonresonant multiphoton ionization processes in the mass spectrometry of explosives. Anal. Chem. 2015, 87, 3027–3031. [Google Scholar] [CrossRef] [PubMed]
- Lozovoy, V.V.; Pastirk, I.; Dantus, M. Multiphoton intrapulse interference. IV. Ultrashort laser pulse spectral phase characterization and compensation. Opt. Lett. 2004, 29, 775–777. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Gunn, J.M.; Dela Cruz, J.M.; Lozovoy, V.V.; Dantus, M. Quantitative investigation of the multiphoton intrapulse interference phase scan method for simultaneous phase measurement and compensation of femtosecond laser pulses. J. Opt. Soc. Am. B 2006, 23, 750–759. [Google Scholar] [CrossRef]
- Coello, Y.; Lozovoy, V.V.; Gunaratne, T.C.; Xu, B.; Borukhovich, I.; Tseng, C.-H.; Weinacht, T.; Dantus, M. Interference without an interferometer: A different approach to measuring, compressing, and shaping ultrashort laser pulses. J. Opt. Soc. Am. B 2008, 25, A140–A150. [Google Scholar] [CrossRef]
- Lozovoy, V.V.; Xu, B.; Coello, Y.; Dantus, M. Direct measurement of spectral phase for ultrashort laser pulses. Opt. Express 2008, 16, 592–597. [Google Scholar] [CrossRef] [PubMed]
- Miranda, M.; Fordell, T.; Arnold, C.; L’Huillier, A.; Crespo, H. Simultaneous compression and characterization of ultrashort laser pulses using chirped mirrors and glass wedges. Opt. Express 2012, 20, 688–697. [Google Scholar] [CrossRef] [PubMed]
- Miranda, M.; Arnold, C.L.; Fordell, T.; Silva, F.; Alonso, B.; Weigand, R.; L’Huillier, A.; Crespo, H. Characterization of broadband few-cycle laser pulses with the d-scan technique. Opt. Express 2012, 20, 18732–18743. [Google Scholar] [CrossRef] [PubMed]
- Loriot, V.; Gitzinger, G.; Forget, N. Self-referenced characterization of femtosecond laser pulses by chirp scan. Opt. Expess 2013, 21, 24879–24893. [Google Scholar] [CrossRef] [PubMed]
- Sellmeier, W. Theory of anomalous light dispersion. Ann. Phys. Chem. 1871, 143, 271. [Google Scholar]
- Malitson, I.H. Interspecimen comparison of refractive index of fused silica. J. Opt. Soc. Am. 1965, 55, 1205–1209. [Google Scholar] [CrossRef]
- Rasskazov, G.; Lozovoy, V.V.; Dantus, M. Spectral amplitude and phase noise characterization of titanium-sapphire lasers. Opt. Express 2015, 23, 23597–23602. [Google Scholar] [CrossRef] [PubMed]




© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Imasaka, T.; Hamachi, A.; Okuno, T.; Imasaka, T. A Simple Method for the Evaluation of the Pulse Width of an Ultraviolet Femtosecond Laser Used in Two-Photon Ionization Mass Spectrometry. Appl. Sci. 2016, 6, 136. https://doi.org/10.3390/app6050136
Imasaka T, Hamachi A, Okuno T, Imasaka T. A Simple Method for the Evaluation of the Pulse Width of an Ultraviolet Femtosecond Laser Used in Two-Photon Ionization Mass Spectrometry. Applied Sciences. 2016; 6(5):136. https://doi.org/10.3390/app6050136
Chicago/Turabian StyleImasaka, Tomoko, Akifumi Hamachi, Tomoya Okuno, and Totaro Imasaka. 2016. "A Simple Method for the Evaluation of the Pulse Width of an Ultraviolet Femtosecond Laser Used in Two-Photon Ionization Mass Spectrometry" Applied Sciences 6, no. 5: 136. https://doi.org/10.3390/app6050136
APA StyleImasaka, T., Hamachi, A., Okuno, T., & Imasaka, T. (2016). A Simple Method for the Evaluation of the Pulse Width of an Ultraviolet Femtosecond Laser Used in Two-Photon Ionization Mass Spectrometry. Applied Sciences, 6(5), 136. https://doi.org/10.3390/app6050136