Abstract
In this paper, we propose a method called temporal correlation support vector machine (TCSVM) for automatic major-minor chord recognition in audio music. We first use robust principal component analysis to separate the singing voice from the music to reduce the influence of the singing voice and consider the temporal correlations of the chord features. Using robust principal component analysis, we expect the low-rank component of the spectrogram matrix to contain the musical accompaniment and the sparse component to contain the vocal signals. Then, we extract a new logarithmic pitch class profile (LPCP) feature called enhanced LPCP from the low-rank part. To exploit the temporal correlation among the LPCP features of chords, we propose an improved support vector machine algorithm called TCSVM. We perform this study using the MIREX’09 (Music Information Retrieval Evaluation eXchange) Audio Chord Estimation dataset. Furthermore, we conduct comprehensive experiments using different pitch class profile feature vectors to examine the performance of TCSVM. The results of our method are comparable to the state-of-the-art methods that entered the MIREX in 2013 and 2014 for the MIREX’09 Audio Chord Estimation task dataset.
1. Introduction
A musical chord can be defined as a set of notes played simultaneously. A succession of chords over time forms the harmony core in a piece of music. Hence, the compact representation of the overall harmonic content and structure of a song often requires labeling every chord in the song. Chord recognition has been applied in many applications such as the segmentation of pieces into characteristic segments, the selection of similar pieces, and the semantic analysis of music [1,2]. With its many applications, automatic chord recognition has been one of the main fields of interest in musical information retrieval in the last few years.
The basic chord recognition system has two main steps: feature extraction and chord classification. In the first step, the features used in chord recognition are typically variants of the pitch class profile (PCP) introduced by Fujishima (1999) [1]. Many publications have improved PCP features for chord recognition by addressing potentially negative influences such as percussion [2], mistuning [3,4], harmonics [5,6,7], or timbre dependency [5,8]. In particular, harmonic contents are abundant in both musical instrument sounds and the human singing voice. However, harmonic patterns in instrument sounds are more regular compared with the singing voice, which often includes ornamental features such as vibrato that lead to significant deviations of the frequency of partials from perfectly harmonic [9]. To attenuate the effect of the singing voice and consider the temporal correlations of music, we separate the singing voice from the accompaniment before obtaining the PCP.
Chord classification is computed once the feature has been extracted. Modeling techniques typically use template-fitting methods [1,3,10,11,12,13], the hidden Markov model (HMM) [14,15,16,17,18,19,20], and dynamic Bayesian networks [21,22] for this recognition process. The template-based method has some advantages, including the fact that it does not require annotated data and has a low computational time. However, its drawbacks include the problem of creating a model of templates of chroma vectors and the selection of a distance measure. The HMM method is a statistical model and its parameter estimation requires substantial training data. The recognition rate of the HMM method is typically relatively high, but it only considers the role of positive training samples without addressing the impact of negative training samples, thereby greatly limiting its discriminative ability. The support vector machine (SVM) method can achieve a high recognition rate, but encounters challenges in the presence of cross-aliasing that cannot be accurately judged. The main difference between HMM and SVM is in the principle of risk minimization [23]. HMM uses empirical risk minimization, which is the simplest induction principle. In contrast, SVM uses structural risk minimization as its induction principle. The difference in risk minimization leads to the better generalization performance of SVM compared with HMM [24]. We present a new method for chord estimation based on a hybrid model of HMM and SVM.
The remainder of this paper is organized as follows: Section 2 reviews related chord estimation work; Section 3 describes our PCP feature vector construction method; Section 4 explains our approach; Section 5 displays the results on the MIREX’09 (Music Information Retrieval Evaluation eXchange) dataset and a provides a comparison with other methods; and Section 6 concludes our work and suggests directions for future work.
2. Related Work
PCP is also called the chroma vector, which is often a 12-dimensional vector whereby each component represents the spectral energy or salience of a semi-tone on the chromatic scale regardless of the octave. The computation of the chroma representation of an audio recording is typically based either on the short-time Fourier transform (STFT) in combination with binning strategies [18,25,26,27] or on the constant Q transform [3,6,15,28,29]. The succession of these chroma vectors over time is often called the chromagram and this forms a suitable representation of the musical content of a piece.
Many features have been used for chord recognition including non-negative least squares [30], chroma DCT (Discrete Cosine Transform)-reduced log pitch (CRP) [31], loudness-based chromagram (LBC) [22], and Mel PCP (MPCP) [32]. In [1], Fujishima developed a real-time chord recognition system using a 12-dimensional pitch class profile derived from the discrete Fourier transform (DFT) of the audio signal, and performed pattern matching using binary chord-type templates. Lee [6] introduced a new input feature called the enhanced pitch class profile (EPCP) using the harmonic product spectrum. Gómez and Herrera [33] used harmonic pitch class profile (HPCP) as the feature vector, which is based on Fujishima’s PCP, and correlated it with a chord or key model adapted from Krumhansl’s cognitive study.
Variants of the pitch class profile (PCP) first introduced by Fujishima (1999) [1] address the potentially negative influences of percussion [2], mistuning [3,4], harmonics [5,6,7] or timbre dependency [5,8]. In addition to these factors, we explore ways to attenuate the influence of the singing voice. Weil introduced an additional pre-processing step for main melody attenuation [34]. To attenuate the negative influence of singing voices, we consider the amplitude similarity of neighborhood musical frames belonging to the same chord and obtain the enhanced PCP. Adding a pre-processing step consisting of robust principal component analysis (RPCA), we expect the low-rank matrix to contain the musical accompaniment and the sparse matrix to contain the vocal signals. Then, the low-rank matrix can be used to calculate the features. The pre-processing considers the temporal correlations of music.
The two most popular chord estimation methods are the template-based model and the hidden Markov model. For the audio chord estimation task of MIREX 2013 and 2014, one of the most popular methods is HMM [35,36,37,38,39,40,41]. A binary chord template with three harmonics was also presented [42].
Template-based chord recognition methods use the chord definition to extract chord labels from a musical piece. Neither training data nor extensive music theory knowledge is used for this purpose [43]. To smooth the resulting representation and exploit the temporal correlation, low-pass and median filters are used to filter the chromagram in the time domain [10]. The template-based method only outputs fragmented transcriptions without considering the temporal correlations of music.
The HMM can model sequences of events in a temporal grid considering hidden and visible variables. In the case of chord recognition, the hidden states correspond to the real chords that are being played, while the observations are the chroma vectors. In [35], Cho and Bello use a K-stream HMM which is then decoded using the standard Viterbi algorithm. Khadkevich and Omologo also use a multi-stream HMM, but the feature is a time-frequency reassignment spectrogram [36]. Steenbergen and Burgoyne present a chord estimation method based on the combination of a neural network and an HMM [40]. In [39], the probabilities of the HMM are not trained through expectation-maximization (EM) or any other machine learning technique, but are instead derived from a number of knowledge-based sub-models. Ni and McVicar proposed a harmony progression HMM topology that consists of three hidden and two observed variables [37]. The hidden variables correspond to the key K, the chord C, and the bass annotations B. These methods usually require a reference dataset for the learning period and entail more parameters to be trained.
In contrast, our method has only one parameter trained from the reference dataset, which is the state transition probability, and the other parameters are obtained from the SVM. The hybrid HMM and SVM model uses the respective advantages of these methods. Our novel method is called the temporal correlation support vector machine (TCSVM).
Our system is composed of two main steps: feature extraction and chord classification, as shown in Figure 1. We pre-process the audio to separate the singing voice. The system then tracks beat intervals in the music and extracts a set of vectors for the PCP. In the chord classification step, our method uses SVM classification and the Viterbi algorithm. Because we employ the temporal correlation of chords, the system can combine the SVM with the Viterbi algorithm, leading to a TCSVM. The Viterbi algorithm uses the transitions between chords to estimate the chords.

Figure 1.
Chord estimation system.
3. Enhanced PCP Feature
3.1. Normalized Logarithmic PCP Feature
Our system begins by extracting suitable feature vectors from the raw audio. Like most chord recognition systems, we use a chromagram or a PCP vector as the feature vector. Müller and Ewert propose a 12-dimensional feature vector–quantized PCP [8,29] that determines the proper frequency resolution and is sufficient for separating musical notes by low-frequency components.
The calculation of PCP feature vectors can be divided into the following steps: (1) using the constant Q transform to calculate the 36-bin chromagram; (2) mapping the spectral chromagram to a particular semitone; (3) median filtering; (4) segmenting the audio signal with a beat-tracking algorithm; (5) reducing the 36-bin chromagram to a 12-bin chromagram based on beat-synchronous segmentation; (6) normalizing the 12-bin chromagram. The reader is referred to [15] for more detailed PCP calculation steps.
In the beat-synchronous (tactus) segmentation, we use the beat-tracking algorithm proposed by Ellis [44]. This method has proven successful for a wide variety of signals. Using beat-synchronous segments has the added advantage that the resulting representation is a function of the beat, or tactus, rather than time.
Unlike most of the traditional PCP methods, we determine the normalized value using the p-norm and logarithm. The formula is as follows:
After applying the logarithm and normalization, the chromagram is called the LPCP.
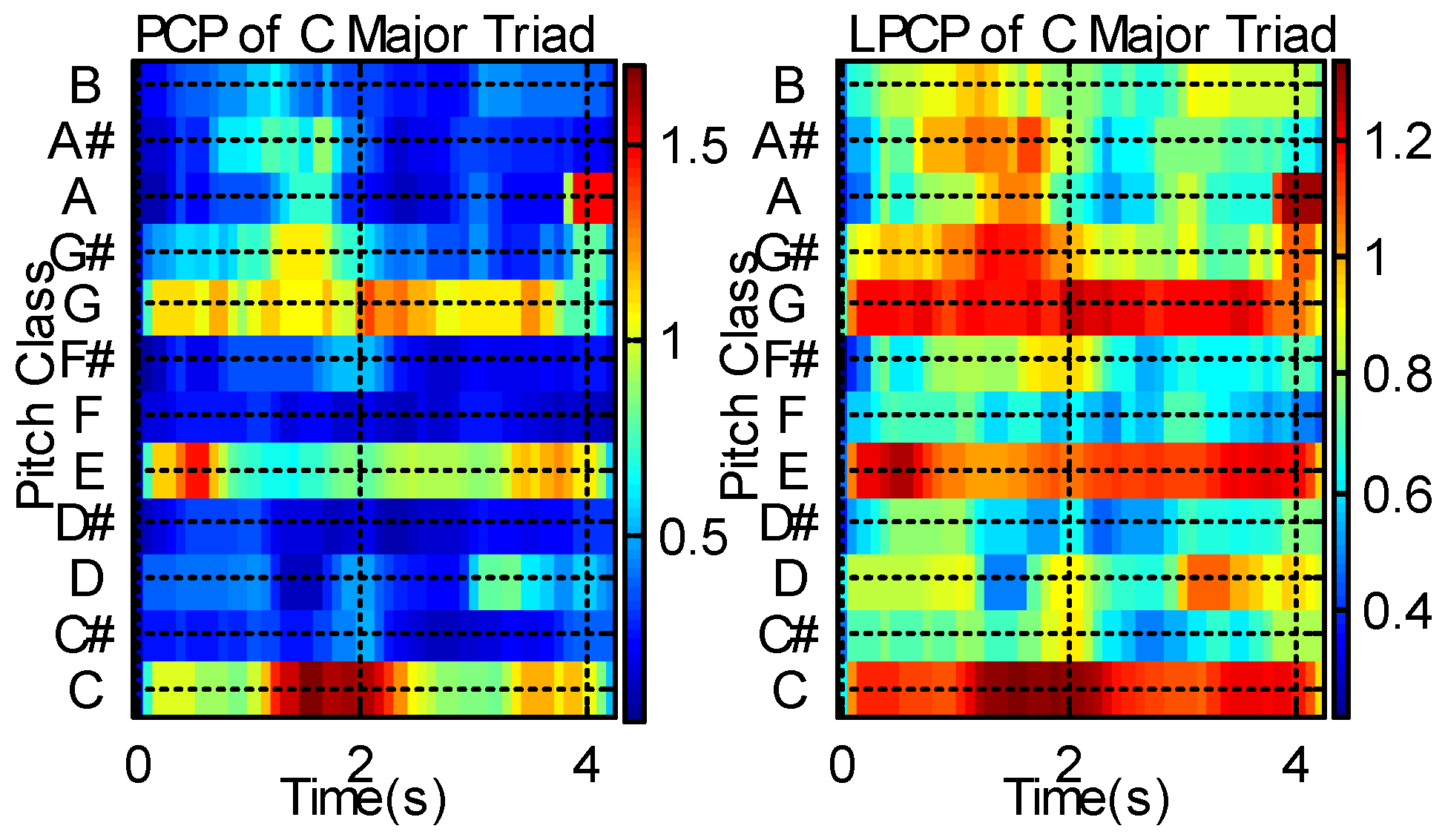
The left image of Figure 2 shows a PCP of the C major triad and the right image shows its LPCP. The strongest peaks are found at C, E, and G because the C major triad comprises three notes at C (root), E (third), and G (fifth). Figure 2 demonstrates that LPCP more clearly approximates the underlying fundamental frequencies than PCP.
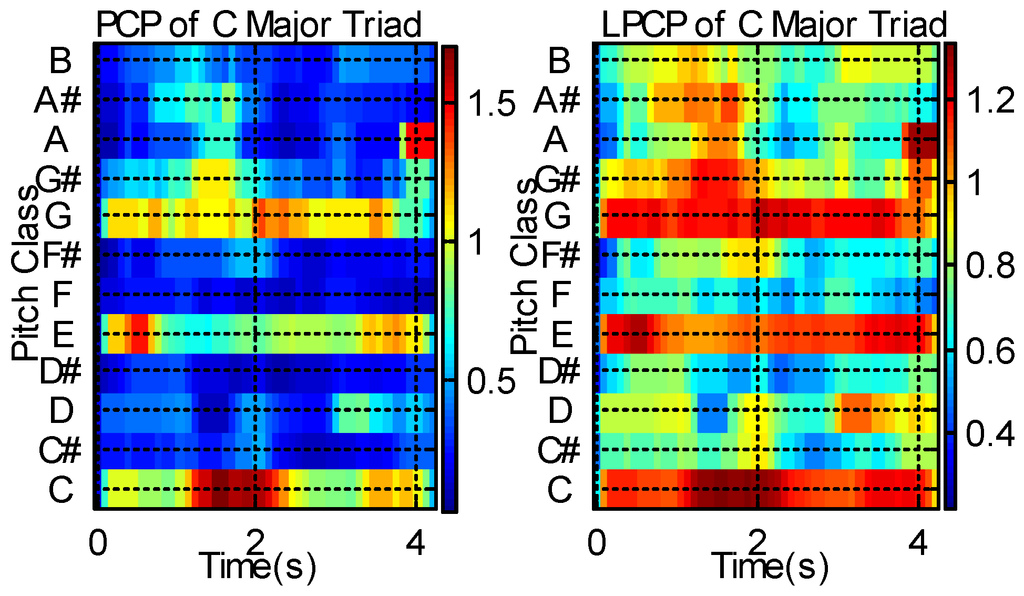
Figure 2.
PCP (pitch class profile) (left) and LPCP (logarithmic pitch class profile) (right) of C major triad.
3.2. Enhanced PCP with Singing-Voice Separation
To attenuate the effect of the singing voice and consider the temporal correlations of the chord, we first separate the singing voice from the accompaniment before calculating the PCP or LPCP. This is denoted as enhanced PCP (EPCP) or enhanced logarithmic PCP (ELPCP). The framework of singing voice separation is shown in Figure 3.

Figure 3.
Calculation of enhanced PCP (EPCP).
In general, because of the underlying repeated musical structure, we assume that music is a low-rank signal. Singing voices offer more variation and have a higher rank but are relatively sparse in the frequency domain. We assume that the low-rank matrix A represents the music accompaniment and the sparse matrix E represents the vocal signals [45]. Then, we perform the separation in two steps. First, we compute the spectrogram of music signals in matrix D, which is calculated from the STFT. Second, we use the inexact augmented Lagrange multiplier (ALM) method [45], which is an efficient algorithm for solving the RPCA problem, to solve A + E = |D|, given the input magnitude of D. Then, using RPCA, we can separate matrices A and E. The low-rank matrix A can be exactly recovered from D = A + E by solving the following convex optimization problem:
where is a positive weighting parameter. The inexact ALM method is as follows [45]:
| Algorithm 1: Inexact ALM Algorithm |
| Input: matrix , parameter |
| 1: . |
| 2: while not converged do |
| 3: // lines 4–5 solve . |
| 4: ; |
| 5: . |
| 6: // line 7 solves . |
| 7: . |
| 8: . |
| 9: . |
| 10: . |
| 11: end while |
| Output: (). |
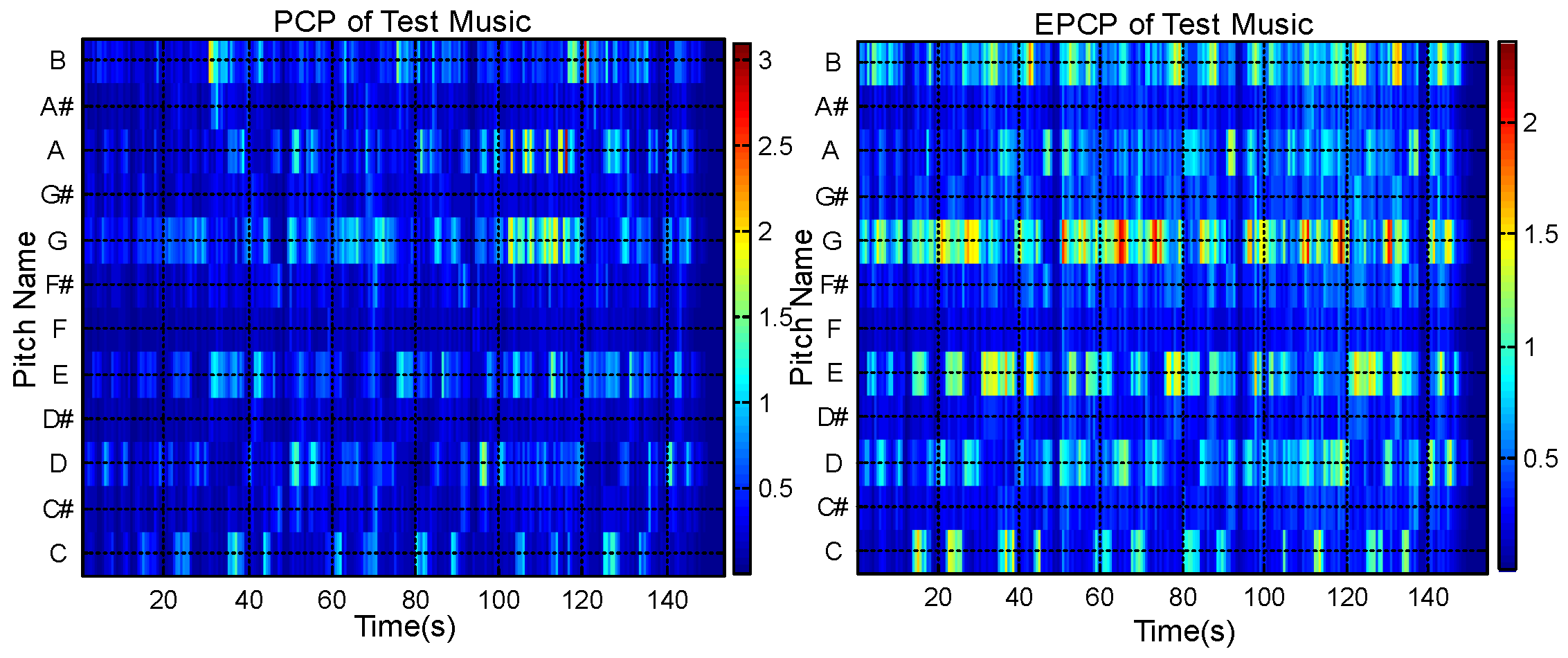
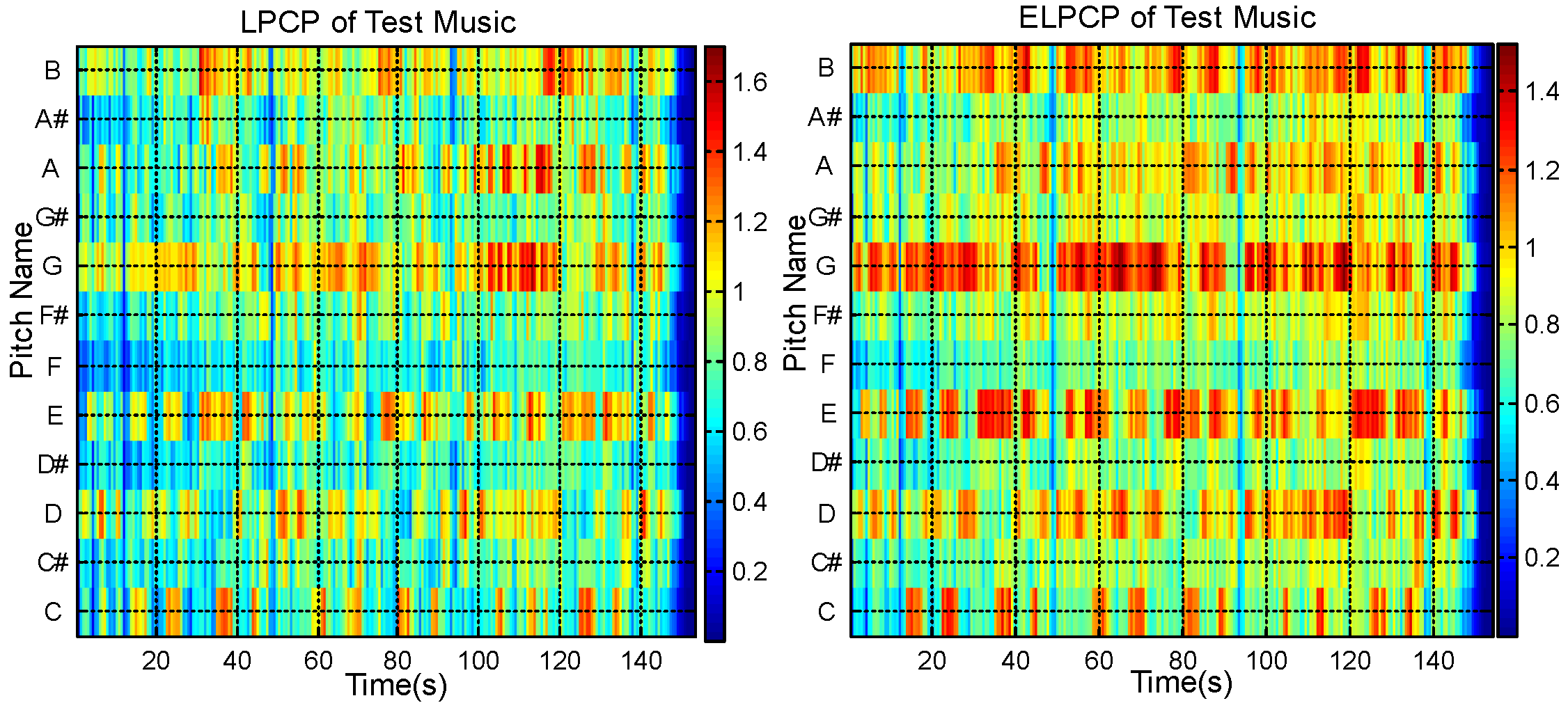
Figure 4 shows the PCP and EPCP of an audio music piece (the music is “Baby It’s You”, from the Beatles’ album Please Please Me). Figure 5 shows the LPCP and ELPCP of the same musical piece.
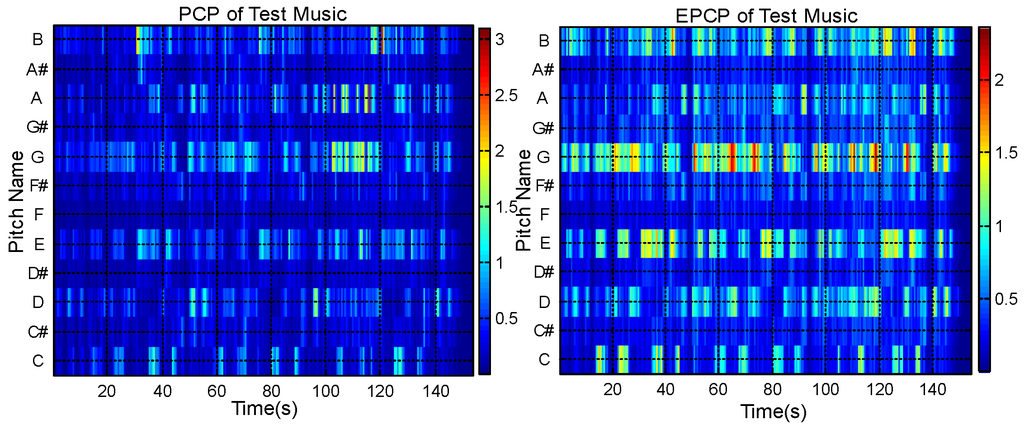
Figure 4.
PCP (left) and EPCP (right) of test music.
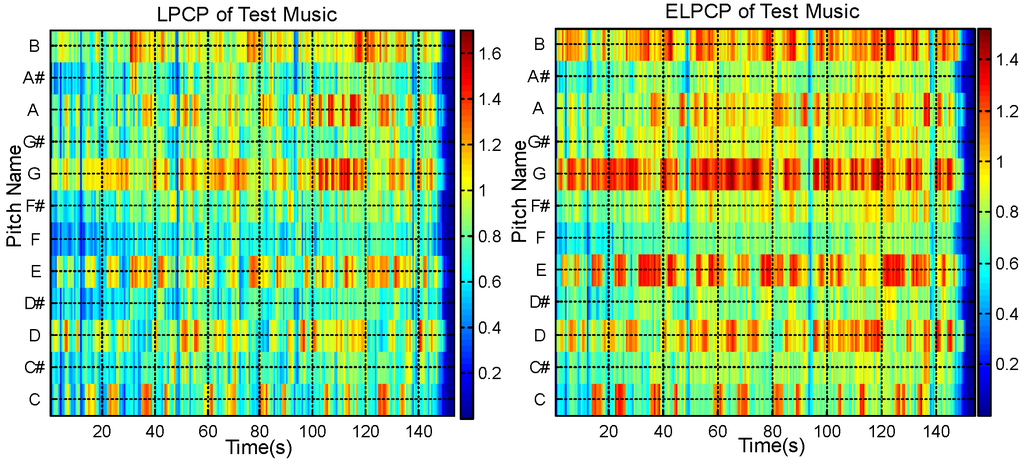
Figure 5.
LPCP (Left) and ELPCP (Right) of test music.
Figure 4 shows that the EPCP has improved continuity compared with the PCP. Figure 5 shows that the ELPCP is further enhanced compared with the LPCP. In Figure 4, it is shown that the EPCP of audio music is more obvious than the PCP. Figure 5 shows that the ELPCP of audio music is clearer than the LPCP. Thus, PCP features for chord recognition are improved by singing voice separation before calculating the PCP or LPCP.
4. Automatic Chord Recognition
Our chord recognition system entails two parts: support vector machine classification and the Viterbi algorithm. For SVM classification, we use LIBSVM (Library for Support Vector Machines) to obtain the chord probability estimates [46]. Then the Viterbi algorithm uses the probability estimates and trained state transition probability to estimate the chord of the music. Because of the temporal correlation of chords, we combine the SVM classification with the Viterbi algorithm and call the system TCSVM (Temporal Correlation Support Vector Machine).
4.1. Support Vector Machine Classification
SVM is a popular machine learning method for classification, regression, and other learning tasks. LIBSVM is currently one of the most widely used SVM software packages. A classification task usually involves a training set where each instance contains the class labels and the features. The goal of SVM is to produce a model to predict the target labels of the test data given only the test data features.
Many methods are available for multi-class SVM classification [47,48]. LIBSVM uses the “one-against-one” approach for multiclass classification. The classification assumes the use of the radial basis function (RBF) kernel of the form . The two parameters of an RBF kernel, and , must be determined by a parameter search as the optimal values vary between tasks. We use the grid-search method to obtain the and parameters.
Once the and parameters are set, the class label and probability information can be predicted. This section discusses the LIBSVM implementation for extending the SVM to output probability estimates. Given K chord classes, for any x, the goal is to estimate .
4.2. Viterbi Algorithm in SVM
The SVM method recognizes the chord based on frame-level classification without considering the inter-frame temporal correlation of chord features. For multiple frames corresponding to the same chord, the recognition results of traditional SVM are independent and fluctuate. Accounting for the inter-frame temporal correlation in the recognition procedure can improve the overall chord recognition rate. Our system combines SVM with the Viterbi algorithm to introduce the temporal correlation prior to a chord. Suppose the system has hidden states, and we denote each state as where the state refers to the chord type. The observed events are , which are PCP features. The current observed chord feature is . represents the transition probability from chord to chord . At an arbitrary time point , for each of the states , a partial probability indicates the probability of the most probable path ending at the state , given the current observed events : . Here, we assume that we already know the probability for any of the previous states at time . is , the current probability estimates of SVM. Once we have all of the objective probabilities for each state at each time point, the algorithm seeks from the end to the beginning to find the most probable path of states for the given sequence of observation events ; indicates the optimal state at time based on the probability computed in the first stage.
The Viterbi algorithm is as follows:
| Algorithm 2: Viterbi algorithm |
| 1 Initialization: |
| ; |
| 2 Recursion: |
| ; |
| 3 Termination: |
| , ; |
| 4 Path backtracking: . |
In our method, we set the initialization observation probability to 1/24. The observed events are PCP features , where is the PCP feature of the tth frame. Generally, SVM predicts only the class label without probability information. The LIBSVM implementation extends SVM to output the probability estimates. The current observation probability corresponds to the probability estimates of SVM and replaces the in the Viterbi algorithm. represents the chord , where is the number of chords and is set to 24.
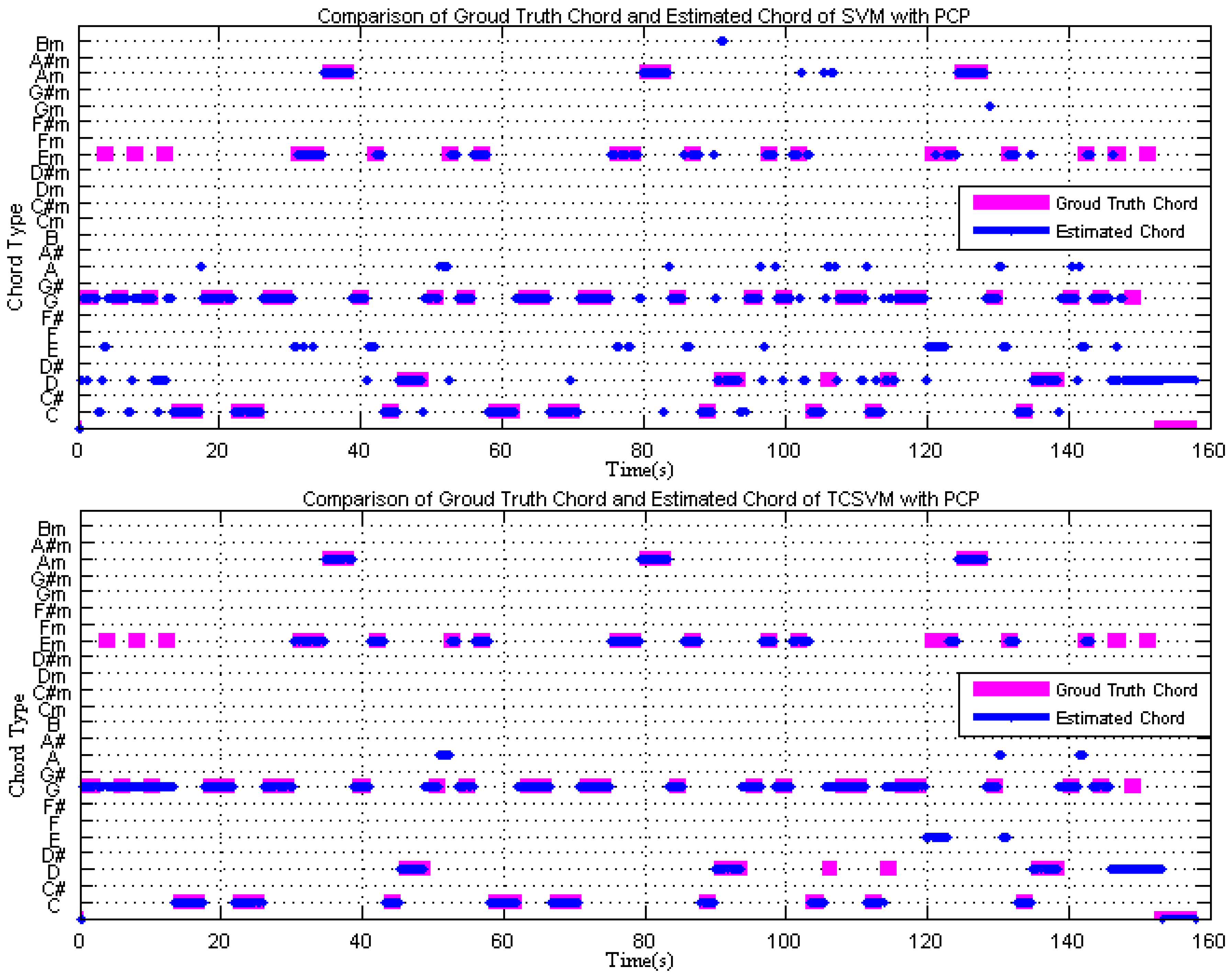
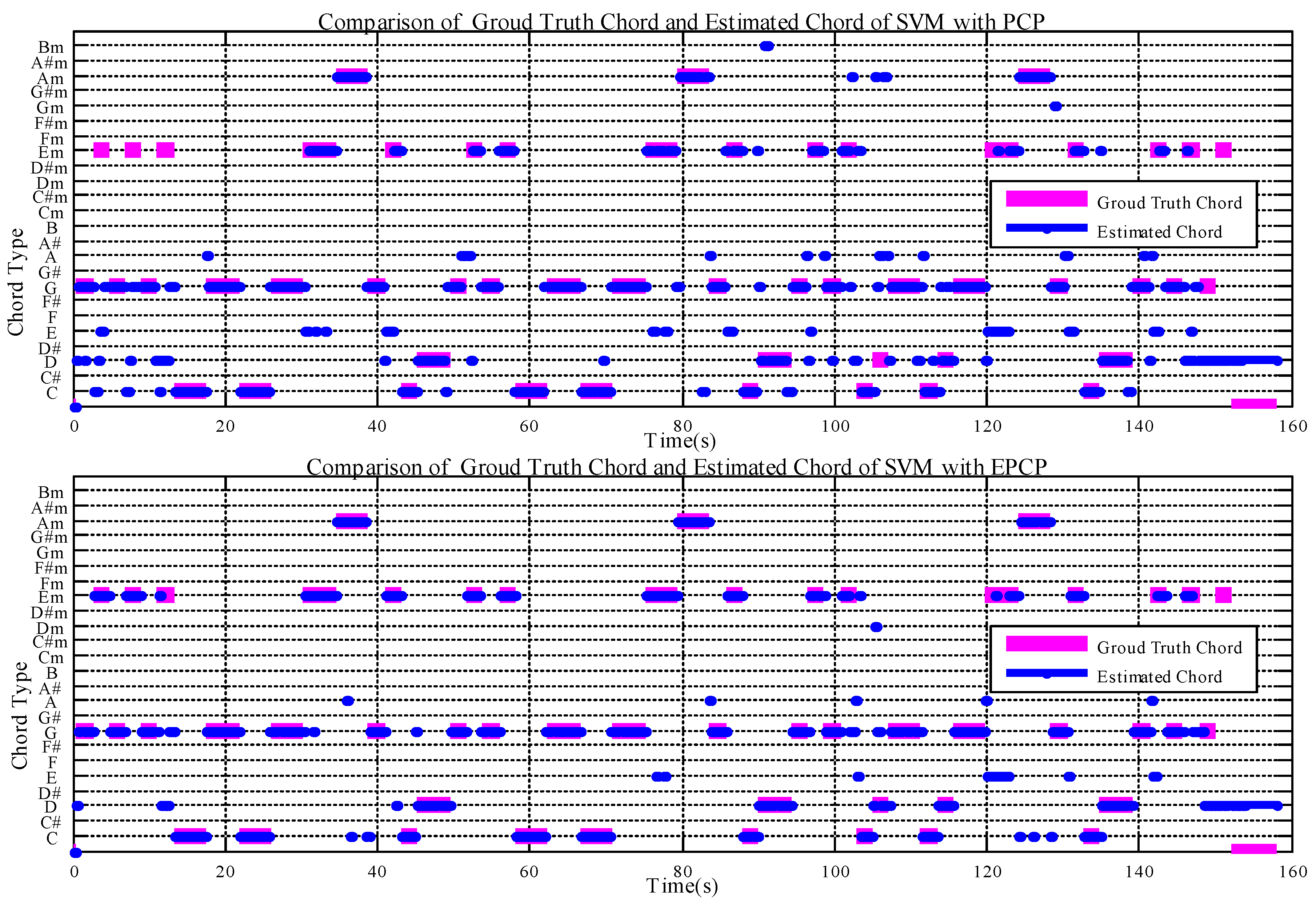
Figure 6 is the comparison of the ground truth chord and estimated chord for the Beatles song “Baby It’s You”. The top figure shows the result of using the SVM method to recognize the chord and the bottom figure uses TCSVM. The ground truth chord is represented in pink and the estimated chord labels are in blue. Figure 6 indicates that the estimation is more stable when using TCSVM.
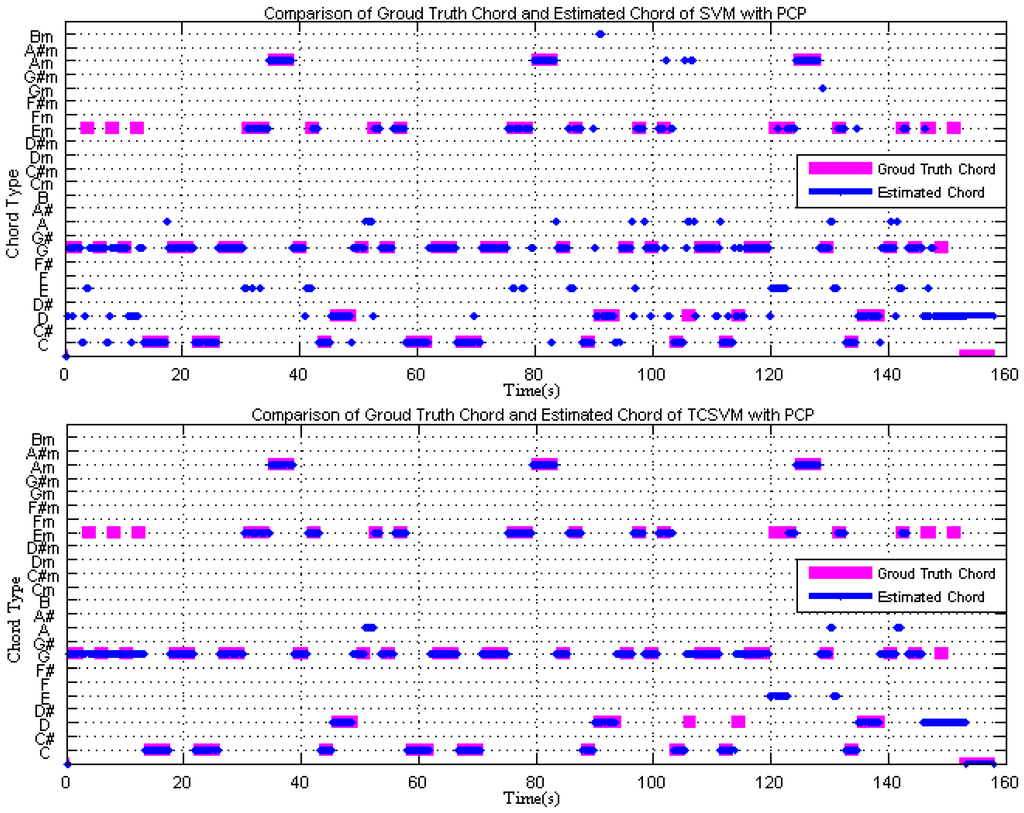
Figure 6.
Comparison of ground truth and estimated chords using SVM (top) and TCSVM (bottom).
5. Experimental Results and Analysis
In this section, we compare the results of chord estimation using different features and methods. We compare our method with the methods that were submitted to MIREX 2013 and MIREX 2014 on the MIREX’09 dataset.
5.1. Corpus and Evaluation Results
For evaluation, we use the MIREX’09 Audio Chord Estimation task dataset which consists of 12 Beatles albums (180 songs, PCM 44 100Hz, 16 bits, mono). Besides the Beatles albums, in 2009, an extra dataset was donated by Matthias Mauch, which consists of 38 songs from Queen and Zweieck [21].
This database has been used extensively for the evaluation of many chord recognition systems, in particular those presented at MIREX 2013 and 2014 for the Audio Chord Estimation task. The evaluation is conducted based on the chord annotations of the Beatles albums provided by Harte and Sandler [49], and the chord annotations of Queen and Zweieck provided by Matthias Mauch [21].
According to [50], chord symbol recall (CSR) is a suitable metric to evaluate chord estimation performance. Since 2013, MIREX has used CSR to estimate how well the predicted chords match the ground truth:
where is the total duration of segments where annotation equals estimation, and is the total duration of the annotated segments.
Because pieces of music vary substantially in length, we weight the CSR by the length of the song when computing the average for a given corpus. This final number is referred to as the weighted chord symbol recall. In this paper, the recognition rate and CSR are equivalent for a song and the recognition rate and weighted chord symbol recall are equivalent for a given corpus or dataset.
In the training stage, we randomly selected 25% of the songs from the Beatles albums to determine the parameters and for the SVM kernel and the state transition probability matrix . For SVM, the training dataset is composed of the PCP features of labeled musical fragments, which are selected from the training songs. The average estimation accuracies or recognition rates are reported.
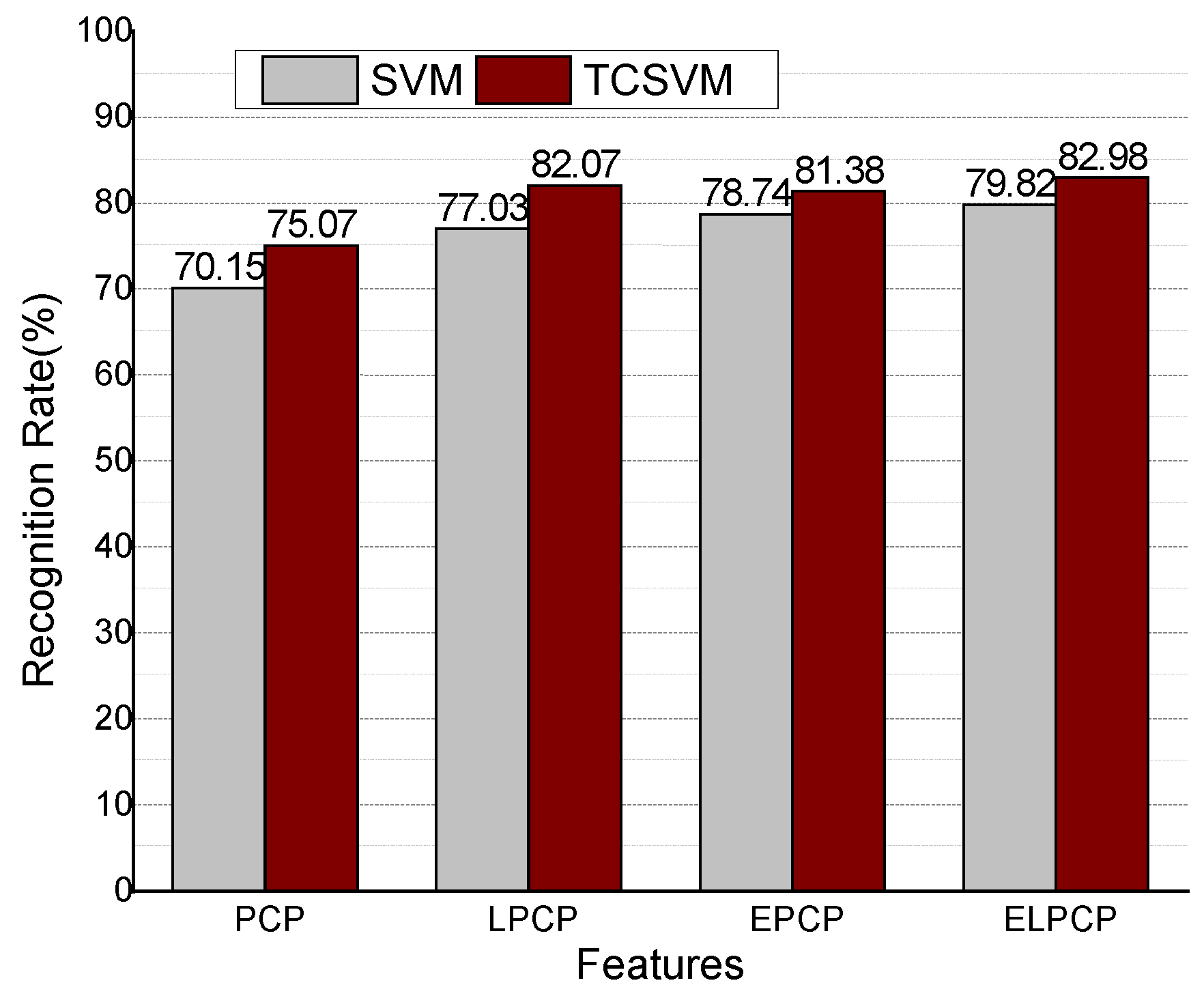
First, we compare the recognition rates of SVM with PCP and EPCP features. The comparison between the ground truth and estimated chord is shown in Figure 7 for the example song (the Beatles song “Baby It’s You”). The top and bottom figures show the results using the SVM method with PCP features and EPCP features, respectively. The ground truth chord is represented in pink and the estimated chord labels are in blue. Figure 7 indicates that EPCP improves the recognition rate. In Figure 8, the recognition rate using SVM with PCP features is 70.15%, while that of TCSVM with the same features is 75.07%. The top image of Figure 6 shows less reliable estimated chords at the times when the chords change. The bottom image considers the inter-frame temporal correlation of chord features and shows more stable estimated chords even when the chords change.
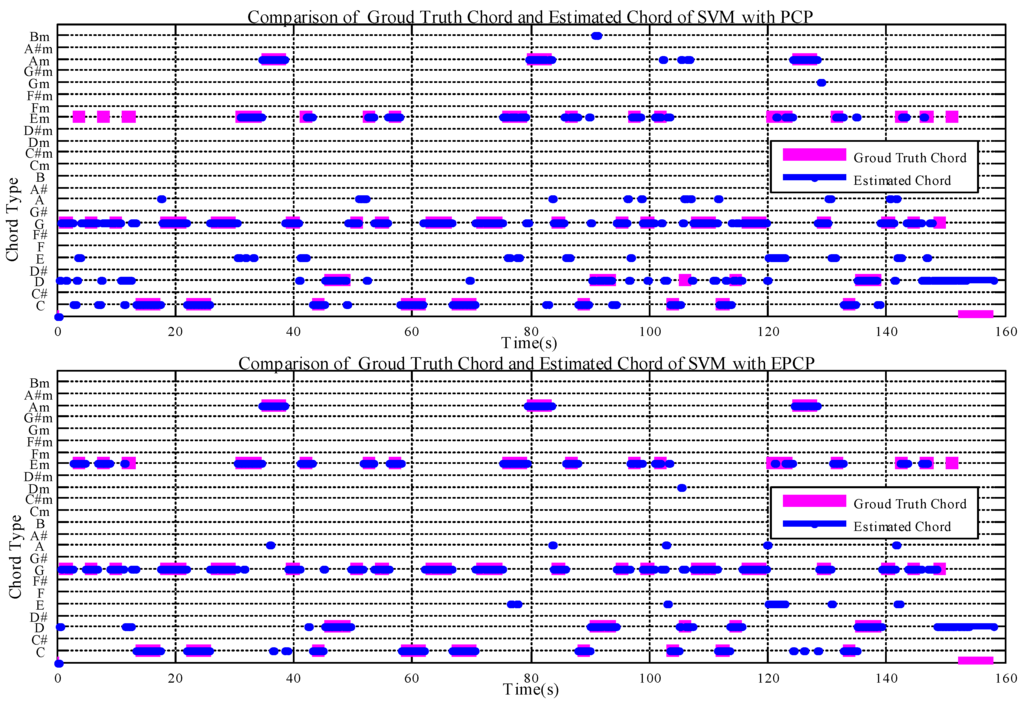
Figure 7.
Comparison of ground truth and estimated chord with PCP (top) and EPCP (bottom).
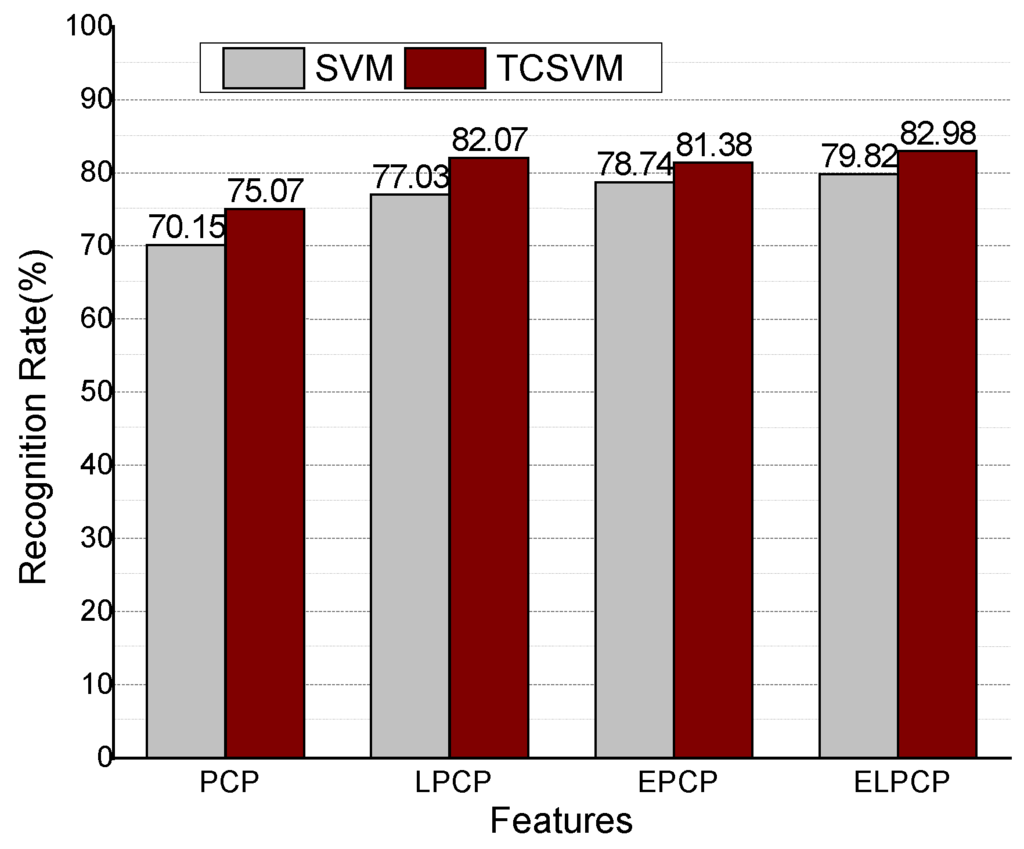
Figure 8.
Recognition rates with different features.
Second, we compare the recognition rates of SVM and TCSVM with different features. The recognition results of the TCSVM method with ELPCP are superior, as shown in Figure 8. Because EPCP and ELPCP consider the temporal correlation of music, the rates show few differences between the SVM and TCSVM.
5.2. Experimental Results Compared with State-of-the-Art Methods
We compare our method with the following methods from MIREX 2013 and MIREX 2014.
MIREX 2013:
- CB4 and CB3: Taemin Cho and Juan P. Bello [35]
- KO1and KO2: Maksim Khadkevich and Maurizio Omologo [36]
- NMSD1 and NMSD2: Yizhao Ni, Matt Mcvicar, Raul Santos-Rodriguez [37]
- CF2 : Chris Cannam, Matthias Mauch, Matthew E. P. Davies [38]
- NG1 and NG2: Nikolay Glazyrin [42]
- PP3 and PP4: Johan Pauwels and Geoffroy Peeters [39]
- SB8: Nikolaas Steenbergen and John Ashley Burgoyne [40]
MIREX 2014:
- KO1: Maksim Khadkevich and Maurizio Omologo [51]
- CM3: Chris Cannam, Matthias Mauch [41]
- JR2: Jean-Baptiste Rolland [52]
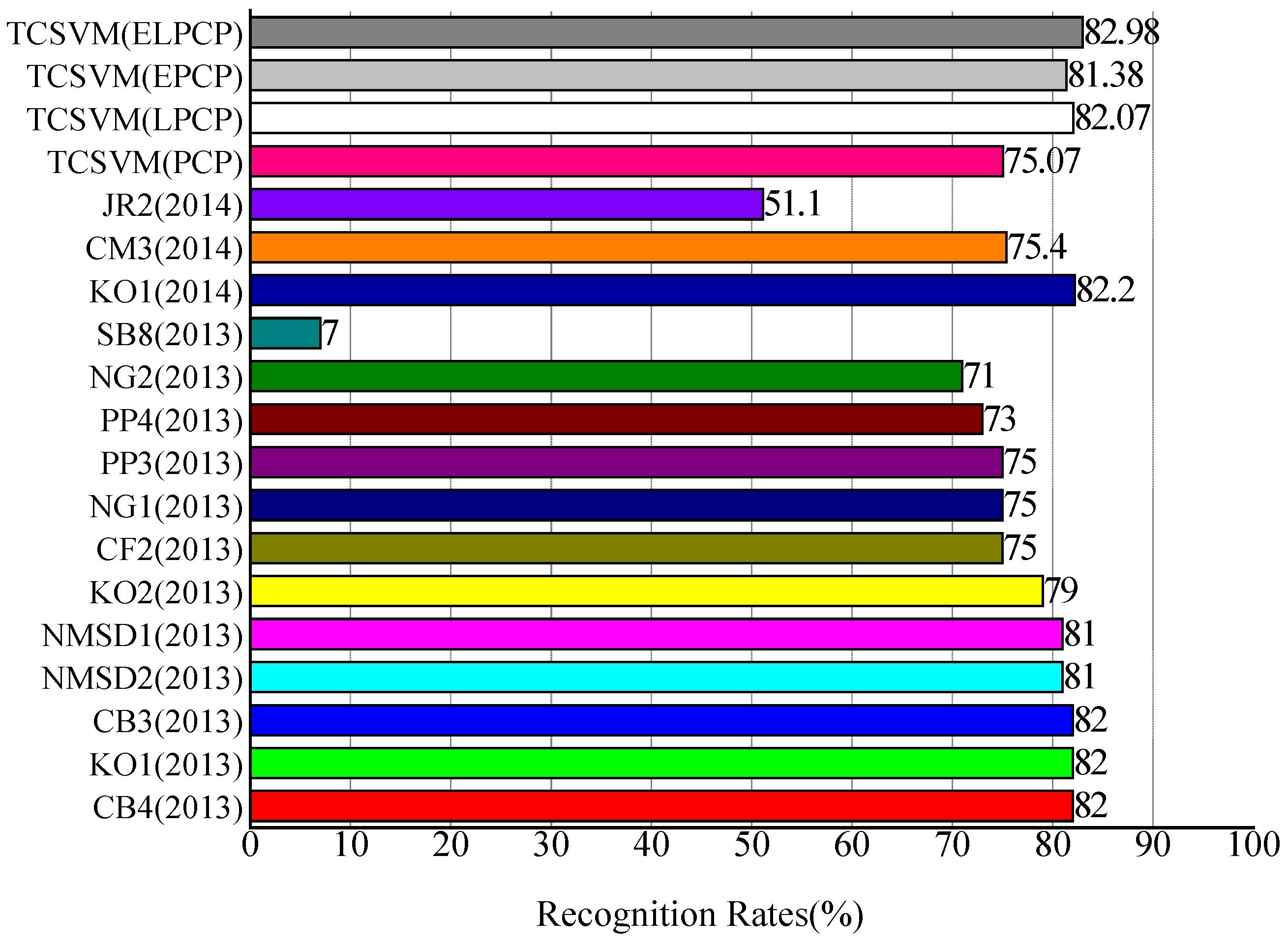
More details about these methods can be found from the corresponding MIREX websites [53]. The results of this comparison are presented in Figure 9.
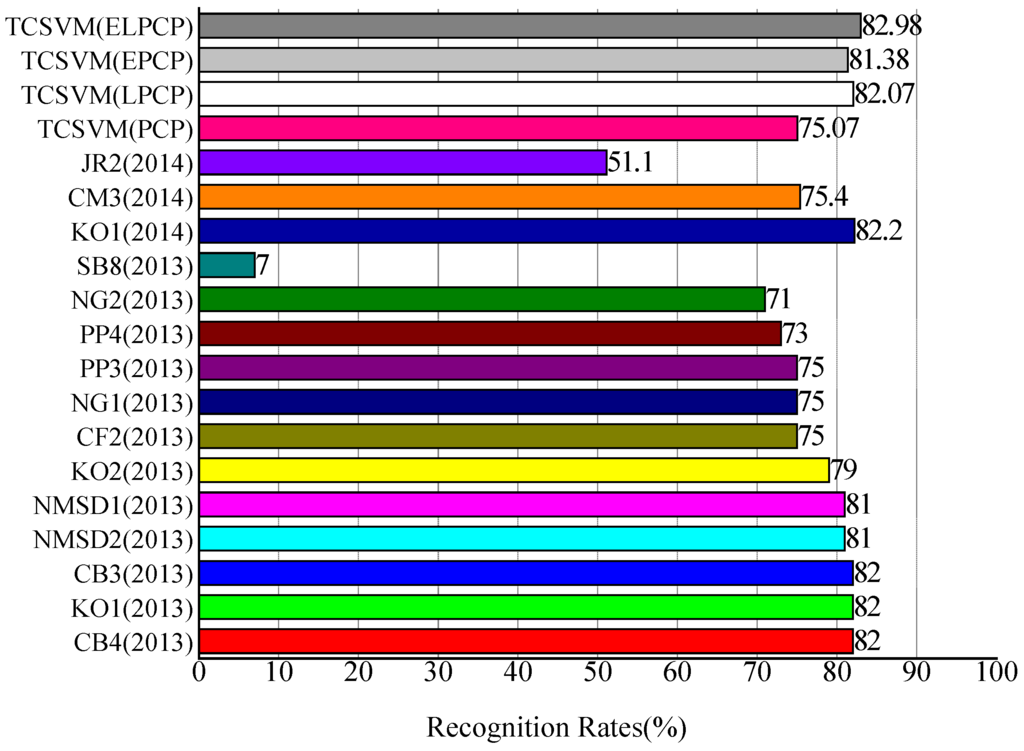
Figure 9.
Comparison of recognition rates with state-of-the-art methods on Mirex’09 dataset.
The recognition rate of our TCSVM method with ELPCP is 82.98%. The recognition rate of our TCSVM (ELPCP) approach is similar to the best-scoring method (KO1) in MIREX 2014.
The results of the 2015 edition of MIREX automatic chord estimation tasks can be found on the corresponding websites [54]. Table 1 shows the comparison of the recognition rates of the 2015 edition on the Isophonics 2009 datasets. The chord classes are as follows: Major and minor(MajMin); Seventh chords(Sevenths); Major and minor with inversions(MajMinInv); Seventh chords with inversions(SeventhsInv). The recognition rate of our TCSVM method is higher than other methods except the rates of the MajMinInv chords.

Table 1.
Comparison of recognition rates of the 2015 edition on Isophonics 2009 datasets.
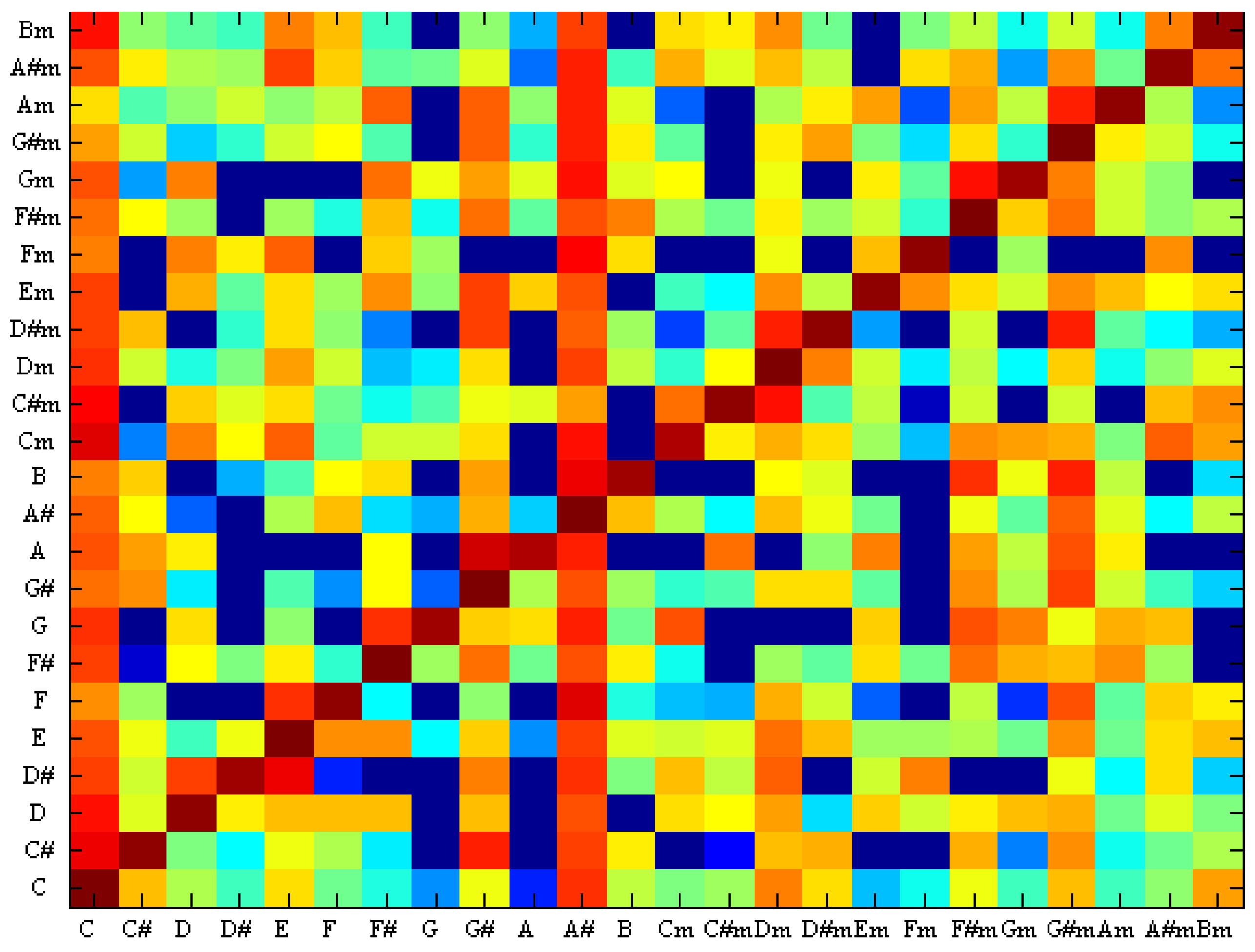
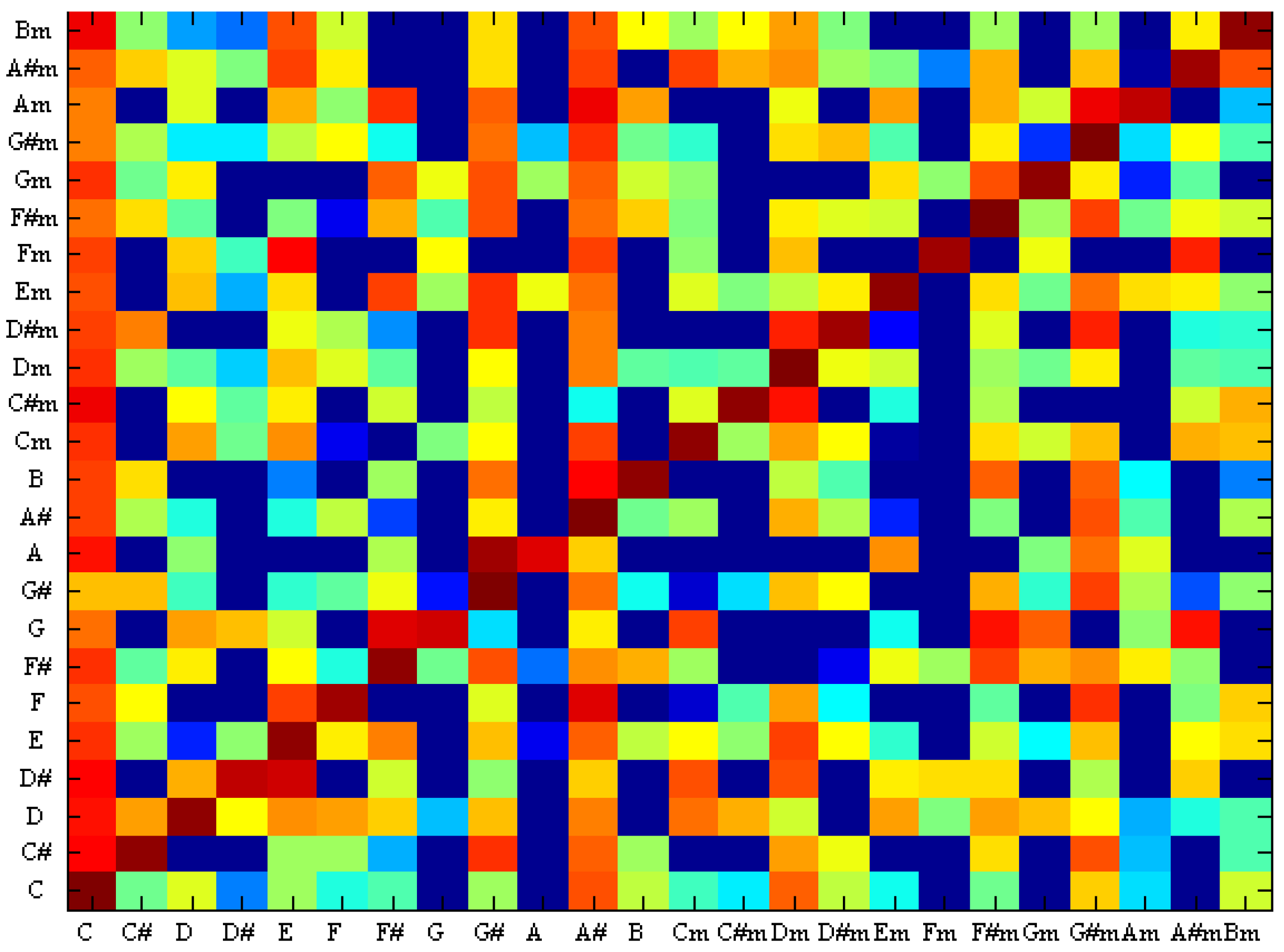
Figure 10 shows the confusion between the chords using SVM and Figure 11 shows the confusion between the chords using TCSVM. The x-axis is the ground truth chord and the y-axis is the estimated chord. Comparing the two images suggests that TCSVM reduces the rate of erroneous identifications for a more reliable result.
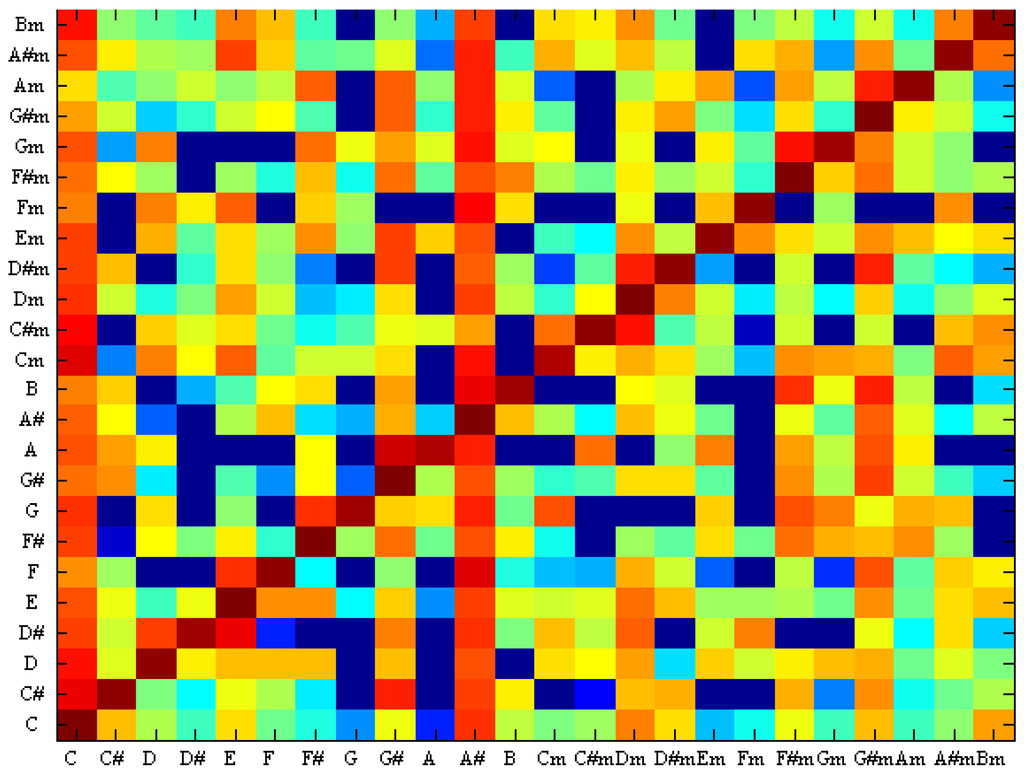
Figure 10.
Confusion between chords with SVM.
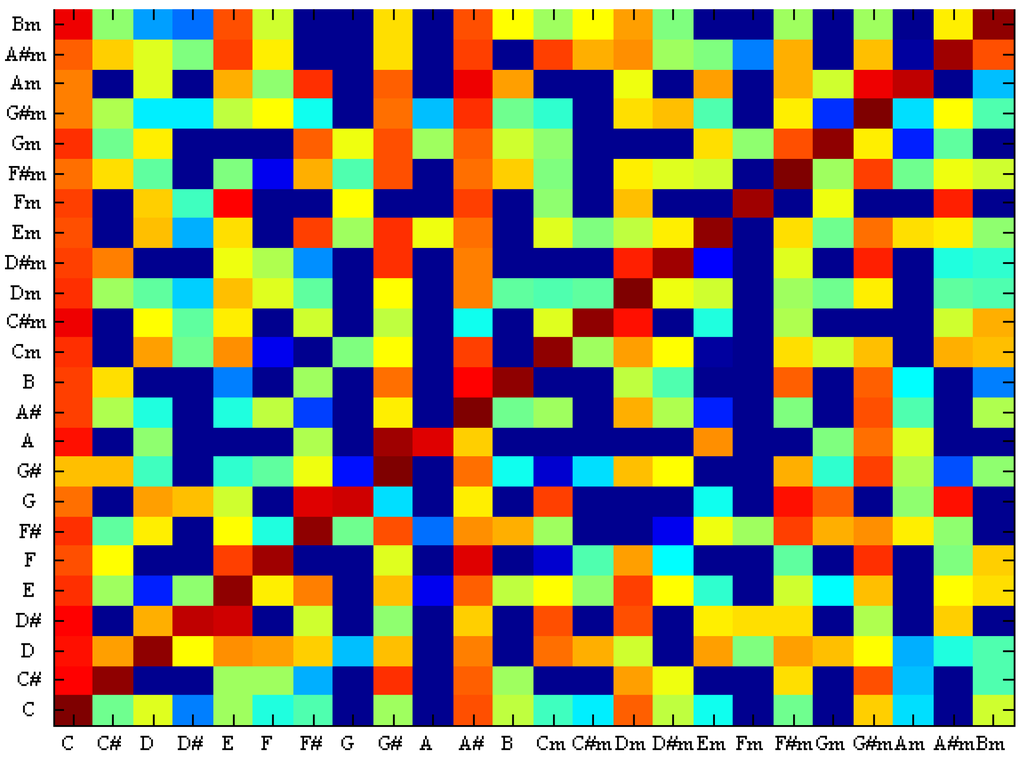
Figure 11.
Confusion between chords with TCSVM.
6. Conclusions
We present a new feature called ELPCP and a machine learning model called TCSVM for chord estimation. We separate the singing voice from the accompaniment to improve the features and consider the temporal correlation of music. Temporal correlation SVM is used to estimate the chord. This system results in more accurate chord recognition and eliminates many spurious chord estimates appearing in the conventional recognition procedure.
Future work should address some limitations. First, this paper only involves common chord estimation as part of the audio chord estimation task. Future work will involve the recognition of more complex chords to increase the applicability of this work in the field of music information retrieval, including song identification, query by similarity, and structure analysis. Second, we consider the effect of the singing voice and the results of Figure 8 show that the recognition rate with singing voice separation is better than without it. There is more room for further improvement of the PCP features to make them more suitable for chord recognition. Finally, we will evaluate the TCSVM method for cases when the audio music contains noise or is corrupted by noise.
Acknowledgments
This work was supported by the national Natural Science Foundation of China (Grant No. 61101225).
Author Contributions
Zhongyang Rao and Xin Guan conceived and designed the experiments; Zhongyang Rao performed the experiments; Zhongyang Rao and Xin Guan analyzed the data; Jianfu Teng contributed materials and analysis tools; Zhongyang Rao and Xin Guan wrote the paper.
Conflicts of Interest
The authors declare that there is no conflict of interests regarding the publication of this paper.
References
- Fujishima, T. Realtime Chord Recognition of Musical Sound: A System Using Common Lisp Music. In Proceedings of the International Computer Music Conference, Beijing, China, 22-27 October 1999; pp. 464–467.
- Ueda, Y.; Uchiyama, Y.; Nishimoto, T.; Ono, N.; Sagayama, S. HMM-based approach for automatic chord detection using refined acoustic features. In Proceedings of the IEEE International Conference on Acoustics Speech and Signal Processing (ICASSP 2010), Dallas, TX, USA, 14–19 March 2010; pp. 5518–5521.
- Harte, C.; Sandler, M. Automatic Chord Identifcation Using a Quantised Chromagram. In Proceedings of the Audio Engineering Society Convention 118, Barcelona, Spain, 28–31 May 2005.
- Degani, A.; Dalai, M.; Leonardi, R.; Migliorati, P. Real-time Performance Comparison of Tuning Frequency Estimation Algorithms. In Proceedings of the 2013 8th International Symposium on Image and Signal Processing and Analysis (ISPA), Trieste, Italy, 4–6 September 2013; pp. 393–398.
- Morman, J.; Rabiner, L. A system for the automatic segmentation and classification of chord sequences. In Proceedings of the 1st ACM Workshop on Audio and Music Computing Multimedia, Santa Barbara, CA, USA, 23–27 October 2006; pp. 1–10.
- Lee, K. Automatic Chord Recognition from Audio Using Enhanced Pitch Class Profile. In Proceedings of the International Computer Music Conference, New Orleans, LA, USA, 6–11 November 2006.
- Varewyck, M.; Pauwels, J.; Martens, J.-P. A novel chroma representation of polyphonic music based on multiple pitch tracking techniques. In Proceedings of the 16th ACM International Conference on Multimedia, Vancouver, BC, Canada, 26–31 October 2008; pp. 667–670.
- Müller, M.; Ewert, S. Towards timbre-invariant audio features for harmony-based music. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 649–662. [Google Scholar]
- Nwe, T.L.; Shenoy, A.; Wang, Y. Singing voice detection in popular music. In Proceedings of the 12th Annual ACM International Conference on Multimedia, New York, NY, USA, 10–16 October 2004; pp. 324–327.
- Oudre, L.; Grenier, Y.; Févotte, C. Template-based Chord Recognition: Influence of the Chord Types. In Proceedings of the International Society for Music Information Retrieval Conference, Kobe, Japan, 26–30 October 2009; pp. 153–158.
- Rocher, T.; Robine, M.; Hanna, P.; Oudre, L.; Grenier, Y.; Févotte, C. Concurrent Estimation of Chords and Keys from Audio. In Proceedings of the International Society for Music Information Retrieval Conference, Utrecht, The Netherlands, 9–13 August 2010; pp. 141–146.
- Cho, T.; Bello, J.P. A Feature Smoothing Method for Chord Recognition Using Rrecurrence Plots. In Proceedings of the Music Information Retrieval Evaluation eXchange (MIREX 2011), Miami, FL, USA, 24–28 October 2011.
- Oudre, L.; Févotte, C.; Grenier, Y. Probabilistic template-based chord recognition. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 2249–2259. [Google Scholar] [CrossRef]
- Papadopoulos, H.; Peeters, G. Large-scale Study of Chord Estimation Algorithms Based on Chroma Representation and HMM. In Proceedings of the International Workshop on Content-Based Multimedia Indexing (CBMI’07), 25–27 June 2007; pp. 53–60.
- Bello, J.P.; Pickens, J. A Robust Mid-Level Representation for Harmonic Content in Music Signals. In Proceedings of the International Society for Music Information Retrieval Conference, London, UK, 11–15 September 2005; pp. 304–311.
- Lee, K.; Slaney, M. Acoustic chord transcription and key extraction from audio using key-dependent HMMs trained on synthesized audio. IEEE Trans. Audio Speech Lang. Process. 2008, 16, 291–301. [Google Scholar] [CrossRef]
- Papadopoulos, H.; Peeters, G. Simultaneous Estimation of Chord Progression and Downbeats from an Audio File. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2008), Bordeaux, France, 25–27 June 2008; pp. 121–124.
- Sheh, A.; Ellis, D.P. Chord Segmentation and Recognition Using EM-Trained Hidden Markov Models. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR 2003), Maryland, MD, USA, 27-30 October 2003; pp. 185–191.
- Scholz, R.; Vincent, E.; Bimbot, F. Robust Modeling of Musical Chord Sequences Using Probabilistic N-grams. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2009), Taipei, Taiwan, 19–24 April 2009; pp. 53–56.
- Yoshii, K.; Goto, M. A Vocabulary-Free Infinity-Gram Model for Nonparametric Bayesian Chord Progression Analysis. In Proceedings of the International Society for Music Information Retrieval Conference, Miami, FL, USA, 24–28 October 2011; pp. 645–650.
- Mauch, M. Automatic Chord Transcription from Audio Using Computational Models of Musical Context. Ph.D. Thesis, University of London, London, UK, 23 March 2010. [Google Scholar]
- Ni, Y.; McVicar, M.; Santos-Rodriguez, R.; de Bie, T. An end-to-end machine learning system for harmonic analysis of music. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 1771–1783. [Google Scholar] [CrossRef]
- Vapnik, V.N. An overview of statistical learning theory. IEEE Trans. Neural Netw. 1999, 10, 988–999. [Google Scholar] [CrossRef] [PubMed]
- Miao, Q.; Huang, H.Z.; Fan, X. A comparison study of support vector machines and hidden Markov models in machinery condition monitoring. J. Mech. Sci. Technol. 2007, 21, 607–615. [Google Scholar] [CrossRef]
- Bartsch, M.A.; Wakefield, G.H. Audio thumbnailing of popular music using chroma-based representations. IEEE Trans. Multimed. 2005, 7, 96–104. [Google Scholar] [CrossRef]
- Gómez, E. Tonal description of polyphonic audio for music content processing. Inf. J. Comput. 2006, 18, 294–304. [Google Scholar] [CrossRef]
- Khadkevich, M.; Omologo, M. Use of Hidden Markov Models and Factored Language Models for Automatic Chord Recognition. In Proceedings of the International Society for Music Information Retrieval Conference, Kobe, Japan, 26–30 October 2009; pp. 561–566.
- Brown, J.C. Calculation of a Constant Q spectral Transform. J. Acoust. Soc. Am. 1991, 89, 425–434. [Google Scholar] [CrossRef]
- Müller, M.; Ewert, S. Chroma Toolbox: MATLAB Implementations for Extracting Variants of Chroma-based Audio Features. In Proceedings of the 12th International Conference on Music Information Retrieval (ISMIR 2011), Miami, FL, USA, 24–28 October 2011.
- Mauch, M.; Dixon, S. Approximate Note Transcription for the Improved Identification of Difficult Chords. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR 2010), Utrecht, The Netherlands, 9–13 August 2010; pp. 135–140.
- Müller, M.; Ewert, S.; Kreuzer, S. Making chroma features more robust to timbre changes. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP 2009), Taipei, Taiwan, 19–24 April 2009; pp. 1877–1880.
- Wang, F.; Zhang, X. Research on CRFs in Music Chord Recognition Algorithm. J. Comput. 2013, 8, 1017. [Google Scholar] [CrossRef]
- Gómez, E.; Herrera, P.; Ong, B. Automatic Tonal Analysis from Music Summaries for Version Identification. In Proceedings of the Audio Engineering Society Convention 121, San Francisco, CA, USA, 5–8 October 2006.
- Weil, J.; Durrieu, J.-L. An HMM-based Audio Chord Detection System: Attenuating the Main Melody. In Proceedings of the Music Information Retrieval Evaluation eXchange (MIREX), Philadelphia, PA, USA, 14–18 September 2008.
- Cho, T.; Bello, J.P. MIREX 2013: Large Vocabulary Chord Recognition System Using Multi-band Features and a Multi-stream HMM. In Proceedings of the Music Information Retrieval Evaluation eXchange (MIREX), Curitiba, Brazil, 4–8 November 2013.
- Khadkevich, M.; Omologo, M. Time-frequency Reassigned Features for Automatic Chord Recognition. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2011), Prague, Czech Republic, 22–27 may 2011; pp. 181–184.
- Ni, Y.; McVicar, M.; Santos-Rodriguez, R.; de Bie, T. Harmony Progression Analyzer for MIREX 2013. In Proceedings of the Music Information Retrieval Evaluation eXchange (MIREX), Curitiba, Brazil, 4–8 November 2013.
- Cannam, C.; Benetos, E.; Mauch, M.; Davies, M.E.P.; Dixon, S.; Landone, C.; Noland, K.; Stowell, D. MIREX 2015: Vamp Plugins from the Centre for Digital Music. In Proceedings of the Music Information Retrieval Evaluation eXchange (MIREX), Malaga, Spain, 26–30 October 2015.
- Pauwels, J.; Peeters, G. The Ircamkeychord Submission for MIREX 2013. In Proceedings of the Music Information Retrieval Evaluation eXchange (MIREX), Curitiba, Brazil, 4–8 November 2013.
- Steenbergen, N.; Burgoyne, J.A. MIREX 2013: Joint Optimization of an Hidden Markov Model-neural Network Hybrid Chord Estimation. In Proceedings of the Music Information Retrieval Evaluation eXchange (MIREX), Curitiba, Brazil, 4–8 November 2013.
- Cannam, C.; Benetos, E.; Mauch, M.; Davies, M.E.; Dixon, S.; Landone, C.; Noland, K.; Stowell, D. MIREX 2014: Vamp Plugins from the Centre for Digital Music. In Proceedings of the Music Information Retrieval Evaluation eXchange (MIREX), Taipei, Taiwan, 27–31 October 2014.
- Glazyrin, N. Audio Chord Estimation Using Chroma Reduced Spectrogram and Self-similarity. In Proceedings of the Music Information Retrieval Evaluation eXchange (MIREX), Curitiba, Brazil, 4–8 November 2013.
- Oudre, L. Template-Based Chord Recognition from Audio Signals. Ph.D. Thesis, TELECOM ParisTech, Paris, France, 3 November 2010. [Google Scholar]
- Ellis, D.P. Beat tracking by dynamic programming. J. New Music Res. 2007, 36, 51–60. [Google Scholar] [CrossRef]
- The Augmented Lagrange Multiplier Method for Exact Recovery of Corrupted Low-Rank Matrices. Available online: http://arxiv.org/abs/1009.5055 (accessed on 18 October 2013).
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 389–396. [Google Scholar] [CrossRef]
- Guo, H.; Wang, W. An active learning-based SVM multi-class classification model. Pattern Recognit. 2015, 48, 1577–1597. [Google Scholar] [CrossRef]
- Tomar, D.; Agarwal, S. A comparison on multi-class classification methods based on least squares twin support vector machine. Knowl.-Based Syst. 2015, 81, 131–147. [Google Scholar] [CrossRef]
- Harte, C.; Sandler, M.B.; Abdallah, S.A.; Gómez, E. Symbolic Representation of Musical Chords: A Proposed Syntax for Text Annotations. In Proceedings of the International Society for Music Information Retrieval Conference, London, UK, 11–15 September 2005; pp. 66–71.
- Pauwels, J.; Peeters, G. Evaluating Automatically Estimated Chord Sequences. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2013), Vancouver, BC, USA, 26–31 May 2013; pp. 749–753.
- Khadkevich, M.; Omologo, M. Time-frequency Reassigned Features for Automatic Chord Recognition. In Proceedings of the Music Information Retrieval Evaluation eXchange (MIREX), Taipei, Taiwan, 27–31 October 2014.
- Rolland, J.-B. Chord Detection Using Chromagram Optimized by Extracting Additional Features. In Proceedings of the Music Information Retrieval Evaluation eXchange (MIREX), Taipei, Taiwan, 27–31 October 2014.
- MIREX HOME. Available online: http://www.music-ir.org/mirex/wiki/MIREX_HOME (accessed on 10 November 2015).
- 2015:Audio Chord Estimation Results. Available online: http://www.music-ir.org/mirex/wiki/2015:Audio_Chord_Estimation_Results#Isophonics_2009 (accessed on 2 December 2015).
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).