Fracture Initiation of an Inhomogeneous Shale Rock under a Pressurized Supercritical CO2 Jet
Abstract
:1. Introduction
2. Field Observations and Experiments
2.1. Field Observations
2.2. Experiments of Perforation Shape
3. Methodology and the Model
3.1. Fluid–Structure Interaction (FSI) Model
- Before the initiation and propagation of fracture, both the fluid and the structure models have fixed boundary profiles, while the FSI boundary has limited deformation.
- In the shale model, due to the short residence time for SC-CO2 jet, the CO2 seepage and phase change did not need to be considered.
- In the SC-CO2 jet model, the temperature does not significantly affect the stress field of the shale rock.
3.2. SC-CO2 Jet Model
3.3. Inhomogeneous Shale Model and User-Defined Material Failure Criterion
3.3.1. Inhomogeneous Mechanism Parameters
3.3.2. Shale Rock Model with User-Defined Constitutive
3.3.3. User-Coded Material Failure Criterion
3.4. Simulation Setup
4. Results and Discussion
4.1. Flow Field and Stress Filed
4.1.1. Flow Field and Stress Filed before Fracture Initiation
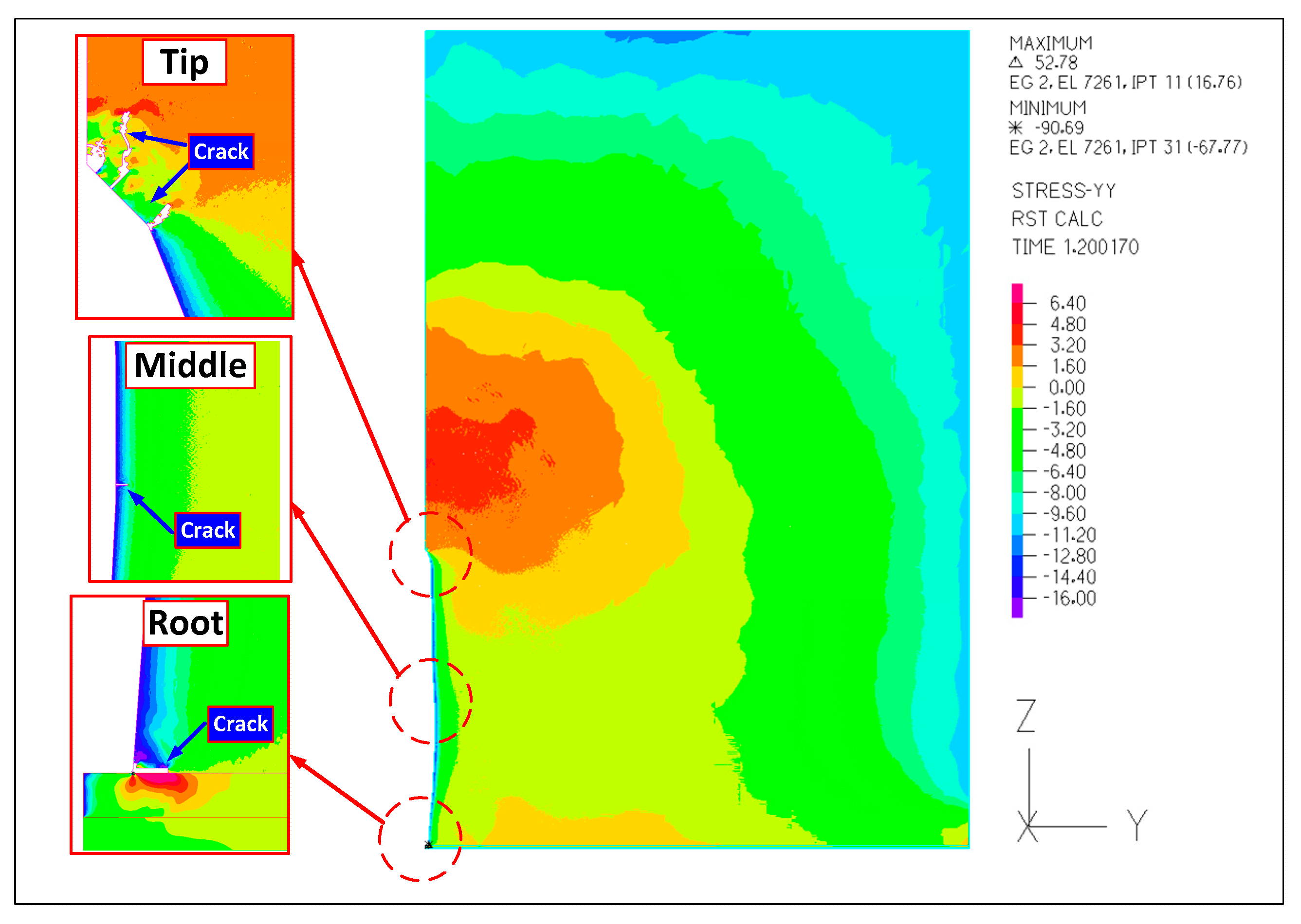
4.1.2. Stress Field after Fracture Initiation
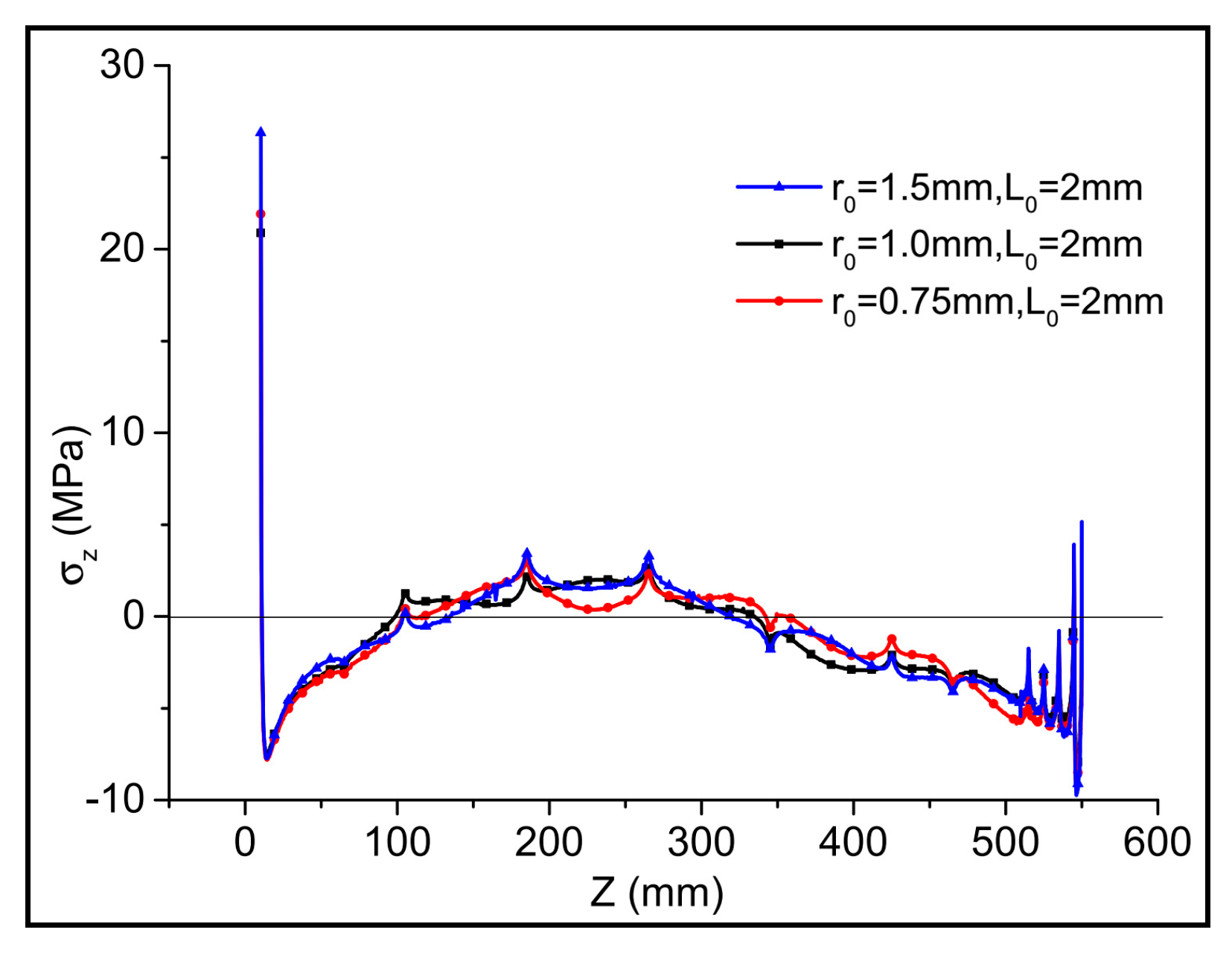
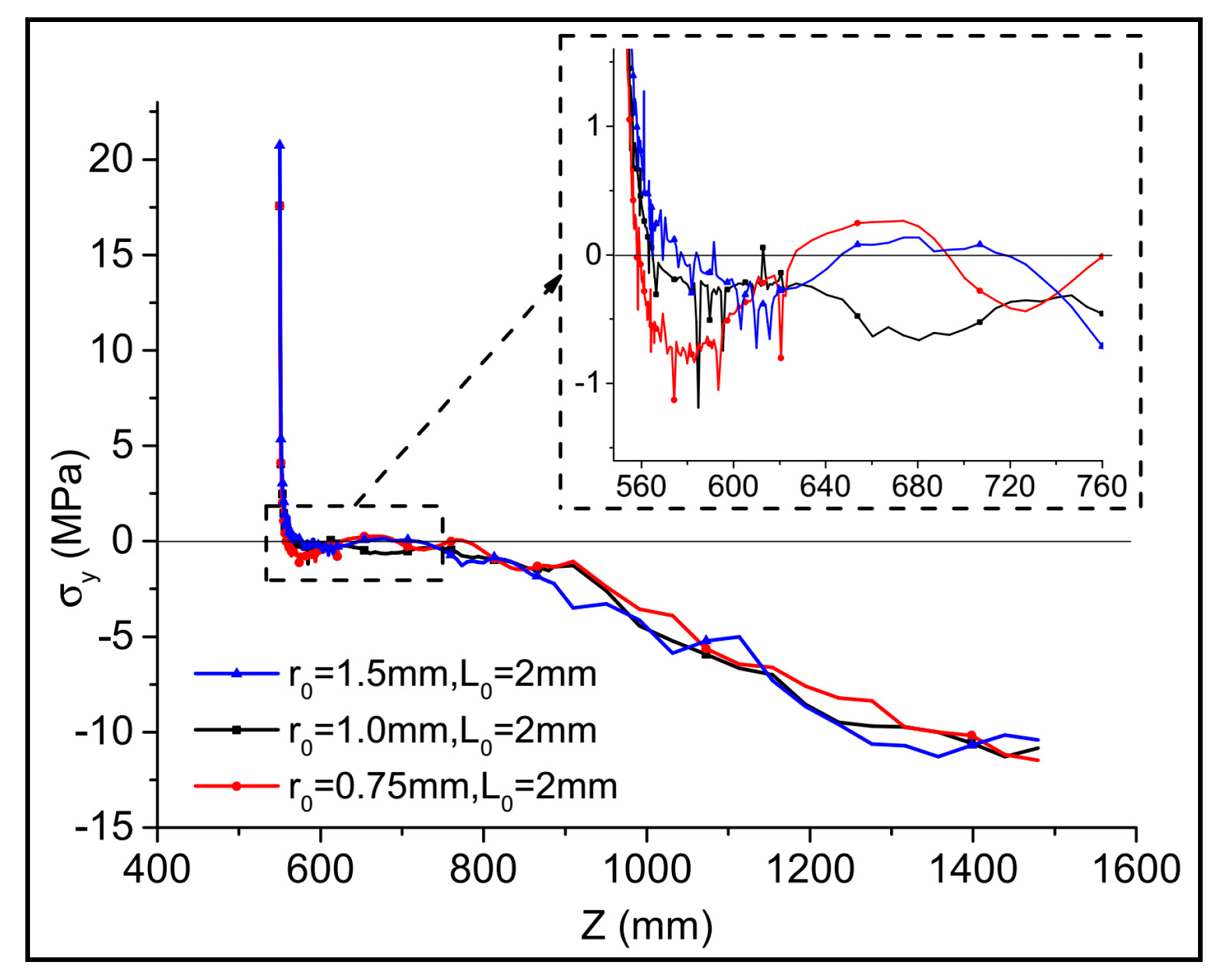
4.1.3. Verification of the Flow Field
4.2. Perforation Pressure
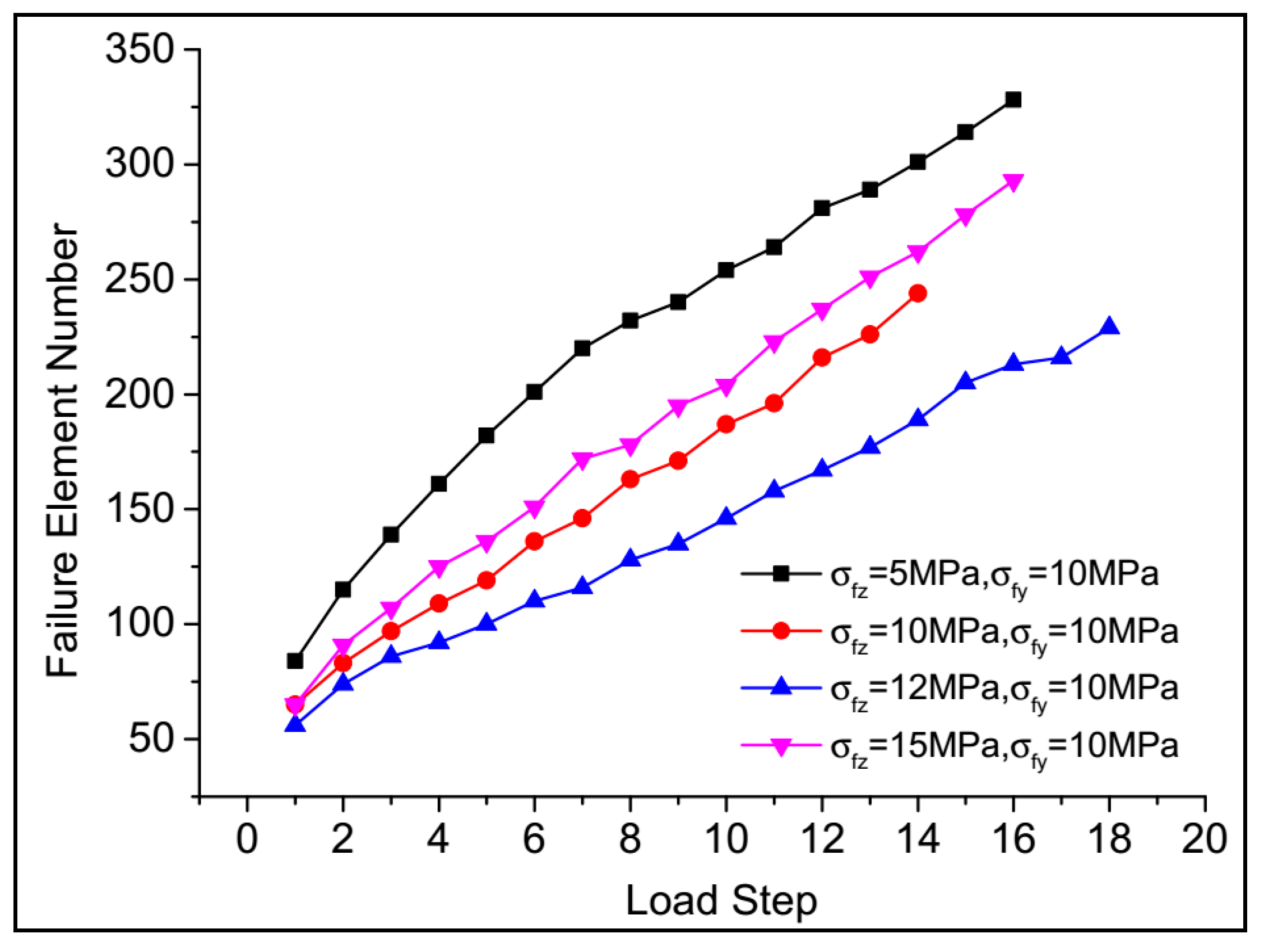
4.3. In-Situ Stress
4.4. Nozzle Outlet Length-to-Diameter Ratio (L/r0)
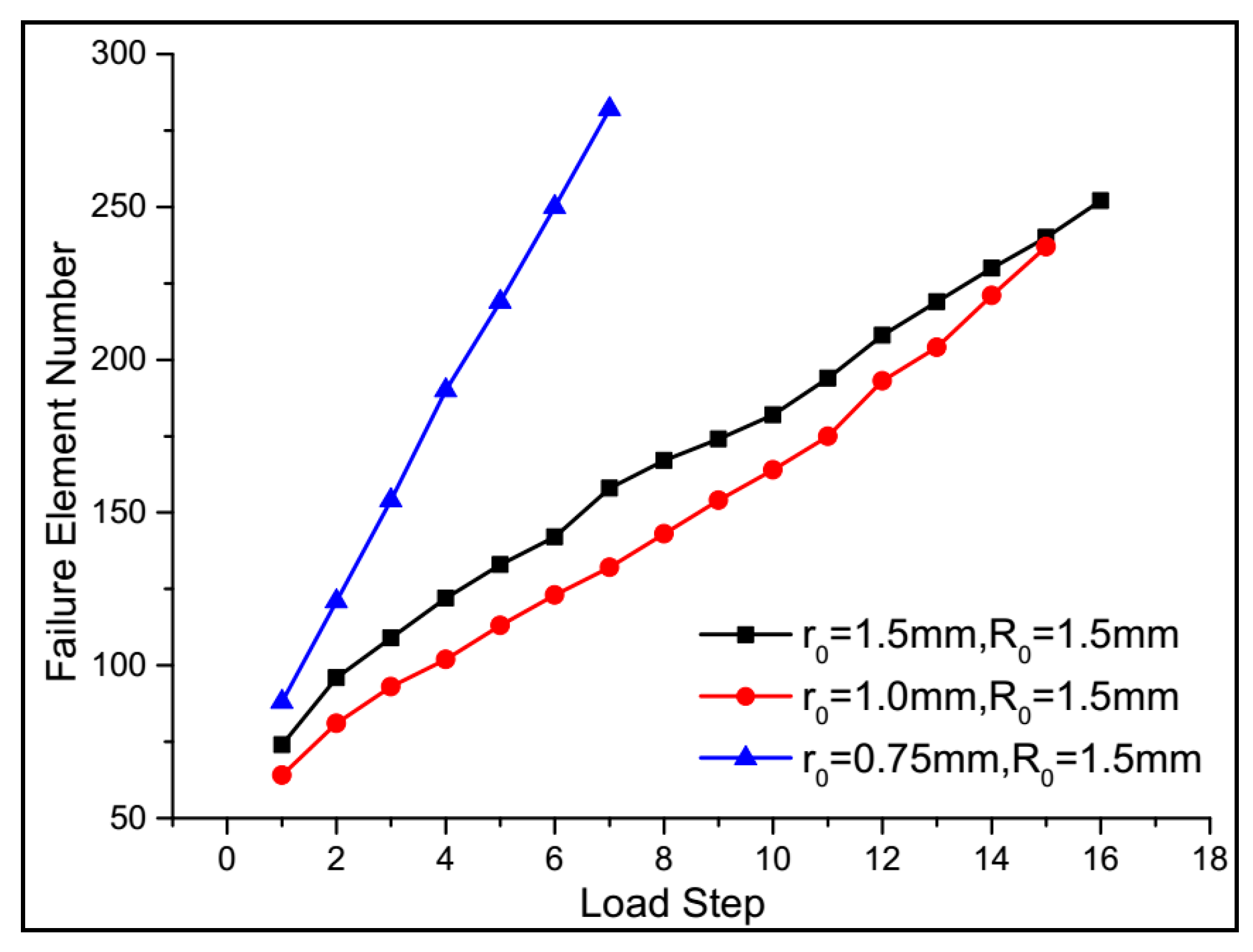
4.5. Aperture Ratio (r0/R)
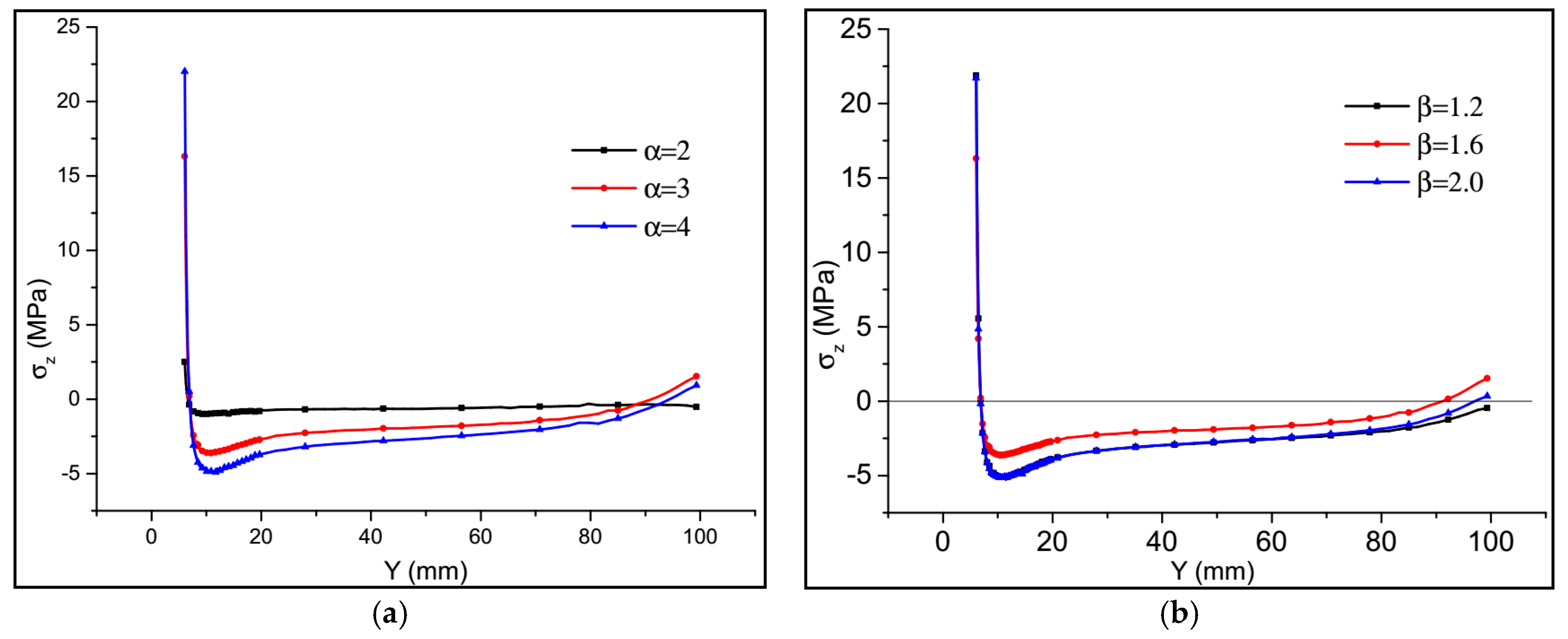
4.6. Weibull Parameter
5. Conclusions
- (1)
- From the experiments and SEM analysis, shale rock exhibited distinct heterogeneity, including elastic modulus, tangent modulus, and Poisson’s ratio. The numerical simulation results indicated that the Weibull probability distribution can be used to analyze fracture initiation. The parameters can explain the distribution of weak elements and can affect the stress field in the shale rock.
- (2)
- A high-velocity SC-CO2 jet not only caused a hydraulic-fracturing ring, but also led to the increase in stress in the shale rock. The tensile stress in the direction parallel to the perforation (z-direction) led to crack initiation at the root and at the middle of the perforation. The tensile stress in the direction vertical to the perforation (y-direction) resulted in crack initiation at the position of the tip of the perforation.
- (3)
- It was found that, with the increase in perforation pressure, more cracks initiated at the tip. In contrast, the length of the cracks initiated at the root decreased. In SC-CO2 hydro-jet fracturing, the in situ stress in the direction perpendicular to the perforation should be greater than that in the direction parallel to the perforation, which is favorable for fracture initiation at the tip and for the prevention of crack initiation at the root.
- (4)
- The structure of the nozzle outlet distinctly affected the pressurization of the SC-CO2 jet. When the diameter of the nozzle outlet was increased, the perforation pressure became higher. These effects were attributed to the non-linear distribution and different maximum values of the stress in shale rock.
- (5)
- The aperture ratio between the nozzle outlet and the casing’s perforation inlet significantly affected the SC-CO2 jet fracturing, which resulted in the disappearance of the “hydraulic isolation ring.” With the increase in aperture ratio, the initiation position of the cracks’ growth and the region of the maximum tensile stress extended, and the number of failure elements also significantly increased.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclatures
| x, y, z | third local coordinate, mm |
| r | radial direction coordinate, mm |
| T | temperature, K |
| Tc | critical temperature, K |
| t | time, s |
| velocity in the y-direction, velocity in the z-direction, m/s | |
| ρ, ρc | density and critical density, kg/m2 |
| Ρ, Ρc | pressure, critical pressure, MPa |
| Ρs, Ρd | static and dynamic pressure, MPa |
| Ρt | total pressure, MPa |
| Ρin | nozzle inlet pressure, MPa |
| Ρam | ambient pressure, MPa |
| perforation pressure, MPa | |
| Tam | ambient temperature, K |
| Vc | critical specific volume, m2/ kg |
| Rsp | specific gas constant, dimensionless |
| K | kinetic energy of turbulence, dimensionless |
| ω | specific dissipation rate of turbulence, dimensionless |
| vz | axial velocity, m/s |
| vmax | max axial velocity, m/s |
| b, a0 | constants of PR equation, dimensionless |
| w | acentric factor, dimensionless |
| V | specific volume, m2/ kg |
| n | constants of PR equation, dimensionless |
| tangent modulus of shale rock, GPa | |
| average tangent modulus of shale rock, GPa | |
| non-uniform parameter of Weibull probability distribution | |
| scale parameter of Weibull probability distribution | |
| y-directional stress, MPa | |
| z-directional stress, MPa | |
| failure tensile stress in the y-direction, MPa | |
| failure tensile stress in the z-direction, MPa | |
| in situ stress in the y-direction, MPa | |
| in situ stress in the z-direction, MPa | |
| d | nozzle outlet diameter, mm |
| l | nozzle outlet length, mm |
| r0 | nozzle outlet radius, mm |
| Dc | inlet diameter of casing, mm |
| R | radius of casing tunnel cross-section, mm |
| Re | Reynolds number, dimensionless |
| RA | control parameter of element failure in ADINA |
| ϕ | dimensionless axial velocity, dimensionless |
| η | dimensionless radius, dimensionless |
| γ | dimensionless radius, dimensionless |
References
- Middleton, R.S.; Carey, J.W.; Currier, R.P.; Hyman, J.D.; Kang, Q.; Karra, S.; Jiménez-Martínez, J.; Porter, M.L.; Viswanathan, H.S. Shale gas and non-aqueous fracturing fluids: Opportunities and challenges for supercritical CO2. Appl. Energy 2015, 147, 500–509. [Google Scholar]
- Middleton, R.; Viswanathan, H.; Currier, R.; Gupta, R. CO2 as a fracturing fluid: Potential for commercial-scale shale gas production and CO2 sequestration. Energy Procedia 2014, 63, 7780–7784. [Google Scholar]
- Liu, H.; Wang, F.; Zhang, J.; Meng, S.; Duan, Y. Fracturing with carbon dioxide: Application status and development trend. Pet. Explor. Dev. 2014, 41, 513–519. [Google Scholar] [CrossRef]
- Matson, D.W.; Petersen, R.C.; Smith, R.D. Production of powders and films by the rapid expansion of supercritical solutions. J. Mater. Sci. 1987, 22, 1919–1928. [Google Scholar]
- Seebald, P.J. Turbulence in Transcritical CO2 Jets. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, January 2014. [Google Scholar]
- Khalil, I.G.; Miller, D.R. The free-jet expansion of supercritical CO2 from a capillary source. In Proceedings of the 24th International Symposium on Rarefied Gas Dynamics, Monopli, Italy, 10–16 July 2004; pp. 343–348. [Google Scholar]
- Gregorio, F.D. Free compressible jet investigation. Exp. Fluid. 2014, 55, 1–21. [Google Scholar]
- Türk, M. Influence of thermodynamic behaviour and solute properties on homogeneous nucleation in supercritical solutions. J. Supercrit. Fluid. 2000, 18, 169–184. [Google Scholar]
- Helfgen, B.; Türk, M.; Schaber, K. Hydrodynamic and aerosol modelling of the rapid expansion of supercritical solutions (RESS-process). J. Supercrit. Fluid. 2003, 26, 225–242. [Google Scholar]
- Ksibi, H.; Tenaud, C.; Subra, P.; Garrabos, Y. Numerical simulation of the rapid expansion of supercritical fluid flow. Eur. J. Mech.B 1996, 15, 569–596. [Google Scholar]
- Yamamoto, S.; Furusawa, T.; Matsuzawa, R. Numerical simulation of supercritical carbon dioxide flows across critical point. Int. J. Heat Mass Transf. 2011, 54, 774–782. [Google Scholar]
- Liu, J.; Do-Quang, M.; Amberg, G. Numerical simulation of rapid expansion of supercritical carbon dioxide. Aiche J. 2015, 61, 317–332. [Google Scholar] [CrossRef]
- He, Z.; Tian, S.; Li, G.; Wang, H.; Shen, Z.; Xu, Z. The pressurization effect of jet fracturing using supercritical carbon dioxide. J. Nat. Gas Sci. Eng. 2015, 27, 842–851. [Google Scholar] [CrossRef]
- Wang, H.Z.; Li, G.S.; Tian, S.C.; Cheng, Y.X.; He, Z.G.; Yu, S.J. Flow field simulation of supercritical carbon dioxide jet: Comparison and sensitivity analysis. J. Hydrodyn. 2015, 27, 210–215. [Google Scholar] [CrossRef]
- Luo, X.; Wang, S.; Wang, Z.; Jing, Z.; Lv, M.; Zhai, Z.; Han, T. Experimental investigation on rheological properties and friction performance of thickened CO2 fracturing fluid. J. Pet. Sci. Eng. 2015, 133, 410–420. [Google Scholar] [CrossRef]
- Khanpour, R.; Sheikhi-Kouhsar, M.R.; Esmaeilzadeh, F.; Mowla, D. Removal of contaminants from polluted drilling mud using supercritical carbon dioxide extraction. J. Supercrit. Fluid. 2014, 88, 1–7. [Google Scholar] [CrossRef]
- Tian, S.; He, Z.; Li, G.; Wang, H.; Shen, Z.; Liu, Q. Influences of ambient pressure and nozzle-to-target distance on SC-CO2 jet impingement and perforation. J. Nat. Gas Sci. Eng. 2016, 29, 232–242. [Google Scholar] [CrossRef]
- Hu, Y.; Kang, Y.; Wang, X.; Li, X.; Huang, M.; Zhang, M. Experimental and theoretical analysis of a supercritical carbon dioxide jet on wellbore temperature and pressure. J. Nat. Gas Sci. Eng. 2016, 36, 108–116. [Google Scholar] [CrossRef]
- He, Z.; Li, G.; Tian, S.; Wang, H.; Shen, Z.; Li, J. SEM analysis on rock failure mechanism by supercritical CO2 jet impingement. J. Pet. Sci. Eng. 2016, 146, 111–120. [Google Scholar] [CrossRef]
- Sheng, M.; Li, G.; Huang, Z.; Tian, S.; Qu, H. Experimental study on hydraulic isolation mechanism during hydra-jet fracturing. Exp. Therm. Fluid Sci. 2013, 44, 722–726. [Google Scholar] [CrossRef]
- Du, Y.K.; Wang, R.H.; Ni, H.J.; Huang, Z.Y.; Li, M.K. Dynamical analysis of high-pressure supercritical carbon dioxide jet in well drilling. J. Hydrodyn. 2013, 25, 528–534. [Google Scholar] [CrossRef]
- Cheng, Y.; Li, G.; Wang, H.; Shen, Z.; Tian, S.; Fan, X. Pressure boosting effect in perforation cavity during supercritical carbon dioxide jet fracturing. At. Sprays 2013, 23, 463–474. [Google Scholar] [CrossRef]
- Biao, F.J.; Liu, H.; Zhang, S.C.; Zhang, J.; Wang, X.X. A numerical study of parameter influences on horizontal hydraulic fracture. Pet. Eng. 2011, 10, 228–235. [Google Scholar]
- Lian, Z.L.; Jing, Z.; Heng-An, W.U.; Wang, X.X.; Xue, B. A simulation study of hydraulic fracturing propagation with a solid-fluid coupling model. Rock Soil Mech. 2008, 11, 3021–3026. [Google Scholar]
- Li, H.; Zou, Y.S.; Liu, S.; Liu, G.Q.; Jing, Y.Z.; Ehlig-Economides, C.A. Prediction of fracture initiation pressure and fracture geometries in elastic isotropic and anisotropic formations. Rock Mech. Rock Eng. 2016, 50, 1–13. [Google Scholar] [CrossRef]
- Hossain, M.M.; Rahman, M.K.; Rahman, S.S. Hydraulic fracture initiation and propagation: Roles of wellbore trajectory, perforation and stress regimes. J. Pet. Sci. Eng. 2000, 27, 129–149. [Google Scholar] [CrossRef]
- Valkó, P.; Economides, M.J. Propagation of hydraulically induced fractures—A continuum damage mechanics approach. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1994, 31, 221–229. [Google Scholar] [CrossRef]
- Fang, C.; Chen, W.; Amro, M. Simulation study of hydraulic fracturing using super critical CO2 in shale. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, UAE, 10–13 November 2014. [Google Scholar]
- Ishida, T.; Aoyagi, K.; Niwa, T.; Chen, Y.; Murata, S.; Chen, Q.; Nakayama, Y. Acoustic emission monitoring of hydraulic fracturing laboratory experiment with supercritical and liquid CO2. Geophys. Res. Lett. 2012, 39, 16309. [Google Scholar] [CrossRef]
- Zolfaghari, N.; Meyer, C.R.; Bunger, A.P. Blade-shaped (PKN) Hydraulic Fracture Driven by a Turbulent Fluid in an Impermeable Rock. J. Eng. Mech. 2016, 143, 04017130. [Google Scholar] [CrossRef]
- Tang, G.; Shi, H.; Wu, Y.; Lu, J.; Li, Z.; Liu, Q.; Zhang, H. A variable turbulent Prandtl number model for simulating supercritical pressure CO2 heat transfer. Int. J. Heat Mass Transf. 2016, 102, 1082–1092. [Google Scholar] [CrossRef]
- Warpinski, N.R. Determining the minimum in situ stress from hydraulic fracturing through perforations. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1989, 26, 523–531. [Google Scholar] [CrossRef]




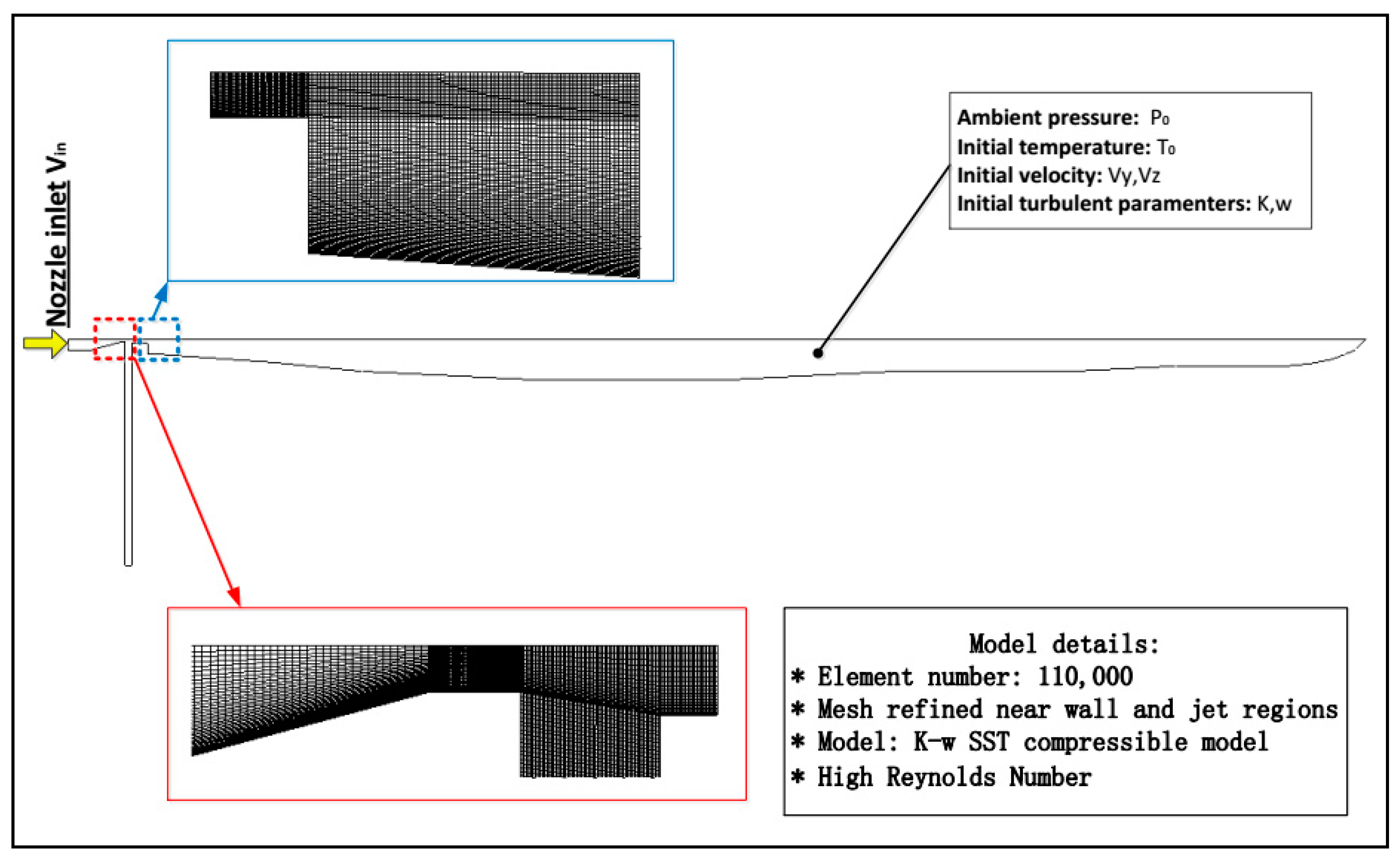

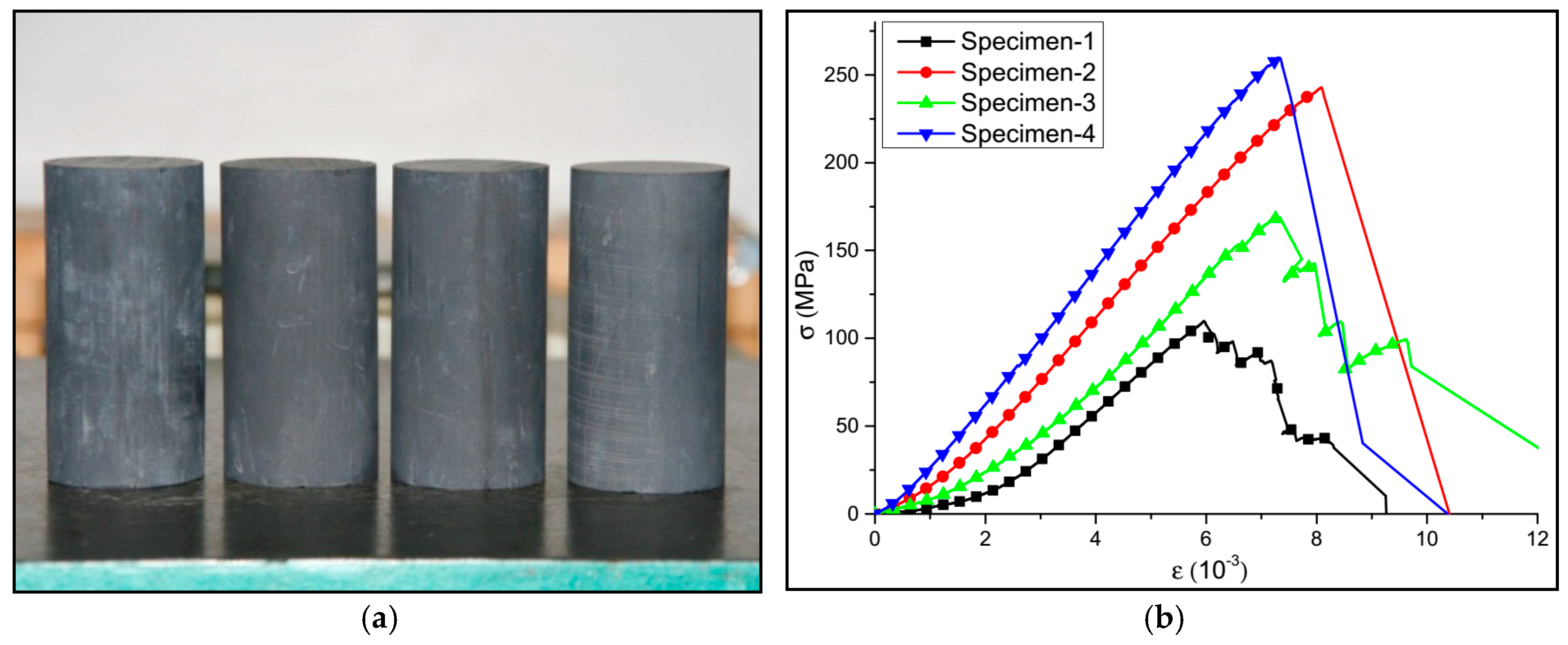
























| Item | Specimen-1 | Specimen-2 | Specimen-3 | Specimen-4 |
|---|---|---|---|---|
| Maximum Stress (MPa) | 109.654 | 242.697 | 168.549 | 259.498 |
| Maximum Strain (E-3) | 5.959 | 8.084 | 7.331 | 7.306 |
| Elasticity Modulus (GPa) | 27.655 | 35.630 | 29.613 | 39.042 |
| Tangent Modulus (GPa) | 14.040 | 28.448 | 18.996 | 34.491 |
| Poisson’s Ratio | 0.244 | 0.220 | 0.159 | 0.173 |
| Item | Symbol | Value |
|---|---|---|
| pressure difference (MPa) | 10 | |
| jet inlet pressure (MPa) | 20 | |
| ambient pressure (MPa) | 10 | |
| nozzle outlet length (mm) | 2 | |
| perforation pressure (MPa) | 3/15/15/20 | |
| in situ stress (MPa) | (5, 10)/(10, 10)/(12, 10)/(15, 10) | |
| nozzle outlet radius (mm) | 0.75/1/1.5 | |
| nozzle-to-casing inlet radius ratio | ||
| Weibull parameter | 2, 3, 4 | |
| Weibull parameter | 1.2, 1.6, 2.0 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Liu, Y.; Cai, C.; Kang, Y.; Wang, X.; Huang, M.; Chen, F. Fracture Initiation of an Inhomogeneous Shale Rock under a Pressurized Supercritical CO2 Jet. Appl. Sci. 2017, 7, 1093. https://doi.org/10.3390/app7101093
Hu Y, Liu Y, Cai C, Kang Y, Wang X, Huang M, Chen F. Fracture Initiation of an Inhomogeneous Shale Rock under a Pressurized Supercritical CO2 Jet. Applied Sciences. 2017; 7(10):1093. https://doi.org/10.3390/app7101093
Chicago/Turabian StyleHu, Yi, Yiwei Liu, Can Cai, Yong Kang, Xiaochuan Wang, Man Huang, and Feng Chen. 2017. "Fracture Initiation of an Inhomogeneous Shale Rock under a Pressurized Supercritical CO2 Jet" Applied Sciences 7, no. 10: 1093. https://doi.org/10.3390/app7101093
APA StyleHu, Y., Liu, Y., Cai, C., Kang, Y., Wang, X., Huang, M., & Chen, F. (2017). Fracture Initiation of an Inhomogeneous Shale Rock under a Pressurized Supercritical CO2 Jet. Applied Sciences, 7(10), 1093. https://doi.org/10.3390/app7101093







