Low-Complexity QRD-M with Path Eliminations in MIMO-OFDM Systems

Abstract

The QR decomposition-M algorithm (QRD-M) is a popular signal detector which has similar error performance with maximum likelihood (ML) in multiple input multiple output-orthogonal frequency division multiplexing (MIMO-OFDM) systems. The QRD-M uses M candidates at each layer, unlike the ML. However, the complexity of the QRD-M is high in huge MIMO-OFDM systems due to unnecessary survival paths at each layer. In this paper, a low-complexity QRD-M with variable number of survival paths at each layer is proposed. In the conventional QRD-M, path eliminations at the previous layer reduce the number of calculations for accumulated squared Euclidean distance (ASED) in subsequent layers. The proposed QRD-M eliminates unnecessary survival paths by comparing the ASED and the calculated threshold at each layer. The simulation results show that the proposed QRD-M maintains the error performance for the conventional QRD-M and has a very low complexity.

1. Introduction

Recently, multiple input multiple output (MIMO) systems have been used to increase spectral efficiency and channel capacity without high transmit power or wide bandwidth in a rich scattering wireless channel [1,2]. A MIMO system has been used in combination with orthogonal frequency division multiplexing (OFDM, a well-known multi-carrier transmission system), and is called MIMO-OFDM [3]. The MIMO-OFDM systems have high frequency efficiency and strong frequency-selective fading. However, since the received signal is composed of many distorted transmit signals by the fading channel, a complex signal detector is required for reliable communication. So, huge MIMO-OFDM systems which use high modulation order and have many antennas require a complex signal detector for accurate estimation of the transmit symbols. The optimal detection in MIMO-OFDM systems is maximum likelihood (ML) [4,5]. The ML calculates squared Euclidean distance (SED) between received symbols and all reference symbols for optimal error performance. However, the main disadvantage of the ML is its extremely high complexity. The number of metrics in the ML increases exponentially with respect to the number of transmit antennas and the modulation order. The QR decomposition-M algorithm (QRD-M) is the simplified ML detection based on tree search. The performance between QRD-M and ML detectors is not the same, but is similar. Unlike the ML, the QRD-M calculates accumulated squared Euclidean distance (ASED) at each layer, and selects only $M$ small distances. These $M$ small distances are usually called survival paths. To approach the error performance of the ML, $M$ must be large, but it requires a very high complexity. The main reason for the high complexity of the QRD-M is that it contains unnecessary survival paths among the $M$ survival paths. Several detections were developed to reduce the complexity of the conventional QRD-M in [6,7,8,9,10,11,12,13,14,15]. Among several detections, an adaptive QRD-M was developed in [10], a modified tree structure QRD-M was developed in [11], and a lattice reduction (LR)-aided adaptive QRD-M was developed in [12]. In [10,11,12], adaptive path eliminations were used at each layer for low complexity. However, these proposed detections still have high complexity since the average number of unnecessary survival paths is high despite the path eliminations. Specifically, modified tree structure QRD-M has high complexity when the number of transmit antennas is high because the conventional QRD-M is applied from the $\lceil N_t/O\rceil$-th layer to the first layer, where $\lceil \cdot \rceil$ denotes rounding function which towards positive infinity and $O$ denotes modulation order. Therefore, this paper proposes very low complexity QRD-M which has the same error performance as ML. At first, the proposed QRD-M calculates the threshold at each layer. Then, ASEDs are compared with the threshold and paths which are larger than the threshold are eliminated. The path eliminations continue until the first layer for very low complexity. For the efficient signal detection, the threshold is calculated adaptively at each layer, depending on the modulation order. The complexity of the proposed QRD-M is much lower than that of other QRD-M detection schemes in [10,11,12] because of the efficient threshold value considering the modulation order.

2. System Model

In this paper, a MIMO-OFDM system which has $N_t$ transmit antennas and $N_r$ receive antennas is considered where $N_r$ is greater than or equal to $N_t$. Figure 1 shows the general structure of the MIMO-OFDM transceiver. Input data is demultiplexed into $N_t$ substreams at the transmitter. Then, $N_t$ substreams go through quadrature amplitude modulation (QAM) mapping, inverse fast Fourier transform (IFFT) processors. Finally, cyclic prefix (CP) is added to decrease the effect of inter-symbol interference (ISI) and inter-carrier interference (ICI). At the receiver, MIMO received vector $Y={\left[\begin{array}{cccc}{Y}_1& Y_2& \cdots & Y_{N_r}\end{array}\right]}^T$ after the fast Fourier transform (FFT) is as follows,

$$\begin{array}{ll}Y& =HX+W\\ & =\left[\begin{array}{cccc}{H}_{11}& H_{12}& \cdots & H_{1N_t}\\ H_{21}& H_{22}& \cdots & H_{2N_t}\\ ⋮& ⋮& \ddots & ⋮\\ H_{N_{r}1}& H_{N_{r}2}& \cdots & H_{N_r{N}_t}\end{array}\right]\left[\begin{array}{c}{X}_1\\ X_2\\ ⋮\\ X_{N_t}\end{array}\right]+\left[\begin{array}{c}{W}_1\\ W_2\\ ⋮\\ W_{N_r}\end{array}\right],\end{array}$$

(1)

where $X$ denotes $N_t\times 1$ MIMO transmit vector, $H$ denotes $N_r\times N_t$ rich scattering complex Rayleigh channel matrix where the element $H_{ij}$, $i=1,2,\cdots ,N_r,j=1,2,\cdots ,N_t$ denotes channel components from the $j$-th transmit antenna to the $i$-th receive antenna, and $W$ denotes $N_r\times 1$ complex additive white Gaussian noise (AWGN) vector.

3. Conventional QRD-M

The conventional QRD-M starts from QR decomposition of the channel matrix $H$ as follows,

$$H=QR,$$

(2)

where $Q$ denotes $N_r\times N_r$ unitary quadrature matrix and $R$ denotes $N_r\times N_t$ upper triangular matrix.

Using Equation (2), the MIMO received vector in Equation (1) is rewritten as follows,

$$Y=HX+W=QRX+W,$$

(3)

Multiplying $Q^H$ on both sides of Equation (3), the modified MIMO received vector $Z={\left[\begin{array}{cccc}{Z}_1& Z_2& \cdots & Z_{N_r}\end{array}\right]}^T$ is as follows,

$$\begin{array}{ll}Z& =Q^{H}Y=RX+\tilde{W}\\ & =\left[\begin{array}{cccc}\begin{array}{c}{R}_{11}\\ 0\\ ⋮\\ 0\end{array}& \begin{array}{c}{R}_{12}\\ R_{22}\\ ⋮\\ 0\end{array}& \begin{array}{c}\cdots \\ \cdots \\ \ddots \\ 0\end{array}& \begin{array}{c}{R}_{1N_t}\\ R_{2N_t}\\ ⋮\\ R_{N_t{N}_t}\end{array}\\ 0& 0& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& 0\end{array}\right]\left[\begin{array}{c}{X}_1\\ X_2\\ ⋮\\ X_{N_t}\end{array}\right]+\left[\begin{array}{c}{\tilde{W}}_1\\ {\tilde{W}}_2\\ ⋮\\ {\tilde{W}}_{N_r}\end{array}\right],\end{array}$$

(4)

where $\tilde{W}=Q^{H}W$ denotes a modified noise vector which has the same statistical properties as the existing noise vector $W$.

In Equation (4), $\left|S\right|$ times SEDs are calculated at the $N_t$-th layer (the $N_t$-th row of $Z$) between $Z_{N_t}$ and the $k$-th reference symbol $C_k$; i.e., $k=1,2,\cdots ,\left|S\right|$, where $\left|S\right|$ denotes constellation size. In all calculated SEDs at the $N_t$-th layer, $M$ paths are selected as survival paths and the remaining $\left|S\right|-M$ paths are discarded. These $M$ survival paths are extended to the $\left(N_t-1\right)$-th layer and operations at the $N_t$-th layer end. The SED $E_{N_t,k}$ between $Z_{N_t}$ and $C_k$ is as follows:

$$E_{N_t,k}={\left|Z_{N_t}-R_{N_t{N}_t}{C}_k\right|}^2.$$

(5)

At the $\left(N_t-1\right)$-th layer, $M\left|S\right|$ times SEDs are calculated. However, for accurate estimation of transmit symbols, the SED in Equation (5) is used to calculate the ASED. The ASED $E_{N_t-1,k}^{d_{N_t}}$ between $Z_{N_t-1}$ and $C_k$ which considers the SED for the $d_{N_t}$-th survival path in Equation (5) is as follows:

$$E_{N_t-1,k}^{d_{N_t}}={\left|Z_{N_t-1}-\left(R_{N_t-1N_t-1}{C}_k+R_{N_t-1N_t}{\widehat{X}}_{N_t}^{d_{N_t}}\right)\right|}^2+E_{N_t,d_{N_t}},$$

(6)

where ${\widehat{X}}_{N_t}^{d_{N_t}}$ is temporarily estimated symbol at the $N_t$-th layer corresponding to the $d_{N_t}$-th survival path.

Like the $N_t$-th layer, $M$ paths are selected as survival paths, and the remaining $M\left|S\right|-M$ paths are discarded. The $M$ survival paths are extended to the next layer and these operations continue until the first layer for accurate estimation of transmit symbols. At the $m$-th layer, $M\left|S\right|$ times ASEDs are calculated. The ASED $E_{m,k}^{d_{m+1}}$ between $Z_m$ and $C_k$ which considers the ASED for the $d_{m+1}$-th survival path is as follows:

$$E_{m,k}^{d_{m+1}}={\left|Z_m-\left(R_{mm}{C}_k+{\displaystyle \sum _{i=m+1}^{N_t^{}}{R}_{mi}{\widehat{X}}_i^{d_i}}\right)\right|}^2+E_{m+1,d_{m+1}}^{d_{m+2}}.$$

(7)

Finally, transmit symbols are estimated by selecting the path with the smallest ASED at the first layer and an algorithm of conventional QRD-M ends.

Figure 2 shows the tree structure for the conventional QRD-M $\left(M=4\right)$ using quadrature phase shift keying (QPSK) modulation in a $4\times 4$ system. In Figure 2, bold lines are survival paths and bold circles are estimated transmit symbols. The conventional QRD-M has extremely high complexity in huge MIMO-OFDM systems because it calculates $M\left|S\right|$ times SEDs at each layer. In Section 4, the authors try to reduce the complexity of the conventional QRD-M by eliminating unnecessary survival paths at all layers. The proposed QRD-M eliminates unnecessary survival paths by comparing the ASEDs and adaptively calculated threshold at each layer. In path eliminations, paths larger than the threshold are regarded as unnecessary survival paths and are eliminated.

4. Proposed Low-Complexity QRD-M

The whole complexity of the conventional QRD-M is very high for achieving the error performance of the ML. The main reason for the high complexity is the calculation of many unnecessary survival paths at all layers. To reduce the complexity of the conventional QRD-M, the authors try to eliminate unnecessary survival paths by comparing the ASEDs and adaptively calculated threshold at each layer. The proposed QRD-M starts with the QR decomposition and performs the same operations from Equations (2) to (5). As a result of Equation (5), $T$ paths are selected in an ascending order, where $T={\log }_2\left|S\right|$ is the number of temporarily selected survival paths at each layer to calculate the threshold and to eliminate unnecessary survival paths. The number of survivor paths increases exponentially as the modulation order increases. The value of $T$ increases linearly as the constellation size increases nonlinearly. So, the used modulation scheme in the system must be considered to calculate the reliable thresholds and successfully eliminate unnecessary survival paths. For general notation of the proposed QRD-M, Equation (5) is rewritten as follows:

$${\left[E_{N_t,k}\right]}_{N_t}={\left|Z_{N_t}-R_{N_t{N}_t}{C}_k\right|}^2,$$

(8)

where ${[\cdot ]}_l$ denotes the $l$-th $\left(2\le l\le N_t\right)$ operation loop to calculate the threshold ${\eta }_l$.

In Equation (8), for easy explanation, it is assumed that ${\left[E_{N_t,k}\right]}_{N_t}$ is sorted in an ascending order with respect to $k$. That is, ${\left[E_{N_t,1}\right]}_{N_t}$ is the smallest SED and ${\left[E_{N_t,\left|S\right|}\right]}_{N_t}$ is the largest SED at the $N_t$-th layer. So, $T$ paths from ${\left[E_{N_t,1}\right]}_{N_t}$ to ${\left[E_{N_t,T}\right]}_{N_t}$ are temporarily selected at the $N_t$-th layer. With each temporarily selected path, the ASED ${\left[E_{N_t-1,k}^{p_{N_t}}\right]}_{N_t}$ between $Z_{N_t-1}$ and $C_k$ which considers the $p_{N_t}$-th temporarily selected path is as follows:

$${\left[E_{N_t-1,k}^{p_{N_t}}\right]}_{N_t}={\left|Z_{N_t}-\left(R_{N_t-1N_t-1}{C}_k+R_{N_t-1N_t}{\widehat{X}}_{N_t}^p\right)\right|}^2+{\left[E_{N_t,p_{N_t}}\right]}_{N_t},$$

(9)

and the error vector with respect to $k$ in Equation (9) is as follows:

$${\left[E_{N_t-1}^{p_{N_t}}\right]}_{N_t}=\left[\begin{array}{cccc}{\left[E_{N_t-1,1}^{p_{N_t}}\right]}_{N_t}& {\left[E_{N_t-1,2}^{p_{N_t}}\right]}_{N_t}& \cdots & {\left[E_{N_t-1,\left|S\right|}^{p_{N_t}}\right]}_{N_t}\end{array}\right].$$

(10)

Then, the smallest element in Equation (10) is selected and these operations continue until the first layer for all $T$ paths. Except for the $N_t$-th layer, all layers calculate $T\left|S\right|$ ASEDs. The matrix of ASEDs at the first layer of the $N_t$-th operation loop is as follows:

$${\left[E\right]}_{N_t}=\left[\begin{array}{c}{\left[E_1^1\right]}_{N_t}\\ {\left[E_1^2\right]}_{N_t}\\ ⋮\\ {\left[E_1^T\right]}_{N_t}\end{array}\right],$$

(11)

where rows denote an index of temporarily selected path at the $N_t$-th layer and columns denote an index of reference symbol.

In ${\left[E\right]}_{N_t}$, the smallest element is selected as the $N_t$-th threshold ${\eta }_{N_t}$ to eliminate the unnecessary survival paths at the $N_t$-th layer. Then, each element in SEDs vector ${\left[E_{N_t}\right]}_{N_t}$ which is the set of ${\left[E_{N_t,k}\right]}_{N_t}$ with respect to all $k$ in Equation (8) is compared with ${\eta }_{N_t}$ and the element larger than ${\eta }_{N_t}$ is eliminated by considering the unnecessary survival path. It is assumed that the number of existing survival paths is $M_{N_t}$ after the eliminations of unnecessary survival paths at the $N_t$-th layer. $\left|S\right|M_{N_t}$ paths are extended to the next layer to select $M$ paths at the $\left(N_t-1\right)$-th layer. The only difference between the $N_t$-th layer and the $\left(N_t-1\right)$-th layer is that ASED is used at the $\left(N_t-1\right)$-th layer, unlike the $N_t$-th layer. To eliminate unnecessary paths at the $\left(N_t-1\right)$-th layer, the $\left(N_t-1\right)$-th threshold ${\eta }_{N_t-1}$ should be calculated like ${\eta }_{N_t}$. The way to calculate ${\eta }_{N_t-1}$ is similar to the calculation of ${\eta }_{N_t}$.

The $l$-th threshold ${\eta }_l$ is calculated on the $l$-th operation loop by selecting the smallest element in ${\left[E\right]}_l$, like in Equation (10). Then, each element in ASEDs vector ${\left[E_l\right]}_l$ is compared with ${\eta }_l$ and the element larger than ${\eta }_l$ is eliminated. It is assumed that the number of existing survival paths is $M_l$ after the elimination of the unnecessary survival paths at the $l$-th layer. The $\left|S\right|M_l$ paths are extended to the next layer to select $M$ paths at the $\left(l-1\right)$-th layer, and these operations continue until the first layer for lower complexity. Finally, MIMO transmit vector ${\widehat{X}}_{\mathrm{P}}={\left[\begin{array}{cccc}{\widehat{X}}_{\mathrm{P},1}& {\widehat{X}}_{\mathrm{P},2}& \cdots & {\widehat{X}}_{\mathrm{P},N_t}\end{array}\right]}^T$ is estimated at the first layer by selecting the path which has the smallest ASED and an algorithm of proposed QRD-M ends.

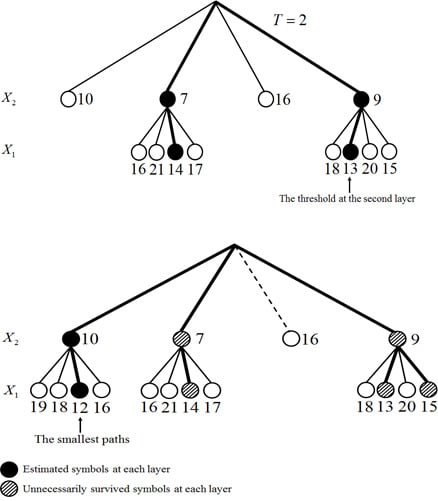
In Figure 3a, the calculation of threshold is illustrated as follows. The value of $T$ is 2 because the used modulation scheme is QPSK $\left(T={\log }_{2}4=2\right)$. At the second layer, SEDs in Equation (8) are calculated as 10, 7, 16, 9. In four SEDs, two small values (7 and 9) are selected. Then, at the first layer, ASEDs in Equation (10) are calculated by using SEDs for 7 and 9. The final ASEDs are 16, 21, 14, and 17 from SED for 7 and 18, 13, 20, and 16 from SED for 9. Among eight ASEDs, the smallest value is 13, and it is selected as threshold for path eliminations at the second layer. Note that the smallest value is not 14, which is extended from SED for 7. So, the used modulation scheme must be considered for low complexity. In Figure 3b, path eliminations are illustrated as follows. At the second layer, the SED for 16 is eliminated because it is larger than the threshold. Then, at the first layer, ASEDs in Equation (10) are calculated for SEDs 10, 7, and 9. Note that ASEDs in Equation (10) are calculated for SEDs 10, 7, 16, and 9 in the conventional QRD-M. The final ASEDs are 19, 18, 12, and 16 for SED 10 and 16, 21, 14, and 17 for SED 7 and 18, 13, 20, and 16 for SED 9. Among twelve ASEDs, the smallest value is 12 and all transmit symbols are estimated.

Figure 4 shows the flow chart of the proposed QRD-M. It is composed of two stages for the calculation of the threshold and path eliminations. The detailed steps of the proposed QRD-M algorithm are presented in

Table 1. The whole algorithm of the proposed QRD-M.

1: $H=QR,Z=Q^{H}Y.$

2: for $k=1:\left|S\right|$

3:   Calculate ${\left[E_{N_t,k}\right]}_{N_t}$ for the $k$-th modulated symbol.

4: end

5: for $l=N_t:-1:1$

6:   for $m=l-1:-1:1$

7:     Select $T$ paths in an ascending order in $\left[E_l\right].$

8:     for $p=1:T$

9:       for $k=1:\left|S\right|$

10:         Calculate ${\left[E_{m,k}^{p_{m+1}}\right]}_l$ for the $k$-th modulated symbol.

11:       end

12:       Find the smallest value in ${\left[E_m^{p_{m+1}}\right]}_l$

13:     end

14:   end

15:   ${\eta }_l=\min \left\{{\left[E\right]}_l\right\}.$

16:   for $k=1:\left|S\right|$

17:     if ${\left[E_{l,k}\right]}_l>{\eta }_l$

18:      Path corresponding to ${\left[E_{l,k}\right]}_l$ is eliminated.

19:     end

20:   end

21:   $\left|S\right|M_l$ paths are extended to the next layer and $M$ paths are selected.

22: end

23: Estimate the ${\widehat{X}}_{\mathrm{P}}$ by selecting the path which has the smallest ASED.

.

Table 2. The number of complex multiplications. DFE: decision feedback equalizer.

Detection Scheme	The Number of Complex Multiplications
Conventional QRD-M	$12N_t^3+4N_t^2+8L+4LM{\displaystyle \sum _{l=2}^{N_t}\left(l+1\right)}$
Proposed QRD-M	$12N_t^3+4N_t^2+8L+4L{\displaystyle \sum _{l=2}^{N_t}{M}_l\left(l+1\right)}$
Extended DFE	$12N_t^3+4N_t^2+4+L+L{\displaystyle \sum _{l=2}^{N_t}\left(4l+1\right)}+4L{N}_t^2+{\mathrm{CLLL}}_{N_t}$

represents the number of complex multiplications for the conventional and the proposed QRD-M. For simple representation, it is assumed that the number of transmit antennas is the same as receive antennas. The number of complex multiplications $12N_t^3+4N_t^2$ is always required for calculating the inverse channel matrix, QR decomposition of the channel and multiplying $Q^H$ with $Y$. Additionally, the number of complex multiplications for the extended decision feedback equalizer (E-DFE) is represented where ${\mathrm{CLLL}}_{N_t}$ is the number of complex multiplications for complex Lenstra–Lenstra–Lovász (CLLL) algorithm in a $N_t\times N_t$ system [16]. The aim of the inverse channel matrix calculation is to decide the detection order at the receiver so as to minimize the error propagation.

5. Simulation Results

This section shows the simulation results for the error performance and the complexity of the proposed QRD-M. As simulation parameters, the size of FFT was 128 and the size of CP was 32. Finally, all transmit symbols go through a Rayleigh fading channel with seven multi-paths.

In Figure 5, bit error rate (BER) performances for the conventional and the proposed QRD-M using 16-QAM modulation are shown in $2\times 2$ and $4\times 4$ systems. Additionally, in Figure 6, BER performances for the conventional and the proposed QRD-M using 64-QAM modulation are shown in $4\times 4$ and $8\times 8$ systems. In Figure 5 and Figure 6, the BER performance for the ML is also shown to present the optimal error performance of the proposed QRD-M. The BER performances for the proposed QRD-M is the same as conventional QRD-M and ML regardless of the used modulation scheme. Thus, the proposed QRD-M successfully eliminates unnecessary survival paths from the $N_t$-th layer to the first layer due to the properly calculated thresholds at all layers. In Figure 7, Figure 8, and Figure 9, complexities for the conventional and the proposed QRD-M using 16-QAM modulation are shown by calculating average number of metric operations in $2\times 2$, $4\times 4$, and $8\times 8$ systems, respectively. In Figure 7, the complexities for the adaptive QRD-M in [10] and LR-aided QRD-M in [12] are also shown for comparison. The average number of metric operations for the conventional QRD-M is shown with $M=1,4,8,16$, and all results are not changed with respect to the signal-to-noise ratio (SNR) because the number of survival paths at all layers is $M.$ However, the average number of metric operations of the proposed QRD-M is lower than the conventional QRD-M $\left(M=4\right)$, and is approximated to the conventional QRD-M $\left(M=1\right)$ with respect to increased SNR because the difference of ASEDs between necessary survival paths and unnecessary survival paths is large. Additionally, the average number of metric operations of the proposed QRD-M is lower than the adaptive QRD-M and LR-aided QRD-M due to more path eliminations by adaptively calculated threshold at each layer.

In Figure 8 and Figure 9, complexities for the conventional and the proposed QRD-M using 16-QAM modulation are shown in $4\times 4$ and $8\times 8$ systems. Specifically, modified tree structure QRD-M is also shown in Figure 9 to provide visible results of complexity improvement for the proposed QRD-M. In Figure 8 and Figure 9, the average number of metric operations for the proposed QRD-M is approximated to the conventional QRD-M $\left(M=1\right)$ with respect to increased SNR. In Figure 9, the average number of metric operations for the proposed QRD-M is lower than the modified tree structure QRD-M in [11] at all SNRs because the modified tree structure QRD-M uses a fixed value of threshold and an accuracy is low when the number of transmit antennas is large. In addition, the modified tree structure QRD-M eliminates unnecessary paths only from the top layer to the $\lceil N_t/O\rceil$-th layer, and the conventional QRD-M is applied under the $\lceil N_t/O\rceil$-th layer.

In Figure 10 and Figure 11, the number of complex multiplications for the conventional and the proposed QRD-M using 16-QAM and 64-QAM modulation is shown with respect to the number of transmit antennas, respectively. For comparison, the number of complex multiplications for the E-DFE, which has poor error performance compared to proposed QRD-M in [16], is also shown. In this simulation, it is assumed that the multiplication of two complex numbers requires four real multiplications. To show the complexity improvements with respect to SNR, the number of complex multiplications for the proposed QRD-M is shown with SNR values of 10, 20, and 30. The complex multiplications for the proposed QRD-M (10 dB) are slightly lower than the conventional QRD-M. However, complex multiplications for the proposed QRD-M (20 dB) are much lower than the conventional QRD-M because many unnecessary paths are eliminated due to relatively small noise power. Finally, complex multiplications for the proposed QRD-M (30 dB) are lower than the E-DFE because the number of unnecessary survival paths for the proposed QRD-M is very low due to high SNR. Additionally, in Figure 11, complex multiplications for the proposed QRD-M (20 dB) are higher than the E-DFE unlike Figure 10 because the complexity of the E-DFE is not significantly affected by nonlinearly increasing constellation size. Instead, the performance degradation is very severe for use in real time systems. So, the proposed QRD-M can be used well with low complexity compared to the E-DFE when the channel environment is good.

For further comparisons,

Table 3. The comparisons for the complexity ratio using 16-QAM modulation in a $4\times 4$ system. SNR: signal-to-noise ratio.

Detection Scheme	The Decreased or Increased Ratio Compared to the Conventional QRD-M	The Increased Ratio in [6,7,8,9] Compared to the Proposed QRD-M with Different SNR
Simplified QRD-M	About 21% decreased	About 55% increased (10 dB) About 63% increased (20 dB)
Combined QRD-M and Kalman filter	About 59% decreased	About 17% increased (10 dB) About 25% increased (20 dB)
Pseudo-inverse based QRD-M	About 50% decreased	About 26% increased (10 dB) About 34% increased (20 dB)
Advanced QRD-M	About 26% increased	About 102% increased (10 dB) About 110% increased (20 dB)
Proposed QRD-M	About 76% decreased (10 dB) About 84% decreased (20 dB)

represents the comparisons for the complexity ratio using 16-QAM modulation in $4\times 4$ system. In Table 3, a simplified QRD-M [6], combined QRD-M and Kalman filter [7], a pseudo-inverse-based QRD-M [8], and an advanced QRD-M [9] are compared with the conventional QRD-M and the proposed QRD-M. The error performances for the conventional QRD-M, existing algorithms, and the proposed QRD-M are almost the same. Therefore, only the complexity is compared. The main advantages for the proposed QRD-M compared to existing QRD-M algorithms are summarized with two factors. First, the number of complex multiplications for the proposed QRD-M is much lower than existing QRD-M algorithms. For example, the complexity for the pseudo-inverse-based QRD-M is about 1.26 times and 1.34 times higher than the proposed QRD-M at 10 dB and 20 dB, respectively. Second, the complexity for the proposed QRD-M is variable with respect to the SNR, while existing QRD-M algorithms have fixed or almost unchanging complexity with respect to the SNR.

6. Conclusions

This paper proposes a low-complexity QRD-M which eliminates unnecessary survival paths by comparing the ASEDs and the calculated threshold at each layer. For efficient path eliminations, the proposed QRD-M calculates thresholds adaptively considering the used modulation scheme. In the simulation results, the BER performances for the proposed QRD-M is the same as conventional QRD-M and ML, despite a high modulation order. Additionally, the average number of metric operations for the proposed QRD-M is approximated to the conventional QRD-M $\left(M=1\right)$ with respect to increased SNR. In order to justify the better performance for the proposed QRD-M, the complexity for several QRD-M algorithms is compared with the proposed QRD-M. The complexity for the proposed QRD-M is lower than several QRD-M algorithms in [6,7,8,9,10,11,12] because the proposed QRD-M eliminates many unnecessary survival paths due to adaptively calculated thresholds at all layers considering the used modulation scheme. For further comparisons, the complexity for the E-DFE in [16] which has poor error performance is also compared with the proposed QRD-M. The complexity for the E-DFE is higher than the proposed QRD-M at 10 dB SNR for 16-QAM and 20 dB for 64-QAM. However, the BER performance for the proposed QRD-M is decreased with respect to increased SNR, and it has lower BER performance than the E-DFE at 20 dB SNR for 16-QAM and 30 dB SNR for 64-QAM. Thus, the proposed QRD-M can be useful for practical implementation in huge MIMO-OFDM systems which require optimal error performance.