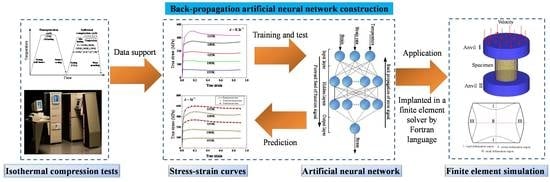
Artificial Neural Network-Based Constitutive Relationship of Inconel 718 Superalloy Construction and Its Application in Accuracy Improvement of Numerical Simulation

Abstract

The application of accurate constitutive relationship in finite element simulation would significantly contribute to accurate simulation results, which play critical roles in process design and optimization. In this investigation, the true stress-strain data of an Inconel 718 superalloy were obtained from a series of isothermal compression tests conducted in a wide temperature range of 1153–1353 K and strain rate range of 0.01–10 s⁻¹ on a Gleeble 3500 testing machine (DSI, St. Paul, DE, USA). Then the constitutive relationship was modeled by an optimally-constructed and well-trained back-propagation artificial neural network (ANN). The evaluation of the ANN model revealed that it has admirable performance in characterizing and predicting the flow behaviors of Inconel 718 superalloy. Consequently, the developed ANN model was used to predict abundant stress-strain data beyond the limited experimental conditions and construct the continuous mapping relationship for temperature, strain rate, strain and stress. Finally, the constructed ANN was implanted in a finite element solver though the interface of “URPFLO” subroutine to simulate the isothermal compression tests. The results show that the integration of finite element method with ANN model can significantly promote the accuracy improvement of numerical simulations for hot forming processes.

1. Introduction

Inconel 718 is a typical nickel-based superalloy extensively applied in aero engines and gas turbines due to its superior corrosion resistance, oxidation resistance, heat resistance and high strength, creep strength [1,2,3]. Exactly because of its high strength and outstanding heat-resistance, it is a hard issue to process Inconel 718 superalloy under low temperature. However, the flow behaviors of Inconel 718 superalloy become extremely complicated under elevated temperature not only due to concomitant hardening and softening behaviors, which mainly include three metallurgical phenomena: work hardening (WH) as well as the subsequent dynamic recovery (DRV) and dynamic recrystallization (DRX) [4,5,6,7] but also due to the precipitation and dissolution of the three different intermetallic precipitation phases, namely γ’, γ” and δ phases [2]. The flow behaviors of materials are generally described by constitutive relationship: the intrinsic relationship among the process variables such as stress, strain, strain rate and temperature. Constitutive relationship is usually applied to the numerical computation to predict the deformation behaviors of materials [8]. Accurate constitutive relationship is the premise of reliable numerical computation results. Therefore, how to accurately construct constitutive relationship has been a problem attracting more and more attention.

For decades, numerous researchers have contributed to three types of constitutive models including phenomenological, analytical and semi-empirical or empirical ones [9]. However, in recent years, a more adaptable and easier modeling approach, artificial neural network (ANN) has been developed and applied in the characterizing and prediction of material flow behaviors. ANN, which emulates the structures, mechanisms and functions of biological neural networks, has a data-driven black-box structure [10] and can automatically learn and grasp the laws of data, even conducted accurate prediction beyond the data already existing. Explicit professional knowledge is not particularly important for the researchers using ANN model, and the critical work is collecting the data of some typical examples. Due to such superiority, the ANN was widely used in various fields, such as the classification of olive farms [11], and the segmentation of the visual object [12]. ANN contains a ‘learning rule’ to modify the weights of the connections on the basis of the input patterns. The commonly used learning rules mainly include Hebbian rule, delta rule, competitive learning rule, and anti-Hebbian rule [13], in which delta rule is often applied in the most widely and successfully used ANN called ‘back-propagation artificial neural network’. In back-propagation ANN, ‘learning’ is a supervised process which follows with each cycle through the feed-forward computation of activations and the backward propagation of error signals for weight adjustments via the generalized delta rule [14]. Recently, considerable efforts have been spent on the constitutive description of several alloys by back-propagation ANN model. Liu et al. [15], Phaniraj et al. [16], Mandal et al. [17], Sabokpa [18] et al. employed back-propagation artificial neural network models to predict the flow behaviors of high-speed steel, carbon steels, type 304L stainless steel, AZ81 magnesium alloy, etc. These reports revealed that back-propagation ANN is an effective tool to predict the complex non-linear hot flow behaviors by self-training.

Despite the fact that plenty of researchers have developed ANN models to describe the constitutive relationships of various materials, further researches with greater depth have been rarely implemented. On the other side, some researchers combined ANN with finite element method (FEM) to handle actual engineering problems. For instance, Meo et al. [19] and Guarize et al. [20] employed ANN and FEM to optimize permanent magnet flux switching generator and analyze the dynamic response of slender marine structures respectively. In these researches, ANN and FEM were still two independent tools. In contrast, in this work, a new application method of ANN and FEM was put forward based on the well-constructed ANN model. Here, the constructed ANN model for the constitutive relationship of Inconel 718 superalloy was successfully integrated with FEM by Fortran language. As is known, the stress-strain data amount and accuracy input into the finite element (FE) model have a significant influence on the simulation accuracy of the hot forming processes. Relative to in the traditional way of importing stress-strain data into the FE solver, in the way described above, the ANN model can predict abundant and accurate stress-strain data automatically for FE solver. Thus, the accuracy of FE simulation could be strongly guaranteed. Before this constitutive relationship with a new style, a continuous mapping relationship was constructed by predicting abundant stress-strain data in extensive deformation conditions. Such a constitutive relationship reflects the continuous mapping of stress to strain, strain rate and temperature.

This work focused on the constitutive relationship construction of Inconel 718 superalloy using ANN model and its application in accuracy improvement of FE numerical simulation. The core of the FE model with high accuracy is the accurate constitutive relationship in wide ranges of temperature, strain and strain rate. In this research, this is guaranteed by a well-trained ANN model taking temperature (T), strain rate ($\dot{\epsilon }$) and true strain ($\epsilon$) as the input variables, and true stress ($\sigma$) as the output variable. Those fundamental data used for the training and test of ANN model were collected from a series of isothermal compression tests conducted by a Gleeble 3500 thermo-mechanical simulator. This work put forward an artificial neural network-based route to improve the FE numerical simulation accuracy of hot forming processes.

2. Experiments

2.1. Material and Experiment Procedures

The detailed chemical compositions of Inconel 718 superalloy are as follows (wt %): Ni 52.5, Cr 18.9, Nb 5.2, Mo 3.2, Ti 1.0, Al 0.6, Co 0.02, C 0.08, and balance Fe. From the raw material, totally 18 cylinders with diameter of 10 mm and height of 12 mm were machined as the specimens by wire-electrode cutting. The experimental schedule of isothermal compression tests was shown in Figure 1. According to the schedule, the specimens were firstly heated to 1373 K and held for 12 h in a furnace to obtained homogenized microstructure. In order to accurately control the temperature in the tests, two K-type thermocouple wires were welded on the specimens to record the real-time temperature of the specimens. Then the specimens were respectively fixed at the exact center of the anvils on a computer-controlled, servo-hydraulic Gleeble 3500 testing machine (in Figure 2a), heated to designated temperatures (1203, 1253, 1303, and 1353 K) with a fixed heating rate of 5 K/s and kept in these temperatures for 180 s to reduce anisotropy and eliminate internal temperature gradients. Subsequently, these specimens were respectively compressed to 40% height with the strain rates of 0.01, 0.1, 1 and 10 s⁻¹. The realistic experimental process was shown in Figure 2b. Besides, two extra experiments under the temperature of 1153 K and strain rates of 0.1 and 1 s⁻¹ were appended. The corresponding results would be used to validate the predictability of ANN and accuracy of FE model. After the isothermal compression tests, the specimens were water quenched immediately to keep the deformed microstructure at elevated temperature. In these tests, a computer control automatic data acquisition system was applied to monitor the experimental data continuously. The recorded normal stress and normal strain were converted into the homologous true stress and true strain according to the formulae in Equations (1) and (2).

$${\sigma }_{\mathrm{T}}={\sigma }_{\mathrm{N}}\left(1+{\epsilon }_{\mathrm{N}}\right)$$

(1)

$${\epsilon }_{\mathrm{T}}=\ln \left(1+{\epsilon }_{\mathrm{N}}\right)$$

(2)

where ${\epsilon }_{\mathrm{N}}$ and ${\epsilon }_{\mathrm{T}}$ are respectively the nominal strain and true strain, ${\sigma }_{\mathrm{N}}$ and ${\sigma }_{\mathrm{T}}$ are the nominal stress and true stress [21].

2.2. Experimental Results

The true stress-strain curves of Inconel 718 superalloy measured by previous isothermal compression tests were shown in Figure 3. As expected, the stress-strain relationship is highly non-linear, and highly susceptible to temperature, strain and strain rate. Via the comparison of one stress-strain curve with another, it can be summarized that the stress level decreases with temperature increase or strain rate decrease. This is due to the following facts. When the strain rate is accelerated, the dislocations participating in deformation in unit time increase, in this situation, deformation is unable to be coordinated duly by dislocation and grain movements, thus, the multiplication of dislocation push the stress value to a higher level. When raising the deformation temperature level, the heat activation increases the average kinetic energy in atoms, and makes atomic diffusion and dislocation movement easier, which induces the decrease in the stress level. As for each stress-strain curve, it shows an initial rapid followed by an increasingly slow work hardening (WH), after which two types of stress-strain evolution exist. In the first case, the stress decreases gradually after a single peak value, an evidence of dynamic recrystallization (DRX) dominated softening, which corresponds to the conditions of 0.01 s⁻¹ and 1203–1253 K, 0.1 s⁻¹ and 1153–1253 K, 1 s⁻¹ and 1153–1303 K and 10 s⁻¹ and 1203–1303 K. In the second case, the stress approximately keeps a steady state, an evidence of dynamic recovery (DRV) dominated softening, under the conditions of 0.01 s⁻¹ and 1303–1353 K, 0.1 s⁻¹ and 1303–1353 K, 1 s⁻¹ and 1353 K and 10 s⁻¹ and 1353 K. The metallographs under the conditions of 1203 K and 0.01 s⁻¹ and 1353 K and 0.01 s⁻¹ were shown in Figure 4. It could be seen that considerable DRX grains were generated but some initial grains are only stretched instead of transforming into new DRX grains at 1203 K, similarly, a small amount of DRX grains generate along the stretched grain boundaries at 1353 K. So it was concluded that DRV and DRX usually coexist even though one of them may play the dominant role. From the previous descriptions, it can be concluded that the compression flow behaviors of Inconel 718 superalloy are extremely complex and highly non-linear, not only due to the effects of temperature and strain rate on stress level, but also due to the evolution characteristics involving WH, DRX, DRV and even the precipitation and dissolution of γ’, γ” and δ phases.

3. ANN model

3.1. Development of ANN Model

In this work, an ANN model for the isothermal compression flow behaviors of Inconel 718 superalloy in respect of dependency of strain, strain rate and temperature, was developed by taking deformation temperature (T), strain rate ($\dot{\epsilon }$) and strain ($\epsilon$) as input variables, and true stress ($\mathsf{\sigma }$) as the only output variable [22]. The schematic representation of the ANN architecture was shown in Figure 5. In this network, all the continuous stress-strain curves measured from the isothermal compression tests were discrete with a strain interval of 0.01, and the discrete points corresponding to the strain of 0.05–0.9 were adopted as the primary data of ANN model. The total 1204 discrete data points from the 18 stress-strain curves except the four curves corresponding to 1153 K and 0.1 s⁻¹, 1303 K and 0.1 s⁻¹, 1153 K and 1 s⁻¹ and 1253 K and 1 s⁻¹ were defined as the training data of the ANN model. Then, a total 344 data points on the other four curves were considered as the test data for the ANN to evaluate of the generalization performance, namely the adaptability of ANN model to fresh forming conditions beyond training. Subsequently, the corresponding 344 experimental data points were picked out and considered as the reference points for the test work. The test work would be conducted between the reference data and the test data.

It is common that the determination of the appropriate number of hidden layers and neurons in each hidden layer is one of the most critical tasks in obtaining an accurate ANN model. It was assumed that the network structure with one or two hidden layers was adopted to test respectively, and then the appropriate number needed to be finally determined through the appropriate tolerance evaluation between the predicted and experimental data. An indicator of mean square error (MSE) as Equation (3) [23] was introduced to evaluate the training performance and the generalization performance of the ANN, and accordingly the optimal hidden layer number and neuron number would be determined by comparing the performance of different networks derived from different network structure parameters. It is noted that a smaller MSE-value indicates better network performance. As for two different network structures, i.e., one or two hidden layers, the relative MSE plots along with the number of neurons in each hidden layer were calculated respectively and shown in Figure 6. The comparison of the MSE plots between the different network structures in Figure 6 shows that the structure of two hidden layers induces lower MSE-value level, and thus it possesses higher generalization performance. Focusing on the cases with two hidden layers, the MSE-values decline with neuron number increasing, while it appears an inverse trend when the neuron number is above ten, which indicates that increasing neuron number up to 10 elevates the network performance significantly. Above all, two hidden layers and 10 neurons in each hidden layer were determined as the final network architecture.

$$MSE=\frac{1}{N}{\displaystyle \sum _{i=1}^N{\left(E_i-P_i\right)}^2}$$

(3)

where E_i and P_i are respectively an experimental stress value and the corresponding predicted stress value; N is the number of data samples.

It is noteworthy that the values of the input and output variables distribute in distinct ranges and even dimensions, which induces poor convergence speed and prediction accuracy of ANN model. Hence, a normalization process for initial true stress-strain data is essential to ensure the input and output variables being dimensionless and in an approximately same magnitude. In this research, the normalization processing was realized by Equation (4). The coefficients of 0.15 and 0.25 in Equation (4) are regulating parameters for the sake of narrowing the magnitude of the normalized data within 0.1 to 0.4. It had been demonstrated by trial and error method that such a magnitude could bring a promotion in convergence speed and prediction accuracy. In particular, ahead of the normalization processing, the logarithm style was adopted for the initial strain rates, which exhibit large magnitude distinction and may cause considerable deviations.

$$x_n=0.15+0.25\times \frac{x-0.95x_{\min }}{1.05x_{\max }-0.95x_{\min }}$$

(4)

in which x is the experimental value of input or output variable; x_min and x_max are respectively the minimum and the maximum value of input or output variable; x_n is the normalization value.

In the present network, transfer functions of the hidden layers and the output layer were chosen as tansig function and purelin function. Meanwhile, Trainbr function was assumed as the training function, and the learning function adopted learngd function. It is well accepted that learning rate directly determines the revised weight in each training cycle, simultaneously plays an important role in the convergence property of networks. Commonly, adopting a high learning rate may cause instability in training, while conversely may get low convergence speed but could keep off the local least values and approach the true least error. Consequently, a lower learning rate is usually selected for better stability and convergence property, here, 0.02 was applied in the present network. In addition, the goal of training error before anti-normalization processing was set as 0.0001.

3.2. Evaluation of ANN Model

To synthetically estimate the predictability of ANN model, two commonly used statistical indicators of correlation coefficient (R) and average absolute relative error (AARE) [24], which were expressed as Equations (5) and (6), were introduced. A high R-value close to 1 illustrates that the predicted values conform to the experimental ones well, meanwhile, a low AARE-value close to 0 indicates that the sum of the errors between the predicted and experimental values tends to be 0. Thereby, such R and AARE are expected.

$$R=\frac{{\displaystyle {\sum }_{i=1}^N(E_i-\overline{E}})(P_i-\overline{P})}{\sqrt{{\displaystyle {\sum }_{i=1}^N(E_i-\overline{E}}{)}^2{\displaystyle {\sum }_{i=1}^N{(P_i-\overline{P})}^2}}}$$

(5)

$$AARE(\%)=\frac{1}{N}{\displaystyle \sum _{i=1}^N\left|\frac{P_i-E_i}{E_i}\right|}\times 100\%$$

(6)

in which E and P are respectively the experimental value and predicted value of true stress; $\overline{E}$ and $\overline{P}$ are the mean values of E and P respectively; N is the number of predicted points.

Using the well-trained ANN model, the true stress values under experimental conditions which include the deformation conditions corresponding to the previous training points and test points were predicted. After that, the correlation relationships between the experimental and predicted true stress were expressed in Figure 7. Each point in Figure 7 takes experimental stress and predicted stress as the horizontal and vertical axis respectively. The straight line at 45 degrees from the axes is the best linear fit line. If the experimental stress is exactly equal to the predicted stress, the corresponding point would lie on this line. Besides, the lines corresponding to 5% error were presented in Figure 7 as well. If a point is within the two 5% error lines, the prediction error corresponding to the deformation condition of this point is lower than 5%. It is clearly observed that all the errors of predicted stress values were lower than 5%. The points in Figure 7, especially the ones in Figure 7a, lie very close to the ideal line, indicating well consistency between the experimental and predicted results. In addition, the R-values for the training part and test part are respectively 0.9991 and 0.9978. As stated above, such high values of correlation coefficient R suggest that the predicted stress values conform very well to the experimental ones in an alternative way. Besides, the AAREs were calculated as well. The AARE-value deriving from the test part is 1.5948%, while that for the training part is merely 0.6314%. Such minor errors signal the high accuracy exhibited in the training and test work by ANN.

The relative error (δ) [17] in Equation (7) represents the percentage error of each predicted stress-strain value relative to the homologous experimental value, in order to further and more detailedly evaluate the ANN model, it was introduced. In the training part, the relative errors range from −2.45% to 3.78%, and for the test part their distribution range is from −3.27% to 3.82%. Figure 8 expresses the columnar distribution maps of the relative errors in the training and test part. In terms of Figure 8, it is not so difficult to find that the relative errors, no matter in training or test part, are within ±4%. However, it is more noteworthy that the most of the δ-values are miraculously concentrated in the vicinity of the ideal value 0: in the training part, the δ-values of 92.8% points are within the interval of [−1%, 1%], and for the test part, 75.5% are concentrated in [−1%, 1%]. These results arisen from unbiased statistical data provide direct evidence that high precise prediction both in the training and test stage was achieved by the ANN model.

$$\delta (\%)=\frac{P_i-E_i}{E_i}\times 100\%$$

(7)

where P is a predicted stress and E is homologous experimental stress.

Figure 9 shows the stress-strain data predicted by the ANN model and their comparison with the initial experimental curves. Obviously, the predicted data can grasp the stress-strain evolution rules precisely, that is, the stress decreases with temperature increasing or strain rate decreasing, predictably indicating that the present ANN model is able to track the work hardening and dynamic softening regions of Inconel 718 superalloy. Moreover, as shown in Figure 9, the predicted points on the 14 training curves almost coincide with the experimental stress-strain curves. Compared with the predicted points on the training curves, the predicted points on the test curves of 1153 K and 0.1 s⁻¹, 1303 K and 0.1 s⁻¹, 1153 K and 1 s⁻¹ and 1253 K and 1 s⁻¹ have relatively larger deviations. Nevertheless, the maximum relative error is merely 3.82%, a quite acceptable value. By comparing the predicted and experimental true stress corresponding to training points and test points, the learning and generalization capabilities of ANN model were validated respectively. Conclusively, the present ANN model has admirable performance in describing and predicting the flow behaviors of Inconel 718 superalloy.

4. Continuous Mapping Relationship

Accurate constitutive relationship is necessary for the accurate numerical simulation. In this work, the constitutive relationship for Inconel 718 superalloy was expressed as a new style: continuous mapping relationship. Due to outstanding generalization capability of the ANN model, it can undoubtedly be employed to predict the true stress of Inconel 718 superalloy outside of the experimental conditions. In this investigation, the true stress-strain data under the temperature range of 1103–1403 K, the strain rate range of 0.01–10 s⁻¹, as well as the strain range of 0.05–0.9 were predicted. The predicted results were expressed as continuous mapping relationship among strain, strain rate, temperature and stress (illustrated in Figure 10). In Figure 10, the X-axis, Y-axis, Z-axis and V-axis respectively represent deformation temperature, strain rate, true strain and true stress. The values on V-axis, that is, the predicted true stress values under different deformation conditions are indicated by different colors. Figure 10a is a global expression of the continuous mapping relationship. It covers all the deformation conditions and homologous predicted true stress values. Therefore, any true stress values in the deformation condition scope can be read and accessed directly. Figure 10b–d, which were constructed by cutting Figure 10a into slices along with the X-axis, Y-axis, Z-axis, respectively intensively reflect the continuous mapping relationships under fixed temperatures, strain rates and strains. It can be clearly observed that, just as the experimental stress-strain data, the stress increases with the strain rate increase and deformation decrease. In addition, the greater color spans under lower temperatures and more modest ones under higher temperatures also indicate DRX and DRV dominated deformation mechanisms. So, such continuous mapping relationship has successfully articulated not only the external quantitative relationships among process parameters but also the intrinsic deformation mechanisms.

The continuous mapping relationship plays an essential part in finite element method (FEM). As is known, the stress-strain data are the most fundamental data to predict the deformation behaviors of materials with FEM. On the basis of the continuous mapping relationship, it is realizable to perform accurate numerical simulations of various hot forming processes. In this way, more reasonable design and optimization of the process parameters such as the deforming temperature, the shape of die cavity, deformation velocity, etc., can be conducted.

5. Application

During the hot deformation process, the material would experience extensive temperature and strain rate regions. Thus, the accurate numerical simulation of hot forming process naturally needs a great deal of stress-train data in wide deformation conditions. However, the measurement of experimental data is undoubtedly a time-consuming and effort-consuming task. In such a situation, the accurate prediction of stress-strain data outside of experimental conditions can actually help a lot. In this investigation, the ANN model was implanted in a finite element solver with the interface of ‘URPFLO’ subroutine of Fortran language. The prediction arithmetic of the ANN model was presented in Equations (8) and (11) [25], according to which the program codes implanting the ANN model into FE solver were written and displayed in the final Appendix A part.

The input net_j of jth node in hidden layer:

$$ne{t}_j={\displaystyle \sum _{i=1}^I{w}_{ij}{x}_i+a_j}$$

(8)

The output y_j of jth node in hidden layer:

$$y_j=\phi \left(ne{t}_j\right)=\phi ({\displaystyle \sum _{i=1}^I{w}_{ij}{x}_i+a_j})$$

(9)

The input net_k of kth node in output layer:

$$ne{t}_k={\displaystyle \sum _{j=1}^J{w}_{jk}{y}_j+b_k}={\displaystyle \sum _{i=1}^q{w}_{jk}\phi \left({\displaystyle \sum _{i=1}^I{w}_{ij}{x}_i+a_j}\right)}+b_k$$

(10)

The output z_k of kth node in output layer:

$$z_k=\psi \left(ne{t}_k\right)=\psi \left({\displaystyle \sum _{j=1}^J{w}_{jk}{y}_j+b_k}\right)=\psi \left({\displaystyle \sum _{i=1}^q{w}_{ki}\phi \left({\displaystyle \sum _{i=1}^I{w}_{ij}{x}_i+a_j}\right)}+b_k\right)$$

(11)

where x_i is the ith input vector; i, j and q are respectively the input, hidden and output layer neuron numbers; a_j and b_k are respectively the jth and kth neuron bias of hidden layer and output layer; w_ij and w_jk are respectively the weights transferring from the ith neuron of output layer to the jth neuron of hidden layer, and the jth neuron of hidden layer to the kth neuron of output layer; net_k and net_j are respectively the received values of the kth neuron for output layer and the jth neuron for hidden layer; $\psi$ and $\phi$ are respectively the transfer functions for the output layer and hidden layers; z_k and y_j are respectively the outcomes of output layer and hidden layers.

The FE solver inserted ANN model was employed to simulate the isothermal compression tests of Inconel 718 superalloy under the conditions of 1153 K and 0.1 s⁻¹, 1303 K and 0.1 s⁻¹, 1153 K and 1 s⁻¹ and 1253 K and 1 s⁻¹. The established FE model was presented in Figure 11. In the FE model, the anvils and specimen were respectively defined as rigid objects and plastic object. During the actual isothermal compression process in Gleeble 3500 test machine, constant temperature is qualitatively ensured for the specimen, so the heat transfer and thermal radiation of the specimen with the anvils and environment as well as the work-heat conversion were ignored in the present FE model. Besides, a constant shear friction coefficient of 0.1 was set to conform to the practical graphite lubricant on the contact surfaces between the anvils and specimen. To meet the demand of fixed strain rates, the compression velocity of the driver anvil (anvil I) was defined according to Equation (12). The compression rate was 60% corresponding to 7.2 mm height reduction of the specimen.

$$v=h_0\dot{\epsilon }\exp (-\dot{\epsilon }t)$$

(12)

where v stands for the instantaneous compression velocity of the driver anvil; h₀ is the original height of the specimen, and here h₀ = 12 mm; $\dot{\epsilon }$ is strain rate and t is the time point.

The effective strain and effective strain rate distributions of the specimens sectioned along the axial direction were presented respectively in Figure 12 and Figure 13. From Figure 12, it can be seen that the deformation of the specimen is inhomogeneous due to the friction between the specimen and anvils. The specimen can be broadly divided into hard deformation region, small deformation region and severe deformation region in accordance with deformation degree just as Figure 14. The friction between the specimen and anvils as well as constraint of anvils would significantly reduce the material flow abilities of the vicinity region of the end plane (region I in Figure 14), so this region is hard deformation region. The central region (region II in Figure 14) is slightly affected by the friction, meanwhile, the extrusion of the hard deformation region would greatly promote the material flow of this region, thus, large deformation would occur in the central region and it is defined as severe deformation region. As for the vicinity region of the cylindrical surface (region III in Figure 14), it is almost not affected by the friction and the extrusion of other regions. The material in this region is roughly in a state of uniaxial compression, and its deformation degree is between the ones of hard deformation region and severe deformation region, so the vicinity region of the cylindrical surface is small deformation region. These simulation results are in good agreement with the real deformation circumstances of the isothermal compression tests. Besides, it could be clearly found from Figure 12 and Figure 13 that the effective strains of the severe deformation regions under the conditions of 1153 K and 0.1 s⁻¹, 1303 K and 0.1 s⁻¹, 1153 K and 1 s⁻¹ and 1253 K and 1 s⁻¹ are all about 0.92, at the same time, the effective strain rates also reach the corresponding values of 0.1, 0.1, 1 and 1 s⁻¹ respectively, which indicate that the simulated process parameters can actually reflect the real experimental conditions.

Corresponding to the simulation experiments above, the controlled simulation experiments using the FE model imported training stress-strain data of ANN in Section 3 were also conducted. Subsequently, the stroke-load curves data were exported from the FE solver. The continuously monitored stroke-load curves by the automatic data acquisition system in the compression tests were assumed to be the ideal curves. The comparisons among the simulated stroke-load curves using different FE models and the ideal curves were presented in Figure 15. From Figure 15, it was known that the simulated evolution rules of forming load with stroke are approximately in accordance with the experimental ones, indicating that the numerical simulation can indeed provide some guidance and reference for the practical processes. However, it is obvious that the predicted stroke-load curves with the FEM-implanted ANN model lie more close to the experimental curves from the global aspect. Especially when the stroke is above 3 mm, the simulated stroke-load curves with the training stress-strain data more and more diverge from the ideal curves, but the ones with the FEM-implanted ANN model can track the ideal curves in relatively high accuracy all along. The 10% error lines were given in Figure 15 as well, from which it was clearly seen that the errors of the predicted stroke-load curves with the FEM-implanted ANN model were always within 10% except the initial deformation stage (below 1 mm of deformation stroke), but the ones with the FEM imported training stress-strain data cannot make it. It is valuable to note that, when the stroke is below 1 mm, all the simulation results appear relatively larger deviations from the ideal ones. This lies in the fact that the elastic deformation stage corresponding to the true strain below 0.05 was ignored in the imported stress-strain data or ANN model. Nevertheless, such errors appearing in the primary deformation stage have little influence on most hot forming processes with large deformation such as extrusion, forging and rolling, thus can be negligible. The above comparisons give the full proof that the present approach, integrating FEM and the ANN model for a constitutive relationship, can significantly improve the numerical simulation accuracy of hot forming processes.

6. Conclusions

(1)

The true stress level of Inconel 718 superalloy decreases with increasing temperature or decreasing strain rate. The true stress varies along with strain highly non-linearly, which represents the non-linear variation of the comprehensive effects of different action mechanisms including work hardening, dynamic recovery, dynamic recrystallization, and the interaction of intermetallic precipitation phases.

(2)

An ANN model taking the deformation temperature (T), strain rate ($\dot{\epsilon }$) and true strain (ε) as input variables and the true stress (σ) as output variable was constructed for the compression flow behaviors of Inconel 718 superalloy. The evaluation via the indicators of correlation coefficient (R), average absolute relative error (AARE) and relative error (δ) revealed that the present ANN model has admirable performance in describing and predicting the flow behaviors.

(3)

The continuous mapping relationship within the temperature range of 1103–1403 K, the strain rate range of 0.01–10 s⁻¹, and the strain range of 0.05–0.9 was constructed. Such a constitutive relationship can provide abundant and accurate stress-strain data in extensive scope for the FE model of Inconel 718 superalloy.

(4)

The simulated isothermal compression tests under the deformation conditions of 1153 K and 0.1 s⁻¹, 1303 K and 0.1 s⁻¹, 1153 K and 1 s⁻¹ and 1253 K and 1 s⁻¹ were conducted in the FE solver. The comparisons between the simulated stroke-load curves based on the FEM-implanted ANN model and the FEM that imported the training stress-strain data revealed the fact that the FE simulation adopting the FE model-implanted ANN model describing the constitutive relationship model can significantly improve the numerical simulation accuracy of hot forming processes.