Driver Fatigue Detection System Using Electroencephalography Signals Based on Combined Entropy Features

Abstract

Driver fatigue has become one of the major causes of traffic accidents, and is a complicated physiological process. However, there is no effective method to detect driving fatigue. Electroencephalography (EEG) signals are complex, unstable, and non-linear; non-linear analysis methods, such as entropy, maybe more appropriate. This study evaluates a combined entropy-based processing method of EEG data to detect driver fatigue. In this paper, 12 subjects were selected to take part in an experiment, obeying driving training in a virtual environment under the instruction of the operator. Four types of enthrones (spectrum entropy, approximate entropy, sample entropy and fuzzy entropy) were used to extract features for the purpose of driver fatigue detection. Electrode selection process and a support vector machine (SVM) classification algorithm were also proposed. The average recognition accuracy was 98.75%. Retrospective analysis of the EEG showed that the extracted features from electrodes T5, TP7, TP8 and FP1 may yield better performance. SVM classification algorithm using radial basis function as kernel function obtained better results. A combined entropy-based method demonstrates good classification performance for studying driver fatigue detection.

1. Introduction

Driver fatigue has become one of the major causes of traffic accidents globally. However, it is a complicated physiological process which is gradual and continuous, so to date there is no effective method to detect the driving fatigue.

For driver fatigue detection, physiological signals in electroencephalography (EEG), electrooculogram (EOG), sweat, saliva and voice have been all investigated. Though functional magnetic resonance imaging (fMRI) was widely used to study the operational organization of the human brain (with considerable clinical significance), it could imply high expense and operate inconveniently for driving fatigue in real driving conditions [1]. Recently, a relatively new classification techniques for functional near-infrared spectroscopy (fNIRS) was also widely used to monitor the occurrence of neuro-plasticity after neuro-rehabilitation and neuro-stimulation, it has low cost, portability, safety, low noise (compared to fMRI), and ease of use [2,3], For example, Khan used fNIRS to discriminate the alert and drowsy states for a passive brain-computer interface, obtaining average accuracies in the right dorsolateral prefrontal cortex of 83.1%, 83.4,% and 84.9% in different time windows respectively [4]. However, fNIRS is mainly at present a confirmatory study with shortcomings of poor time resolution compared with EEG/ERP (event-related potential) and signal acquisition without covering the whole brain. Comparatively speaking, EEG is most common non-invasive way to identify driver fatigue. A lot of related research in this field had been published. Simon et al. [5] used EEG alpha principal axis measurement in real traffic situation as the driver fatigue index. They found that, compared with EEG power, the alpha principal parameters gave better fatigue test sensitivity as well as specificity. Kaur et al. [6] achieved a success rate of 84.8% in the use of empirical mode decomposition (EMD) to process the EEG signal for fatigue detection. Mousa Kadhim et al. [7] used discrete wavelet transforms (DWT) to process the EEG signal for fatigue detection. DWT and fast Fourier transformation (FFT) methods were combined to correlate the distracted, fatigue, alert states corresponding to alpha-, delta-, theta- and beta-wave features, before db4, db8, sym8, coif5 wavelet transforms were performed on the EEG bands. The db4 wavelet transform yielded the highest accuracy of 85%. Correa et al. [8] studied the automated fatigue detection system with EEG-based multi-mode analysis. They found that there are 19 features for differentiation in the signal from just a single EEG channel. Based on the Wiles test, feature indices were fed into neural network classifier. A total of 18 EEG signals were analyzed with this method, and achieved an accuracy of 83.6%. The discrimination accuracy was as high as 94.25%. Steady-state visual evoked potential (SSVEP) was applied in the study by Resalat [9], who used different scan times in the optical stimulation on drivers. Two Fourier transforms were used in the feature extraction and three different linear discriminant analysis classifiers to obtain an accuracy of 98.20%.

In the EEG signal analysis, information entropies, such as fuzzy entropy, sample entropy, approximate entropy, wave entropy, power spectrum entropy and sort entropy, are often used as entropy-based feature extraction method [10,11,12,13]. These entropies are often used for quantification in the cognitive analysis of EEG signals in different mental state and sleep state, indicating that entropy index is a rather useful tool for EEG analysis.

In this paper, spectrum entropy, approximate entropy, sample entropy and fuzzy entropy are all used for EEG signals collected in normal (rest) state and fatigue driving states in order to extract features. Current research indicates that different calculation methods about entropy features have different advantages. In this study, spectrum entropy, approximate entropy, sample entropy and fuzzy entropy can be used to describe the features about the power spectrum, periodicity and approximation degree of a time series signals. In order to discuss these features based on EEG signals under the driving condition of fatigue and normal states, the above four different entropies had been used to discuss and analyze the EEG signals. The difference between the four entropy features and the comparison of the average accuracy with respect to single entropy and combined entropy were all calculated in this paper. The good results show that the performance based on the combined entropy is superior to that of the single entropy. For single entropy, we also found that the fuzzy entropy obtained a better performance.

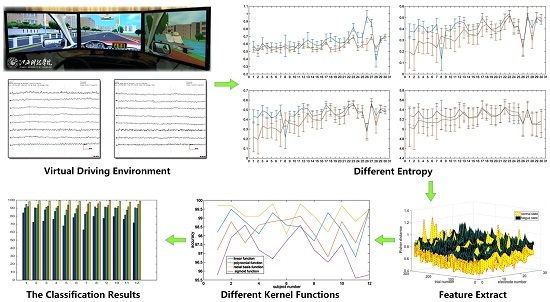
2. Materials and Methods

2.1. Entropy-Based Feature Extraction

Initially a quantity describing the degree of disorder in a thermodynamic system, entropy is later widely used to assess the uncertainty of a system [14]. From the perspective of information theory, entropy is the amount of information contained in a generalized probability distribution. As the nonlinear parametric which quantifies the complexity of a time series, it can be used to describe the non-linear, unstable dynamic EEG signals [15].

2.1.1. Spectral Entropy

Spectral entropy is evaluated using the normalized Shannon entropy, which quantifies the spectral complexity of the time series [16,17]. Spectral entropy uses the power spectrum of the signal to estimate the regularity of time series; its amplitude components are used to compute the probabilities in entropy computation. Furthermore, Fourier transformation is used to obtain the power spectral density of the time series, which represents the distribution of power of the signal according to the frequencies present in the signal. In order to obtain the power level for each frequency, the Fourier transform of the signal is computed, and the power level of the frequency component is denoted by $Y_i$. The normalization of the power is performed by computing the total power as $\sum Y_i$ and dividing the power level corresponding to each frequency by the total power as:

$$y_i=Y_i/{\displaystyle \sum Y_i}$$

(1)

The entropy is computed by multiplying the power level in each frequency and the logarithm of the inverse of the same power level. Finally, the spectral entropy of the time series is computed using the following formula [14]:

$$spectralEn={\displaystyle \sum _i{y}_i}\log (1/y_i)$$

(2)

2.1.2. Approximate Entropy

Approximate entropy is, as proposed by Pincus, a statistically quantified nonlinear dynamic parameter that measures the complexity of a time series [18]. It is an EEG complexity measure analysis method without coarse graining. A non-negative number is used to represent the complexity of a time series and the incidence of new information. The more complex a time series, the greater the approximate entropy value. Studies have shown that approximate entropy can characterize a person’s physiological state change. Compared with other nonlinear dynamics parameters, approximate entropy needs shorter data segment input for calculation, and comes with certain noise immunity. It is widely used in the field of EEG analysis. The procedure for the ApproxEn-based algorithm is described in detail as follows:

(1)

Considering a time series t(i) of length L, a set of m-dimensional vectors are obtained according to the sequence order of t(i):

$$T_i^m=[t(i),t(i+1),...,t(i+m-1)];1\le i\le L-m+1$$

(3)

(2)

$d[T_i^m,T_j^m]$ is the distance between two vectors $T_i^m$ and $T_j^m$, defined as the maximum difference values between the corresponding elements of two vectors:

$$d[T_i^m,T_j^m]=\underset{k\in (0,m-1)}{{\displaystyle \max \left\{\right|t(i+k)-t(j+k)\left|\right\},(i,j=1~L-m+1,i\ne j)}}$$

(4)

(3)

For a given $T_i^m$ calculate the number of $j(1\le j\le L-m+1,j\ne i)$ of any vectors $T_j^m$ that are similar to $T_i^m$ within r as $S_i^m(s)$. Then, for $1\le i\le L-m+1$,

$$S_i^m(s)=\frac{1}{L-m+1}{S}_i$$

(5)

(4)

where $S_i$ is the number of vectors $T_j$ that are similar to $T_i$, subject to the criterion of similarity $d[T_i^m,T_j^m]\le s$.

(5)

Define the function ${\mathsf{\gamma }}^m(s)$ as:

$${\mathsf{\gamma }}^m(s)=\frac{1}{L-m+1}{\displaystyle \sum _{i=1}^{L-m+1}\ln S_i^m(s)}$$

(6)

(6)

Set m = m + 1, and repeat steps (1) to (5) to obtain $S_i^{m+1}(s)$ and ${\mathsf{\gamma }}^{m+1}(s)$, then:

$${\mathsf{\gamma }}^{m+1}(s)=\frac{1}{L-m+1}{\displaystyle \sum _{i=1}^{L-m+1}\ln S_i^{m+1}(s)}$$

(7)

(7)

The approximate entropy can be expressed as:

$$ApprpxEn={\mathsf{\gamma }}^m(s)-{\mathsf{\gamma }}^{m+1}(s)$$

(8)

2.1.3. Sample Entropy

The sample entropy’s algorithm is similar to that of approximate entropy. It is actually an optimized approximate entropy, a new measure of time series complexity proposed by Richman and Moorman [19]. The steps forming (1) to (2) can be defined in the same way as the ApproxEn-based algorithm; other steps in the SampleEn-based algorithm are described in detail as follows:

(1)

For a given $T_i^m$, calculate the number of $j(1\le j\le L-m,j\ne i)$, of any vector $T_j^m$, similar to $T_i^m$ within s as $A_i^m(s)$. Then, for $1\le i\le L-m$,

$$A_i^m(s)=\frac{1}{L-m-1}{A}_i$$

(9)

(2)

where $A_i$ is the number of vectors $T_j$ that are similar to $T_i$ subject to the criterion of similarity $d[T_i^m,T_j^m]\le s$.

(3)

Define the function ${\mathsf{\gamma }}^m(s)$ as:

$${\mathsf{\gamma }}^m(s)=\frac{1}{L-m}{\displaystyle \sum _{i=1}^{L-m}{A}_i^m(s)}$$

(10)

(4)

Set m = m + 1, and repeat steps (1) to (3) to obtain $A_i^{m+1}(s)$ and ${\mathsf{\gamma }}^{m+1}(s)$, then

$${\mathsf{\gamma }}^{m+1}(s)=\frac{1}{L-m}{\displaystyle \sum _{i=1}^{L-m}{A}_i^{m+1}(s)}$$

(11)

(5)

The sample entropy can be expressed as:

$$SampleEn=\log ({\mathsf{\gamma }}^m(s)-{\mathsf{\gamma }}^{m+1}(s))$$

(12)

2.1.4. Fuzzy Entropy

To deal with some of the issues with sample entropy, Chen et al. proposed the use of fuzzy membership function in computing the vector similarity to replace the binary function in sample entropy algorithm [20], so that the entropy value is continuous and smooth. While maintaining the merits of sample entropy algorithm, the new algorithm obtains stable results for different parameters, and offers better noise resistance. It is more suitable than the sample entropy as a measure of time series complexity [21]. The procedure for the FuzzyEn-based algorithm is described in detail as follows:

(1)

Set a L-point sample sequence: $\{v(i):1\le i\le L\}$;

(2)

The phase-space reconstruction is performed on v(i) according to the sequence order, and a set of m-dimensional vectors are obtained as $(m\le L-2)$. The reconstructed vector can be written as:

$$T_i^m=\{v(i),v(i+1),...,v(i+m-1)\}-v_0(i)$$

(13)

where $i=1,2,...,L-m+1$, and $v_0(i)$ is the average value described as the following equation:

$$v_0(i)=\frac{1}{m}{\displaystyle \sum _{j=0}^{m-1}v(i+j)}$$

(14)

(3)

$d_{ij}^m$, the distance between two vectors $T_i^m$ and $T_j^m$, is defined as the maximum difference values between the corresponding elements of two vectors:

$$\begin{array}{l}{d}_{ij}^m=d[T_i^m,T_j^m]={\displaystyle \sum _{k\in (0,m-1)}\{|v(i+k)-v_0(i)}-(v(j+k)-v_0(j))|\}\\ (i,j)=1~L-m,i\ne j)\end{array}$$

(15)

(4)

According to the fuzzy membership function $\mathsf{\sigma }(d_{ij}^m,n,s)$, the similarity degree $D_{ij}^m$ between two vectors $T_i^m$ and $T_j^m$ is defined as:

$$D_{ij}^m=\mathsf{\sigma }(d_{ij}^m,n,s)=\exp (-{(d_{ij}^m)}^n/s)$$

(16)

where the fuzzy membership function $\mathsf{\sigma }(d_{ij}^m,n,s)$ is an exponential function, while n and s are the gradient and width of the exponential function, respectively.

(5)

Define the function ${\mathsf{\gamma }}^m(n,s)$:

$${\mathsf{\gamma }}^m(n,s)=\frac{1}{L-m}{\displaystyle \sum _{i=1}^{L-m}\frac{1}{L-m-1}{\displaystyle \sum _{j=1,j\ne 1}^{L-m}{D}_{ij}^m]}}$$

(17)

(6)

Repeat the steps from (1) to (4) in the same manner, a set of (m + 1)-dimensional vectors can be reconstructed according to the order of sequence. Define the function:

$${\mathsf{\gamma }}^{m+1}(n,s)=\frac{1}{L-m}{\displaystyle \sum _{i=1}^{L-m}\frac{1}{L-m-1}{\displaystyle \sum _{j=1,j\ne 1}^{L-m}{D}_{ij}^{m+1}]}}$$

(18)

(7)

The fuzzy entropy can be expressed as:

$$FuzzyEn(m,s,L)=\ln {\mathsf{\gamma }}^m(n,s)-\ln {\mathsf{\gamma }}^{m+1}(n,s)$$

(19)

In these four entropies, m and s are the dimensions of phase space and similarity tolerance, respectively. Generally, a too-large similarity tolerance will lead to a loss of useful information. The larger the similarity tolerance, the more information may be missed. However, if the similarity tolerance is underestimated, the sensitivity to noise will be increased significantly. In the present study, m = 2, n = 4 while s = 0.2 * SD, where SD denotes the standard deviation of the time series.

2.2. Fisher-Based Distance Metric

In the real application, EEG signals collected by some electrodes might serve mostly as noise which interferences with classification performance, reducing the accuracy rate of the authentication. Electrode selection, which picks those electrodes whose EEG signal could be used for feature extraction to identify the sample class, is therefore necessary. Fisher distance, which is often applied in classification research to represent the dissimilarity between classes, is used in this study. Fisher distance is proportional to the dissimilarity between classes. The bigger the dissimilarity degree, the larger the Fisher distance. The calculation of Fisher distance is as following [22]:

$$F=\frac{{({\mathsf{\mu }}_1-{\mathsf{\mu }}_2)}^2}{{\mathsf{\sigma }}_1^2-{\mathsf{\sigma }}_2^2}$$

(20)

where F is Fisher distance, $\mathsf{\mu }$ and $\mathsf{\sigma }$ are the mean and variance, respectively, and the subscripts 1, 2 denote the classes. For each data point, the Fisher distance indicates the contribution to classification of a particular electrode’s data points. A greater Fisher distance implies that the classification result is obvious. The Fisher distance is calculated with all data in the data set for a certain electrode at each time point.

2.3. Support Vector Machine (SVM)

In this study, SVM was used as the operation engine. In many machine learning algorithms, SVM belongs to the family of kernel-based classifiers, and they are very powerful classifiers, as they can perform both linear and non-linear classification simply by changing the “kernel” function utilized [23]. SVM has been widely used in the realm of EEG [24,25,26,27]. The basic idea of SVM is to transform the data into a high dimensional feature space, and then determine the optimal separating hyperplane using a kernel function. For a brief formulation of SVM and how it works, see paper [28]; for more details on SVM, see [29].

In this study, the LIBSVM package was used as an implementation of SVM [30]. Furthermore, the radial basis function (RBF) was taken as the kernel function to study the classification results, which is commonly used in support vector machine classification. The RBF kernel on two samples x_i and x_j, represented as feature vectors in some input space, is defined as follows [31]:

$$K(x_i,x_j)=\exp (-\frac{|x_i-x_j{|}^2}{2{\mathsf{\sigma }}^2})$$

(21)

where $|x_i-x_j{|}^2$ may be recognized as the squared Euclidean distance between the two feature vectors, and $\mathsf{\sigma }$ is a free parameter. When ${\mathsf{\sigma }}^2\to \infty$, the classification accuracy of using the RBF kernel is at least as good as using the linear kernel after selecting a suitable parameter. The RBF kernel may be the most used kernel in training nonlinear SVM, so we also take it as SVM kernel function.

2.4. Performance Evaluation

To provide a more intuitive and easier-to-understand method to measure the prediction quality, the following equation set is often used in literature for examining performance quality as follows [32]:

$$\{\begin{array}{c}Sn=\frac{TP}{TP+FN}\\ Sp=\frac{TN}{TN+FP}\\ Acc=\frac{TP+TN}{TP+TN+FP+FN}\\ MCC=\frac{(TP\times TN)-(FP\times FN)}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}\end{array}$$

(22)

where TP (true positive) represents the number of fatigue EEG signals identified as fatigue EEG signals; TN (true negative), the number of normal EEG signals classified as normal EEG signals; FP (false positive), the number of normal EEG signals recognized as fatigue EEG signals; FN (false negative), the number of fatigue EEG signals distinguished as normal EEG signals; Sn represents sensitivity; Sp represents specificity; Acc represents accuracy; and MCC represents Mathew’s correlation coefficient.

3. Experiment and Results

In this paper we present the EEG signal feature analysis with four entropy values. SVM is used for feature classification, and the steps are shown in Figure 1. At first, the subject goes through driving training in a virtual environment under the instruction of the operator while the EEG signal is collected. This original signal then goes though the pre-processing step, which includes filtering, signal baseline correction, segmentation and manual check. The original EEG records of the two states (normal state and fatigue state) are converted into 1-s segmented data sets. The next step is computation of entropy value for the segmented EEG signals, in which spectrum entropy, approximate entropy, sample entropy and fuzzy entropy are used. Once the sets of entropy value are obtained, the analysis on electrode selection and combination of entropy features can be performed. Feature combination is carried out to differentiate the dataset of the two states.

3.1. Data Source

The EEG data were collected by the Brain–Computer Interface Lab, Jiangxi University of Technology, from university students (12 subjects: 8 male and 4 female, average age 21.5 years). In the 24 h prior to the experiments, these subjects were to consume no tea or coffee and have 8 h sleep at night before the experiment. The subject was given an operation introduction while an electrode cap was put on his/her head. After the subject was familiar with driving in the road conditions, EEG signal collection began. For a short time of driving, it is difficult to enter into a state of fatigue to produce a reliable and effective EEG. Unfortunately, for a longer period of driving, most participants experience uncomfortable and unpleasant feelings including boredom, testiness and nausea. Therefore, according to previous experience in a fatigue-related experiment, each subject was asked to drive for 40 min without a break before taking a questionnaire to check the status, based on the Li’s subjective fatigue scale and Borg’s CR-10 scale. The questionnaire results showed the subject was in driving fatigue. The experiments were authorized by Academic Ethics Committee of Jiangxi University of Technology.

The sample set of the experiment was divided into training sample (400 samples) and test sample (200 samples). With a 32-electrodes Neuroscan data acquisition device, the international 10–20 system was used for the EEG collection protocol. All channel data were referenced to two electrically linked mastoids at A1 and A2, digitized at 1000 Hz from a 32-channel electrode cap (including 30 effective channels and 2 reference channels) based on the international 10–20 system and stored in a computer for the offline analysis [33,34,35,36]. Eye movements and blinking were monitored by recording the horizontal and vertical EOG.

After the EEG signals were collected, the main steps of data preprocessing was carried out by the Scan 4.3 software of Neuroscan (El Paso, TX, USA, 2003). The raw signals were first filtered by a 50 Hz notch filter and a 0.15 Hz to 45 Hz band-pass filter to remove the noise. We defined two types of state for every subject within the 40-min EEG recordings: the 10-min of EEG signals before the 40-min virtual driving operation was defined as the normal state, and the last 10 min of EEG signals within the 40-min virtual driving operation was defined as the fatigue state.

Figure 2 shows a comparison between EEG signals on normal state and fatigue state. As can be seen from the figure, EEG signals in the time domain are mixed and disordered, containing a lot of noise data, with the resulting features not being obvious. Therefore, it is necessary to transform EEG signals before extracting features for describing the fatigue state.

3.2. Entropy Function Selection

The entropy functions for EEG identification are set as Entropy_Approximate (A, m, r), Entropy_Fuzzy(A, m, n, r), Entropy_Sample(A, m, r) and Entropy_Spectral (A), where A is the input matrix. Based on EEG acquisition frequency, Fs = 1000 and segment length of each sample N = 1000; the data reconstruction dimension is m = 2. For fuzzy entropy index gradient n, we set n = 4; while for spectrum entropy, the Pburg algorithm was selected for power spectrum estimation, and the spectrum estimation order is 7. The entropy tolerance r has direct influence on the entropy value. Too-large tolerance would let in redundant signals that interfere with genuine features. If the selected r value is too small, feature sensitivity is increased so that the entropy value is disordered by the noise. Proper r is needed for feature stability and the quality of classification index.

3.3. Classification Result

SVM classifier enjoys unique advantages over other classifiers in small-sample, non-linear and high-dimension pattern recognition, which is the case for the identification of the positive and negative sample described in this paper. Each of the entropies comes with its unique features. To obtain the most suitable features, we selected four entropies: spectrum entropy, approximate entropy, sample entropy and fuzzy entropy. For each type of entropy, certain electrodes are selected for SVM as the input feature. Figure 3 shows, in term of mean and variance, the four entropy values of a randomly selected subject. The x-axis is for the EEG label and y-axis denotes the entropy value. Both the mean and variance indicate that the entropy dissimilarity varies from different electrodes and that the fuzzy entropy has strong stability and obvious effect. In addition, from the Figure 3, it can be obviously observed that the sample entropy and the approximate entropy had similar entropy dissimilarity and the spectrum entropy had a weak dissimilarity.

Figure 4 is the comparison of fisher distance on fuzzy entropy among multiple samples, which shows the obvious two-state sample feature difference between different electrodes. For 12 subjects, the t test is performed for the features of two type states with data from the whole electrode, the maximum p value reached 6 × 10⁻⁵. The results of Figure 3 and Figure 4 show that the features of the two states based on fuzzy entropy have a significant difference under the criteria with the Fisher distance. Similarly, for each subject, if performed for the four combined entropy features of the two states with data from the same electrode, the p values with 27 electrodes in the international 10–20 system are (0.18, 0.34, 0.68, 0.30, 0.77, 0.60, 0.76, 0.33, 0.22, 0.21, 0.57, 0.19, 0.77, 0.49, 0.53, 0.26, 0.24, 0.16, 0.45, 0.48, 0.34, 0.14, 0.11, 0.60, 0.32, 0.34, 0.68) × 10⁻³, which obtained the result that the T5, TP7, TP8 and FP1 electrodes had a significant difference. In addition, Figure 5 shows a comparison with the combined entropy between the normal state and fatigue state, which selected 30 electrodes sorted by the Fisher distance according to the descending order.

The classification performance thus obtained by the jackknife test using fusion of the four types of entropies are given in

Table 1. The classification results. Acc: accuracy; Sn: sensitivity; Sp: specificity; MCC: Mathew´s correlation coefficient

Entropies	Acc	Sp	Sn	MCC
SpectralEn	75.00	78.00	72.00	47.08
ApproxEn	87.25	84.05	87.50	73.57
SampleEn	89.75	84.50	91.00	78.66
FuzzyEn	93.50	92.50	91.50	85.02
CombinedEn	98.75	97.50	96.00	93.51

, from which we can see that FuzzyEn-based method owns maximum classification accuracy, using the SVM classifier with the RBF function. The parameter Sn indicates the ability of the classifier to accurately identify the proportion of true positive samples from the test set. Similarly, the parameter Sp indicates the ability of the classifier to accurately identify the proportion of true negative samples from the test set. In this work, we have achieved the highest Sn and Sp of 91.50% and 92.50% for the FuzzyEn, respectively. It appears that the FuzzyEn-based method exhibits a remarkably higher accuracy, sensitivity and specificity than that of the SampleEn-based or else methods. In terms of classification accuracy with respect to entropy, the fuzzy entropy and sample entropy shows a stable performance for RBF kernel function and is suitable for the EEG-signal classification. Mathew’s correlation coefficient (MCC) evaluates the classification accuracy of imbalanced positive and negative samples in a dataset. The highest value of the MCC parameter, 85.02% and 78.66%, also indicates when the radial basis function is used as the kernel function of SVM, the characteristics of sample entropy and fuzzy entropy are obvious. The result indicates that the accuracy is improved with combined entropies.

Furthermore,

Table 2. The classification results.

No.	SpectralEn	ApproxEn	SampleEn	FuzzyEn	CombinedEn
1	84.2108	90.3983	94.8875	91.8033	98.3625
2	72.4208	90.4583	90.1075	94.4533	99.2325
3	73.9208	87.8983	91.1175	92.4733	98.8825
4	76.0708	85.9283	90.3975	92.4933	99.6925
5	67.9408	80.9783	87.7875	94.0633	99.3725
6	78.2808	83.2783	89.3975	93.2733	98.8725
7	62.9308	82.4783	85.4575	95.3433	97.5425
8	79.6808	91.6483	89.9775	95.4333	98.0625
9	77.2308	91.5383	90.7775	93.4333	99.6925
10	79.5308	90.4383	89.8175	92.3833	98.6825
11	76.0208	81.4883	87.5675	91.7333	97.7025
12	71.7608	90.4683	89.7075	95.1133	98.9025

shows that classification accuracies of each subject with respect to single entropy and combined entropy. In order to analysis the results with a statistical significance, we calculated the p value of the t test. Using p1 as the t test with the SpectralEn and CombinedEn, p2 as ApproxEn and CombinedEn, p3 as SampleEn and CombinedEn, and p4 as FuzzyEn and CombinedEn, (p1, p2, p3, p4) = (1.7, 90, 1.6, 20) × 10⁻⁵ was obtained, from which we know that an obvious difference between single entropy as features and combined entropy as features is shown.

Table 3. The variation of entropy values on different electrodes.

No.	T5			TP7			TP8			FP1
	Normal	Fatigue	Variation	Normal	Fatigue	Variation	Normal	Fatigue	Variation	Normal	Fatigue	Variation
1	0.507	0.655	0.148↑	0.63	0.62	0.010↓	0.353	0.579	0.226↑	0.19	0.674	0.484↑
2	0.694	0.819	0.125↑	0.519	0.683	0.164↑	0.633	0.672	0.039↑	0.518	0.568	0.050↑
3	0.737	0.682	0.055↓	0.811	0.696	0.115↓	0.751	0.625	0.126↓	0.712	0.632	0.080↓
4	0.845	0.507	0.338↓	0.946	0.551	0.395↓	0.582	0.588	0.006↑	0.68	0.778	0.098↑
5	0.46	0.559	0.099↑	0.454	0.53	0.076↑	0.438	0.551	0.113↑	0.541	0.578	0.037↑
6	0.653	0.499	0.154↓	0.643	0.485	0.158↓	0.543	0.38	0.163↓	0.695	0.430	0.265↓
7	0.762	0.731	0.031↓	0.607	0.552	0.055↓	0.71	0.674	0.036↓	0.697	0.597	0.100↓
8	0.597	0.624	0.027↑	0.592	0.41	0.182↓	0.672	0.645	0.027↓	0.679	0.626	0.053↓
9	0.327	0.288	0.039↓	0.477	0.291	0.186↓	0.247	0.366	0.119↑	0.323	0.304	0.019↓
10	0.765	0.774	0.009↑	0.774	0.782	0.008↑	0.755	0.766	0.011↑	0.799	0.776	0.023↓
11	0.467	0.366	0.101↓	0.583	0.474	0.109↓	0.561	0.547	0.014↓	0.442	0.475	0.033↑
12	0.95	0.845	0.105↓	0.843	0.752	0.091↓	0.755	0.682	0.073↓	0.805	0.692	0.113↓

also shows that the average success rates based on combined entropy had better performance than that using single entropy. In addition, approximate entropy and sample entropy have a similar degree of detection of EEG signals of fatigue and normal state because of the p value of the t test is 0.01, implying that there is little difference.

When single entropy is used for classification, fuzzy entropy gives the highest average discrimination rate at 93.50%. Approximate entropy and sample entropy come next with scores around 88%, and spectrum entropy comes up with the lowest accuracy with 75%. Furthermore, as the top performer, fuzzy entropy’s three parameter averages are, 91.50%, 92.50% and 85.02%, respectively. Next in order is sample entropy, whose three parameter average are 91.00%, 84.50% and 78.66%, respectively. These results indicate that, in the case of driver fatigue detection, fuzzy entropy and sample entropy are more effective and stable EEG features for classification.

It is well-known that the feature distance and the difference significance as class features vary from electrode to electrode. For EEG analysis, therefore, it is necessary to conduct backtracking to single out those electrodes most sensitive to driver fatigue, based on the signal feature. In order to demonstrate the difference significance in various electrodes for the 300 samples of each type, the t test is performed for the two types with data from a certain electrode. The p value of the t test is listed in descending order, and for the n subjects, the top four electrodes are shown in Table 3, which displays the mean values of entropy for the subjects and the related test results during normal state and fatigue state, respectively. The row labeled by variation in Table 3 represents the variation of the fatigue state compared with normal state; specifically, ↑ denotes an increase of entropy value in fatigue state, while ↓ denotes a reduction of entropy value in fatigue state.

As known to all, the kernel function can affect the classification performance of the SVM classifier. In order to study the different influence on classification results, we used the linear function, the polynomial function, the radial basis function and the sigmoid function as the kernel function, respectively. Shown as Figure 6, the comparison of the average accuracies for 12 subjects with four different kernel functions was made; its average accuracies are 98.5%, 98.3%, 98.7% and 97.1%, respectively, which indicated that classification performance using the radial basis function as kernel function obtained a better result.

4. Discussion

It is generally accepted that entropy is an index used to measure the complexity of a system. Progress in understanding the difference between normal and fatigue period has been vigorous as a result of gains achieved by investigators employing the study of brain entropy. The indexes and the related classification performance adopted in previous studies are listed in

Table 4. Studies regarding driver fatigue detection using different types of entropy. EOG: electrooculogram.

Research Group	Number of Subjects	Feature Types	Classifier	Adopted Entropy	Acc
Zhang [37]	20	EEG + EOG + EMG	neural network	Approximate	96.50%
Khushaba [38]	31	EEG + EOG	The Fuzzy Mutual Information based Wavelet Packet Algorithm	Fuzzy	95%
Zhao [39]	28	EEG	Threshold of ROC curve	Sample	95%
This paper	12	EEG	SVM (support vector machine)	Combined Entropy	98.75%

. Zhang [37] used the approximate entropy and combined a variety of physiological signals for 20 subjects, by using the method of multi feature combined analysis method with a high success rate of 96.5%. Khushaba [38] employed 31 subjects to participate in the study, combining EEG and EOG to analyze with the final classification accuracy of 95%. Zhao [39] used the sample entropy to study EEG signals. The results of reference [37,38,39] show that using various physiological features and a variety of entropy fusion method could obtain an obvious improvement for the classification accuracy. However, various physiological features could increase the difficulty of signal acquisition and result in a difficult comparison with different entropies for different signal sources. From the use of a single entropy feature, the results of this paper indicated that the combined entropy features could have better performance based on the EEG signal, which reduced the difficulty of signal collection. In short, compared with other existing EEG based driver fatigue analysis methods, the combined entropy feature analysis gives better classification result.

For different analysis targets, using different entropies may have different impacts on the classification accuracy. In this paper we selected four types of entropies for detecting driver fatigue. Table 1 and Table 4 indicate that, for the same data source, the classification parameters of the four entropies are notably different. In our experiment paradigm, the fuzzy entropy has the highest accuracy if single entropy is used as input, followed by sample entropy and approximate entropy, while the spectrum entropy records the lowest performance. The results are satisfactory: using the FuzzyEn and the SampleEn as features, the average accuracies are 93.50% and 89.75%, respectively.

As we can see from Figure 2 and Table 4, using a FuzzyEn-based classification, the accuracy of the different data sets was different. The accuracy of the No. 8 dataset was 87.05%, and the average accuracy of the No. 2 dataset was as high as 96.75%. The accuracy was a little different, and the reason for this slight discrepancy might be that the No. 2 dataset was collected from T5 electrode, while the No. 8 dataset was collected from FP2 electrode. For the whole dataset, FuzzyEn-based classification greatly enhanced detection performance. Considering the ease of data acquisition, the present results implied that T5 electrode data with analysis with FuzzyEn-based classification also had very high detection performance and are suitable for research into the detection of driving fatigue.

In addition, the existing driving fatigue analysis results show that the frequency features of EEG signals have obviously changed when the drivers were in fatigue driving. Therefore, this paper selected fuzzy entropy, approximate entropy, sample entropy and spectral entropy as feature extraction methods. Seen from the analysis results, it can clearly obtain an improvement in detection of driver fatigue via use of combined entropy features. However, in the analysis of EEG signals, many types of entropy had been broadly applied recently. Of special note, one review introduced the application of various entropies for automated diagnosis of epilepsy using EEG signals [40]; the authors used a total of 13 entropy features such as approximate entropy, fuzzy entropy, sample entropy, Renyi’s entropy, spectral entropy, permutation entropy, wavelet entropy and so on to discriminate normal, interictal and ictal EEG signals of epilepsy, finding that most of the entropy features are best suitable for the classification of epileptic EEG signals. This study concluded that Renyi’s entropy, sample entropy, spectral entropy and permutation entropy are highly discriminative features to classify normal, interictal and ictal EEG signals. The fact that many types of entropy were applied in that paper [40] indicated that in future work we can use and fuse more different entropies to analyze different fatigue states such as normal, alert, and fatigued. Therefore, due to the fact that different entropy features have their own advantages, we will study the influence of other entropies and their different combination on the classification results for detecting driver fatigue in the future.

5. Conclusions

In this paper, four types of common entropies were used to extract feature for detecting driver fatigue and EEG signals were used as the signal source, which reduced the difficulty of signal collection. Experimental results show that, for the 12 subjects, the highest classification rate reached 98.75%, and it can be concluded that fuzzy and sample entropies are highly discriminative features to classify normal and fatigue EEG signals. It is anticipated that this will be a useful revelation for driver fatigue detection in the relevant areas, or at the very least play a complementary role to the existing method. Still, there are some issues that need to be discussed in the future, such as computational complexity of feature extraction for using a variety of entropies. Therefore, one of the future works will aim to reduce algorithm complexity for real-time detection of driver fatigue.