Predictive Modelling and Analysis of Process Parameters on Material Removal Characteristics in Abrasive Belt Grinding Process
Abstract
:1. Introduction
2. Theoretical Basis
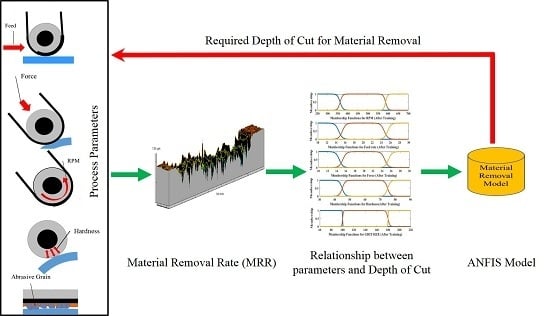
2.1. Abrasive Belt Grinding Process
2.2. Adaptive Neuro-Fuzzy Inference System
- Rule 1: If x is A1 and y is B1, then f1 = p1x +q1y + r1;
- Rule 2: If x is A2 and y is B2, then f2 = p2x +q2y + r2;
- where p1, p2, q1, q2, r1, and r2 are linear parameters and A1, A2, B1, and B2 are nonlinear parameters. The output of the ith node in layer 1 is denoted as Ol,i.
- Layer 1: Every adaptive node i in the layer 1 has a node function.where x (or y) is the input to nodes i and Ai (or Bi–2) generating a linguistic label coupled with the node as given by Equation (2). The membership function for A (or B) can be any, parameterized as a sigmoidal membership function given by Equation (3).where (ci, ai) is the parameter set. These are called premise parameters. As the values of the parameters change, the shape of the membership function varies.
- Layer 2: Every node in layer 2 is a fixed node labelled ∏. Each node calculates the firing strength of each rule, which is the output using the simple product operator. Evaluating the rule premises results as a product of all of the incoming signals given by Equation (4)
- Layer 3: The ratio of the ith rule’s firing strength to the sum of all of the rule’s firing strengths is calculated by Equation (5) in layer 3. The output of this layer is called normalized firing strengths.
- Layer 4: Every node i in layer 4 is an adaptive node with a node function. The nodes compute a parameter function on the layer output. Parameters in this layer will be referred to as consequent parameters.where wi is a normalised firing strength from layer 3 and (pi, qi, ri) is the parameter set for the node.
- Layer 5: This layer has a fixed single node labelled Σ, which computes the overall output as the summation of all of the incoming signals, as shown in Equation (7). The Σ gives the overall output of the constructed adaptive network, having same functionality as the Sugeno fuzzy model.
3. Experimental Procedures
3.1. Experiment Design Based on Taguchi Method
3.1.1. Experimental Setup
3.1.2. Toolpath Planning
3.1.3. Taguchi Based DoE (Design of Experiments)
3.2. Experimental Conditions
- The contact head of the belt grinder is kept at normal angle to keep uniformity in contact conditions throughout machining.
- Tool wear effect was ignored as the tests were conducted in the useful lifetime of the belt tool.
- The surface condition of the machined aluminium 6061 coupons was uniform with a surface roughness of 0.8 microns (μm).
- Experiments are carried out in dry conditions.
- Experiments were carried out with three passes for each trial. On each pass, the depth of cut was measured at three different locations, as shown in Figure 6, resulting in nine measurements. According to the parameter combinations from the Taguchi method, which obtained 27 trials as presented in Table 2, 243 depth of cut readings were obtained.
3.3. Prediction of Depth of Cut
4. Results and Analysis
4.1. Analysis of Variance (ANOVA)
4.2. Predictive Modelling of Material Removal Using ANFIS
4.2.1. Membership Functions for the Input and Output Variables
4.2.2. ANFIS Rules Employed in Model
4.2.3. Training the Network and Prediction Performance
5. Conclusions
- ANOVA determined the level of significance of the machining parameters on the material depth of cut. Based on the analysis of variance (ANOVA) results at a 95% confidence level, the highly dominant parameters of material removal are identified. Namely, the grit size grinding parameter is the primary factor that has the highest influence on the material removal, and this parameter is about five times greater than the second ranking parameters (RPM and force imparted). The feed rate and polymer wheel hardness parameters do not seem to have much of an influence on the depth of cut, i.e., material removal. Results from ANOVA interactions also suggests that the experimental trials can further be optimised using Taguchi Interaction instead of orthogonal design.
- Based on the signal-to-noise ratio results in Figure 9, we can construe that 750 RPM, 10 mm/s feed rate, 30 N force, 90 Shore A hardness, and 60 grit size are the optimal grinding parameters for achieving maximum depth of cut.
- A method of modelling and calculating the material removal using ANFIS is proposed in this paper. The ANFIS model developed is validated with experimental trials for given conditions. It has been identified that results produced by the designed regression model have acceptable deviations between the predicted and the actual experimental results with 93.5% accuracy. The ANFIS model developed in this research work is viable and could be used to predict the depth of cut, i.e., material removal for an Abrasive Belt Grinding process.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, X.; Kuhlenkötter, B.; Kneupner, K. An efficient method for solving the Signorini problem in the simulation of free-form surfaces produced by belt grinding. Int. J. Mach. Tools Manuf. 2005, 45, 641–648. [Google Scholar] [CrossRef]
- Jourani, A.; Dursapt, M.; Hamdi, H.; Rech, J.; Zahouani, H. Effect of the belt grinding on the surface texture: Modeling of the contact and abrasive wear. Wear 2005, 259, 1137–1143. [Google Scholar] [CrossRef]
- Ren, X.; Cabaravdic, M.; Zhang, X.; Kuhlenkötter, B. A local process model for simulation of robotic belt grinding. Int. J. Mach. Tools Manuf. 2007, 47, 962–970. [Google Scholar] [CrossRef]
- Ren, X.; Kuhlenkötter, B.; Müller, H. Simulation and verification of belt grinding with industrial robots. Int. J. Mach. Tools Manuf. 2006, 46, 708–716. [Google Scholar] [CrossRef]
- Hamann, G. Modellierung des Abtragsverhaltens Elastischer Robotergefuehrter Schleifwerkzeuge; University of Stuttgart: Stuttgart, Germany, 1998. [Google Scholar]
- Rufeng, X.; Chen, Z.; Chen, W.; Wu, X.; Zhu, J. Dual drive curve tool path planning method for 5-axis NC machining of sculptured surfaces. Chin. J. Aeronaut. 2010, 23, 486–494. [Google Scholar] [CrossRef]
- Zhang, X.; Kneupner, K.; Kuhlenkötter, B. A new force distribution calculation model for high-quality production processes. Int. J. Adv. Manuf. Technol. 2006, 27, 726–732. [Google Scholar] [CrossRef]
- Radzevich, S.P. A closed-form solution to the problem of optimal tool-path generation for sculptured surface machining on multi-axis NC machine. Math. Comput. Model. 2006, 43, 222–243. [Google Scholar] [CrossRef]
- Pi, J.; Red, E.; Jensen, G. Grind-free tool path generation for five-axis surface machining. Comput. Integr. Manuf. Syst. 1998, 11, 337–350. [Google Scholar] [CrossRef]
- Taguchi, G. Introduction to Quality Engineering: Designing Quality into Products and Processes; Asian Producativity Organization: Tokyo, Japan, 1986. [Google Scholar]
- Lindman, H.R. Analysis of Variance in Experimental Design; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Gill, S.S.; Singh, J. An Adaptive Neuro-Fuzzy Inference System modeling for material removal rate in stationary ultrasonic drilling of sillimanite ceramic. Expert Syst. Appl. 2010, 37, 5590–5598. [Google Scholar] [CrossRef]
- Çaydaş, U.; Hasçalık, A.; Ekici, S. An adaptive neuro-fuzzy inference system (ANFIS) model for wire-EDM. Expert Syst. Appl. 2009, 36, 6135–6139. [Google Scholar] [CrossRef]
- Jang, J.-S.R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Wang, S.; Li, C. Application and development of high-efficiency abrasive process. Int. J. Adv. Manuf. Technol. 2012, 47, 51–64. [Google Scholar]
- Huang, H.; Gong, Z.M.; Chen, X.Q.; Zhou, L. Robotic grinding and polishing for turbine-vane overhaul. J. Mater. Process. Technol. 2002, 127, 140–145. [Google Scholar] [CrossRef]
- Lei, Y.; He, Z.; Zi, Y. A new approach to intelligent fault diagnosis of rotating machinery. Expert Syst. Appl. 2008, 35, 1593–1600. [Google Scholar] [CrossRef]
- Ying, L.-C.; Pan, M.-C. Using adaptive network based fuzzy inference system to forecast regional electricity loads. Energy Convers. Manag. 2008, 49, 205–211. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Werbos, P.J. Backpropagation through time: What it does and how to do it. Proc. IEEE 1990, 78, 1550–1560. [Google Scholar] [CrossRef]
- Yilmaz, O.; Bozdana, A.T.; Okka, M.A. An intelligent and automated system for electrical discharge drilling of aerospace alloys: Inconel 718 and Ti-6Al-4V. Int. J. Adv. Manuf. Technol. 2014, 74, 1323–1336. [Google Scholar] [CrossRef]

















| Parameter | Unit | Levels | ||
|---|---|---|---|---|
| L1 | L2 | L3 | ||
| RPM | (m/min) | 250 | 500 | 700 |
| Feed | (mm/s) | 10 | 20 | 30 |
| Force | (N) | 10 | 20 | 30 |
| Rubber hardness | (Shore A) | 30 | 60 | 90 |
| Grit Size | - | 60 | 120 | 220 |
| Trial No. | Factors | MRR | |||||
|---|---|---|---|---|---|---|---|
| RPM | Feed | Force | Hardness | Grit | Depth of Cut | S/N Ratio | |
| 1 | 250 | 10 | 10 | 30 | 60 | 65.60076 | 36.338177 |
| 2 | 250 | 10 | 10 | 30 | 120 | 25.87109 | 28.256295 |
| 3 | 250 | 10 | 10 | 30 | 220 | 13.34471 | 22.506183 |
| 4 | 250 | 20 | 20 | 60 | 60 | 86.10453 | 38.70052 |
| 5 | 250 | 20 | 20 | 60 | 120 | 44.20156 | 32.908752 |
| 6 | 250 | 20 | 20 | 60 | 220 | 23.53456 | 27.434122 |
| 7 | 250 | 30 | 30 | 90 | 60 | 93.8753 | 39.451027 |
| 8 | 250 | 30 | 30 | 90 | 120 | 54.33391 | 34.701419 |
| 9 | 250 | 30 | 30 | 90 | 220 | 23.55062 | 27.440047 |
| 10 | 500 | 10 | 20 | 90 | 60 | 142.9324 | 43.102614 |
| 11 | 500 | 10 | 20 | 90 | 120 | 86.37583 | 38.727845 |
| 12 | 500 | 10 | 20 | 90 | 220 | 59.38035 | 35.472855 |
| 13 | 500 | 20 | 30 | 30 | 60 | 120.6638 | 41.63154 |
| 14 | 500 | 20 | 30 | 30 | 120 | 57.50747 | 35.194485 |
| 15 | 500 | 20 | 30 | 30 | 220 | 45.55799 | 33.171291 |
| 16 | 500 | 30 | 10 | 60 | 60 | 77.47286 | 37.782992 |
| 17 | 500 | 30 | 10 | 60 | 120 | 26.08495 | 28.3278 |
| 18 | 500 | 30 | 10 | 60 | 220 | 13.54166 | 22.633438 |
| 19 | 750 | 10 | 30 | 60 | 60 | 134.8952 | 42.59993 |
| 20 | 750 | 10 | 30 | 60 | 120 | 76.88529 | 37.716865 |
| 21 | 750 | 10 | 30 | 60 | 220 | 58.97687 | 35.413634 |
| 22 | 750 | 20 | 10 | 90 | 60 | 103.8255 | 40.326081 |
| 23 | 750 | 20 | 10 | 90 | 120 | 56.9663 | 35.11236 |
| 24 | 750 | 20 | 10 | 90 | 220 | 35.31606 | 30.959445 |
| 25 | 750 | 30 | 20 | 30 | 60 | 114.009 | 41.138783 |
| 26 | 750 | 30 | 20 | 30 | 120 | 56.65924 | 35.065415 |
| 27 | 750 | 30 | 20 | 30 | 220 | 44.31528 | 32.93107 |
| Machining Parameter | Degrees of Freedom | Sum of Squares | Mean Square | F Ratio | Contribution (%) |
|---|---|---|---|---|---|
| RPM | 2 | 5055.5 | 2527.7 | 26.42 | 13.54 |
| Feed | 2 | 1249.1 | 624.5 | 6.53 | 3.34 |
| Force | 2 | 4782.8 | 2391.4 | 25.00 | 12.79 |
| Hardness | 2 | 867.1 | 433.6 | 4.53 | 2.31 |
| Grit | 2 | 23,903.7 | 11,951.9 | 124.93 | 63.93 |
| Error | 16 | 1530.7 | 95.7 | - | 4.09 |
| Total | 26 | 37,388.8 | - | - | - |
| Parameter | Value |
|---|---|
| Neuron level | 5 |
| Size of input data set | 243 |
| Training Set | 70% |
| Testing Set | 30% |
| andMethod | Prod |
| orMethod | Max |
| defuzzMethod | Wtaver |
| impMethod | Prod |
| aggMethod | Max |
| Number of output | 1 |
| Membership function | Sigmoidal membership |
| Learning rules | Least square estimation-Gradient descent algorithm |
| Number of epoch | 250 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pandiyan, V.; Caesarendra, W.; Tjahjowidodo, T.; Praveen, G. Predictive Modelling and Analysis of Process Parameters on Material Removal Characteristics in Abrasive Belt Grinding Process. Appl. Sci. 2017, 7, 363. https://doi.org/10.3390/app7040363
Pandiyan V, Caesarendra W, Tjahjowidodo T, Praveen G. Predictive Modelling and Analysis of Process Parameters on Material Removal Characteristics in Abrasive Belt Grinding Process. Applied Sciences. 2017; 7(4):363. https://doi.org/10.3390/app7040363
Chicago/Turabian StylePandiyan, Vigneashwara, Wahyu Caesarendra, Tegoeh Tjahjowidodo, and Gunasekaran Praveen. 2017. "Predictive Modelling and Analysis of Process Parameters on Material Removal Characteristics in Abrasive Belt Grinding Process" Applied Sciences 7, no. 4: 363. https://doi.org/10.3390/app7040363
APA StylePandiyan, V., Caesarendra, W., Tjahjowidodo, T., & Praveen, G. (2017). Predictive Modelling and Analysis of Process Parameters on Material Removal Characteristics in Abrasive Belt Grinding Process. Applied Sciences, 7(4), 363. https://doi.org/10.3390/app7040363