Research on the Transportation of Low-Strength Composites Sheets

Abstract

The novel non-combustible sandwich panel is extremely fragile in manufacturing and cannot be tensioned between rolls. Previous studies on the roll-to-roll system, which mainly focused on the high-tension situations and little described the low-strength materials, are insufficient. To explore the transportation of low-strength materials, we study the tension distribution of continuous moving flexible one-dimensional materials on a steady-state track. First, we propose a numerical method to calculate the steady-state track of low-strength sheet between rolls considering the gravity, as well as size and position of rolls. Then we obtain the optimum sag at different size and position of rolls. We find out that there is a lower limit of the sheet’s strength-density ratio (the Minimum Specific Strength) for a specific set of size and position of rolls. Finally, we establish a method to calculate the lower limit approximately for engineering use. Our method can be generalized in manufacturing other low-strength flexible thin-sheet materials as well.

1. Introduction

The non-combustible sandwich panel is a new type of building material. Its core layer consists of less than 25 wt % polyacrylate and more than 75 wt % inorganic powders, which significantly enhances the safety of traditional sandwich panels. During the continuous manufacturing process of the core layer, fluidized state compound of polyacrylate and inorganic powder are transported through several machines to form solid-state panels [1]. As the majority of core panel precursors is inorganic powder, the material is extremely fragile and prone to crack, especially when being transported between rolls.

The placement of the rolls and the sheet has an important influence on the tension in the sheet when the low-strength sheet is transported between rolls. To figure out the optimum placement, multiple experiments are needed at different transporting speeds and different polyacrylate portions in core panel. This trial and error method is inefficient since the non-contact measurement or processing equipment between the upstream and downstream rolls (as shown in Figure 1) is hard to move after installation.

Previous studies on the roll-to-roll system mainly focused on the high-tension situation, most of which neglected the influence of the gravity, the shape and the relative position of rolls. Those approximations lead to the consequence that the track of the traveling materials is an approximately straight line. For example, the studies on the transverse vibrations of axially moving materials [2,3,4,5,6,7,8,9,10,11,12,13,14] and studies on the transverse vibration control technique of axially moving materials [15,16,17,18,19,20] all neglected the effect of gravity on the sheet and treated the traveling materials as tensioned. This means that the sag of the moving sheet is small compared to the distance between two rolls. The studies on the speed or tension control of axially moving materials [21,22,23,24,25,26] assumed the moving materials as a 1D elastic beam and simplified the track of materials as a straight line. Stump studied the low-tension, large-deflection shape of a transporting sheet hanging under gravity [27]. Banichuk studied the gravity’s influence on the stability of the travelling elastic beam using analytical and numerical methods [28]. However, they did not give the explicit expression of the relationship between positions of rolls and tension in the sheet.

However, many novel composite materials (such as flame retardant composites) possess very low strength in processing [29,30,31] that even tension caused by gravity may cause the crack. Ignoring gravity is inappropriate for these novel materials. Moreover, engineering practice demonstrates that the size and position of rolls, as well as the sag of thin-sheet materials, influence the maximum tension in the moving thin-sheet material. Those parameters are also neglected in conventional studies.

Since conventional models are not good at predicting thin-sheet material’s behavior between rolls, a thorough study in tension distribution and motion state of thin-sheet materials between rolls is of great significance to the manufacturing of the non-combustible core panel and such low strength material sheets.

In this study, we propose a model describing the steady-state behavior of low-tension moving thin-sheet materials. This model is developed from the previous studies on hanging materials [32,33,34,35,36,37] and axially moving materials [19,27]. We introduce a numerical method to calculate the shape of moving thin-sheet materials between rolls, taking into account the position and size of rolls. We further discuss how the sag of the thin-sheet material and placement of rolls influence the maximum tension in the thin-sheet material. Finally, we present approximate estimation methods to predict the optimum shape and the lower limit of the material’s strength-density ratio (the Minimum Specific Strength) that two rolls can transport.

2. Problem Formulation

Figure 2 shows the axially moving sheet travelling between two rolls with the constant linear velocity v. The geometric parameters of the sheet and rolls are: b is the width, t is the thickness, l is the sheet length between it and rolls’ contact points, $D_h$ is the vertical (y direction) distance between two rolls’ axes, $2D_l$ is the horizontal (x direction) distance between two rolls’ axes. The ratio between thickness t and length l is very small: $t/l\ll O\left(1\right)$. The material properties are the mass density $\rho$, the Young’s modulus E. ${\sigma }_x$ is the stress at position x in tangent direction and ${\epsilon }_x$ is the strain at position x in tangent direction.

This study focuses on the scenario that the tension in the sheet is mainly caused by gravity that is enough to break some low-strength materials. This means that ${\sigma }_x/\left(\rho gl\right)\approx O\left(1\right)$. In the international system of units (SI), $\rho gl\approx O\left({10}^4\right)$ and $E>O\left({10}^6\right)$ for most materials. Thus ${\epsilon }_x={\sigma }_x/E<O\left({10}^{-2}\right)$. So the elastic effect can be negligible and it can be considered as a 2D problem. Since that many polymer composites are plastic when processing and $t/l\ll O\left(1\right)$, the bending moment in the sheet is assumed to be 0. The sheet is perpendicular to plane $xy$ and its projection in plane $xy$ is $y=f\left(x\right)$. The gravity is in the direction of $-y$. At equilibrium, the kinetic energy T, the potential energy U are given as:

$$T=\frac{1}{2}\rho bt{\int }_l\mathbf{v}\times \mathbf{v}\mathrm{d}l$$

(1)

$$U=\rho btg{\int }_{l}y\mathrm{d}l$$

(2)

When the system is steady, f satisfies:

$$f=\arg \underset{f}{\min }{\int }_l(\rho btgy+\frac{1}{2}\rho bt{v}^2)\mathrm{d}l$$

(3)

Introduce Lagrange multiplier $\lambda$, $L=(\rho btgy+\frac{1}{2}\rho bt{v}^2-\lambda )\sqrt{1+{\dot{y}}^2}$. The Euler-Lagrange equation of this problem is:

$$\frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{\partial L}{\partial \dot{y}}\right)-\frac{\partial L}{\partial y}=0,\Rightarrow \frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{\rho btgy\dot{y}+\frac{1}{2}\rho bt{v}^2\dot{y}-\lambda \dot{y}}{\sqrt{1+{\dot{y}}^2}}\right)-\rho btg\sqrt{1+{\dot{y}}^2}=0$$

(4)

Solve the equation for y :

$$y\left(x\right)=\frac{C_1}{\rho btg}cosh\left(\frac{\rho btg(x-C_2)}{C_1}\right)+\frac{\lambda }{\rho btg}-\frac{v^2}{g}$$

(5)

$\lambda ,C_1$ and $C_2$ can be determined by boundary conditions.

The free-body diagram of the forces acting on the element is shown in Figure 3. $T\left(x\right)$ is the tension in the sheet at position x and G is the gravity.

Equilibrium equation of the forces is:

$$T(x+\mathrm{d}x)\overrightarrow{e_u}(x+\mathrm{d}x)-T\left(x\right)\overrightarrow{e_u}\left(x\right)-G\overrightarrow{e_y}=\frac{\mathrm{d}\overrightarrow{v}}{\mathrm{d}t}\rho bt\sqrt{1+{\dot{y}}^2}\mathrm{d}x$$

(6)

That is:

$$\frac{\mathrm{d}}{\mathrm{d}x}(T\left(x\right)\overrightarrow{e_u})-\rho btg\sqrt{1+{\dot{y}}^2}\overrightarrow{e_y}=\frac{\mathrm{d}\overrightarrow{v}}{\mathrm{d}t}\rho bt\sqrt{1+{\dot{y}}^2}$$

(7)

in which, $\overrightarrow{e_y}$ is the unit vector in the y direction. $\overrightarrow{e_u}$ and $\overrightarrow{e_v}$ is the unit tangent vector and unit normal vector of v, respectively:

$$\overrightarrow{e_y}=\left[\begin{array}{c}0\\ 1\end{array}\right],\overrightarrow{e_u}=\left[\begin{array}{c}\frac{1}{\sqrt{1+{\dot{y}}^2}}\\ \frac{\dot{y}}{\sqrt{1+{\dot{y}}^2}}\end{array}\right],\overrightarrow{e_v}=\left[\begin{array}{c}-\frac{\dot{y}}{\sqrt{1+{\dot{y}}^2}}\\ \frac{1}{\sqrt{1+{\dot{y}}^2}}\end{array}\right],\overrightarrow{v}=v\overrightarrow{e_u}$$

(8)

In the equilibrium state, each point of the sheet has a linear velocity of v, so:

$$\frac{\mathrm{d}\overrightarrow{e_u}}{\mathrm{d}t}=v\frac{\mathrm{d}\overrightarrow{e_u}}{\mathrm{d}s}=\frac{v}{\sqrt{1+{\dot{y}}^2}}·\frac{\mathrm{d}\overrightarrow{e_u}}{\mathrm{d}x}$$

(9)

Substitute Equations (8) and (9) in Equation (7), and solve Equation (7) for $T\left(x\right)$ :

$$T\left(x\right)=\rho bt{v}^2+\frac{1+{\dot{y}}^2}{\ddot{y}}\rho btg$$

(10)

Substitute Equation (5) into Equation (10):

$$T\left(x\right)=\rho bt{v}^2+C_{1}cosh\left(\frac{\rho btg(x-C_2)}{C_1}\right)$$

(11)

Equation (11) is the explicit expression of the tension in the sheet.

With Equations (5) and (11), it can be inferred that the stress at the higher position of the steady-state continuous moving sheet is larger than that at the lower position. The track of the sheet is catenary and there is a square relationship between tension and transporting speed v.

3. Problem Solution

When the thin-sheet material is transported from one roll to another, its projection curve along the rolls’ axes between two contact points with rolls can be described with Equation (5). As shown in Figure 4, the upstream roll is located at coordinate $O_1(0,D_h)$, the downstream roll is located at coordinate $O_2(2D_l,0)$. The radius of the upstream roll and the downstream roll is $R_1$ and $R_2$ respectively. The touchpoints between the sheet and the two rolls are B and C. The upper external co-tangents of $O_1$ and $O_2$ is $AD$. The angles between the vertical direction and $O_{1}B$ and $O_{2}C$ are ${\theta }_1$ and ${\theta }_2$, respectively.

The first derivative of the track is continuous at point B and point C. The boundary conditions of this problem are:

$$\left\{\begin{array}{c}{y}_B=D_h+R_{1}cos{\theta }_1\\ y_C=R_{2}cos{\theta }_2\\ {\dot{y}}_B=-tan{\theta }_1\\ {\dot{y}}_C=tan{\theta }_2\end{array}\right.\Rightarrow \left\{\begin{array}{c}y(R_{1}sin{\theta }_1)=D_h+R_{1}cos{\theta }_1\\ y(2D_l-R_{2}sin{\theta }_2)=R_{2}cos{\theta }_2\\ \dot{y}(R_{1}sin{\theta }_1)=-tan{\theta }_1\\ \dot{y}(2D_l-R_{2}sin{\theta }_2)=tan{\theta }_2\end{array}\right.$$

(12)

Substitute Equation (5) in Equation (12):

$$\left\{\begin{array}{c}-D_h-R_{1}cos{\theta }_1+\frac{C_1}{\rho btg}cosh\left(\frac{\rho btg}{C_1}(R_{1}sin{\theta }_1-C_2)\right)+\frac{\lambda -\rho bt{v}^2}{\rho btg}=0\\ -R_{2}cos{\theta }_2+\frac{C_1}{\rho btg}cosh\left(\frac{\rho btg}{C_1}(2D_l-R_{2}sin{\theta }_2-C_2)\right)+\frac{\lambda -\rho bt{v}^2}{\rho btg}=0\\ tan{\theta }_1+sinh\left(\frac{\rho btg}{C_1}(R_{1}sin{\theta }_1-C_2)\right)=0\\ -tan{\theta }_2+sinh\left(\frac{\rho btg}{C_1}(2D_l-R_{2}sin{\theta }_2-C_2)\right)=0\end{array}\right.$$

(13)

Define dimensionless variables as follows:

$$\widetilde{D_l}\equiv \frac{D_l}{R_1},\tilde{r}\equiv \frac{R_2}{R_1},\widetilde{D_h}\equiv \frac{D_h}{R_1},\widetilde{C_1}\equiv \frac{C_1}{R_1\rho btg},\widetilde{C_2}\equiv \frac{C_2}{R_1},\widetilde{C_3}\equiv \frac{\lambda -\rho bt{v}^2}{R_1\rho btg}$$

(14)

So, the dimensionless form of Equation (13) is:

$$\left\{\begin{array}{c}-\widetilde{D_h}-cos{\theta }_1+\widetilde{C_1}cosh\frac{sin{\theta }_1-\widetilde{C_2}}{\widetilde{C_1}}+\widetilde{C_3}=0\\ -\tilde{r}cos{\theta }_2+\widetilde{C_1}cosh\frac{2\widetilde{D_l}-\tilde{r}sin{\theta }_2-\widetilde{C_2}}{\widetilde{C_1}}+\widetilde{C_3}=0\\ tan{\theta }_1+sinh\frac{sin{\theta }_1-\widetilde{C_2}}{\widetilde{C_1}}=0\\ -tan{\theta }_2+sinh\frac{2\widetilde{D_l}-\tilde{r}sin{\theta }_2-\widetilde{C_2}}{\widetilde{C_1}}=0\end{array}\right.$$

(15)

These four equations contains four unknown varibles. For any given ${\theta }_1\in ({\theta }_s,\frac{\pi }{2})$, the unkown ${\theta }_2,\widetilde{C_1},\widetilde{C_2},\widetilde{C_3}$ can be solved with Equation (15) where ${\theta }_s$ is the angle between $AD$ and the horizontal direction and given by

$${\theta }_s=arctan\frac{\widetilde{D_h}}{2\widetilde{D_l}}-arcsin\frac{\tilde{r}-1}{\sqrt{{\widetilde{D_h}}^2+4{\widetilde{D_l}}^2}}$$

(16)

It is hard to obtain analytical solution to Equation (15). Numerical methods are used to solve it. In fact, Equation (15) has multiple solutions, as shown in Figure 5, and only the one with ${\theta }_2\in (-{\theta }_s,\frac{\pi }{2})$ accords with the actual circumstance. In many cases, the numerical methods cannot converge because of the high nonlinearity of Equation (15). It is found that the convergence of many numerical methods and which solution of the multiple solutions will be given are highly sensitive to the initial value ${[{\theta }_2^{\left(0\right)},{\widetilde{C_1}}^{\left(0\right)},{\widetilde{C_2}}^{\left(0\right)},{\widetilde{C_3}}^{\left(0\right)}]}^T$.

To solve this problem, an approximate value of the solution is given in Equation (17). This value is calculated by first assuming that the relationship between ${\theta }_1$ and ${\theta }_2$ is linear (${\theta }_1\in ({\theta }_s,\frac{\pi }{2})\to {\theta }_2\in (-{\theta }_s,\frac{\pi }{2})$) and then calculating ${\widetilde{C_1}}^{\left(0\right)},{\widetilde{C_2}}^{\left(0\right)},{\widetilde{C_3}}^{\left(0\right)}$ with ${\theta }_1$ and hypothetical ${\theta }_2$. Using this approximate value as the initial value in the process of finding the wanted numerical solution for Equation (15) is proved to be very efficient and effective.

$$\left[\begin{array}{c}{\theta }_2^{\left(0\right)}\\ {\widetilde{C_1}}^{\left(0\right)}\\ {\widetilde{C_2}}^{\left(0\right)}\\ {\widetilde{C_3}}^{\left(0\right)}\end{array}\right]=\left[\begin{array}{c}\frac{\frac{\pi }{2}+{\theta }_s}{\frac{\pi }{2}-{\theta }_s}\left({\theta }_1-{\theta }_s\right)-{\theta }_s\\ \frac{{\widetilde{C_2}}^{\left(0\right)}-sin{\theta }_1}{\mathrm{arcsinh}tan{\theta }_1}\\ \frac{(2\widetilde{D_l}-\tilde{r}sin{\theta }_2^{\left(0\right)})\mathrm{arcsinh}tan{\theta }_1+sin{\theta }_1\mathrm{arcsinh}tan{\theta }_2^{\left(0\right)}}{\mathrm{arcsinh}tan{\theta }_1+\mathrm{arcsinh}tan{\theta }_2^{\left(0\right)}}\\ \widetilde{D_h}+cos{\theta }_1-\frac{{\widetilde{C_1}}^{\left(0\right)}}{cos{\theta }_1}\end{array}\right]$$

(17)

Algorithm 1 present an example way to solve Equation (15) for $[{\theta }_2,\widetilde{C_1},\widetilde{C_2},\widetilde{C_3}]$.

Algorithm 1 Calculate ${[{\theta }_2,\widetilde{C_1},\widetilde{C_2},\widetilde{C_3}]}^T$ when given $R_1,R_2,D_l,D_h,{\theta }_1$.

Require: $2D_l>R_1+R_2,{\theta }_1\in ({\theta }_s,\frac{\pi }{2})$

Calculate $\tilde{r},\widetilde{D_l},\widetilde{D_h}$

Calculate ${[{\theta }_2^{\left(0\right)},{\widetilde{C_1}}^{\left(0\right)},{\widetilde{C_2}}^{\left(0\right)},{\widetilde{C_3}}^{\left(0\right)}]}^T$ with Equation (17)

$\mathrm{tol}={10}^{-7},\mathrm{factor}={10}^{-3}$

Find ${[{\theta }_2,\widetilde{C_1},\widetilde{C_2},\widetilde{C_3}]}^T$ minimize Equation (15) with ${[{\theta }_2^{\left(0\right)},{\widetilde{C_1}}^{\left(0\right)},{\widetilde{C_2}}^{\left(0\right)},{\widetilde{C_3}}^{\left(0\right)}]}^T$ as the initial value and factor as the initial step

return${[{\theta }_2,\widetilde{C_1},\widetilde{C_2},\widetilde{C_3}]}^T$

The convergence of this algorithm is verified using the exhaustive method when $\widetilde{D_h}\in [-20,20]$, $\widetilde{D_l}\in [1.5,50]$. Figure 6 shows the shape of the moving thin-sheet materials (solid) between rolls when position of rolls varies and $\tilde{r}=2$. Figure 6 also shows the track of the lowest point on the sheet (dash). This work uses HYBRID of MINPACK [38] in numerical computation.

For a given set of position and size parameters $R_1,R_2,D_l,D_h$ and ${\theta }_1\in ({\theta }_s,\frac{\pi }{2})$, by using above method, the parameters ${\theta }_2,\widetilde{C_1},\widetilde{C_2},\widetilde{C_3}$ can be determined. This method can be applied in the design of the production line, to determine if the track of a sheet is appropriate or to avoid the possible mechanical interference of the sheets with other equipment.

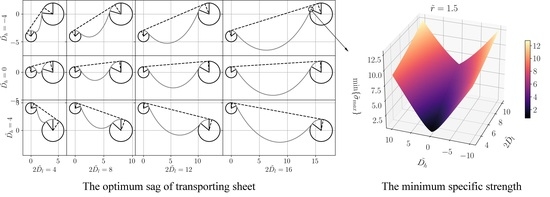
4. The Optimal Sag

If the sheet between rolls is too long or too short, it will have large tensions inside. To determine the relationship between the length of the sheet between rolls, the maximum tension in the sheet, and the position and size of rolls, define the length between rolls L as the length of the sheet between A and D as shown in Figure 4. For a given ${\theta }_1$, L can be expressed as:

$$\begin{array}{cc}\hfill L& \equiv \stackrel{⌢}{AB}+\stackrel{⌢}{BC}+\stackrel{⌢}{CD}\hfill \\ & =R_1({\theta }_1-{\theta }_s)+{\int }_{x_B}^{x_C}\sqrt{1+{\dot{y}}^2}\mathrm{d}x+R_2({\theta }_2+{\theta }_s)\hfill \\ & =\frac{C_1}{\rho btg}(tan{\theta }_1+tan{\theta }_2)+R_1({\theta }_1-{\theta }_s)+R_2({\theta }_2+{\theta }_s)\hfill \end{array}$$

(18)

Equation (11) indicates that the maximum tension exists at either point B or point C (the higher one). So the maximum stress in the sheet is:

$$\begin{array}{cc}\hfill {\sigma }_{max}& =\frac{T_{max}}{bt}=\frac{max\{T_B,T_C\}}{bt}\hfill \\ & =2\rho v^2-\frac{\lambda }{bt}+\rho gmax\{y_B,y_C\}\hfill \\ & =2\rho v^2-\frac{\lambda }{bt}+\rho gmax\{D_h+R_{1}cos{\theta }_1,R_{2}cos{\theta }_2\}\hfill \end{array}$$

(19)

Define the dimensionless forms of L and ${\sigma }_{max}$ as:

$$\tilde{L}\equiv \frac{L}{R_1}=\widetilde{C_1}(tan{\theta }_1+tan{\theta }_2)+{\theta }_1+\tilde{r}{\theta }_2+(\tilde{r}-1){\theta }_s$$

(20)

$${\tilde{\sigma }}_{max}\equiv \frac{{\sigma }_{max}-\rho v^2}{R_1\rho g}=max\{\widetilde{D_h}+cos{\theta }_1,\tilde{r}cos{\theta }_2\}-\widetilde{C_3}$$

(21)

It should be pointed out that for some specific parameters $R_1,R_2,D_l,D_h$ (when $(R_1-R_2+D_h)D_h<0$), the maximum tension point may change between B and C as the length changes. For example, when $R_1=0.2,R_2=1.0,D_l=3.0,D_h=0.4$, as shown in Figure 7, point C has greater tension when the sheet is tensioned and point B posesses greater tension when the sheet is relaxed.

The relationship between ${\tilde{\sigma }}_{max}$ and $\tilde{L}$ is calculated with Equations (20) and (21) when $\widetilde{D_l}$ varied and $\widetilde{D_h}=0$ is shown in Figure 8. Figure 8 (A), (B), (C), (D) for $\tilde{r}=0.2,1.0,1.5,1.8$ respectly.

The plot of ${\tilde{\sigma }}_{max}$ as a function of $\tilde{L}$ is shown in Figure 9, when $\widetilde{D_h}$ varied and $\widetilde{D_l}=2.5$. Figure 9 (A), (B), (C), (D) for $\tilde{r}=0.2,1.0,1.5,1.8$ respectly.

Figure 8 and Figure 9 show that ${\tilde{\sigma }}_{max}$ increases fast when $\tilde{L}$ is close to the length of $AD$, which means that the sheet is tensioned. It is also shown that the slope of ${\tilde{\sigma }}_{max}-\tilde{L}$ curve coverges to $0.5$ when $\tilde{L}$ increases. It has been shown that for a set of specific position and size parameters $R_1,R_2,D_l,D_h$, there is one optimum length $\widehat{L}$ which minimizes the maximum stress inside the sheet. Examples of this optimum pose are shown in Figure 10.

$$\widehat{L}=\arg \underset{L}{\min }{\sigma }_{max}$$

(22)

In practical engineering, $\widehat{L}$ can be estimated from the length of $AD$. Define $L_0=AD$. Figure 11 shows $\widehat{L}/L_0$ when $\widetilde{D_l}\in [1.5,5],\widetilde{D_h}\in [-10,10]$. Figure 11 (A), (B), (C), (D) for $\tilde{r}=0.2,1.0,1.5,1.8$ respectly.

The approximate value of $\widehat{L}$ is:

$$\widehat{L}\approx 1.25L_0=1.25\sqrt{D_h^2+4D_l^2+{(R_1-R_2)}^2}$$

(23)

The estimation method of the optium sheet sag shown in Equation (23) is a fast way to know how the sheet should be located to lower the maximum stress in the sheet.

5. The Minimum Specific Strength

When the radius of the rolls $(R_1,R_2)$ and positions $(D_l,D_h)$ are fixed, there exists an optium sheet position which makes the maximum dimensionless stress (${\tilde{\sigma }}_{max}$, defined in Equation (21)) in the sheet minimum.

$${\tilde{\sigma }}_{max}=\frac{{\sigma }_{max}-\rho v^2}{\rho g{R}_1}>min\left\{{\tilde{\sigma }}_{max}\right\}$$

(24)

In another word, when the rolls’ radius and positions are given, there is a lower limit for the material’s specific strength to be transported between these rolls.

$$\frac{{\sigma }_{max}}{\rho }>g{R}_{1}min\left\{{\tilde{\sigma }}_{max}\right\}+v^2$$

(25)

Define this lower limit as the Minimum Specific Strength, ${\widehat{\sigma }}_{Smin}$.

$${\sigma }_{Smin}\equiv g{R}_{1}min\left\{{\tilde{\sigma }}_{max}\right\}+v^2$$

(26)

To calculate $min\left\{{\tilde{\sigma }}_{max}\right\}$ with $R_1,R_2,D_l,D_h$, a numerical approach using varible step Newton’s Method is proposed as Algorithm 2. In this algorithm, factor $\alpha$ is introduced to control the Newton step to make the algorithm converge in some extreme examples. ${\tilde{\sigma }}_{max}\left({\theta }_1^{\left(t\right)}\right)$ can be calculated using method proposed in former sections. $min\left\{{\tilde{\sigma }}_{max}\right\}$ are calculated when $\widetilde{D_l}\in [1.5,5],\widetilde{D_h}\in [-10,10]$ and the results are shown in Figure 12. Figure 12 (A), (B), (C), (D) for $\tilde{r}=0.2,1.0,1.5,1.8$ respectly. As shown, the relationship between $min\left\{{\tilde{\sigma }}_{max}\right\}$, $|D_h|$ and $2D_l-R_1-R_2$ is approximately linear.

Algorithm 2 Calculate $min\left\{{\tilde{\sigma }}_{max}\right\}$ when given $R_1,R_2,D_l,D_h$.

Require: $2D_l>R_1+R_2$

${\theta }_1^{\left(0\right)}=1.1,t=0,\alpha =1,\Delta {\theta }_1={10}^{-3},\mathrm{tol}={10}^{-7}$

repeat

${\theta }_1^{(t+1)}={\theta }_1^{\left(t\right)}-\alpha \frac{\Delta {\theta }_1}{2}\frac{{\tilde{\sigma }}_{max}({\theta }_1^{\left(t\right)}+\Delta {\theta }_1)-{\tilde{\sigma }}_{max}({\theta }_1^{\left(t\right)}-\Delta {\theta }_1)}{{\tilde{\sigma }}_{max}({\theta }_1^{\left(t\right)}+\Delta {\theta }_1)+{\tilde{\sigma }}_{max}({\theta }_1^{\left(t\right)}-\Delta {\theta }_1)-2{\tilde{\sigma }}_{max}({\theta }_1^{\left(t\right)})}$

$t=t+1,\alpha =\alpha \ast 0.995$

until $\mathrm{abs}({\theta }_1^{(t+1)}-{\theta }_1^{\left(t\right)})<\mathrm{tol}$

return $min\left\{{\tilde{\sigma }}_{max}\right\}={\tilde{\sigma }}_{max}({\theta }_1^{\left(t\right)})$

To provide an estimation method for ${\sigma }_{Smin}$, let $min\left\{{\tilde{\sigma }}_{max}\right\}\approx k_1(2D_l-R_1-R_2)+k_2\left|D_h\right|$. $k_1,k_2$ are identified with the least square method when the $\tilde{r}$ took different values, as shown in

Table 1. Fitting results when $\tilde{r}$ varies. $D_h\in [0,10]$ or $[-10,0]$, $D_l\in [1.5,5]$.

${\mathit{R}}_1$	${\mathit{R}}_2$	${\mathit{D}}_{\mathit{h}}$	${\mathit{k}}_1$	${\mathit{k}}_2$		${\mathit{R}}_1$	${\mathit{R}}_2$	${\mathit{D}}_{\mathit{h}}$	${\mathit{k}}_1$	${\mathit{k}}_2$
1.0	0.2	$[0,10]$	0.704	0.809		1.0	0.2	$[-10,0]$	0.662	0.766
1.0	0.3	$[0,10]$	0.701	0.806		1.0	0.3	$[-10,0]$	0.664	0.769
1.0	0.4	$[0,10]$	0.698	0.804		1.0	0.4	$[-10,0]$	0.666	0.771
1.0	0.5	$[0,10]$	0.695	0.801		1.0	0.5	$[-10,0]$	0.669	0.774
1.0	0.6	$[0,10]$	0.692	0.798		1.0	0.6	$[-10,0]$	0.671	0.776
1.0	0.7	$[0,10]$	0.689	0.795		1.0	0.7	$[-10,0]$	0.673	0.779
1.0	0.8	$[0,10]$	0.686	0.792		1.0	0.8	$[-10,0]$	0.675	0.781
1.0	0.9	$[0,10]$	0.683	0.789		1.0	0.9	$[-10,0]$	0.677	0.784
1.0	1.0	$[0,10]$	0.679	0.786		1.0	1.0	$[-10,0]$	0.679	0.786
1.0	1.1	$[0,10]$	0.677	0.783		1.0	1.1	$[-10,0]$	0.682	0.789
1.0	1.2	$[0,10]$	0.674	0.779		1.0	1.2	$[-10,0]$	0.684	0.791
1.0	1.3	$[0,10]$	0.671	0.776		1.0	1.3	$[-10,0]$	0.686	0.794
1.0	1.4	$[0,10]$	0.668	0.772		1.0	1.4	$[-10,0]$	0.688	0.797
1.0	1.5	$[0,10]$	0.666	0.768		1.0	1.5	$[-10,0]$	0.69	0.799
1.0	1.6	$[0,10]$	0.663	0.764		1.0	1.6	$[-10,0]$	0.691	0.802
1.0	1.7	$[0,10]$	0.661	0.76		1.0	1.7	$[-10,0]$	0.693	0.805
1.0	1.8	$[0,10]$	0.659	0.755		1.0	1.8	$[-10,0]$	0.694	0.808

.

Based on the fitting results, the method for calculating ${\sigma }_{Smin}$ is given as:

$${\sigma }_{Smin}\approx g[0.68(2D_l-R_2-R_1)+0.79|D_h\left|\right]+v^2$$

(27)

Define relative error of this method as $\epsilon$:

$$\epsilon =\frac{{\sigma }_{Smin}-g[0.68(2D_l-R_2-R_1)+0.79|D_h\left|\right]-v^2}{{\sigma }_{Smin}-v^2}$$

(28)

The relative error $\epsilon$ is calculated when $\tilde{r},\widetilde{D_l},\widetilde{D_h}$ took different values, as shown in Figure 13. Figure 13 (A), (B), (C), (D) for $\tilde{r}=0.2,1.0,1.5,1.8$ respectly. In most cases, relative error of estimation value given by Equation (27) is less than 25%.

The concept of the Minimum Specific Strength has high practical significance in the production of the low-strength sheet. It is the property of the production system, and it does not depend on the sheet material or size. In real manufacturing, each machine has fixed roll size and position. Our Minimum Specific Strength model determines whether a certain type of material can be manufactured on this machine or not, and hence prevent the potential failures.

6. Discussion

This work derives the track and tension distribution for steady-state continuous moving flexible sheet under gravity (Equations (5) and (11)). Compared to previous studies (view the track of the sheet as a straight line), our work has a better prediction of the thin-sheet materials’ behavior when being transported in the low-tension state between rolls.

This study proposes a numerical method to model the track of the thin-sheet material considering the size and position of rolls (Algorithm 1). It is hardly studied before since in high-tension condition the size and position of rolls are insignificant. However, in the low-tension condition, they are important when modeling the shape and the maximum stress of the hanging sheet (Figure 8 and Figure 9). This study further finds that there exists a special shape of the thin-sheet material which minimizes the maximum stress in the sheet (Figure 10). The concept of the Minimum Specific Strength is developed, which depends only on the size, position, and the transporting speed (Equation (27)). This Minimum Specific Strength means the lower limit of thin-sheet material’s strength-density ratio that two fixed rolls can transport without damaging it.

7. Conclusions

This study proposes the concept of the Minimum Specific Strength that determines if a specific roll-to-roll system would be able to convey a certain low-strength sheet. The essential part of this work is the low-tension roll-to-roll system model. This study also presents an algorithm used to solve the complex problems when considering the size and position of rolls. This study further discusses how the sheet sag, rolls’ position, and rolls’ size would influence the maximum stress in the sheet. This study eventually leads to the concept of the Minimum Specific Strength and how to calculate and estimate it with rolls’ size and position. The relative error of this method to estimate the Minimum Specific Strength is less than 25% when $\widetilde{D_l}\in [1.5,5],\widetilde{D_h}\in [-10,10]$ in most cases.

The models and methods developed have already been applied in the design and intelligent control of noncombustible composite panel production line, which also can be applied to the manufacturing process of other low-strength flexible thin-sheet materials as well.