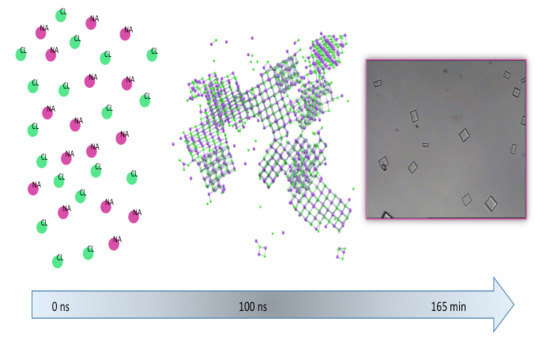
Membrane-Assisted Crystallization: A Molecular View of NaCl Nucleation and Growth

Featured Application

Investigation and prediction of crystallization and nucleation of mono and bivalent crystals with a new class of materials in advanced membrane separations.

Abstract

Membrane-assisted crystallization, aiming to induce supersaturation in a solution, has been successfully tested in the crystallization of ionic salts, low molecular organic acids, and proteins. Membrane crystallization is an emerging membrane process with the capability to simultaneously extract fresh water and valuable components from various streams. Successful application of crystallization for produced water treatment, seawater desalination, and salt recovery has been demonstrated. Recently, membrane crystallization has been developed to recover valuable minerals from highly concentrated solutions, since the recovery of high-quality minerals is expected to impact agriculture, pharmaceuticals, and household activities. In this work, molecular dynamics simulations were used to study the crystal nucleation and growth of sodium chloride in bulk and with hydrophobic polymer surfaces of polyvinylidene fluoride (PVDF) and polypropylene (PP) at a supersaturated concentration of salt. In parallel, membrane crystallization experiments were performed utilizing the same polymeric membranes in order to compare the experimental results with the computational ones. Moreover, the comparison in terms of nucleation time between the crystallization of sodium chloride (NaCl) using the traditional evaporation process and the membrane-assisted crystallization process was performed. Here, with an integrated experimental–computational approach, we demonstrate that the PVDF and PP membranes assist the crystal growth for NaCl, speeding up crystal nucleation in comparison to the bulk solution and leading to smaller and regularly structured face-centered cubic lattice NaCl crystals. This results in a mutual validation between theoretical data and experimental findings and provides the stimuli to investigate other mono and bivalent crystals with a new class of materials in advanced membrane separations.

1. Introduction

Crystallization is one of the oldest chemical operations to produce, purify, or separate solid products. Membrane crystallization refers to a hybrid membrane separation–crystallization process introduced in 2001 [1,2,3,4,5]. It denotes an advanced process where crystal nucleation and growth are carried out in a well-controlled pathway by using a porous hydrophobic membrane. In particular, a membrane crystallizer is a system where a membrane is in contact on one side with the feed solution (containing a nonvolatile component to be crystallized) and on the other side with a permeate solution (Figure 1).

The gradient of vapor pressure between the two subsystems induces the evaporation of the volatile component (i.e., the solvent) from feed solution and its migration through the porous membrane. The continuous removal of solvent increases solute concentration, thus generating supersaturation. Although the membrane does not act as sieving barrier for the selective transport of specific components, a solute–membrane interaction occurs due to the direct contact of the feed solution with the membrane surface. By considering the interactions between solute and solid substrate in terms of contact angle θ (which the crystallizing solution forms with the solid substrate), the reduction of ΔG due to heterogeneous nucleation is equal to [6,7,8]

$$\frac{\Delta G_{heter}}{\Delta G_{homog}}=\frac{1}{4}\left(2+\cos \theta \right){\left(1-\cos \theta \right)}^2{\left[1-\epsilon \frac{{\left(1+\cos \theta \right)}^2}{{\left(1-\cos \theta \right)}^2}\right]}^3$$

(1)

where ε is the overall surface porosity defined as the ratio between the area of the pores to the total membrane surface area. In the case of a nonporous system (ε = 0), when the contact angle is equal to 180°, then $\Delta G_{heter} =\Delta G_{homog}$, whereas if the contact angle is equal to 90°, then $\Delta G_{heter} =\frac{1}{2}\Delta G_{homog}$. Therefore, we can conclude that the presence of a hydrophobic membrane with 90° < θ < 180° promotes nucleation. The special effect of the heterogeneous contribution allows crystals to nucleate faster and/or by using a lower initial amount of substance with respect to the usual comparable techniques. An example can be found in [9], where the kinetics of lysozyme crystallization carried out with microporous hydrophobic membranes were investigated. Di Profio et al. [9] found considerably shorter induction periods (ranging between 1.2 and 10 h), compared with those measured by using conventional crystallization techniques, and high values of the growth rate constant at low supersaturation ratios. Their findings clearly demonstrate the effect of the membrane surface as a heterogeneous support for crystal nucleation and growth. Because the relation between ΔG_heter and ΔG_homog depends on the contact angle value, different polymeric membrane structures exhibit dissimilar interactions with a liquid phase. It is noteworthy that controlling interfacial forces are also contingent with local chemical environments dispersed in the membrane surface [10]. These kinds of interactions can also affect the induction time of nucleation, resulting in a very short time of crystallization. Gugliuzza et al. demonstrated that an increase in the cohesive energy between a protein solution and membrane surface was increased by functionalization of the membrane surface. An amphiphilic additive was used, thereby increasing the number of interaction sites without substantially affecting the hydrophobic character of the membrane surface. The result was an increasingly lower free energy of interfacial interaction, which is an expression of affinity between protein and membrane immersed in water. Consequently, a reduction of the crystallization induction time was achieved with formation of nanosized crystals in a range of 3–7 h [11].

The understanding of crystal nucleation is far from complete [12,13]. This is because the molecular details of the process appear in a very small length scale of the order of nanometers, and they are, by definition, unstable and therefore form only transiently, so they are quite challenging to probe even in real time. However, today, with state-of-the-art measurements, nucleation has also been observed at the molecular scale [12,14,15,16]. The rapid advance of experimental techniques such as in situ atomic force microscopy [17], liquid-cell transmission electron microscopy [18], and cryo-TEM [15] will deliver novel results in order to refine the understanding of crystal nucleation and growth [19]. Computational modelling and in particular molecular dynamics (MD), where the temporal evolution of the liquid into the crystal is studied, complementary experiments provide exciting insights into the mechanisms of such phenomena and enable kinetic and thermodynamic quantities to be estimated. Surely, the rapid progress in computational methodology has unraveled crucial aspects of crystal nucleation in liquids. Several studies have been performed to depict the mechanism of heterogeneous crystal nucleation by simulation [13,20,21,22,23], such as atomic simulation [24,25,26] and phase field theory [27], while there are limited publications for heterogeneous salt crystal nucleation from an aqueous solution [25,28,29]. Moreover, the mechanics of the earliest stages of the crystallization assisted by membranes still remain an important fundamental issue. However, there have been a series of papers discussing crystal nucleation in aqueous solutions [30,31,32,33,34], focusing on available force fields and models. Here, we present the results from molecular dynamics simulations of the crystal nucleation and growth of a sodium chloride solution in contact with hydrophobic polymer surfaces of polyvinylidene fluoride (PVDF) and polypropylene (PP) at a supersaturated concentration of salt. The crystallization of NaCl from aqueous solutions was chosen because it is a typical example of most inorganic crystallizing systems. First, crystal nucleation and growth were simulated in a slightly supersaturated aqueous bulk solution as performed by Chakraborty [33]. Then, PVDF and PP membrane surfaces interfacing an NaCl solution were studied and the results were compared with that of bulk solutions and with experimental data. In parallel, membrane crystallization experiments were performed utilizing the same kind of polymeric membranes in order to compare the experimental findings with the computational data. Moreover, the comparison in terms of nucleation time between the crystallization of sodium chloride using the traditional evaporation process and the membrane-assisted crystallization process was performed. By means of molecular dynamics simulations, we demonstrate that the PVDF and PP membranes assist the crystal growth of NaCl, speeding up crystal nucleation in comparison to the bulk solution and leading to smaller and regularly structured face-centered cubic lattice NaCl crystals. A mutual validation between theoretical data and experimental findings was found. These preliminary simulations shed light on their application capability to predict crystallization with different complex polymeric matrices.

2. Materials and Methods

2.1. Experiments

The description of the lab-scale apparatus utilized for performing the tests (Figure 1) can be found elsewhere [34]. In all the tests, the feed solution was charged in the crystallizer tank and recirculated through the membrane modules. The solvent evaporated at the interface of microporous hydrophobic membranes on the warm (retentate/feed) side, diffused through the pores, and condensed on the opposite (permeate/distillate) side (Figure 1). A pump ensured the counter-current recycle also of the cold permeate stream (constituted by distilled water), the function of which was to condense the water vapor passing across the membrane pores. The driving force of the process was a vapor pressure difference across the membrane which was imposed by a temperature difference across the membrane. Therefore, the feed/retentate line was heated by an ISCO GTR 2000 heater whilst the permeate/distillate side was cooled by an NESLAB RTE 17 refrigerated bath. A crucial requirement for an MCr is to prevent crystal deposition inside the membrane module and on the membrane surface. The recirculation of the feed solution helps in removing crystals eventually deposited and/or grown on the membrane surface.

In

Table 1. Structural parameters of the utilized membranes.

Fiber Type	Outer Diameter (mm)	Inner Diameter (mm)	Thickness (mm)	Pore Size (μm)	Porosity (%)	Contact Angle (°)
PVDF	1.75	0.94	0.40	0.47	80.8	91
PP	1.80	1.56	0.12	0.20	70.0	115

, the characteristics of the utilized membranes can be found. In both cases, experiments were performed at the same temperature of the feed (34 ± 1 °C).

Since the crystals appeared every 30 min, a suspension sample of them was extracted carefully and with alacrity. For each test, three different samples were analyzed (the first one at the onset of crystallization, the second one after 30 min, and the third one after 1 h). Particles were extracted, examined visually with an optic microscope (model Axiovert 25, ZEISS, Oberkochen, Germany), and pictures recorded with a video camera module VISIOSCOPE Modular System equipped with an optical head (10/100X) in order to determine the crystal growth rate (G), which was determined according to the following equations [18]:

$$\ln \left(n\right)=\frac{-L}{Gt}+ln(n^0)$$

(2)

and

$$B^0=n^{0}G$$

(3)

where n is the crystal population density, L is the crystal size, t is the retention time, and $n^0$ is the population density at L equal to zero.

2.2. Modelling

Unbiased molecular dynamics simulations using all atoms were performed for the investigation of the feasibility of growing NaCl crystals. The initial amorphous PVDF and PP structures with a density of 1.9 and 0.9 g/cc, respectively, were constructed using the amorphous cell module in the commercial software Material Studio package (version 7.0) (Dassault Systèmes BIOVIA, San Diego, 2013) [35] and the COMPASS (Condensed-phase Optimized Molecular Potentials for Atomistic Simulation Studies) force field [36]. The polymeric models were grown in a 3D cubic box under periodic boundary conditions at 298 K using the algorithm developed by Theodorou and Suter [17] and the scanning method proposed by Meirovitch [38]. All MD simulations, both considering only the bulk solution and with the polymeric membrane models, were then performed using the GROMACS (Groningen MAchine for Chemical Simulation, developed at the University of Groningen, Groningen, The Netherlands) software package, version 5.1.4 [39]. The force field parameters of the PVDF polymer developed by Byutner and Smith [40] were used in this study and are listed in

Table 2. Force field parameters for polyvinylidene fluoride (PVDF) [40,41].

Bonds			${\mathit{b}}_{\mathit{i}\mathit{j}}$ (nm)		${\mathit{k}}_{\mathit{i}\mathit{j}}^{\mathit{b}}$ (kJ/mol nm2)
CH–H			0.1085		274,135.68
CF–F			0.1357		417,814.24
CF–CH			0.1534		258,487.52
Angles			${\theta }_{ijk}^0$ (deg)		$k_{ijk}^{\theta }$(kJ/mol rad2)
F–CF–F			105.27		1004.1600
F–CF–CH			107.74		753.1200
CH–CF–CH			118.24		671.9504
H–CH–H			109.27		322.1680
H–CH–CF			108.45		358.9872
CF–CH–CF			118.24		671.9504
Torsions (kJ/mol)	$k_{\varphi }(1)$	$k_{\varphi }(2)$	$k_{\varphi }(3)$	$k_{\varphi }(4)$	$k_{\varphi }(5)$	$k_{\varphi }(6)$
CF–CH–CF–CH	1.65268	3.01248	−1.58992	−0.85772	1.77820	−0.10460
F–CF–CH–CF	1.48532	1.44348	−1.58992	0.58576	0.60668	−0.10460

.

The size of the PVDF model was 9.72 × 6.18 × 6.2 nm, that of the PP model was 5.61 × 5.61 × 10.1 nm, whereas the size of the bulk NaCl solution was 5.83 × 5.83 × 7.7 nm. The simulation boxes of three models were filled with 6919 SPC/E water molecules [42]. Slightly supersaturated conditions were considered with a concentration of solution of 5.94 ± 0.2 M (crystallization of NaCl to occur at sodium chloride concentrations larger than 5:4 mol/L [43]) with almost 741 pairs of Na⁺ and Cl⁻ ions chosen in order to simulate the condition near a membrane surface during crystallization experiments. The ion parameters with the OPLS force field [44] were used. All pair interactions consisted of Lennard-Jones (LJ) and Columbic terms, and the Lorentz–Berthelot combining rules [45] were chosen to generate LJ parameters between different types of atoms. Other LJ parameters utilized in this study are shown in

Table 3. Nonbonded force field parameters and charges of the Lennard-Jones potential for water, ion, and PVDF ^a.

Atom Type	σ (Å)	ε (kJ/mol)	Charge (e)
Ow	3.166	0.6501	−0.847600
Hw	0.0	0.0	+0.423800
Na+	3.330	0.0116	+1
Cl−	4.417	0.4928	−1
CPVDF, H	3.500	0.2763	−0.650250
CPVDF, F	3.500	0.2763	+0.765000
HPVDF	2.500	0.1256	+0.225875
FPVDF	2.983	0.2512	−0.283250

^a The O_w and H_w parameters are for water and from [42], and the Na⁺ and Cl⁻ parameters are from [50,51], respectively. The parameters of C_{PVDF, H}, C_{PVDF, F}, H_PVDF, and F_PVDF are for PVDF and from [52].

. The total energy of the materials calculated is given by [39,40]

$$\begin{array}{cc}\hfill V& ={\displaystyle \sum _{i,j}\frac{1}{2}{k}_{ij}^b{\left(r_{ij}-b_{ij}\right)}^2}+{\displaystyle \sum _{i,j,k}\frac{1}{2}{k}_{ijk}^{\theta }{\left({\theta }_{ijk}-{\theta }_{ijk}^0\right)}^2}+{\displaystyle \sum _{i,j,k,l}{\displaystyle \sum _n\frac{1}{2}{k}_{ijkl}^{\varphi }\left(n\right)\left(1+\cos \left(n{\varphi }_{ijkl}-{\varphi }_s\right)\right)}}\hfill \\ & +{\displaystyle \sum _{i>j}4{\epsilon }_{ij}\left({\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{12}-{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^6\right)}+{\displaystyle \sum _{i>j}\frac{1}{4\pi {\epsilon }_0}\left(\frac{q_i{q}_j}{{\epsilon }_r{r}_{ij}}\right)}\hfill \end{array}$$

(4)

where $r_{ij}$, ${\theta }_{ijk}$, and ${\varphi }_{ijkl}$ are the distance, angle, and torsional angle between the bonded atoms i and j, i, j and k, i, j, k, and l, respectively. ${\varphi }_s$ is 180°. ${\epsilon }_{ij}$ and ${\sigma }_{ij}$ are the well depth and size of Lennard-Jones. ${\epsilon }_0$ is the permittivity of vacuum, and ${\epsilon }_r$ is the relative dielectric constant, and in this case, it is 1. $q_i$ and $q_j$ are the respective charges of atoms i and j. Other LJ parameters utilized in this study are shown Table 3. Periodic boundary conditions were applied. Long-range Columbic interactions were calculated using the particle-mesh Ewald (PME) summation method [46].

The cutoff radius for LJ interactions and for short-range Columbic interactions was set to 1 nm. The leapfrog algorithm with a time step of 2 fs was used for integration of equations of motion. The simulations were conducted in the isothermal–isobaric ensemble (NPT) at 300 K and 1 atm using the velocity rescaling thermostat [47] (τ_t = 0.1 ps) for temperature coupling and the Berendsen barostat [48] with the compressibility of 4.5 × 105 bar⁻¹ (τ_p = 2 ps) for pressure coupling. The initial configuration for the models were obtained by minimizing the total energy in the box, then equilibrated via isothermal ensemble (NVT) followed by NPT for each 2000 ps with a time step of 0.2 fs. Finally, the systems were carried out with a production run of 100 ns. All trajectories were visualized using Visual Molecular Dynamics, version 1.9.3 [49].

3. Results and Discussion

Crystals obtained from crystallization experiments reported in this work show the characteristic cubic block-like form in accordance with the expected geometry of the NaCl crystals (Figure 2).

The molecular view of the crystals was reached observing the crystal obtained by molecular simulations both in the bulk solution of NaCl and in the presence of PVDF and PP membrane surfaces.

Crystals achieved from bulk solutions are indicated in Figure 3, wherein the lattice of Na⁺ and Cl⁻ ions is visible. Crystal growth was observed within 100 ns from supersaturated solutions (about 6 M). The salt concentration was set at a relatively high value because it facilitates nucleation during the MD simulations. NaCl crystallized into a face-centered cubic lattice, a cubic with space group Fm3m and Z = 4 (four formula units per cell). The lattice parameter is a = 5.6601 Å at room temperature, slightly larger than the experimental value of 0.564 nm determined by X-ray diffraction measurements by Walker et al. [53] on synthetic NaCl powders. This is due to small inaccuracies in the interaction potentials and the finite size of the crystal. Similar regular structures of face-centered cubic NaCl crystals appeared when the supersaturated solutions (about 6 M) were in contact with polymeric PVDF and PP membranes, in agreement with the crystal forms obtained from experimental screening (Figure 2).

Crystal growth is a relatively slow process but is accessible to MD simulations for simple systems. Nucleation, on the other hand, is an activated process belonging to a class of rare event phenomena [13].

The simulations indicated that crystallization in both the NaCl solution and PVDF and PP membrane surfaces follow an Ostwald-like process [34,54,55,56,57,58]. Firstly, local regions of relatively high salt concentration in the supersaturated solution appear prior to visible spatial ordering with the early-stage salt nucleus containing a significant amount of water, followed by a second step that includes nucleation and development of spatial ordering of the ions. This is due to the fact that formation of several small nuclei is entropically favorable [59,60].

Na⁺ and Cl⁻ ions, both in the bulk solution and with PVDF and PP membrane surfaces, during the simulation time organize themselves in regions of highly concentrated disordered ions and then the initial formation of ordered clusters and growth followed the Ostwald-like process during the simulation time, as observed for the NaCl solution at different concentrations by Chakraborty and Patey [34]. Figure 4 gives a qualitative overview of crystal nucleation of NaCl crystals from the bulk solution and in the presence of the PP membrane surface. Small size aggregates of ions appeared in both systems and combined gradually to form larger aggregates (Figure 4a,c). For the bulk solution, some initial small nuclei of crystals (with a partial but visible order of Na⁺ and Cl⁺ ions) started forming at 16.5 ns (Figure 4b). The nucleation of small visible crystals in PVDF started at 6–6.5 ns of simulation (not shown here), whilst 3.5–4 ns were necessary for PP systems (Figure 4d). Therefore, in the presence of the membrane surface, crystals formed in a shorter time than that observed for the bulk solution.

Similarly, the experimental data reported in

Table 4. Kinetic parameters of the NaCl crystallization tests.

	PVDF	PP
Minimum time for detecting and recovering crystals [min]	360	from 165 to 283 a)
Crystals growth rate [mm/min] a)	from 6.5 × 10−5 to 2.2 × 10−4	from 2.5 × 10−5 to 5.7 × 10−5

^a) For each membrane, the lowest and highest crystals growth rate of the three analyzed samples are reported.

showed that the time for detecting and collecting crystals from the feed solution was lower for PP membranes with respect to PVDF membranes. These data are in accordance with the estimated Gibbs free energies’ ratio (Equation (1) equal to 0.40 and 0.56 for PP and PVDF membranes, respectively. The lower the ΔG_{heterogeneous}/ΔG_homogeneous ratio, the lower the energy barrier to overcome for forming a critical nucleus formation.

For comparison, Cui et al. [61] determined a nucleation time for NaCl crystals produced via the traditional evaporation method equal to 386 min.

Moreover, the experimental data reported in Table 4 prove that the crystal growth in the PVDF membrane is almost the same, just slightly higher than in PP membrane. The shape and dimension of crystals in both membrane systems are similar, as confirmed by the modelled crystals in Figure 2.

After 100 ns of simulations, significant differences between the NaCl bulk solution and the system containing membrane surfaces were observed. PP and PVDF models produced multiple regularly structured face-centered cubic lattice NaCl crystals, suggesting a more controlled nucleation and higher growth of the crystals. These high numbers of crystal were of a smaller dimension compared to that obtained from the NaCl bulk solution (Figure 5a–c).

This is in accordance with the fact that in the bulk solution, the nucleation is slower and the supersaturation in the solution decreases gradually because the nucleation of the formed crystals continues and different sizes can be obtained. Instead, with PVDF and PP surfaces, the nucleation is faster than in the bulk solution and many crystals form nearly simultaneously [12]. Moreover, the percentage of free ions after 100 ns of simulation in the bulk NaCl solution was about 14.3%, whereas in PVDF and PP, it was about 4.5% and 3.6%, respectively. The growth of crystals in PVDF and PP diminishes the solution of solute and leads to the termination of nucleation at the advanced stages of crystallization. Therefore, the majority of crystals grow to approximately identical sizes [12].

In order to analyze the evolution of the NaCl crystals during simulation time, a quantitative overview is given in Figure 6, where we have plotted r²h₊₋(r) for times ranging from 5 to 100 ns. Here, h₊₋(r) = g(r)⁻¹, where g(r) is the radial distribution function and multiplied by r² to magnify the structural details [31]. The function h₊₋(r) is averaged over all ions in the system. However, ions in the growing crystal contributed to the long-range structure. At 5, 10, and up to 20 ns, r²h₊₋(r) is very short ranged and refers to the metastable solution with one discernable peak indicating few ordered ions. At 100 ns of simulation, the structural peaks related to the ion−ion correlation are visible, indicating the growth of NaCl crystals. When the function r²h₊₋(r) becomes negative, a rough indication of the “crystal magnitude” is obtained: the positive region reflects the increase in the ion density in the crystal, and the negative region is the corresponding decrease in the ion density in the surrounding solution [30,33]. This effect is evident in the bulk NaCl solution. For the bulk NaCl solution, a larger order is visible up to 2 nm, whereas for NaCl in contact with the hydrophobic membranes, it is up to 1.5 nm.

The presence of PP and PVDF membranes modified the shape of the r²h₊₋(r) function. Only positive regions are present in both Figure 6b,c, indicating the augmented ion density in the crystal. However, the disorder in the figure visible at larger separations could be related to the distinct crystal distribution in the PP (PVDF) systems, with a higher number of small crystals, and to the presence of water molecules (discussed below).

Snapshots referring to specific simulation times, i.e., 5 ns (Figure 7a), 20 ns (Figure 7b), and 100 ns (Figure 5c) of PP model were related to the radial distribution function g(r) (Figure 7c) of the interaction of Na⁺ and Cl⁻ (the PP model was used as a reference, showing similar behavior to PVDF).

Here, both water molecules and polymeric membranes are not shown. After 5 ns of simulation, several crystals with small dimensions were distinguishable. So, a distinct order among the ions existed (Figure 7a), although the nuclei were immersed in amorphous NaCl agglomerates (disorder), showing that the crystal structures were not completely stable yet. After 20 ns, larger crystals were found and the central part of the system appeared to be stable (Figure 7b). This reveals how rapidly the crystals grow over time, such as to form significant aggregates even at 20 ns. At 100 ns of simulations, stable crystals are made with few free ions available in the solution (Figure 5c).

The analysis of the dimension is reflected by the analysis of the g(r). At 5 ns of simulations, one sharp peak and a second peak, less resolved at larger interionic distances referring to the increased spatial ordering of the ions, are visible. The evolution of the g(r) at 20 ns indicated well-defined peaks demonstrating nucleation and spatial ordering of the ions as reported also for the NaCl bulk solution at different concentrations [62,63]. A similar g(r) plot appears at 100 ns as indicated by the crystal dimension at 20 ns (Figure 7b) and at 100 ns (Figure 5c).

The contribution of water molecules to the formation of crystals is reflected by analyzing the Na⁺ ion−water interaction (Figure 8). The peaks of the g(r) plot refer to the area corresponding to the growth of the crystal that decreased with time. At 5 ns, the peaks referring to the ion–water interaction are high and at a value corresponding to the first shell of solvation of Na⁺ (0.23 and 0.25 nm) and in agreement with ab initio MD [64], neutron diffraction data [65], and with large-angle X-ray scattering (LAXS) data [66]. After 20 and 100 ns of simulation, the corresponding peaks are smaller and smaller but present, indicating that some residual water remained within the crystals both in the bulk solution and in the presence of the membrane surfaces.

The place where crystals nucleate and grow is an important parameter to consider in the entire process because it is dependent on the strong repulsion between water and ions approaching the hydrophobic PVDF and PP surfaces.

Figure 9 shows the density profiles of the PVDF system composed of the PVDF surface, water molecules, and ions at 5 and 100 ns of simulations. The density profile of the PP system is similar and for this reason not shown here. The analysis of the atomic fraction distribution indicated at 100 ns an increase of the ions’ density profile (Figure 9b) at about 2 nm away from the PVDF surface resulting in an increase in the crystal density. In parallel, there is a partial reduction of the density profile relative to water in correspondence of the ions’ increase. This is an indication of the removal of water molecules and ion–ion aggregation, which preludes the crystal formation as shown in Figure 8. Due to the hydrophobicity of the membrane surface, water molecules are “shifted” far away from the surface and ions are physically constrained in a smaller region wherein attractive ion–ion Coulomb interactions take place. This effect could be related to a kind of “extra supersaturation” induced by hydrophobic surfaces that catalyze ion aggregation through reinforcement of Coulomb interactions when compared with the model of bulk NaCl.

These findings are in agreement with the results of Chakraborty and Patey [33] at high concentrations and with recent fallouts coming from polymeric hydrophobic matrices with complementary functions such as bismuth selenide confined inside PVDF that produce a quicker and controlled growth rate of NaCl salts [67]. These preliminary simulations shed light on their application capability to predict crystallization with different complex polymeric matrices.

4. Conclusions

Molecular dynamics simulations were used to investigate crystal nucleation and growth of NaCl in membrane-assisted crystallization. The results were compared with a bulk NaCl solution at the same concentration. In parallel, membrane crystallization tests were performed utilizing the same polymeric membranes in order to compare experimental results with the computational ones. Additionally, the comparison in terms of nucleation time between the crystallization of sodium chloride using the traditional evaporation process and the membrane-assisted crystallization process was performed.

The analysis of shape and growth of crystals indicated the formation of smaller and regularly structured face-centered cubic lattice NaCl crystals when the solution was in contact with PVDF and PP membrane surfaces in comparison with that obtained from the bulk solution, where fewer and larger crystals were visible, suggesting a more controlled nucleation and higher growth of the crystals.

The integrated experimental–computational approach showed that both polymeric surfaces speeded up crystal nucleation in comparison with the bulk solution, confirming the experimental results and thus resulting in a reciprocal validation and in useful correlations between MD and the experimental analysis.

These preliminary simulations provide the stimuli to investigate other mono and bivalent crystals and related mixtures in view to predict crystallization with different complex polymeric matrices [67].