Postbuckling and Free Vibration of Multilayer Imperfect Nanobeams under a Pre-Stress Load
Abstract
:1. Introduction
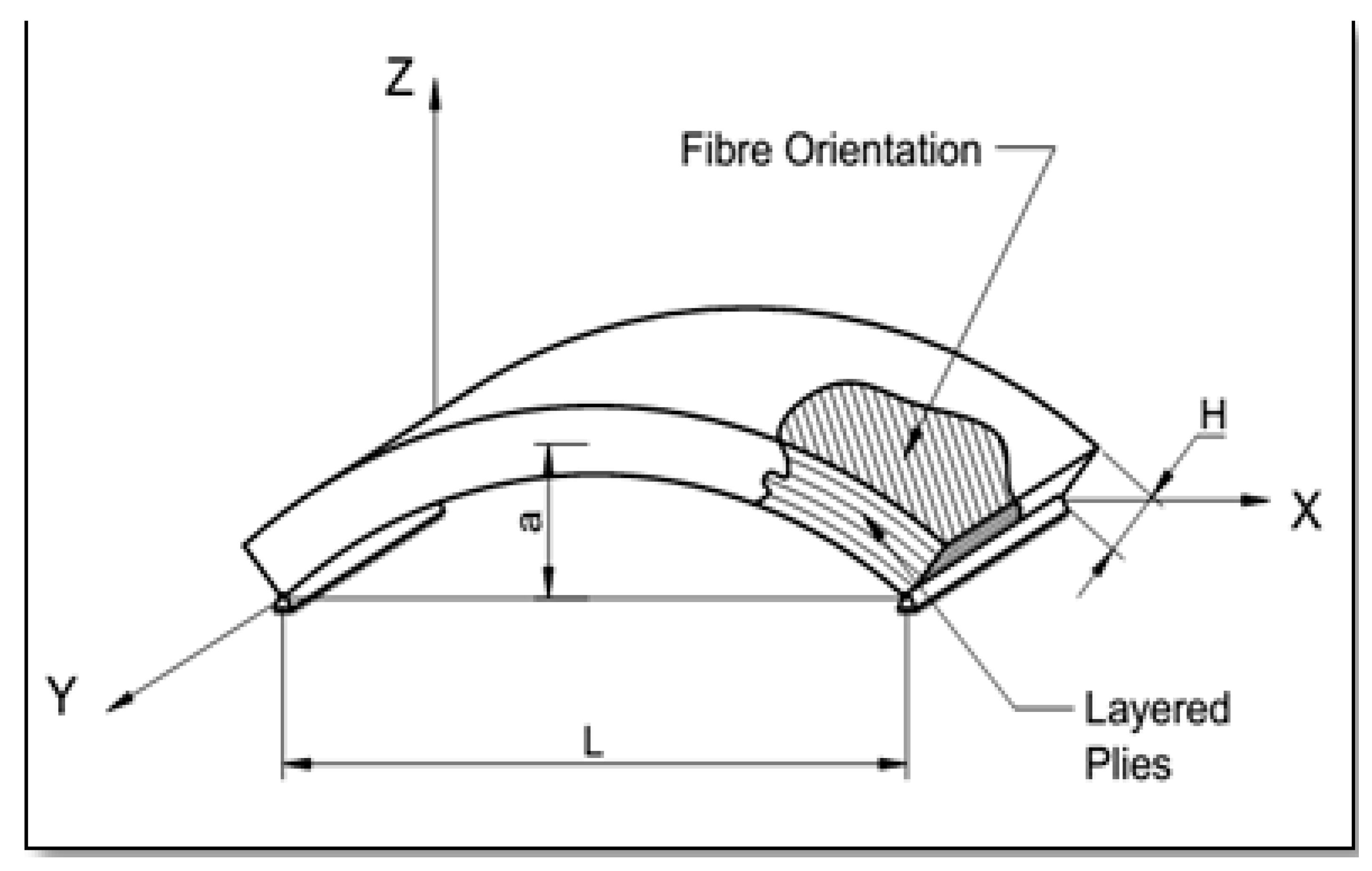
2. Problem Formulation
2.1. Kinematic Relations
2.2. Equations of Motion
2.3. Constitutive Equations
3. Static Analysis
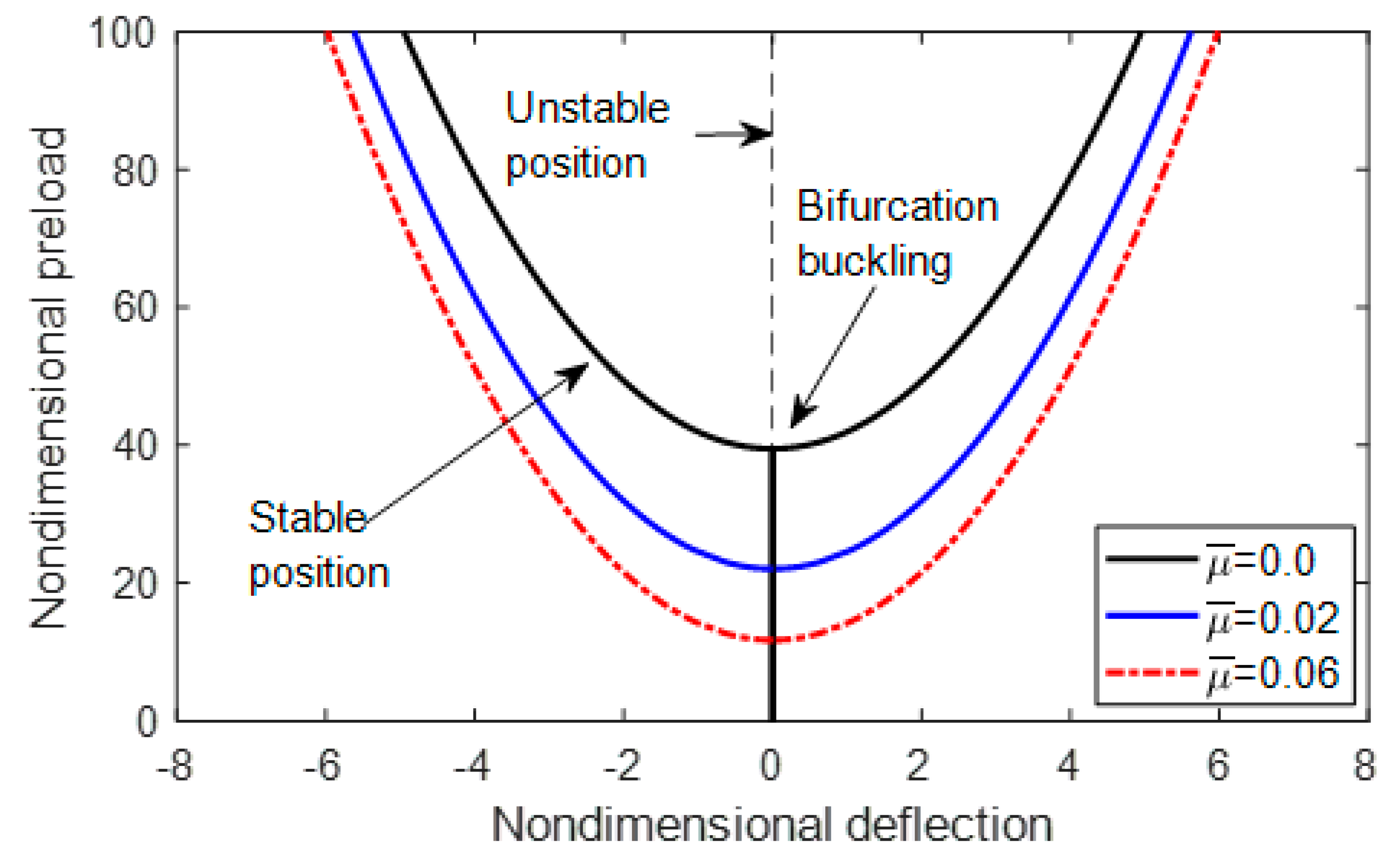
3.1. Buckling Load of Imperfect, Multilayer Nanobeams
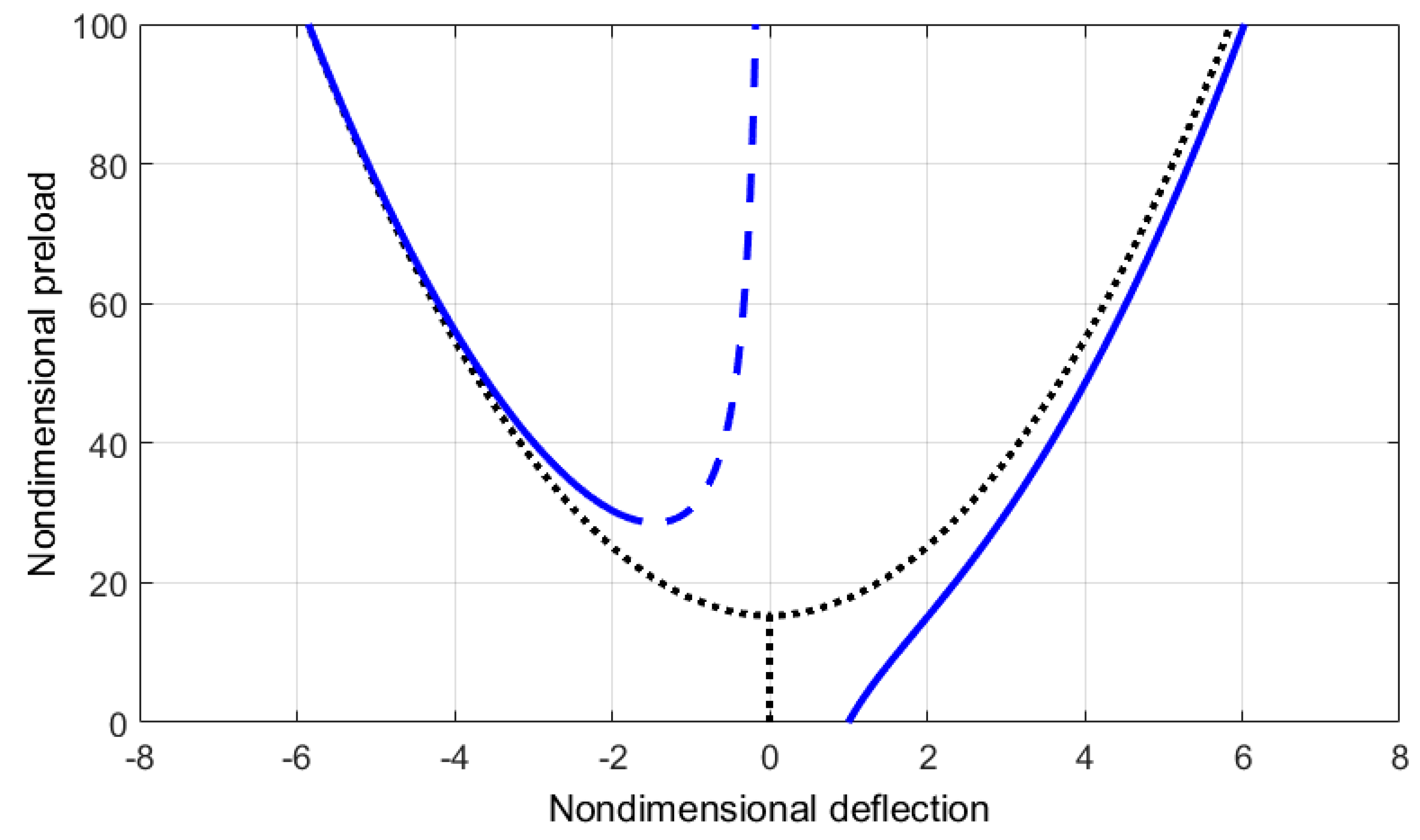
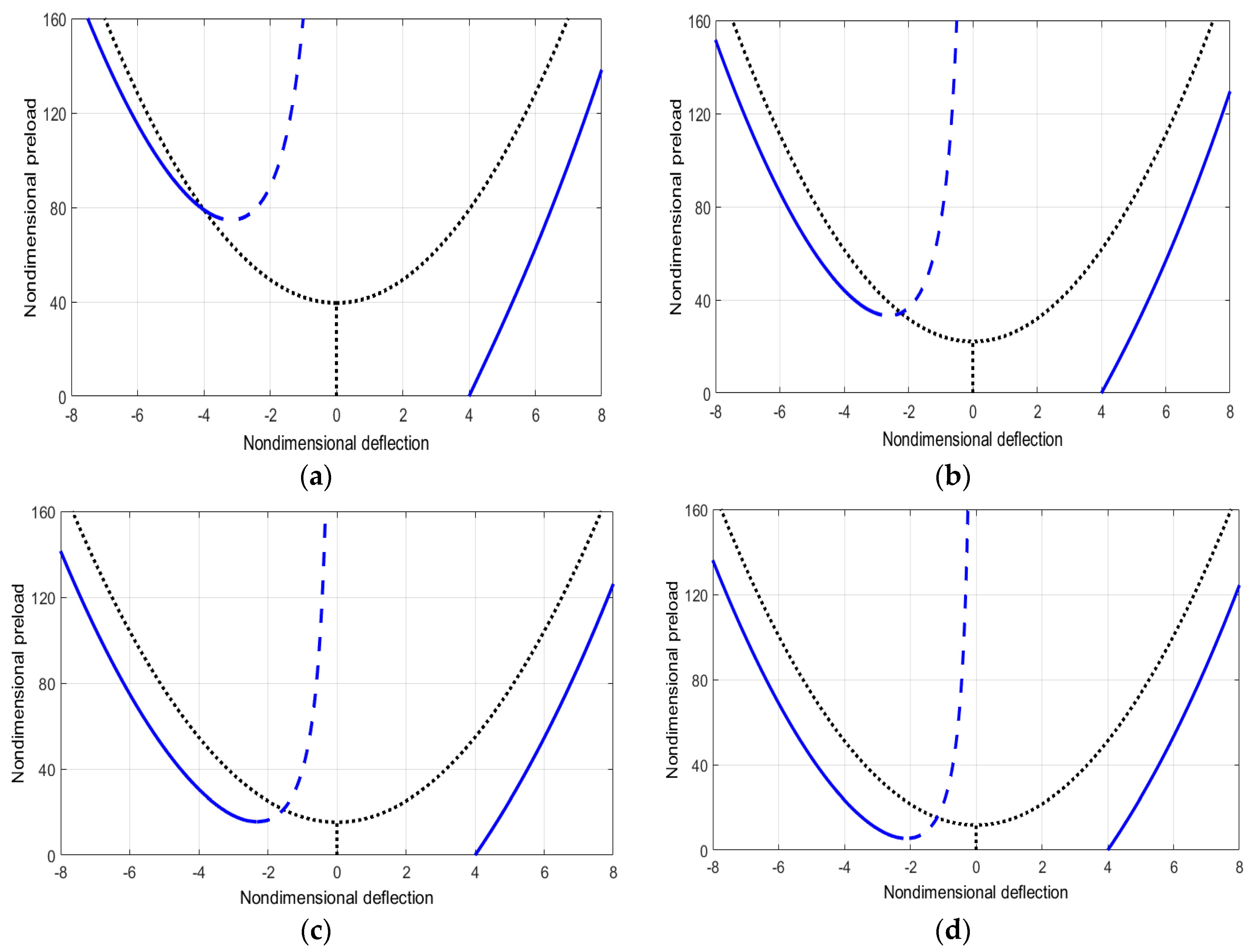
3.2. Postbuckling of Imperfect, Multilayer Nanobeams under Pre-Stress Loading
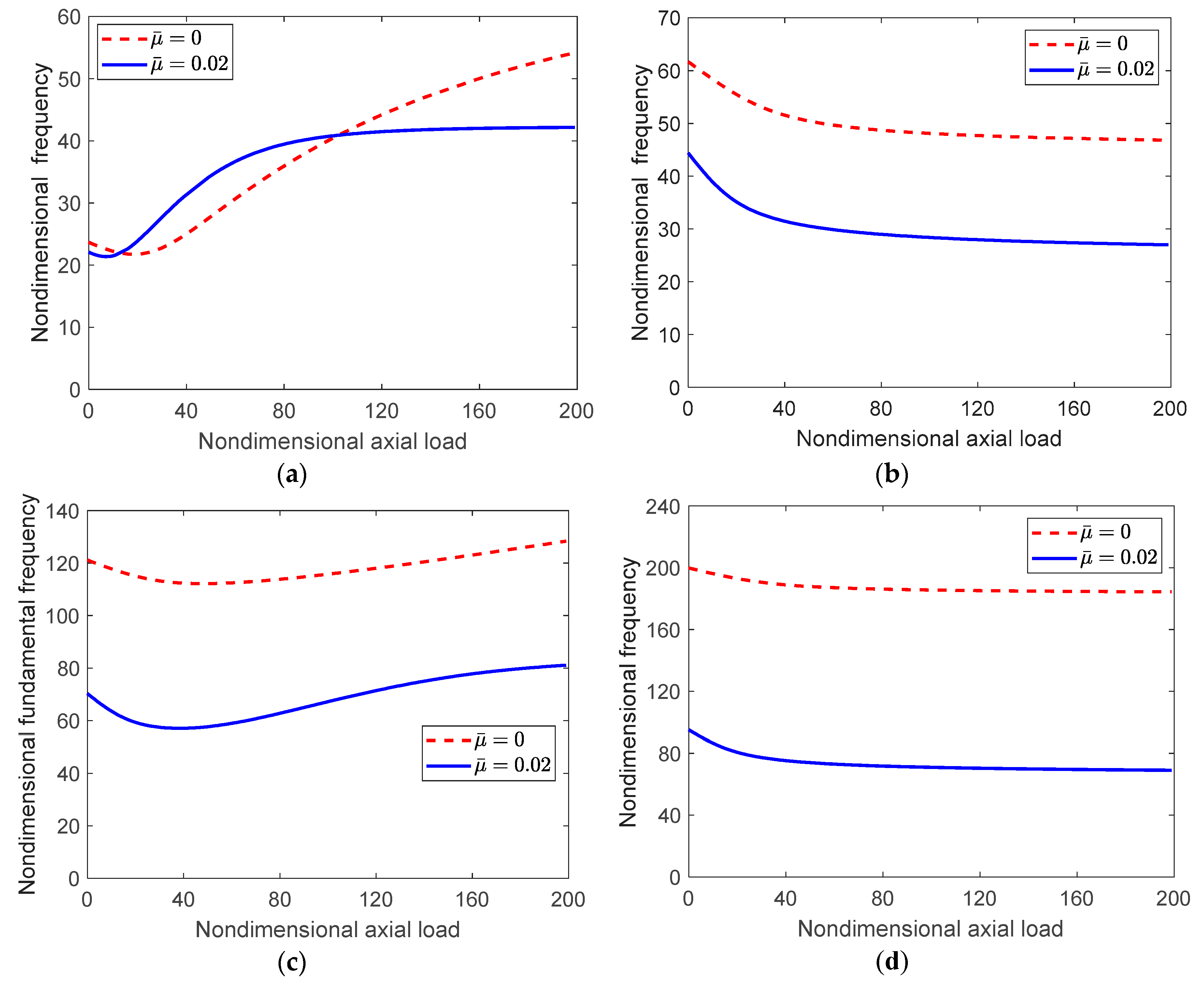
4. Free Vibrations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bortz, J.; Shatz, N. Nanolayered polymer diffusive spectral filters. In Proceedings of the SPIE 8485, Nonimaging Optics: Efficient Design for Illumination and Solar Concentration IX, San Diego, CA, USA, 11 October 2012. [Google Scholar]
- Legtenberg, R.; Gilbert, J.; Senturia, S.D.; Elwenspoek, M. Electrostatic curved electrode actuators. J. Microelectromech. Syst. 1997, 6, 257–265. [Google Scholar] [CrossRef] [Green Version]
- Torri, P.; Hirvonen, J.P.; Kung, H.; Lu, Y.C.; Nastasi, M.; Gibson, P.N. Mechanical properties, stress evolution and high-temperature thermal stability of nanolayered Mo–Si–N/SiC thin films. J. Vac. Sci. Technol. B 1999, 17, 1329–1335. [Google Scholar] [CrossRef]
- Li, Z.; Dharap, P.; Nagarajaiah, S.; Nordgren, R.P.; Yakobson, B. Nonlinear analysis of a SWCNT over a bundle of nanotubes. Int. J. Solids Struct. 2004, 41, 6925–6936. [Google Scholar] [CrossRef]
- Verma, N.; Jayaram, V. Role of interface curvature on stress distribution under indentation for ZrN/Zr multilayer coating. Thin Solid Films 2014, 571, 283–289. [Google Scholar] [CrossRef]
- Senturia, S.D. Microsystem Design; Kluwer Academic Publishers: Boston, MA, USA, 2001. [Google Scholar]
- Chidamparam, P.; Leissa, A.W. Vibrations of planar curved beams, rings, and arches. Appl. Mech. Rev. 1993, 46, 467–483. [Google Scholar] [CrossRef]
- Petyt, M.; Fleischer, C.C. Free vibration of a curved beam. J. Sound Vib. 1971, 18, 17–30. [Google Scholar] [CrossRef]
- Palani, G.S.; Rajasekaran, S. Finite element analysis of thin-walled curved beams made of Composites. J. Struct. Eng. 1992, 118, 2039–2061. [Google Scholar] [CrossRef]
- Lacarbonara, W. A theoretical and experimental investigation of nonlinear vibrations of buckled beams. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 1997. [Google Scholar]
- Howson, W.P.; Jemah, A.K. Exact out-of-plane natural frequencies of curved Timoshenko beams. J. Eng. Mech. 1999, 125, 19–25. [Google Scholar] [CrossRef]
- Raveendranath, P.; Singh, G.; Pradhan, B. A two-noded locking-free shear flexible curved beam element. Int. J. Numer. Methods Eng. 1999, 44, 265–280. [Google Scholar] [CrossRef]
- Lacarbonara, W.; Yabuno, H. Closed-loop non-linear control of an initially imperfect beam with non-collocated input. J. Sound Vib. 2004, 273, 695–711. [Google Scholar] [CrossRef]
- Lacarbonara, W.; Arafat, H.N.; Nayfeh, A.H. Non-linear interactions in imperfect beams at veering. Int. J. Non-Linear Mech. 2005, 40, 987–1003. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, M.Z.; Zhao, B.S. The refined theory of rectangular curved beams. Acta Mech. 2007, 189, 141–150. [Google Scholar] [CrossRef]
- Chang, C.S.; Hodges, D. Vibration characteristics of curved beams. J. Mech. Mater. Struct. 2009, 4, 675–692. [Google Scholar] [CrossRef] [Green Version]
- Emam, S.A. A static and dynamic analysis of the postbuckling of geometrically imperfect beams. Structures 2009, 90, 247–253. [Google Scholar] [CrossRef]
- Shooshtari, A.; Kalhori, H.; Masoodian, A. Investigation for dimension effect on mechanical behavior of a metallic curved micro-cantilever beam. Measurement 2011, 44, 454–465. [Google Scholar] [CrossRef]
- Stanciulescu, I.; Mitchell, T.; Chandra, Y.; Eason, T.; Spottswood, M. A lower bound on snap-through instability of curved beams under thermomechanical loads. Int. J. Non-Linear Mech. 2012, 47, 561–575. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Deng, Z.; Zhang, K.; Zhou, J. Dynamic analysis of embedded curved double-walled carbon nanotubes based on nonlocal Euler-Bernoulli Beam theory. Multidiscipl. Model. Mater. Struct. 2012, 8, 432–453. [Google Scholar] [CrossRef]
- Wu, J.S.; Lin, F.T.; Shaw, H.J. Free in-plane vibration analysis of a curved beam (arch) with arbitrary various concentrated elements. Appl. Math. Model. 2013, 37, 7588–7610. [Google Scholar] [CrossRef]
- Dastgerdi, J.; Marquis, G.; Salimi, M. The effect of nanotubes waviness on mechanical properties of CNT/SMP composites. Compos. Sci. Technol. 2013, 86, 164–169. [Google Scholar] [CrossRef]
- Lee, S.Y.; Yan, Q.Z. An analytical solution for out-of-plane deflection of a curved Timoshenko beam with strong nonlinear boundary conditions. Acta Mech. 2015, 226, 3679–3694. [Google Scholar] [CrossRef]
- Truesdell, C.; Noll, W. The Nonlinear Field Theories of Mechanics; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Eringen, A.C. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Eringen, A.C.; Edelen, D. On nonlocal elasticity. Int. J. Eng. Sci. 1972, 10, 233–248. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Qian, D.; Dickey, E.C.; Andrews, R.; Rantell, T. Load transfer and deformation mechanisms in carbon nanotube-polystyrene Composites. Appl. Phys. Lett. 2000, 76, 2868–2870. [Google Scholar] [CrossRef]
- Wang, Z.L.; Poncharal, P.; De Heer, W.A. Nanomeasurements of individual carbon nanotubes by in situ TEM. Pure Appl. Chem. 2000, 72, 209–219. [Google Scholar] [CrossRef]
- Mikata, Y. Complete solution of elastica for a clamped-hinged beam, and its applications to a carbon nanotube. Acta Mech. 2007, 190, 133–150. [Google Scholar] [CrossRef]
- Mayoof, F.N.; Hawwa, M.A. Chaotic behavior of a curved carbon nanotube under harmonic excitation. Chaos Solitons Fractals 2009, 42, 1860–1867. [Google Scholar] [CrossRef]
- Formica, G.; Lacarbonara, W.; Alessi, R. Vibrations of carbon nanotube-reinforced s. J. Sound Vib. 2010, 329, 1875–1889. [Google Scholar] [CrossRef]
- Ouakad, H.M.; Younis, M.I. Natural frequencies and mode shapes of initially curved carbon nanotube resonators under electric excitation. J. Sound Vib. 2011, 330, 3182–3195. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R.; Diaco, M.; de Sciarra, F.M. Constitutive boundary conditions and paradoxes in nonlocal elastic nanobeams. Int. J. Mech. Sci. 2017, 121, 151–156. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R. Stress-driven versus strain-driven nonlocal integral model for elastic nano-beams. Compos. Part B 2017, 114, 184–188. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R. Nonlocal elasticity in nanobeams: The stress-driven integral model. Int. J. Eng. Sci. 2017, 115, 14–27. [Google Scholar] [CrossRef]
- Glavardanov, V.B.; Spasic, D.T.; Atanackovic, T.M. Stability and optimal shape of Pflüger micro/nano beam. Int. J. Solids Struct. 2012, 49, 2559–2567. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Emam, S.A.; Mahmoud, F.F. Free vibration analysis of functionally graded size-dependent nanobeams. Appl. Math. Comput. 2012, 218, 7406–7420. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Emam, S.A.; Mahmoud, F.F. Static and stability analysis of nonlocal functionally graded nanobeams. Compos. Struct. 2013, 96, 82–88. [Google Scholar] [CrossRef]
- Wang, L.; Dai, H.L.; Qian, Q. Dynamics of simply supported fluid-conveying pipes with geometric imperfections. J. Fluids Struct. 2012, 29, 97–106. [Google Scholar] [CrossRef]
- Wang, B.; Deng, Z.; Zhang, K.; Zhou, J. Nonlinear vibration of embedded single-walled carbon nanotube with geometrical imperfection under harmonic load based on nonlocal Timoshenko beam theory. Appl. Math. Mech. 2013, 34, 269–280. [Google Scholar] [CrossRef]
- Emam, S.A. A general nonlocal nonlinear model for buckling of nanobeams. Appl. Math. Model. 2013, 37, 6929–6939. [Google Scholar] [CrossRef]
- Thongyothee, C.; Chucheepsakul, S. Postbuckling behaviors of nanorods including the effects of nonlocal elasticity theory and surface stress. J. Appl. Phys. 2013, 114, 243507. [Google Scholar] [CrossRef]
- Mohammadi, H.; Mahzoon, M.; Mohammadi, M.; Mohammadi, M. Postbuckling instability of nonlinear nanobeam with geometric imperfection embedded in elastic foundation. Nonlinear Dyn. 2014, 76, 2005–2016. [Google Scholar] [CrossRef]
- Khater, M.; Eltaher, M.; Abdel-Rahman, E.; Yavuz, M. Surface and Thermal Load Effects on the Buckling of Curved Nanowires. J. Eng. Sci. Technol. 2014, 17, 279–283. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Khater, M.E.; Emam, S.A. A review on nonlocal elastic models for bending, buckling, vibrations, and wave propagation of nanoscale beams. Appl. Math. Model. 2016, 40, 4109–4128. [Google Scholar] [CrossRef]
- Eltaher, M.A.; El-Borgi, S.; Reddy, J.N. Nonlinear analysis of size-dependent and material-dependent nonlocal CNTs. Multilayer Struct. 2016, 153, 902–913. [Google Scholar] [CrossRef]
- Ghadiri, M.; Shafiei, N. Nonlinear bending vibration of a rotating nanobeam based on nonlocal Eringen’s theory using differential quadrature method. Microsyst. Technol. 2016, 22, 2853–2867. [Google Scholar] [CrossRef]
- Kaghazian, A.; Hajnayeb, A.; Foruzande, H. Free vibration analysis of a piezoelectric nanobeam using nonlocal elasticity theory. Struct. Eng. Mech. 2017, 61, 617–624. [Google Scholar] [CrossRef]
- Khetir, H.; Bouiadjra, M.B.; Houari, M.S.A.; Tounsi, A.; Mahmoud, S.R. A new nonlocal trigonometric shear deformation theory for thermal buckling analysis of embedded nanosize FG plates. Struct. Eng. Mech. 2017, 64, 391–402. [Google Scholar]
- Mohamed, N.; Eltaher, M.A.; Mohamed, S.A.; Seddek, L.F. Numerical analysis of nonlinear free and forced vibrations of buckled curved beams resting on nonlinear elastic foundations. Int. J. Non Linear Mech. 2018, 101, 157–173. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R. Axial magnetic field effects on dynamic characteristics of embedded multiphase nanocrystalline nanobeams. Microsyst. Technol. 2018, 24, 3521–3536. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Kabeel, A.M.; Almitani, K.H.; Abdraboh, A.M. Static bending and buckling of perforated nonlocal size-dependent nanobeams. Microsyst. Technol. 2018, 24, 4881–4893. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Abdraboh, A.M.; Almitani, K.H. Resonance frequencies of size dependent perforated nonlocal nanobeam. Microsyst. Technol. 2018, 24, 3925–3937. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R. Vibration analysis of embedded size dependent FG nanobeams based on third-order shear deformation beam theory. Struct. Eng. Mech. 2017, 61, 721–736. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R. A unified formulation for modeling of inhomogeneous nonlocal beams. Struct. Eng. Mech. 2018, 66, 369–377. [Google Scholar]
- Challamel, N.; Wang, C.M. The small length scale effect for a non-local cantilever beam: A paradox solved. Nanotechnology 2008, 19, 345703. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Yao, L.; Chen, W.; Li, S. Comments on nonlocal effects in nano-cantilever beams. Int. J. Eng. Sci. 2015, 87, 47–57. [Google Scholar] [CrossRef]
- Benvenuti, E.; Simone, A. One-dimensional nonlocal and gradient elasticity: Closed-form solution and size effect. Mech. Res. Commun. 2013, 48, 46–51. [Google Scholar] [CrossRef]
- Fernández-Sáez, J.; Zaera, R.; Loya, J.A.; Reddy, J.N. Bending of Euler–Bernoulli beams using Eringen’s integral formulation: A paradox resolved. Int. J. Eng. Sci. 2016, 99, 107–116. [Google Scholar] [CrossRef]
- Tuna, M.; Kirca, M. Exact solution of Eringen’s nonlocal integral model for bending of Euler-Bernoulli and Timoshenko beams. Int. J. Eng. Sci. 2016, 105, 80–92. [Google Scholar] [CrossRef]
- Apuzzo, A.; Barretta, R.; Luciano, R.; de Sciarra, F.M.; Penna, R. Free vibrations of Bernoulli-Euler nano-beams by the stress-driven nonlocal integral model. Compos. Part B Eng. 2017, 123, 105–111. [Google Scholar] [CrossRef]
- Fang, W.; Wickert, J.A. Post buckling of micromachined beams. J. Micromech. Microeng. 1994, 4, 116–122. [Google Scholar] [CrossRef]
- Emam, S.A. Analysis of shear-deformable composite beams in postbuckling. Compos. Struct. 2011, 94, 24–30. [Google Scholar] [CrossRef]
- Eltaher, M.; Khater, M.; Abdel-Rahman, E.; Yavuz, M. Model for nano-scale bonding wires under thermal loading. In Proceedings of the 14th IEEE International Conference on Nanotechnology, Toronto, ON, Canada, 18–21 August 2014; pp. 382–385. [Google Scholar]
- Reddy, J.N. On laminated plates with integrated sensors and actuators. Eng. Struct. 1999, 21, 568–593. [Google Scholar] [CrossRef]
- Wang, Q. Wave propagation in carbon nanotubes via nonlocal continuum mechanics. J. Appl. Phys. 2005, 98, 124301. [Google Scholar] [CrossRef]
- Jones, R.M. Buckling of Bars, Plates and Shells; Bull Ridge Publishing: Blacksburg, VA, USA, 2006. [Google Scholar]
- Nayfeh, A.H.; Balachandran, B. Applied Nonlinear Dynamics, Analytical, Computational, and Experimental Methods; Wiley Series in Nonlinear Sciences; Wiley Interscience: New York, NY, USA, 2000; ISBN 0471593486. [Google Scholar]
- Aydogdu, M. A general nonlocal beam theory: Its application to nanobeam bending, buckling and vibration. Phys. E Low Dimens. Syst. Nanostruct. 2009, 41, 1651–1655. [Google Scholar] [CrossRef]
- Srubshchik, L.S. Precritical equilibrium of a thin shallow shell of revolution and its stability. J. Appl. Math. Mech. 1980, 44, 229–235. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Emam, S.A. Exact solution and stability of postbuckling configurations of beams. Nonlinear Dyn. 2008, 54, 395–408. [Google Scholar] [CrossRef]






| Nondimensional Imperfection Amplitude | Nondimensional Size Parameter | |||||
|---|---|---|---|---|---|---|
| 0 | 0.02 | 0.04 | 0.06 | 0.08 | 0.1 | |
| 0 | 39.4784 | 22.0603 | 15.3068 | 11.7192 | 9.4939 | 7.9789 |
| 1 | 66.6198 | 39.6802 | 28.5831 | 22.4276 | 18.4767 | 15.7086 |
| 2 | 76.6099 | 44.0773 | 30.4287 | 22.7649 | 17.8004 | 14.2962 |
| 3 | 78.8606 | 41.6370 | 25.8483 | 16.9195 | 11.1047 | 6.9832 |
| 4 | 74.6095 | 33.1988 | 15.4999 | 5.4418 | −1.1318 | −5.8044 |
| Nondimensional Imperfection Amplitude | Nondimensional Size Parameter | |||||
|---|---|---|---|---|---|---|
| 0 | 0.02 | 0.04 | 0.06 | 0.08 | 0.1 | |
| 0 | 39.4784 | 22.0603 | 15.3068 | 11.7192 | 9.4939 | 7.9789 |
| 1 | 71.8484 | 42.4339 | 30.2078 | 23.3849 | 18.9855 | 15.8917 |
| 2 | 78.9568 | 42.4957 | 27.0549 | 18.3317 | 12.6551 | 8.6339 |
| 3 | 72.6622 | 30.2908 | 12.1536 | 1.8365 | −4.9113 | −9.7103 |
| 4 | 54.5237 | 6.8768 | −13.6671 | −25.4069 | −33.1108 | −38.6041 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Emam, S.A.; Eltaher, M.A.; Khater, M.E.; Abdalla, W.S. Postbuckling and Free Vibration of Multilayer Imperfect Nanobeams under a Pre-Stress Load. Appl. Sci. 2018, 8, 2238. https://doi.org/10.3390/app8112238
Emam SA, Eltaher MA, Khater ME, Abdalla WS. Postbuckling and Free Vibration of Multilayer Imperfect Nanobeams under a Pre-Stress Load. Applied Sciences. 2018; 8(11):2238. https://doi.org/10.3390/app8112238
Chicago/Turabian StyleEmam, S. A., M. A. Eltaher, M. E. Khater, and W. S. Abdalla. 2018. "Postbuckling and Free Vibration of Multilayer Imperfect Nanobeams under a Pre-Stress Load" Applied Sciences 8, no. 11: 2238. https://doi.org/10.3390/app8112238
APA StyleEmam, S. A., Eltaher, M. A., Khater, M. E., & Abdalla, W. S. (2018). Postbuckling and Free Vibration of Multilayer Imperfect Nanobeams under a Pre-Stress Load. Applied Sciences, 8(11), 2238. https://doi.org/10.3390/app8112238





