Lightweight Design of Multi-Objective Topology for a Large-Aperture Space Mirror
Abstract
:1. Introduction
2. Lightweight Design of the Primary Mirror
2.1. Fundamental Concepts
2.2. Formulation of the Optimization Problem
3. Application Examples of the Topology Optimization Method
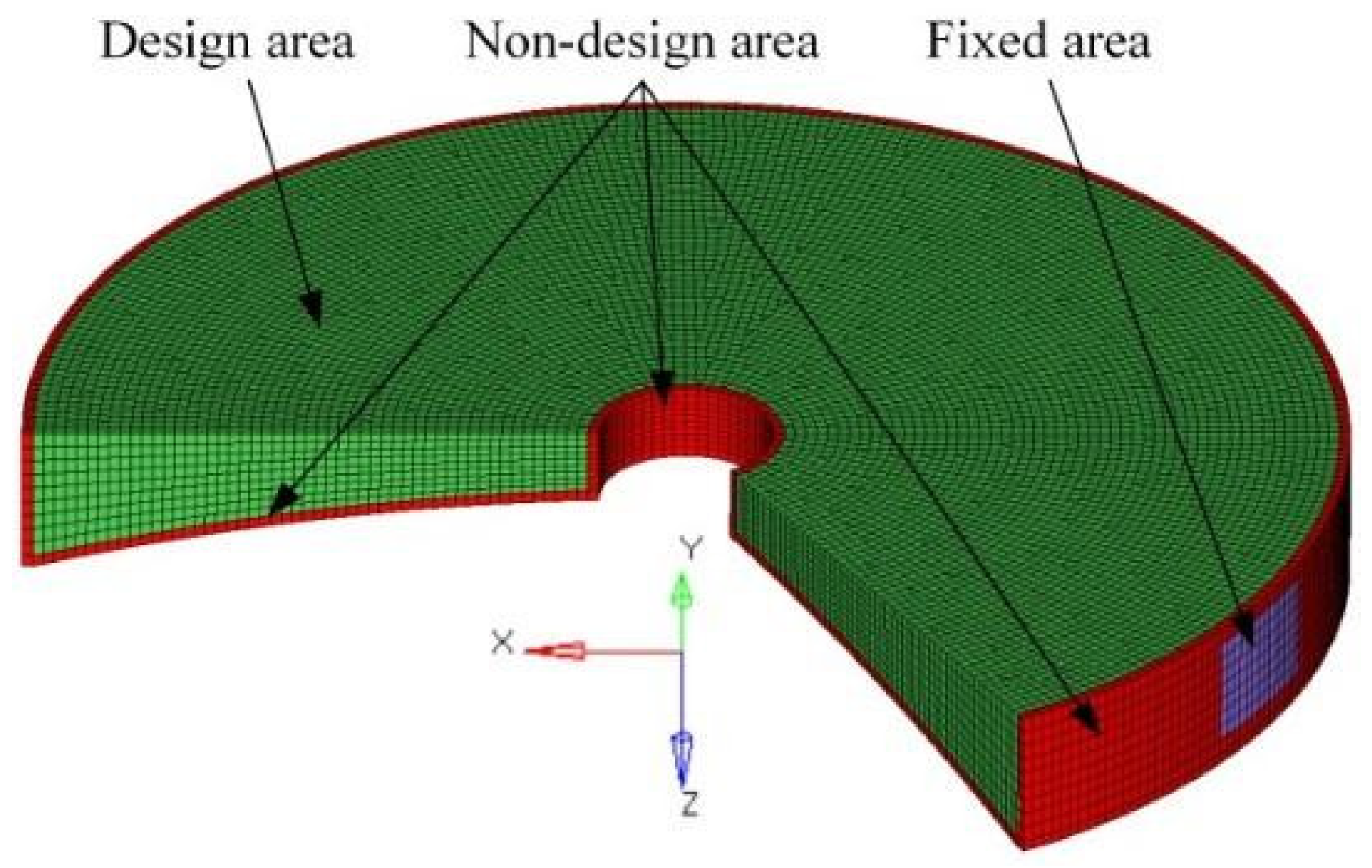
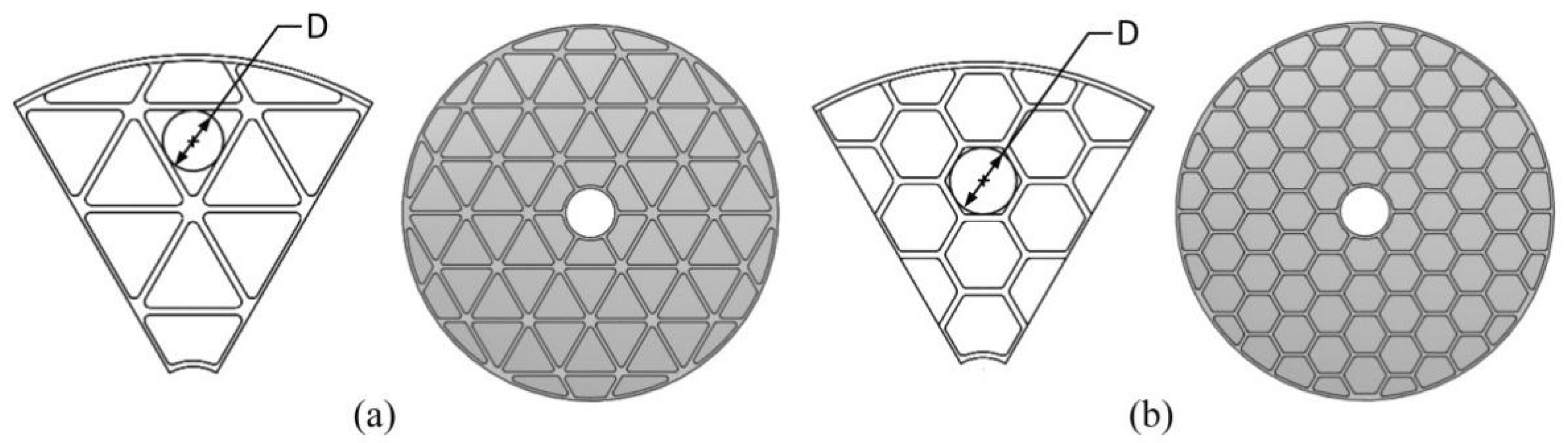
3.1. Initial Design of the Primary Mirror
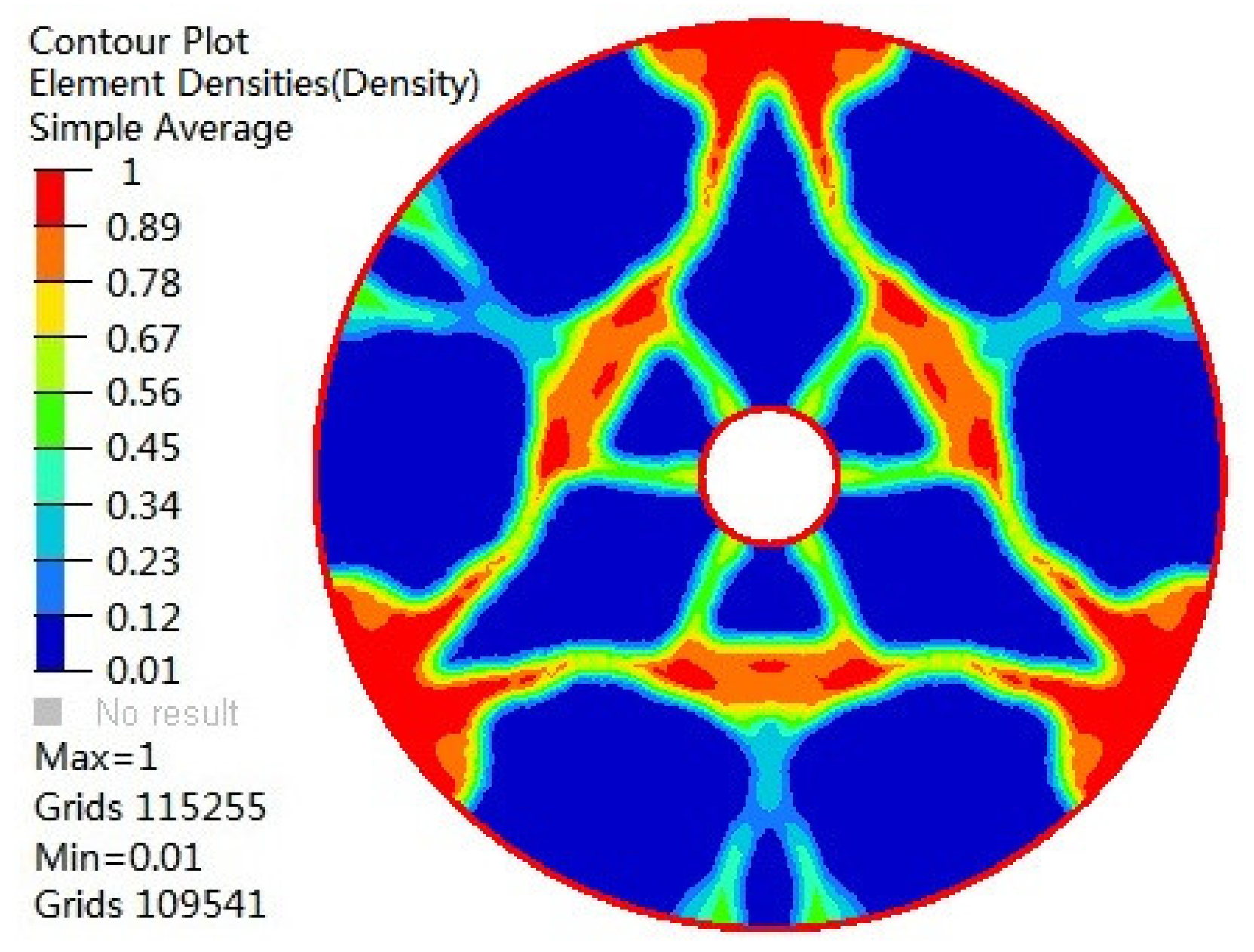
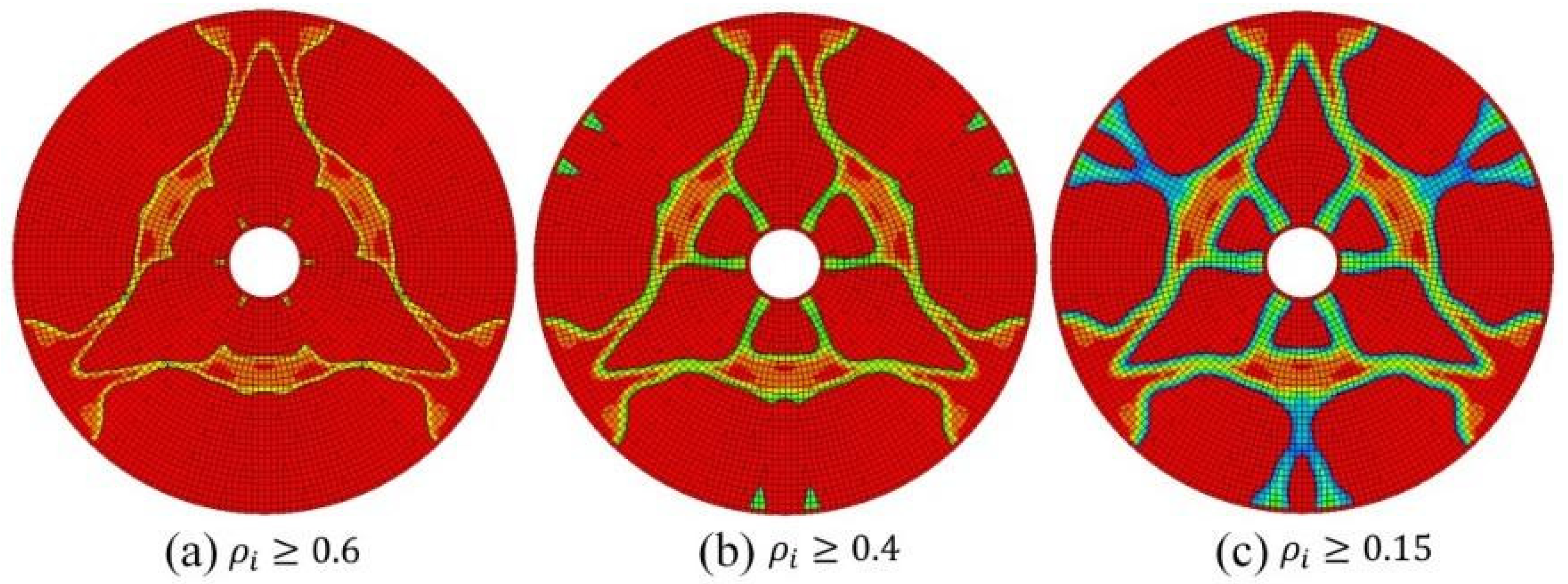
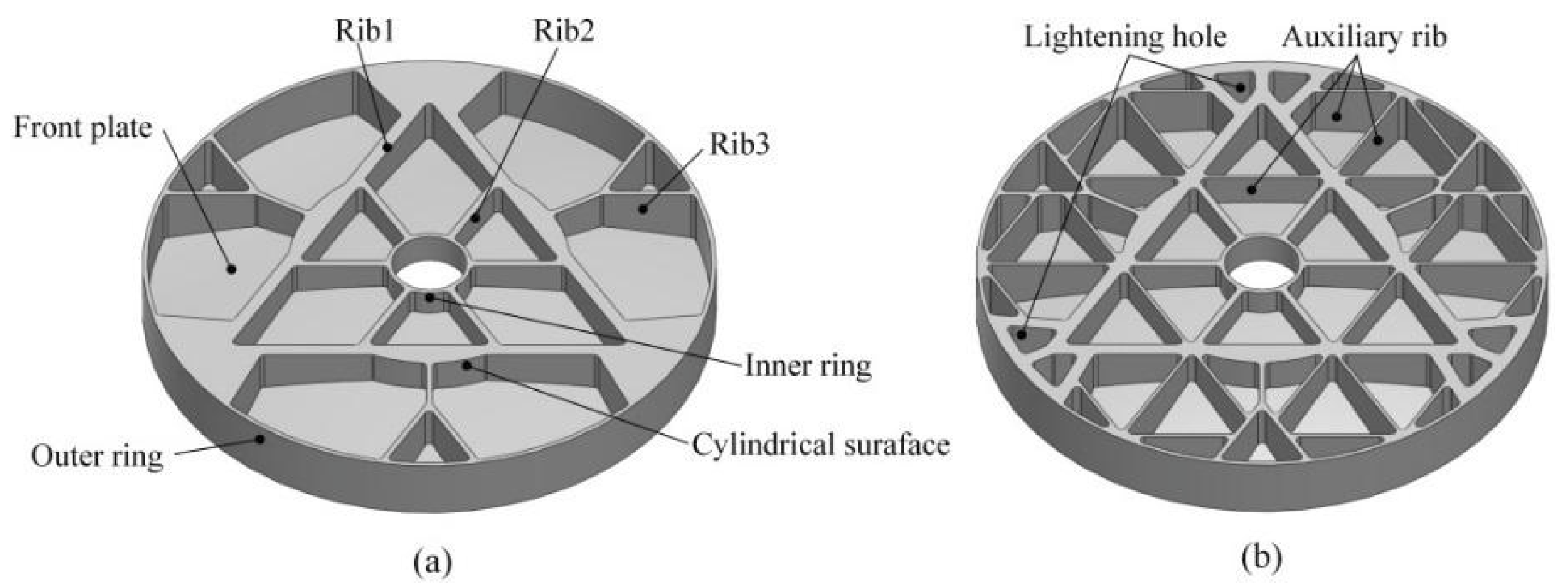
3.2. Topology Optimization Results
- (1)
- The additional ribs pass through the center of the areas without material filling to reduce the local deformation;
- (2)
- The additional ribs pass through the intersection of the main ribs to shorten the transmission path of the force;
- (3)
- The arrangement of the additional ribs must not affect the cyclic symmetry of the mirror;
- (4)
- Increasing lightening holes in the areas where the material is excessively concentrated.
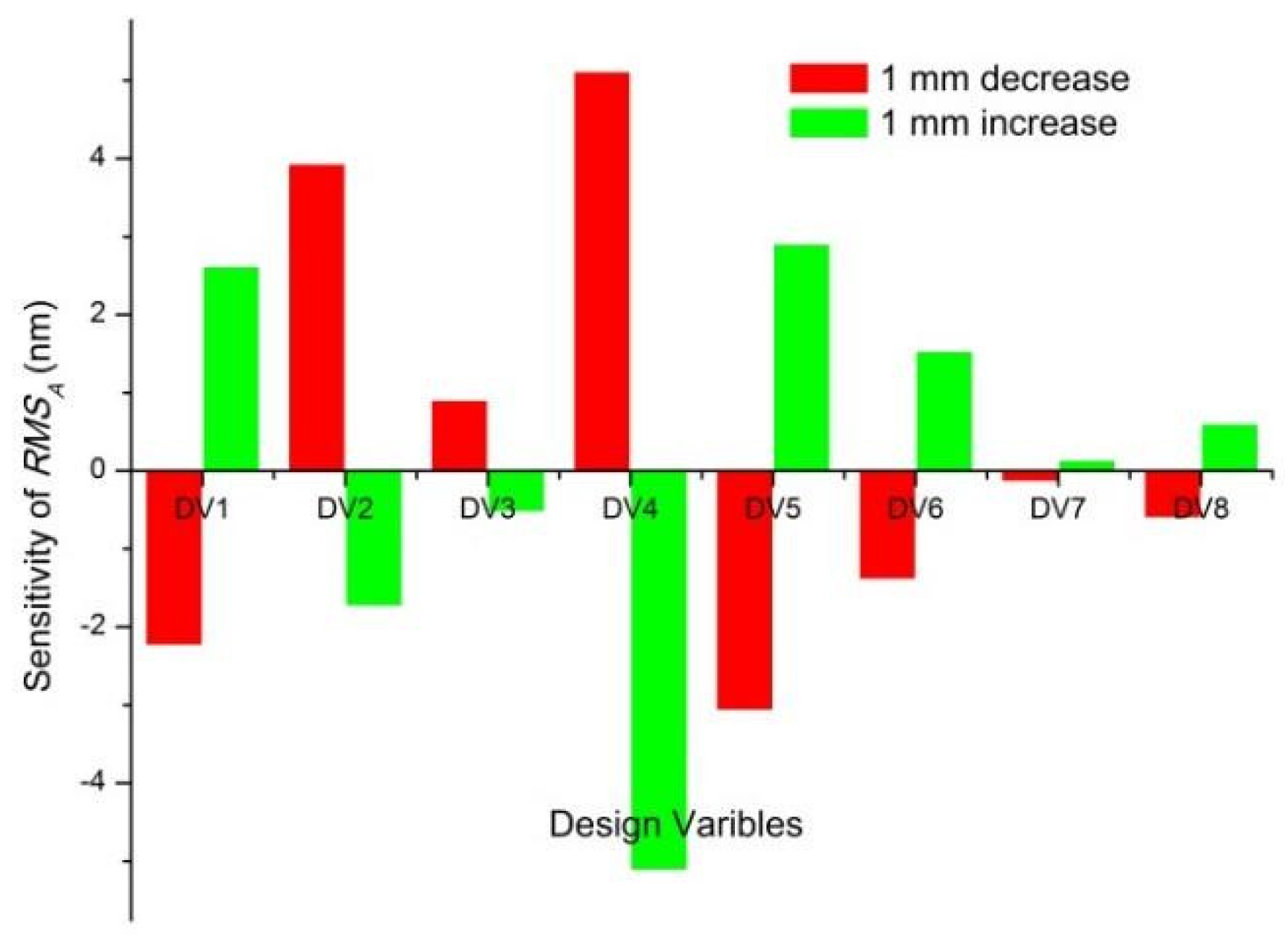
3.3. Sensitive Analysis and Size Optimization
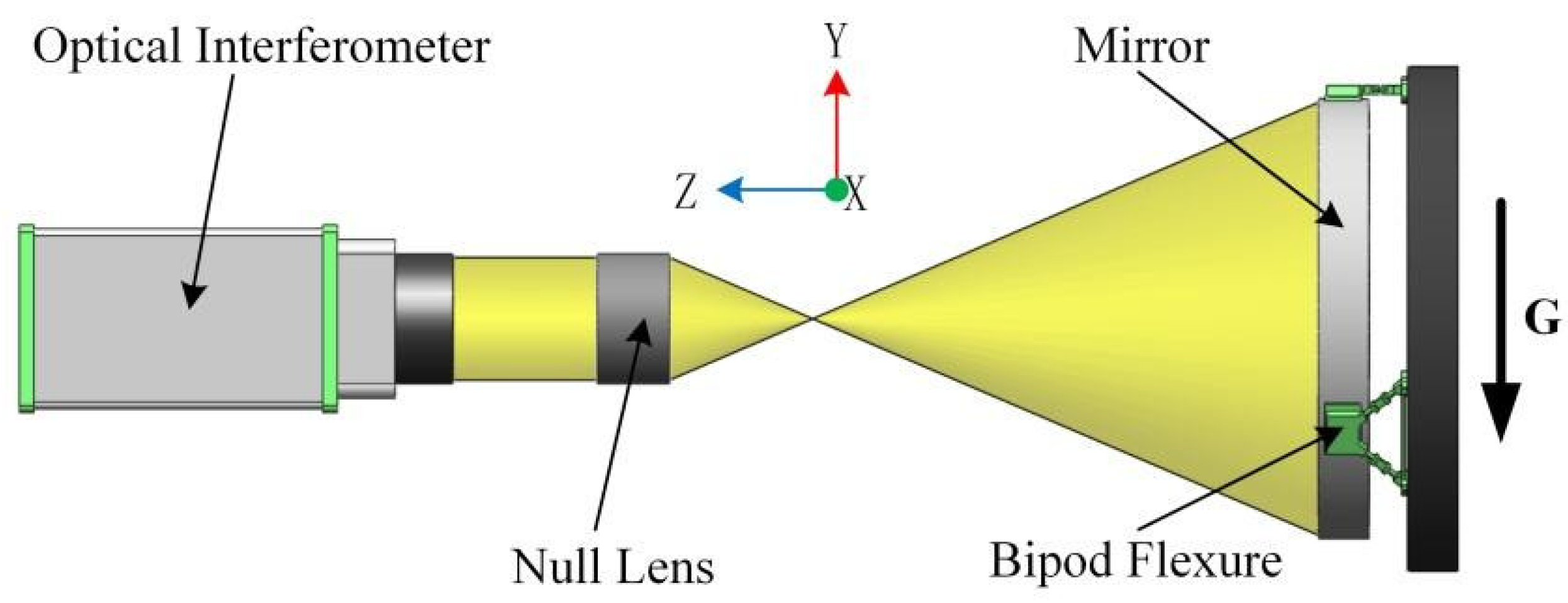
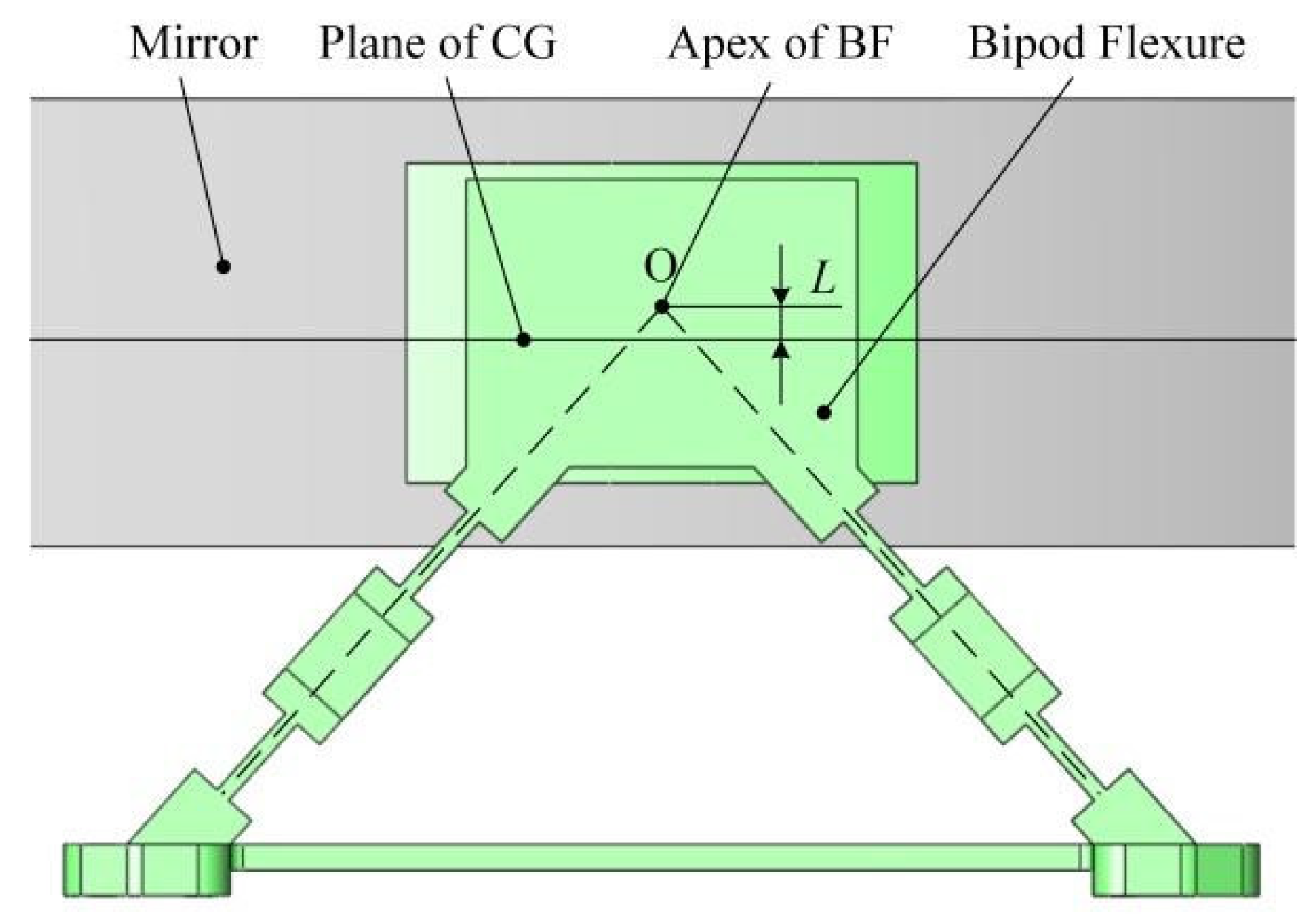
4. Performance Evaluation of the New Configuration
4.1. Comparison of Optical Performance of Three Naked Mirrors
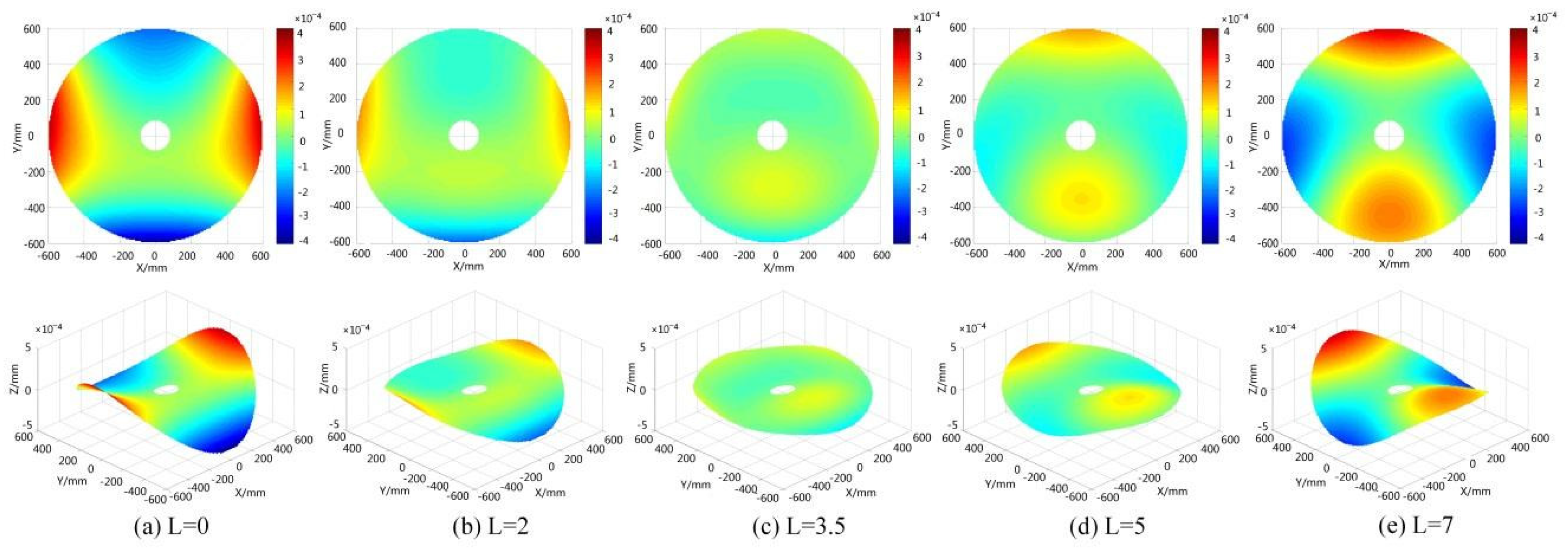
4.2. Optical Performance of the PMA
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, B.; Wang, W.; Qu, Y.; Li, X.; Wang, X. Design of an adjustable bipod flexure for a large-aperture mirror of a space camera. Appl. Opt. 2018, 57, 4048–4055. [Google Scholar] [CrossRef] [PubMed]
- Wang, X. Research on 800 mm Reflect Mirror and It’s Support Structure of Space Camera. Master’s Thesis, University of Chinese Academy of Sciences, Beijing, China, 2014. [Google Scholar]
- Nelson, J.E.; Lubliner, J.; Mast, T.S. Telescope mirror supports: Plate deflection on point supports. Proc. SPIE 1982, 332, 212–228. [Google Scholar] [CrossRef]
- Wan, D.S.; Angel, J.R.P.; Parks, R.E. Mirror deflection on multiple axial supports. Appl. Opt. 1989, 28, 354–362. [Google Scholar] [CrossRef] [PubMed]
- Kihm, H.; Yang, H.S. Design optimization of a 1-m lightweight mirror for a space telescope. Opt. Eng. 2013, 52, 091806. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, B.; You, Z.; Chan, C.; Huang, T. Optimization of lightweight structure and supporting bipod flexure for a space mirror. Appl. Opt. 2016, 55, 10382–10391. [Google Scholar] [CrossRef] [PubMed]
- Mici, J.; Rothenberg, B.; Brisson, E.; Wicks, S.; Stubbs, D.M. Optomechanical performance of 3D-printed mirrors with embedded cooling channels and substructures. Proc. SPIE 2015, 9573, 957306. [Google Scholar] [CrossRef]
- Roulet, M.; Atkins, C.; Hugot, E.; Lemared, S.; Lombardo, S.; Ferrari, M. 3D printing for astronomical mirrors. Proc. SPIE 2018, 10675, 1067504. [Google Scholar] [CrossRef] [Green Version]
- Park, K.S.; Lee, J.H.; Youn, S.K. Lightweight mirror design method using topology optimization. Opt. Eng. 2005, 44, 053002. [Google Scholar] [CrossRef]
- Liu, S.; Hu, R.; Li, Q. Topology optimization-based lightweight primary mirror design of a large-aperture space telescope. Appl. Opt. 2014, 53, 8318–8325. [Google Scholar] [CrossRef] [PubMed]
- Qu, Y.; Wang, W.; Liu, B.; Li, X. Topology optimization design of space rectangular mirror. Proc. SPIE 2016, 154, 1015421. [Google Scholar] [CrossRef]
- Hu, R.; Liu, S.; Li, Q. Topology-optimization-based design method of flexures for mounting the primary mirror of a large-aperture space telescope. Appl. Opt. 2017, 56, 4551–4560. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Chen, X.; Wang, S.; Jin, G. Optimal design of a Φ760 mm lightweight SiC mirror and the flexure mount for a space telescope. Rev. Sci. Instrum. 2017, 88, 125107. [Google Scholar] [CrossRef] [PubMed]
- Bittner, H.; Erdmann, M. SOFIA Primary Mirror Assembly: Structural Properties and Optical Performance. Proc. SPIE 2003, 4857, 266–273. [Google Scholar] [CrossRef]
- Petrovsky, G.T.; Tolstoy, M.N. 2.7-meter-diameter silicon carbide primary mirror for the SOFIA telescope. Proc. SPIE 1994, 2199, 263–270. [Google Scholar] [CrossRef]
- Kaneda, H. Cryogenic optical performance of the ASTRO-F SiC telescope. Appl. Opt. 2005, 44, 6823–6832. [Google Scholar] [CrossRef] [PubMed]
- Sholl, M.; Lampton, M. Snap Telescope: Optical, Infrared, and Millimeter Space Telescopes. Proc. SPIE 2004, 5487, 1473–1483. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J.; Han, J. Large-scale fabrication of lightweight Si/SiC ceramic composite optical mirror. Mater. Lett. 2004, 58, 1204–1208. [Google Scholar] [CrossRef]
- Cho, M. The design of support structure of mirror subassembly of space remote sensor. Proc. SPIE 2014, 9280, 928002. [Google Scholar] [CrossRef]
- Wang, K. Research on the Lightweight Design and Compound Support of the Large-Aperture Mirror for Space-Based Telescope. Ph.D. Thesis, University of Chinese Academy of Sciences, Beijing, China, 2016. [Google Scholar]
- Zhang, L.; Wang, F. Application of bipod to supporting structure of minitype reflector. Opt. Precis. Eng. 2015, 23, 438–443. [Google Scholar] [CrossRef]
- Mahajan, V.N. Zernike circle polynomials and optical aberrations of systems with circular pupils. App. Opt. 1994, 33, 8121–8124. [Google Scholar] [CrossRef] [PubMed]
- Dai, G.M.; Mahajan, V.N. Orthonormal polynomials in wavefront analysis: Error analysis. Appl. Opt. 2008, 47, 3433–3445. [Google Scholar] [CrossRef] [PubMed]
- Wyatt, J.; Creath, K. Basic wavefront aberration theory for optical metrology. In Applied Optics and Optical Engineering; Shannon, R.R., Wyant, J.C., Eds.; Academics Press: New York, NY, USA, 1992; Volume XI, ISBN 0-12-408611-X. [Google Scholar]





| γ, η, μ | α | D1 | D2 | P |
|---|---|---|---|---|
| 0.33 | 0.3 | 25 nm | 160 nm | 0.2 kPa |
| Outside Diameter | Inside Diameter | Outer Edge Thickness | SiC | ||
|---|---|---|---|---|---|
| E0 | μ | ρ | |||
| 610 mm | 86 mm | 70 mm | 280 GPa | 0.17 | 2800 kg/m3 |
| Design Variable | Term | Value |
|---|---|---|
| DV1 | Front plate thickness | 5 mm |
| DV2 | Outer ring thickness | 5 mm |
| DV3 | Inner ring thickness | 5 mm |
| DV4 | Rib1 thickness | 15 mm |
| DV5 | Rib2 thickness | 8 mm |
| DV6 | Rib3 thickness | 6 mm |
| DV7 | Cylindrical structure radius | 162 mm |
| DV8 | Auxiliary rib thickness | 4 mm |
| Design Variable | Lower Bound | Upper Bound | Optimum Value |
|---|---|---|---|
| DV1 | 4 mm | 8 mm | 4 mm |
| DV2 | 4 mm | 8 mm | 5.6 mm |
| DV4 | 12 mm | 18 mm | 16.4 mm |
| DV5 | 4 mm | 10 mm | 5.2 mm |
| DV6 | 4 mm | 10 mm | 4 mm |
| Terms | Tri-Configuration | Hex-Configuration | New Configuration |
|---|---|---|---|
| PVA & RMSA | 125.73 & 28.65 nm | 150.57 & 34.43 nm | 119.53 & 27.58 nm |
| PVL & RMSL | 8.08 & 1.68 nm | 10.38 & 1.92 nm | 7.03 & 1.28 nm |
| PVP & RMSP | 55.80 & 13.56 nm | 60.74 & 14.05 nm | 45.65 & 10.10 nm |
| PV & RMS (+2 °C) | 61.6 & 10.48 nm | 100.5 & 17.5 nm | 50.1 & 8.78 nm |
| Frequency | 1400.8 Hz | 1344.5 Hz | 1555.3 Hz |
| Mass | 13.48 kg | 11.54 kg | 11.08 kg |
| Lightweight ratio | 68.4% | 72.9% | 74.0% |
| Name | Term | L = 1 mm, Coefficient/nm | L = 3.5 mm, Coefficient/nm | L = 6 mm, Coefficient/nm |
|---|---|---|---|---|
| Focus | 2r2 − 1 | 3.73 × 10−2 | 2.19 × 10−2 | 9.78 × 10−3 |
| Pri Astig-A | r2cos(2θ) | 9.06 | 2.31 × 10−1 | −8.72 |
| Pri Astig-B | r2sin(2θ) | −5.19 × 10−2 | −2.67 × 10−2 | −5.66 × 10−2 |
| Pri Coma-A | (3r2 − 2r)cos(θ) | 1.37 × 10−2 | 2.15 × 10−2 | 1.65 × 10−2 |
| Pri Coma-B | (3r2 − 2r)sin(θ) | 2.77 × 10−1 | 2.97 × 10−1 | 3.17 × 10−1 |
| Pri Spherical | 6r4 − 6r2 − 1 | −2.15 × 10−2 | −9.32 × 10−3 | −3.46 × 10−4 |
| Pri Trefoil-A | r3cos(3θ) | 9.62 × 10−1 | 1.04 × 10−2 | −1.02 × 10−2 |
| Pri Trefoil-B | r3sin(3θ) | −6.53 × 10−3 | −7.83 × 10−3 | −8.05 × 10−3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, Y.; Jiang, Y.; Feng, L.; Li, X.; Liu, B.; Wang, W. Lightweight Design of Multi-Objective Topology for a Large-Aperture Space Mirror. Appl. Sci. 2018, 8, 2259. https://doi.org/10.3390/app8112259
Qu Y, Jiang Y, Feng L, Li X, Liu B, Wang W. Lightweight Design of Multi-Objective Topology for a Large-Aperture Space Mirror. Applied Sciences. 2018; 8(11):2259. https://doi.org/10.3390/app8112259
Chicago/Turabian StyleQu, Yanjun, Yanru Jiang, Liangjie Feng, Xupeng Li, Bei Liu, and Wei Wang. 2018. "Lightweight Design of Multi-Objective Topology for a Large-Aperture Space Mirror" Applied Sciences 8, no. 11: 2259. https://doi.org/10.3390/app8112259
APA StyleQu, Y., Jiang, Y., Feng, L., Li, X., Liu, B., & Wang, W. (2018). Lightweight Design of Multi-Objective Topology for a Large-Aperture Space Mirror. Applied Sciences, 8(11), 2259. https://doi.org/10.3390/app8112259




