Interpolation of Turbulent Boundary Layer Profiles Measured in Flight Using Response Surface Methodology
Abstract
:1. Introduction
2. Flight Test Bed, Measurement System and Equipment, and Test Conditions
2.1. Flight Test Bed and Measurement System Onboard
2.2. Paint-Based Riblets
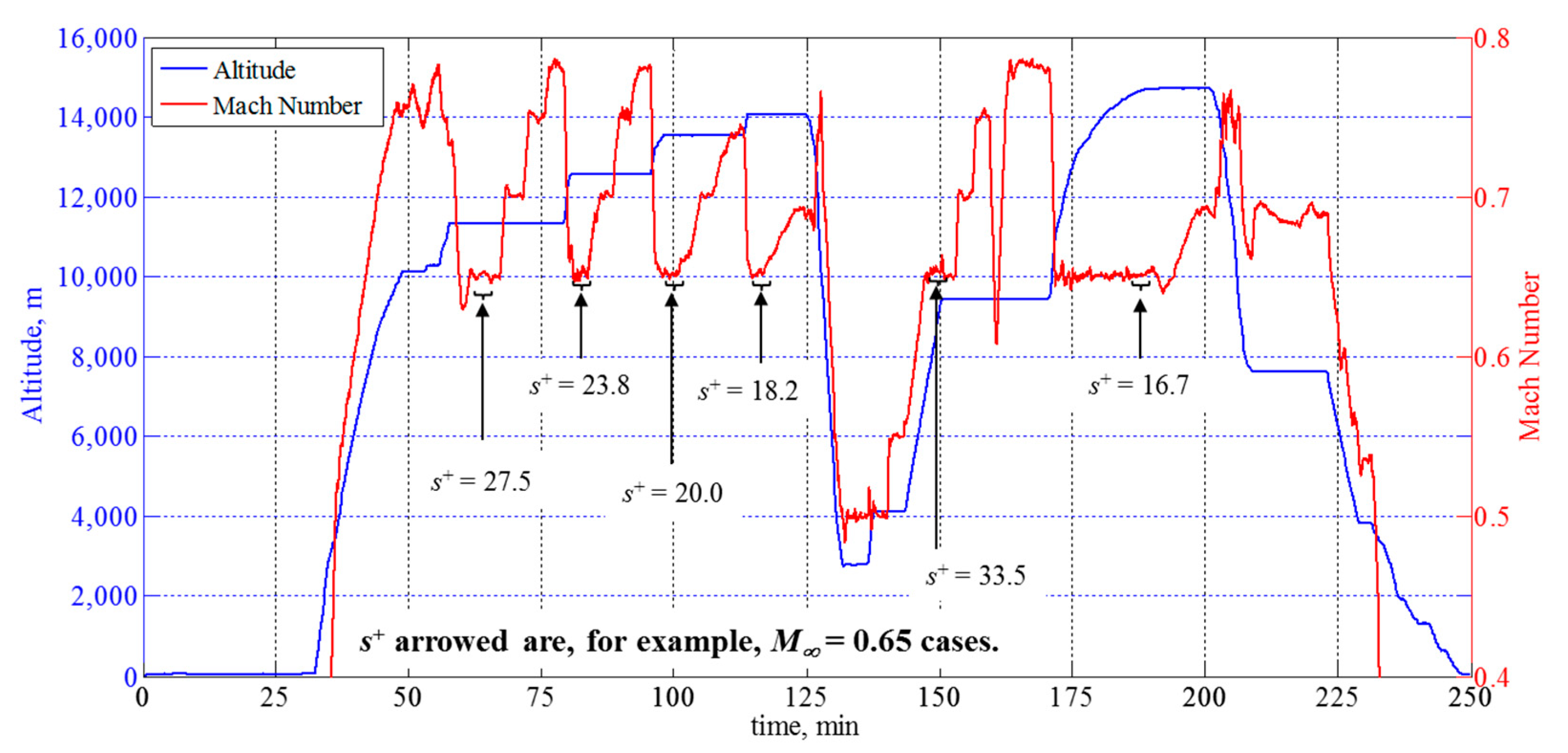
2.3. Test Conditions
3. Data Reduction Methodologies
3.1. Application of Response Surface Methodology (RSM) to Flight Data
- Reference Case
- (i)
- First, flight experimental data obtained with a smooth wall surface on the aircraft airframe without involving any flow control device such as riblets were considered as reference data to be compared. The dataset for the reference case (as well as other flight cases) contains pitot pressure data and flight condition data such as Mach number, Reynolds number, etc. (hereinafter, flight data) measured by ADS onboard. The pressure coefficient based on pitot pressure divided by flight dynamic pressure was considered the primary parameter of interest and is expressed as follows:From Equation (4), the pitot pressure at each pitot-probe is obtained as follows:Based on Equation (5) and assuming the isentropic flow process, the Mach number at each pitot-probe is obtained by Equation (6) by further assuming that the pitot pressure at each pitot-probe is considered to be the local total pressure at each probe tip. Here, an assumption was made that no total pressure loss was involved in the shock wave formation in front of each pitot-probe, since the entire flowfield is considered to be subsonic in accounting for flight speed conditions.Rewriting Equation (6) in terms of U-velocity yields the U-velocity (Upitot) at each pitot-probe as Equation (7).
- Compared case
- (ii)
- Similar to the reference case, the pressure coefficient for the compared case, , is created by pitot pressures and flight data for the compared case (Equation (8)).
- (iii)
- Assuming that the pressure coefficient at each pitot-probe can be expressed by using some measured variables yields an expression of shown as Equation (9).Here, x1, x2, … are variables obtained by flight experiments such as α, Reu∞, β, U∞, T0∞, and P0∞. Each variable is independent of each other. ε is the uncertainty arising from reconstructing Cp with the interpolation technique.
- (iv)
- Equation (9) is then expressed by applying response surface methodology as follows. Since the fitting curve being used for interpolation would be a curvature response, the 3rd-degree response surface model was employed. Detailed reason behind the usage of the 3rd-degree response surface model will be presented in a later section along with a comparison of interpolated boundary layer profile using the 2nd-degree response surface model. Note that this process is only meaningful for the compared case; the interpolated reference data are identical to the original reference data.Here, N is the total number of variables and each variable is chosen as, for instance, N = 4, x1 = M∞, x2 = Re∞, x3 = P∞, and x4 = α. a and b are coefficients for calculating the response surface. It should be noted that each variable would be non-dimensionalized prior to making a fitting curve using Equation (10). The cross terms in Equation (10) appear to introduce the curvature of the response surface since the fitting curve for this case would not be linear.
- (v)
- Coefficients appearing in Equation (10) can be obtained by expressing Equation (10) in matrix notation as follows:where is a vector of the parameter being reconstructed by the fitting dataset for interpolation, X is the matrix of values of the design variables at each flight condition, A is the vector of tuning parameters, and ε is a vector of errors inherent in the curve fitting using the response surface model (equivalent to the one expressed in Equation (10)). n is the total number of experimental cases and k is the total number of variables. A can be estimated using the least-square error method as:
- (vi)
- The interpolated pressure coefficient for compared case , which is interpolated for equivalent flight conditions of the reference case (x1~xN)|ref, is now obtained.
- (vii)
- Then the interpolated pitot pressure is expressed as:The interpolated pitot pressure and Mach number at each pitot-probe are expressed using the above relationships and isentropic relationships as follows:
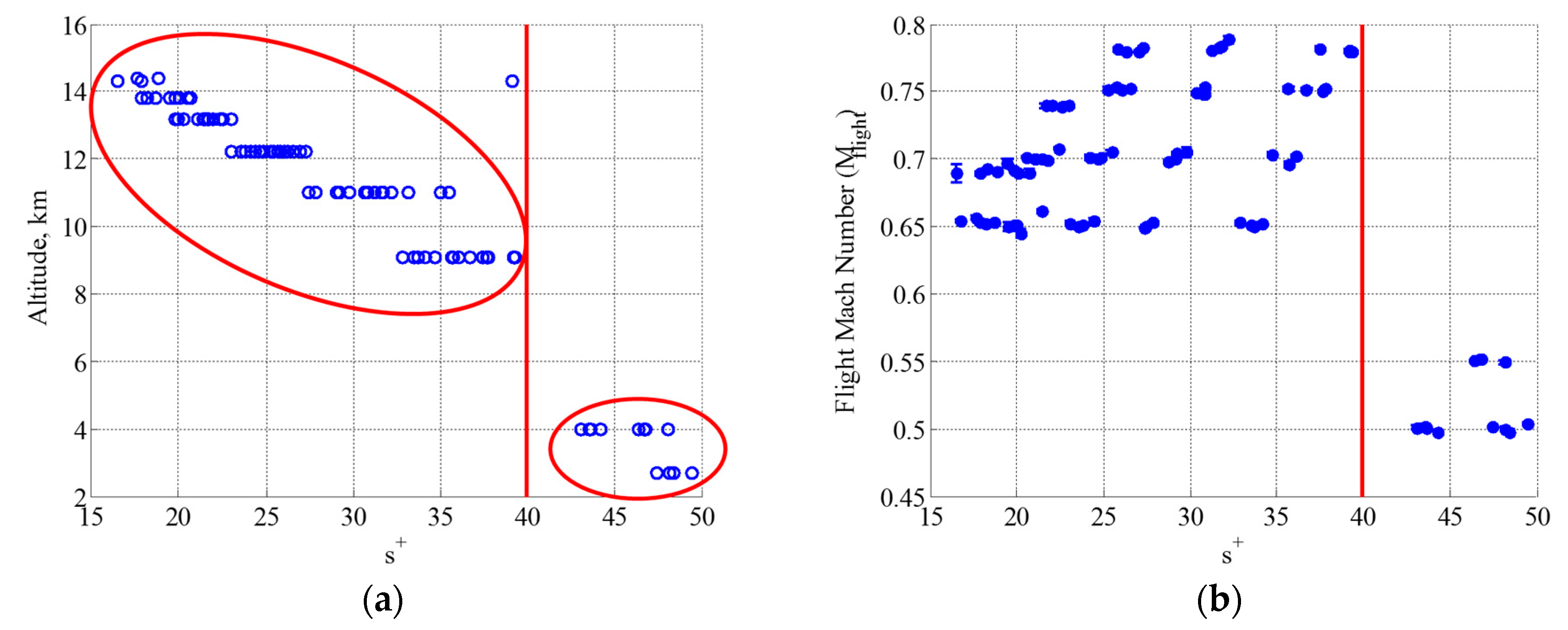
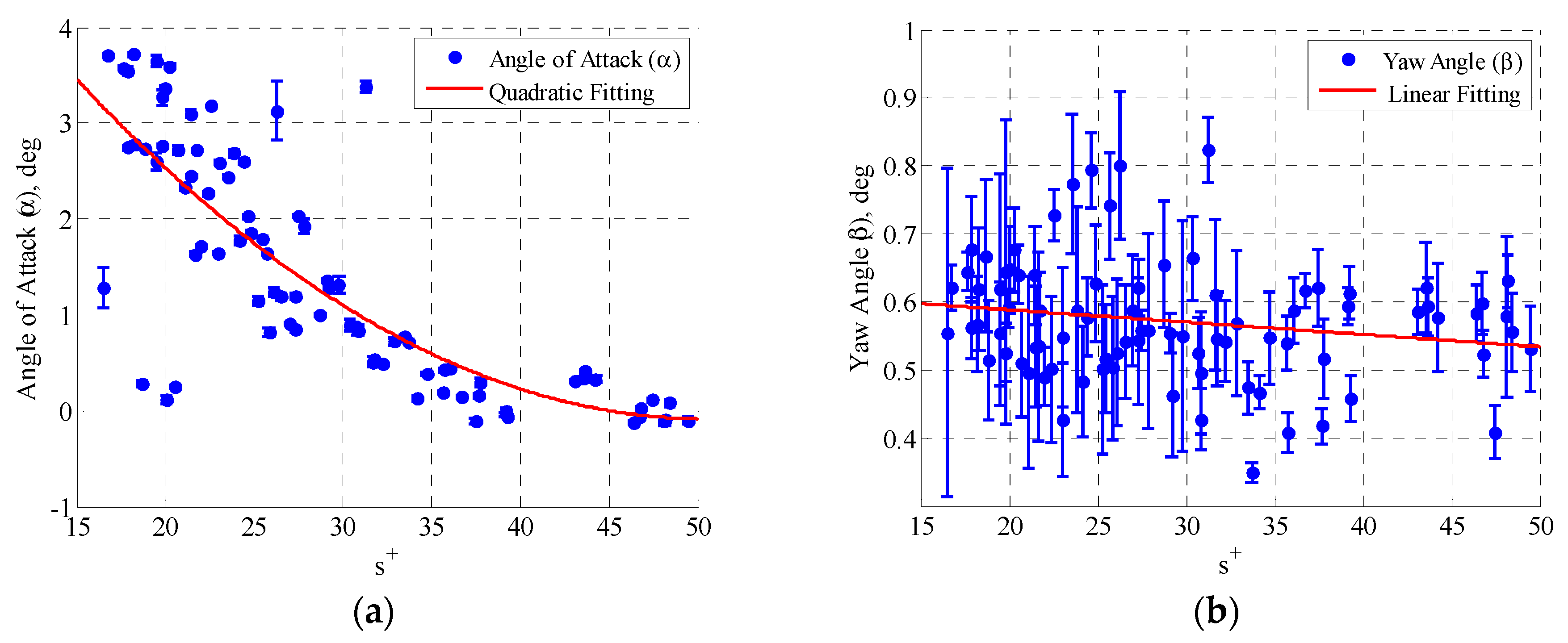
3.2. Governing Parameters and Data Screening
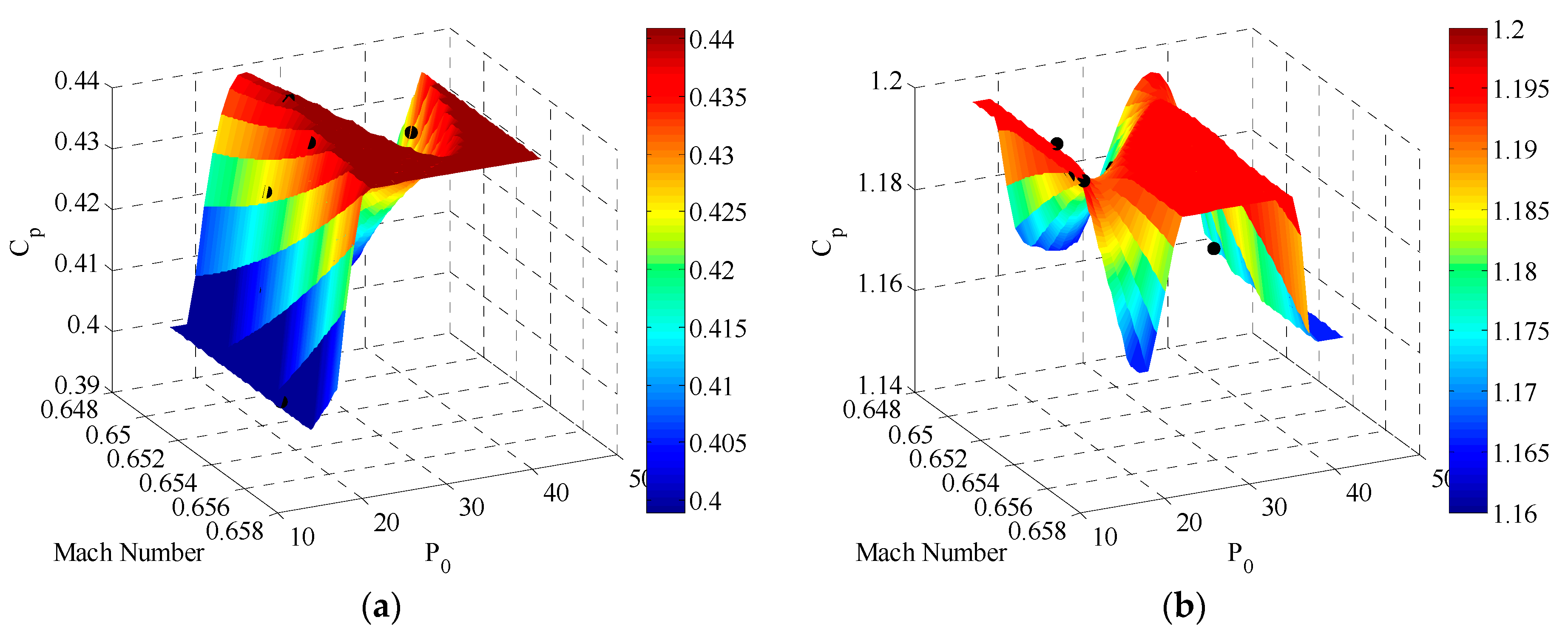
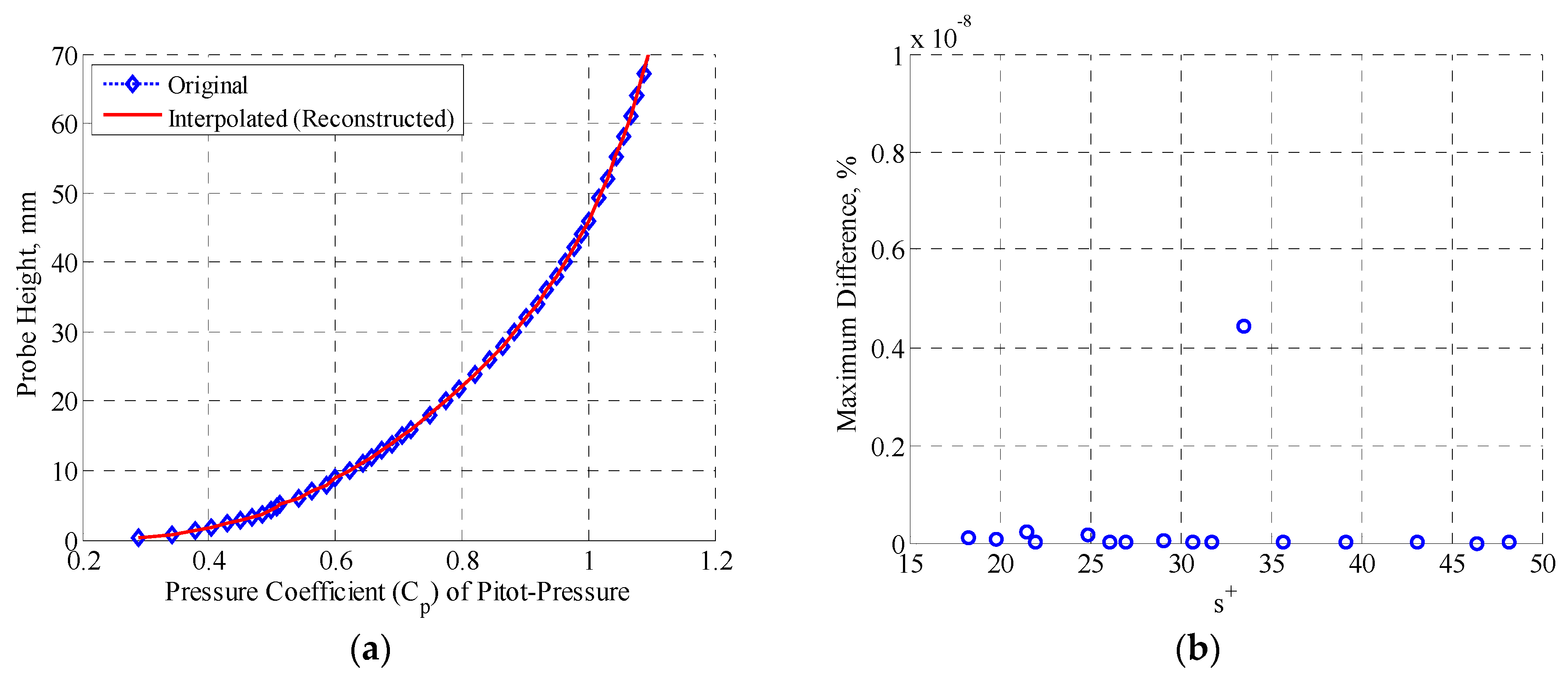
3.3. Response Surface Model (Interpolation of Boundary Layer Profile)
4. Results and Discussion
4.1. Accuracy of Interpolation
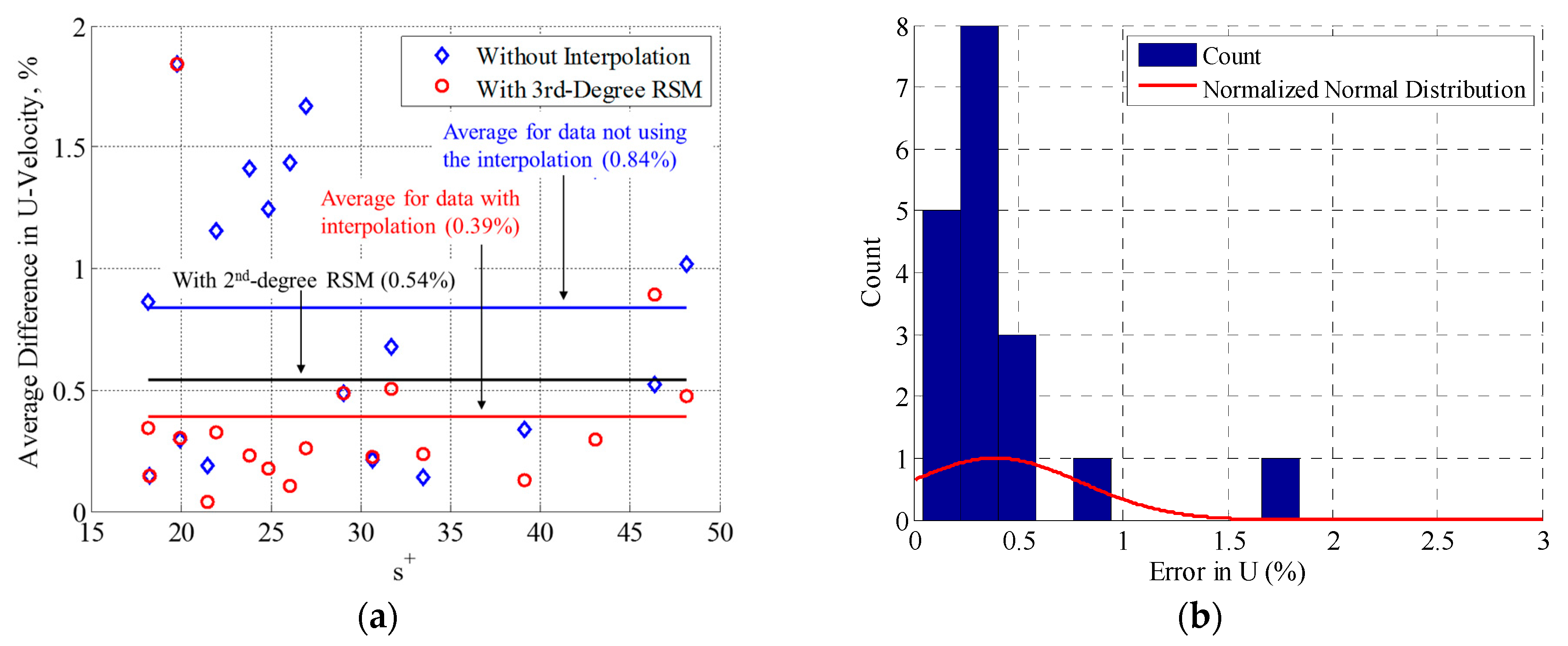
4.2. Uncertainty Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| cf | local skin friction coefficient |
| Cp | pressure coefficient |
| M | Mach number |
| q | uncertainty |
| R | gas constant |
| Re | Reynolds number |
| s | width of riblet, μm |
| s+ | non-dimensional width of riblet |
| T | temperature, K or °C |
| U | streamwise velocity component (U-velocity), m/s |
| Uτ | friction velocity |
| x | coordinate in streamwise direction |
| y | coordinate in spanwise direction |
| z | coordinate in vertical direction |
| α | angle of attack, deg |
| β | yaw angle or angle of sideslip, deg |
| δ | boundary layer thickness, mm |
| ε | tiny amount or uncertainty |
| γ | specific heat ratio |
| μ | dynamic viscosity |
| ν | kinematic viscosity, m2/s |
| ρ | density, kg/m3 |
| σ | standard deviation |
| Subscripts | |
| 0 | stagnation condition |
| com | compared case |
| fit | fitted data |
| flight | flight condition |
| i, j | index number |
| interpolated | interpolated data |
| pitot | pitot-rake data |
| ref | reference case |
| s | static condition |
| total | total value |
| u | unit value |
| ∞ | freestream condition |
References
- Szodruch, J. Viscous Drag Reduction on Transport Aircraft Reno. In Proceedings of the AIAA 29th Aerospace Sciences Meeting, Reno, NV, USA, 7–10 January 1991. AIAA Paper 91-0685. [Google Scholar]
- Yousefi, K.; Saleh, R. Three-dimensional suction flow control and suction jet length optimization of NACA 0012 wing. Meccanica 2015, 50, 1481–1494. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.Y.; Zhang, W.L.; Chen, Z.; Sun, X.H.; Xia, C.C. Suction control of flow separation of a low-aspect-ratio wing at low Reynolds-number. Fluid Dyn. Res. 2018, 50, 065504. [Google Scholar]
- Yousefi, K.; Saleh, R.; Zahedi, P. Numerical study of blowing and suction slot geometry optimization on NACA 0012 airfoil. J. Mech. Sci. Technol. 2014, 28, 1297–1310. [Google Scholar] [CrossRef] [Green Version]
- You, D.; Moin, P. Active control of flow separation over an airfoil using synthetic jets. J. Fluids Struct. 2008, 24, 1349–1357. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, B.; Qiu, Q.; Xu, X. Flow control on the NREL S809 wind turbine airfoil using vortex generators. Energy 2017, 118, 1210–1221. [Google Scholar] [CrossRef]
- Saravi, S.S.; Cheng, K. A Review of Drag Reduction by Riblets and Micro-Textures in the Turbulent Boundary Layers. Eur. Sci. J. 2013, 9, 62–81. [Google Scholar]
- Walsh, M.J. Riblets, Viscous Drag Reduction in Boundary Layers; Bushness, H., Ed.; Progress in Astronautics and Aeronautics; American Institute of Aeronautics and Astronautics: Washington, DC, USA, 1989; Volume 123, pp. 203–261. [Google Scholar]
- Walsh, M.J. Riblets as a Viscous Drag Reduction Technique. AIAA J. 1983, 21, 485–486. [Google Scholar] [CrossRef]
- Sareen, A.; Deters, R.W.; Henry, S.P.; Selig, M.S. Drag reduction using riblet film applied to airfoils for wind turbines. J. Sol. Energy Eng. 2014, 136, 021007. [Google Scholar] [CrossRef]
- Raayai-Ardakani, S.; McKinley, G.H. Drag reduction using wrinkled surfaces in high Reynolds number laminar boundary layer flows. Phys. Fluids 2017, 29, 093605. [Google Scholar] [CrossRef]
- Sasamori, M.; Iihama, O.; Mamori, H.; Iwamoto, K.; Murata, A. Parametric Study on a Sinusoidal Riblet for Drag Reduction by Direct Numerical Simulation. Flow Turbul. Combust. 2017, 99, 47–69. [Google Scholar] [CrossRef]
- Bushnell, D.M.; Hefner, J.N.; Ash, R.L. Effect of Compliant Wall Motion on Turbulent Boundary Layers. Phys. Fluids 1977, 20, S31–S48. [Google Scholar] [CrossRef]
- Suzuki, Y.; Kasagi, N. Turbulent Drag Reduction Mechanism Above a Riblet Surface. AIAA J. 1994, 32, 1781–1790. [Google Scholar] [CrossRef]
- Dean, B.; Bhushan, B. Shark-Skin Surfaces for Fluid-Drag Reduction in Turbulent Flow: A Review. Philos. Trans. R. Soc. A 2010, 368, 4775–4806. [Google Scholar] [CrossRef] [PubMed]
- Viswanath, P.R. Aircraft Viscous Drag Reduction Using Riblets. Prog. Aerosp. Sci. 2002, 38, 571–600. [Google Scholar] [CrossRef]
- Okabayashi, K.; Matsue, T.; Asai, M. Development of Turbulence Model to Simulate Drag Reducing Effects of Riblets. J. Jpn. Soc. Aeronaut. Space Sci. 2016, 64, 41–49. (In Japanese) [Google Scholar]
- Sawyer, W.; Winter, K. An Investigation of the Effect on Turbulent Skin Friction of Surface with Streamwise Grooves. In Turbulent Drag Reduction by Passive Means; The Royal Aeronautical Society: London, UK, 1987; pp. 330–362. [Google Scholar]
- Walsh, M.J. Turbulent Boundary Layer Drag Reduction Using Riblets. In Proceedings of the AIAA 20th Aerospace Sciences Meeting, Orlando, FL, USA, 11–14 January 1982. AIAA Paper 82-0169. [Google Scholar]
- Bechert, D.W.; Bruse, M.; Hage, W.; Van Der Hoeven, J.G.T.; Hoppe, G. Experiments on Drag-Reducing Surfaces and their Optimization with an Adjustable Geometry. J. Fluid Mech. 1997, 338, 59–87. [Google Scholar] [CrossRef]
- MBB Transport Aircraft Group. Microscopic Rib Profiles Will Increase Aircraft Economy in Flight. Aircr. Eng. 1988, 60, 11. [Google Scholar] [CrossRef]
- Kurita, M.; Nishizawa, A.; Okabayashi, K.; Koga, S.; Kwak, T.; Nakakita, K.; Naka, Y. FINE: Flight Investigation of Skin-Friction Reducing Eco-Coating. In Proceedings of the 54th Aircraft Symposium, Toyama, Japan, 31 October–2 November 2016. JSASS-2016-5180 (In Japanese). [Google Scholar]
- Koga, S.; Kurita, M.; Iijima, H.; Okabayashi, K.; Nishizawa, A.; Takahashi, H.; Endo, S. Wind Tunnel Tests for Measurement System Design of Flight Investigation of Skin-Friction Reducing Eco-Coating (FINE). In Proceedings of the 54th Aircraft Symposium, Toyama, Japan, 31 October–2 November 2016. JSASS-2016-5105 (In Japanese). [Google Scholar]
- Rosenbaum, B.; Schulz, V. Response Surface Methods for Efficient Aerodynamic Surrogate Models. Comput. Flight Test. 2013, 123, 113–129. [Google Scholar]
- Sevant, N.E.; Bloor, M.I.G.; Wilson, M.J. Aerodynamic Design of a Flying Wing Using Response Surface Methodology. J. Aircr. 2000, 37, 562–569. [Google Scholar] [CrossRef]
- Zhang, M.; He, L. Combining Shaping and Flow Control for Aerodynamic Optimization. AIAA J. 2015, 53, 888–901. [Google Scholar] [CrossRef]
- Papila, M.; Haftka, R.T. Response Surface Approximations: Noise, Error Repair, and Modeling Errors. AIAA J. 2000, 38, 2336–2343. [Google Scholar] [CrossRef]
- Madsen, J.; Shyy, W.; Haftka, R.T. Response Surface Techniques for Diffuser Shape Optimization. AIAA J. 2000, 38, 1512–1518. [Google Scholar] [CrossRef]
- Walsh, M.J.; Sellers, W.L., III; McGinley, C.B. Riblet Drag at Flight Conditions. J. Aircr. 1989, 26, 570–575. [Google Scholar] [CrossRef]
- Takahashi, H.; Tomioka, S.; Sakuranaka, N.; Tomita, T.; Kuwamori, K.; Masuya, G. Effects of Plume Impingements of Clustered Nozzles on the Surface Skin Friction. J. Propuls. Power 2015, 31, 485–495. [Google Scholar] [CrossRef]
- Marshakov, A.V.; Scheta, J.A.; Kiss, T. Direct Measurement of Skin Friction in a Turbine Cascade. J. Propuls. Power 1996, 12, 245–249. [Google Scholar] [CrossRef]
- Allen, J.M. An Improved Sensing Element for Skin-Friction Balance Measurements. In Proceedings of the AIAA 18th Aerospace Sciences Meeting, Pasadena, CA, USA, 14–16 January 1980. AIAA Paper 1980-0049. [Google Scholar]
- Walsh, M.J.; Sellers, W.L.; McGinley, C.B. Riblet Drag Reduction at Flight Conditions. In Proceedings of the AIAA 6th Applied Aerodynamics Conference, Williamsburg, VA, USA, 6–8 Junuary1988. AIAA Paper 88-2554. [Google Scholar]
- Liu, T. Extraction of Skin-Friction Fields from Surface Flow Visualizations as an Inverse Problem. Meas. Sci. Technol. 2013, 24, 124004. [Google Scholar] [CrossRef]
- Bottini, H.; Kurita, M.; Iijima, H.; Fukagata, K. Effects of Wall Temperature on Skin-Friction Measurements by Oil-Film Interferometry. Meas. Sci. Technol. 2015, 26, 105301. [Google Scholar] [CrossRef]
- Mclean, J.D.; George-Falvy, D.N.; Sullivan, P.P. Flight-Test of Turbulent Skin-Friction Reduction by Riblets. In Turbulent Drag Reduction by Passive Means; The Royal Aeronautical Society: London, UK, 1987; pp. 408–424. [Google Scholar]
- Larson, T.J. Evaluation of a Flow Direction Probe and a Pitot-Static Probe on the F-14 Airplane at High Angles of Attack and Sideslip; NASA Technical Memorandum 84911; National Aeronautics and Space Administration: Washington, DC, USA, 1984.
- Kurita, M.; Nishizawa, A.; Kwak, D.; Iijima, H.; Iijima, Y.; Takahashi, H.; Sasamori, M.; Abe, H.; Koga, S.; Nakakita, K. Flight Test of a Paint-Riblet for Reducing Skin-Friction. In Proceedings of the AIAA 2018 Applied Aerodynamics Conference, Atlanta, GA, USA, 25–29 Junuary 2018. AIAA paper 2018-3005. [Google Scholar]
- Bushnell, D.M.; Hefner, J.; Walsh, M.J. Viscous Drag Reduction in Boundary Layers; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 1990. [Google Scholar]
- Box, G.E.P.; Draper, N.R. Empirical Model-Building and Response Surfaces; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Khuri, A.I.; Mukhopadhyay, S. Response Surface Methodology. Wires Comput. Stat. 2010, 2, 128–149. [Google Scholar] [CrossRef]






| Uncertainty Source | Symbol | Value, % | Note |
|---|---|---|---|
| Total pressure | q1 | 0.025 | Atmospheric air pressure measured by the air-data sensing system onboard |
| Mach number | q2 | 1.01 | Obtained by the air-data sensing system onboard |
| Pitot measurement | q3 | 3.5 | Max. percent uncertainty obtained as 1σ over an averaged value for 1-min duration for all probes |
| Response surface methodology (RSM) (Interpolation) | q4 | 1.8 | Uncertainty obtained from Figure 10, including pitot pressure measurement error |
| Cumulative error (Total uncertainty) | qtotal | 4.1 (4.06) | Total uncertainty and corresponding to ε in Equation (9) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takahashi, H.; Kurita, M.; Iijima, H.; Sasamori, M. Interpolation of Turbulent Boundary Layer Profiles Measured in Flight Using Response Surface Methodology. Appl. Sci. 2018, 8, 2320. https://doi.org/10.3390/app8112320
Takahashi H, Kurita M, Iijima H, Sasamori M. Interpolation of Turbulent Boundary Layer Profiles Measured in Flight Using Response Surface Methodology. Applied Sciences. 2018; 8(11):2320. https://doi.org/10.3390/app8112320
Chicago/Turabian StyleTakahashi, Hidemi, Mitsuru Kurita, Hidetoshi Iijima, and Monami Sasamori. 2018. "Interpolation of Turbulent Boundary Layer Profiles Measured in Flight Using Response Surface Methodology" Applied Sciences 8, no. 11: 2320. https://doi.org/10.3390/app8112320
APA StyleTakahashi, H., Kurita, M., Iijima, H., & Sasamori, M. (2018). Interpolation of Turbulent Boundary Layer Profiles Measured in Flight Using Response Surface Methodology. Applied Sciences, 8(11), 2320. https://doi.org/10.3390/app8112320





