Experimental Simulation of Lightning Current Discharge on Rocks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Target Rocks
2.2. X-Ray Powder Diffraction
2.3. Experimental Hardware Setup
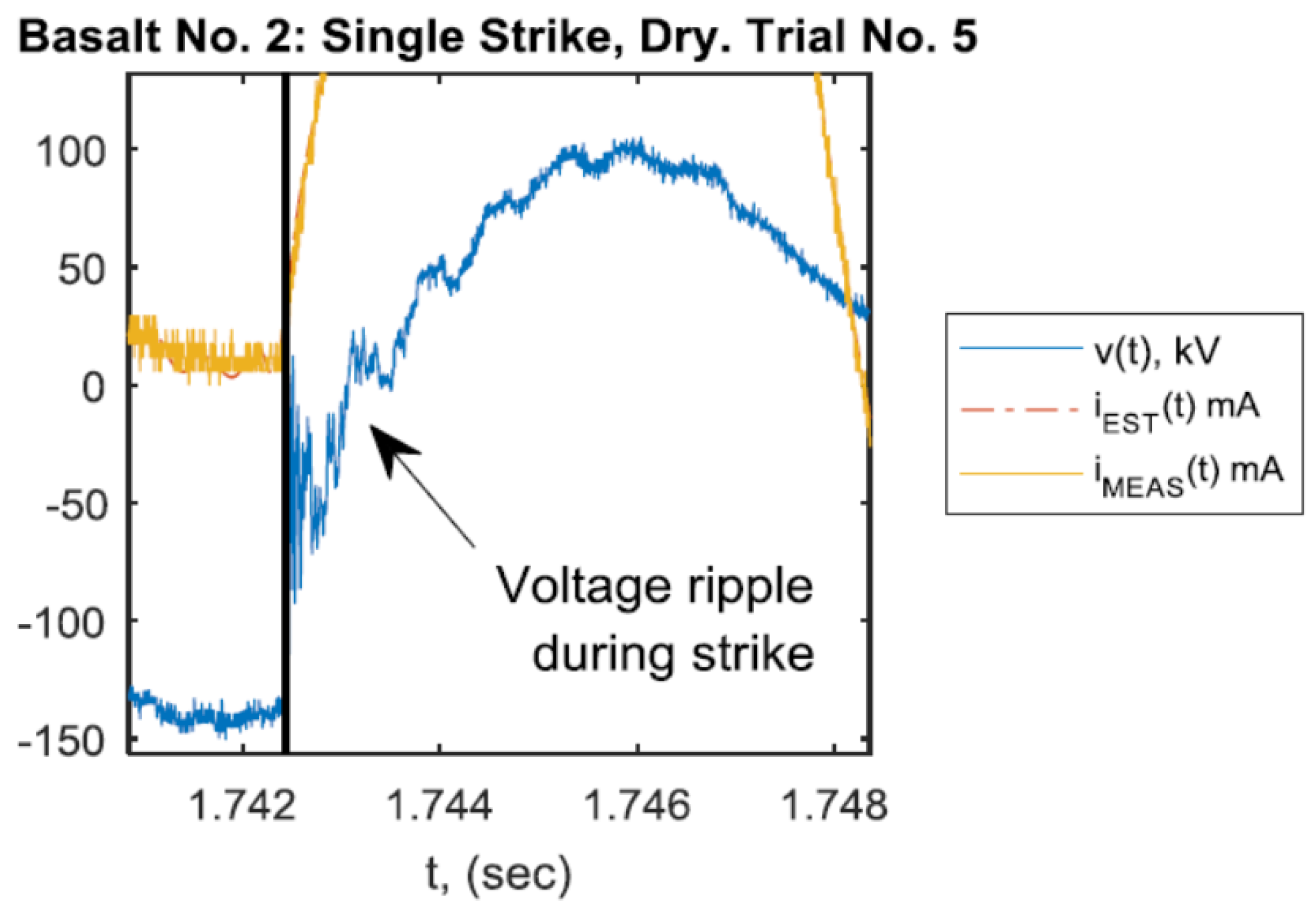
2.4. Electrical Measurements and Calculations
2.5. Fault Onset
2.6. Fault Extinction
- Characterize the pre-fault (open-circuit) noise level in the current measurement using the standard deviation (assume noise is Gaussian with mean estimated from the data):
- Find the post-onset sample for which all later data samples could be considered noise:
3. Results
3.1. Mineralogy of Target Rocks
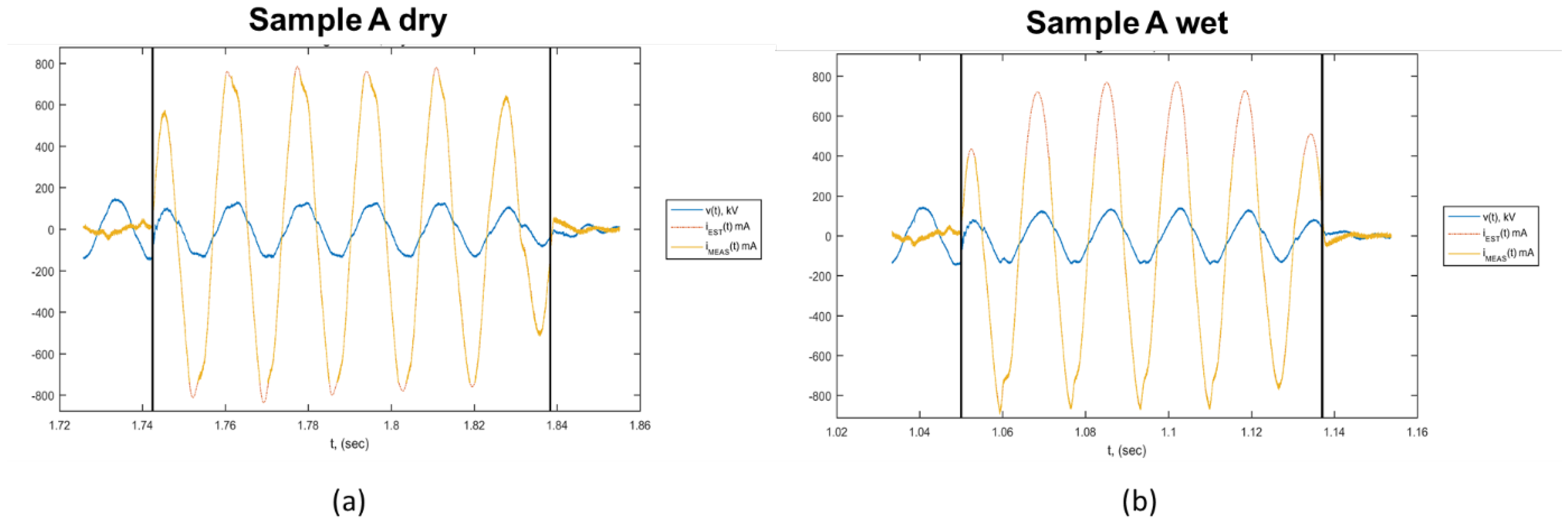
3.2. Arc Discharge Experiment Results
4. Discussion
4.1. Lightning Simulation
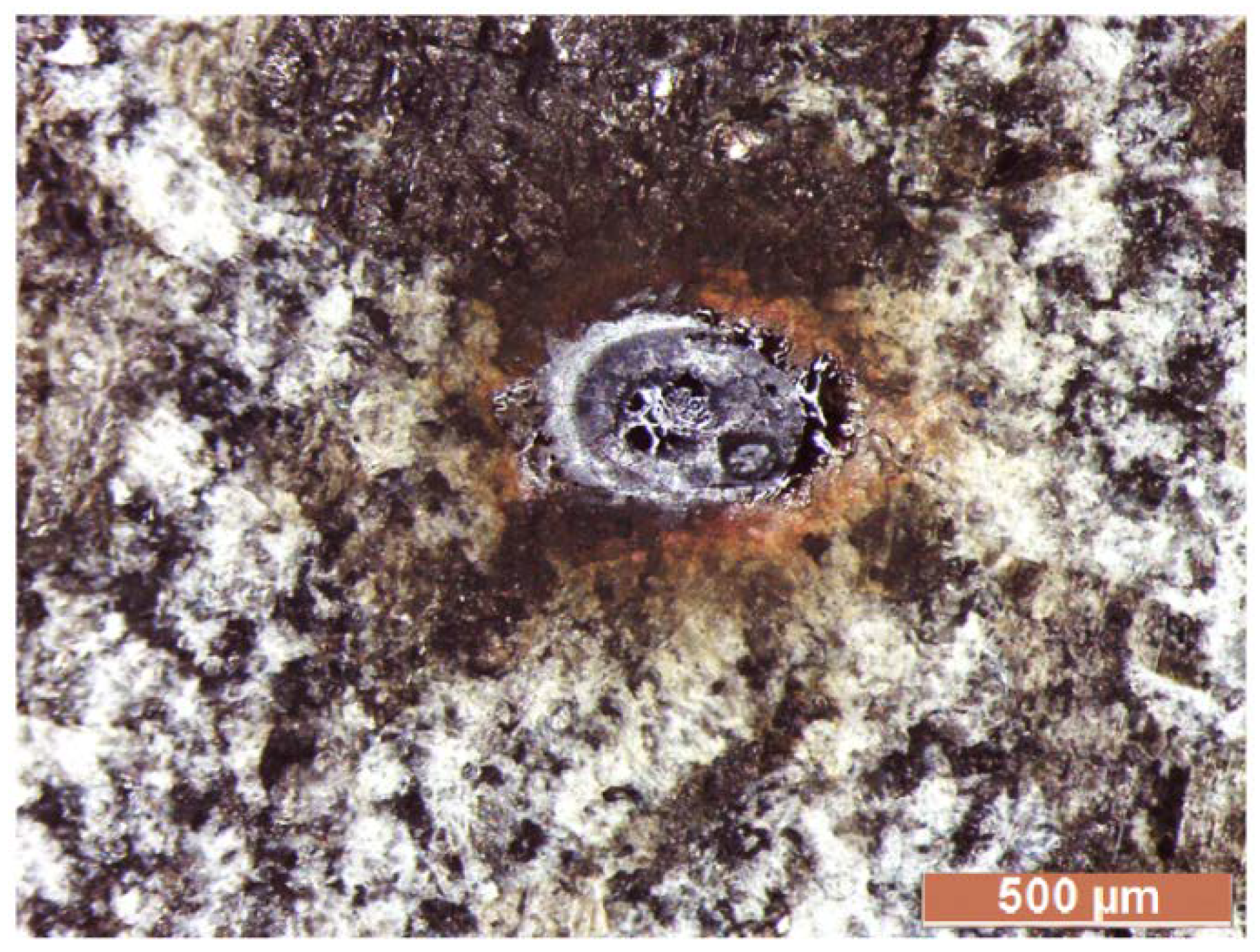
4.2. Fulgurite Glass Formation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Uman, M.A.; Krider, E.P. Natural and Artificially Initiated Lightning. Science 1989, 246, 457–464. [Google Scholar] [CrossRef] [PubMed]
- Cooray, V. Lightning and Global Temperature Change. In Lightning Flash, 2nd ed.; Cooray, V., Ed.; Institution of Engineering and Technology: London, UK, 2014; pp. 861–878. [Google Scholar]
- Glushakow, B. Effective Lightning Protection for Wind Turbine Generators. IEEE Trans. Energy Convers. 2007, 22, 214–222. [Google Scholar] [CrossRef]
- Cooray, V.; Cooray, C.; Andrews, C.J. Lightning caused injuries in humans. J. Electrost. 2007, 65, 386–394. [Google Scholar] [CrossRef]
- Ritenour, A.E.; Morton, M.J.; McManus, J.G.; Barillo, D.J.; Cancio, L.C. Lightning injury: A review. Burns 2008, 34, 585–594. [Google Scholar] [CrossRef] [PubMed]
- Curran, E.B.; Holle, R.L.; López, R.E. Lightning Casualties and Damages in the United States from 1959 to 1994. J. Clim. 2000, 13, 3448–3464. [Google Scholar] [CrossRef]
- Mason, J. The Generation of Electric Charges and Fields in Thunderstorms. Proc. R. Soc. A Math. Phys. Eng. Sci. 1988, 415, 303–315. [Google Scholar] [CrossRef]
- US-NSSL. Available online: http://www.nssl.noaa.gov/research/lightning/ (accessed on 22 September 2018).
- Saikia, B.J.; Parthasarathy, G.; Sarmah, N.C.; Baruah, G.D. Fourier-transform infrared spectroscopic characterization of naturally occurring glassy fulgurites. Bull. Mater. Sci. 2008, 31, 155–158. [Google Scholar] [CrossRef]
- Rakov, V.A. Lightning makes glass. In Proceedings of the 29th Annual Conference of the Glass Art Society, Tampa, FL, USA, 29 April–2 May 1999; pp. 45–50. [Google Scholar]
- Martin Crespo, T.; Lozano Fernandez, R.P.; Gonzalez Laguna, R. The fulgurite of Torre de Moncorvo (Portugal): Description and analysis of the glass. Eur. J. Miner. 2009, 21, 783–794. [Google Scholar] [CrossRef]
- Rakov, V.A.; Uman, M.A. Lightning: Physics and Effects; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Allibone, T.E.; Dring, D. Lightning and the Long Spark. The Significance of Leader-Stroke Velocity. Proc. R. Soc. A Math. Phys. Eng. Sci. 1977, 357, 15–35. [Google Scholar] [CrossRef]
- Uman, M.A. The peak temperature of lightning. J. Atmos. Terr. Phys. 1964, 26, 123–128. [Google Scholar] [CrossRef]
- Uman, M.A. Lightning; McGraw-Hill: New York, NY, USA, 1969. [Google Scholar]
- Pasek, M.A.; Hurst, M. A Fossilized Energy Distribution of Lightning. Nat. Sci. Rep. 2016, 6, 30586. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lay, E.H.; Jacobson, A.R.; Holzworth, R.H.; Rodger, C.J.; Dowden, R.L. Local time variation in land/ocean lightning flash density as measured by the World Wide Lightning Location Network. J. Geophys. Res. 2007. [Google Scholar] [CrossRef]
- Elmi, C.; Chen, J.; Goldsby, D.; Gieré, R. Mineralogy and chemistry of lightning-struck rocks: A study of fulgurites from Mount Mottarone, Baveno (Italy). Am. Miner. 2017, 102, 1470–1481. [Google Scholar] [CrossRef]
- O’Connor, B.H.; Raven, M.D. Application of the Rietveld Refinement Procedure in Assaying Powdered Mixtures. Powder Diffr. 1988, 3, 2–6. [Google Scholar] [CrossRef]
- Degen, T.; Sadki, M.; Bron, E.; Konig, U.; Nenert, G. The HighScore suite. Powder Diffr. 2014, 29, S13–S18. [Google Scholar] [CrossRef] [Green Version]
- Vetterli, M.; Kovacevic, J. Wavelets and Subband Coding; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1995; p. 488. [Google Scholar]
- Daubechies, I. Ten Lectures on Wavelets; SIAM: Philadelphia, PA, USA, 1992; p. 357. [Google Scholar]
- Coleman, N.S.; Schegan, C.; Miu, K.N. A Study of Power Distribution System Fault Classification with Machine Learning Techniques. In Proceedings of the 2015 North American Power Symposium (NAPS), Charlotte, NC, USA, 4–6 October 2015. [Google Scholar]
- Santoso, S.; Grady, W.M.; Powers, E.J.; Lamoree, J.; Bhatt, S.C. Characterization of distribution power quality events with Fourier and wavelet transforms. IEEE Trans. Power Deliv. 2000, 15, 247–254. [Google Scholar] [CrossRef]
- Schegan, C.M. A Hardware/Software Platform for Fault Detection and Identification in Electric Power Distribution Systems for Testing Various Detection Schemes; Drexel University: Philadelphia, PA, USA, 2008. [Google Scholar]
- Stolper, E.; Walker, D. Melt Density and the Average Composition of Basalt. Contrib. Miner. Pet. 1980, 74, 7–12. [Google Scholar] [CrossRef]
- Ahrens, T.J.; O’Keefe, J.D. Shock melting and vaporization of lunar rocks and minerals. Moon 1972, 4, 214–249. [Google Scholar] [CrossRef]
- Navarre-Sitchler, A.; Brantley, S. Basalt weathering across scales. Earth Planet. Sci. Lett. 2007, 261, 321–334. [Google Scholar] [CrossRef]
- Bazelyan, E.M.; Raizer, Y.P. Introduction: Lightning, its destructive effects and protection. In Lightning Physics and Lightning Protection; Bazelyan, E.M., Raizer, Y.P., Eds.; CRC Press: Boca Raton, FL, USA, 2000; pp. 1–26. [Google Scholar]
- Cornell, R.M.; Schwertmann, U. The Iron Oxides: Structure, Properties, Reactions, Occurrences and Uses; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Keller, G.V. Electrical properties of rocks and minerals. In Handbook of Physical Constants; Clark, S.P., Ed.; The Geological Society of America Memoir: Boulder, CO, USA, 1966; Volume 97, pp. 553–577. [Google Scholar]
- Telford, W.M.; Geldart, L.; Sheriff, R.E. Electrical Properties of Rocks and Minerals. In Applied Geophysics, 2nd ed.; Telford, W.M., Geldart, L., Sheriff, R.E., Eds.; Cambridge University Press: Cambridge, UK, 1990; pp. 283–292. [Google Scholar]
- Olhoeft, G.R. Electrical properties of granite with implications for the lower crust. J. Geophys. Res. Solid Earth 1981, 86, 931–936. [Google Scholar] [CrossRef]
- Stone, G.C.; Culbert, I.; Boulter, E.A.; Dhirani, H. Historical development of insulation materials and systems In Electrical Insulation for Rotating Machines: Design, Evaluation, Aging, Testing, and Repair, 2nd ed.; Stone, G.C., Culbert, I., Boulter, E.A., Dhirani, H., Eds.; Wiley: Hoboken, NJ, USA, 2014; pp. 83–110. [Google Scholar]
- Dearman, W.R.; Baynes, F.J.; Irfan, T.Y. Engineering grading of weathered granite. Eng. Geol. 1978, 12, 345–374. [Google Scholar] [CrossRef]

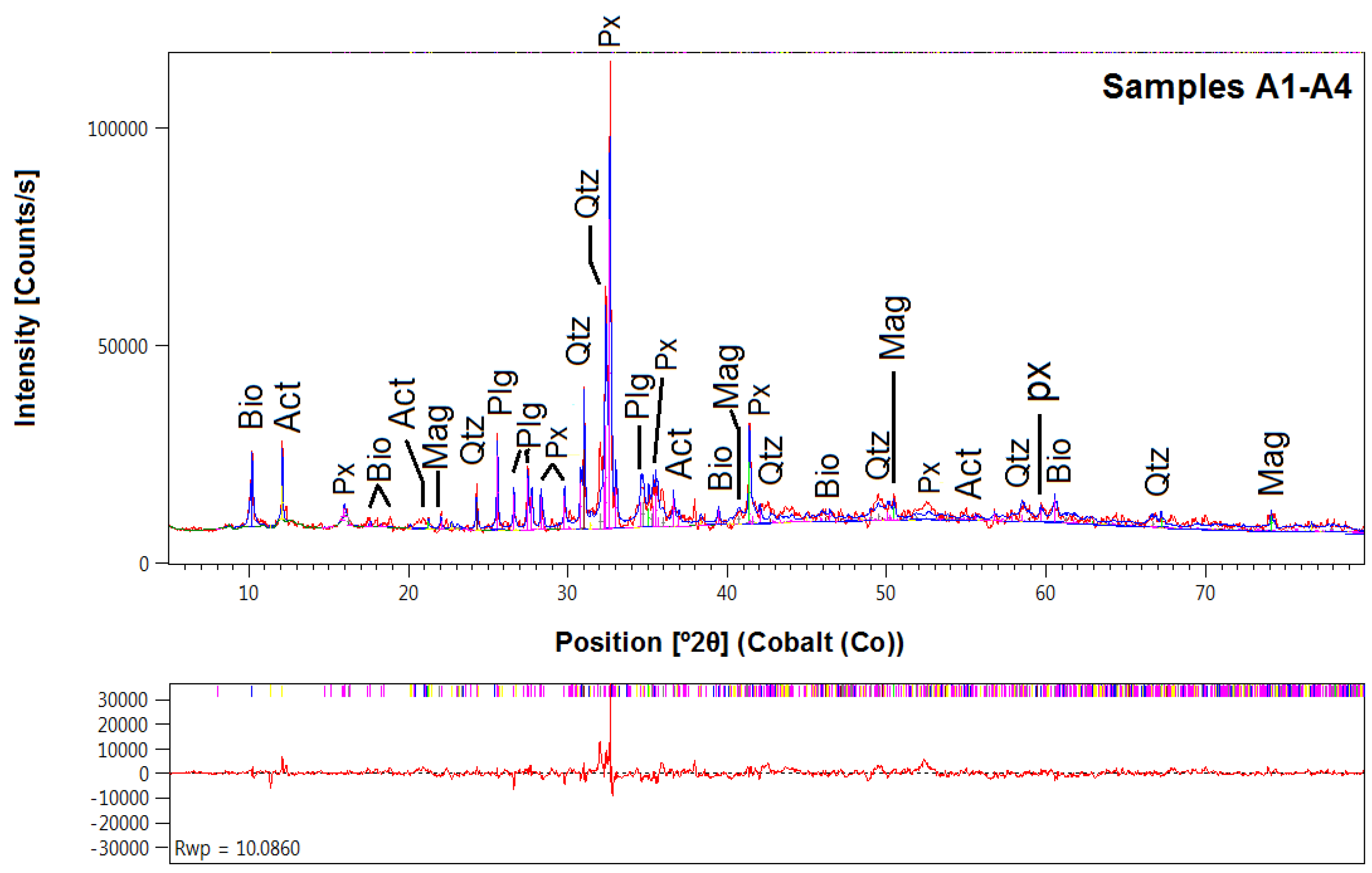





| Weight % | Samples A1–A4 | Samples B1–B2 |
|---|---|---|
| Quartz | 10.2(3) | 54.6(2) |
| Plagioclase | 49.6(4) | 15.7(4) |
| K-feldspar | 21.0(2) | |
| Pyroxene | 18.5(4) | |
| Biotite | 5.6(2) | 7.5(2) |
| Chlorite | 1.2(4) | |
| Actinolite | 6.3(5) | |
| Magnetite | 3.6(2) | |
| Amorphous | 6.2(4) |
| Specimen | Strike Number | TF (ms) | VR (kV) | IR (A) | P (kW) | (kW) | E (kJ) |
|---|---|---|---|---|---|---|---|
| Average A0 dry | 96.86 | 85.26 | 0.53 | 42.25 | 116.28 | 4.09 | |
| Sample A1 dry | 1 | 95.97 | 85.13 | 0.52 | 42.07 | 124.65 | 4.04 |
| Sample A2 dry | 1 | 103.74 | 82.82 | 0.51 | 39.72 | 107.28 | 4.12 |
| 2 | 88.04 | 83.01 | 0.52 | 40.18 | 102.62 | 3.54 | |
| 3 | 96.26 | 85.57 | 0.53 | 42.25 | 129.27 | 4.07 | |
| 4 | 88.61 | 85.65 | 0.53 | 42.52 | 121.36 | 3.77 | |
| 5 | 96.03 | 84.93 | 0.52 | 41.67 | 123.31 | 4.00 | |
| 6 | 103.78 | 79.68 | 0.50 | 36.78 | 117.00 | 3.82 | |
| Average A2 | 96.08 | 83.61 | 0.52 | 40.52 | 116.81 | 3.89 | |
| Sample A3 wet | 1 | 87.04 | 86.26 | 0.53 | 43.08 | 121.10 | 3.75 |
| Sample A4 wet | 1 | 95.67 | 83.21 | 0.52 | 40.28 | 122.78 | 3.85 |
| 2 | 96.24 | 86.32 | 0.53 | 43.02 | 121.48 | 4.14 | |
| 3 | 102.42 | 81.23 | 0.51 | 38.38 | 122.67 | 3.93 | |
| 4 | 96.56 | 85.22 | 0.52 | 41.91 | 121.36 | 4.05 | |
| Average A4 | 97.72 | 84.00 | 0.52 | 40.90 | 122.07 | 3.99 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elmi, C.; Coleman, N.S.; Miu, K.; Schruba, E. Experimental Simulation of Lightning Current Discharge on Rocks. Appl. Sci. 2018, 8, 2394. https://doi.org/10.3390/app8122394
Elmi C, Coleman NS, Miu K, Schruba E. Experimental Simulation of Lightning Current Discharge on Rocks. Applied Sciences. 2018; 8(12):2394. https://doi.org/10.3390/app8122394
Chicago/Turabian StyleElmi, Chiara, Nicholas S. Coleman, Karen Miu, and Edward Schruba. 2018. "Experimental Simulation of Lightning Current Discharge on Rocks" Applied Sciences 8, no. 12: 2394. https://doi.org/10.3390/app8122394
APA StyleElmi, C., Coleman, N. S., Miu, K., & Schruba, E. (2018). Experimental Simulation of Lightning Current Discharge on Rocks. Applied Sciences, 8(12), 2394. https://doi.org/10.3390/app8122394






