Systematic Quantum Cluster Typical Medium Method for the Study of Localization in Strongly Disordered Electronic Systems
Abstract
1. Introduction
2. Background: Electron Localization in Disordered Medium
2.1. Anderson Localization
2.2. Order Parameter of Anderson Localization
- We approximate the effect of coupling the block to the reminder of the lattice via Fermi’s golden rule—coupling which is proportional to the density of accessible states.
- Since on average each cluster is equivalent to all the others, this density will also be proportional to some appropriate block DOS.
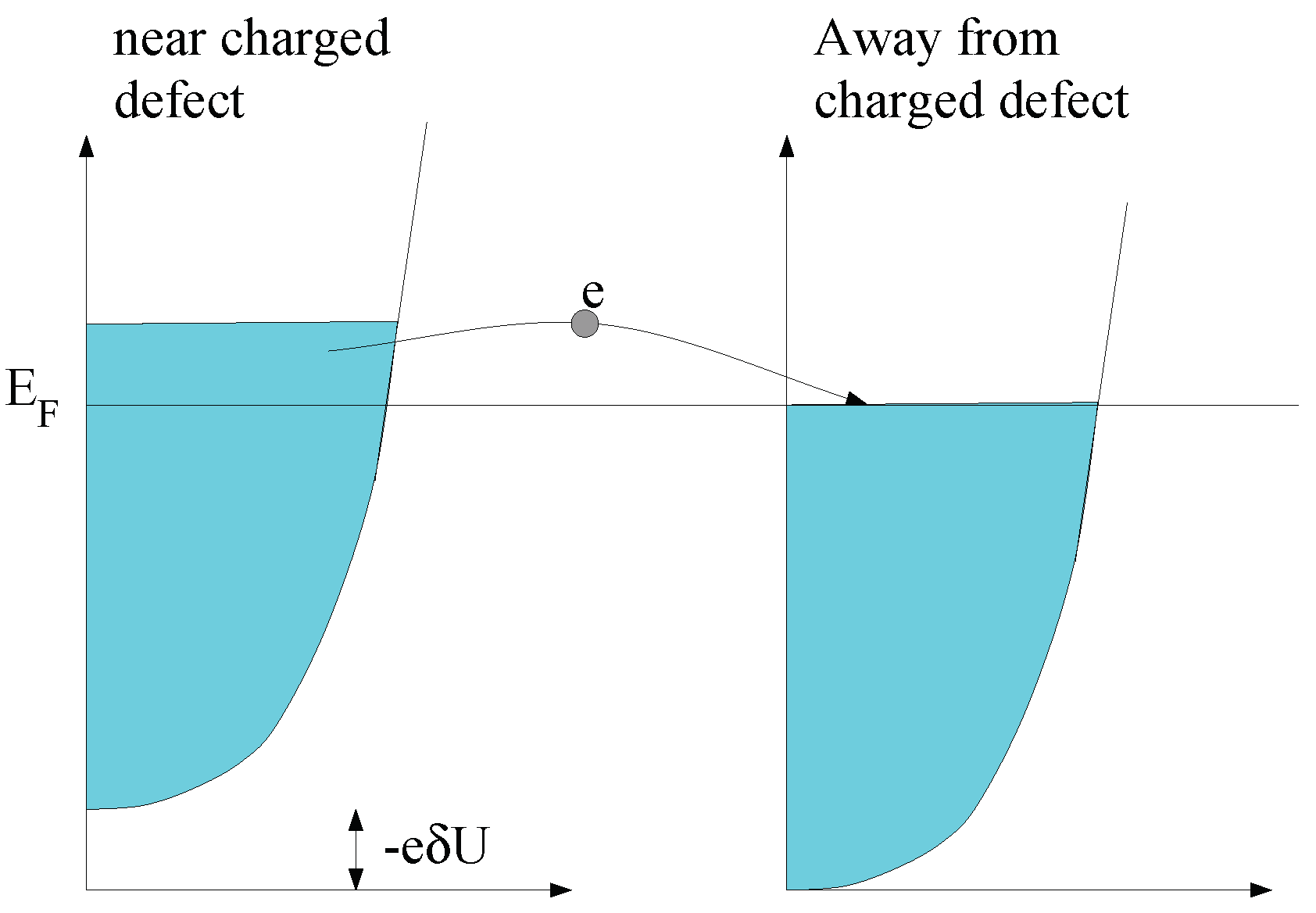
2.3. On the Role of Interactions: Thomas-Fermi Screening
2.4. The Mott Transition
2.5. Interacting Disordered Systems: Beyond the Single-Particle Description
3. Direct Numerical Methods for Strongly Disordered Systems
3.1. Transfer Matrix Method
3.2. Kernel Polynomial Method
3.3. Diagonalization Methods
4. Coarse-Grained Methods
4.1. A Few Fundamentals
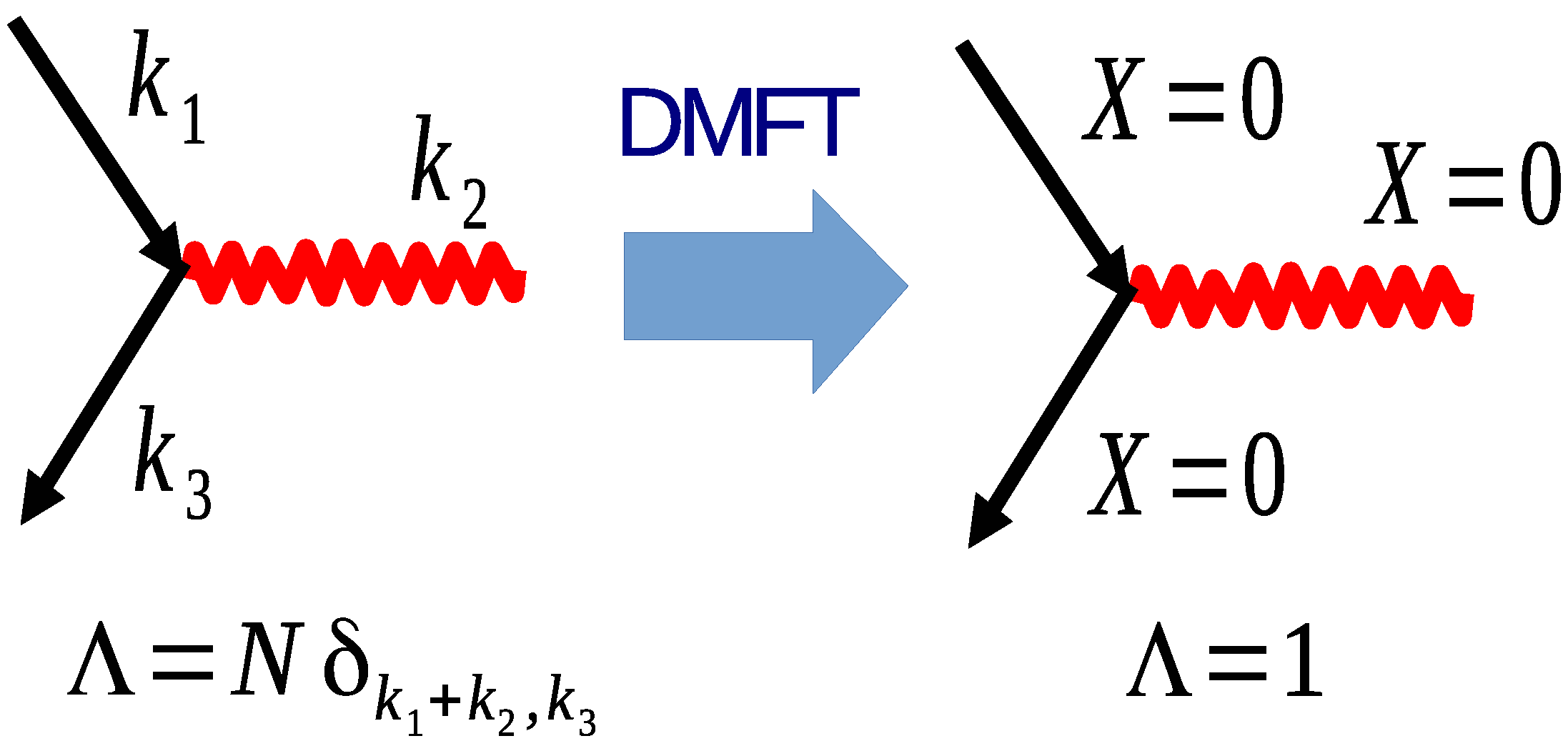
4.2. The Laue Function and the Limit of Infinite Dimension
4.3. The DCA
4.3.1. Coarse-Graining
4.3.2. DCA: A Diagrammatic Derivation
4.3.3. DCA: A Generating Functional Derivation
5. Typical Medium Theories of Anderson Localization: Model Studies
5.1. Building Quantum Cluster Theories for the Study of Localization
- We approximate the coupling of the clusters to their lattice environment at the single-particle level (akin to the Fermi golden rule) neglecting two-particle and higher processes. This coupling is proportional to the square of a matrix element between the cluster and its host, times an appropriate DOS which describes the states available on the surrounding clusters.
- Since on average each cluster is equivalent to all the others, this DOS will also be proportional to some appropriate cluster density of states. In addition, since the distribution of the DOS is highly skewed, the typical DOS is quite different than the average DOS. The typical cluster DOS, which is clearly more representative of the local environment, will be used to define the effective medium.
- 3.
- Maintain the translational invariance of the impurity averaged cluster, i.e., there should be no distinction between, e.g., sites in the center and those at the boundary of the cluster.
- 4.
- The clusters should maintain the point group symmetries of the lattice.
- 5.
- The method should be fully causal, with positive definite spectra
- 6.
- It should recover the DCA when the disorder is weak.
- 7.
- it should recover the TMT when
- 8.
- In lieu of interactions, the scatterings at different energies are completely independent of each other.
- 9.
- For large it should become exact while avoiding self-averaging effects.
- 10.
- It should be extensible to multiple bands, and realistic models with longer ranged diagonal and off-diagonal disorder
5.2. Typical Medium Dynamical Cluster Approximation (TMDCA)
- Ansatz 1When the cluster size = 1, this Ansatz [10] recovers the local TMT with . For weak disorder, the TMDCA recovers the average DCA results, with . In addition, in the limit of → ∞, the TMDCA becomes exact. Hence, between these limits, this Ansatz 1 of the TMDCA systematically incorporates non-local correlations into the local TMT. Since, this Ansatz uses the TDOS, to get typical cluster Green’s function , we use a Hilbert transformation, with
- Ansatz 2While Ansatz 1 works rather well for simple single-band models with local and non-local disorder, we find that it can suffer from numerical instabilities when applied to complex first-principle effective Hamiltonians with many orbitals and non-local disorder potentials. Such numerical instabilities arise due to the Hilbert transformation which is used to calculate the Green’s function from the TDOS . To avoid such numerical instabilities, we constructed the following Ansatz 2 [172] where we calculate directly asThis Ansatz 2 again incorporates the typical value of the local DOS, the resulting formalism again becomes exact in the limit of , promotes numerical stability of the algorithm, and converges quickly with cluster size. As noted in Table 1 it does not reproduce the TMT when . This is due to the lack of a limit where the formalism is exact so that the Ansatz may be uniquely defined.
- We start with a guess for the cluster self-energy , usually set to zero.
- Then we calculate the coarse-grained cluster Green’s function as
- The cluster problem is now set up by calculating the cluster-excluded Green’s function as
- Since the cluster problem is solved in real space, we then Fourier transform (K,) to real space: .
- We solve the cluster problem using, e.g., a random sampling simulation. Here, we stochastically generate random configurations of the disorder potential V. For each disordered configuration, we construct the new fully dressed cluster Green’s function asWe then calculate the disorder-averaged, typical cluster Green’s function via the Hilbert transform using Equation (46) for Ansatz 1, or we can directly calculate the from Equation (47) if we use Ansatz 2.
- With the cluster problem solved, we use the obtained typical cluster Green’s function to obtain a new estimate for the cluster self-energy
- We repeat this procedure starting from 2, until converges to the desired accuracy.
5.3. Off-Diagonal Disorder
5.3.1. DCA with Off-Diagonal Disorder
5.3.2. TMDCA with Off-Diagonal Disorder
5.4. TMDCA for Multi-Orbital Systems
5.5. Disorder in Interacting Systems
5.5.1. SOPT
5.5.2. Stat DMFT Approach
5.6. Two-Particle Calculations
6. Methodology for First-Principles Studies of Localization
6.1. From DFT to the EDHM
- In the first step two DFT calculations are performed: a normal cell calculation of the pure host material and a supercell calculation of the host material with a single impurity in it. For example, for KFeSe, an iron-based superconductor that contains Fe vacancies, the normal cell of the host will be KFeSe. To capture the impurity potential of an Fe vacancy one can run a DFT calculation for a KFeSe supercell containing a single Fe vacancy [199].
- The second step is to derive the low-energy Hamiltonians using a projected Wannier function transformation in which a set of atomic orbitals is projected on the bands close to the Fermi level [75,76,202]. For the case of KFeSe, one can project Fe-d and Se-p orbitals on the bands within [−6, 2] eV [199]. This results in two ordered tight-binding Hamiltonians. One for the normal cell , and one for the single-impurity supercell .
- Finally, a superposition of these ordered Hamiltonians is used to build Hamiltonians of arbitrary impurity configurations. Specifically, the difference between the single impurity and pure Hamiltonian is taken to derive the single-impurity potential: . To remove the influence of the periodically repeated impurities in the single-impurity supercell calculation a partitioning procedure is necessary. A detailed account of this procedure is given in [202]. From single-impurity potential the effective Hamiltonian of a disordered impurity configuration with N impurities can be assembled as follows: .
6.2. From the EDHM to TMDCA
7. Applications of the Typical Medium DCA to Systems with Disorder
7.1. Results for the Anderson Model
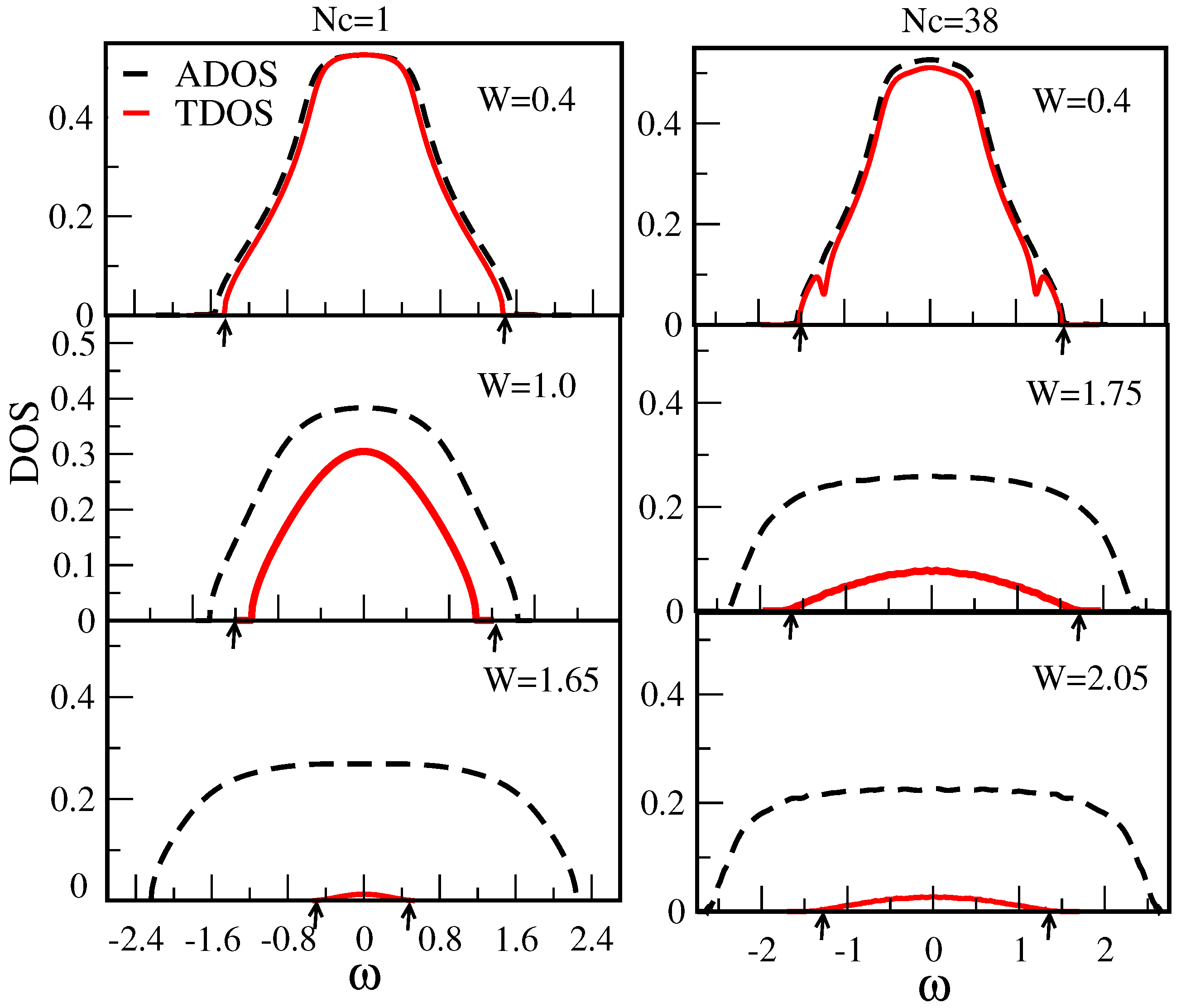
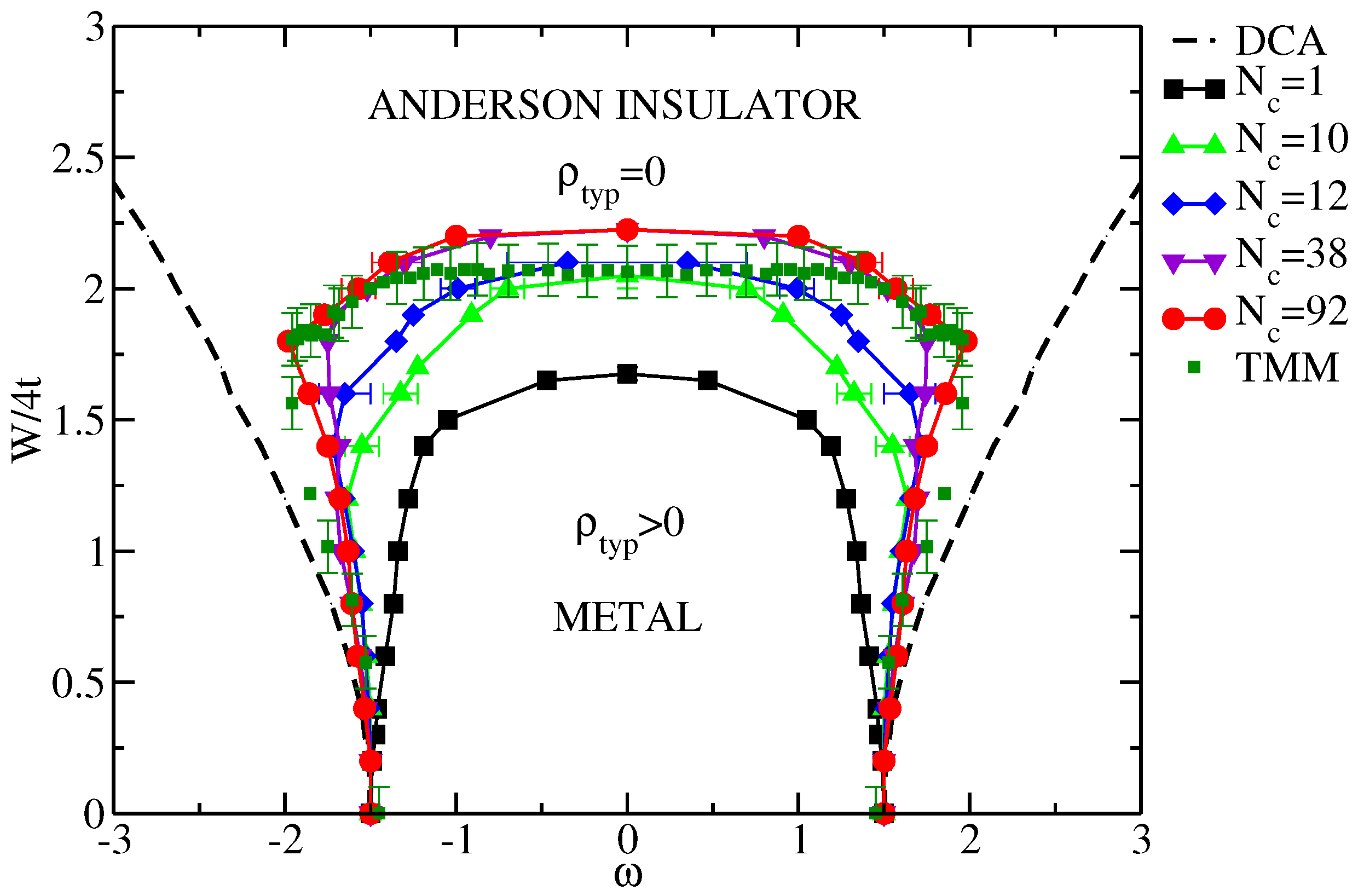
7.1.1. Typical DOS as an Order Parameter for Anderson Localization
7.1.2. Cluster Size Convergence
7.2. Results for Models with More Realistic Parameters
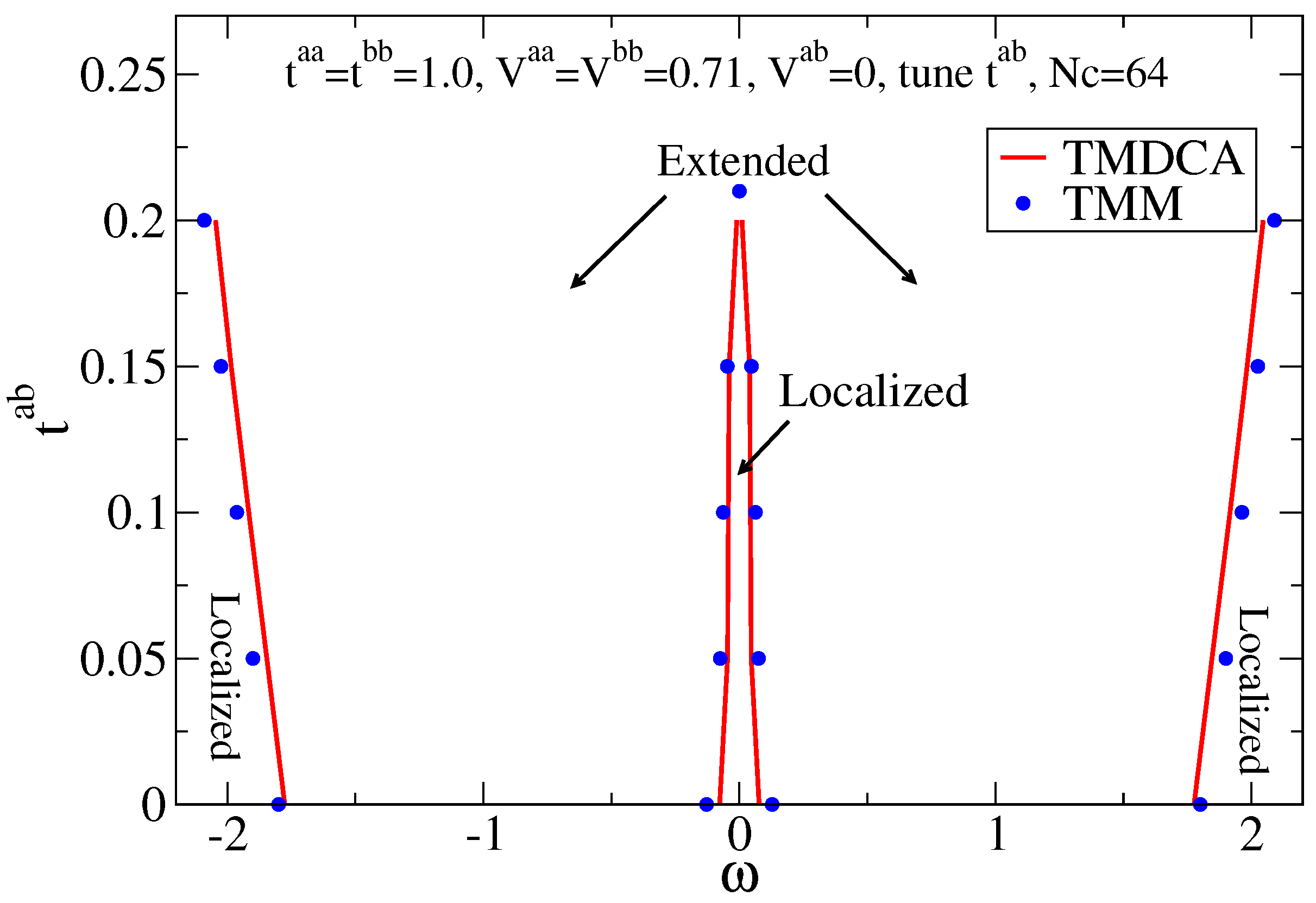
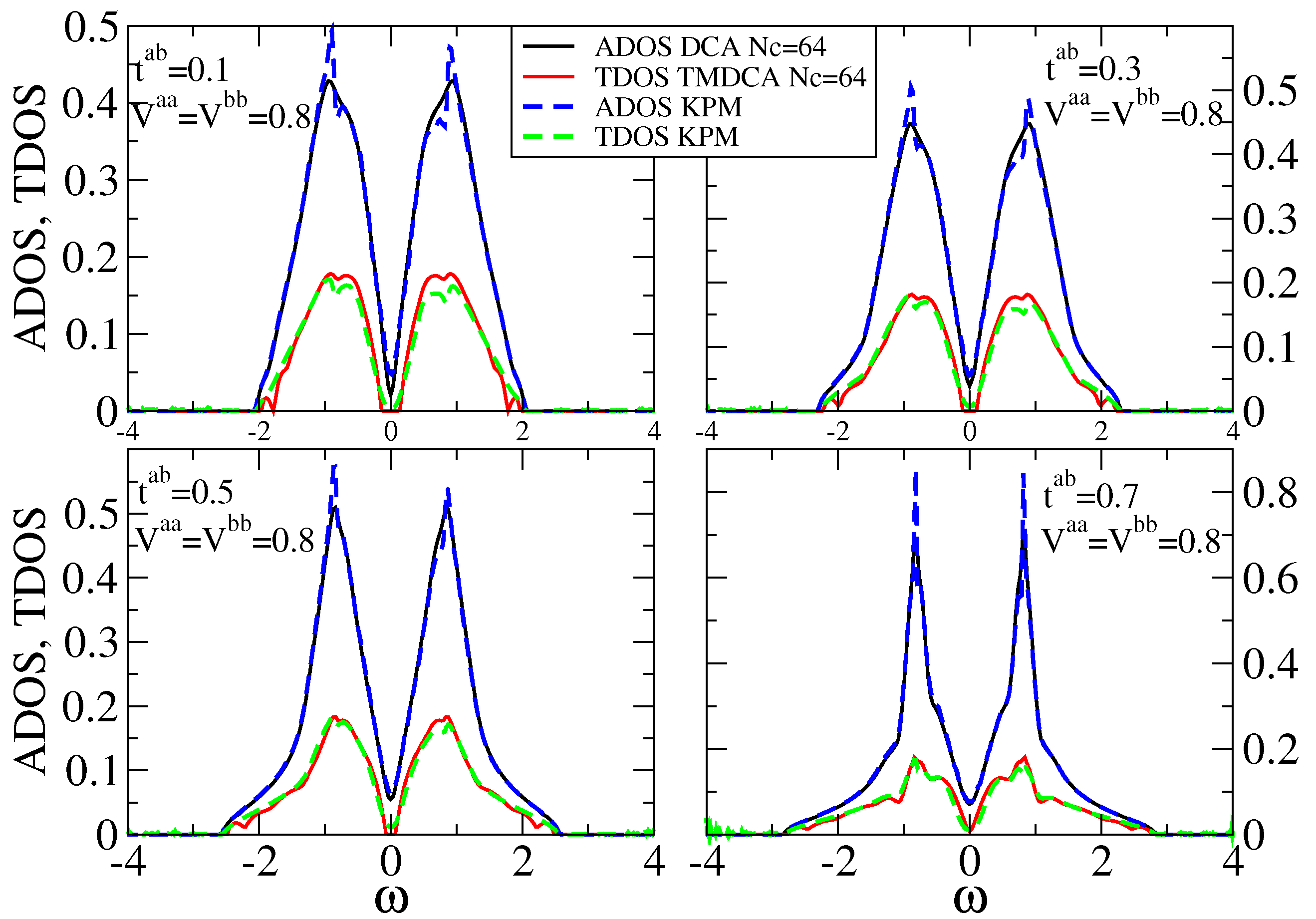
7.2.1. Off-Diagonal Disorder
7.2.2. Multiple Orbitals
7.3. Results for Two-Particle Calculations
7.4. Results for Interacting Models
7.4.1. Results from SOPT
7.4.2. Results from Stat-DMFT
7.5. Results of First-Principles Studies of Localization
7.5.1. Application to KFeSe
7.5.2. Application to (Ga,Mn)N
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Acronym | Description |
| ADOS | Average Density of States |
| AL | Anderson Localization |
| BEB | Blackman Esterling Berk |
| CPA | Coherent Potential Approximation |
| DCA | Dynamical Cluster Approximation |
| DFT | Density-Functional Theory |
| CDMFT | Cluster Dynamical Mean-Field Theory |
| EDHM | Effective Disorder Hamiltonian Method |
| JDM | Jacobi-Davidson Method |
| KKR | Korringa-Kohn-Rostoker method |
| KPM | Kernel Polynomial Method |
| LAPW | Linear Augmented Plane Wave |
| LDOS | Local Density of States |
| LMA | Local Moment Approach |
| MCPA | Molecular Coherent Potential Approximation |
| MS | Multiple-Scattering |
| NLCPA | Non-Local Coherent Potential Approximation |
| ODD | Off-Diagonal Disorder |
| QC | Quantum-Critical |
| QMC | Quantum Monte Carlo |
| SOPT | Second Order Perturbation Theory |
| TDOS | Typical Density of States |
| TMDCA | Typical Medium Dynamical Cluster Approximation |
| TMM | Transfer Matrix Method |
| TMT | Typical Medium Theory |
| Symbol | Description |
| wavenumber | |
| Cluster wavenumber | |
| lattice site coordinate | |
| Cluster site coordinate | |
| N | Number of lattice sites |
| Number of cluster sites | |
| Real and complex frequencies | |
| DCA coarse-graining many to one map | |
| Density of states | |
| V | Electronic potential |
| Electronic energy | |
| Electronic chemical potential | |
| spin index | |
| t | Electronic Hopping matrix element (energy) |
| m | Magnetization |
| h | Magnetic Field |
| Two-particle Green’s function (tensor) | |
| F | Full vertex function (tensor) |
| G | Single-particle Green’s function |
| A | Single-particle spectral function |
| Mean-field hybridization between cluster and host | |
| Host or cluster-excluded Green’s function | |
| Single-particle self-energy | |
| Irreducible vertex function | |
| Laue function | |
| A superscript “c” designates a cluster quantity | |
| A superscript “l” designates a lattice quantity | |
| A subscript “typ” designates a cluster quantity | |
| denotes a coarse-grained quantity | |
| uppercase subscripts indicate indices in cluster space | |
| lowercase subscripts indicate indices in lattice space | |
| denotes a matrix in the Blackman formalism or in the multi-orbital system |
References
- Woods, D. Power, Pollution and the Internet. New York Times, 23 September 2012. [Google Scholar]
- How Dirty Is Your Data? A Look at the Energy Choices that Power Cloud Computing; Greenpeace International: Amsterdam, The Netherlands, 2011.
- Imada, M.; Fujimori, A.; Tokura, Y. Metal-insulator transitions. Rev. Mod. Phys. 1998, 70, 1039–1263. [Google Scholar] [CrossRef]
- Mott, N.F. Metal-Insulator Transition. Rev. Mod. Phys. 1968, 40, 677–683. [Google Scholar] [CrossRef]
- Belitz, D.; Kirkpatrick, T.R. The Anderson-Mott transition. Rev. Mod. Phys. 1994, 66, 261–380. [Google Scholar] [CrossRef]
- Evers, F.; Mirlin, A.D. Anderson transitions. Rev. Mod. Phys. 2008, 80, 1355–1417. [Google Scholar] [CrossRef]
- Dobrosavljević, V.; Trivedi, N.; Valles, J.M., Jr. Conductor Insulator Quantum Phase Transitions; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Jarrell, M.; Krishnamurthy, H.R. Systematic and causal corrections to the coherent potential approximation. Phys. Rev. B 2001, 63, 125102. [Google Scholar] [CrossRef]
- Dobrosavljević, V.; Pastor, A.A.; Nikolić, B.K. Typical medium theory of Anderson localization: A local order parameter approach to strong-disorder effects. EPL 2003, 62, 76. [Google Scholar] [CrossRef]
- Ekuma, C.E.; Moore, C.; Terletska, H.; Tam, K.M.; Moreno, J.; Jarrell, M.; Vidhyadhiraja, N.S. Finite-cluster typical medium theory for disordered electronic systems. Phys. Rev. B 2015, 92, 014209. [Google Scholar] [CrossRef]
- Ekuma, C.E.; Yang, S.X.; Terletska, H.; Tam, K.M.; Vidhyadhiraja, N.S.; Moreno, J.; Jarrell, M. Metal-insulator transition in a weakly interacting disordered electron system. Phys. Rev. B 2015, 92, 201114. [Google Scholar] [CrossRef]
- Zhang, Y.; Terletska, H.; Moore, C.; Ekuma, C.; Tam, K.M.; Berlijn, T.; Ku, W.; Moreno, J.; Jarrell, M. Study of multiband disordered systems using the typical medium dynamical cluster approximation. Phys. Rev. B 2015, 92, 205111. [Google Scholar] [CrossRef]
- Metzner, W.; Vollhardt, D. Correlated lattice fermions in d = ∞ dimensions. Phys. Rev. Lett. 1989, 62, 324–327. [Google Scholar] [CrossRef] [PubMed]
- Müller-Hartmann, E. Correlated fermions on a lattice in high dimensions. Z. Phys. B Condens. Matter 1989, 74, 507–512. [Google Scholar] [CrossRef]
- Müller-Hartmann, E. The Hubbard model at high dimensions: Some exact results and weak coupling theory. Z. Phys. B Condens. Matter 1989, 76, 211–217. [Google Scholar] [CrossRef]
- Georges, A.; Kotliar, G. Hubbard model in infinite dimensions. Phys. Rev. B 1992, 45, 6479–6482. [Google Scholar] [CrossRef]
- Jarrell, M. The Hubbard Model in Infinite Dimensions: A Quantum Monte Carlo Study. Phys. Rev. Lett. 1992, 69, 168–171. [Google Scholar] [CrossRef] [PubMed]
- Pruschke, T.; Jarrell, M.; Freericks, J. Anomalous normal-state properties of high-Tc superconductors: intrinsic properties of strongly correlated electron systems? Adv. Phys. 1995, 44, 187–210. [Google Scholar] [CrossRef]
- Georges, A.; Kotliar, G.; Krauth, W.; Rozenberg, M. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 1996, 68, 13–125. [Google Scholar] [CrossRef]
- Soven, P. Coherent-Potential Model of Substitutional Disordered Alloys. Phys. Rev. 1967, 156, 809–813. [Google Scholar] [CrossRef]
- Velický, B.; Kirkpatrick, S.; Ehrenreich, H. Single-Site Approximations in the Electronic Theory of Simple Binary Alloys. Phys. Rev. 1968, 175, 747–766. [Google Scholar] [CrossRef]
- Elliott, R.J.; Krumhansl, J.A.; Leath, P.L. The theory and properties of randomly disordered crystals and related physical systems. Rev. Mod. Phys. 1974, 46, 465–543. [Google Scholar] [CrossRef]
- Hettler, M.; Tahvildar-Zadeh, A.; Jarrell, M.; Pruschke, T.; Krishnamurthy, H. Nonlocal dynamical correlations of strongly interacting electron systems. Phys. Rev. B 1998, 58, 7475–7478. [Google Scholar] [CrossRef]
- Hettler, M.; Mukherjee, M.; Jarrell, M.; Krishnamurthy, H. Dynamical cluster approximation: Nonlocal dynamics of correlated electron systems. Phys. Rev. B 2000, 61, 12739–12756. [Google Scholar] [CrossRef]
- Anderson, P.W. Absence of Diffusion in Certain Random Lattices. Phys. Rev. 1958, 109, 1492–1505. [Google Scholar] [CrossRef]
- Dagotto, E. Complexity in Strongly Correlated Electronic Systems. Science 2005, 309, 257–262. [Google Scholar] [CrossRef] [PubMed]
- Rokhinson, L.P.; Lyanda-Geller, Y.; Ge, Z.; Shen, S.; Liu, X.; Dobrowolska, M.; Furdyna, J.K. Weak localization in Ga1−xMnxAs: Evidence of impurity band transport. Phys. Rev. B 2007, 76, 161201. [Google Scholar] [CrossRef]
- Dobrowolska, M.; Tivakornsasithorn, K.; Liu, X.; Furdyna, J.K.; Berciu, M.; Yu, K.M.; Walukiewicz, W. Controlling the Curie temperature in (Ga,Mn)As through location of the Fermi level within the impurity band. Nat. Mater. 2012, 11, 444–449. [Google Scholar] [CrossRef] [PubMed]
- Sawicki, M.; Chiba, D.; Korbecka, A.; Nishitani, Y.; Majewski, J.; Matsukura, F.; Dielt, T.; Ohno, H. Experimental probing of interplay between ferromagnetism and localization in (Ga,Mn)As. Nat. Phys. 2010, 6, 22. [Google Scholar] [CrossRef]
- Flatte, M.E. Dilute magnetic semiconductors: Hidden order revealed. Nat. Phys. 2011, 7, 285–286. [Google Scholar] [CrossRef]
- Samarth, N. Ferromagnetic semiconductors: Battle of the bands. Nat. Mater. 2012, 11, 360–361. [Google Scholar] [CrossRef] [PubMed]
- Luque, A.; Martí, A. A metallic intermediate band high efficiency solar cell. Prog. Photovolt. Res. Appl. 2001, 9, 73–86. [Google Scholar] [CrossRef]
- Okada, Y.; Ekins-Daukes, N.J.; Kita, T.; Tamaki, R.; Yoshida, M.; Pusch, A.; Hess, O.; Phillips, C.C.; Farrell, D.J.; Yoshida, K.; et al. Intermediate band solar cells: Recent progress and future directions. Appl. Phys. Rev. 2015, 2, 021302. [Google Scholar] [CrossRef]
- Zhang, J.; He, H.; Pan, B. Fe/Co doped molybdenum diselenide: A promising two-dimensional intermediate-band photovoltaic material. Nanotechnology 2015, 26, 195401. [Google Scholar] [CrossRef] [PubMed]
- Manley, M.; Lynn, J.; Abernathy, D.; Specht, E.; Delaire, O.; Bishop, A.; Sahul, R.; Budai, J. Phonon localization drives polar nanoregions in a relaxor ferroelectric. Nat. Commun. 2014, 5, 3683. [Google Scholar] [CrossRef] [PubMed]
- Anderson, P.W.; Mott, N.F.; van Vleck, J.H. The Nobel Prize in Physics 1977. Available online: https://www.nobelprize.org/nobel_prizes/physics/laureates/1977/ (accessed on 10 November 2018).
- Lagendijk, A.; van Tiggelen, B.; Wiersma, D.S. Fifty years of Anderson localization. Phys. Today 2009, 62, 24–29. [Google Scholar] [CrossRef]
- Abrahams, E. (Ed.) 50 Years of Anderson Localization; World Scientific: Singapore, 2010. [Google Scholar]
- Kramer, B.; MacKinnon, A.; Ohtsuki, T.; Slevin, K. Finite size scaling analysis of the anderson transition. Int. J. Mod. Phys. B 2010, 24, 1841. [Google Scholar] [CrossRef]
- Markos, P. Numerical Analysis of the Anderson Localization. Acta Phys. Slovaca 2006, 56, 561–685. [Google Scholar] [CrossRef]
- Kramer, B.; MacKinnon, A. Localization: Theory and experiment. Rep. Prog. Phys. 1993, 56, 1469. [Google Scholar] [CrossRef]
- Weiße, A.; Wellein, G.; Alvermann, A.; Fehske, H. The kernel polynomial method. Rev. Mod. Phys. 2006, 78, 275–306. [Google Scholar] [CrossRef]
- Vollhardt, D. Dynamical Mean-Field Theory of Electronic Correlations in Models and Materials. AIP Conf. Proc. 2010, 1297, 339–403. [Google Scholar]
- Jarrell, M.; Akhlaghpour, H.; Pruschke, T. The Periodic Anderson Model in Infinite Dimensions. Phys. Rev. Lett. 1993, 70, 1670–1673. [Google Scholar] [CrossRef] [PubMed]
- Freericks, J.K.; Jarrell, M.; Scalapino, D.J. Holstein model in infinite dimensions. Phys. Rev. B 1993, 48, 6302–6314. [Google Scholar] [CrossRef]
- Maier, T.; Jarrell, M.; Pruschke, T.; Hettler, M.H. Quantum cluster theories. Rev. Mod. Phys. 2005, 77, 1027–1080. [Google Scholar] [CrossRef]
- Kotliar, G.; Savrasov, S.; Palsson, G.; Biroli, G. Cellular Dynamical Mean Field Approach to Strongly Correlated Systems. Phys. Rev. Lett. 2001, 87, 186401. [Google Scholar] [CrossRef]
- Jarrell, M.; Pruschke, T. The Magnetic and Dynamic Properties of the Hubbard Model in Infinite Dimensions. Z. Phys. B. 1993, 90, 187–194. [Google Scholar] [CrossRef]
- Maier, T.; Jarrell, M.; Schulthess, T.; Kent, P.; White, J. A systematic study of superconductivity in the 2D repulsive Hubbard model. Phys. Rev. Lett. 2005, 95, 237001. [Google Scholar] [CrossRef] [PubMed]
- Yonezawa, F.; Morigaki, K. Coherent Potential Approximation. Basic concepts and applications. Suppl. Prog. Theor. Phys. 1973, 53, 1. [Google Scholar] [CrossRef]
- Ziman, J.M. Models of Disorder; Cambridge University Press: New York, NY, USA, 1979. [Google Scholar]
- Taylor, D. Vibrational Properties of Imperfect Crystals with Large Defect Concentrations. Phys. Rev. 1967, 156, 1017–1029. [Google Scholar] [CrossRef]
- Györffy, B. Coherent-Potential Approximation for a Nonoverlapping-Muffin-Tin-Potential Model of Random Substitutional Alloys. Phys. Rev. B 1972, 5, 2382. [Google Scholar] [CrossRef]
- Johnson, D.; Nicholson, D.; Pinski, F.; Gyorffy, B.; Stocks, G. Density-Functional Theory for Random Alloys: Total Energy within the Coherent-Potential Approximation. Phys. Rev. Lett. 1986, 56, 2088–2091. [Google Scholar] [CrossRef] [PubMed]
- Vitos, L.; Abrikosov, I.A.; Johansson, B. Anisotropic Lattice Distortions in Random Alloys from First-Principles Theory. Phys. Rev. Lett. 2001, 87, 156401. [Google Scholar] [CrossRef] [PubMed]
- Singh, P.P.; Gonis, A.; Turchi, P.E.A. Toward a unified approach to the study of metallic alloys: Application to the phase stability of Ni-Pt. Phys. Rev. Lett. 1993, 71, 1605–1608. [Google Scholar] [CrossRef] [PubMed]
- Faulkner, J.S. The modern theory of alloys. Prog. Mater. Sci. 1982, 27, 1. [Google Scholar] [CrossRef]
- Johnson, D.D.; Pinski, F.J. Inclusion of charge correlations in calculations of the energetics and electronic structure for random substitutional alloys. Phys. Rev. B 1993, 48, 11553–11560. [Google Scholar] [CrossRef]
- Korzhavyi, P.A.; Ruban, A.V.; Abrikosov, I.A.; Skriver, H.L. Madelung energy for random metallic alloys in the coherent potential approximation. Phys. Rev. B 1995, 51, 5773–5780. [Google Scholar] [CrossRef]
- Ruban, A.V.; Abrikosov, I.A.; Skriver, H.L. Ground-state properties of ordered, partially ordered, and random Cu-Au and Ni-Pt alloys. Phys. Rev. B 1995, 51, 12958–12968. [Google Scholar] [CrossRef]
- Györffy, B.L.; Stocks, G.M. Concentration Waves and Fermi Surfaces in Random Metallic Alloys. Phys. Rev. Lett. 1983, 50, 374–377. [Google Scholar] [CrossRef]
- Althoff, J.D.; Johnson, D.D.; Pinski, F.J. Commensurate and Incommensurate Ordering Tendencies in the Ternary fcc Cu-Ni-Zn System. Phys. Rev. Lett. 1995, 74, 138–141. [Google Scholar] [CrossRef] [PubMed]
- Abrikosov, I.A.; Ruban, A.V.; Kats, D.Y.; Vekilov, Y.H. Theory of substitutionally disordered Heisenberg ferromagnets. J. Phys. Condens. Matter 1993, 5, 1271. [Google Scholar] [CrossRef]
- Vitos, L. Computational Quantum Mechanics for Materials Engineers; Springer: London, UK, 2007. [Google Scholar]
- Akai, H.; Dederichs, P.H. Local moment disorder in ferromagnetic alloys. Phys. Rev. B 1993, 47, 8739–8747. [Google Scholar] [CrossRef]
- Turek, I.; Kudrnovský, J.; Drchal, V.; Weinberger, P. Itinerant magnetism of disordered Fe-Co and Ni-Cu alloys in two and three dimensions. Phys. Rev. B 1994, 49, 3352–3362. [Google Scholar] [CrossRef]
- Abrikosov, I.A.; Eriksson, O.; Söderlind, P.; Skriver, H.L.; Johansson, B. Theoretical aspects of the FecNi1−c Invar alloy. Phys. Rev. B 1995, 51, 1058–1063. [Google Scholar] [CrossRef]
- Kudrnovský, J.; Turek, I.; Drchal, V.; Weinberger, P.; Christensen, N.E.; Bose, S.K. Self-consistent Green’s-function method for random overlayers. Phys. Rev. B 1992, 46, 4222–4228. [Google Scholar] [CrossRef]
- MacLaren, J.M.; Gonis, A.; Schadler, G. First-principles calculation of stacking-fault energies in substitutionally disordered alloys. Phys. Rev. B 1992, 45, 14392–14395. [Google Scholar] [CrossRef]
- Abrikosov, I.A.; Skriver, H.L. Self-consistent linear-muffin-tin-orbitals coherent-potential technique for bulk and surface calculations: Cu-Ni, Ag-Pd, and Au-Pt random alloys. Phys. Rev. B 1993, 47, 16532–16541. [Google Scholar] [CrossRef]
- Ruban, A.V.; Abrikosov, I.A.; Kats, D.Y.; Gorelikov, D.; Jacobsen, K.W.; Skriver, H.L. Self-consistent electronic structure and segregation profiles of the Cu-Ni (001) random-alloy surface. Phys. Rev. B 1994, 49, 11383–11396. [Google Scholar] [CrossRef]
- Pasturel, A.; Drchal, V.; Kudrnovský, J.; Weinberger, P. First-principles study of surface segregation in Cu-Ni alloys. Phys. Rev. B 1993, 48, 2704–2710. [Google Scholar] [CrossRef]
- Minár, J.; Ebert, H.; Chioncel, L. A self-consistent, relativistic implementation of the LSDA+DMFT method. Eur. Phys. J. Spec. Top. 2017, 226, 2477–2498. [Google Scholar] [CrossRef]
- Marzari, N.; Vanderbilt, D. Maximally localized generalized Wannier functions for composite energy bands. Phys. Rev. B 1997, 56, 12847–12865. [Google Scholar] [CrossRef]
- Ku, W.; Rosner, H.; Pickett, W.E.; Scalettar, R.T. Insulating Ferromagnetism in La4Ba2Cu2O10: An Ab Initio Wannier Function Analysis. Phys. Rev. Lett. 2002, 89, 167204. [Google Scholar] [CrossRef] [PubMed]
- Anisimov, V.I.; Kondakov, D.; Kozhevnikov, A.V.; Nekrasov, I.; Pchelkina, Z.; Allen, J.; Mo, S.K.; Kim, H.; Metcalf, P.; Suga, S.; et al. Full orbital calculation scheme for materials with strongly correlated electrons. Phys. Rev. B 2005, 71, 125119. [Google Scholar] [CrossRef]
- Gonis, A. Green Functions for Ordered and Disordered Systems; North-Holland: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Kotliar, G.; Savrasov, S.Y.; Haule, K.; Oudovenko, V.S.; Parcollet, O.; Marianetti, C.A. Electronic structure calculations with dynamical mean-field theory. Rev. Mod. Phys. 2006, 78, 865–951. [Google Scholar] [CrossRef]
- Bergmann, G. Weak localization in thin films: A time-of-flight experiment with conduction electrons. Phys. Rep. 1984, 107, 1–58. [Google Scholar] [CrossRef]
- Langer, J.S. Theory of Impurity Resistance in Metals. Phys. Rev. 1960, 120, 714–725. [Google Scholar] [CrossRef]
- Langer, J.S.; Neal, T. Breakdown of the Concentration Expansion for the Impurity Resistivity of Metals. Phys. Rev. Lett. 1966, 16, 984–986. [Google Scholar] [CrossRef]
- Dobrosavljević, V. Typical medium theory of Mott-Anderson localization. Int. J. Mod. Phys. B 2010, 24, 1680–1726. [Google Scholar] [CrossRef]
- Mott, N. Electrons in disordered structures. Adv. Phys. 1967, 16, 49–144. [Google Scholar] [CrossRef]
- Cohen, M.H.; Fritzsche, H.; Ovshinsky, S.R. Simple Band Model for Amorphous Semiconducting Alloys. Phys. Rev. Lett. 1969, 22, 1065–1068. [Google Scholar] [CrossRef]
- Economou, E.N.; Cohen, M.H. Existence of Mobility Edges in Anderson’s Model for Random Lattices. Phys. Rev. B 1972, 5, 2931–2948. [Google Scholar] [CrossRef]
- Edwards, J.T.; Thouless, D.J. Numerical studies of localization in disordered systems. J. Phys. C: Solid State Phys. 1972, 5, 807. [Google Scholar] [CrossRef]
- Licciardello, D.C.; Thouless, D.J. Constancy of Minimum Metallic Conductivity in Two Dimensions. Phys. Rev. Lett. 1975, 35, 1475–1478. [Google Scholar] [CrossRef]
- Abrahams, E.; Anderson, P.W.; Licciardello, D.C.; Ramakrishnan, T.V. Scaling Theory of Localization: Absence of Quantum Diffusion in Two Dimensions. Phys. Rev. Lett. 1979, 42, 673. [Google Scholar] [CrossRef]
- Gor’kov, L.P.; Larkin, A.I.; Khmel’nitskii, D.E. Particle Conductivity in a two-dimensonal random potential. JETP 1979, 30, 248–252. [Google Scholar]
- Aharony, A.; Imry, Y. The mobility edge as a spin-glass problem. J. Phys. C Solid State Phys. 1977, 10, L487. [Google Scholar] [CrossRef]
- Wegner, F. The mobility edge problem: Continuous symmetry and a conjecture. Z. Phys. B Condens. Matter 1979, 35, 207–210. [Google Scholar] [CrossRef]
- Wegner, F. Inverse participation ratio in 2+ϵ dimensions. Z. Phys. B Condens. Matter 1980, 36, 209–214. [Google Scholar]
- Schäfer, L.; Wegner, F. Disordered system withn orbitals per site: Lagrange formulation, hyperbolic symmetry, and goldstone modes. Z. Phys. B Condens. Matter 1980, 38, 113–126. [Google Scholar] [CrossRef]
- Castellani, C.; Peliti, L. Multifractal wavefunction at the localisation threshold. J. Phys. A Math. Gener. 1986, 19, L429. [Google Scholar] [CrossRef]
- Hikami, S.; Larkin, A.I.; Nagaoka, Y. Spin-Orbit Interaction and Magnetoresistance in the Two Dimensional Random System. Prog. Theor. Phys. 1980, 63, 707–710. [Google Scholar] [CrossRef]
- Efetov, K.B. Supersymmetry method in localization theory. JETP 1982, 82, 872–887. [Google Scholar]
- Vollhardt, D.; Wölfle, P. Diagrammatic, self-consistent treatment of the Anderson localization problem in d ≤ 2 dimensions. Phys. Rev. B 1980, 22, 4666–4679. [Google Scholar] [CrossRef]
- Vollhardt, D.; Wölfle, P. Chapter 1. Self-Consistent Theory of Anderson Localization. In Electronic Phase Transitions; Modern Problems in Condensed Matter Sciences; Hanke, W., Kopaev, Y., Eds.; Elsevier: Amsterdam, The Netherlands, 1992; Volume 32, pp. 1–78. [Google Scholar]
- Vollhardt, D.; Wölfle, P. Scaling Equations from a Self-Consistent Theory of Anderson Localization. Phys. Rev. Lett. 1982, 48, 699–702. [Google Scholar] [CrossRef]
- Altland, A.; Zirnbauer, M.R. Nonstandard symmetry classes in mesoscopic normal-superconducting hybrid structures. Phys. Rev. B 1997, 55, 1142–1161. [Google Scholar] [CrossRef]
- Schnyder, A.P.; Ryu, S.; Furusaki, A.; Ludwig, A.W.W. Classification of topological insulators and superconductors in three spatial dimensions. Phys. Rev. B 2008, 78, 195125. [Google Scholar] [CrossRef]
- Chiu, C.K.; Teo, J.C.Y.; Schnyder, A.P.; Ryu, S. Classification of topological quantum matter with symmetries. Rev. Mod. Phys. 2016, 88, 035005. [Google Scholar] [CrossRef]
- Zirnbauer, M.R. Localization transition on the Bethe lattice. Phys. Rev. B 1986, 34, 6394–6408. [Google Scholar] [CrossRef]
- Efetov, K.B. Density-density correlator in a model of a disordered metal on a Bethe lattice. JETP 1987, 65, 360. [Google Scholar]
- Mirlin, A.D.; Fyodorov, Y.V. Distribution of local densities of states, order parameter function, and critical behavior near the Anderson transition. Phys. Rev. Lett. 1994, 72, 526–529. [Google Scholar] [CrossRef] [PubMed]
- Schubert, G.; Schleede, J.; Byczuk, K.; Fehske, H.; Vollhardt, D. Distribution of the local density of states as a criterion for Anderson localization: Numerically exact results for various lattices in two and three dimensions. Phys. Rev. B 2010, 81, 155106. [Google Scholar] [CrossRef]
- Thomas, L.H. The calculation of atomic fields. Math. Proc. Camb. Philos. Soc. 1927, 23, 542. [Google Scholar] [CrossRef]
- Fermi, E. Eine statistische Methode zur Bestimmung einiger Eigenschaften des Atoms und ihre Anwendung auf die Theorie des periodischen Systems der Elemente. Z. Phys. 1928, 48, 73–79. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Note on Exchange Phenomena in the Thomas Atom. Math. Proc. Camb. Philos. Soc. 1930, 26, 376–385. [Google Scholar] [CrossRef]
- Ibach, H.; Lüth, H. Solid-State Physics: An Introduction to Principles of Materials Science; Advanced Texts in Physics; Springer: Berlin/Heidelberg, Germnay, 2009. [Google Scholar]
- Mott, N.F. The Basis of the Electron Theory of Metals, with Special Reference to the Transition Metals. Proc. Phys. Soc. Sect. A 1949, 62, 416. [Google Scholar] [CrossRef]
- Li, Y.; Luo, X.; Kröger, H. Bound states and critical behavior of the Yukawa potential. Sci. China Ser. G 2006, 49, 60–71. [Google Scholar] [CrossRef]
- Pergament, A.; Stefanovich, G.; Markova, N. The Mott criterion: So simple and yet so complex. arXiv, 2014; arXiv:cond-mat.str-el/1411.4372. [Google Scholar]
- Kravchenko, S.V.; Mason, W.E.; Bowker, G.E.; Furneaux, J.E.; Pudalov, V.M.; D’Iorio, M. Scaling of an anomalous metal-insulator transition in a two-dimensional system in silicon at B=0. Phys. Rev. B 1995, 51, 7038–7045. [Google Scholar] [CrossRef]
- Kravchenko, S.V.; Kravchenko, G.V.; Furneaux, J.E.; Pudalov, V.M.; D’Iorio, M. Possible metal-insulator transition at B=0 in two dimensions. Phys. Rev. B 1994, 50, 8039–8042. [Google Scholar] [CrossRef]
- Radonjić, M.c.v.M.; Tanasković, D.; Dobrosavljević, V.; Haule, K. Influence of disorder on incoherent transport near the Mott transition. Phys. Rev. B 2010, 81, 075118. [Google Scholar] [CrossRef]
- Radonjić, M.M.; Tanasković, D.; Dobrosavljević, V.; Haule, K.; Kotliar, G. Wigner-Mott scaling of transport near the two-dimensional metal-insulator transition. Phys. Rev. B 2012, 85, 085133. [Google Scholar] [CrossRef]
- Finkel’stein, A.M. Spin fluctuations in disordered systems near the metal-insulator transition. JETP Lett. 1984, 40, 796. [Google Scholar]
- Finkel’stein, A.M. Metal-insulator transiton in a disordered system. JETP 1984, 59, 212. [Google Scholar]
- Finkel’stein, A.M. Weak localization and coulomb interaction in disordered systems. Z. Phys. B Condens. Matter 1984, 56, 189–196. [Google Scholar] [CrossRef]
- Finkl’stein, A.M. Influence of Coulomb interaction on the properties of disordered metals. JETP 1983, 57, 97. [Google Scholar]
- Lee, P.A.; Ramakrishnan, T.V. Disordered electronic systems. Rev. Mod. Phys. 1985, 57, 287–337. [Google Scholar] [CrossRef]
- Belitz, D.; Kirkpatrick, T.R. Critical behavior of the density of states at the metal-insulator transition. Phys. Rev. B 1993, 48, 14072–14079. [Google Scholar] [CrossRef]
- Castellani, C.; Di Castro, C.; Lee, P.A.; Ma, M. Interaction-driven metal-insulator transitions in disordered fermion systems. Phys. Rev. B 1984, 30, 527–543. [Google Scholar] [CrossRef]
- Aguiar, M.C.O.; Dobrosavljević, V.; Abrahams, E.; Kotliar, G. Critical Behavior at the Mott-Anderson Transition: A Typical-Medium Theory Perspective. Phys. Rev. Lett. 2009, 102, 156402. [Google Scholar] [CrossRef] [PubMed]
- Byczuk, K.; Hofstetter, W.; Vollhardt, D. Mott-Hubbard Transition versus Anderson Localization in Correlated Electron Systems with Disorder. Phys. Rev. Lett. 2005, 94, 056404. [Google Scholar] [CrossRef] [PubMed]
- Byczuk, K.; Hofsletter, W.; Yu, U.; Vollhardt, D. Correlated electrons in the presence of disoder. Eur. Phys. J. Spec. Top. 2009, 180, 135–151. [Google Scholar] [CrossRef]
- Derrida, B.; Gardner, E. Lyapounov exponent of the one dimensional Anderson model: Weak disorder expansions. J. Phys. Fr. 1984, 45, 1283–1295. [Google Scholar] [CrossRef]
- Oseledets, V.I. A multiplicative ergodic theorem. Characteristic Ljapunov, exponents of dynamical systems. Tr. Mosk. Mat. Obs. 1968, 19, 179–210. [Google Scholar]
- Pichard, J.L. The one-dimensional Anderson model: Scaling and resonances revisited. J. Phys. C Solid State Phys. 1986, 19, 1519. [Google Scholar] [CrossRef]
- Furstenberg, H. Non-commuting random products. Trans. Am. Math. Soc. 1963, 108, 377–428. [Google Scholar] [CrossRef]
- MacKinnon, A.; Kramer, B. The scaling theory of electrons in disordered solids: Additional numerical results. Z. Phys. B Condens. Matter 1983, 53, 1–13. [Google Scholar] [CrossRef]
- Furstenberg, H.; Kesten, H. Products of random matrices. Ann. Math. Stat. 1960, 31, 457–469. [Google Scholar] [CrossRef]
- Pichard, J.L.; Sarma, G. Finite size scaling approach to Anderson localisation. J. Phys. C Solid State Phys. 1981, 14, L127. [Google Scholar] [CrossRef]
- Wang, L.W. Calculating the density of states and optical-absorption spectra of large quantum systems by the plane-wave moments method. Phys. Rev. B 1994, 49, 10154–10158. [Google Scholar] [CrossRef]
- Silver, R.; Röder, H. Densities of states of mega-dimensional hamiltonian matrices. Int. J. Mod. Phys. C 1994, 5, 735–753. [Google Scholar] [CrossRef]
- Silver, R.; Roeder, H.; Voter, A.; Kress, J. Kernel Polynomial Approximations for Densities of States and Spectral Functions. J. Comput. Phys. 1996, 124, 115–130. [Google Scholar] [CrossRef]
- Silver, R.N.; Röder, H. Calculation of densities of states and spectral functions by Chebyshev recursion and maximum entropy. Phys. Rev. E 1997, 56, 4822–4829. [Google Scholar] [CrossRef]
- Jackson, D. The theory of approximation. J. Appl. Math. Mech. 1930, 11, 77. [Google Scholar]
- Lancoz, C. An iteration method for the solution of the eigenvalue problem of linear differential and integral operators. J. Res. Natl. Bur. Std. 1950, 45, 255–282. [Google Scholar]
- Arnoldi, W.E. The principle of minimized iterations in the solution of the matrix eigenvalue problem. Q. Appl. Math. 1951, 9, 17–29. [Google Scholar] [CrossRef]
- Lin, H.; Gubernatis, J. Exact Diagonalization Methods for Quantum Systems. Comput. Phys. 1993, 7, 400–407. [Google Scholar] [CrossRef]
- Weiße, A.; Fehske, H. Exact Diagonalization Techniques. In Computational Many-Particle Physics; Fehske, H., Schneider, R., Weiße, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 529–544. [Google Scholar]
- Noack, R.M.; Manmana, S.R. Diagonalization- and Numerical Renormalization-Group-Based Methods for Interacting Quantum Systems. AIP Conf. Proc. 2005, 789, 93–163. [Google Scholar]
- Ericsson, T.; Ruhe, A. The spectral transformation Lanczos Method for the numerical solution of large sparse generalized symmetric eigenvalue problems. Math. Comp. 1980, 35, 1251–1268. [Google Scholar]
- Kawamura, M.; Yoshimi, K.; Misawa, T.; Yamaji, Y.; Todo, S.; Kawashima, N. Quantum lattice model solver HΦ. Comput. Phys. Commun. 2017, 217, 180–192. [Google Scholar] [CrossRef]
- Davidson, E.R. The iterative calculation of a few of the lowest eigenvalues and corresponding eigenvectors of large real-symmetric matrices. J. Comput. Phys. 1975, 17, 87–94. [Google Scholar] [CrossRef]
- Dupont, T.; Kendall, R.; Rachford, H., Jr. An Approximate Factorization Procedure for Solving Self-Adjoint Elliptic Difference Equations. SIAM J. Numer. Anal. 1968, 5, 559–573. [Google Scholar] [CrossRef]
- Meijerink, J.A.; van der Vorst, H.A. An Iterative Solution Method for Linear Systems of Which the Coefficient Matrix is a Symmetric M-Matrix. Math. Comput. 1977, 31, 148–162. [Google Scholar]
- Bollhöfer, M.; Notay, Y. JADAMILU: A software code for computing selected eigenvalues of large sparse symmetric matrices. Comput. Phys. Commun. 2007, 177, 951–964. [Google Scholar] [CrossRef]
- Rodriguez, A.; Vasquez, L.J.; Slevin, K.; Römer, R.A. Critical Parameters from a Generalized Multifractal Analysis at the Anderson Transition. Phys. Rev. Lett. 2010, 105, 046403. [Google Scholar] [CrossRef] [PubMed]
- Ujfalusi, L.; Varga, I. Finite-size scaling and multifractality at the Anderson transition for the three Wigner-Dyson symmetry classes in three dimensions. Phys. Rev. B 2015, 91, 184206. [Google Scholar] [CrossRef]
- Hubbard, J. Electron Correlations in Narrow Energy Bands. Proc. R. Soc. A 1963, 276, 238–257. [Google Scholar] [CrossRef]
- Anderson, P.W. Present status of the theory of the high-Tc cuprates. Low Temp. Phys. 2006, 32, 282–289. [Google Scholar] [CrossRef]
- Metzner, W.; Vollhardt, D. Ground-state energy of the d=1,2,3 dimensional Hubbard model in the weak-coupling limit. Phys. Rev. B 1989, 39, 4462. [Google Scholar] [CrossRef]
- Jarrell, M.; Pang, H.; Cox, D.; Luk, K. Two-Channel Kondo Lattice: An Incoherent Metal. Phys. Rev. Lett. 1996, 77, 1612–1615. [Google Scholar] [CrossRef] [PubMed]
- Weik, M.H. Nyquist theorem. In Computer Science and Communications Dictionary; Springer: Boston, MA, USA, 2001; p. 1127. [Google Scholar]
- Jarrell, M.; Maier, T.; Huscroft, C.; Moukouri, S. Quantum Monte Carlo algorithm for nonlocal corrections to the dynamical mean-field approximation. Phys. Rev. B 2001, 64, 195130. [Google Scholar] [CrossRef]
- Zlatic, V.; Horvatic, B. The local approximation for correlated systems on high dimensional lattices. Solid State Commun. 1990, 75, 263–267. [Google Scholar] [CrossRef]
- Baym, G.; Kadanoff, L.P. Conservation Laws and Correlation Functions. Phys. Rev. 1961, 124, 287–299. [Google Scholar] [CrossRef]
- Baym, G. Self-Consistent Approximations in Many-Body Systems. Phys. Rev. 1962, 127, 1391–1401. [Google Scholar] [CrossRef]
- Jarrell, M.; Gubernatis, J. Bayesian Inference and the Analytic Continuation of Imaginary-Time Quantum Monte Carlo Data. Phys. Rep. 1996, 269, 133–195. [Google Scholar] [CrossRef]
- Terletska, H.; Yang, S.X.; Meng, Z.Y.; Moreno, J.; Jarrell, M. Dual fermion method for disordered electronic systems. Phys. Rev. B 2013, 87, 134208. [Google Scholar] [CrossRef]
- Rammer, J.; Smith, H. Quantum field-theoretical methods in transport theory of metals. Rev. Mod. Phys. 1986, 58, 323–359. [Google Scholar] [CrossRef]
- Keldysh, L.V. Diagram Technique for Nonequilibrium Processes. JETP 1965, 20, 1018. [Google Scholar]
- Wagner, M. Expansions of nonequilibrium Green’s functions. Phys. Rev. B 1991, 44, 6104–6117. [Google Scholar] [CrossRef]
- Edwards, S.F.; Anderson, P.W. Theory of spin glasses. J. Phys. F Met. Phys. 1975, 5, 965. [Google Scholar] [CrossRef]
- Betts, D.D.; Stewart, G.E. Estimation of zero-temperature properties of quantum spin systems on the simple cubic lattice via exact diagonalization on finite lattices. Can. J. Phys. 1997, 75, 47–66. [Google Scholar] [CrossRef]
- Betts, D.D.; Lin, H.Q.; Flynn, J.S. Improved finite-lattice estimates of the properties of two quantum spin models on the infinite square lattice. Can. J. Phys. 1999, 77, 353–369. [Google Scholar] [CrossRef]
- Kent, P.R.C.; Jarrell, M.; Maier, T.A.; Pruschke, T. Efficient calculation of the antiferromagnetic phase diagram of the 3D Hubbard model. Phys. Rev. B 2005, 72, 060411. [Google Scholar] [CrossRef]
- Ekuma, C.E.; Terletska, H.; Meng, Z.Y.; Moreno, J.; Jarrell, M.; Mahmoudian, S.; Dobrosavljevic, V. Effective cluster typical medium theory for diagonal Anderson disorder model in one- and two-dimensions. J. Phys. Condens. Matter 2014, 26, 274209. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Nelson, R.; Siddiqui, E.; Tam, K.M.; Yu, U.; Berlijn, T.; Ku, W.; Vidhyadhiraja, N.S.; Moreno, J.; Jarrell, M. Generalized multiband typical medium dynamical cluster approximation: Application to (Ga,Mn)N. Phys. Rev. B 2016, 94, 224208. [Google Scholar] [CrossRef]
- Blackman, J.A.; Esterling, D.M.; Berk, N.F. Generalized Locator—Coherent-Potential Approach to Binary Alloys. Phys. Rev. B 1971, 4, 2412–2428. [Google Scholar] [CrossRef]
- Ekuma, C.E.; Terletska, H.; Tam, K.M.; Meng, Z.Y.; Moreno, J.; Jarrell, M. Typical medium dynamical cluster approximation for the study of Anderson localization in three dimensions. Phys. Rev. B 2014, 89, 081107. [Google Scholar] [CrossRef]
- Altshuler, B.; Aronov, A. Zero bias anomaly in tunnel resistance and electron-electron interaction. Solid State Commun. 1979, 30, 115–117. [Google Scholar] [CrossRef]
- Efros, A.L.; Shklovskii, B.I. Coulomb gap and low temperature conductivity of disordered systems. J. Phys. C Solid State Phys. 1975, 8, L49. [Google Scholar] [CrossRef]
- Dobrosavljević, V.; Abrahams, E.; Miranda, E.; Chakravarty, S. Scaling Theory of Two-Dimensional Metal-Insulator Transitions. Phys. Rev. Lett. 1997, 79, 455–458. [Google Scholar] [CrossRef]
- Atland, A.; Simons, B. Condensed Matter Field Thory; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Miranda, E.; Dobrosavljević, V. Dynamical mean-field theories of correlation and disorder. In Conductor-Insulator Quantum Phase Transitions; Dobrosavljevic, V., Trivedi, N., Valles, J., Eds.; Oxford University Press: Oxford, UK, 2013; pp. 161–243. [Google Scholar]
- Galpin, M.R.; Gilbert, A.B.; Logan, D.E. A local moment approach to the degenerate Anderson impurity model. J. Phys. Condens. Matter 2009, 21, 375602. [Google Scholar] [CrossRef] [PubMed]
- Bulla, R.; Costi, T.A.; Pruschke, T. Numerical renormalization group method for quantum impurity systems. Rev. Mod. Phys. 2008, 80, 395–450. [Google Scholar] [CrossRef]
- Gull, E.; Millis, A.J.; Lichtenstein, A.I.; Rubtsov, A.N.; Troyer, M.; Werner, P. Continuous-time Monte Carlo methods for quantum impurity models. Rev. Mod. Phys. 2011, 83, 349–404. [Google Scholar] [CrossRef]
- Assaad, F.F. Exact Diagonalization Techniques. In DMFT at 25: Infinite Dimensions; Pavarini, E., Koch, E., Vollhardt, D., Lichtenstein, A., Eds.; Verlag des Forschungszentrum Jülich: Jurlich, Germany, 2014. [Google Scholar]
- Miranda, E.; Dobrosavljević, V.; Kotliar, G. Kondo disorder: A possible route towards non-Fermi liquid behviour. J. Phys. Condens. Matter 1996, 8, 9871. [Google Scholar] [CrossRef]
- Miranda, E.; Dobrosavljević, V.; Kotliar, G. Disorder-Driven Non-Fermi-Liquid Behavior in Kondo Alloys. Phys. Rev. Lett. 1997, 78, 290–293. [Google Scholar] [CrossRef]
- Chattopadhyay, A.; Jarrell, M.; Krishnamurthy, H.R.; Ng, H.K.; Sarrao, J.; Fisk, Z. Weak magnetoresistance of disordered heavy fermion systems. arXiv, 1998; arXiv:cond-mat/9805127. [Google Scholar]
- Sen, S.; Terletska, H.; Moreno, J.; Vidhyadhiraja, N.S.; Jarrell, M. Local theory for Mott-Anderson localization. Phys. Rev. B 2016, 94, 235104. [Google Scholar] [CrossRef]
- Aguiar, M.C.O.; Dobrosavljević, V.; Abrahams, E.; Kotliar, G. Scaling behavior of an Anderson impurity close to the Mott-Anderson transition. Phys. Rev. B 2006, 73, 115117. [Google Scholar] [CrossRef]
- Sen, S.; Vidhyadhiraja, N.S.; Jarrell, M. Emergence of non-Fermi liquid dynamics through nonlocal correlations in an interacting disordered system. Phys. Rev. B 2018, 98, 075112. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.F.; Yang, S.X.; Tam, K.M.; Vidhyadhiraja, N.S.; Jarrell, M. Calculation of two-particle quantities in the typical medium dynamical cluster approximation. Phys. Rev. B 2017, 95, 144208. [Google Scholar] [CrossRef]
- Terletska, H.; Zhang, Y.; Chioncel, L.; Vollhardt, D.; Jarrell, M. Typical-medium multiple-scattering theory for disordered systems with Anderson localization. Phys. Rev. B 2017, 95, 134204. [Google Scholar] [CrossRef]
- Berlijn, T.; Volja, D.; Ku, W. Can Disorder Alone Destroy the e′g Hole Pockets of NaxCoO2? A Wannier Function Based First-Principles Method for Disordered Systems. Phys. Rev. Lett. 2011, 106, 077005. [Google Scholar] [CrossRef] [PubMed]
- Soler, J.M.; Artacho, E.; Gale, J.D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA method for ab initio order- N materials simulation. J. Phys. Condens. Matter 2002, 14, 2745. [Google Scholar] [CrossRef]
- Junquera, J.; Paz, O.; Sánchez-Portal, D.; Artacho, E. Numerical atomic orbitals for linear-scaling calculations. Phys. Rev. B 2001, 64, 235111. [Google Scholar] [CrossRef]
- Blum, V.; Gehrke, R.; Hanke, F.; Havu, P.; Havu, V.; Ren, X.; Reuter, K.; Scheffler, M. Ab initio molecular simulations with numeric atom-centered orbitals. Comput. Phys. Commun. 2009, 180, 2175–2196. [Google Scholar] [CrossRef]
- Koskinen, P.; Mäkinen, V. Density-functional tight-binding for beginners. Comput. Mater. Sci. 2009, 47, 237–253. [Google Scholar] [CrossRef]
- Van der Ven, A.; Aydinol, M.K.; Ceder, G.; Kresse, G.; Hafner, J. First-principles investigation of phase stability in LixCoO2. Phys. Rev. B 1998, 58, 2975–2987. [Google Scholar] [CrossRef]
- Berlijn, T.; Lin, C.H.; Garber, W.; Ku, W. Do Transition-Metal Substitutions Dope Carriers in Iron-Based Superconductors? Phys. Rev. Lett. 2012, 108, 207003. [Google Scholar] [CrossRef] [PubMed]
- Berlijn, T.; Hirschfeld, P.J.; Ku, W. Effective Doping and Suppression of Fermi Surface Reconstruction via Fe Vacancy Disorder in KxFe2−ySe2. Phys. Rev. Lett. 2012, 109, 147003. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Berlijn, T.; Wang, Y.; Lin, C.H.; Hirschfeld, P.J.; Ku, W. Effects of Disordered Ru Substitution in BaFe2As2: Possible Realization of Superdiffusion in Real Materials. Phys. Rev. Lett. 2013, 110, 037001. [Google Scholar] [CrossRef] [PubMed]
- Berlijn, T.; Cheng, H.P.; Hirschfeld, P.J.; Ku, W. Doping effects of Se vacancies in monolayer FeSe. Phys. Rev. B 2014, 89, 020501. [Google Scholar] [CrossRef]
- Berlijn, T. Effects of Disordered Dopants on the Electronic Structure of Functional Materials: Wannier Function-Based First Principles Methods for Disordered Systems. Ph.D. Thesis, Stony Brook University, Stony Brook, NY, USA, 2011. [Google Scholar]
- Anisimov, V.I.; Gunnarsson, O. Density-functional calculation of effective Coulomb interactions in metals. Phys. Rev. B 1991, 43, 7570–7574. [Google Scholar] [CrossRef]
- Cococcioni, M. The LDA+U Approach: A Simple Hubbard Correction for Correlated Ground States. In Correlated Electrons: From Models to Materials Modeling and Simulation; Verlag des Forschungszentrum Jülich: Jülich, Germany, 2012. [Google Scholar]
- Nelson, R.; Berlijn, T.; Moreno, J.; Jarrell, M.; Ku, W. What is the Valence of Mn in Ga1−xMnxN? Phys. Rev. Lett. 2015, 115, 197203. [Google Scholar] [CrossRef] [PubMed]
- Aryasetiawan, F.; Imada, M.; Georges, A.; Kotliar, G.; Biermann, S.; Lichtenstein, A.I. Frequency-dependent local interactions and low-energy effective models from electronic structure calculations. Phys. Rev. B 2004, 70, 195104. [Google Scholar] [CrossRef]
- Chandrasekharan, S.; Wiese, U.J. Meron-Cluster Solution of Fermion Sign Problems. Phys. Rev. Lett. 1999, 83, 3116–3119. [Google Scholar] [CrossRef]
- Delaire, O.; Al-Qasir, I.I.; May, A.F.; Li, C.W.; Sales, B.C.; Niedziela, J.L.; Ma, J.; Matsuda, M.; Abernathy, D.L.; Berlijn, T. Heavy-impurity resonance, hybridization, and phonon spectral functions in Fe1−xMxSi(M = Ir,Os). Phys. Rev. B 2015, 91, 094307. [Google Scholar] [CrossRef]
- Bulka, B.; Kramer, B.; MacKinnon, A. Mobility edge in the three dimensional Anderson model. Z. Phys. B Condens. Matter 1985, 60, 13–17. [Google Scholar] [CrossRef]
- Slevin, K.; Ohtsuki, T. Critical exponent for the Anderson transition in the three-dimensional orthogonal universality class. New J. Phys. 2014, 16, 015012. [Google Scholar] [CrossRef]
- Terletska, H.; Ekuma, C.E.; Moore, C.; Tam, K.M.; Moreno, J.; Jarrell, M. Study of off-diagonal disorder using the typical medium dynamical cluster approximation. Phys. Rev. B 2014, 90, 094208. [Google Scholar] [CrossRef]
- Weiße, A. Chebyshev expansion approach to the AC conductivity of the Anderson model. Eur. Phys. J. B 2004, 40, 125–128. [Google Scholar] [CrossRef]
- Leconte, N.; Ferreira, A.; Jung, J. Chapter Two—Efficient Multiscale Lattice Simulations of Strained and Disordered Graphene. In 2D Materials; Semiconductors and Semimetals; Francesca Iacopi, J.J.B., Jagadish, C., Eds.; Elsevier: Burlington, ON, Canada, 2016; Volume 95, pp. 35–99. [Google Scholar]
- Garcia, J.H.; Covaci, L.; Rappoport, T.G. Real-Space Calculation of the Conductivity Tensor for Disordered Topological Matter. Phys. Rev. Lett. 2015, 114, 116602. [Google Scholar] [CrossRef] [PubMed]
- Tanasković, D.; Dobrosavljević, V.; Abrahams, E.; Kotliar, G. Disorder Screening in Strongly Correlated Systems. Phys. Rev. Lett. 2003, 91, 066603. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Jin, S.; Wang, G.; Wang, S.; Zhu, K.; Zhou, T.; He, M.; Chen, X. Superconductivity in the iron selenide KxFe2Se2 (0 ≤ x ≤ 1.0). Phys. Rev. B 2010, 82, 180520. [Google Scholar] [CrossRef]
- Wei, B.; Qing-Zhen, H.; Gen-Fu, C.; Green, M.A.; Du-Ming, W.; Jun-Bao, H.; Yi-Ming, Q. A Novel Large Moment Antiferromagnetic Order in K 0.8 Fe 1.6 Se 2 Superconductor. Chin. Phys. Lett. 2011, 28, 086104. [Google Scholar]
- Jungwirth, T.; Sinova, J.; Mavsek, J.; Kuvcera, J.; MacDonald, A.H. Theory of ferromagnetic (III,Mn)V semiconductors. Rev. Mod. Phys. 2006, 78, 809–864. [Google Scholar] [CrossRef]
- Dietl, T.; Ohno, H.; Matsukura, F. Hole-mediated ferromagnetism in tetrahedrally coordinated semiconductors. Phys. Rev. B 2001, 63, 195205. [Google Scholar] [CrossRef]
- Zajac, M.; Gosk, J.; Kamińska, M.; Twardowski, A.; Szyszko, T.; Podsiadlo, S. Paramagnetism and antiferromagnetic d-d coupling in GaMnN magnetic semiconductor. Appl. Phys. Lett. 2001, 79, 2432. [Google Scholar] [CrossRef]
- Dhar, S.; Brandt, O.; Trampert, A.; Friedland, K.J.; Sun, Y.J.; Ploog, K.H. Observation of spin-glass behavior in homogeneous (Ga,Mn)N layers grown by reactive molecular-beam epitaxy. Phys. Rev. B 2003, 67, 165205. [Google Scholar] [CrossRef]
- Overberg, M.E.; Abernathy, C.R.; Pearton, S.J.; Theodoropoulou, N.A.; McCarthy, K.T.; Hebard, A.F. Indication of ferromagnetism in molecular-beam-epitaxy-derived N-type GaMnN. Appl. Phys. Lett. 2001, 79, 1312. [Google Scholar] [CrossRef]
- Stefanowicz, S.; Kunert, G.; Simserides, C.; Majewski, J.A.; Stefanowicz, W.; Kruse, C.; Figge, S.; Li, T.; Jakieła, R.; Trohidou, K.N.; et al. Phase diagram and critical behavior of the random ferromagnet Ga1−xMnxN. Phys. Rev. B 2013, 88, 081201. [Google Scholar] [CrossRef]
- Sasaki, T.; Sonoda, S.; Yamamoto, Y.; Suga, K.I.; Shimizu, S.; Kindo, K.; Hori, H. Magnetic and transport characteristics on high Curie temperature ferromagnet of Mn-doped GaN. J. Appl. Phys. 2002, 91, 7911. [Google Scholar] [CrossRef]
- Li, J.; Chu, R.L.; Jain, J.K.; Shen, S.Q. Topological Anderson Insulator. Phys. Rev. Lett. 2009, 102, 136806. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.M.; Rosenberg, G.; Refael, G.; Franz, M. Topological Anderson Insulator in Three Dimensions. Phys. Rev. Lett. 2010, 105, 216601. [Google Scholar] [CrossRef] [PubMed]















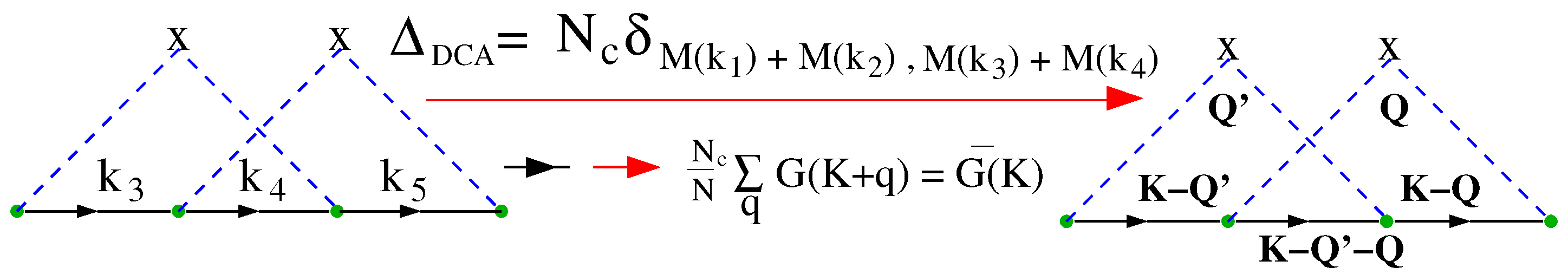


















| System/Ansatz | Characteristics | ODP | VDP |
|---|---|---|---|
| Single Band Local (diagonal) Disorder Ansatz Equation (45) | Recovers TMT at . Recovers DCA for Calculate Hilbert trans. for | 8 | 7 |
| Single Band Local (diagonal) Disorder Ansatz Equation (47) | Not TMT when . Recovers DCA for Calculate directly | 7 | 8 |
| Single Band Off-Diagonal Disorder Ansatz Equation (59) | matrix Calculate matrix HT to get matrix | 8 | 7 |
| Multiband Systems Local Disorder Ansatz Equation (61) | Matrix in orbital space Calculate matrix HT to get matrix Recovers DCA for | 8 | 7 |
| Realistic Material Systems Complex Disorder Potentials with full DFT detail Ansatz Equation (47) | Matrix in orbital space Recovers DCA for | 7 | 8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Terletska, H.; Zhang, Y.; Tam, K.-M.; Berlijn, T.; Chioncel, L.; Vidhyadhiraja, N.S.; Jarrell, M. Systematic Quantum Cluster Typical Medium Method for the Study of Localization in Strongly Disordered Electronic Systems. Appl. Sci. 2018, 8, 2401. https://doi.org/10.3390/app8122401
Terletska H, Zhang Y, Tam K-M, Berlijn T, Chioncel L, Vidhyadhiraja NS, Jarrell M. Systematic Quantum Cluster Typical Medium Method for the Study of Localization in Strongly Disordered Electronic Systems. Applied Sciences. 2018; 8(12):2401. https://doi.org/10.3390/app8122401
Chicago/Turabian StyleTerletska, Hanna, Yi Zhang, Ka-Ming Tam, Tom Berlijn, Liviu Chioncel, N. S. Vidhyadhiraja, and Mark Jarrell. 2018. "Systematic Quantum Cluster Typical Medium Method for the Study of Localization in Strongly Disordered Electronic Systems" Applied Sciences 8, no. 12: 2401. https://doi.org/10.3390/app8122401
APA StyleTerletska, H., Zhang, Y., Tam, K.-M., Berlijn, T., Chioncel, L., Vidhyadhiraja, N. S., & Jarrell, M. (2018). Systematic Quantum Cluster Typical Medium Method for the Study of Localization in Strongly Disordered Electronic Systems. Applied Sciences, 8(12), 2401. https://doi.org/10.3390/app8122401





