A New Rotor Position Measurement Method for Permanent Magnet Spherical Motors
Abstract
:1. Introduction
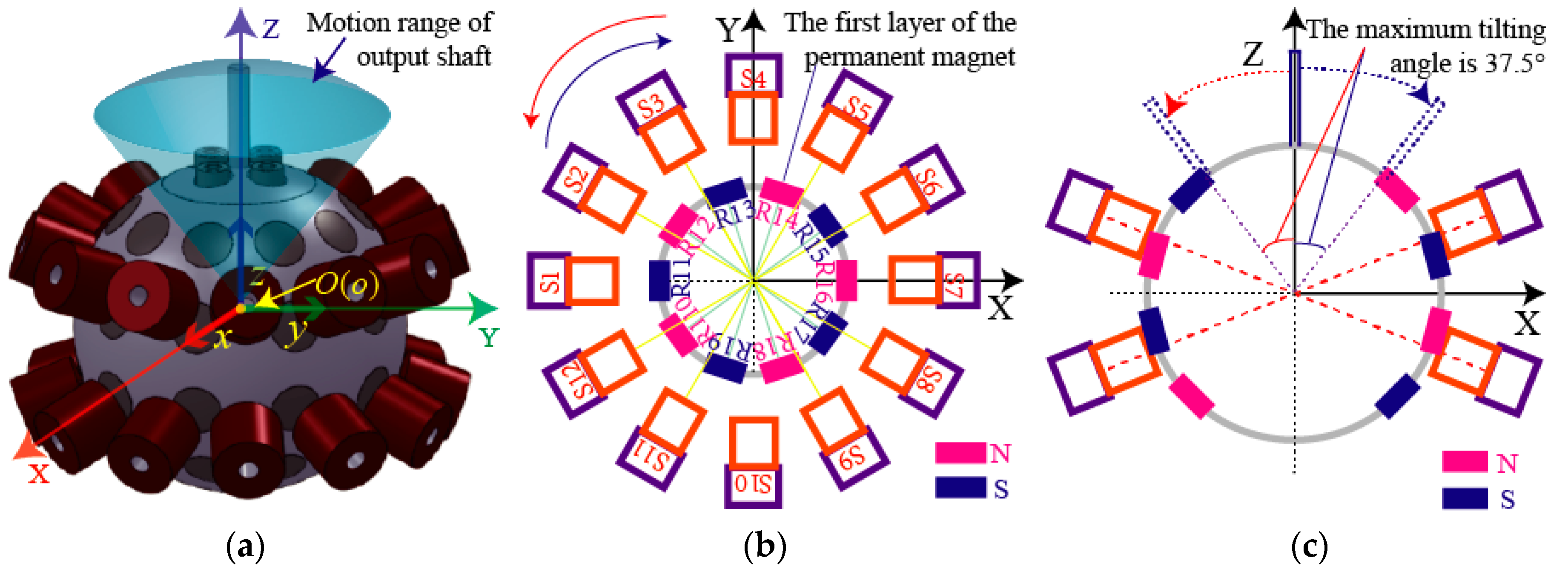
2. Structure of a PMSM
3. Rotor Position Measurement for a PMSM
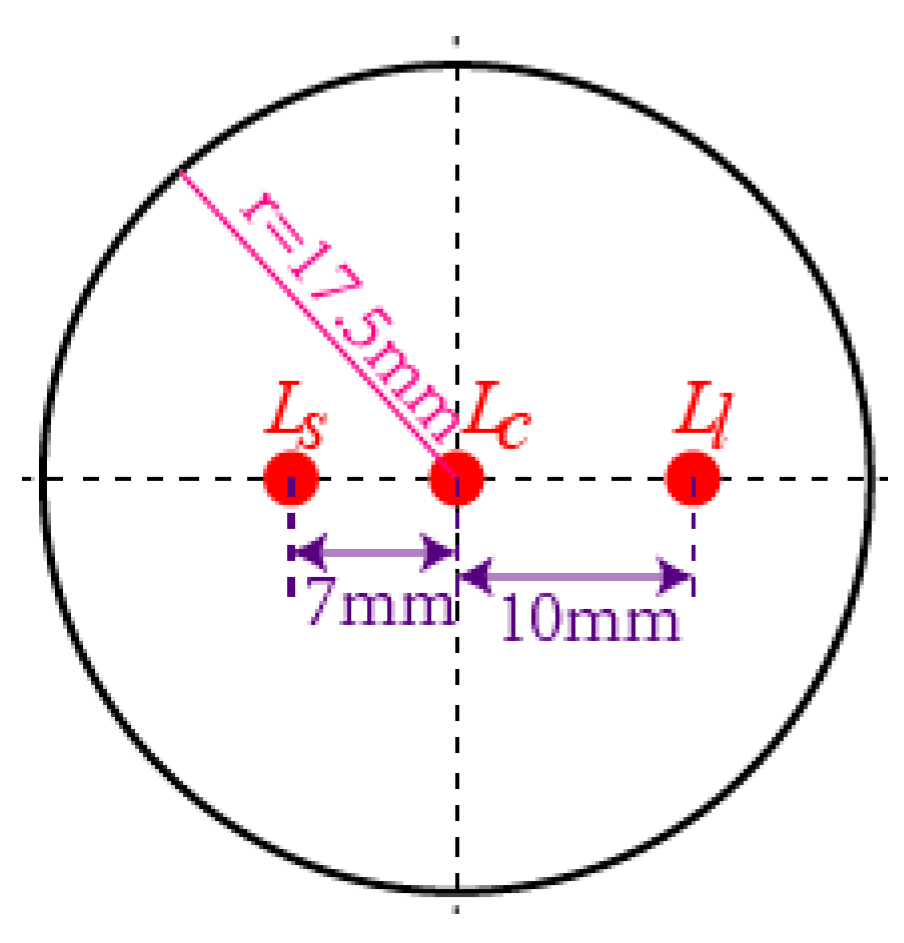
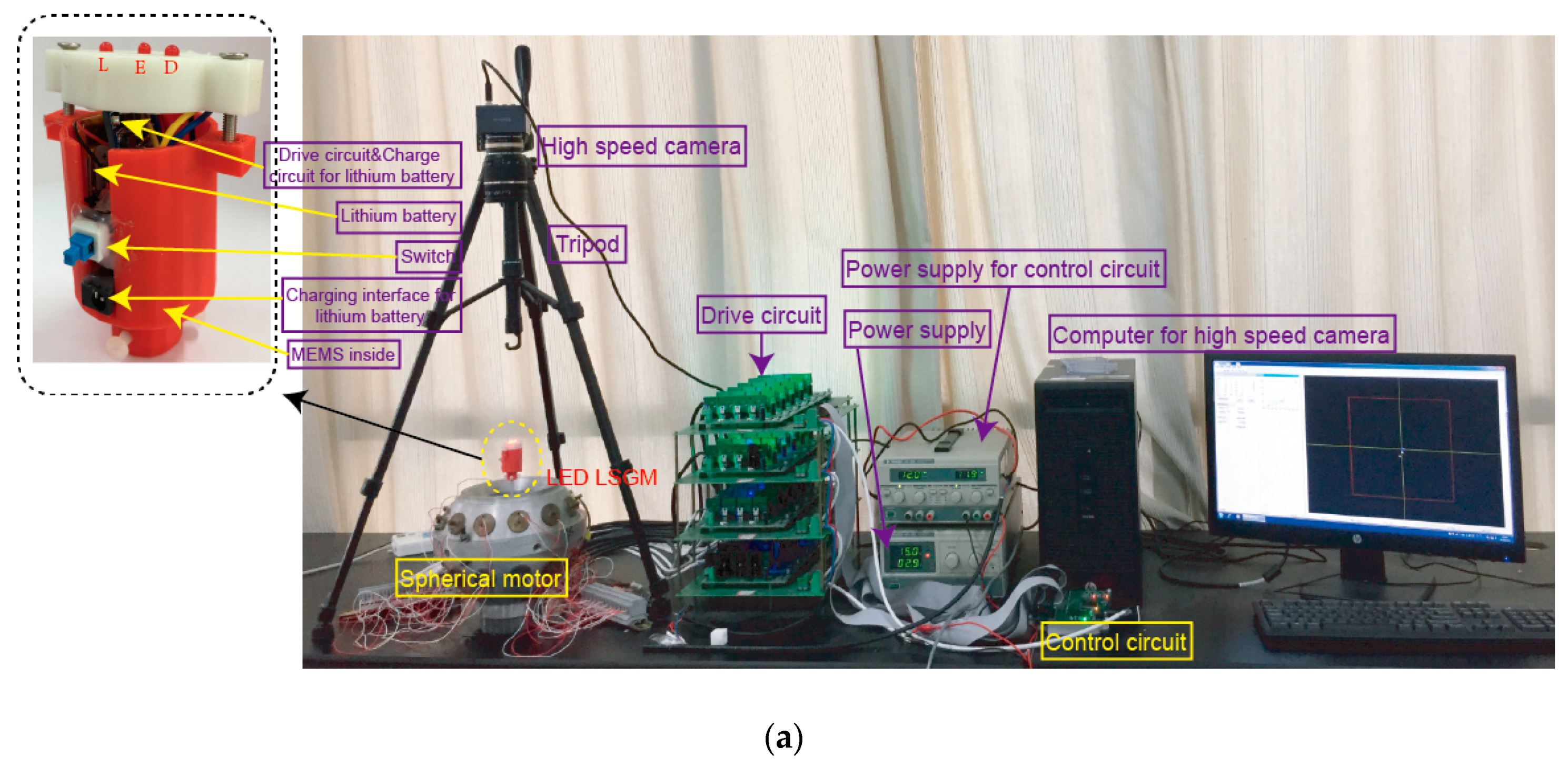
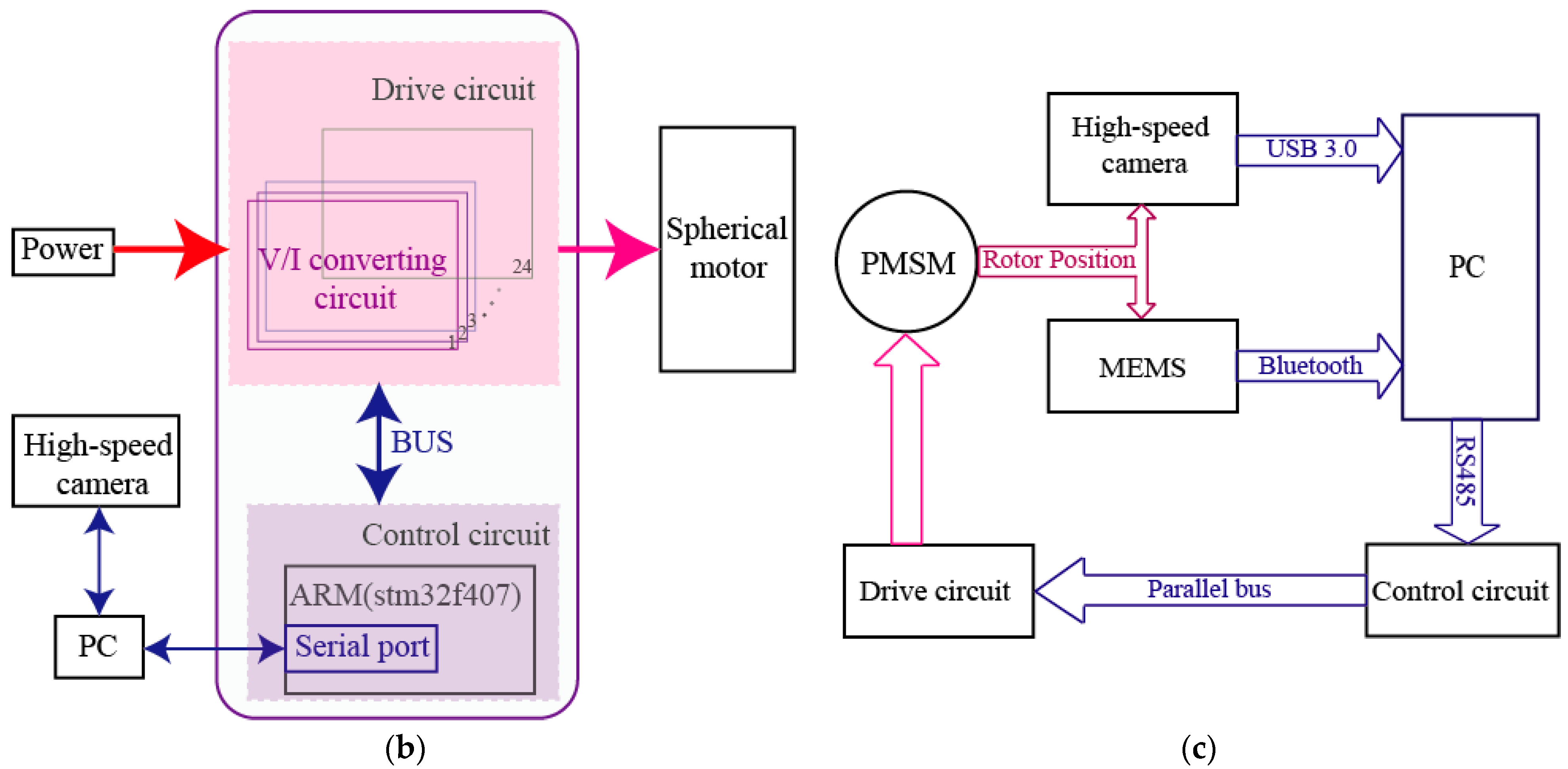
3.1. The Structure of the Measurement Device
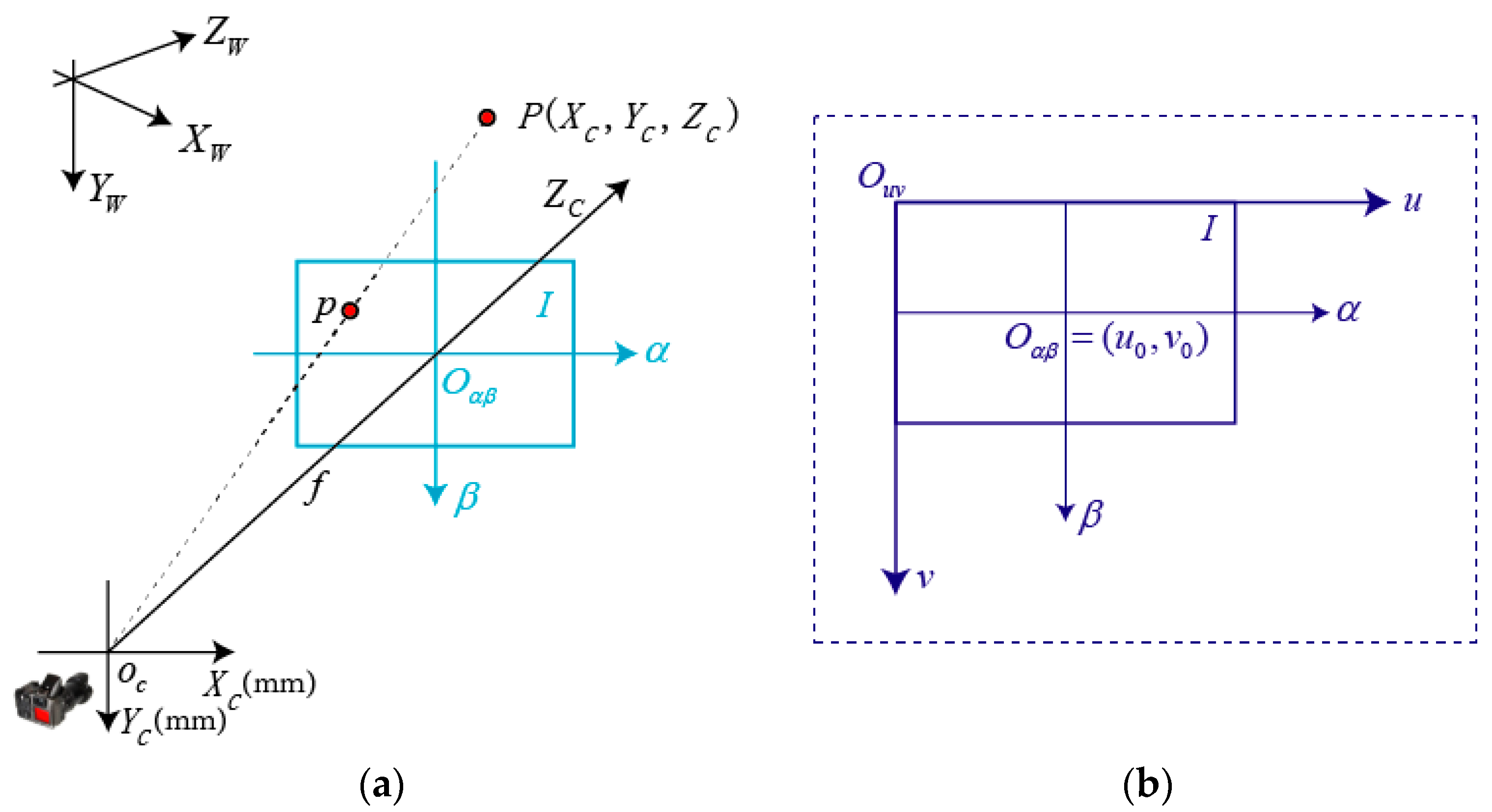
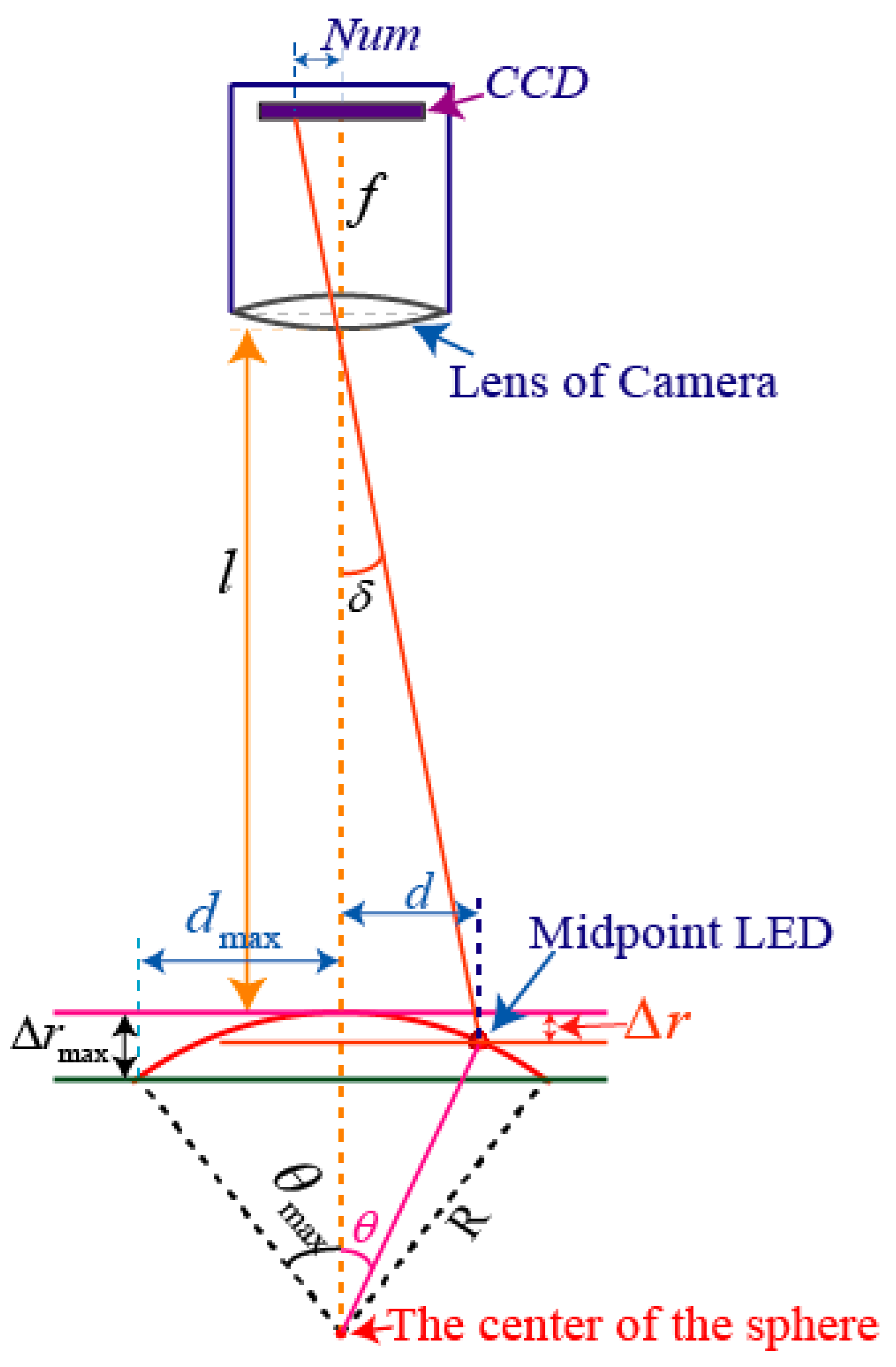
3.2. The Principle of Camera Imaging Based on Pin-Hole Model
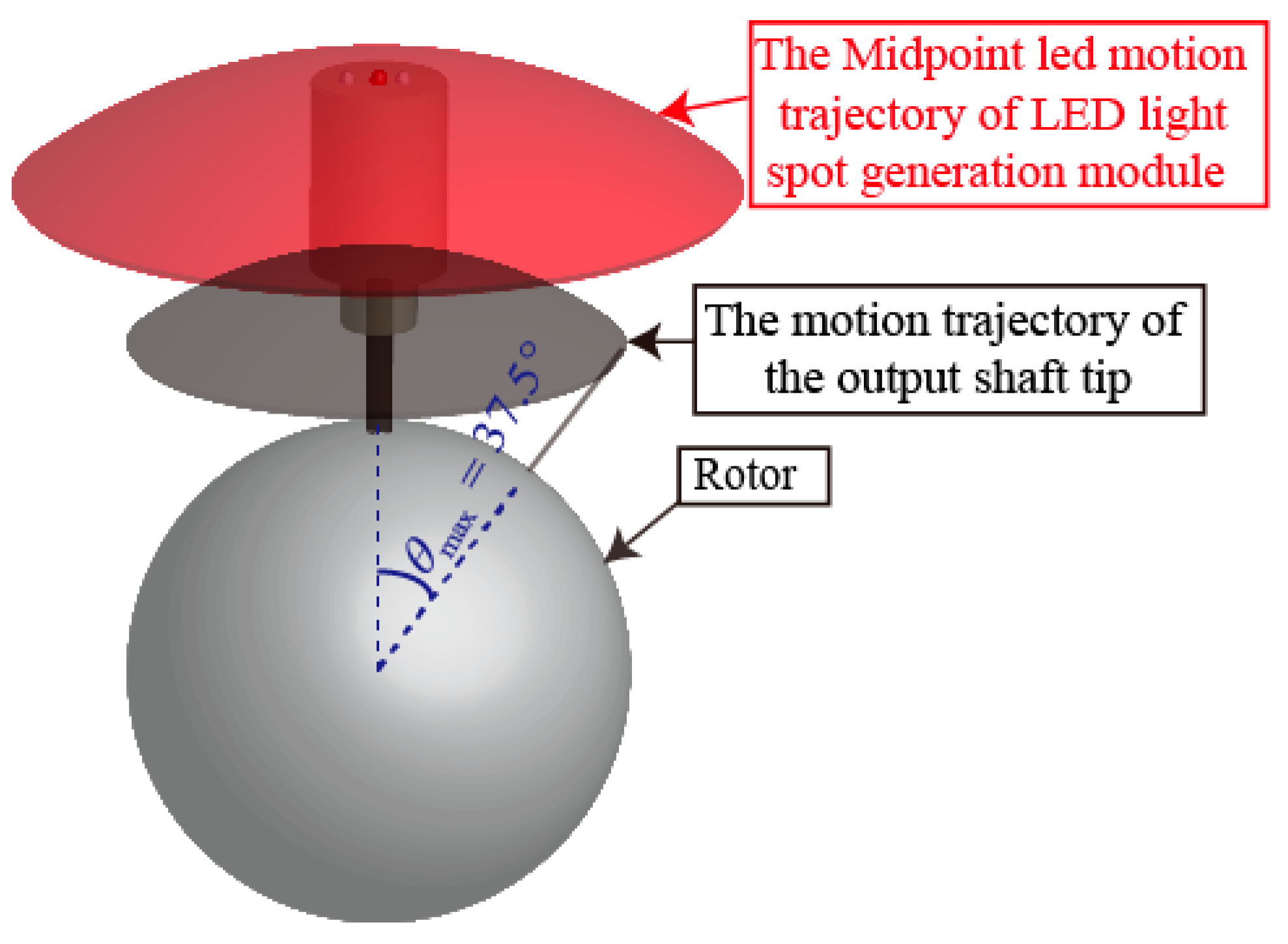
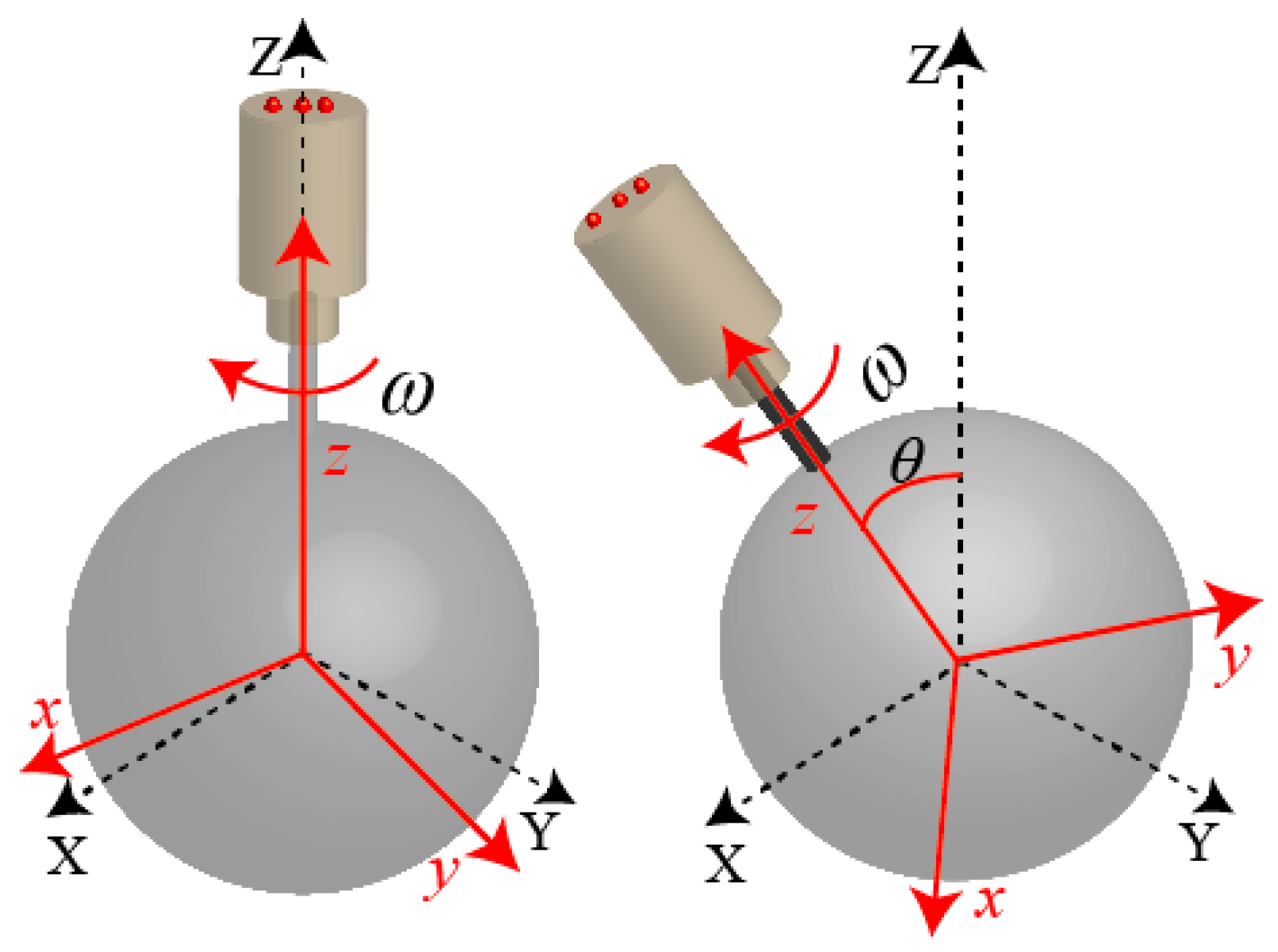
3.3. Analysis of Rotor Motion in a PMSM
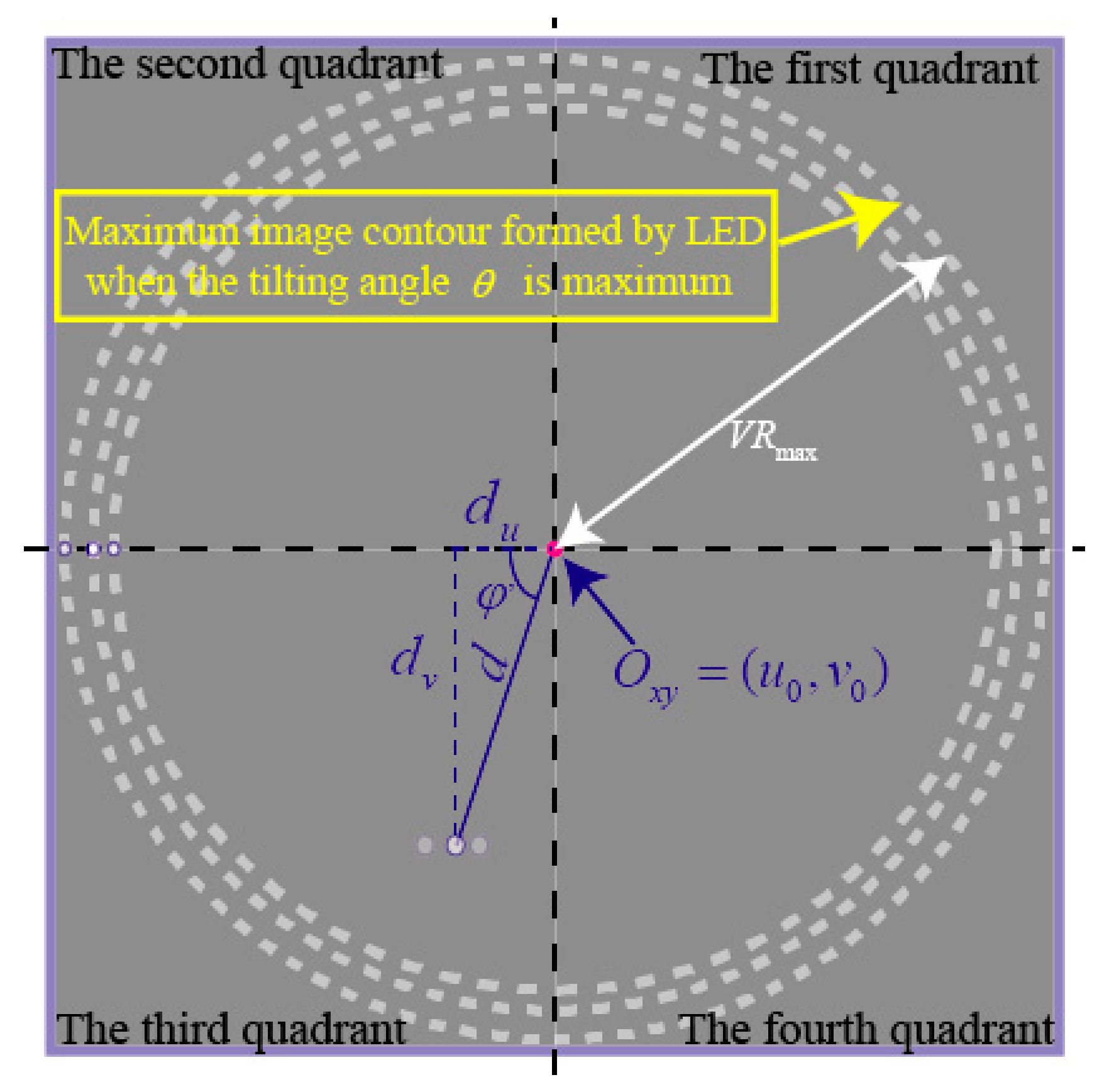
3.3.1. Calculation of the Rotor Position in a PMSM
3.3.2. Calculation of the Tilting angle_
3.3.3. Calculation of the Yaw angle_
3.3.4. Calculation of the Spinning angle_
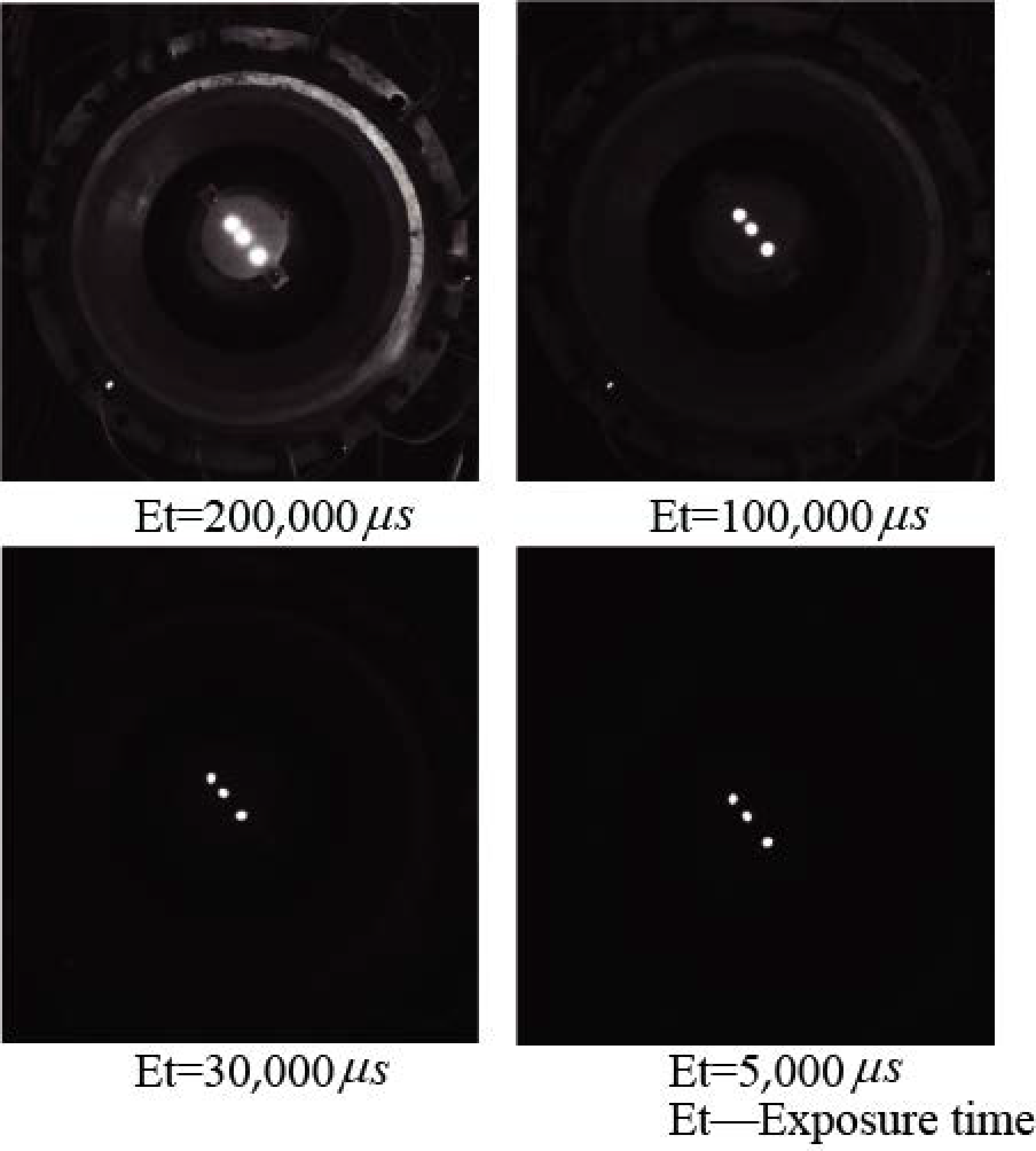
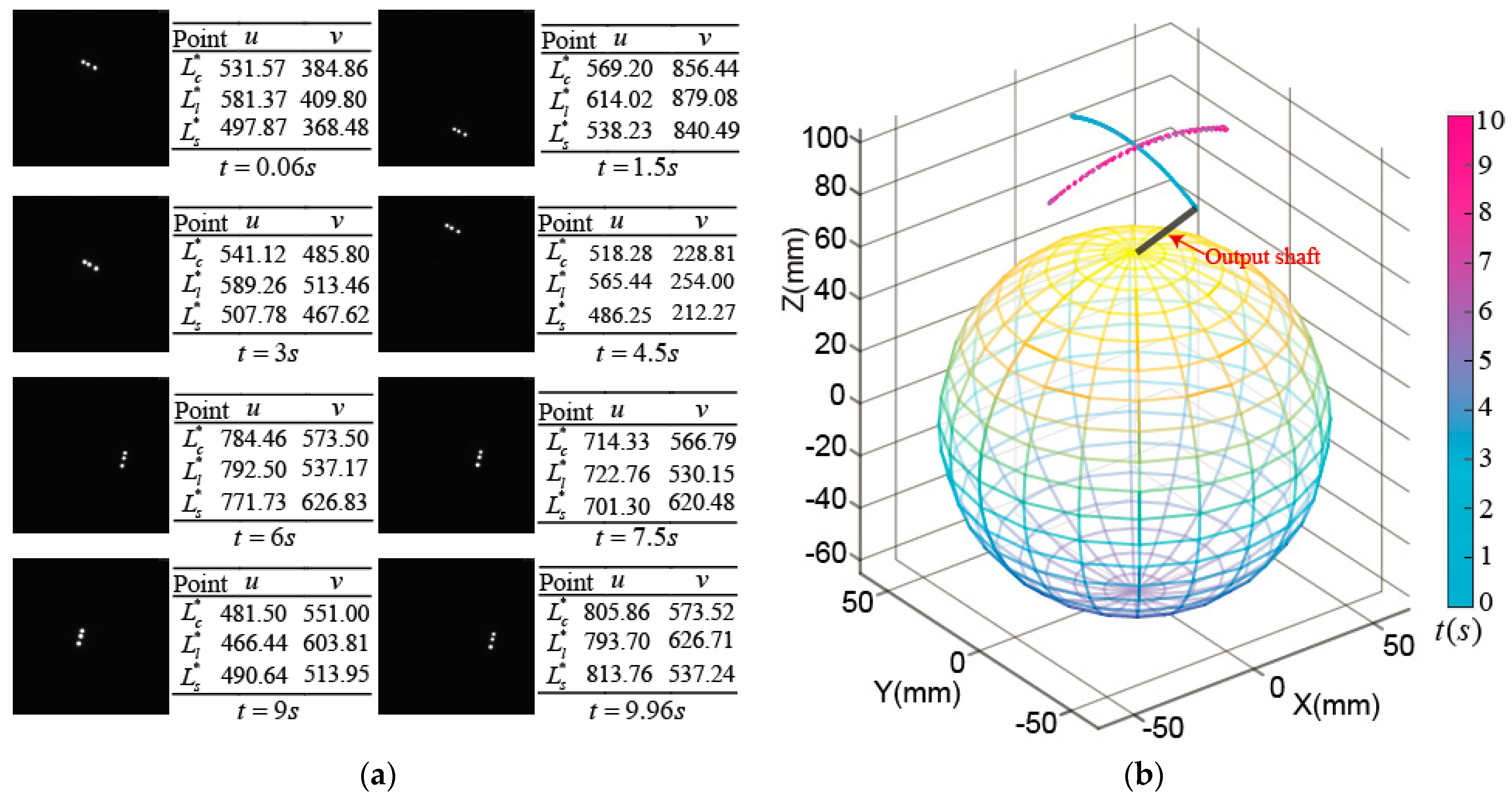
4. Experimental Results
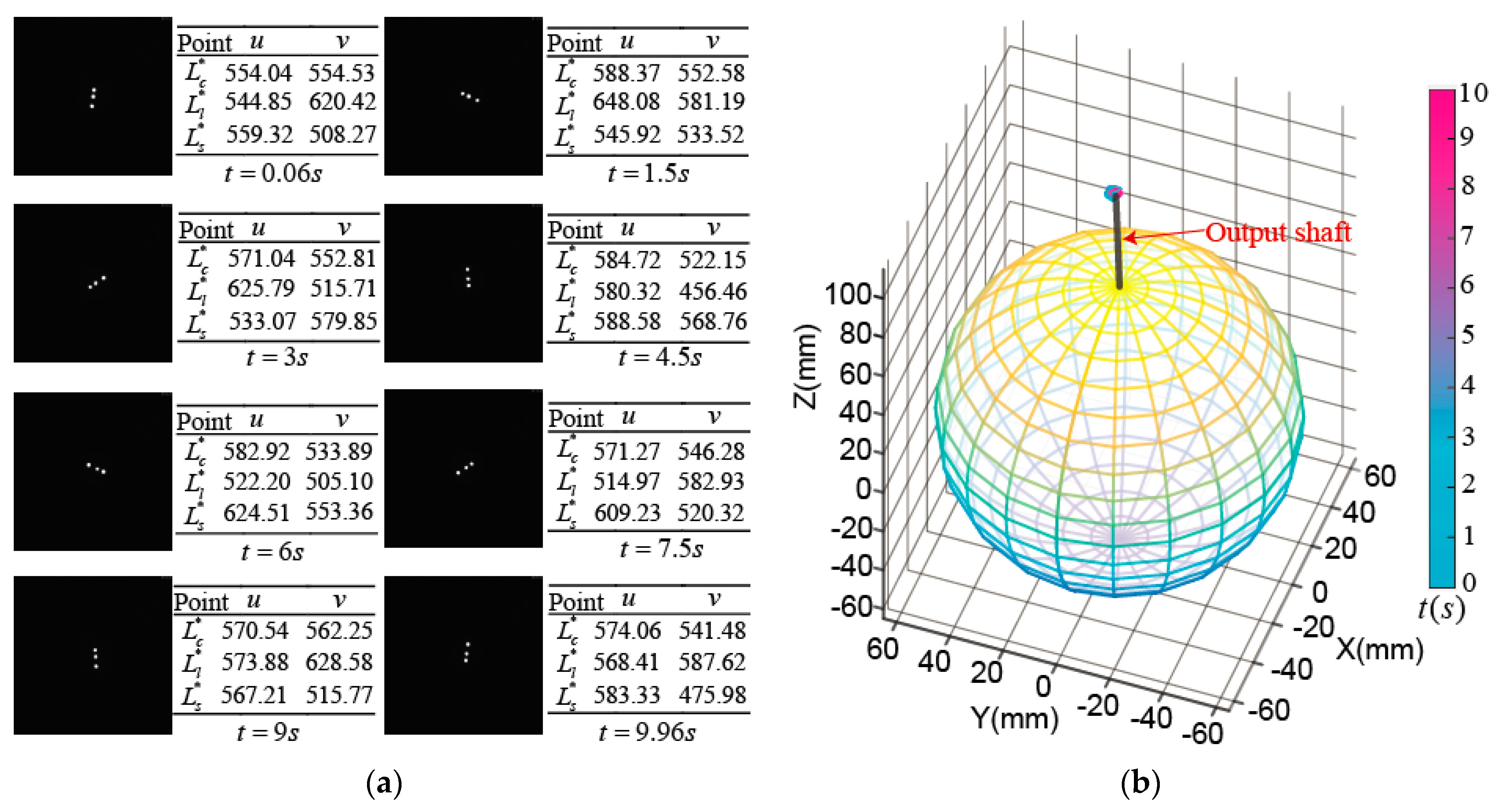
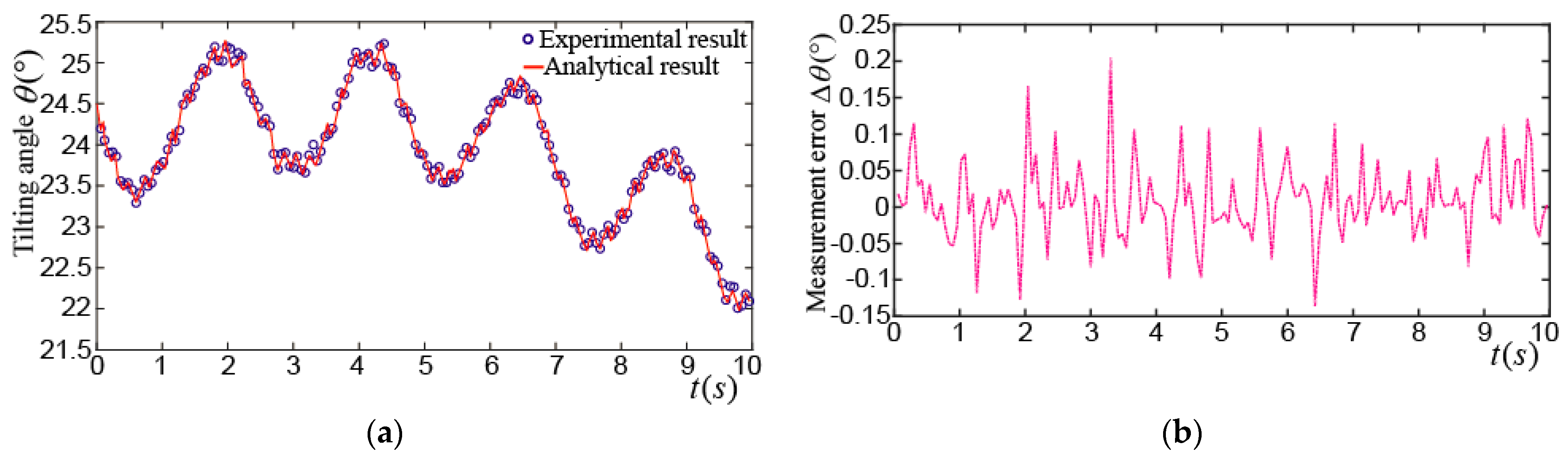
4.1. Experimental Measurement on Tilting Motion of PMSM Rotor
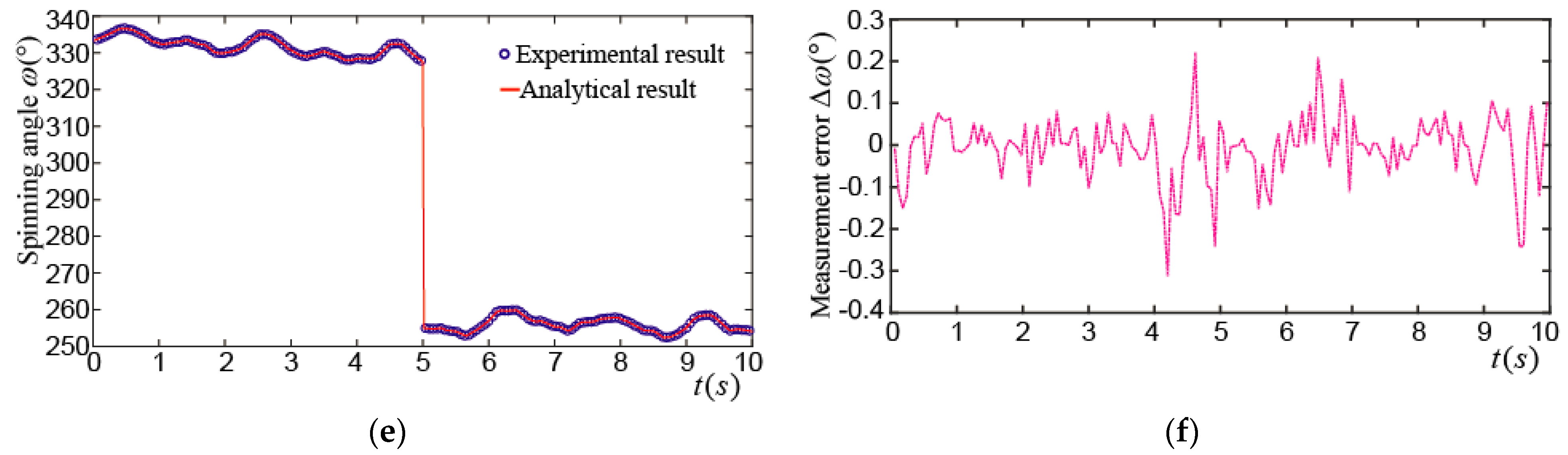
4.2. Experimental Measurement on Spinning Motion of PMSM Rotor at the Center Point
4.3. Experimental Measurement on Edge Spinning Motion of PMSM Rotor
4.4. Comparison of Different Rotor Position Measurement Methods
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Glowacz, A. Fault diagnosis of single-phase induction motor based on acoustic signals. Mech. Syst. Signal Process. 2019, 117, 65–80. [Google Scholar] [CrossRef]
- Singh, G.; Naikan, V.N.A. Infrared thermography based diagnosis of inter-turn fault and cooling system failure in three phase induction motor. Infrared Phys. Technol. 2017, 87, 134–138. [Google Scholar] [CrossRef]
- Williams, F.C.; Laithwaite, E.R.; Eastham, J.F. Development and design of spherical induction motors. Proc. IEE Part A Power Eng. 1959, 106, 471–484. [Google Scholar] [CrossRef]
- Lee, K.M.; Vachtsevanos, G.; Kwan, C. Development of a spherical stepper wrist motor. J. Intell. Robot. Syst. 1988, 1, 225–242. [Google Scholar] [CrossRef]
- Son, H.; Lee, K.M. Open-Loop controller design and dynamic characteristics of a spherical wheel Motor. IEEE Trans. Ind. Electron. 2010, 57, 3475–3482. [Google Scholar] [CrossRef]
- Kahlen, K.; Voss, I.; Priebe, C.; Doncker, R.W.D. Torque control of a spherical machine with variable pole pitch. IEEE Trans. Power Electron. 2002, 19, 1628–1634. [Google Scholar] [CrossRef]
- Chirikjian, G.S.; Stein, D. Kinematic design and commutation of a spherical stepper motor. IEEE/ASME Trans. Mechatron. 1999, 4, 342–353. [Google Scholar] [CrossRef]
- Amano, T.; Ishii, T.; Nakamura, K.; Ueha, S. An ultrasonic actuator with multidegree of freedom using bending and longitudinal vibrations of a single stator. In Proceedings of the IEEE Ultrasonics Symposium, Sendai, Japan, 5–8 October 1998; pp. 667–670. [Google Scholar]
- Guo, J.; Kim, D.H.; Son, H. Effects of magnetic pole design on orientation torque for a spherical motor. IEEE/ASME Trans. Mechatron. 2013, 18, 1420–1425. [Google Scholar]
- Sakaidani, Y.; Hirata, K.; Maeda, S.; Niguchi, N. Feedback control of the 2-dof actuator specialized for 2-axes rotation. IEEE Trans. Magn. 2013, 49, 2245–2248. [Google Scholar] [CrossRef]
- Liu, J.; Deng, H.; Chen, W.; Bai, S. Robust dynamic decoupling control for permanent magnet spherical actuators based on extended state observer. IET Control Theory Appl. 2017, 11, 619–631. [Google Scholar] [CrossRef]
- Liu, J.; Deng, H.; Hu, C.; Hua, Z.; Chen, W. Adaptive backstepping sliding mode control for 3-dof permanent magnet spherical actuator. Aerosp. Sci. Technol. 2017, 67, 62–71. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, W.; Liu, J.; Wen, C. A robust adaptive iterative learning control for trajectory tracking of permanent-magnet spherical actuator. IEEE Trans. Ind. Electron. 2015, 63, 291–301. [Google Scholar] [CrossRef]
- Bai, K.; Lee, K.M. Direct field-feedback control of a ball-joint-like permanent-magnet spherical motor. IEEE/ASME Trans. Mechatron. 2014, 19, 975–986. [Google Scholar] [CrossRef]
- Stein, D.; Scheinerman, E.R.; Chirikjian, G.S. Mathematical models of binary spherical-motion encoders. IEEE/ASME Trans. Mechatron. 2003, 8, 234–244. [Google Scholar] [CrossRef] [Green Version]
- Strumik, M.; Wawrzaszek, R.; Banaszkiewicz, M.; Seweryn, K. Analytical model of eddy currents in a reaction sphere actuator. IEEE Trans. Magn. 2014, 50, 1–7. [Google Scholar]
- Rossini, L.; Mingard, S.; Boletis, A.; Forzani, E.; Onillon, E.; Perriard, Y. Rotor design optimization for a reaction sphere actuator. IEEE Trans. Ind. Appl. 2014, 50, 1706–1716. [Google Scholar] [CrossRef]
- Garner, H.; Klement, M.; Lee, K.M. Design and analysis of an absolute non-contact orientation sensor for wrist motion control. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Como, Italy, 8–12 July 2001. [Google Scholar]
- Yan, L.; Chen, I.M.; Guo, Z.; Lang, Y.; Li, Y. A three degree-of-freedom optical orientation measurement method for spherical actuator applications. IEEE Trans. Autom. Sci. Eng. 2011, 8, 319–326. [Google Scholar] [CrossRef]
- Wang, J.; Jewell, G.W.; Howe, D. Analysis, design and control of a novel spherical permanent-magnet actuator. IEE Proc. Electr. Power Appl. 1998, 145, 61–71. [Google Scholar] [CrossRef]
- Li, H.; Liu, W.; Li, B. A sensing system of the halbach array permanent magnet spherical motor based on 3-D hall sensor. J. Electr. Eng. Technol. 2018, 13, 352–361. [Google Scholar]
- Wang, J.; Wang, W. Jewell, G.W.; Howe, D. A novel spherical permanent magnet actuator with three degrees-of-freedom. IEEE Trans. Magn. 1998, 34, 2078–2080. [Google Scholar] [CrossRef]
- Wang, W.; Wang, J.; Jewell, G.W.; Howe, D. Design and control of a novel spherical permanent magnet actuator with three degrees of freedom. IEEE/ASME Trans. Mechatron. 2003, 8, 457–468. [Google Scholar] [CrossRef]
- Jin, H.Z.; Lu, H.; Cho, S.K.; Lee, J.M. Nonlinear Compensation of a New Noncontact Joystick Using the Universal Joint Mechanism. IEEE/ASME Trans. Mechatron. 2007, 12, 549–556. [Google Scholar] [CrossRef]
- Rossini, L.; Chetelat, O.; Onillon, E.; Perriard, Y. Force and torque analytical models of a reaction sphere actuator based on spherical harmonic rotation and decomposition. IEEE/ASME Trans. Mechatron. 2013, 18, 1006–1018. [Google Scholar] [CrossRef]
- Li, B.; Li, Z.; Li, G. Magnetic field model for permanent magnet spherical motor with double polyhedron structure. IEEE Trans. Magn. 2017, 53, 1–5. [Google Scholar] [CrossRef]
- Li, B.; Zhang, S.; Li, G.; Li, H. Synthesis strategy for stator magnetic field of permanent magnet spherical motor. IEEE Trans. Magn. 2018, 99, 1–5. [Google Scholar] [CrossRef]
- Li, H.; Li, T. End-effect magnetic field analysis of the halbach array permanent magnet spherical motor. IEEE Trans. Magn. 2018, 99, 1–9. [Google Scholar] [CrossRef]
- Zhao, L.; Li, G.; Guo, X.; Li, S.; Wen, Y.; Ye, Q. Time-optimal trajectory planning of permanent magnet spherical motor based on genetic algorithm. In Proceedings of the 2017 12th IEEE Conference on Industrial Electronics and Applications (ICIEA), Siem Reap, Cambodia, 18–20 June 2017; pp. 828–833. [Google Scholar]
- Zhang, Z. A Flexible New Technique for Camera Calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]












| Maximum Resolution | ||
| Pixel Size | ||
| Frame rate (USB3.0 Interfaces) | Frame Rate | Resolution |
| 96 | ||
| 180 | ||
| 360 | ||
| 490 | ||
| 1000 | ||
| 1400 | ||
| Dynamic Range | 60 dB | |
| Accuracy | 8 bit | |
| Sensitivity | 5200 DN/Lux.S, 550 nm | |
| Exposure time | >2 μS | |
| Size | ||
| Working voltage | 24 V |
| Maximum input voltage | 55 V |
| Total driver unit number | 24 |
| Maximum output current (per every driver unit) | ±5 A |
| Constant-current precision | ±20 mA |
| Maximum output frequency | 200 Hz |
| Module Type | MPU6050 | |
|---|---|---|
| Measurement dimension | Acceleration | 3-DOF |
| Angular velocity | 3-DOF | |
| Attitude angle | 3-DOF | |
| Measurement range | Acceleration | ±16 g |
| Angular velocity | ±2000°/s | |
| Resolution | Acceleration | 0.01 g |
| Angular velocity | 0.05°/s | |
| Attitued angle | 0.01° | |
| Data output frequency | 100 Hz | |
| Measurement Method | Photoelectric Sensor | Hall-Effect Sensor | High-Speed Camera | |
|---|---|---|---|---|
| Tilting motion | (°) | 0.65 | 1.55 | 0.32 |
| (°) | 0.58 | 1.62 | 0.3 | |
| (°) | 0.49 | 1.47 | 0.31 | |
| Spinning motion at Center point | (°) | 0.59 | 1.29 | 0.25 |
| (°) | 0.51 | 1.36 | 0.3 | |
| (°) | 0.47 | 1.28 | 0.3 | |
| Edge spinning motion | (°) | 0.69 | 1.87 | 0.22 |
| (°) | 0.62 | 1.83 | 0.3 | |
| (°) | 0.51 | 1.31 | 0.45 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Hu, C.; Wang, Q.; Hong, Y.; Shen, W.; Zhou, C. A New Rotor Position Measurement Method for Permanent Magnet Spherical Motors. Appl. Sci. 2018, 8, 2415. https://doi.org/10.3390/app8122415
Lu Y, Hu C, Wang Q, Hong Y, Shen W, Zhou C. A New Rotor Position Measurement Method for Permanent Magnet Spherical Motors. Applied Sciences. 2018; 8(12):2415. https://doi.org/10.3390/app8122415
Chicago/Turabian StyleLu, Yin, Cungang Hu, Qunjing Wang, Yi Hong, Weixiang Shen, and Chengquan Zhou. 2018. "A New Rotor Position Measurement Method for Permanent Magnet Spherical Motors" Applied Sciences 8, no. 12: 2415. https://doi.org/10.3390/app8122415
APA StyleLu, Y., Hu, C., Wang, Q., Hong, Y., Shen, W., & Zhou, C. (2018). A New Rotor Position Measurement Method for Permanent Magnet Spherical Motors. Applied Sciences, 8(12), 2415. https://doi.org/10.3390/app8122415







