Numerical Study on Evaluating the Concrete-Bedrock Interface Condition for Hydraulic Tunnel Linings Using the SASW Method
Abstract
:1. Introduction
2. Materials and Methods
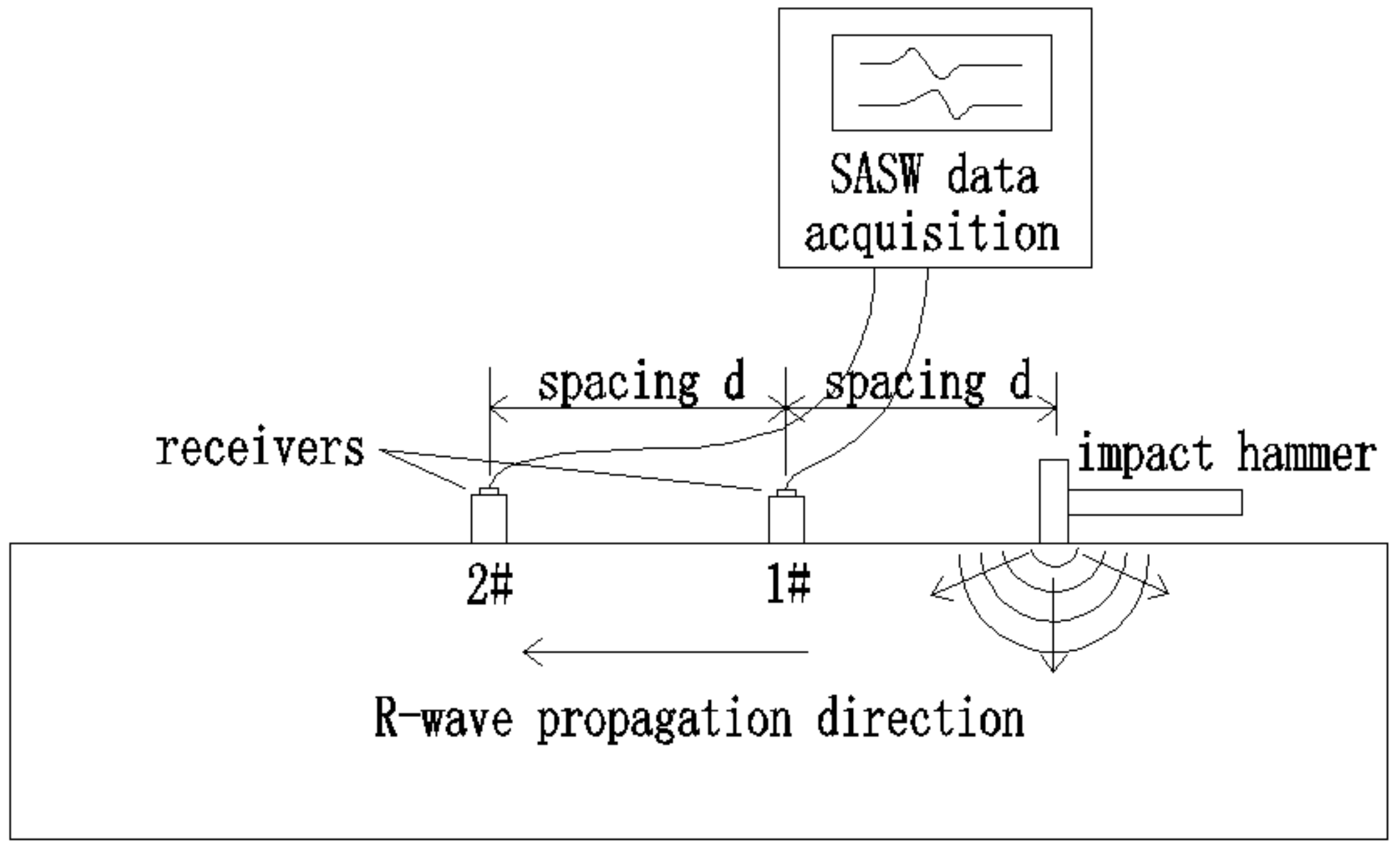
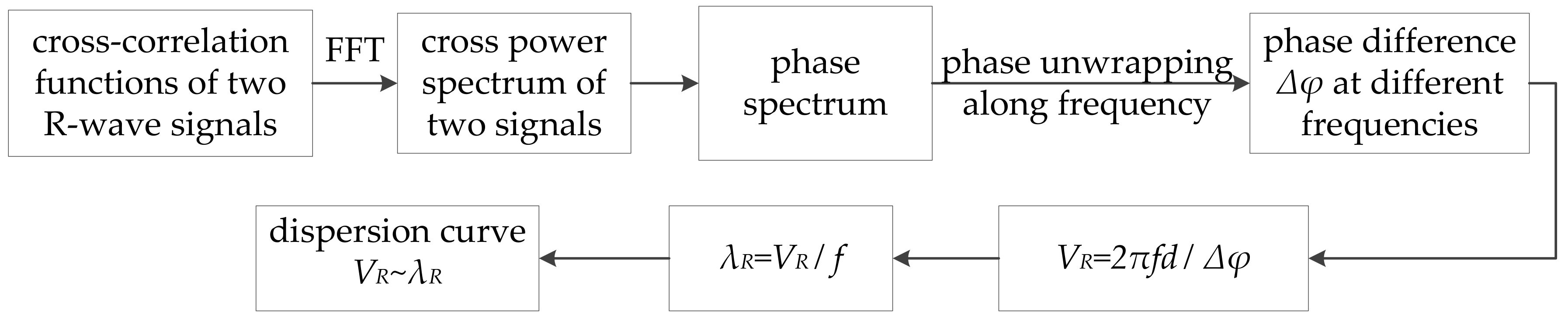
2.1. Processing Method of Collecting Signals
2.2. Description of Finite Element Calculation
3. Results and Discussion
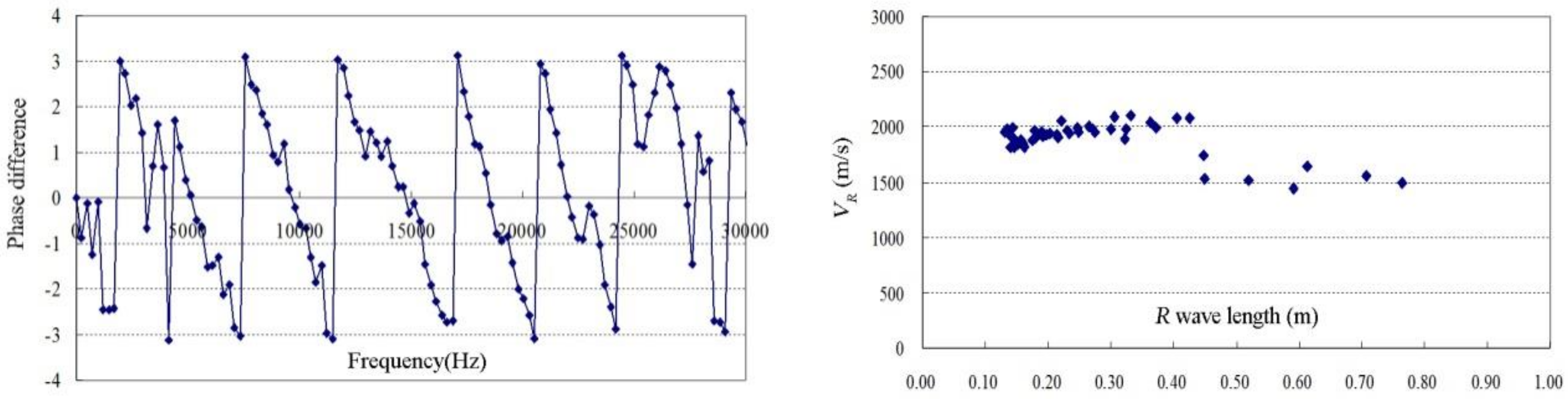
3.1. Dispersion Curves of Different Models
3.2. Dispersion Curves of Receiver Spacing
3.3. Dispersion Curves of Impact Duration
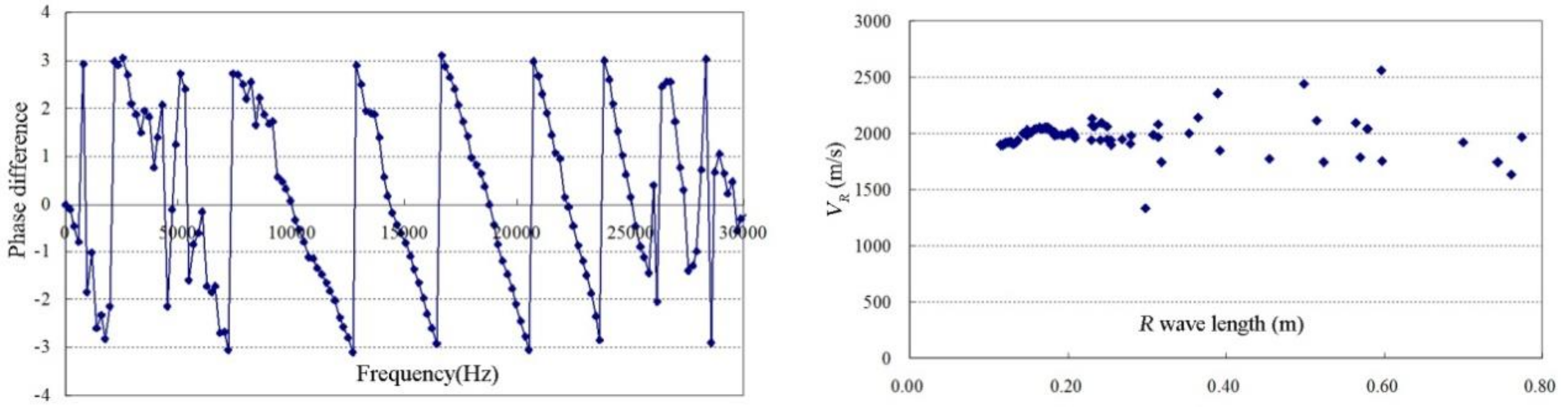
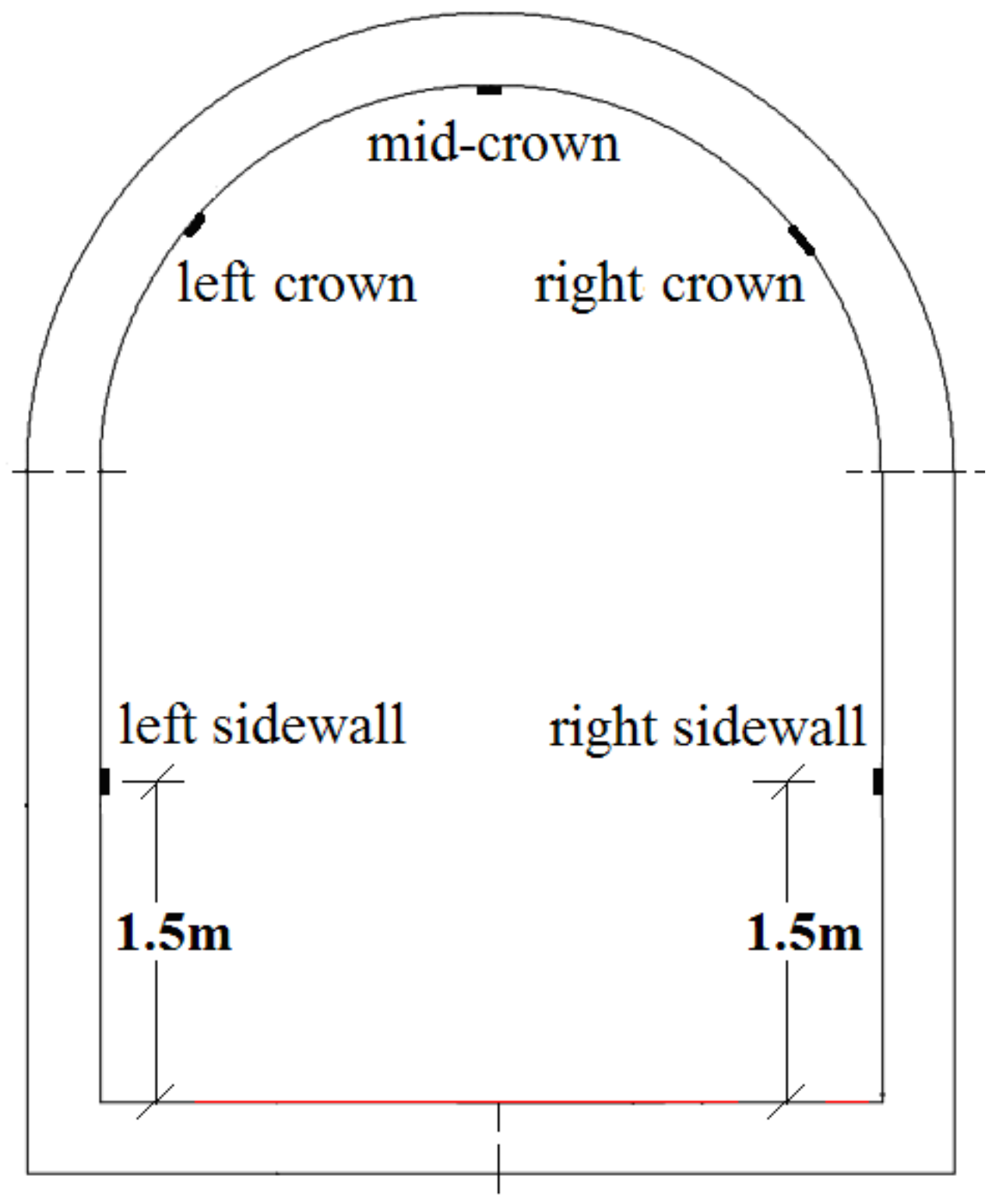
3.4. Field Test
4. Conclusions
- (1)
- The finite element analysis results of different uniform or layered models show that the SASW method can accurately identify the interface contact condition between the concrete lining and bedrock, especially the existence of voids.
- (2)
- When the receiver spacing is 1.0–1.5 times that of the thickness of the target object to be inspected, the quality of the collected signal data is the best, which is conducive to improving the accuracy of defect identification.
- (3)
- Under a certain reasonable range, the impact duration has an insignificant effect on the phase spectra and dispersion curves of a concrete-weak layer model.
- (4)
- The results of the in-situ SASW inspection are consistent with those of the finite element model analysis, which can accurately tell whether the voids exist at the concrete-bedrock interface. It shows the SASW method may be applied as an effective supplement to the ground penetrating radar in inspecting the densely reinforced concrete tunnels.
- (5)
- The data processing program of the SASW method based on the MATLAB platform is accurate, convenient, and worth promoting.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Goodman, D. Ground-penetrating radar simulation in engineering and archaeology. Geophysics 1994, 59, 224–232. [Google Scholar] [CrossRef]
- Annan, A.P. The history of ground penetrating radar. Subsurf. Sens. Technol. Appl. 2002, 3, 303–320. [Google Scholar] [CrossRef]
- Fisher, E.; Mcmechan, G.A.; Annan, A.P.; Cosway, S.W. Examples of reverse-time migration of single-channel, ground-penetrating radar profiles. Geophysics 1992, 57, 577–586. [Google Scholar] [CrossRef]
- Kohler, B.; Schubert, F. Study of Impact Excited Elastic Waves in Concrete by Scanning Laser Vibrometry. Quant. Nondestruct. Eval. 2006, 820, 1328–1334. [Google Scholar] [CrossRef]
- Wieczorek, G.F.; Snyder, J.B.; Waitt, R.B.; Morrissey, M.M.; Uhrhammer, R.A.; Harp, E.L.; Norris, R.D.; Bursik, M.I.; Finewood, L.G. Unusual July 10, 1996, rock fall at happy isles, Yosemite National Park, California. Geol. Soc. Am. Bull. 2000, 112, 75–85. [Google Scholar] [CrossRef]
- Mutlib, N.K.; Baharom, S.; Nuawi, M.Z.; El-Shafie, A. Ultrasonic surface wave monitoring for steel fibre-reinforced concrete using gel-coupled piezoceramic sensors: A case study. Arab. J. Sci. Eng. 2016, 41, 1–9. [Google Scholar] [CrossRef]
- Karaman, K.; Kesimal, A. Correlation of schmidt rebound hardness with uniaxial compressive strength and p-wave velocity of rock materials. Arab. J. Sci. Eng. 2015, 40, 1897–1906. [Google Scholar] [CrossRef]
- Hawwa, M.A. Shear waves in an initially stressed elastic plate with periodic corrugations. Arab. J. Sci. Eng. 2016, 42, 1–10. [Google Scholar] [CrossRef]
- Olson, L.D.; Miller, P. Comparison of Surface Wave Tests for Pavement System Thicknesses/Moduli. In Proceedings of the GeoHunan International Conference: Challenges and Recent Advances in Pavement Technologies and Transportation Geotechnics, Changsha, China, 3–6 August 2009; Volume 189, pp. 174–179. [Google Scholar]
- Ismail, M.A.; Samsudin, A.R.; Rafek, A.G.; Nayan, K.A.M. In Situ Determination of Layer Thickness and Elastic Moduli of Asphalt Pavement Systems by Spectral Analysis of Surface Waves (SASW) Method. In Proceedings of the GeoHunan International Conference: Challenges and Recent Advances in Pavement Technologies and Transportation Geotechnics, Changsha, China, 3–6 August 2009. [Google Scholar]
- Cho, Y.S. Ndt response of spectral analysis of surface wave method to multi-layer thin high-strength concrete structures. Ultrasonics 2002, 40, 227–230. [Google Scholar] [CrossRef]
- Barkan, D.D.; Drashevska, L. Dynamics of Bases and Foundations; McGraw-Hill Book Company Inc.: New York, NY, USA, 1962. [Google Scholar]
- Volti, T.; Burbidge, D.; Collins, C.; Asten, M.; Odum, J.; Pascal, C.H.; Holzschuh, J. Comparisons between vs30 and spectral response for 30 sites in Newcastle, Australia, from collocated seismic cone penetrometer, active- and passive-source vs. data comparisons between vs30 and spectral response for 30 sites in Australia. Bull. Seismol. Soc. Am. 2016, 106, 1690–1709. [Google Scholar] [CrossRef]
- Lu, Y.; Cao, Y.; Mcdaniel, J.G.; Wang, M.L. Fast Inversion of Air-Coupled Spectral Analysis of Surface Wave (SASW) Using in situ Particle Displacement. ISPRS Int. J. Geo-Inf. 2015, 4, 2619–2637. [Google Scholar] [CrossRef] [Green Version]
- Nazarian, S.; Stoke, K.H., II. In-Situ Determination of Elastic Moduli of Pavements Systems by Spectral Analysis of Surface Waves Method (Practical Aspects); Research Report Number 368-1F; US Department of Transportation, Federal Highway Administration: Washington, DC, USA, 1985. [Google Scholar]
- Kim, D.S.; Seo, W.S.; Lee, K.M. IE–SASW method for nondestructive evaluation of concrete structure. NDT E Int. 2006, 39, 143–154. [Google Scholar] [CrossRef]
- Lu, X.; Sun, Q.; Feng, W.; Tian, J. Evaluation of dynamic modulus of elasticity of concrete using impact-echo method. Constr. Build. Mater. 2013, 47, 231–239. [Google Scholar] [CrossRef]
- Ma, F.; Wang, R.; Lu, X.; Luke, A. Assessing frost resistance of concrete by impact-echo method. Mag. Concr. Res. 2015, 67, 1–8. [Google Scholar]
- Kang, S.L.; Choi, J.I.; Kim, S.K.; Lee, B.K.; Hwang, J.S.; Bang, Y.L. Damping and mechanical properties of composite composed of polyurethane matrix and preplaced aggregates. Constr. Build. Mater. 2017, 145, 68–75. [Google Scholar] [CrossRef]
- Kim, D.S.; Kim, H.W.; Seo, W.S.; Choi, K.C.; Woo, S.K. Feasibility study of the IE-SASW method for nondestructive evaluation of containment building structures in nuclear power plants. NDT E Int. 2003, 219, 97–110. [Google Scholar] [CrossRef]
- Chen, Z.S.; Jiang, B.F.; Song, J.J.; Wang, W.T. Accurate Sparse Recovery of Rayleigh Wave Characteristics Using Fast Analysis of Wave Speed (FAWS) Algorithm for Soft Soil Layers. Appl. Sci. 2018, 8, 1204. [Google Scholar] [CrossRef]
- Harley, J.B.; Moura, J.M. Sparse recovery of the multimodal and dispersive characteristics of lamb waves. J. Acoust. Soc. Am. 2013, 133, 2732–2745. [Google Scholar] [CrossRef] [PubMed]
- Song, X.; Tang, L.; Lv, X.; Fang, H.; Gu, H. Application of particle swarm optimization to interpret rayleigh wave dispersion curves. J. Appl. Geophys. 2012, 84, 1–13. [Google Scholar] [CrossRef]
- Snowball, P.S.I. Spectral Analysis of Signals. Leber Magen Darm 2005, 13, 57–63. [Google Scholar]
- Rao, K.D.; Swamy, M.N.S. Spectral Analysis of Signals. In Digital Signal Processing; Springer Singapore: Cham, Switzerland, 2018. [Google Scholar]
- Lee, U. Spectral Analysis of Signals. Spectral Element Method in Structural Dynamics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2005; pp. 57–63. [Google Scholar]
- Singh, A.; Derybel, T.; Marti, J.R. FFT tutor: A matlab-based instructional tool for FFT parameter exploration. Acoust. Week Can. 2008, 36, 82–83. [Google Scholar]
- Xu, Y.; Zhang, X.M.; Wang, Y.; Sun, Q.B.; Wang, Z.M.; Sun, Y. A new method of spectrum analysis based on DFT. Power Syst. Prot. Control 2011, 39, 38–43. [Google Scholar]
- Zeng, S.; Shen, H.; Zhen, Y.U. FFT based spectrogram analysis and display of signals using matlab. Bull. Sci. Technol. 2000. [Google Scholar]
- Lyon, D.A. The Discrete Fourier Transform, Part 6: Cross-Correlation. J. Object Technol. 2010, 9, 17–22. [Google Scholar] [CrossRef]
- Pei, S.; Ding, J.; Chang, J. Efficient implementation of quaternion Fourier transform, convolution, and correlation by 2-D complex FFT. IEEE Trans. Signal Process. 2001, 49, 2783–2797. [Google Scholar] [CrossRef]















| Number | Material | Thickness (cm) | Model Type |
|---|---|---|---|
| 1 | concrete | 200 | Uniform |
| 2 | concrete | 40 | Layered model 1 |
| bedrock | 160 | ||
| 3 | concrete | 40 | Layered model 2 |
| weak interlayer | 2 | ||
| bedrock | 158 | ||
| 4 | concrete | 40 | Layered model 3 |
| weak layer | 160 |
| Material | Dynamic Elastic Modulus (GPa) | Poisson’s Ratio | Density (kg/m3) |
|---|---|---|---|
| concrete | 30 | 0.2 | 2450 |
| bedrock | 10 | 0.3 | 2500 |
| weak interlayer | 1 | 0.3 | - |
| weak layer | 1 | 0.3 | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Lu, X.; Li, M.; Hao, J.; Xu, Y. Numerical Study on Evaluating the Concrete-Bedrock Interface Condition for Hydraulic Tunnel Linings Using the SASW Method. Appl. Sci. 2018, 8, 2428. https://doi.org/10.3390/app8122428
Li X, Lu X, Li M, Hao J, Xu Y. Numerical Study on Evaluating the Concrete-Bedrock Interface Condition for Hydraulic Tunnel Linings Using the SASW Method. Applied Sciences. 2018; 8(12):2428. https://doi.org/10.3390/app8122428
Chicago/Turabian StyleLi, Xiulin, Xiaobin Lu, Meng Li, Jutao Hao, and Yao Xu. 2018. "Numerical Study on Evaluating the Concrete-Bedrock Interface Condition for Hydraulic Tunnel Linings Using the SASW Method" Applied Sciences 8, no. 12: 2428. https://doi.org/10.3390/app8122428
APA StyleLi, X., Lu, X., Li, M., Hao, J., & Xu, Y. (2018). Numerical Study on Evaluating the Concrete-Bedrock Interface Condition for Hydraulic Tunnel Linings Using the SASW Method. Applied Sciences, 8(12), 2428. https://doi.org/10.3390/app8122428





