First-Principles Investigation of Atomic Hydrogen Adsorption and Diffusion on/into Mo-doped Nb (100) Surface

Abstract

To investigate Mo doping effects on the hydrogen permeation performance of Nb membranes, we study the most likely process of atomic hydrogen adsorption and diffusion on/into Mo-doped Nb (100) surface/subsurface (in the Nb₁₂Mo₄ case) via first-principles calculations. Our results reveal that the (100) surface is the most stable Mo-doped Nb surface with the smallest surface energy (2.75 J/m²). Hollow sites (HSs) in the Mo-doped Nb (100) surface are H-adsorption-favorable mainly due to their large adsorption energy (−4.27 eV), and the H-diffusion path should preferentially be HS→TIS (tetrahedral interstitial site) over HS→OIS (octahedral interstitial site) because of the correspondingly lower H-diffusion energy barrier. With respect to a pure Nb (100) surface, the Mo-doped Nb (100) surface has a smaller energy barrier along the HS→TIS pathway (0.31 eV).

1. Introduction

The interaction between hydrogen and metal surfaces is an interesting topic in science and engineering, and has been investigated by both experimental [1,2,3] and theoretical [4,5] approaches. Over 80 percent of synthetic chemicals are produced with the application of catalysts, meaning that the interactions of hydrogen with catalytic metal surfaces during heterogeneous catalysis are of great interest for several important processes [6,7,8] including petrochemical processing, pharmaceutical production [9], highly efficient electrocatalysis [10], fine chemical production [11], and conversion of biomass to fuels and chemicals [12]. Meanwhile, hydrogen–metal interactions have attracted further attention due to the central role of hydrogen as a clean and efficient energy source [13,14]. With the increasing demand for high purity hydrogen in the fields of fuel cell, new materials for hydrogen separation/purification are being explored. Consequently, the study of the behavior of both absorbed and adsorbed hydrogen on/into the metal surface/subsurface is important for achieving a deep understanding of the hydrogen-permeation properties of such metallic membranes [15,16].

Considerable experimental and theoretical studies of the hydrogen sorption on many single-crystal metal surfaces have been carried out. For example, Ferrin et al. [4,15] performed a comprehensive theoretical study addressing adsorption and absorption energies and subsurface penetration barriers of hydrogen on different low-index surface terminations of 17 transition metals (TM) by first-principles calculations. Lauhon et al. further studied the diffusion of atomic hydrogen on Cu (001) via scanning tunneling microscope (STM) measurements. The diffusion of H atoms was measured as a function of temperature, and a transition from thermally activated diffusion to quantum tunneling was observed at 60 K [16]. Recently, Gómez et al. reported an extensive study of adsorption and diffusion of hydrogen atoms on the (100) surfaces of fcc Au, Cu, Ag, and Pt, performed by means of density functional theory (DFT) calculations [17,18]. Based on elucidating the preferential adsorption sites of hydrogen on each metal, they calculated the adsorption distances and energies of atomic hydrogen at the top, hollow, and bridge sites of the (100) surfaces. The numerous studies focused on this topic have proved the importance of understanding the mechanism of hydrogen–metal-surface-related phenomena.

Pd and its alloys are excellent materials for hydrogen separation and purification, but their high cost and scarcity should be noted. Currently, niobium (Nb), a Group VB (e.g., V, Nb, Ta, etc.) TM, has attracted much attention as one of the most promising hydrogen separation materials due to its relatively low price [3], excellent high-temperature mechanical properties, and corrosion resistance [19,20,21]. However, Nb often exhibit poor resistance to hydrogen embrittlement and therefore is limited in the practical application [22,23,24,25]. Experimental and theoretical studies have verified that alloying Nb with other metals is an effective approach to solve this problem [26,27,28,29,30]. Hu et al. [31] reported that the W doping is supposed to be the key role in enhancing the mechanical properties of Nb₁₆H, and is not conducive to the structural stability of the Nb₁₅WH (TIS) phase. Moreover, doping Nb with W can reduce the diffusion barrier of H, and enhance diffusion paths for H [32].

Both W and Mo are high-Z refractory metals (i.e., refractory metals containing impurities with high atomic numbers (Z) with similar physical properties. Comparing with W, Mo has a lower melting point (2883 K) and a lower erosion rate. Moreover, H has higher diffusivity and lower solubility in Mo, leading to lower H retention [33,34,35]. These characteristics make Mo an important alloying candidate of Nb-based membranes for hydrogen permeation.

To gain a detailed understanding of the hydrogen-permeation behavior of Mo-doped Nb membranes, adsorption and diffusion of hydrogen atoms on a Mo-doped Nb (Nb₁₂Mo₄) surface have been investigated by first-principles calculations in this work. Furthermore, we discuss the most favorable process of H adsorption and diffusion on/into a Mo-doped Nb (100) surface/subsurface. We believe this work is important to comprehensively understand the basic mechanism of atomic hydrogen sorption on TM surfaces and the influence of element doping, and contribute to the design of Nb-based alloys for H-storage and H-separation applications.

2. Computational Details

Our calculations were carried out with the use of the Vienna Ab-initio Simulation Package (VASP) [36,37]. The interactions between the core and valence electrons were described with the projector augmented wave (PAW) approach [38,39]. Exchange correlation functions were generalized gradient approximations (GGA) developed by Perdew et al. [40]. An energy cutoff of 360 eV was used for the plane-wave basis sets, and a grid with 2π × 0.03 Å⁻¹ resolution in the Brillouin zone was used for all calculations to minimize the error from the k-point meshes. During structure relaxation, the lattice parameters, volume, and atomic positions were fully optimized with in-symmetry restrictions until the total energy converged to 10⁻⁵ eV in the self-consistent loop. Relaxed until the maximum force on each atom was less than 0.01 eV/Å. The electrons of the Nb 4d⁴5s¹ and the Mo 4d⁵5s¹ orbitals were treated as valence electrons. To study the diffusion properties of atomic hydrogen from the surface into the subsurface of Mo-doped Nb (100), we used the climbing image nudged elastic band (CI-NEB) method [41] to determine the diffusion barriers between the initial and final positions.

3. Results and Discussion

3.1. Surface Model of Mo-doped Nb

In Nb_16−xMo_xH system, Nb₁₂Mo₄H has the highest absolute value of ΔH_f, which is favorable for dehydrogenation. Therefore, Nb₁₂Mo₄H was selected to build the slab model for further study, which is depicted in Figure 1a. There are two high symmetrical interstitial sites in the region between the first and second atomic layer, which are tetrahedral interstitial site (TIS) and octahedral interstitial site (OIS), as shown in Figure 1b and Figure 1c. Due to the similar atomic radius of Mo compared to Nb, the crystal keeps the cubic structure after Mo-doping. The equilibrium lattice constant (3.304 Å) of bulk Nb agrees well with experimental values (3.305 Å) [42]. For the (100) surface, we built a slab model with seven atomic layers, which is depicted in Figure 1d.

Surface energy is an important parameter of a metal surface that can be utilized to explain the physical and chemical processes and surface stability. Cutting surfaces from bulk crystal breaking various chemical bonds, which increases the energy of the system, thereby resulting in instability of the surface systems. The surface energy is defined as [14]

$$\sigma =\left(E_{slab}-n\times E_{bulk}\right)/\left(2A\right)$$

(1)

Here, E_slab, E_bulk, n, and A represent the total energy of the slab, the total energy of the corresponding bulk material, the number of atoms contained in the slab and the area of the surface, respectively. In the structure optimization calculations, the atoms in the top three layers were fully relaxed, and the atoms in the other layers were fixed at their bulk positions.

Table 1. Calculated surface energies of pure Nb (100), Nb₁₂Mo₄ (100) and (111) for of different numbers of atomic layers. Experimental value [43] is listed for comparison.

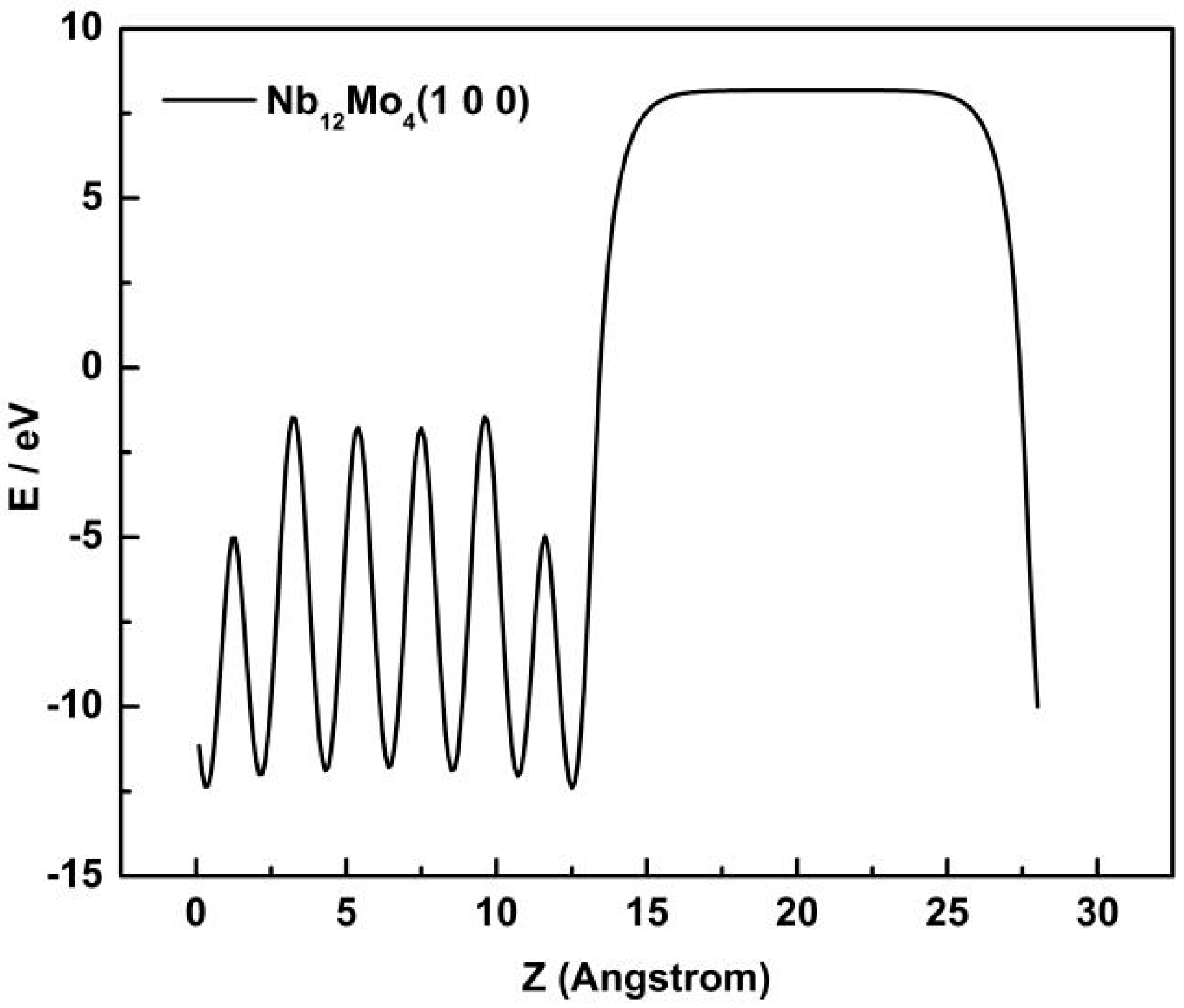
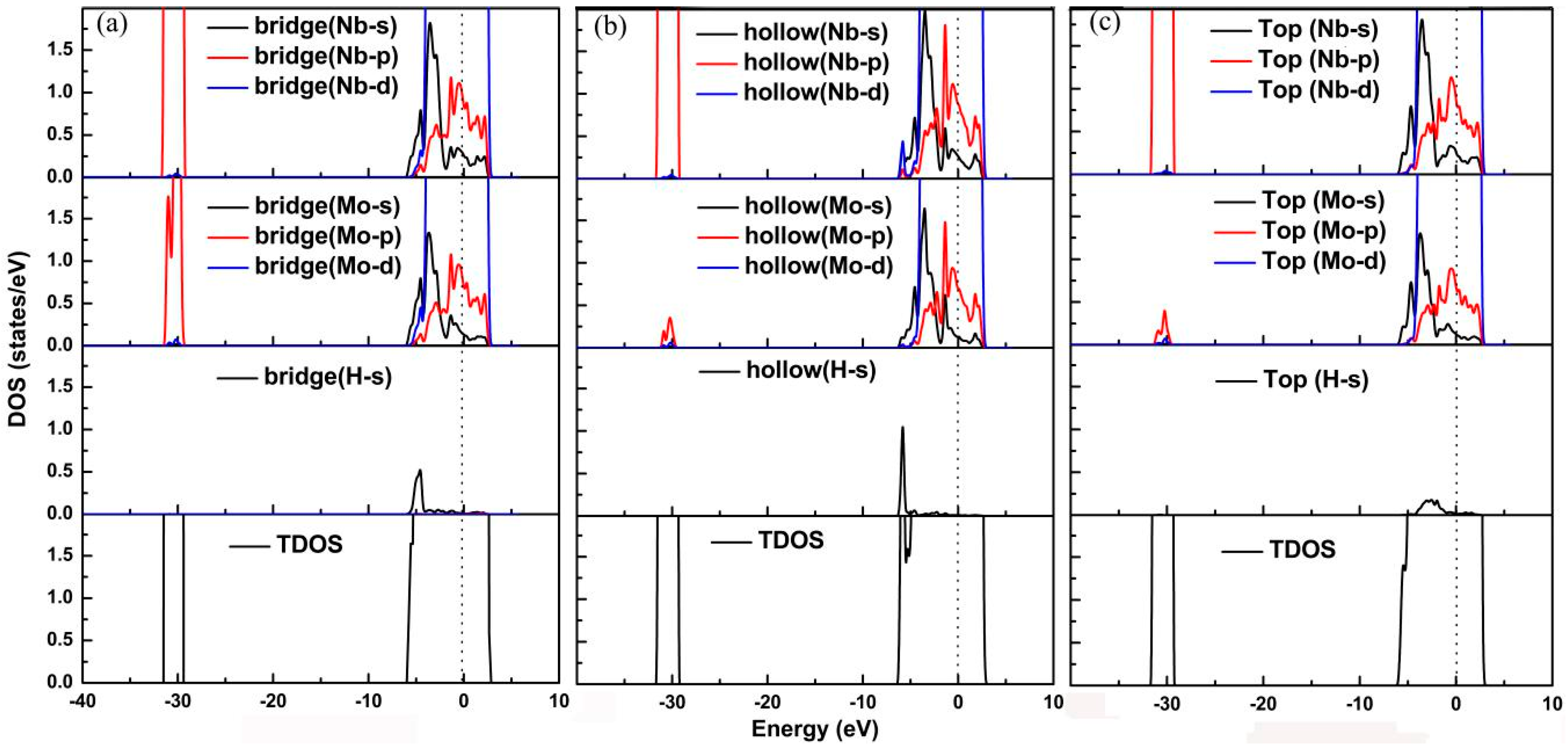
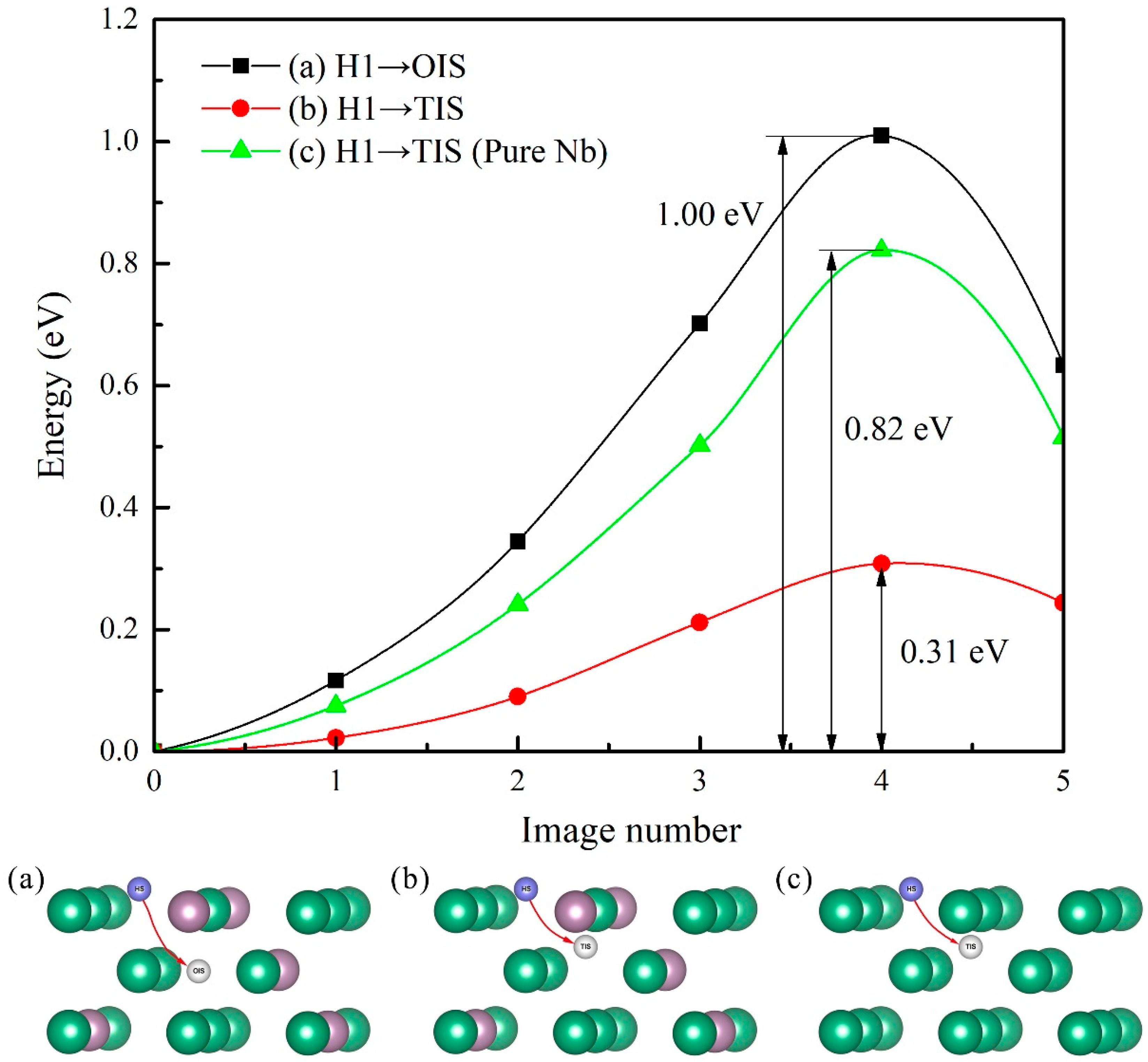
	Surface Energies (eV)
	4 Layers	5 Layers	6 Layers	7 Layers	8 Layers	9 Layers	10 Layers
Pure Nb (100)	2.63	2.45	2.43	2.42	2.44	2.44	2.44
Pure Nb (100) a		2.3–2.7
Nb12Mo4 (100)	2.72	2.73	2.74	2.75	2.75	2.75	2.75
Nb12Mo4 (111)	3.28	3.31	3.32	3.32	3.32	3.32	3.32

^a Ref. [43].

lists the calculated surface energies of slab models with different numbers of atomic layers. The surface energy of pure Nb (100) surface is also calculated for comparison. The results agree well with the values from Baskes et al. [43]. The surface energy of Nb₁₂Mo₄(100) surface and Nb₁₂Mo₄(111) surface tend to be stable when there are more than five atomic layers. Moreover, the Nb₁₂Mo₄(100) surface is the most stable one with the smallest surface energy (2.75 J/m²). Therefore, we select Nb₁₂Mo₄(100) surface for further study.

To determine a practicable number of atomic layers and the vacuum region of Mo-doped Nb (100) surface model, we calculate the changes of the interlayer distances during structure relaxation as the following relationship [44,45]

$$\Delta d_{i-j}=d_{i-j}-d_0$$

(2)

Here, d₀ denotes the layer distance between the i- and j-layers of the unrelaxed slab model established from a geometry-optimized bulk model and d_i−j denotes the corresponding layer distance of the optimized slab model. From the calculated results depicted in Figure 2, we can infer that the interlayer distance between the outermost layer and secondary outer layer tends to be stable when there are more than six atomic layers. According to the previously calculated surface energies, seven atomic layers are sufficient to avoid the effects of external forces in z-axis.

In addition, to ensure that hydrogen permeation process is not influenced by periodicity, a vacuum region between the atomic layers in the (100) surface is required. Thus, the work function of (100) surface model with seven atomic layers and a 12 Å vacuum layer along the surface normal direction (z-axis) is calculated, and is depicted in Figure 3. The flat line in the figure indicating that the work function converges in the vacuum region. Therefore, we employed a slab model of seven atomic layers with a 12 Å vacuum layer of (100) surface for further hydrogen permeation analysis.

3.2. H Atom Adsorption Sites of Mo-doped Nb (100) Surface

Based on the slab model of Mo-doped Nb (100) surface, there are three possible adsorption sites for hydrogen atoms, i.e., top site (TS), bridge site (BS), and hollow site (HS), as shown in Figure 4. The adsorption energies (E_ads) are calculated to characterize the preferred location of the adsorbed hydrogen atom. When Nb doping is considered, E_ads can be expressed as

$$E_{ads}=E\left(N{b}_{n}M{o}_{m-n}H\right)-E\left(N{b}_{n}M{o}_{m-n}\right)-E\left(H\right)$$

(3)

Here, m represents the total number of atoms, n represents the number of Nb atoms in the slab model, E(H) = −0.019 eV, E(Nb_nMo_m−n) and E(Nb_nMo_m−nH) the total energies of the corresponding crystal structures. The calculated E_ads values are summarized in

Table 2. Calculated adsorption energy (E_ads), average distance between H atom and metal atom (d_H-TM) as well as average distance between H atom and the top layer (d_H-Surf) in slab model of Mo-doped Nb (100) surface for adsorbed hydrogen atoms at different sites indicated in Figure 4

Site	Eads (eV)	dH-TM (Å)	dH-Surf (Å)
T2	−3.41	1.77	1.85
T1	−3.26	1.85	1.93
B2	−3.77	1.97	1.30
B1	−3.75	1.97	1.21
H2	−4.24	1.98	0.46
H1	−4.27	1.99	0.44

. Among the possible positions, the largest adsorption energy (−4.27 eV) belongs to the hollow site on top of Nb atom (H1), which indicates that H1 sites are the preferential sites of adsorbed hydrogen atoms. In addition, the average vertical distance between adsorbed H atom and the top layer (d_H-Surf) as well as the distance between H atom and TM atoms (d_H-TM ) are also calculated and listed in Table 2. The bonding lengths (d_H-TM) between the hydrogen-atom and TM atom show the descending on the hollow, bridge and top sites, respectively. The smallest d_H-Surf (0.44 Å) belongs to the H1 site, indicating that there exists a very strong interaction between H atom and (100) surface. Similar results were obtained by Gong and co-authors [46].

3.3. Electronic Properties of Mo-doped Nb (100) Surface

To examine the interaction between atoms, we investigated the electronic properties of the Mo-doped Nb (100) surface. The calculated density of states (DOS) of H atom adsorbed at the bridge, hollow, and top sites are shown in Figure 5a–c, respectively. The Partial DOS (PDOS) peaks at about −30 eV with respect to the Fermi level are mainly contributed by Nb-p and Mo-p states for Mo-doped Nb (100) surface. The PDOS peaks near −5 eV are contributed by the H-s state. In the case of H1 model (Figure 5b), an obvious peak of Nb-d is observed at −5 eV, but it is absent in the case of B1 and T1 models, indicating that the hybridization between H-s and Nb-d states in B1 model is adjusted by Mo-doping.

3.4. Diffusion of Hydrogen Atom into Mo-doped Nb (100) Subsurface

To further understand the behavior of H atoms diffusion, we investigate the subsequent H-diffusion process from the surface into the subsurface. The possible H-diffusion paths are H1→TIS and H1→OIS. We utilize CI-NEB method to determine the minimum energy and energy barrier for H-diffusion at both paths. The energy barrier of H1→TIS is 0.31 eV (Figure 6b), which is smaller than the corresponding value (1.0 eV) of H1→OIS (Figure 6a), meaning that the H-diffusion path should mainly be H1→TIS. In addition, the energy barrier of H1→TIS of the pure Nb (100) surface is 0.82 eV (Figure 6c), indicating Mo-doping improves the performance of H-atom diffusion for Nb (100) surface.

4. Conclusions

The probable processes of atomic hydrogen adsorption, and diffusion behaviors on/into Mo-doped Nb (100) surface/subsurface are investigated using first-principles calculations in combination with empirical theory. Considering the above mentioned, we can come to the following conclusion:

(1) Comparing with the (111) surface, the (100) surface is more stable with smaller surface energy (2.75 J/m²) for Mo-doped Nb.

(2) Among the three possible sites for H adsorption (BS, HS, and TS), H1 is most favorable due to its larger adsorption energy (−4.27 eV) and smaller average vertical distance between H atoms and the top layer of surface (0.44 Å). The optimal H-diffusion path is H1→TIS for its low energy barrier of H-diffusion.

(3) The optimal H-diffusion path is H1→TIS. Furthermore, compared with pure Nb, Mo-doped Nb (100) surface offers a smaller energy barrier for H1→TIS path (0.31 eV), indicating that Mo-doping improves H adsorption and diffusion performance for Nb (100) surface.