Performance Analysis of Satellite-to-Ground Coherent Optical Communication System with Aperture Averaging

Abstract

The satellite-to-ground optical communication system suffers from atmosphere turbulence severely. It is well-known that the coherent detection can increase the receiver sensitivity and performing aperture averaging can reduce the scintillation caused by the atmosphere turbulence. In this paper, the bit error rate, the outage probability and the average capacity of a coherent satellite-to-ground optical communication downlink with aperture averaging are analyzed. The Log-normal atmosphere turbulence model and BPSK (Binary Phase Shift Keying) modulation is employed. The analyzing focuses on the improvement of aperture averaging with different atmospheric conditions and zenith angles of the satellite. The bit error rate performance based on measuring data is given too. The results demonstrate the bit error rate and the outage probability can be reduced and the average capacity can be improved by aperture averaging efficiently. When the turbulence is stronger and the zenith angle is larger, the effect of aperture averaging is more obvious. The aperture averaging effect on BER (Bit Error Rate) is better than the effect on average capacity.

1. Introduction

Compared with the radio-frequency satellite to ground communication link, the optical communication link has lower power consumption, higher transmission rate and greater security [1]. It has attracted significant attention for these advantages. One significant experiment is the LLCD (Lunar Laser Communication Demonstration) carried out by NASA [2]. However, as a result of the atmosphere channel, the received signal of the receiver on the ground is fluctuated and weak [1]. A number of studies are devoted to improve the sensitivity of the receiver and alleviate the signal fluctuation.

Taking the advantage of the local oscillator laser, the receiver employing the coherent detection method is more sensitive than the intensity modulation direct detection (IM/ID) method [3,4]. In particular, with the development of the digital signal processing technology, the frequency offset and the phase offset between the local laser and the received signal can be estimated and compensated in a coherent system [5,6,7,8]. To alleviate the signal fluctuation, two important schemes can be used. The one is adopting a lager receiving aperture, and the other is employing a receiving array consisting of multiple apertures called spatial diversity [9,10,11,12,13,14,15]. The lager aperture method cannot only alleviate signal fluctuation, but can also receive more signal power by larger lens. So, employing coherent detection and aperture averaging together in the satellite-to-ground optical link, higher sensitivity, higher average SNR and lower scintillation index can be provided.

At present, there is some study in terms of the satellite to ground link with on-off keying modulation scheme [16,17] and point receiver model with which the ground receiver is assumed as a point [18]. The use of coherent detection and aperture averaging is considered together in this paper. The aperture averaging performance of a coherent satellite-to-ground optical communication system using BPSK scheme is analyzed. The BER, the outage probability and average capacity of this system with different receiving aperture diameters, different atmospheric conditions and different satellite angles are analyzed. The BER performance based on measuring data is given too.

2. Atmosphere Channel

2.1. Scintillation Index with Aperture Averaging

The scintillation index in the receiving aperture is an important coefficient to describe the fluctuation of the optical signal. For satellite-to-ground optical downlink, when the height of the satellite is over 20 km, the scintillation index can be expressed as [19]:

$${\sigma }_I(d)=8.70k^{7/6}{(H-h_0)}^{5/6}{\sec }^{11/6}(\zeta )\times \mathrm{Re}{\displaystyle {\int }_{h_0}^H{C}_n^2}(h)\left[{\left(\frac{k{d}^2}{16(H-h_0)\sec \zeta }+i\frac{h-h_0}{H-h_0}\right)}^{5/6}-{\left(\frac{k{d}^2}{16L}\right)}^{5/6}\right]dh$$

(1)

$k$ is the wave number of the optical signal and it is defined as:

$$k=\frac{2\pi }{\lambda }$$

(2)

$d$ is the diameter of the receiving aperture. $\lambda$ is the wave length. $H$ and $h_0$ are the altitude height of the satellite and the receiver. $\zeta$ and $L$ are the zenith angle of the satellite and the distance from the ground receiver to the satellite. $C_n^2(h)$ is the refractive-index structure parameter. Here, the Hufnagel-Valley (H-V) model is employed as [19]:

$$C_n^2(h)=0.00594{\left(\frac{w}{27}\right)}^2{\left({10}^{-5}h\right)}^{10}\exp (-\frac{h}{1000})+2.7\times {10}^{-16}\exp (-\frac{h}{1500})+A\exp (-\frac{h}{100})$$

(3)

$h$, $w$, and $A$ are the altitude, the rms windspeed and the nominal value of $C_n^2(0)$. The rms wind speed depends on the ground wind speed and the slew rate associated with the satellite moving relative to the observer on the ground. $A$ can be estimated by the altitude of the ground station. If $d$ in Equation (1) is 0 (point receiver case), Equation (1) reduces to the scintillation index described as [18,19]

$${\sigma }_I=2.25k^{7/6}{\sec }^{11/6}(\zeta ){\displaystyle {\int }_{h_0}^H{C}_n^2}(h){(h-h_0)}^{5/6}dh$$

(4)

2.2. Log-Normal Model

Log-normal model describes the optical signal intensity PDF with weak turbulence as:

$$f(I)=\frac{1}{\sqrt{2\pi {\sigma }_l^2}}\frac{1}{I}\exp \left\{-\frac{{(\ln \frac{I}{I_0}-E[l])}^2}{2{\sigma }_l^2}\right\}\hspace{1em}\hspace{1em}I\ge 0$$

(5)

For satellite-to-ground downlink channel, the value of the scintillation index expressed in (4) is typically 0.07~0.23 [19] and it can get smaller at the presence of aperture averaging. For weak turbulence, the Rytov variance ${\sigma }_l$ in (5) is simply the scintillation index [20]. After normalization, the average irradiance $I_0$ is set to be 1. The Log average irradiance value $E(l)$ is obtained as:

$$E(l)=-\frac{{\sigma }_l^2}{2}$$

(6)

with the Rytov variance ${\sigma }_l$ increasing, more sample values move towards zero and more low SNR bits appear in the communication link.

3. Receiver Model

The coherent receiver aims at improving the sensitivity taking the advantage of the local optical oscillator. After the coherent mixing of the optical signal and the local laser, the output current of detector $i$ includes DC and AC terms expressed by $i_d$ and $i_a$ [3]:

$$i(t)=i_d+i_a(t)+n(t)$$

(7)

where

$$i_d(t)=R_d(P_s+P_{LO})$$

(8)

$$i_a(t)=2R_d\sqrt{P_s{P}_{LO}}\cos (w_{if}t+\Delta \phi +\phi )$$

(9)

$R_d$, $P_S$ and $P_{LO}$ are the detector responsibility, the power of optical signal and local laser respectively. $n(t)$ is the shot noise considered as AWGN (addictive white Gaussian noise). The $w_{if}$ and $\Delta \phi$ are the frequency offset and phase offset between the optical carrier and the local oscillator. $\phi \in \{0,\pi \}$ is the phase information of BPSK.

The SNR of coherent receiver is defined as [18]

$$\gamma =\frac{\langle i_a^2(t)\rangle }{{\sigma }_n^2}=\frac{2R_d^2{P}_s{P}_{LO}}{2q{R}_d{P}_{LO}\Delta f}=\frac{R_{d}AI}{q\Delta f}$$

(10)

where

$$P_s=AI$$

(11)

${\sigma }_n^2$ is the total variance of the shot noise. $A$ and $I$ are the aperture area and normalized optical radiance through the receiving aperture. $\Delta f$ and $q$ are the noise equivalent bandwidth and the electronic charge respectively.

Assuming the received optical signal as plane wave, the average SNR in unit aperture area is

$${\rho }_0=\frac{R_d}{q\Delta f}$$

(12)

Considering the aperture diameter as a constant, the average SNR is

$${\gamma }_0=\frac{A{R}_d}{q\Delta f}$$

(13)

According to this section, large aperture area can improve the average SNR of the receiver efficiently. In addition, the noise equivalent bandwidth and the electronic charge should be limited in a suitable range.

4. Performance Analysis

To evaluate the performance of a communication system, the BER, the outage probability, and the average capacity are employed commonly. In this section, the above criterions are used to analyze the coherent satellite-to-ground optical communication system with aperture averaging. BPSK is used as the modulation.

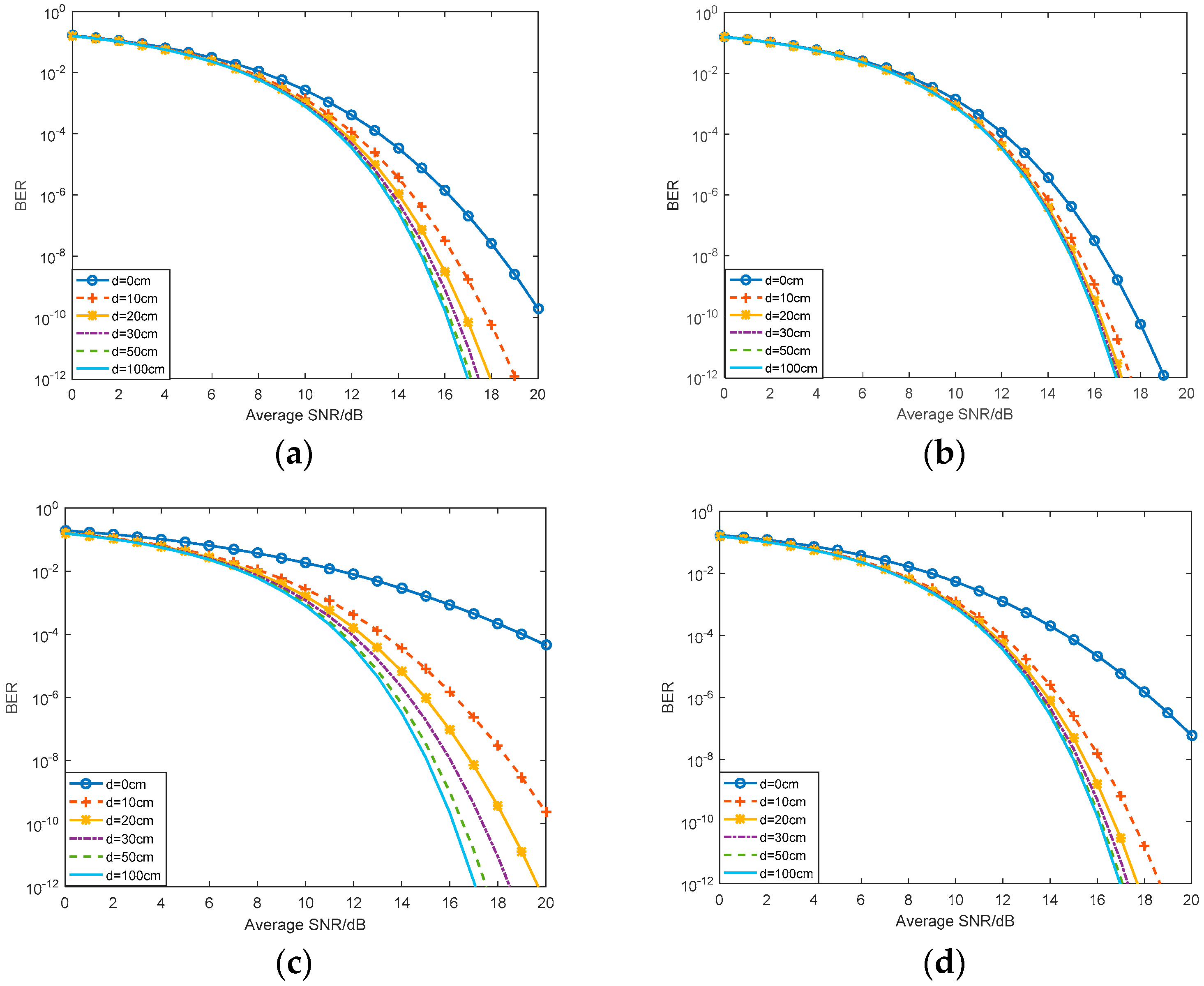
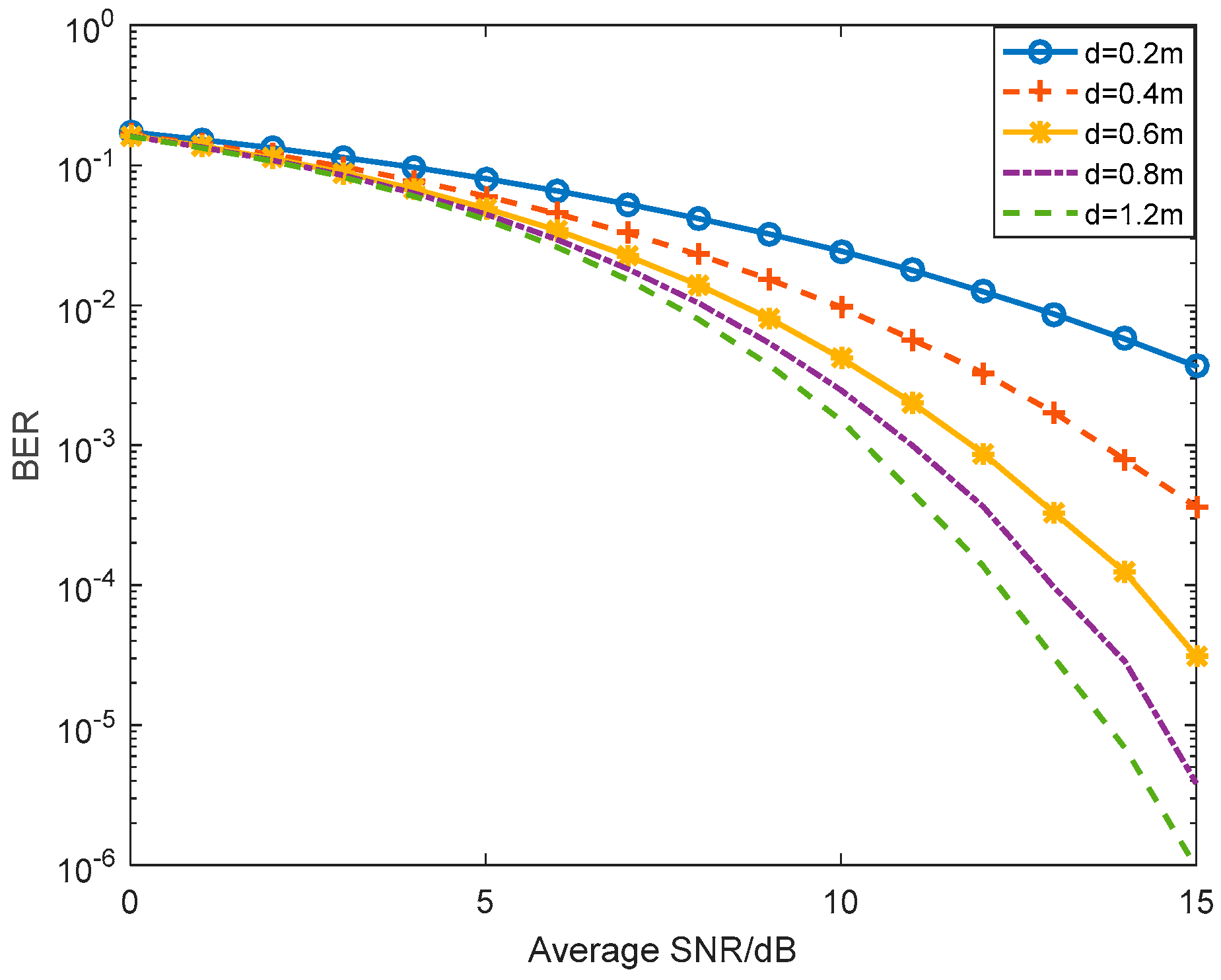
4.1. Bit Error Rate

Assuming the frequency offset $w_{if}$ and the phase offset $\Delta \phi$ between the signal and the local laser are estimated and compensated ideally, the BER of a BPSK system is expressed as [21]:

$$P_e=\frac{1}{2}{\displaystyle {\int }_0^{\infty }erfc(\sqrt{\frac{\gamma }{2}}})d\gamma$$

(14)

where $\gamma$ is the SNR described in (10). For an optical communication system with channel fading the bit error rate can be obtained as

$$P_e=\frac{1}{2}{\displaystyle {\int }_0^{\infty }f(I)erfc(\sqrt{\frac{{\gamma }_0}{2}I}})dI$$

(15)

$f(I)$ is the probability density function of irradiance $I$ described by (5). According to (5), (10), (13) and (15), $P_e$ can be expressed as:

$$P_e=\frac{1}{2}{\displaystyle {\int }_0^{\infty }\frac{1}{\sqrt{2\pi {\sigma }_l^2}}\frac{1}{I}\exp \left\{-\frac{{[\ln (\frac{I}{I_0})-E(l)]}^2}{2{\sigma }_l^2}\right\}erfc(\sqrt{\frac{{\gamma }_0}{2}I}})dI$$

(16)

$f(I)$ is determined by ${\sigma }_l$, and ${\sigma }_l$ is influenced by the aperture diameter described in (1).

If the aperture area is considered as variable as described in (11) and (12), the BER is expressed as:

$$P_e=\frac{1}{2}{\displaystyle {\int }_0^{\infty }\frac{1}{\sqrt{2\pi {\sigma }_l^2}}\frac{1}{I}\exp \left\{-\frac{{[\ln (\frac{I}{I_0})-E(l)]}^2}{2{\sigma }_l^2}\right\}erfc(\sqrt{A\frac{{\rho }_0}{2}I}})dI$$

(17)

If the frequency offset and the phase offset are not estimated ideally, the constellation of information bits rotates within certain range, and the BER may higher than the above results.

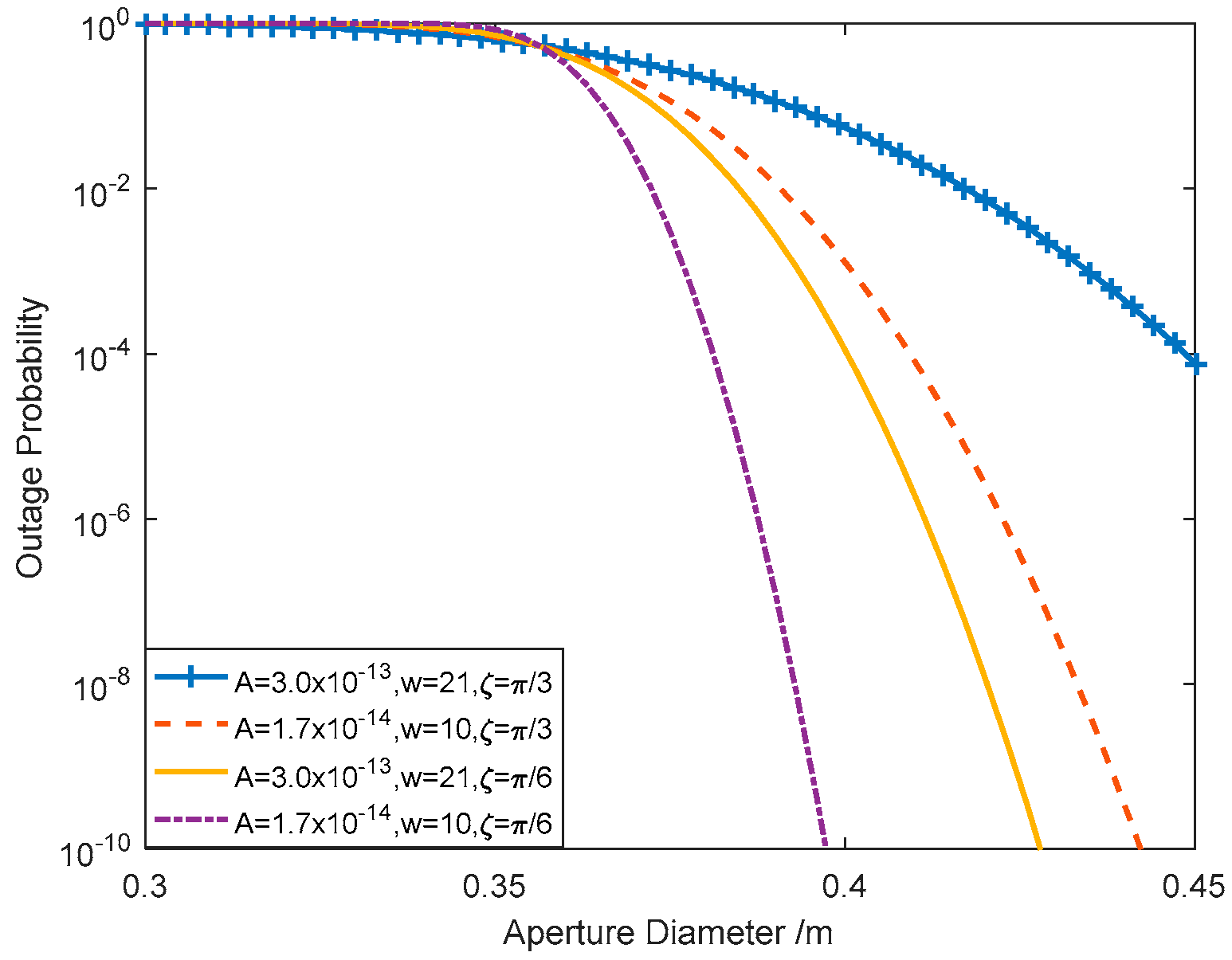
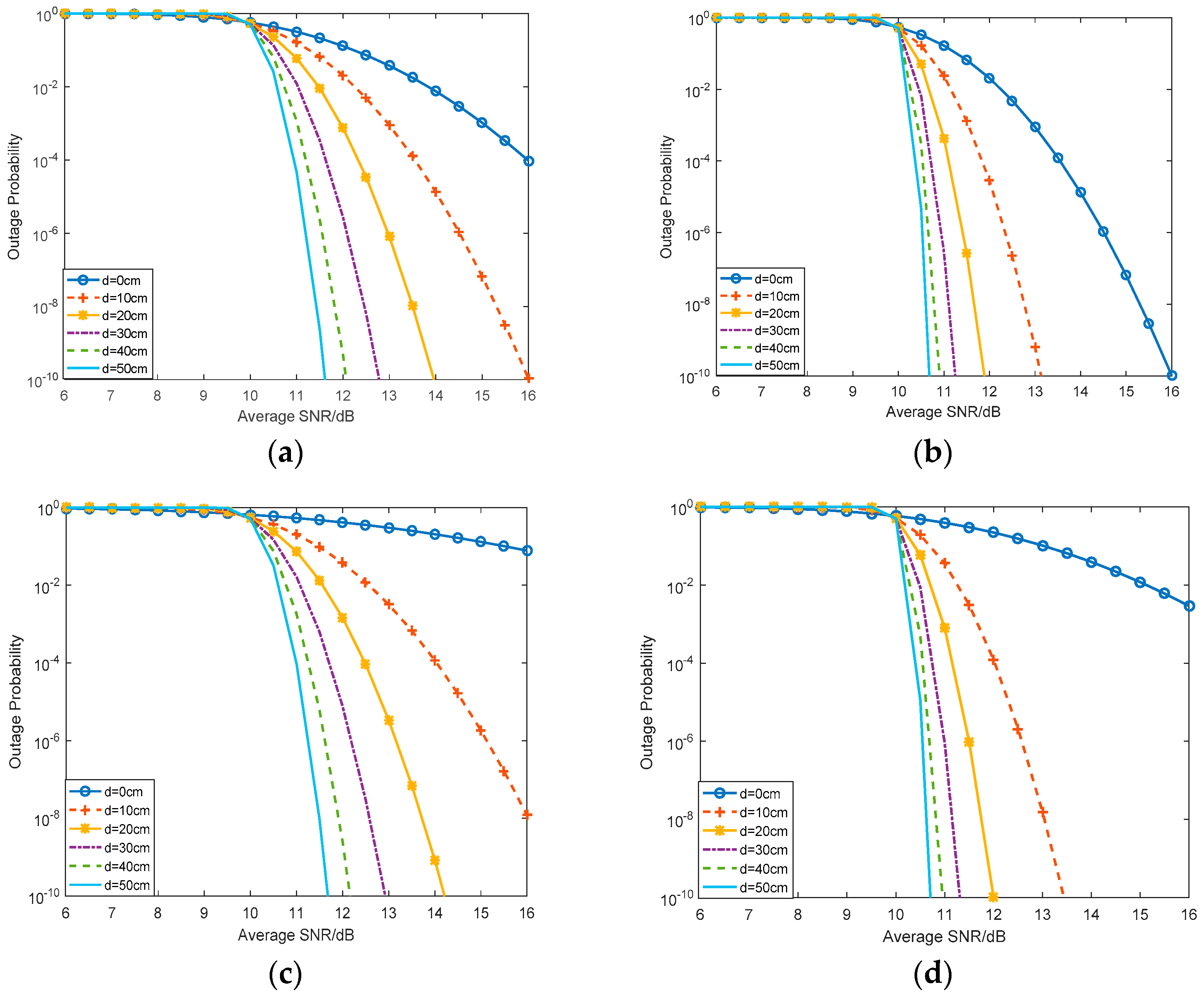
4.2. Outage Probability

Outage probability $P_o$ is another criterion evaluating the reliability of communication and it is defined as the probability when the BER is higher than a certain threshold. So, the outage probability can be described by the probability when the SNR is lower than a certain threshold. $P_o$ is expressed as:

$$P_o=P\left\{\gamma \le {\gamma }_{th}\right\}=P\left\{\frac{R_{d}AI}{q\Delta f}\le {\gamma }_{th}\right\}=P\left\{I\le \frac{{\gamma }_{th}q\Delta f}{R_{d}A}\right\}$$

(18)

where ${\gamma }_{th}$ is the SNR threshold, according to (5) and (18), $P_o$ can be rewritten as:

$$P_O={\displaystyle {\int }_0^{\frac{{\gamma }_{th}q\Delta f}{R_{d}A}}f(I)dI}={\displaystyle {\int }_0^{\frac{{\gamma }_{th}q\Delta f}{R_{d}A}}\frac{1}{\sqrt{2\pi {\sigma }_l^2}}\frac{1}{I}\exp \left\{-\frac{{[\ln (\frac{I}{I_0})-E(l)]}^2}{2{\sigma }_l^2}\right\}}dI$$

(19)

$f(I)$ is the irradiance PDF. The same as $P_e$, $P_o$ is influenced by the aperture diameter. According to (13), the upper limit in (19) can be rewritten as:

$$\frac{{\gamma }_{th}q\Delta f}{R_{d}A}=\frac{{\gamma }_{th}}{{\gamma }_0}$$

(20)

Assuming the aperture area is variable, the outage probability is:

$$P_o=\left\{A{\rho }_{0}I\le {\gamma }_{th}\right\}=P\left\{I\le \frac{{\gamma }_{th}}{A{\rho }_0}\right\}={\displaystyle {\int }_0^{\frac{{\gamma }_{th}}{A{\rho }_0}}f(I)dI}$$

(21)

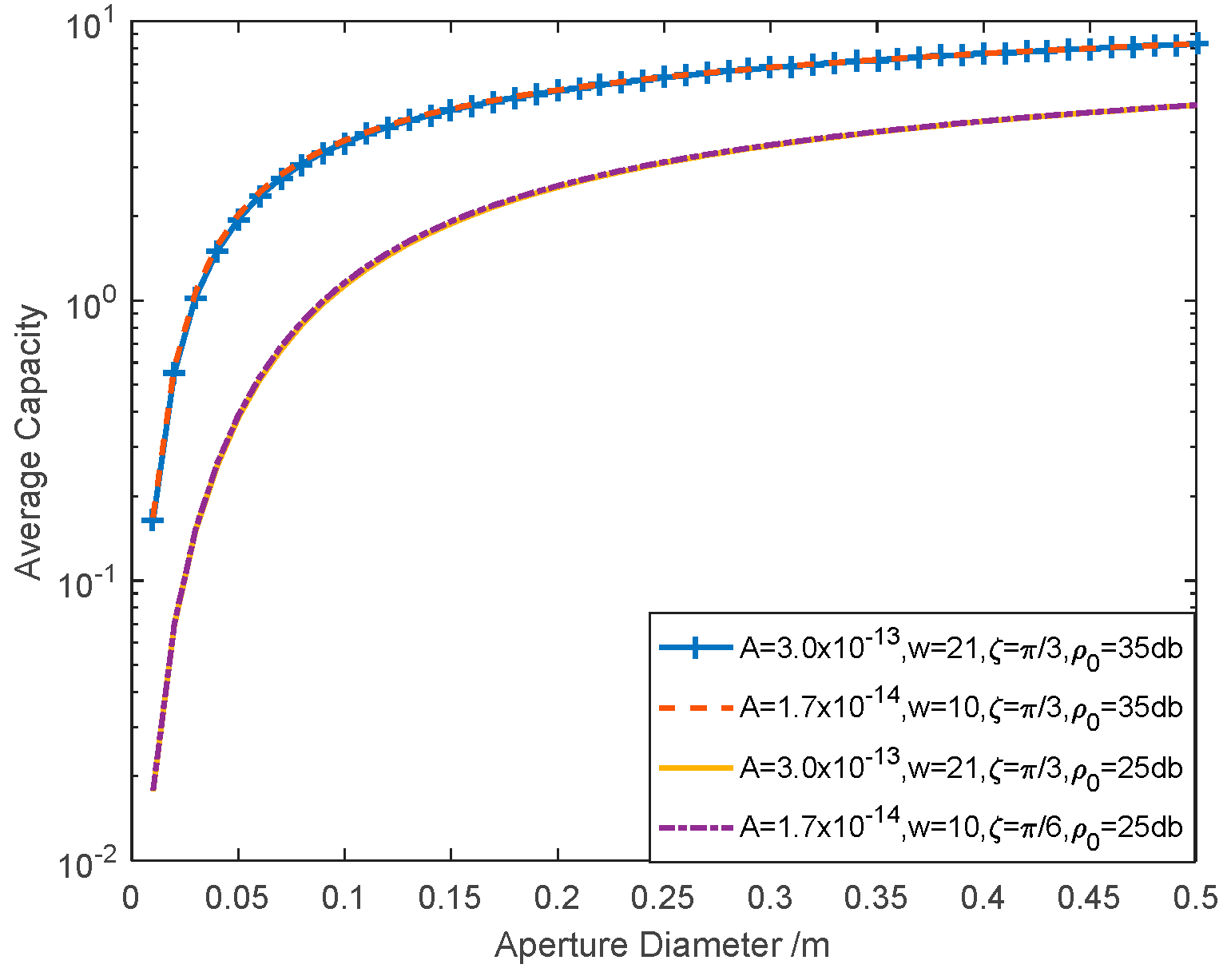
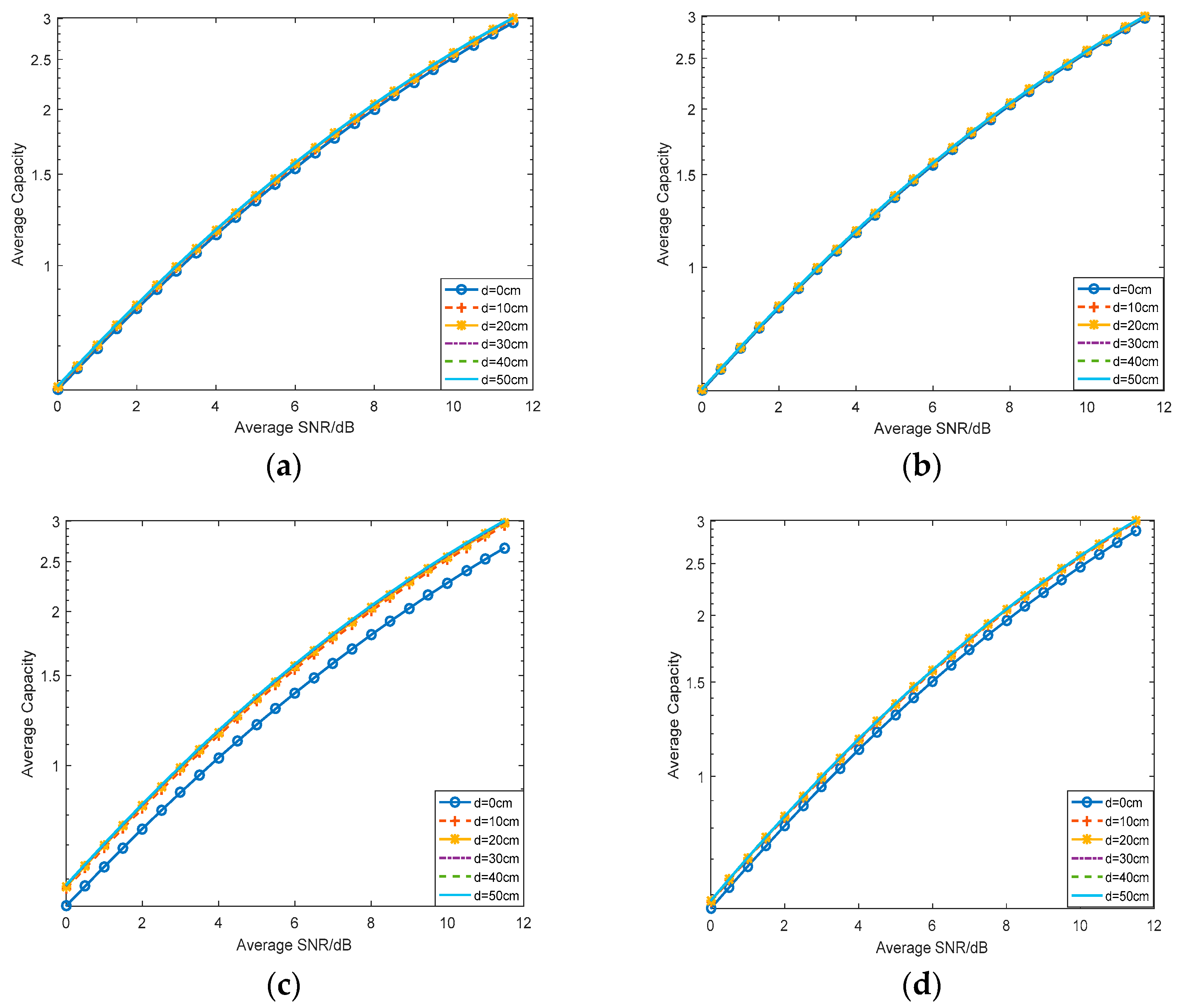
4.3. Average Capacity

If the state of the transmitter, the receiver and the channel are known, the average capacity of FSO system $<C>$ is [22]:

$$<C>=B{\displaystyle {\int }_0^{\infty }{\log }_2}(1+\frac{\gamma }{2})f(I)dI$$

(22)

$B$ is the bandwidth and is normalized to be 1 in this paper. The average capacity is also influenced by the aperture diameter. According to (12) and (13), the average capacity can be rewritten as:

$$<C>={\displaystyle {\int }_0^{\infty }{\log }_2}(1+\frac{R_{d}AI}{2q\Delta f})f(I)dI={\displaystyle {\int }_0^{\infty }{\log }_2}(1+A\frac{{\rho }_0}{2}I)f(I)dI={\displaystyle {\int }_0^{\infty }{\log }_2}(1+\frac{{\gamma }_0}{2}I)f(I)dI$$

(23)

The above three criterions depend on the average SNR and the optical intensity probability density. With the receiving aperture area decreasing, the Rytov variance increases and more low SNR bits cause higher BER, higher outage rate and lower average capacity.

5. Numerical Results

In this paper, the satellite height is 3.6 × 10³ km and the altitude of receiver is 0. According to simulation, $C_n^2(h)$ changes little with satellite height increasing, when the height is over 20 km. The satellite slew rate is related to the height, which influences the rms wind speed. The laser wavelength is 1550 nm.

It is assumed that the aperture area is variable, the power of the signal received by the aperture increases and the scintillation index of irradiance decreases with the aperture diameter increasing. The BER against aperture area are shown in Figure 1. Each curve has its certain satellite zenith angle, atmospheric parameter, and ${\rho }_0$ in (17).

To investigate the improvement of aperture averaging in further, Figure 2 shows BER of the receiver with different apertures against the average SNR ${\gamma }_0$. When the zenith angle is larger and the atmosphere turbulence is stronger, the effect of aperture averaging is more obvious. According Figure 2b with weak turbulence and small zenith angle, the improvement of aperture averaging is limited, when $d\ge 50\mathrm{cm}$. In Figure 2c, when BER = 10⁻⁸, the noise endurance differences between d = 10 cm and d = 20 cm is nearly 2 dB, the same as the noise endurance difference between d = 20 cm and d = 50 cm.

Similar to the analyzing of BER, the outage probability is analyzed in two ways. In Figure 3, the outage probability decreases rapidly with aperture diameter increasing, once the average SNR is over the threshold. Here the average SNR in unit aperture area ${\rho }_0$ is set to be 20 dB, and the threshold value of the SNR ${\gamma }_{th}$ is 10 dB. When the diameter is smaller than 0.36 m, the outage probability values are all nearly 1 as a result of lower SNR and higher scintillation index.

The effect made by different aperture diameters, different zenith angles and atmospheric conditions on the outage probability is shown in Figure 4. The SNR threshold ${\gamma }_{th}$ is set to be 10 dB. When the SNR exceeds the threshold, the curves of point receiver model ($d=0$) drop more slowly than others. When the outage probability is 10⁻⁴ in Figure 4c, the aperture with d = 20 cm needs more than 1 dB higher SNR than d = 50 cm.

The average capacity against the aperture diameter when ${\rho }_0=25\mathrm{dB}$ and ${\rho }_0=35\mathrm{dB}$ is shown in Figure 5. Each curve with the same average SNR overlaps with each other nearly in spite of the different atmospheric conditions and satellite zenith angles. To some extent, enough average SNR play more important role in average capacity than the atmospheric condition.

The average capacity against the average SNR is shown in Figure 6. When the zenith angle is larger and the turbulence is stronger, the differences of the average capacity with different aperture diameters are more obvious. According to the curves, the aperture averaging effect of average capacity is less obvious than the effect of BER. The curves overlap with each other nearly when d = 10 cm, 20 cm, 30 cm, 40 cm, 50 cm, especially in Figure 6b.

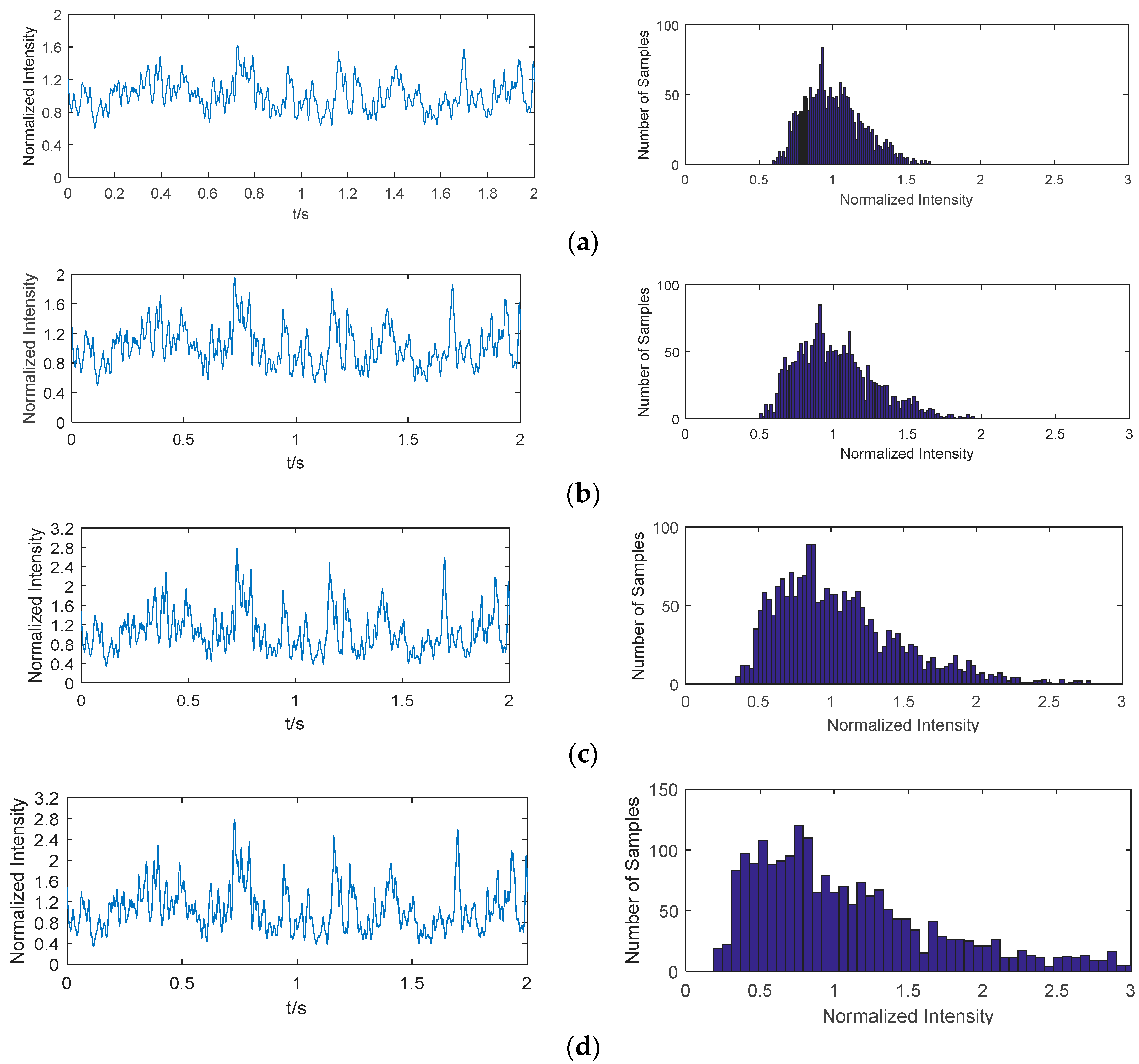
6. BER Performance Based on Measuring Data

To evaluate the performance of coherent optical link with aperture averaging further, a group of channel gain data collected by the ground station of the LEO quantum communication satellite located Xinjiang of China is employed. The channel gain data of apertures with various diameters can be obtained by changing the statistical parameter of the data collected by the telescope with 1.2 m diameter.

Figure 7 shows the channel gain curve collected by 1.2 m telescope within 2 s and the histogram with 2042 samples (1041 samples/s). The zenith angle is 61° and the rms wind speed is 76 m/s. The altitude of the ground station is 2080 m and the $C_n^2$ at this altitude is estimated as $9.86\times {10}^{-17}$. The satellite altitude is assumed as 500 km. The theoretical scintillation index at the experience condition is 0.0136 and the realistic scintillation index is 0.0150.

Changing the scintillation index of the data shown as Figure 7, according to Equation (1) and [23], we obtain the channel gain curves of different aperture diameters shown as Figure 8.

Using the channel gain data, the BER performance with various aperture diameters is shown as Figure 9. The coherent BPSK scheme is employed. This result has agreement to the theorical results of Figure 2 and the BER of the same aperture diameter is higher than Figure 2 as a result of stronger turbulence.

7. Conclusions and Future Work

The performance of satellite-to-ground coherent optical communication downlink with aperture averaging is investigated. The results demonstrate that aperture averaging can improve the reliability of communication efficiently, especially with stronger turbulence and larger zenith angles. With the aperture increasing continuously, the wave front aberration can degrade the communication performance inevitably, especially for the coherent optical link. An adaptive system installed in the large aperture receiver on the ground can compensate the wave front aberration effectively [24]. To improve the reliability of the communication system in further, a coherent multiple apertures diversity receiving system will be investigated. The amount and diameters of the apertures of a diversity receiving system will be analyzed.