Improving Security and Reliability in Merkle Tree-Based Online Data Authentication with Leakage Resilience
Abstract
:1. Introduction
- We analyze potential information leakage during the online verification process. It includes partial information of the Merkle tree and size information, which weaken the security and reliability of authentication (Section 3).
- We evaluate efficiency of the proposed scheme by implementing it in a real-world application. It shows that our approach can flexibly be adjusted to required system resources with minimal overhead. Nonetheless, it still supports leakage resilience that was not guaranteed in previous research (Section 6).
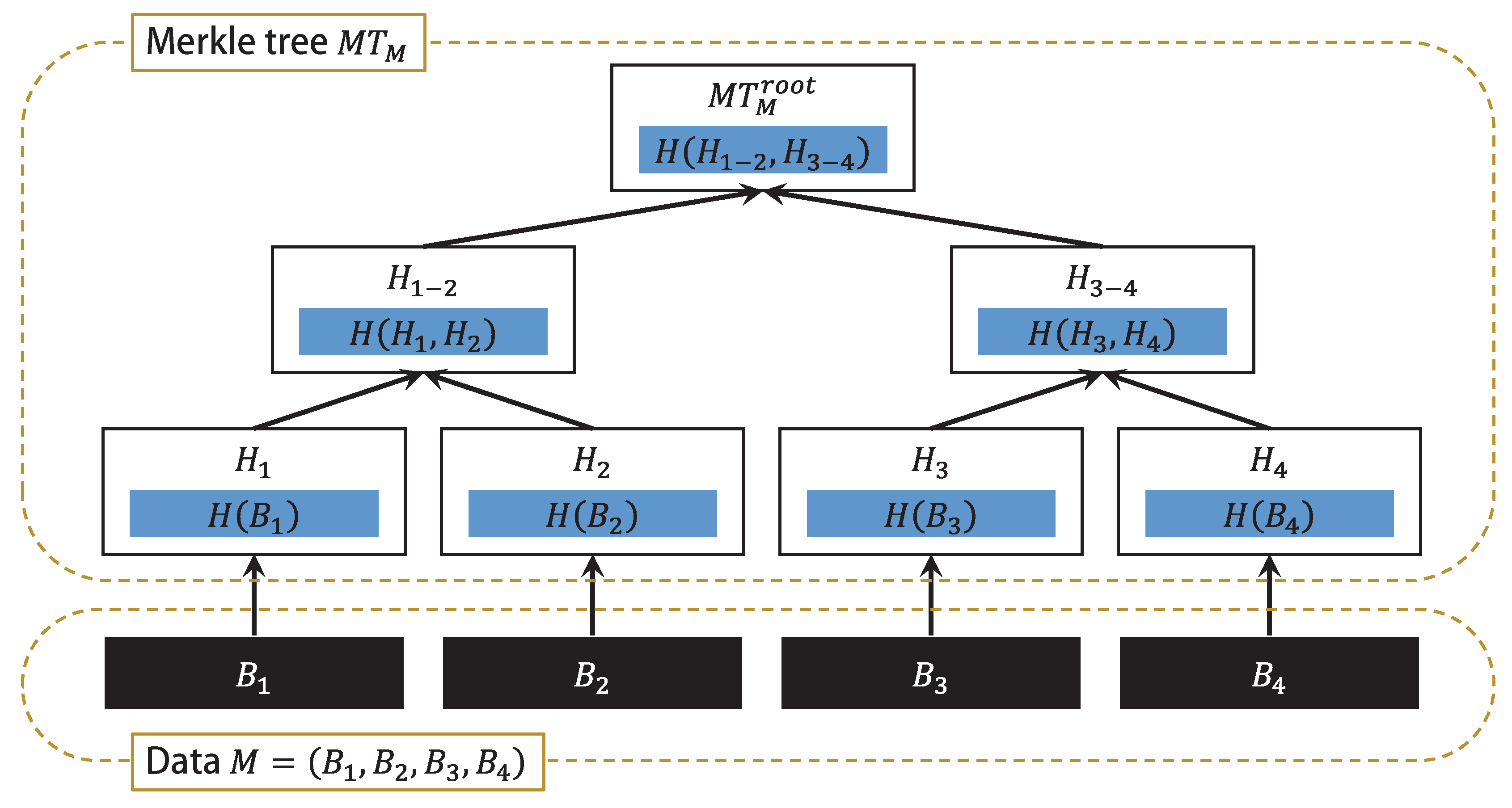
2. Merkle Tree-Based Authentication
- Prover is an entity who attempts to convince the other party (i.e., the verifier ) that it owns all of the data. To converve network bandwidth, the prover sends a small piece of verifiable information instead of all of the content.
- Verifier is another entity who tries to determine whether prover ’s claim is correct or not. To reduce storage requirements, the verifier usually stores only the value of the root node of the Merkle tree instead of all nodes of the tree.
3. Information Leakage Analysis of Merkle Tree-Based Authentication Schemes
3.1. Analysis of Merkle Tree-Based Authentication
3.1.1. Leakage of Data Size Information
3.1.2. Leakage of Merkle Tree Hash Values
3.2. Previous Schemes and Their Vulnerabilities
3.2.1. Generic Merkle Tree-Based Authentication
3.2.2. Authentication without a Merkle Tree
| Algorithm 1 Randomized online authentication exploiting a hardcore function |
 |
3.2.3. Merkle Tree-Based Authentication of Encrypted Data
3.2.4. Merkle Tree-Based Authentication with Transmission in Encrypted Form
| Algorithm 2 Merkle tree-based online authentication with encrypted communication |
 |
4. Randomized Online Authentication
4.1. Adversarial Model
4.2. Goal
- Prevention of size information leakage: The authentication mechanism should block the outflow of information about the size of the target data, which can be used by adversaries to select and predict the required number of authentication proofs.
- Prevention of replay attacks: The protocol should not allow adversaries to launch replay attacks, in which a collected valid set of authentication proofs are used in subsequent authentication requests. In other words, the adversary cannot learn any information from the disclosed information via public channels during the authentication process.
- Minimal requctions in efficiency: The effective handling of side channels should be achieved with acceptable computation and communication overhead, maintaining the advantages of the Merkle tree-based approach.
- Compatability: Given that the Merkle tree-based approach is widely deployed in industry and academia due to its intuitive nature and ease of utilization, the proposed approach should be applicable to existing uses. This includes adaptability to lightweight devices with limited resources and restrictions on the installation of additional libraries depending on the system architecture, such as IoT terminal devices and sensors.
4.3. Construction
| Algorithm 3 Merkle tree-based online authentication with randomized input |
 |
4.3.1. Authentication Initiation
4.3.2. Randomized Challenge Generation
4.3.3. Original Challenge Restoration
4.3.4. Proof Generation
4.3.5. Proof Obfuscation
4.3.6. (Original) Proof Restoration
4.3.7. Proof Verification
5. Security Analysis
5.1. Security of Merkle Tree-based Authentication
5.2. Security of the Proposed Scheme
5.2.1. Security of One-time Secret Delivery
5.2.2. Security of the Proposed Scheme
6. Efficiency Analysis
6.1. Experimental Environment
6.2. Computation Overhead
6.2.1. Authentication Based on Merkle Tree
6.2.2. Authentication Based on the Hardcore Function
6.2.3. Authentication Based on Merkle Tree with Transmission in Encrypted Form
6.2.4. Authentication Based on the Proposed Approach
6.2.5. Analysis of Computation Overhead
6.3. Communication Overhead
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- CPA Practice Advisor. The Top Cyber Risks to Accounting Firms Come from Inside the Firm. Available online: https://www.cpapracticeadvisor.com/news/12427308/the-top-cyber-risks-to-accounting-firms-come-from-inside-the-firm (accessed on 13 September 2018).
- Chen, C.; Deng, I. Tencent Cloud Says Ímproper Operationsĺed to Data Loss for Client as It Seeks to Implement Improvements. Available online: https://www.scmp.com/tech/article/2158785/tencent-cloud-says-improper-operations-led-data-loss-client-it-seeks-implement (accessed on 13 September 2018).
- Zeng, K. Publicly Verifiable Remote Data Integrity. In Information and Communications Security; Springer: New York, NY, USA, 2008; pp. 419–434. [Google Scholar] [CrossRef]
- Henry, J. These 5 Types of Insider Threats Could Lead to Costly DAta Breaches. Available online: https://securityintelligence.com/these-5-types-of-insider-threats-could-lead-to-costly-data-breaches/ (accessed on 13 September 2018).
- Sambit, k. Global Cloud Data Loss Prevention (DLP) Market 2023 Growth Factors, Regional Analysis by Types, Applications, & Manufacturers with Forecasts. Available online: https://thetradereporter.com/global-cloud-data-loss-prevention-dlp-market-2023-growth-factors-egional-analysis-by-types-applications-manufacturers-with-forecasts/139976/ (accessed on 13 September 2018).
- Vacca, J.R. Cloud Computing Security: Foundations and Challenges; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Symantec Corporation. Symantec Data Loss Prevention. Available online: https://www.symantec.com/products/data-loss-prevention/ (accessed on 13 September 2018).
- Trustwave Holdings, Inc. Trustwave Data Loss Prevention. Available online: https://www.trustwavecompliance.com/solutions/compliance-technologies/data-loss-prevention/ (accessed on 13 September 2018).
- McAfee, LLC. McAfee Total Protection for Data Loss Prevention. Available online: https://www.mcafee.com/enterprise/en-ca/products/total-protection-for-data-loss-prevention.html/ (accessed on 13 September 2018).
- Check Point Software Technologies, Ltd. Data Loss Prevention Software Blade. Available online: https://www.checkpoint.com/products/dlp-software-blade/ (accessed on 13 September 2018).
- Digital Guardian. Digital Guardian Encpoint DLP. Available online: https://digitalguardian.com/products/endpoint-dlp/ (accessed on 13 September 2018).
- Merkle, R.C. A Digital Signature Based on a Conventional Encryption Function. In Advances in Cryptology—CRYPTO; Springer: Berlin/Heidelberg, Germany, 1988; pp. 369–378. [Google Scholar] [CrossRef]
- Swan, M. Blockchain Thinking: The Brain as a Decentralized Autonomous Corporation [Commentary]. IEEE Technol. Soc. Mag. 2015, 34, 41–52. [Google Scholar] [CrossRef]
- Liang, X.; Shetty, S.; Tosh, D.; Kamhoua, C.; Kwiat, K.; Njilla, L. ProvChain: A Blockchain-based Data Provenance Architecture in Cloud Environment with Enhanced Privacy and Availability. In Proceedings of the 2017 IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing (CCGrid ’17), Madrid, Spain, 14–17 May 2017; pp. 468–477. [Google Scholar] [CrossRef]
- Bitcoin. Available online: https://www.bitcoin.com/ (accessed on 13 September 2018).
- Halevi, S.; Harnik, D.; Pinkas, B.; Shulman-Peleg, A. Proofs of Ownership in Remote Storage Systems. In Proceedings of the 2011 ACM Conference on Computer and Communications Security (CCS), Chicago, IL, USA, 17–21 October 2011; pp. 491–500. [Google Scholar] [CrossRef]
- Yang, C.; Ren, J.; Ma, J. Provable Ownership of Files in Deduplication Cloud Storage. Secur. Commun. Netw. 2015, 8, 2457–2468. [Google Scholar] [CrossRef]
- Armknecht, F.; Boyd, C.; Davies, G.T.; Gjøsteen, K.; Toorani, M. Side Channels in Deduplication: Trade-offs Between Leakage and Efficiency. In Proceedings of the 2017 ACM on Asia Conference on Computer and Communications Security (ASIA CCS ’17), Abu Dhabi, UAE, 2–6 April 2017; pp. 266–274. [Google Scholar] [CrossRef]
- Koo, D.; Shin, Y.; Yun, J.; Hur, J. An Online Data-Oriented Authentication Based on Merkle Tree with Improved Reliability. In Proceedings of the 2017 IEEE International Conference on Web Services (ICWS), Honolulu, HI, USA, 25–30 June 2017; pp. 840–843. [Google Scholar] [CrossRef]
- Merkle, R.C. A Certified Digital Signature. In Advances in Cryptology—CRYPTO; Springer: New York, NY, USA, 1990; pp. 218–238. [Google Scholar]
- Lamport, L. Constructing Digital Signatures from a One-Way Function; Technical Report, Technical Report CSL-98; SRI International Palo Alto: Menlo Park, CA, USA, 1979. [Google Scholar]
- Kundu, A.; Atallah, M.J.; Bertino, E. Leakage-free Redactable Signatures. In Proceedings of the 2012 ACM Conference on Data and Application Security and Privacy, CODASPY ’12, San Antonio, TX, USA, 7–9 February 2012; ACM: New York, NY, USA, 2012; pp. 307–316. [Google Scholar] [CrossRef]
- Buldas, A.; Laur, S. Knowledge-Binding Commitments with Applications in Time-Stamping. In Public Key Cryptography—PKC; Springer: Berlin/Heidelberg, Germany, 2007; pp. 150–165. [Google Scholar]
- Wikipedia. Binary Tree. Available online: https://en.wikipedia.org/wiki/Binary_tree/ (accessed on 13 September 2018).
- Ateniese, G.; Burns, R.; Curtmola, R.; Herring, J.; Kissner, L.; Peterson, Z.; Song, D. Provable Data Possession at Untrusted Stores. In Proceedings of the ACM Conference on Computer and Communications Security (CCS), Alexandria, VA, USA, 28–31 October 2007; pp. 598–609. [Google Scholar] [CrossRef]
- Zhao, Y.; Chow, S.S.M. Towards Proofs of Ownership Beyond Bounded Leakage. In Proceedings of the 2016 International Conference on Provable Security (ProvSec), Nanjing, China, 10–11 November 2016; pp. 340–350. [Google Scholar] [CrossRef]
- Atallah, M.J.; Cho, Y.; Kundu, A. Efficient Data Authentication in an Environment of Untrusted Third-Party Distributors. In Proceedings of the IEEE 24th International Conference on Data Engineering, Cancun, Mexico, 7–12 April 2008; pp. 696–704. [Google Scholar] [CrossRef]
- Atallah, M.J.; Li, J. Enhanced smart-card based license management. In Proceedings of the 2003 IEEE International Conference on E-Commerce, CEC 2003, Newport Beach, CA, USA, 24–27 June 2003; pp. 111–119. [Google Scholar] [CrossRef] [Green Version]
- Benjamin, D.; Atallah, M.J. Private and Cheating-Free Outsourcing of Algebraic Computations. In Proceedings of the 2008 Annual Conference on Privacy, Security and Trust, Fredericton, NB, Canada, 1–3 October 2008; pp. 240–245. [Google Scholar] [CrossRef]
- Keelveedhi, S.; Bellare, M.; Ristenpart, T. DupLESS: Server-Aided Encryption for Deduplicated Storage. In Proceedings of the 22nd USENIX Security Symposium, Washington, DC, USA, 14–16 August 2013; pp. 179–194. [Google Scholar]
- Xu, J.; Chang, E.C.; Zhou, J. Weak Leakage-resilient Client-side Deduplication of Encrypted Data in Cloud Storage. In Proceedings of the 2013 ACM SIGSAC Symposium on Information, Computer and Communications Security, ASIA CCS ’13, Berlin, Germany, 4–8 November 2013; pp. 195–206. [Google Scholar] [CrossRef]
- Li, H.; Lu, R.; Zhou, L.; Yang, B.; Shen, X. An Efficient Merkle-Tree-Based Authentication Scheme for Smart Grid. IEEE Syst. J. 2014, 8, 655–663. [Google Scholar] [CrossRef]
- Rogaway, P.; Shrimpton, T. Cryptographic Hash-Function Basics: Definitions, Implications, and Separations for Preimage Resistance, Second-Preimage Resistance, and Collision Resistance. In Fast Software Encryption; Springer: Berlin/Heidelberg, Germany, 2004; pp. 371–388. [Google Scholar]
- Merkle, R.C. Protocols for Public Key Cryptosystems. In Proceedings of the 1980 IEEE Symposium on Security and Privacy, Oakland, CA, USA, 14–16 April 1980; p. 122. [Google Scholar] [CrossRef]
- Becker, G. Merkle Signature Schemes, Merkle Trees and Their Cryptanalysis; Technical Report; Ruhr-University Bochum: Bochum, Germany, 2008. [Google Scholar]
- Koblitz, N.; Menezes, A.J. Cryptocash, cryptocurrencies, and cryptocontracts. Des. Codes Cryptogr. 2016, 78, 87–102. [Google Scholar] [CrossRef]
- Bellare, M.; Pointcheval, D.; Rogaway, P. Authenticated Key Exchange Secure against Dictionary Attacks. In Advances in Cryptology—EUROCRYPT 2000; Springer: Berlin/Heidelberg, Germany, 2000; pp. 139–155. [Google Scholar]
- Wikipedia. Entropy (Information Theory). Available online: https://en.wikipedia.org/wiki/Entropy_(information_theory) (accessed on 13 September 2018).
- Information Assurance by the National Security Agency. Commercial National Security Algorithm (CNSA) Suite. Available online: https://www.iad.gov/iad/customcf/openAttachment.cfm?FilePath=/iad/library/ia-guidance/ia-solutions-for-classified/algorithm-guidance/assets/public/upload/Commercial-National-Security-Algorithm-CNSA-Suite-Factsheet.pdf&WpKes=aF6woL7fQp3dJiShxsuwyRvADMxf4cwBTYEUSz (accessed on 13 September 2018).
- Python Software Foundation. pycrypto. Available online: https://pypi.org/project/pycrypto/ (accessed on 13 September 2018).
- Python Software Foundation. python. Available online: https://www.python.org/ (accessed on 13 September 2018).
- Python Software Foundation. pysha3. Available online: https://pypi.org/project/pysha3/ (accessed on 13 September 2018).











| Notation | Description |
|---|---|
| Cryptographic hash function | |
| Size of the hash value (in bits) | |
| n | Number of data blocks for the entire data D |
| Merkle tree constructed from data D | |
| Root node in the Merkle tree | |
| h | Height of the Merkle tree |
| L | Required length of the sibling path in the authentication proof |
| Value of the given node N | |
| Sibling node in the sibling path for the given node N | |
| i-th element in sequence A (cardinality) | |
| Number of elements in set A | |
| Random selection of element a in set A | |
| Assignment of the result of the deterministic algorithm (operation) B to b | |
| Assignment of the result of the probabilistic algorithm (operation) B to b |
| 100 B | 1 KB | 10 KB | 100 KB | 1 MB | 10 MB | 100 MB | 1 GB | |
|---|---|---|---|---|---|---|---|---|
| Merkle tree generation | 0.00461 | 0.01748 | 0.11897 | 1.05451 | 10.67579 | 107.07319 | 1134.07592 | 11,191.59684 |
| (0.00062) | (0.00080) | (0.00247) | (0.00723) | (0.09199) | (1.07465) | (19.51252) | (33.31233) | |
| Challenge generation | 0.00086 | 0.00086 | 0.00099 | 0.00101 | 0.00100 | 0.00100 | 0.00087 | 0.00087 |
| (0.00019) | (0.00017) | (0.00020) | (0.00021) | (0.00021) | (0.00023) | (0.00017) | (0.00016) | |
| Sibling path generation | 0.00201 | 0.00389 | 0.00662 | 0.00863 | 0.01101 | 0.01258 | 0.02032 | 0.02273 |
| (0.00024) | (0.00066) | (0.00048) | (0.00038) | (0.00059) | (0.00054) | (0.00159) | (0.00168) | |
| Verification | 0.00127 | 0.00417 | 0.00937 | 0.01398 | 0.01836 | 0.02369 | 0.02840 | 0.03294 |
| (0.00034) | (0.00030) | (0.00077) | (0.00075) | (0.00096) | (0.00149) | (0.00085) | (0.00096) |
| 100 B | 1 KB | 10 KB | 100 KB | 1 MB | 10 MB | 100 MB | 1 GB | |
|---|---|---|---|---|---|---|---|---|
| Seed generation | 0.00065 | 0.00075 | 0.00092 | 0.00223 | 0.00313 | 0.00420 | 0.00822 | 0.01068 |
| (0.00016) | (0.00018) | (0.00020) | (0.00061) | (0.00037) | (0.00054) | (0.00101) | (0.00119) | |
| Pseudorandom bitstring | 0.01106 | 0.01417 | 0.03730 | 0.28324 | 4.12432 | 44.29721 | 450.26368 | 4690.52351 |
| generation | (0.00085) | (0.00133) | (0.00351) | (0.02986) | (0.79537) | (8.69847) | (89.4971) | (488.92123) |
| Proof generation | 0.04765 | 0.57035 | 7.20359 | 84.95004 | 1058.25365 | 12,523.93617 | 139,315.96462 | 1,666,976.31436 |
| (0.00148) | (0.01614) | (0.09508) | (0.86894) | (2.32808) | (8.65474) | (236.08956) | (2663.86754) | |
| Verification | 0.00018 | 0.00019 | 0.00022 | 0.00032 | 0.00036 | 0.00036 | 0.00036 | 0.00100 |
| (0.00014) | (0.00014) | (0.00013) | (0.00013) | (0.00013) | (0.00013) | (0.00014) | (0.00023) |
| 100 B | 1 KB | 10 KB | 100 KB | 1 MB | 10 MB | 100 MB | 1 GB | |
|---|---|---|---|---|---|---|---|---|
| Parameter | 9468.19790 | 9538.16482 | 9794.65946 | 9532.98866 | 9452.51795 | 9727.44050 | 9064.76798 | 9633.54744 |
| generation | (8493.82876) | (8975.20449) | (9175.01323) | (8829.14856) | (8759.71474) | (9374.65954) | (7981.16155) | (8863.74385) |
| Partial key | 4.80688 | 4.79883 | 4.78975 | 4.79192 | 4.80195 | 4.80006 | 4.81253 | 4.96501 |
| generation | (0.18776) | (0.18395) | (0.18719) | (0.18367) | (0.18475) | (0.18142) | (0.19221) | (0.25943) |
| Key | 4.57732 | 4.57399 | 4.56398 | 4.56755 | 4.57577 | 4.57745 | 4.57501 | 4.57433 |
| agreement | (0.13962) | (0.14449) | (0.14221) | (0.15151) | (0.15099) | (0.14848) | (0.14461) | (0.14200) |
| Challenge | 0.00087 | 0.00098 | 0.00091 | 0.00088 | 0.00100 | 0.00087 | 0.00099 | 0.00087 |
| generation | (0.00018) | (0.00020) | (0.00020) | (0.00016) | (0.00021) | (0.00016) | (0.00023) | (0.00018) |
| Encryption of | 0.02674 | 0.02647 | 0.02668 | 0.02702 | 0.03341 | 0.03457 | 0.03739 | 0.05227 |
| the challenge | ( 0.00145) | (0.00140) | (0.00117) | (0.0013) | (0.00210) | (0.00235) | (0.00323) | (0.00281) |
| Decryption of | 0.01458 | 0.01567 | 0.01597 | 0.01776 | 0.01967 | 0.02292 | 0.02444 | 0.02568 |
| the challenge | (0.00068) | (0.00065) | (0.00042) | (0.00088) | (0.00118) | (0.00097) | (0.00064) | (0.00066) |
| Merkle tree | 0.00324 | 0.01570 | 0.11664 | 1.05112 | 10.55169 | 106.34833 | 1072.881132 | 11,196.73308 |
| generation | (0.00024) | (0.00043) | (0.00184) | (0.03182) | (0.08447) | (0.36833) | (6.69879) | (33.06858) |
| Sibling path | 0.00271 | 0.00429 | 0.00655 | 0.00808 | 0.01018 | 0.01172 | 0.01773 | 0.02247 |
| generation | (0.00033) | (0.00042) | (0.00047) | (0.00054) | (0.00079) | (0.00047) | (0.00100) | (0.00101) |
| Encryption of | 0.01639 | 0.01751 | 0.01866 | 0.02067 | 0.02978 | 0.04813 | 0.05219 | 0.05405 |
| the sibling path | (0.00061) | (0.00043) | (0.00089) | (0.00117) | (0.00323) | (0.00177) | (0.00118) | (0.00357) |
| Decryption of | 0.01782 | 0.01776 | 0.01895 | 0.01714 | 0.01790 | 0.01957 | 0.02026 | 0.02090 |
| the sibling path | (0.00061) | (0.00071) | (0.00062) | (0.00085) | (0.00058) | (0.00102) | (0.00080) | (0.00129) |
| Verification | 0.00130 | 0.00454 | 0.00981 | 0.01408 | 0.01836 | 0.02378 | 0.02848 | 0.03252 |
| (0.00018) | (0.00041) | (0.00078) | (0.00091) | (0.00112) | (0.00121) | (0.00088) | (0.00041) |
| 100 B | 1 KB | 10 KB | 100 KB | 1 MB | 10 MB | 100 MB | 1 GB | |
|---|---|---|---|---|---|---|---|---|
| Requested proof length | 49.04100 | 50.84400 | 52.70700 | 52.58500 | 52.22300 | 51.67100 | 50.86000 | 50.81600 |
| (27.97269) | (28.63403) | (27.93591) | (28.83915) | (28.47626) | (28.3989) | (27.28825) | (28.78524) | |
| Merkle tree generation | 0.00299 | 0.01417 | 0.11407 | 1.04286 | 10.53377 | 106.27209 | 1081.34281 | 11,178.68500 |
| (0.00098) | (0.00324) | (0.03135) | (0.29979) | (3.02505) | (30.96492) | (320.58949) | (354.27592) | |
| Challenge generation | 0.00216 | 0.00226 | 0.00247 | 0.00243 | 0.00216 | 0.00240 | 0.00243 | 0.00238 |
| (0.00068) | (0.00067) | (0.00062) | (0.00053) | (0.00070) | (0.00056) | (0.00059) | (0.00068) | |
| Sibling path generation | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00002 | 0.00002 | 0.00003 | 0.00002 |
| (0.00000) | (0.00000) | (0.00000) | (0.00000) | (0.00000) | (0.00000) | (0.00000) | (0.00000) | |
| Sibling path obfuscation | 0.04547 | 0.06643 | 0.10507 | 0.13948 | 0.17899 | 0.23363 | 0.26413 | 0.29186 |
| (0.00596) | (0.00338) | (0.01607) | (0.01782) | (0.02655) | (0.03630) | (0.04581) | (0.06181) | |
| Random bitstring padding | 0.89665 | 0.87894 | 0.85868 | 0.78980 | 0.72994 | 0.66017 | 0.59333 | 0.55448 |
| (0.54933) | (0.53655) | (0.53474) | (0.53037) | (0.51176) | (0.49959) | (0.46923) | (0.47786) | |
| Mask removal | 0.02384 | 0.04487 | 0.08232 | 0.11417 | 0.14501 | 0.17849 | 0.20863 | 0.23202 |
| (0.00310) | (0.00207) | (0.01486) | (0.01715) | (0.02501) | (0.03532) | (0.04438) | (0.06090) | |
| Verification | 0.00886 | 0.01602 | 0.01936 | 0.02576 | 0.02953 | 0.03799 | 0.04319 | 0.04763 |
| (0.00358) | (0.08621) | (0.00421) | (0.05892) | (0.00504) | (0.01028) | (0.00676) | (0.00924) |
| Features | Authentication Based on | |||
|---|---|---|---|---|
| Merkle Tree | Hardcore Function | Merkle Tree with Encrypted Communication | Proposed Scheme | |
| Resilience against size information leakage | X | X | X | O |
| Resilience against replay attacks | X | O | O | O |
| Requirement for an additional trusted authority | X | X | O | X |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koo, D.; Shin, Y.; Yun, J.; Hur, J. Improving Security and Reliability in Merkle Tree-Based Online Data Authentication with Leakage Resilience. Appl. Sci. 2018, 8, 2532. https://doi.org/10.3390/app8122532
Koo D, Shin Y, Yun J, Hur J. Improving Security and Reliability in Merkle Tree-Based Online Data Authentication with Leakage Resilience. Applied Sciences. 2018; 8(12):2532. https://doi.org/10.3390/app8122532
Chicago/Turabian StyleKoo, Dongyoung, Youngjoo Shin, Joobeom Yun, and Junbeom Hur. 2018. "Improving Security and Reliability in Merkle Tree-Based Online Data Authentication with Leakage Resilience" Applied Sciences 8, no. 12: 2532. https://doi.org/10.3390/app8122532
APA StyleKoo, D., Shin, Y., Yun, J., & Hur, J. (2018). Improving Security and Reliability in Merkle Tree-Based Online Data Authentication with Leakage Resilience. Applied Sciences, 8(12), 2532. https://doi.org/10.3390/app8122532






