Stochastic Analysis of the Gas Flow at the Gas Diffusion Layer/Channel Interface of a High-Temperature Polymer Electrolyte Fuel Cell
Abstract
Featured Application
Abstract
1. Introduction
2. Methods
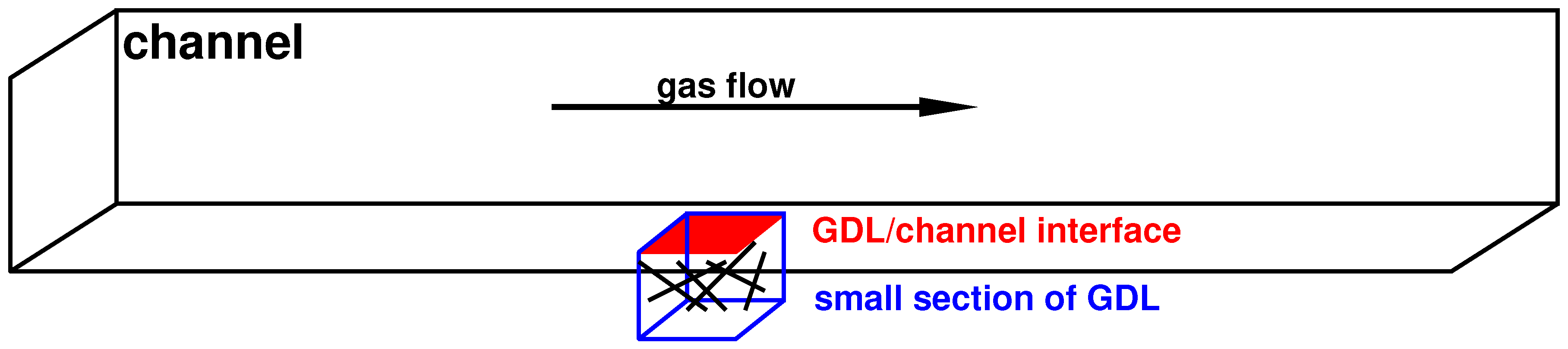
2.1. Geometric Data
2.2. Lattice Boltzmann Method
2.3. Simulation Frame
2.4. Analysis of the Interface
3. Results
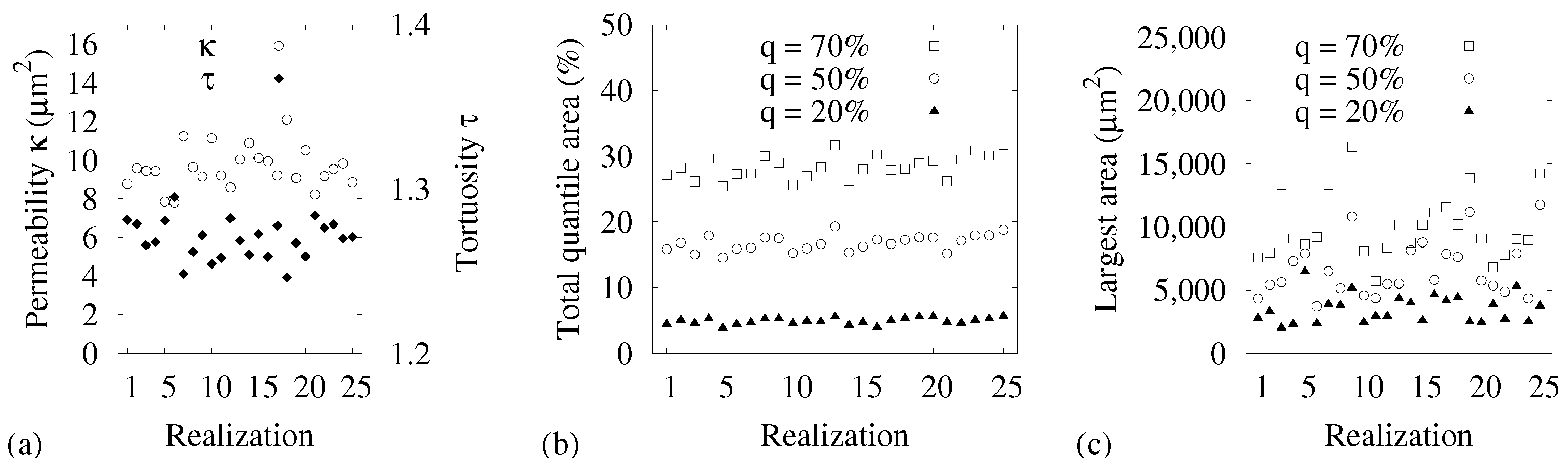
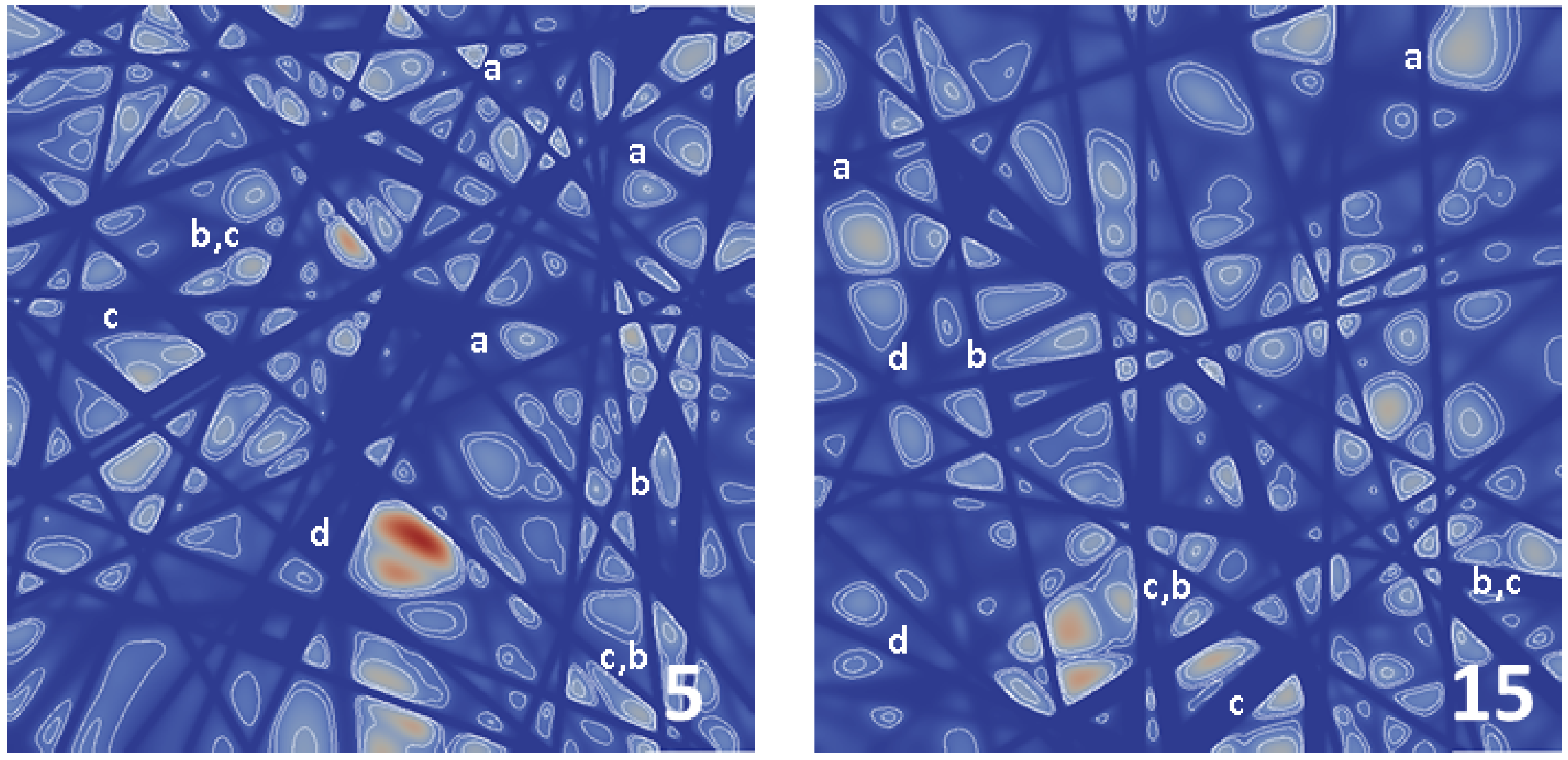
3.1. Analysis of the GDL Surface
3.2. Statistical Evaluation
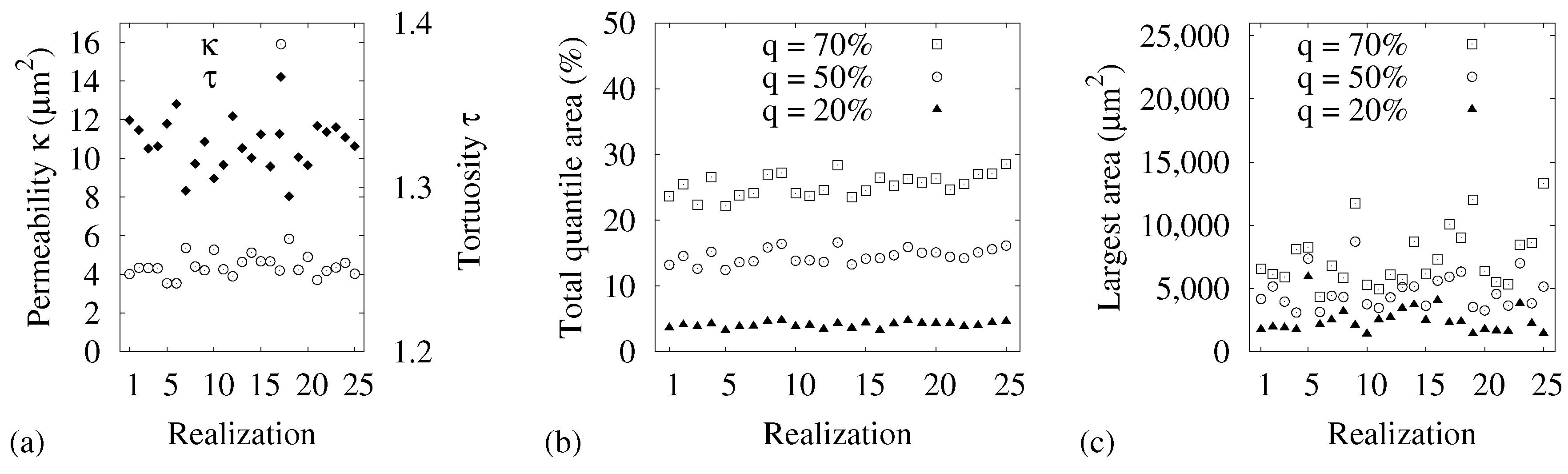
3.3. Impact of the Compression
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Weber, A.Z.; Borup, R.L.; Darling, R.M.; Das, P.K.; Dursch, T.J.; Gu, W.; Harvey, D.; Kusoglu, A.; Litster, S.; Mench, M.M.; et al. A Critical Review of Modeling Transport Phenomena in Polymer-Electrolyte Fuel Cells. J. Electrochem. Soc. 2014, 161, F1254–F1299. [Google Scholar] [CrossRef]
- Andersson, M.; Beale, S.B.; Espinoza, M.; Wu, Z.; Lehnert, W. A review of cell-scale multiphase flow modeling, including water management, in polymer electrolyte fuel cells. Appl. Energy 2016, 180, 757–778. [Google Scholar] [CrossRef]
- Molaeimanesh, G.; Googarchin, H.S.; Moqaddam, A.Q. Lattice Boltzmann simulation of proton exchange membrane fuel cells—A review on opportunities and challenges. Int. J. Hydrogen Energy 2016, 41, 22221–22245. [Google Scholar] [CrossRef]
- Froning, D.; Brinkmann, J.; Reimer, U.; Schmidt, V.; Lehnert, W.; Stolten, D. 3D analysis, modeling and simulation of transport processes in compressed fibrous microstructures, using the Lattice Boltzmann method. Electrochim. Acta 2013, 110, 325–334. [Google Scholar] [CrossRef]
- Froning, D.; Gaiselmann, G.; Reimer, U.; Brinkmann, J.; Schmidt, V.; Lehnert, W. Stochastic Aspects of Mass Transport in Gas Diffusion Layers. Transp. Porous Media 2014, 103, 469–495. [Google Scholar] [CrossRef]
- Froning, D.; Yu, J.; Gaiselmann, G.; Reimer, U.; Manke, I.; Schmidt, V.; Lehnert, W. Impact of compression on gas transport in non-woven gas diffusion layers of high temperature polymer electrolyte fuel cells. J. Power Sources 2016, 318, 26–34. [Google Scholar] [CrossRef]
- van Doormaal, M.A.; Pharoah, J.G. Determination of permeability in fibrous porous media using the lattice Boltzmann method with application to PEM fuel cells. Int. J. Numer. Meth. Fluids 2009, 59, 75–89. [Google Scholar] [CrossRef]
- Thiedmann, R.; Fleischer, F.; Hartnig, C.; Lehnert, W.; Schmidt, V. Stochastic 3D Modeling of the GDL Structure in PEMFCs Based on Thin Section Detection. J. Electrochem. Soc. 2008, 155, B391–B399. [Google Scholar] [CrossRef]
- Mangal, P.; Pant, L.M.; Carrigy, N.; Dumontier, M.; Zingan, V.; Mitra, S.; Secanell, M. Experimental study of mass transport in PEMFCs: Through plane permeability and molecular diffusivity in GDLs. Electrochim. Acta 2015, 167, 160–171. [Google Scholar] [CrossRef]
- Salomov, U.R.; Chiavazzo, E.; Asinari, P. Pore-scale modeling of fluid flow through gas diffusion and catalyst layers for high temperature proton exchange membrane (HT-PEM) fuel cells. Comput. Math. Appl. 2014, 67, 393–411. [Google Scholar] [CrossRef]
- Nabovati, A.; Hinebaugh, J.; Bazylak, A.; Amon, C.H. Effect of porosity heterogeneity on the permeability and tortuosity of gas diffusion layers in polymer electrolyte membrane fuel cells. J. Power Sources 2014, 248, 83–90. [Google Scholar] [CrossRef]
- Rosén, T.; Eller, J.; Kang, J.; Prasianakis, N.I.; Mantzaras, J.; Büchi, F.N. Saturation Dependent Effective Transport Properties of PEFC Gas Diffusion Layers. J. Electrochem. Soc. 2012, 159, F536–F544. [Google Scholar] [CrossRef]
- Eller, J.; Lamibrac, A.; Marone, F.; Büchi, F.N. Influence of Binder Porosity on GDL Gas Phase Transport. ECS Meet. Abstr. 2016, 230, 2747. [Google Scholar]
- Simaafrookhteh, S.; Shakeri, M.; Baniassadi, M.; Sahraei, A.A. Microstructure Reconstruction and Characterization of the Porous GDLs for PEMFC Based on Fibers Orientation Distribution. Fuel Cells 2018, 18, 160–172. [Google Scholar] [CrossRef]
- Tamayol, A.; McGregor, F.; Bahrami, M. Single phase through-plane permeability of carbon paper gas diffusion layers. J. Power Sources 2012, 204, 94–99. [Google Scholar] [CrossRef]
- Zamel, N.; Li, X. Effective transport properties for polymer electrolyte membrane fuel cells—With a focus on the gas diffusion layer. Prog. Energy Combust. Sci. 2013, 39, 111–146. [Google Scholar] [CrossRef]
- Rashapov, R.R.; Gostick, J.T. In-Plane Effective Diffusivity in PEMFC Gas Diffusion Layers. Transp. Porous Media 2016, 115, 411–433. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, C.; Cho, C. An Investigation of the Compressive Behavior of Polymer Electrode Membrane Fuel Cell’s Gas Diffusion Layers under Different Temperatures. Polymers 2018, 10, 971. [Google Scholar] [CrossRef]
- Taira, H.; Liu, H. In-situ measurements of GDL effective permeability and under-land cross-flow in a PEM fuel cell. Int. J. Hydrogen Energy 2012, 37, 13725–13730. [Google Scholar] [CrossRef]
- Reshetenko, T.V.; St-Piere, J.; Rocheleau, R. Effects of local gas diffusion layer gas permeability variations on spatial proton exchange membrane fuel cells performance. J. Power Sources 2013, 241, 597–607. [Google Scholar] [CrossRef]
- Kvesić, M.; Reimer, U.; Froning, D.; Lüke, L.; Lehnert, W.; Stolten, D. 3D modeling of a 200 cm2 HT-PEFC short stack. Int. J. Hydrogen Energy 2012, 37, 2430–2439. [Google Scholar] [CrossRef]
- Sousa, T.; Mamlouk, M.; Scott, K.; Rangel, C.M. Three Dimensional Model of a High Temperature PEMFC. Study of the Flow Field Effect on Performance. Fuel Cells 2012, 12, 566–576. [Google Scholar] [CrossRef]
- Chippar, P.; Ju, H. Numeric modeling and investigation of gas crossover effects in high temperature proton exchange membrane (PEM) fuel cells. Int. J. Hydrogen Energy 2013, 38, 7704–7714. [Google Scholar] [CrossRef]
- Yuan, X.Z.; Li, H.; Gu, E.; Qian, W.; Girard, F.; Wang, Q.; Biggs, T.; Jaeggle, M. Measurements of GDL Properties for Quality Control in Fuel Cell Mass Production Line. World Electr. Veh. J. 2016, 8, 422. [Google Scholar] [CrossRef]
- Breitwieser, M.; Klingele, M.; Vierrath, S.; Zengerle, R.; Thiele, S. Tailoring the Membrane-Electrode Interface in PEM Fuel Cells: A Review and Perspective on Novel Engineering Approaches. Adv. Energy Mater. 2018, 8, 1701257. [Google Scholar] [CrossRef]
- Froning, D.; Yu, J.; Reimer, U.; Lehnert, W. Stochastic Analysis of the Gas Flow at the Gas Diffusion Layer/Electrode Interface of a High-Temperature Polymer Electrolyte Fuel Cell. Transp. Porous Media 2018, 123, 403–420. [Google Scholar] [CrossRef]
- Kaneko, H.; Ohta, K.; Shimuzu, M.; Araki, T. Measurements of Anisotropy of the Effective Diffusivity through PEFC GDL and Mass Transfer Resistance at GDL and Channel Interface. Trans. Jpn. Soc. Mech. Eng. Ser. B 2013, 79, 71–81. [Google Scholar] [CrossRef]
- Yoon, Y.; Jo, Y.; Kim, H.S. Experimental investigation of liquid water droplet removal in a simulated polymer electrolyte membrane fuel cell gas channel with gas diffusion layer characteristics. J. Mech. Sci. Technol. 2014, 28, 5221–5230. [Google Scholar] [CrossRef]
- Wang, Y.; Cho, S.; Thiedmann, R.; Schmidt, V.; Lehnert, W.; Feng, X. Stochastic modeling and direct simulation of the diffusion media for polymer electrolyte fuel cells. Int. J. Heat Mass Transf. 2010, 53, 1128–1138. [Google Scholar] [CrossRef]
- Niu, Z.; Jiao, K.; Zhang, F.; Du, Q.; Yin, Y. Direct numerical simulation of two-phase turbulent flow in fuel cell flow channel. Int. J. Hydrogen Energy 2016, 41, 3147–3152. [Google Scholar] [CrossRef]
- Kim, H.Y.; Jeon, S.; Song, M.; Kim, K. Numerical simulations of water droplet dynamics in hydrogen fuel cell gas channel. J. Power Sources 2014, 246, 679–695. [Google Scholar] [CrossRef]
- Koz, M.; Kandlikar, S.G. Oxygen transport resistance at gas diffusion layer—Air channel interface with film flow of water in a proton exchange membrane fuel cell. J. Power Sources 2016, 302, 331–342. [Google Scholar] [CrossRef]
- Chen, L.; Feng, Y.L.; Song, C.X.; Chen, L.; He, Y.L.; Tao, W.Q. Multi-scale modeling of proton exchange membrane fuel cell by coupling finite volume method and lattice Boltzmann method. Int. J. Heat Mass Transf. 2013, 63, 268–283. [Google Scholar] [CrossRef]
- Yu, J.; Froning, D.; Reimer, U.; Lehnert, W. Apparent contact angles of liquid water droplet breaking through a gas diffusion layer of polymer electrolyte membrane fuel cell. Int. J. Hydrogen Energy 2018, 43, 6318–6330. [Google Scholar] [CrossRef]
- Qin, C. Water Transport in the Gas Diffusion Layer of a Polymer Electrolyte Fuel Cell: Dynamic Pore-Network Modeling. J. Electrochem. Soc. 2015, 162, F1036–F1046. [Google Scholar] [CrossRef]
- Qin, C.Z.; Hassanizadeh, S.M.; van Oosterhout, L.M. Pore-Network Modeling of Water and Vapor Transport in the Micro Porous Layer and Gas Diffusion Layer of a Polymer Electrolyte Fuel Cell. Computation 2016, 4, 21. [Google Scholar] [CrossRef]
- Aghighi, M.; Hoeh, M.A.; Lehnert, W.; Merle, G.; Gostick, J. Simulation of a Full Fuel Cell Membrane Electrode Assembly Using Pore Network Modeling. J. Electrochem. Soc. 2016, 163, F384–F392. [Google Scholar] [CrossRef]
- Niu, Z.; Bao, Z.; Wu, J.; Wang, Y.; Jiao, K. Two-phase flow in the mixed-wettability gas diffusion layer of proton exchange membrane fuel cells. Appl. Energy 2018, 232, 443–450. [Google Scholar] [CrossRef]
- Yang, G.; Weigand, B.; Terzis, A.; Weishaupt, K.; Helmig, R. Numerical Simulation of Turbulent Flow and Heat Transfer in a Three-Dimensional Channel Coupled with Flow Through Porous Structures. Transp. Porous Media 2018, 122, 145–167. [Google Scholar] [CrossRef]
- Kulikovsky, A.A. Analytical Modelling of Fuel Cells; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Chevalier, S.; Josset, C.; Auvity, B. Analytical solutions and dimensional analysis of pseudo 2D current density distribution model in PEM fuel cells. Renew. Energy 2018, 125, 738–746. [Google Scholar] [CrossRef]
- Thiedmann, R.; Hartnig, C.; Manke, I.; Schmidt, V.; Lehnert, W. Local Structural Characteristics of Pore Space in GDLs of PEM Fuel Cells Based on Geometric 3D Graphs. J. Electrochem. Soc. 2009, 156, B1339–B1347. [Google Scholar] [CrossRef]
- Succi, S. The Lattice Boltzmann Equation; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Wolf-Gladrow, D. Lattice-Gas Cellular Automata and Lattice Boltzmann Models; Springer: Berlin, Germany, 2000. [Google Scholar]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- Hänel, D. Molekulare Gasdynamik; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Tomadakis, M.M.; Robertson, T.J. Viscous Permeability of Random Fiber Structures: Comparison of Electrical and Diffusional Estimates with Experimental and Analytical Results. J. Compos. Mater. 2005, 39, 163–188. [Google Scholar] [CrossRef]
- Koponen, A.; Kataja, M.; Timonen, J. Tortuous flow in porous media. Phys. Rev. E 1996, 54, 406–410. [Google Scholar] [CrossRef]
- Kitware, Inc. Paraview—Open Source Scientific Visualization; Kitware, Inc.: Clifton Park, NY, USA, 2009. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Hedderich, J.; Sachs, L. Angewandte Statistik, 14th ed.; Springer: Heidelberg/Berlin, Germany; Dordrecht, The Netherlands; London, UK; New York, NY, USA, 2012. [Google Scholar]
- Adler, J. R in a Nutshell, 2nd ed.; O’Reilly: Sebastopol, CA, USA, 2012. [Google Scholar]
- Pharoah, J.G.; Karan, K.; Sun, W. On effective transport coefficients in PEM fuel cell electrodes: Anisotropy of the porous transport layers. J. Power Sources 2006, 161, 214–224. [Google Scholar] [CrossRef]
- Kvesić, M.; Reimer, U.; Froning, D.; Lüke, L.; Lehnert, W.; Stolten, D. 3D modeling of an HT-PEFC stack using reformate gas. Int. J. Hydrogen Energy 2012, 37, 12438–12450. [Google Scholar] [CrossRef]
- Cao, Q.; Beale, S.B.; Reimer, U.; Froning, D.; Lehnert, W. The Importance of Diffusion Mechanisms in High Temperature Polymer Electrolyte Fuel Cells. ECS Trans. 2015, 69, 1089–1103. [Google Scholar] [CrossRef]
- Horgue, P.; Soulaine, C.; Franc, J.; Guibert, R.; Debenest, G. An open-source toolbox for multiphase flow in porous media. Comput. Phys. Commun. 2015, 187, 217–226. [Google Scholar] [CrossRef]
- Kazmouz, S.J.; Giusti, A.; Mastorakos, E. Numerical simulation of shale gas flow in three-dimensional fractured porous media. J. Unconv. Oil Gas Resour. 2016, 16, 90–112. [Google Scholar] [CrossRef]
- Wörner, M. Numerical modeling of multiphase flows in microfluidics and micro process engineering: A review of methods and applications. Microfluid. Nanofluid. 2012, 12, 841–886. [Google Scholar] [CrossRef]
- Cai, Y.; Chen, T.; Yang, T.; Xiao, J. Mechanism of water transport in serpentine cathode channels of proton exchange membrane fuel cells. J. Power Sources 2012, 209, 90–104. [Google Scholar] [CrossRef]


| Condition | Value |
|---|---|
| Average current density | 1 A/cm |
| Volumetric flow rate H | |
| (normal conditions) | 7 mL/min |
| Volumetric flow rate O | |
| (normal conditions) | 3.5 mL/min |
| Operating temperature | 160 |
| Superficial velocity HO | 1.8 × 10 m/s |
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| q/% | |||||||||||||||
| 70 | 160 | 166 | 154 | 175 | 150 | 161 | 161 | 177 | 171 | 151 | 159 | 167 | 187 | 155 | |
| #reg. | 190 | 156 | 158 | 178 | 181 | 194 | 133 | 144 | 130 | 150 | 161 | 164 | 150 | 123 | |
| 843 | 1067 | 977 | 981 | 828 | 830 | 1214 | 1230 | 1317 | 1007 | 987 | 1019 | 1244 | 1260 | ||
| 7592 | 7965 | 13,329 | 9070 | 8640 | 9191 | 12,587 | 7256 | 16,323 | 8075 | 5699 | 8343 | 10,154 | 8744 | ||
| 50 | 93 | 99 | 89 | 106 | 86 | 94 | 95 | 104 | 103 | 90 | 94 | 98 | 114 | 90 | |
| #reg. | 144 | 125 | 112 | 132 | 144 | 149 | 91 | 119 | 113 | 119 | 129 | 132 | 113 | 84 | |
| 648 | 793 | 791 | 800 | 596 | 629 | 1039 | 873 | 914 | 755 | 729 | 743 | 1008 | 1077 | ||
| 4329 | 5432 | 5623 | 7292 | 7889 | 3726 | 6496 | 5137 | 10,816 | 4570 | 4358 | 5488 | 5524 | 8147 | ||
| 20 | 26 | 30 | 27 | 31 | 23 | 26 | 28 | 31 | 31 | 27 | 29 | 28 | 33 | 25 | |
| #reg. | 55 | 41 | 52 | 60 | 51 | 52 | 42 | 58 | 48 | 58 | 64 | 57 | 47 | 27 | |
| 476 | 726 | 520 | 518 | 444 | 502 | 655 | 534 | 650 | 464 | 450 | 494 | 701 | 931 | ||
| 2788 | 3292 | 2012 | 2302 | 6453 | 2358 | 3884 | 3807 | 5171 | 2455 | 2927 | 2927 | 4311 | 3980 | ||
| No. | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | aver. | var. | ||
| /% | 1–25 | coef. | |||||||||||||
| 70 | 165 | 178 | 164 | 166 | 170 | 173 | 154 | 174 | 182 | 178 | 187 | 167 | |||
| #reg. | 155 | 150 | 172 | 147 | 160 | 135 | 163 | 140 | 156 | 150 | 148 | 155 | |||
| 1064 | 1189 | 956 | 1127 | 1065 | 1281 | 948 | 1241 | 1167 | 1184 | 1281 | 1092 | ||||
| 10,177 | 11,144 | 11,540 | 10,193 | 13,840 | 9086 | 6780 | 7796 | 9041 | 8969 | 14,227 | 9831 | ||||
| 50 | 96 | 102 | 98 | 102 | 104 | 104 | 90 | 101 | 106 | 106 | 111 | 99 | |||
| #reg. | 106 | 116 | 131 | 118 | 131 | 98 | 111 | 116 | 112 | 124 | 117 | 115 | |||
| 903 | 880 | 749 | 862 | 801 | 1059 | 807 | 871 | 945 | 854 | 948 | 843 | ||||
| 8771 | 5805 | 7862 | 7612 | 11,192 | 5749 | 5362 | 4869 | 7904 | 4347 | 11,756 | 6642 | ||||
| 20 | 28 | 23 | 29 | 32 | 33 | 33 | 28 | 27 | 29 | 31 | 33 | 29 | |||
| #reg. | 48 | 37 | 51 | 53 | 63 | 59 | 43 | 46 | 44 | 61 | 65 | 51 | |||
| 580 | 629 | 583 | 594 | 520 | 557 | 648 | 588 | 667 | 508 | 513 | 578 | ||||
| 2588 | 4637 | 4147 | 4412 | 2484 | 2412 | 3888 | 2702 | 5310 | 2504 | 3767 | 3501 |
| 0.833 | 0.48 | 0.113 | −0.053 | |
| 0.593 | 0.12 | −0.087 | ||
| −0.127 | −0.133 | |||
| −0.593 |
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| q/% | |||||||||||||||
| 70 | 139 | 150 | 132 | 157 | 131 | 140 | 142 | 159 | 160 | 142 | 140 | 145 | 167 | 139 | |
| #reg. | 234 | 203 | 184 | 212 | 219 | 229 | 159 | 173 | 179 | 190 | 188 | 208 | 182 | 150 | |
| 595 | 748 | 717 | 740 | 597 | 612 | 894 | 919 | 897 | 748 | 744 | 697 | 920 | 925 | ||
| 6568 | 6124 | 5906 | 8089 | 8237 | 4352 | 6788 | 5843 | 11,723 | 5288 | 4943 | 6109 | 5715 | 8712 | ||
| 50 | 78 | 86 | 74 | 86 | 73 | 80 | 81 | 94 | 97 | 82 | 82 | 80 | 98 | 78 | |
| #reg. | 177 | 145 | 137 | 153 | 149 | 185 | 121 | 143 | 144 | 152 | 158 | 151 | 150 | 103 | |
| 440 | 592 | 544 | 585 | 492 | 434 | 670 | 654 | 672 | 537 | 520 | 533 | 654 | 760 | ||
| 4174 | 5159 | 3962 | 3096 | 7362 | 3139 | 4421 | 4322 | 8708 | 3755 | 3458 | 4295 | 5112 | 5159 | ||
| 20 | 21 | 24 | 22 | 25 | 19 | 22 | 23 | 27 | 28 | 23 | 24 | 20 | 25 | 21 | |
| #reg. | 62 | 64 | 62 | 64 | 44 | 63 | 49 | 68 | 76 | 58 | 68 | 56 | 52 | 37 | |
| 345 | 375 | 362 | 391 | 432 | 355 | 467 | 399 | 372 | 390 | 351 | 359 | 487 | 572 | ||
| 1751 | 1951 | 1890 | 1753 | 5920 | 2144 | 2504 | 3182 | 2097 | 1406 | 2538 | 2711 | 3443 | 3708 | ||
| No. | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | aver. | var. | ||
| /% | 1–25 | coef. | |||||||||||||
| 70 | 144 | 156 | 149 | 155 | 152 | 155 | 145 | 150 | 159 | 160 | 168 | 150 | |||
| #reg. | 178 | 192 | 204 | 174 | 192 | 165 | 200 | 166 | 176 | 194 | 195 | 190 | |||
| 811 | 814 | 729 | 891 | 791 | 941 | 727 | 906 | 905 | 824 | 864 | 798 | ||||
| 6156 | 7299 | 10,089 | 9029 | 12,020 | 6370 | 5522 | 5312 | 8442 | 8609 | 13,309 | 7462 | ||||
| 50 | 84 | 84 | 87 | 94 | 89 | 89 | 85 | 84 | 89 | 92 | 95 | 86 | |||
| #reg. | 134 | 141 | 162 | 146 | 143 | 124 | 146 | 136 | 136 | 157 | 159 | 146 | |||
| 623 | 595 | 534 | 644 | 621 | 718 | 583 | 616 | 655 | 585 | 599 | 594 | ||||
| 3632 | 5621 | 5922 | 6332 | 3528 | 3265 | 4563 | 3645 | 6995 | 3825 | 5146 | 4744 | ||||
| 20 | 26 | 19 | 25 | 28 | 26 | 26 | 25 | 23 | 23 | 26 | 27 | 24 | |||
| #reg. | 60 | 47 | 62 | 66 | 71 | 61 | 65 | 63 | 44 | 68 | 68 | 60 | |||
| 431 | 408 | 406 | 423 | 360 | 419 | 390 | 360 | 532 | 382 | 400 | 406 | ||||
| 2495 | 4055 | 2293 | 2374 | 2422 | 1766 | 1661 | 1613 | 3814 | 2232 | 1442 | 2486 |
| Quantile Level q | Uncompressed | Compressed (30%) |
|---|---|---|
| 70% | 28.3% | 23.6% |
| 50% | 16.8% | 13.2% |
| 20% | 4.9% | 3.6% |
| Quantile Level q | |||
|---|---|---|---|
| 70% | 0.78 | 0.75 | 0.43 |
| 50% | 0.70 | 0.81 | 0.34 |
| 20% | 0.65 | 0.42 | 0.46 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Froning, D.; Yu, J.; Reimer, U.; Lehnert, W. Stochastic Analysis of the Gas Flow at the Gas Diffusion Layer/Channel Interface of a High-Temperature Polymer Electrolyte Fuel Cell. Appl. Sci. 2018, 8, 2536. https://doi.org/10.3390/app8122536
Froning D, Yu J, Reimer U, Lehnert W. Stochastic Analysis of the Gas Flow at the Gas Diffusion Layer/Channel Interface of a High-Temperature Polymer Electrolyte Fuel Cell. Applied Sciences. 2018; 8(12):2536. https://doi.org/10.3390/app8122536
Chicago/Turabian StyleFroning, Dieter, Junliang Yu, Uwe Reimer, and Werner Lehnert. 2018. "Stochastic Analysis of the Gas Flow at the Gas Diffusion Layer/Channel Interface of a High-Temperature Polymer Electrolyte Fuel Cell" Applied Sciences 8, no. 12: 2536. https://doi.org/10.3390/app8122536
APA StyleFroning, D., Yu, J., Reimer, U., & Lehnert, W. (2018). Stochastic Analysis of the Gas Flow at the Gas Diffusion Layer/Channel Interface of a High-Temperature Polymer Electrolyte Fuel Cell. Applied Sciences, 8(12), 2536. https://doi.org/10.3390/app8122536






