Size-Dependent Free Vibration of Axially Moving Nanobeams Using Eringen’s Two-Phase Integral Model
Abstract
:1. Introduction
2. Model Equations
3. Free Vibrations
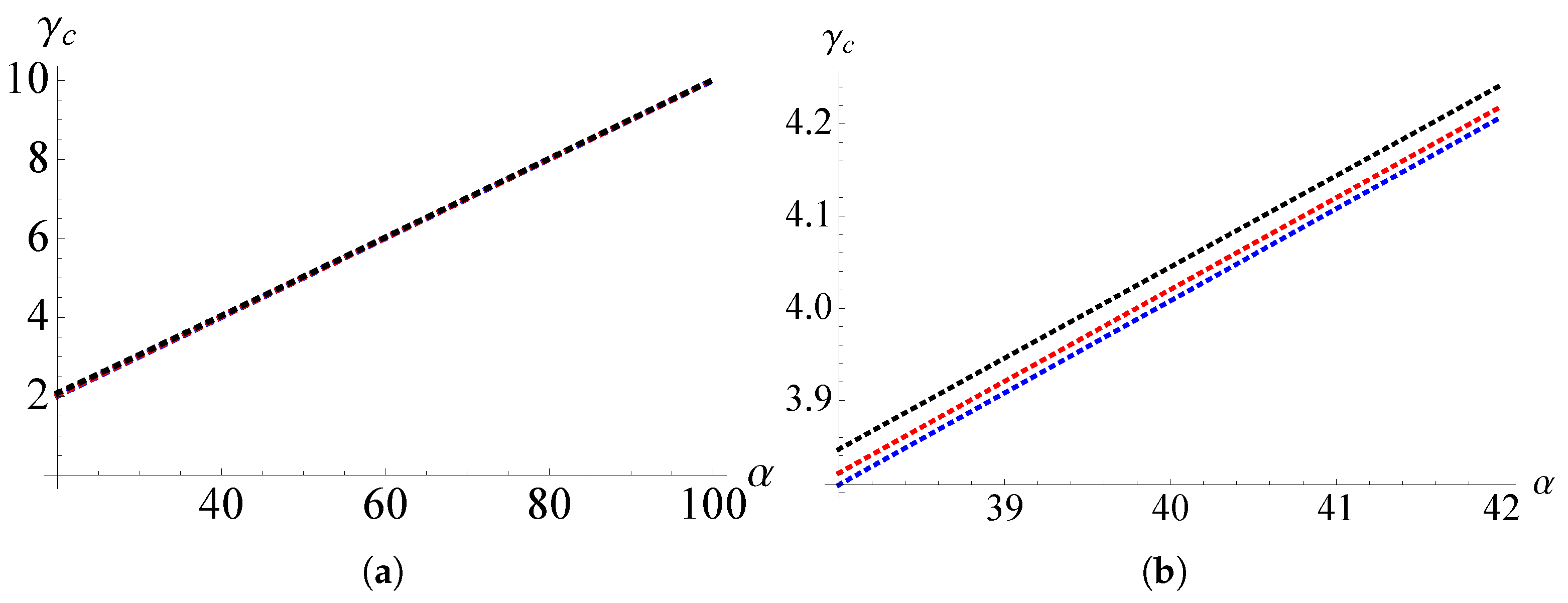
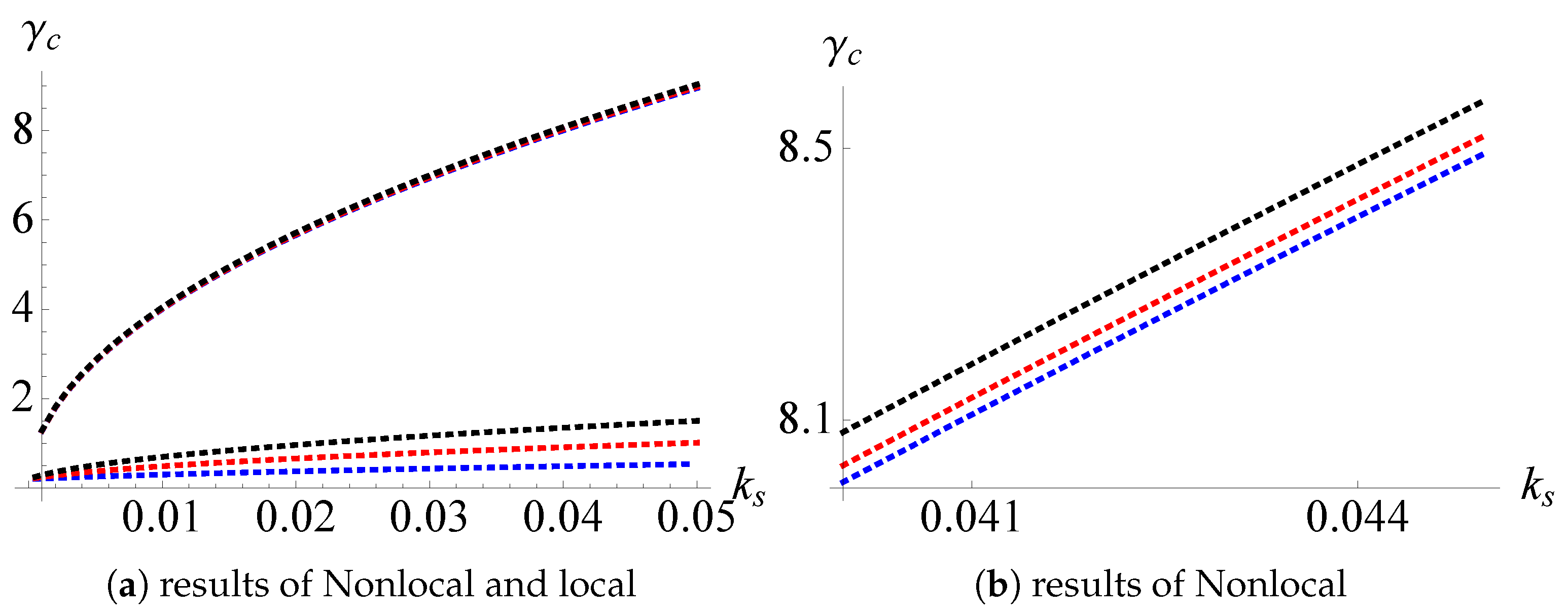
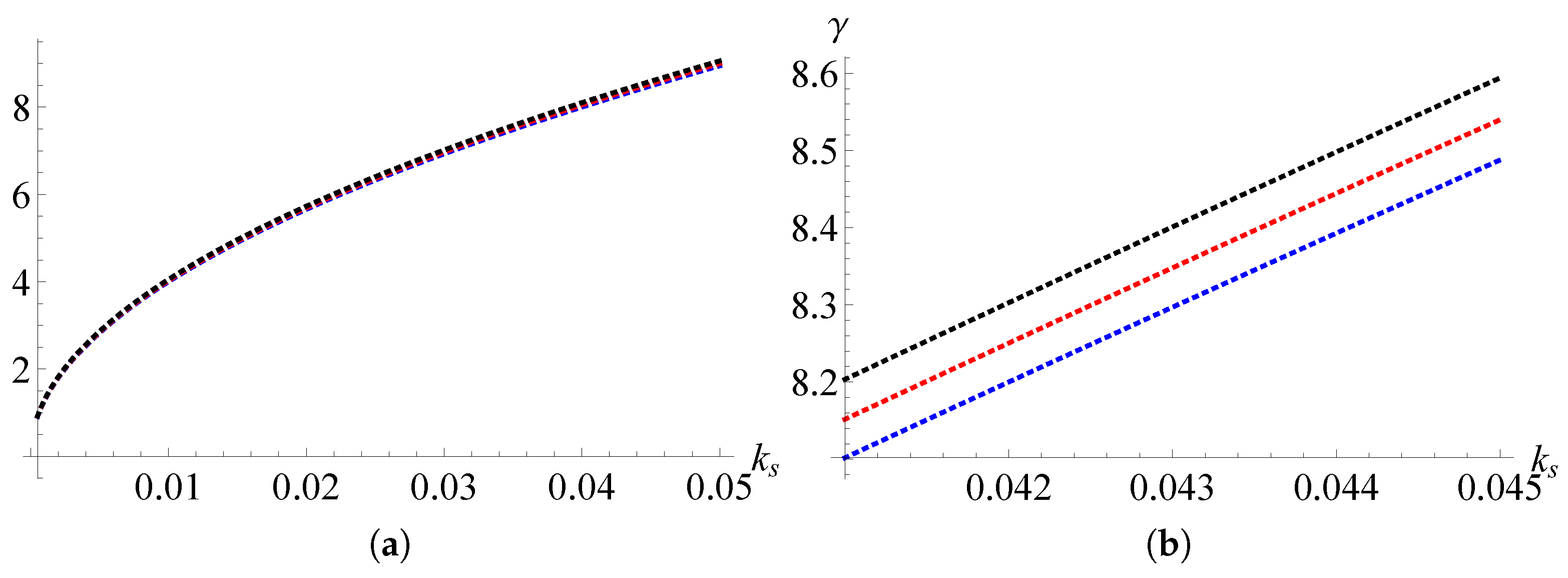
3.1. Critical Velocity
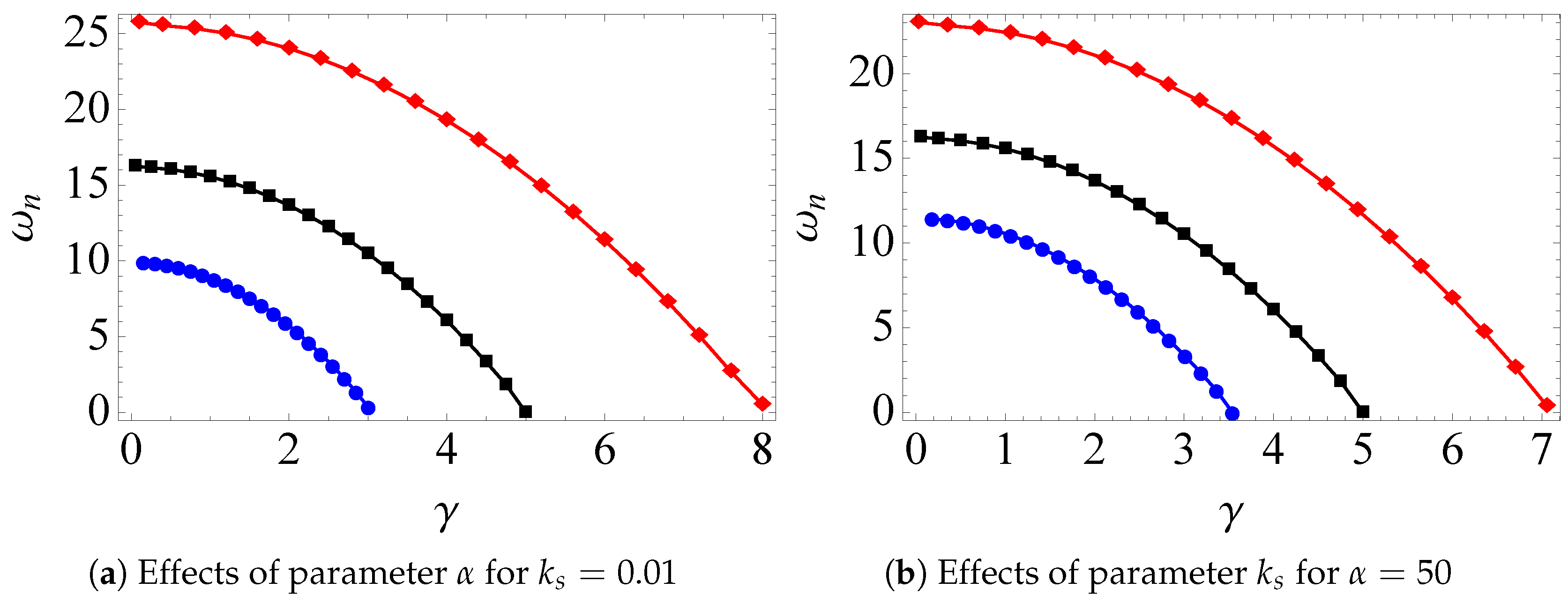
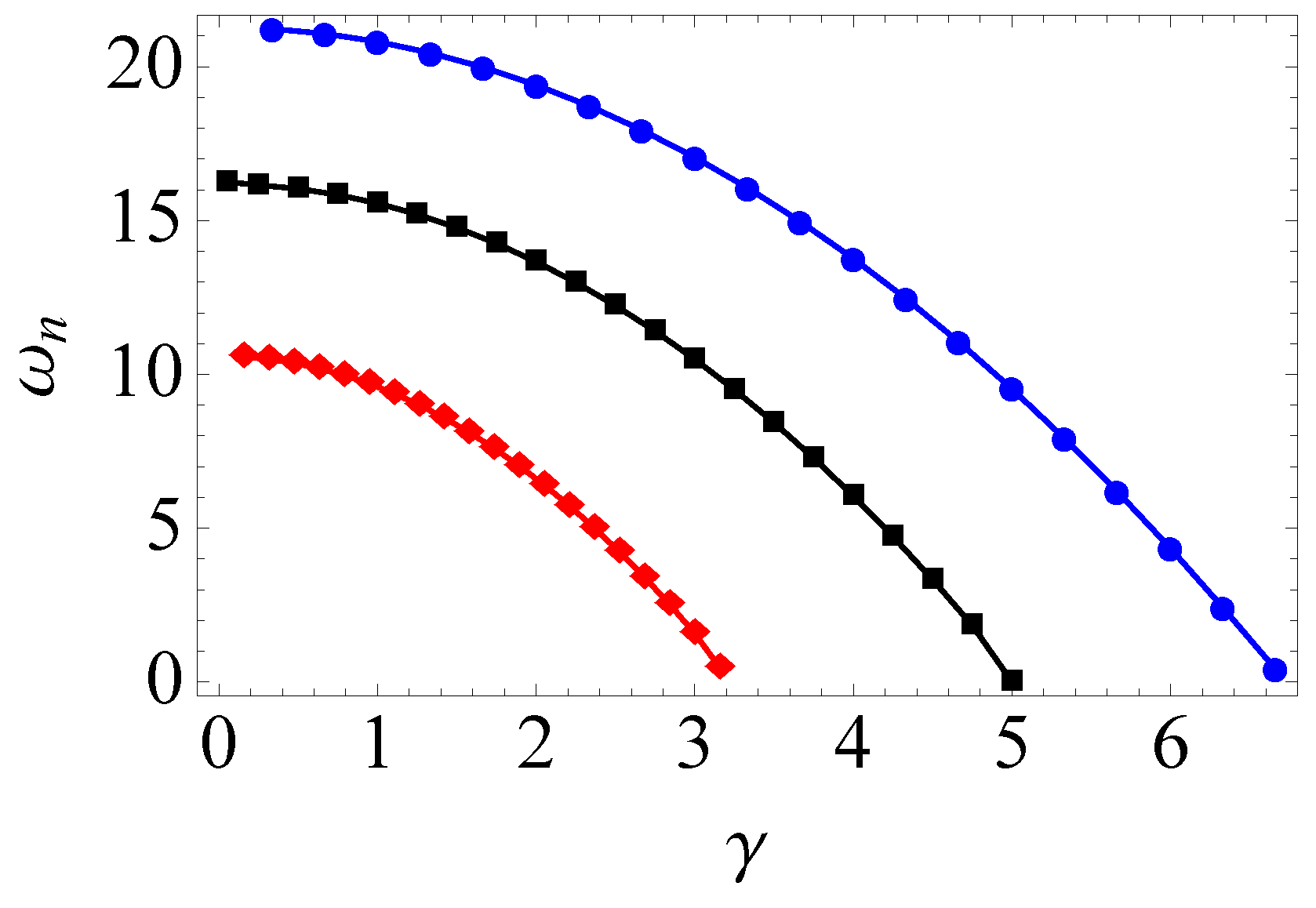
3.2. Natural Frequencies
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hu, D.; Tang, Y.T.; Chen, L.Q. Frequencies of transverse vibration of an axially moving viscoelastic beam. J. Vib. Control 2015. [Google Scholar] [CrossRef]
- Wickert, J.A. Non-linear vibration of a traveling tensioned beam. Int. J. Nonlinear Mech. 1992, 27, 503–517. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Amabili, M. Nonlinear dynamics of an axially moving Timoshenko beam with an internal resonance. Nonlinear Dyn. 2013, 73, 39–52. [Google Scholar] [CrossRef]
- Hu, D.; Chen, L.Q. Galerkin methods for natural frequencies of high-velocity axially moving beams. J. Sound Vib. 2010, 329, 3484–3494. [Google Scholar]
- Ghayesh, M.H.; Amabili, M.; Farokhi, H. Global dynamics of an axially moving buckling beam. J. Vib. Control 2015, 21, 195–208. [Google Scholar] [CrossRef]
- Challamel, N.; Wang, C.M. The small length scale effect for a non-local cantilever beam: A paradox solved. Nanotechnology 2008, 19, 345703. [Google Scholar] [CrossRef] [PubMed]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983. [Google Scholar] [CrossRef]
- Reddy, J.N. Nonlocal theories for bending, buckling and vibration of beams. Int. J. Eng. Sci. 2007, 45, 288–307. [Google Scholar] [CrossRef]
- Reddy, J.N.; Pang, S.D. Nonlocal continuum theories of beams for the analysis of carbon nanotubes. J. Appl. Phys. 2007, 103. [Google Scholar] [CrossRef]
- Lim, C.W.; Zhang, G.; Reddy, J.N. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J. Mech. Phys. Solids 2007, 78, 298–313. [Google Scholar] [CrossRef]
- Kiani, K. Longitudinal, transverse and torsional vibrations and stabilities of axially moving single-walled carbon nanotubes. Curr. Appl. Phys. 2013, 13, 1651–1660. [Google Scholar] [CrossRef]
- Rezaee, M.; Lotfan, S. Non-linear nonlocal vibration and stability analysis of aixally moving nanoscale beams with time-dependent velocity. Int. J. Mech. Sci. 2015, 96, 36–46. [Google Scholar] [CrossRef]
- Lim, C.W.; Li, C.; Yu, J.L. Dynamic behaviour of axially moving nanobeams based on nanolocal elasticity approach. Acta Mech. Sin.-PRC 2010, 26, 755–765. [Google Scholar] [CrossRef]
- Li, C. Nonlocal Thermo-Electro-Mechanical coupling vibrations of axially moving piezoelectric nanobeams. Mech. Based Des. Struct. 2017, 45, 463–478. [Google Scholar] [CrossRef]
- Liu, J.J.; Li, C. Dynamical responses and stabilities of axially moving nanoscale beams with time-dependent velocity using a nonlocal stress gradient theory. J. Vib. Control 2016. [Google Scholar] [CrossRef]
- Wang, J.; Shen, H.M. Complex modal analysis of transverse free vibrations for axially moving nanobeams based on the nonlocal strain gradient theory. Physica E 2018, 101, 85–93. [Google Scholar] [CrossRef]
- Fernández-Sáez, J.; Zaera, R.; Loya, J.A.; Reddy, J.N. Bending of Euler-Bernoulli beams using Eringen’s integral formulation: A paradox resolved. Int. J. Eng. Sci. 2016, 99, 107–116. [Google Scholar] [CrossRef]
- Tuna, M.; Kirca, M. Exact solutions of Eringen’s nonlocal integral model for bending of Euler-Bernoulli and Timoshenko beams. Int. J. Eng. Sci. 2016, 105, 80–92. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R.; Diaco, M.; Sciarra, F.M.D. Constitutive boundary conditions and paradoxes in nonlocal elastic nanobeams. Int. J. Mech. Sci. 2016, 121, 151–156. [Google Scholar] [CrossRef]
- Li, C.; Yao, L.Q.; Chen, W.Q.; Li, S. Comments on nonlocal effects in nano-cantilever beams. Int. J. Eng. Sci. 2015, 87, 47–57. [Google Scholar] [CrossRef]
- Barretta, R.; Feo, L.; Luciano, R.; Diaco, M.; Sciarra, F.M.D. Application of an enhanced version of the Eringen differential model to nanotechnology. Compos. Part B-Eng. 2016, 96, 274–280. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R.; Diaco, M. On nonlocal integral models for elastic nano-beams. Int. J. Mech. Sci. 2017, 131–132, 490–499. [Google Scholar] [CrossRef]
- Romano, G.; Luciano, R.; Barretta, R.; Diaco, M. Nonlocal integral elasticity in nanostructures, mixtures, boundary effects and limit behaviours. Continuum Mech. Therm. 2018, 30, 641–655. [Google Scholar] [CrossRef]
- Wang, Y.B.; Zhu, X.W.; Dai, H.H. Exact solutions for the static bending of Euler-Bernoulli beams using Eringen’s two-phase local/nonlocal model. AIP Adv. 2016, 6. [Google Scholar] [CrossRef]
- Zhu, X.W.; Wang, Y.B.; Dai, H.H. Buckling analysis of Euler-Bernoulli beams using Eringen’s two-phase nonlocal model. Int. J. Eng. Sci. 2017, 116, 130–140. [Google Scholar] [CrossRef]
- Fernández-Sáez, J.; Zaera, R. Vibrations of Bernoulli-Euler beams using the two-phase nonlocal elasticity theory. Int. J. Eng. Sci. 2017, 119, 232–248. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R. Nonlocal elasticity in nanobeams: The stress-driven integral model. Int. J. Eng. Sci. 2017, 115, 14–27. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R. Stress-driven versus strain-driven nonlocal integral model for elastic nano-beams. Compos. Part B-Eng. 2017, 114, 184–188. [Google Scholar] [CrossRef]
- Barretta, R.; Diaco, M.; Feo, L.; Luciano, R.; Sciarra, F.M.D.; Penna, R. Stress-driven integral elastic theory for torsion of nano-beams. Mech. Res. Commun. 2018, 87, 35–41. [Google Scholar] [CrossRef]
- Barretta, R.; Ali Faghidian, S.; Luciano, R.; Medaglia, C.M.; Penna, R. Stress-driven two-phase integral elasticity for torsion of nano-beams. Compos. Part B-Eng. 2018, 145, 62–69. [Google Scholar] [CrossRef]
- Barretta, R.; Čanadija, M.; Luciano, R.; Sciarra, F.M.D. Stress-driven modeling of nonlocal thermoelastic behavior of nanobeams. Int. J. Eng. Sci. 2018, 126, 53–67. [Google Scholar] [CrossRef]





© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Lou, Z.; Huang, K.; Zhu, X. Size-Dependent Free Vibration of Axially Moving Nanobeams Using Eringen’s Two-Phase Integral Model. Appl. Sci. 2018, 8, 2552. https://doi.org/10.3390/app8122552
Wang Y, Lou Z, Huang K, Zhu X. Size-Dependent Free Vibration of Axially Moving Nanobeams Using Eringen’s Two-Phase Integral Model. Applied Sciences. 2018; 8(12):2552. https://doi.org/10.3390/app8122552
Chicago/Turabian StyleWang, Yuanbin, Zhimei Lou, Kai Huang, and Xiaowu Zhu. 2018. "Size-Dependent Free Vibration of Axially Moving Nanobeams Using Eringen’s Two-Phase Integral Model" Applied Sciences 8, no. 12: 2552. https://doi.org/10.3390/app8122552
APA StyleWang, Y., Lou, Z., Huang, K., & Zhu, X. (2018). Size-Dependent Free Vibration of Axially Moving Nanobeams Using Eringen’s Two-Phase Integral Model. Applied Sciences, 8(12), 2552. https://doi.org/10.3390/app8122552



