Parameter Optimization Method for Identifying the Optimal Nonlinear Parameters of a Miniature Transducer with a Metal Membrane
Abstract
:1. Introduction
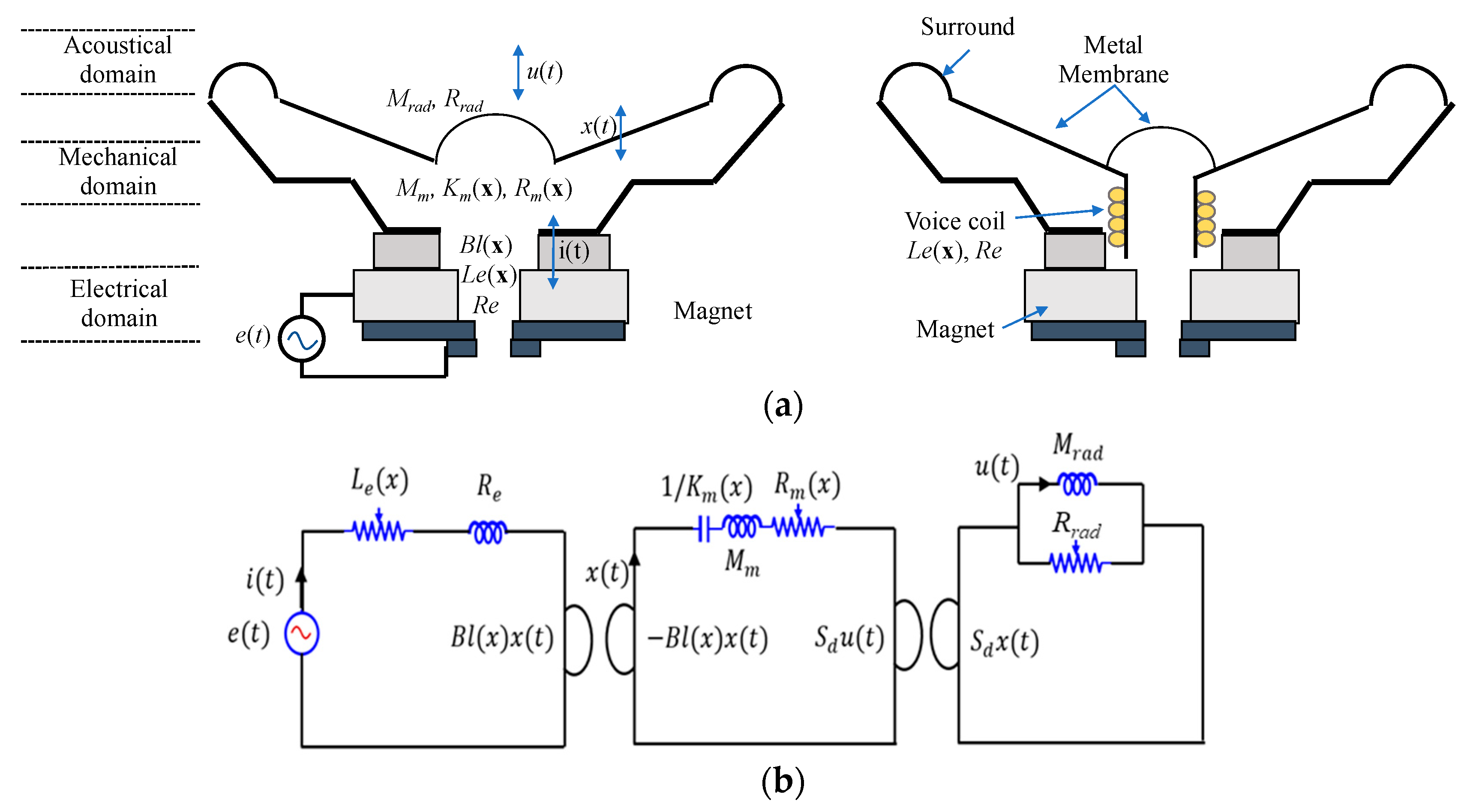
2. Mathematical Model
2.1. Transmission Equation
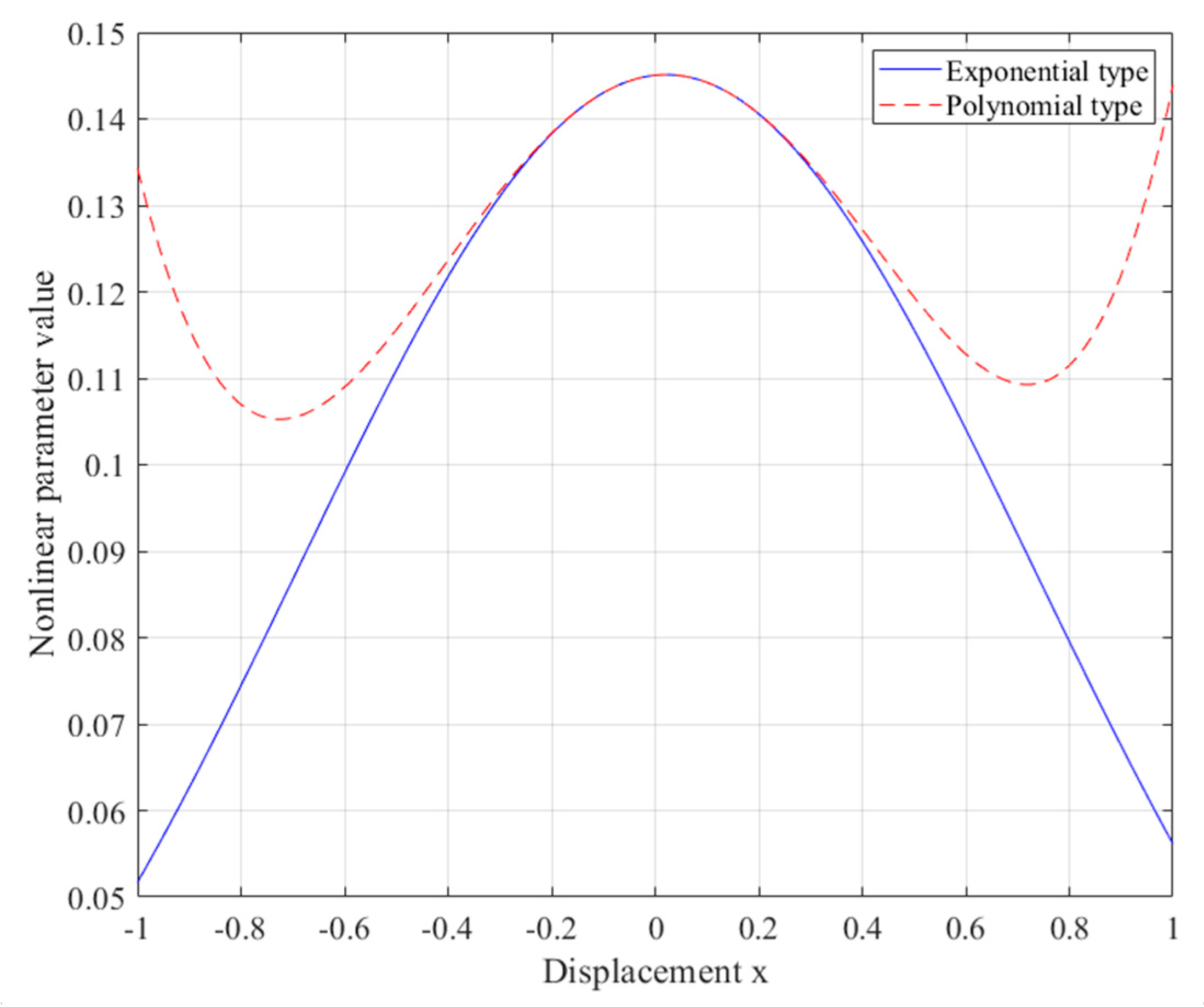
2.2. Nonlinear Parameter Fitting Equations
2.3. Calculation of Nonlinear Optimization Parameters
2.4. Broyden–Fletcher–Goldfarb–Shanno (BFGS) Algorithm
2.5. Brent’s Algorithm
- The selected value must be within the [a, c] interval.
- The variation approaching the optimum value cannot exceed the previous variation by more than half, which means that the following inequality must be met: .
2.6. Constraint Equations
2.7. Computational Algorithm
- Step 1
- Let the search index n = 0, and arbitrarily choose a set of initial values of a vector as w(0).
- Step 2
- Substitute w(n) into transmission Equations (1)–(4) using numerical solver as finite difference method to obtain the values of x(t;w) and i(t;w), and use Equation (8) to obtain J(w).
- Step 3
- Solve Equations (13) and (14) for and substitute it into Equation (12) to obtain E(n). Let when k = 0; otherwise, substitute E(n) into Equation (11) to obtain A(n). Then, substitute and A(n) into Equation (10) to get search direction P(n).
- Step 4
- For the step length, the two methods are proposed. The first is to solve Equation (16) to obtain step length . The second is to use the Brent’s method (Equation (17a)), which is described in Section 2.5 to get .
- Step 5
- After obtaining P(n) and , the new w(n+1) can be obtained from Equation (9). If constraint equations in Section 2.6 are applied, substitute , , and w(n+1) into Equations (20)–(23) to make sure w(n+1) are matching the constraints, if not, update the w(n+1) from constraint Equations (20)–(23).
- Step 6
- Set the search iteration to n = n + 1 and determine whether J(w) is smaller than the preset tolerance of convergence criteria or the specified number of iterations. If the constraint of the convergence criteria is satisfied, end the iteration process; otherwise, start from Step 2 again.
3. Simulation Results and Empirical Results Verifications
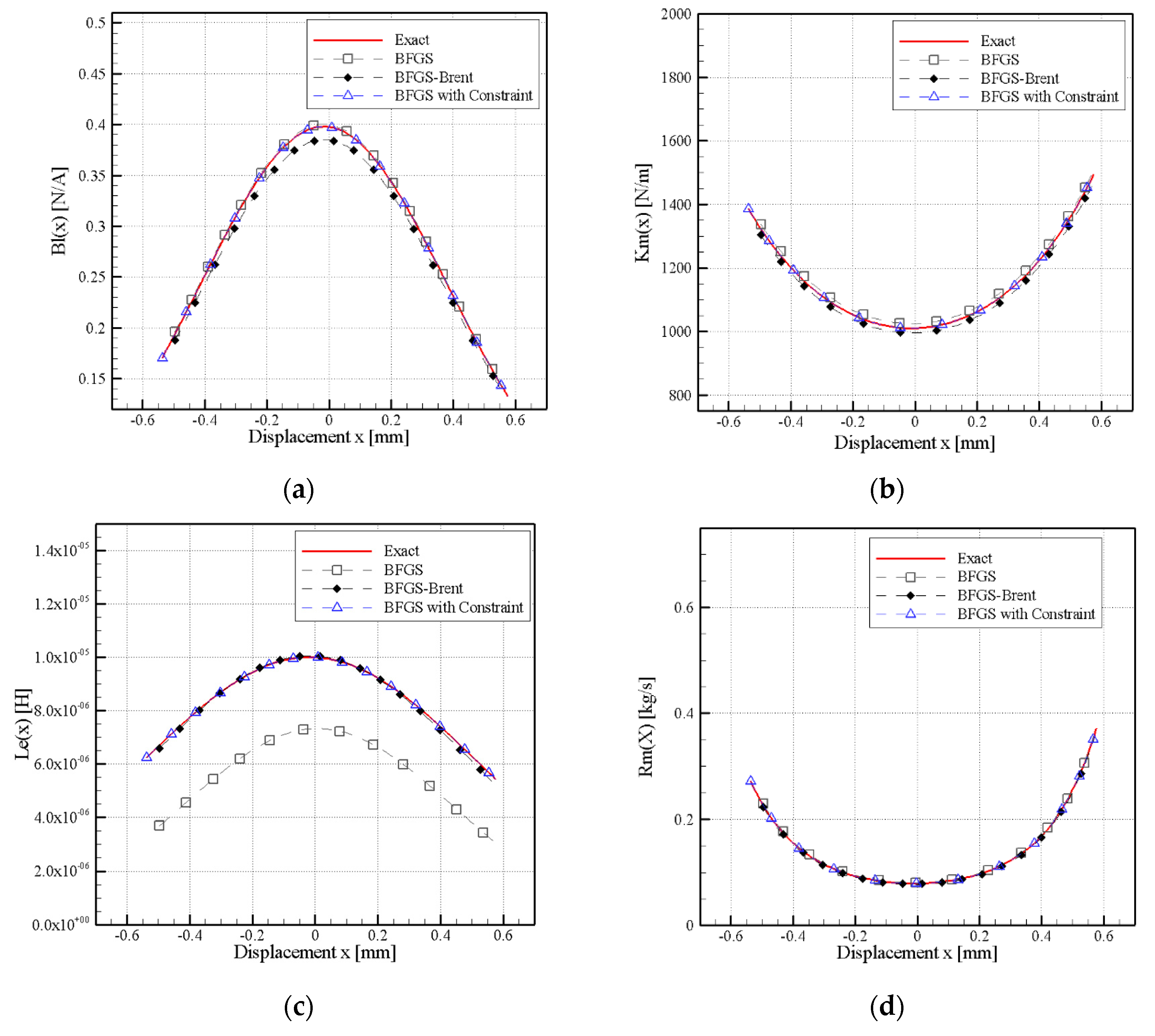
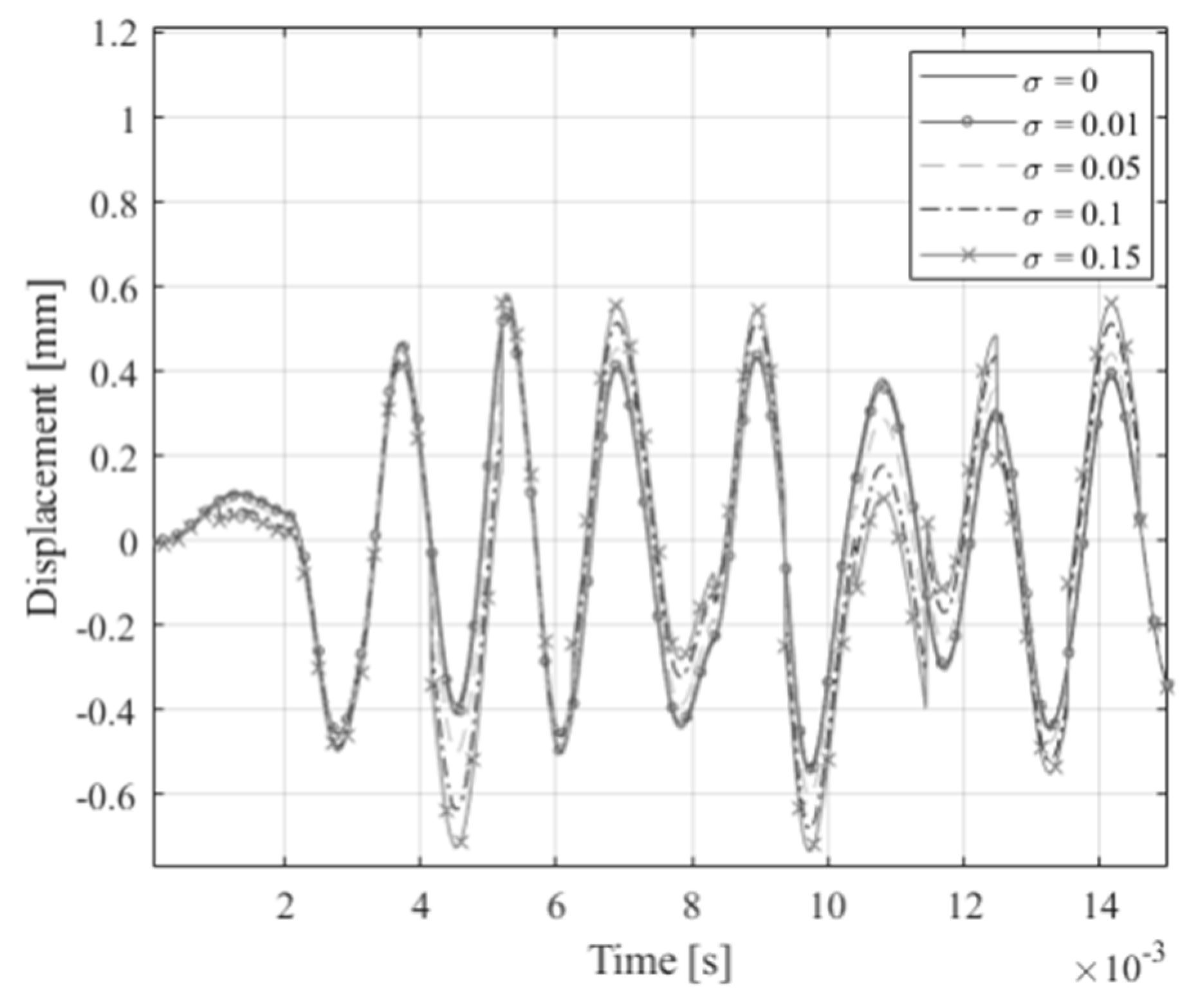
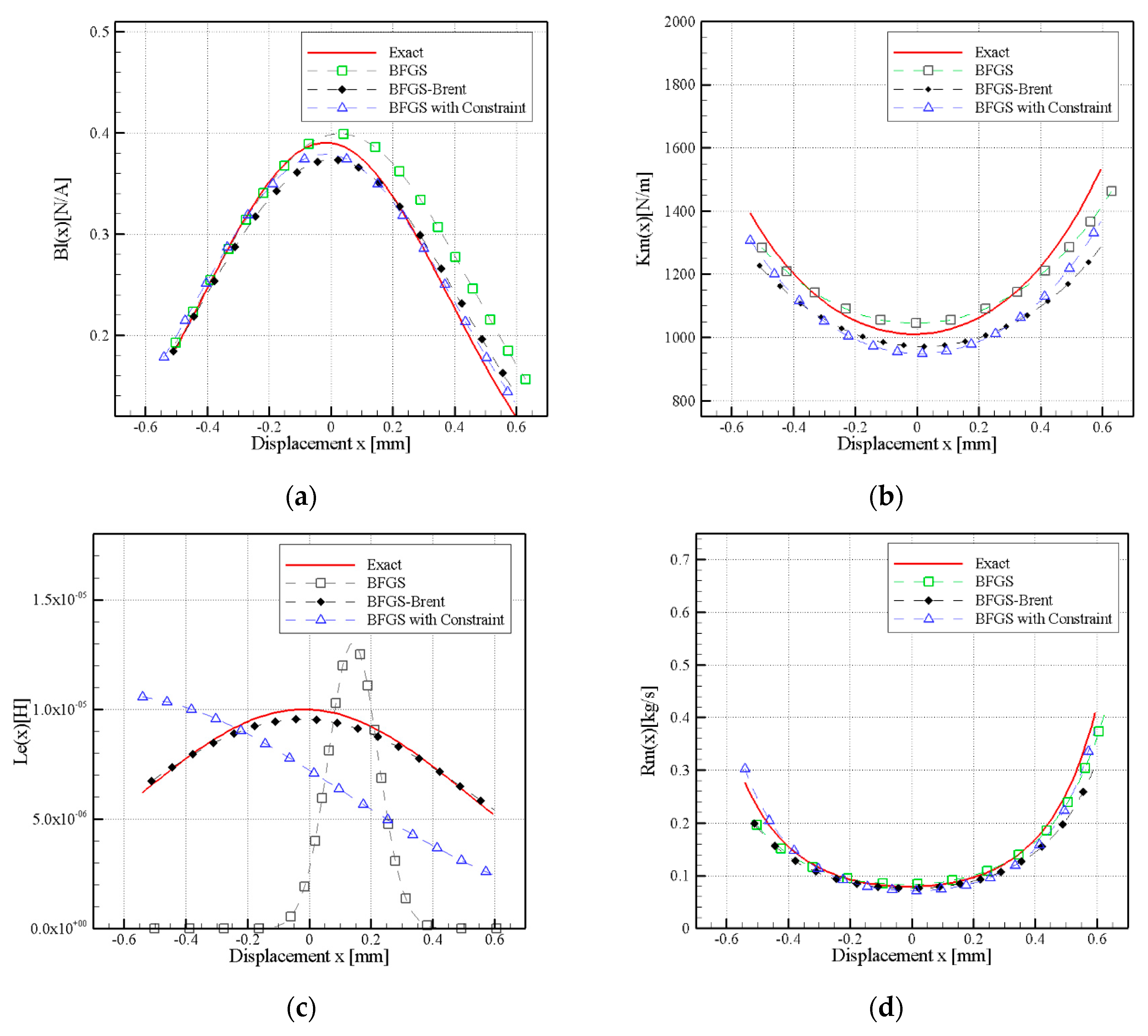
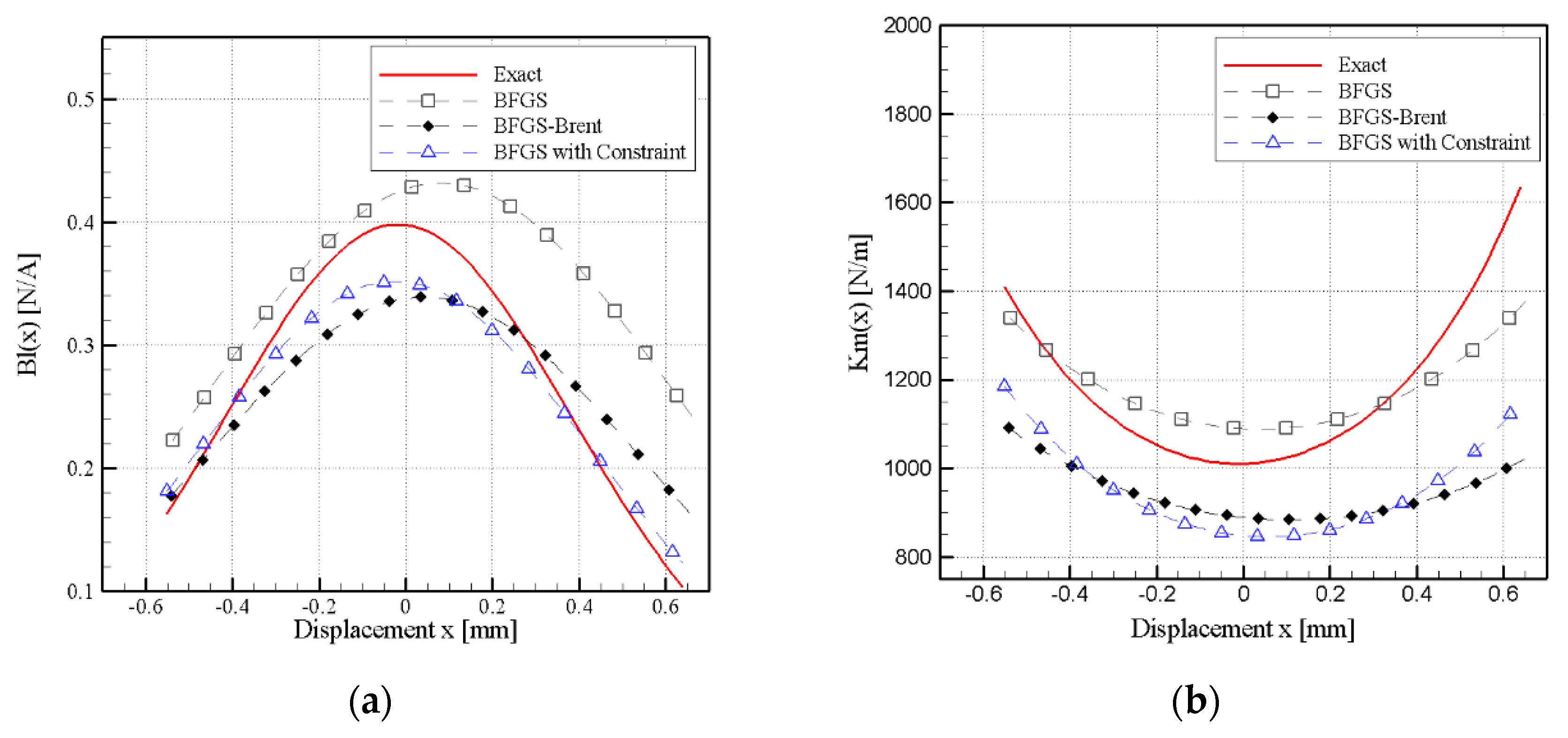
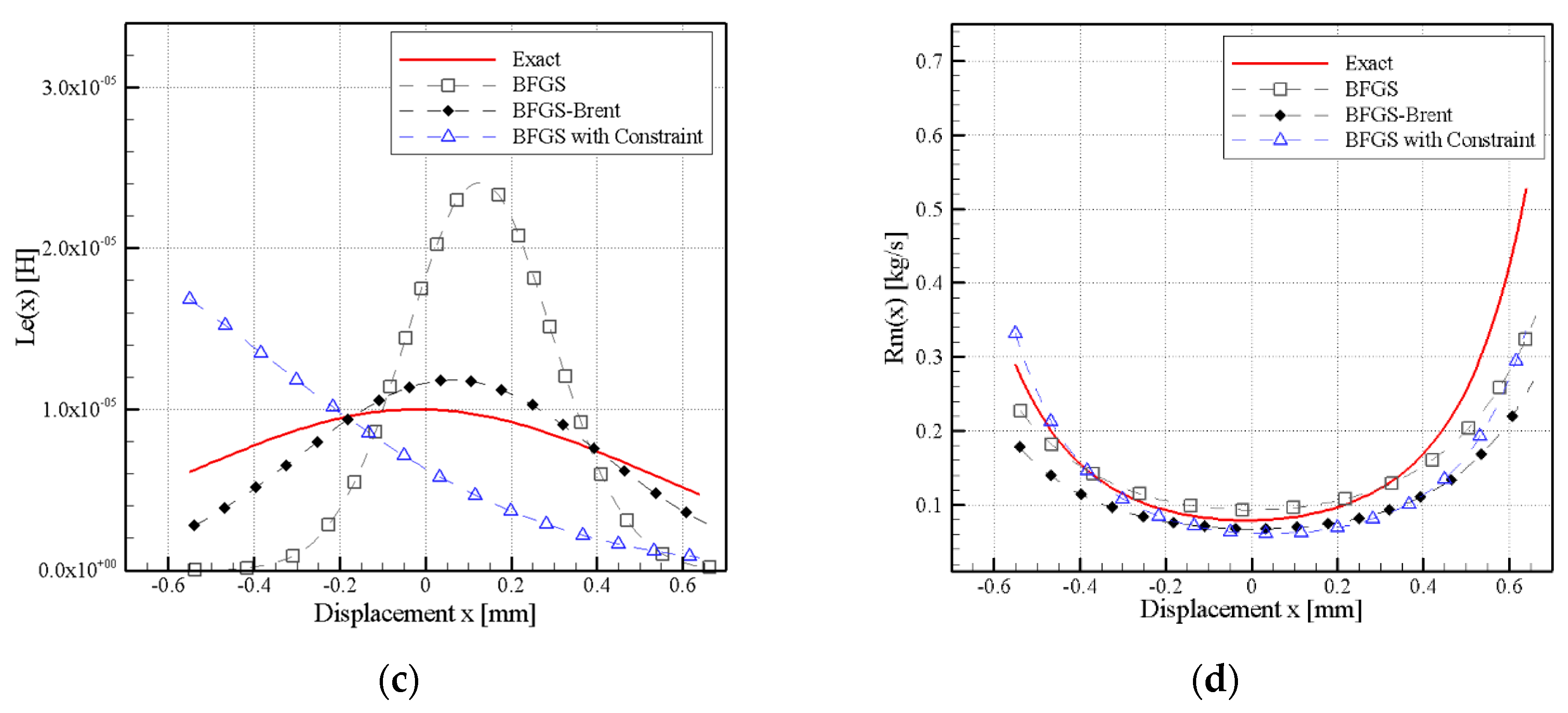
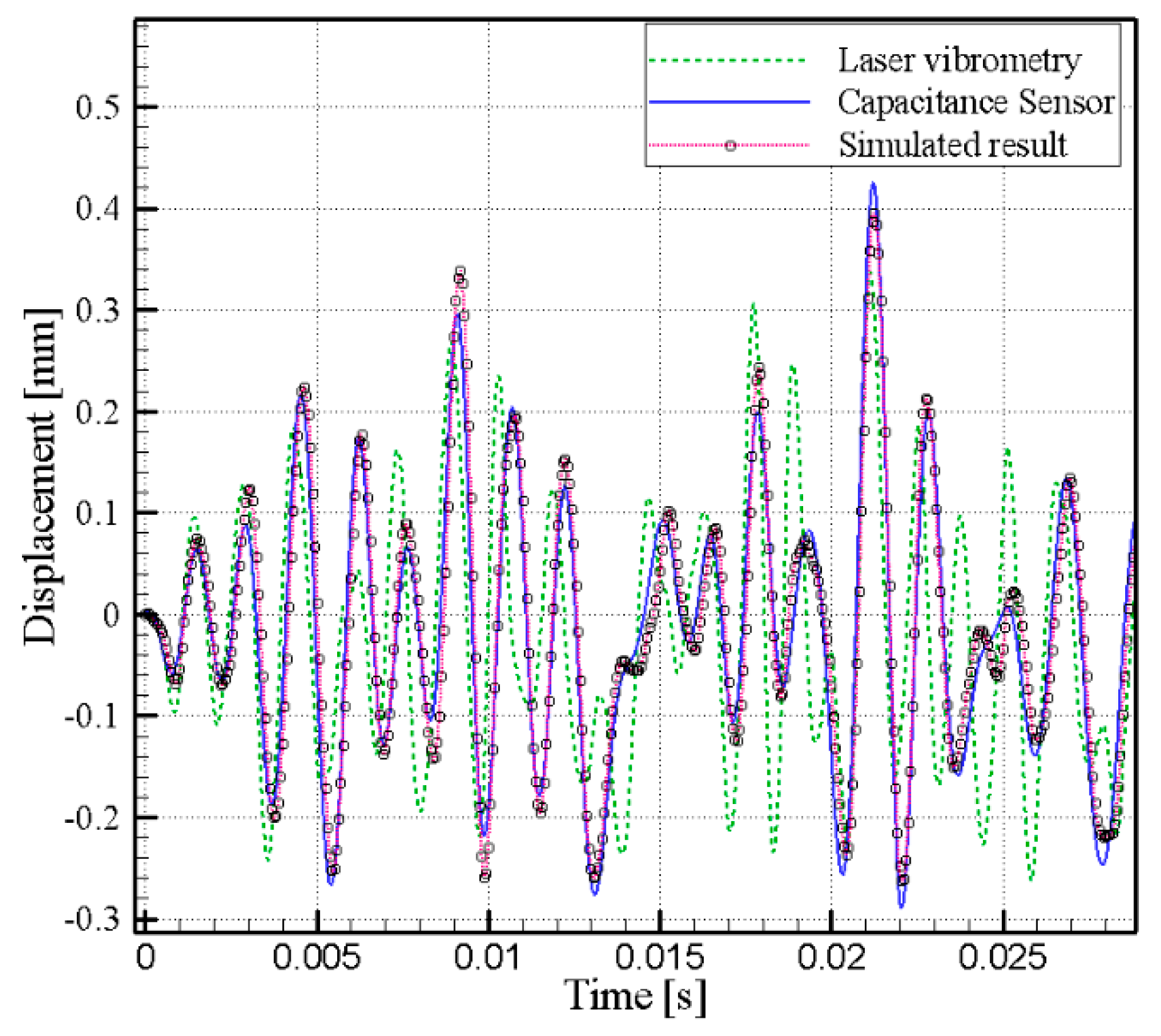
3.1. Simulation Results
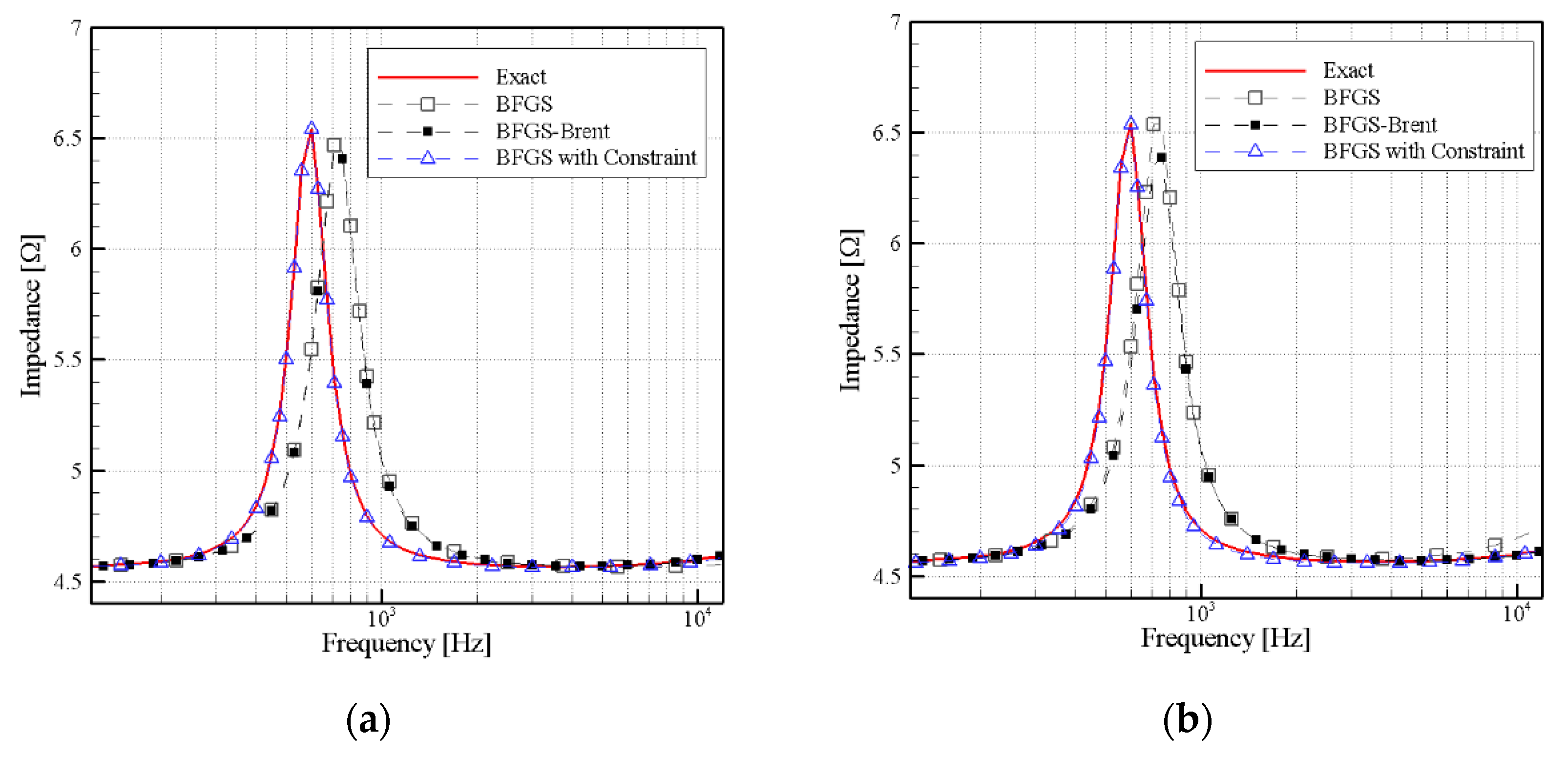
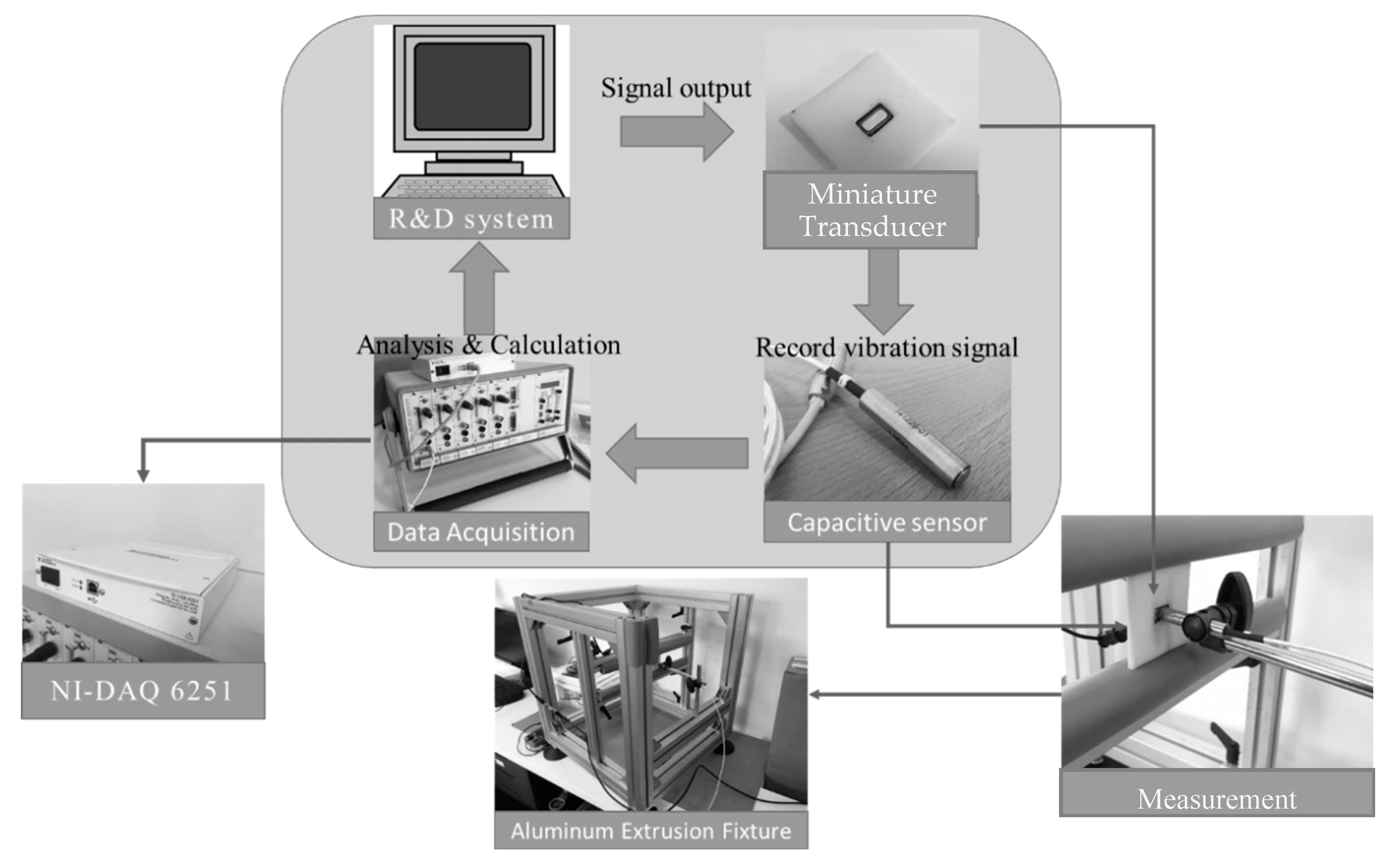
3.2. Experimental Equipment Establishment
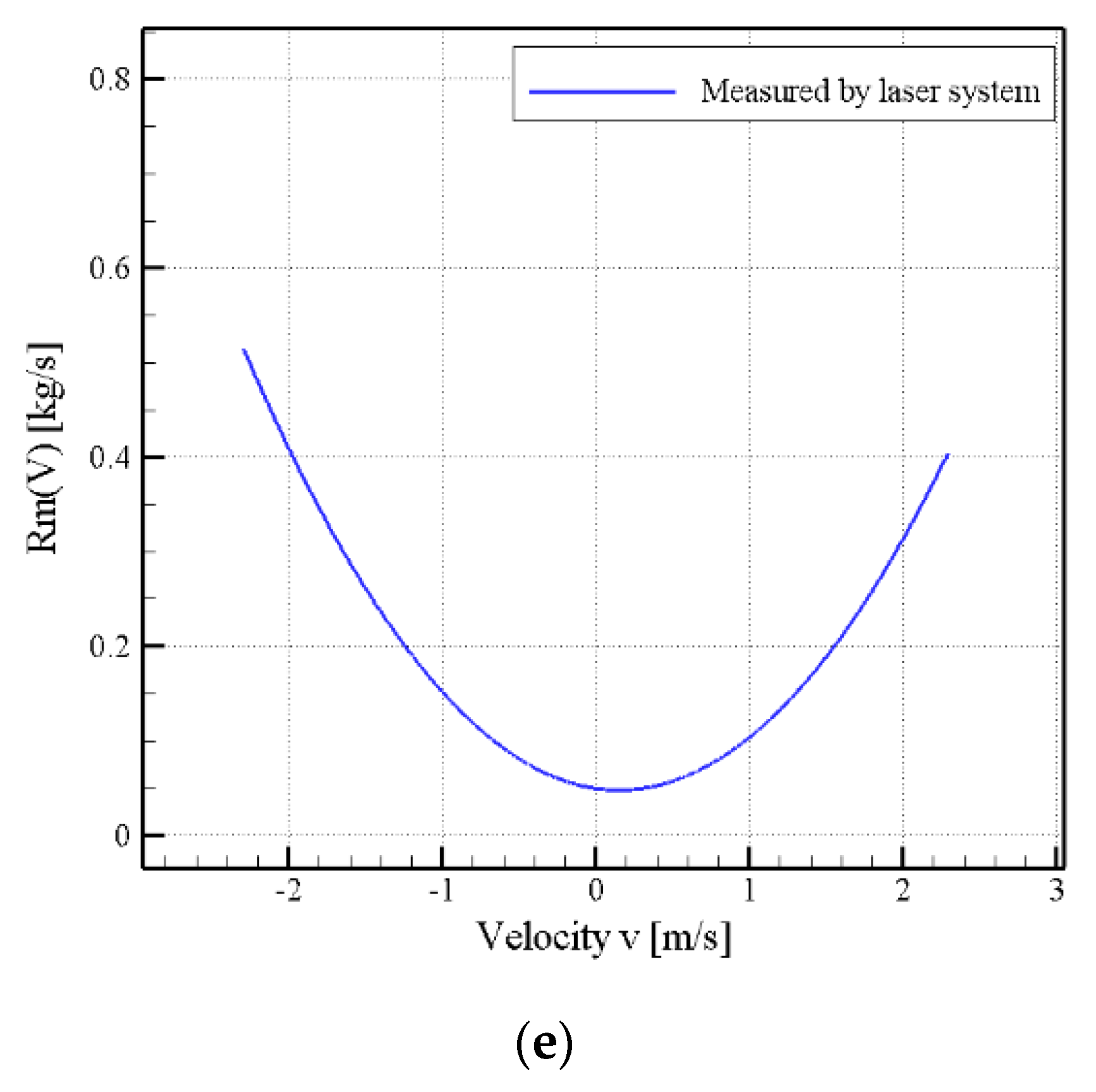
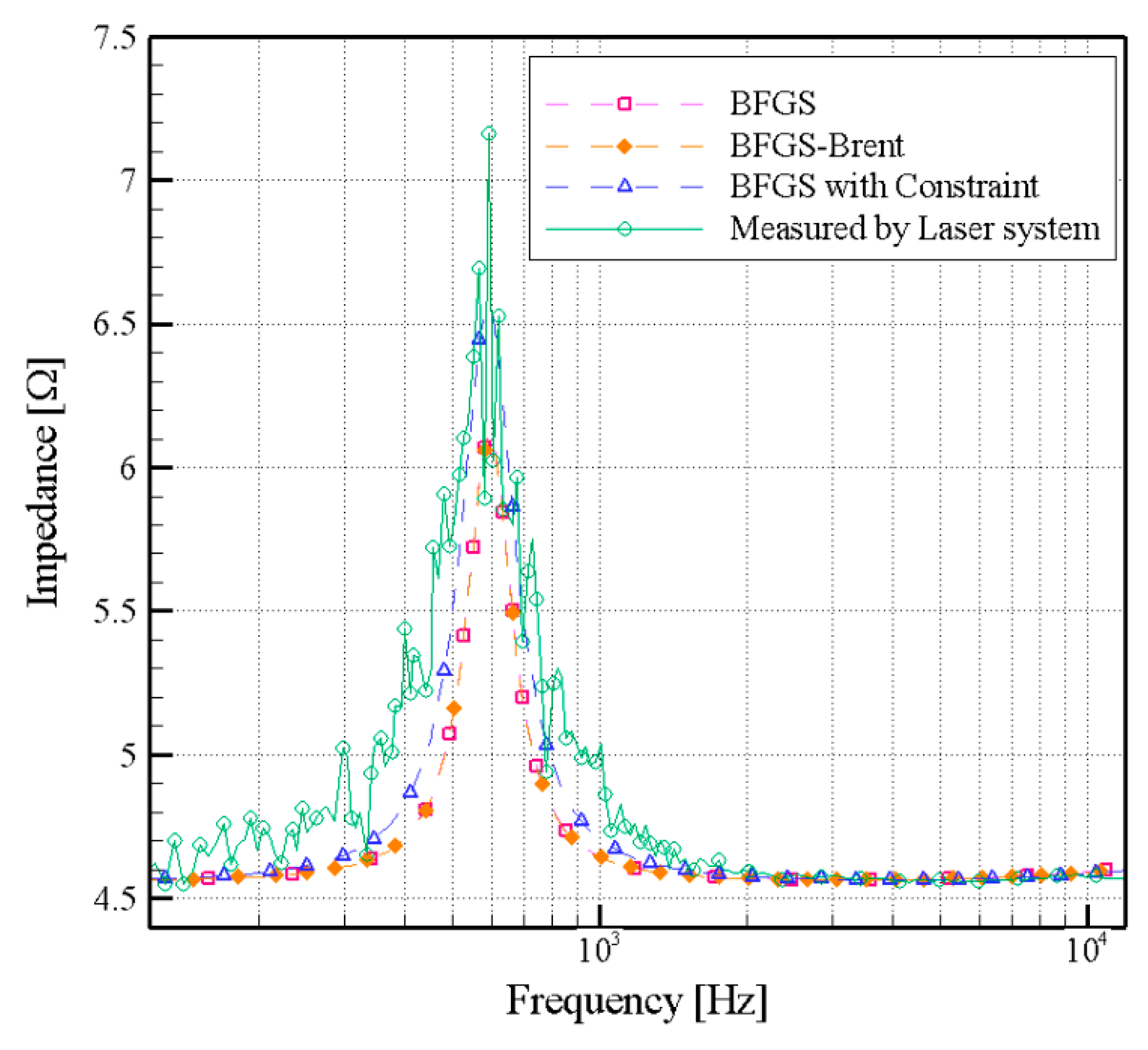
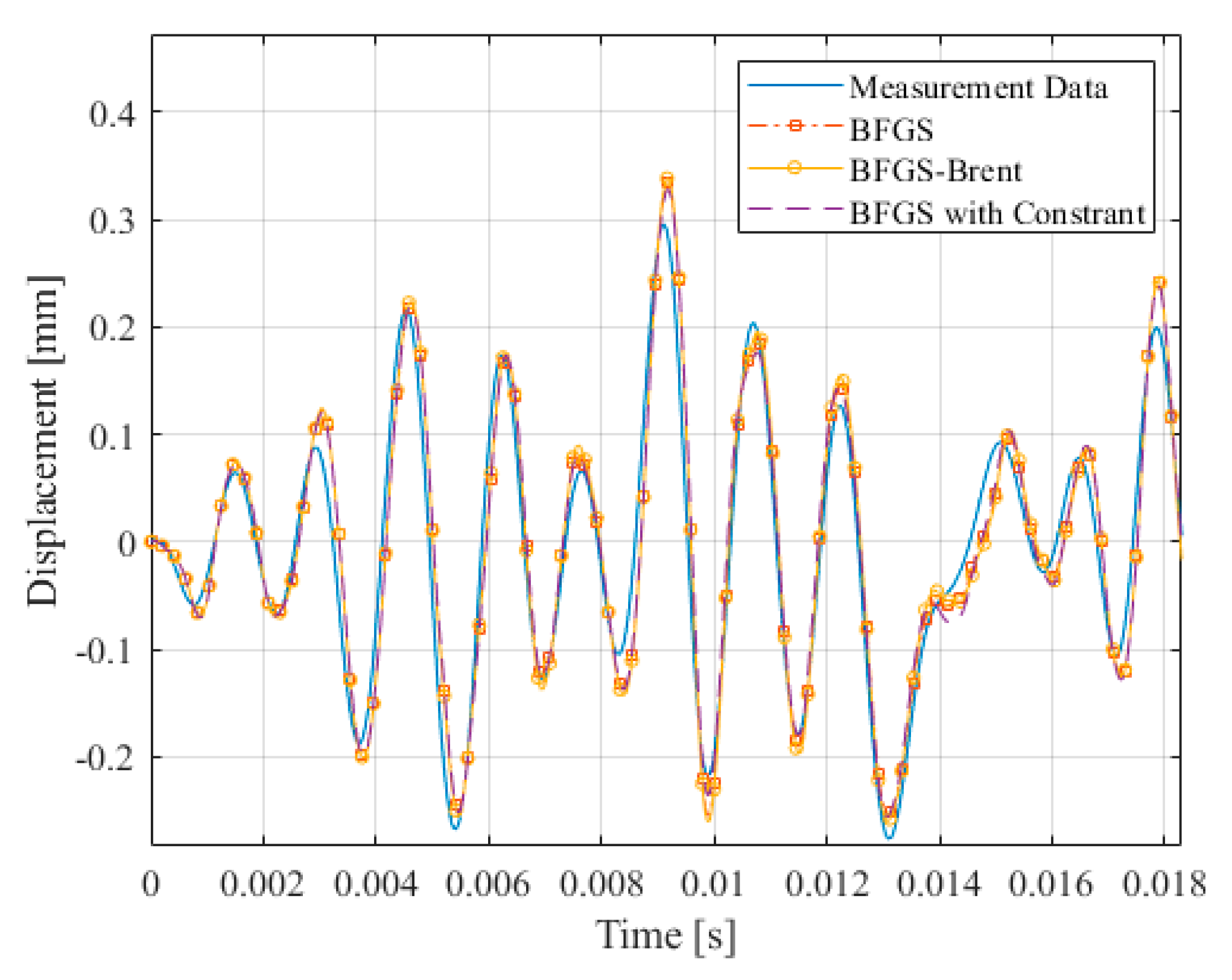
3.3. Discussion of Empirical Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Weems, D.B. How to Design, Build, & Test Complete Speaker Systems; Tab Books: Blue Ridge Summit, PA, USA, 1978. [Google Scholar]
- Carlson, D.E. Loudspeaker parameter determination. J. Acoust. Soc. Am. 1977, 61, S53. [Google Scholar] [CrossRef]
- Gomez-Meda, R. Measurement of the Thiele-Small parameters for a given loudspeaker, without using a box. In Proceedings of the Audio Engineering Society Convention 91, Jalisco, Mexico, 4–8 October 1991; p. 3162. [Google Scholar]
- Struck, C. ZFIT: A MATLAB tool for Thiele-Small parameter fitting and optimization. In Proceedings of the AES Convention 129th, San Francisco, CA, USA, 4–7 November 2010; pp. 8220–8227. [Google Scholar]
- Klippel, W. Tutorial: Loudspeaker nonlinearities—Causes, parameters, symptoms. J. Audio Eng. Soc. 2006, 54, 907–939. [Google Scholar]
- Clark, D. Precision measurement of loudspeaker parameters. J. Audio Eng. Soc. 1997, 45, 129–141. [Google Scholar]
- Schurer, H.; Slump, C.H.; Herrmann, O.E. Theoretical and experimental comparison of three methods for compensation of electrodynamic transducer nonlinearity. J. Audio Eng. Soc. 1998, 46, 723–740. [Google Scholar]
- Klippel, W. Dynamic measurement and interpretation of the nonlinear parameters of electrodynamic loudspeakers. J. Audio Eng. Soc. 1990, 38, 944–955. [Google Scholar]
- Heng, W.; Shen, Y.; Xia, J.; Feng, Z.; Liu, Y. Analysis and prediction of loudspeaker large-signal symptoms. Sci. China Phys. Mech. Astron. 2013, 56, 1355–1360. [Google Scholar] [CrossRef]
- Faifer, M.; Ottoboni, R.; Toscani, S. A novel, cost-effective method for loudspeakers parameters measurement under non-linear conditions. In Proceedings of the 2008 IEEE Autotestcon, Salt Lake City, UT, USA, 8–11 September 2008; pp. 562–568. [Google Scholar]
- Mowry, S. Simplified Simulation Method for Nonlinear Loudspeaker Parameters. Voice Coil Mag. 2007, 9, 1–8. [Google Scholar]
- Mihelich, R.J. Loudspeaker nonlinear parameter estimation: An optimization method. In Proceedings of the AES Convention 111th, New York, NY, USA, 21–24 September 2001. [Google Scholar]
- Pedersen, B.R.; Rubak, P. Online identification of linear loudspeakers parameters. In Proceedings of the AES Convention 122th, Vienna, Austria, 5–8 May 2007. [Google Scholar]
- Knudsen, M.H. Loudspeaker Modelling and Parameter Estimation. In Proceedings of the Audio Engineering Society Convention 100th, Copenhagen, Denmark, 11–14 May 1996. [Google Scholar]
- Lei, H.; Chen, X.D.; Yao, Y.; Li, X.Y. Novel Quartz Crystal Capacitive Sensor for Micro Displacement Detection. IEEE Sens. J. 2012, 12, 2145–2149. [Google Scholar] [CrossRef]
- Kang, D.; Moon, W. Electrode configuration method with surface profile effect in a contact-type area-varying capacitive displacement sensor. Sens. Actuator A-Phys. 2013, 189, 33–44. [Google Scholar] [CrossRef]
- Mei, S.; Montanari, A.; Nguyen, P.M. A mean field view of the landscape of two-layer neural networks. Proc. Natl. Acad. Sci. USA 2018, 115, E7665–E7671. [Google Scholar] [CrossRef] [PubMed]
- De, S.; Mukherjee, A.; Ullah, E. Convergence guarantees for RMSProp and ADAM in non-convex optimization and an empirical comparison to Nesterov acceleration. arXiv, 2018; arXiv:1807.06766. [Google Scholar]
- Dai, Y.H.; Yuan, Y. A nonlinear conjugate gradient method with a strong global convergence property. SIAM J. Optim. 1999, 10, 177–182. [Google Scholar] [CrossRef]
- Mokhtari, A.; Ribeiro, A. RES: Regularized Stochastic BFGS Algorithm. IEEE Trans. Signal Process. 2014, 62, 6089–6104. [Google Scholar] [CrossRef] [Green Version]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipesn: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: New York, NY, USA, 2007; p. 1256. [Google Scholar]
- Andersen, M.R. Compensation of Nonlinearities in Transducers; Technical University of Denmark: Lyngby, Denmark, 2005. [Google Scholar]
- Capacitive Linear Displacement Sensors an Overview. Available online: http://www.lionprecision.com/capacitive-sensors/ (accessed on 16 December 2018).
- National Instruments NI-DAQ 6251, datasheet, National Instruments Corporation, US. Available online: http://www.ni.com/datasheet/pdf/en/ds-22 (accessed on 16 December 2018).



| Parameters | Values |
|---|---|
| Mm | 0.049 ×10−3 (kg) |
| Re | 4.560 (Ohm) |
| Bl(x) | (N/A) |
| Rm(x) | (kg/s) |
| Le(x) | (H) |
| Km(x) | (N/m) |
| Parameters (Unit) | Values | ||
|---|---|---|---|
| Case1 | Case2 | Case3 | |
| Mm (kg) | 0.049 × 10−3 | 0.003 | 0.065× 10−6 |
| Re (Ohm) (fixed) | 4.560 | 4.560 | 4.560 |
| Bl(x) (N/A) | |||
| Rm(x) (kg/s) | |||
| Le(x) (H) | |||
| Km(x) (N/m) | |||
| Case | Iteration Numbers | Minimal Value of J | Average Error for Each Parameters (%) | ||||
|---|---|---|---|---|---|---|---|
| Mm | Bl(x) | Rm(x) | Le(x) | Km(x) | |||
| 1 | 51 | ||||||
| 2 | 143 | ||||||
| 3 | 130 | ||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jian, Y.-C.; Tsai, Y.-T.; Pawar, S.J. Parameter Optimization Method for Identifying the Optimal Nonlinear Parameters of a Miniature Transducer with a Metal Membrane. Appl. Sci. 2018, 8, 2647. https://doi.org/10.3390/app8122647
Jian Y-C, Tsai Y-T, Pawar SJ. Parameter Optimization Method for Identifying the Optimal Nonlinear Parameters of a Miniature Transducer with a Metal Membrane. Applied Sciences. 2018; 8(12):2647. https://doi.org/10.3390/app8122647
Chicago/Turabian StyleJian, Yin-Cheng, Yu-Ting Tsai, and S. J. Pawar. 2018. "Parameter Optimization Method for Identifying the Optimal Nonlinear Parameters of a Miniature Transducer with a Metal Membrane" Applied Sciences 8, no. 12: 2647. https://doi.org/10.3390/app8122647





