Ocean Color Analytical Model Explicitly Dependent on the Volume Scattering Function
Abstract
:Featured Application
Abstract
1. Introduction
2. Forward Model Development
2.1. Diffuse Attenuation of Upwelling Radiance
2.2. Average Cosine of the Asymptotic Light Field
2.3. Backward Phase Function β(ψ)/bb
2.4. Backscattering Ratio
2.5. Shape Factor fL
2.6. Remote Sensing Reflectance Formulation
2.7. Average Cosine of the Downwelling Light Field
2.8. Including Inelastic Water Raman Effects
2.9. ZTT Model Summary
3. Methods
3.1. Synthetic Dataset
3.2. Radiative Transfer Simulations
3.3. Field Data Sets
3.4. Depth Weighting IOPs
3.5. Metrics for Error Assessment
4. Results
4.1. Developing an Expression for the fL Term
4.2. Assessing Assumption of Constant βp(ψ)/bbp
4.3. Assessment with High Quality Validation Data
4.4. Assessment with Global NOMAD Data Set
5. Discussion
5.1. Assessing Residual Bias in the Model
5.2. Suitability for Inversion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Symbol | Description | Units |
|---|---|---|
| a | total absorption coefficient | m−1 |
| ax | absorption coefficient, where subscript x = w, p, d, ph, g, pg, pico, and micro specifies water, particulate, non-phytoplankton particulate, phytoplankton, dissolved, particulate plus dissolved, picoplankton, and microplankton | m−1 |
| a* | specific absorption coefficient | m2 mg−1 |
| b | total scattering coefficient | m−1 |
| bp | particulate scattering coefficient | m−1 |
| bf | forward scattering coefficient | m−1 |
| bbx | backscattering coefficient, where subscript x = w and p specifies water and particulate | m−1 |
| backscattering ratio | - | |
| particulate backscattering ratio | - | |
| β | total volume scattering function (VSF) | m−1 sr−1 |
| βx | volume scattering function (VSF), where subscript x = w and p specifies seawater and particulate | m−1 sr−1 |
| c | total attenuation coefficient | m−1 |
| [Chl] | chlorophyll concentration | mg m−3 |
| δx | error, where subscript x = abs and rel specifies absolute and relative | - |
| Ex | planar irradiance, where subscript x = d, ds, and dd specifies downwelling, diffuse downwelling, and direct downwelling | W m−2 nm−1 |
| Eod | downwelling scalar irradiance | W m−2 nm−1 |
| f | model coefficient for relating irradiance reflectance to bb/a | - |
| fb, fL | radiance shape factors | - |
| Φ | azimuth angle relative to solar plane | °, rad |
| G | model coefficient for above-surface remote sensing reflectance | sr−1 |
| ψ | scattering angle | °, rad |
| H | fraction of diffuse downwelling light (Eds/Ed) | - |
| ηbb | fraction of total backscattering contributed by bbw | - |
| Kx | diffuse attenuation coefficient, where subscript x = Lu, u, d, and ∞ specifies upwelling radiance, upwelling irradiance, downwelling irradiance, and asymptotic | m−1 |
| Lu | upwelling radiance | W m−2 nm−1 sr−1 |
| Lw | water-leaving radiance | W m−2 nm−1 sr−1 |
| λ | Wavelength | nm |
| Atmospheric component of | - | |
| IOP component of | - | |
| average cosine of the asymptotic light field | - | |
| average cosine of the downwelling light field | - | |
| μw | cosine of the in-water solar zenith | - |
| np | particulate refractive index, relative to water | - |
| P | phase function (β/b) | sr−1 |
| Px | particulate phase function (βp/bp), where subscript x = p, ps, and pl specifies particulate, particulate small-dominant, and particulate large-dominant | sr−1 |
| Pbb,x | backward particulate phase function (βp/bbp), where subscript x = ST and FF specifies functions from References [26,44] | sr−1 |
| Q | ratio of upwelling irradiance to nadir radiance | sr |
| rrs | remote sensing reflectance, the ratio of upwelling subsurface radiance to downwelling irradiance | sr−1 |
| Rrs | remote sensing reflectance, the ratio of water-leaving radiance to downwelling irradiance | sr−1 |
| Rd | scaling factor for ad | - |
| Rg | scaling factor for ag | - |
| Sf | mixing factor for aph | - |
| θx | zenith angle, where x = s and v specifies solar and viewing | °, rad |
| θs’ | above water solar zenith angle | °, rad |
| v | exponent of empirical spectral bp function | - |
| V | atmospheric horizontal visibility | km |
| ω | albedo (b/c) | - |
| ratio of diffuse upwelling attenuation coefficient to asymptotic attenuation coefficient | - | |
| z | depth | m |
| Equation | Symbol | Value |
|---|---|---|
| Equation (3) | −5.98948784303628 × 10−8 | |
| 5.95904039870752 × 10−6 | ||
| −6.975283717755 × 10−4 | ||
| 2.07111856771792 × 10−3 | ||
| 2.69046922858858 × 10−2 | ||
| Equation (4) | −3.79435531537314 × 10−7 | |
| 2.42117623125973 × 10−4 | ||
| −5.76056692150838 × 10−2 | ||
| 6.04944577004764 | ||
| −236.166389774491 | ||
| Equation (16) | −3.37021020153209 × 10−12 | |
| 2.25040435584125 × 10−10 | ||
| −2.25897880448836 × 10−9 | ||
| 4.98402568695743 × 10−10 | ||
| −3.67440351688922 × 10−8 | ||
| 4.02677827509591 × 10−7 | ||
| −2.52448256032736 × 10−8 | ||
| 2.09631870150827 × 10−6 | ||
| −2.43068373614361 × 10−5 | ||
| 5.98295717192273 × 10−7 | ||
| −5.36922068813161 × 10−5 | ||
| 6.84105803724285 × 10−4 | ||
| −5.34168078899319 × 10−6 | ||
| 4.95201118318049 × 10−4 | ||
| −6.09578731164684 × 10−3 | ||
| 5.32097604773773 × 10−4 | ||
| −2.91276619216202 × 10−2 | ||
| 0.589340234481004 | ||
| Equation (17) | 0.00611094400155735 | |
| −0.00104841847722295 | ||
| 0.0498255758922950 | ||
| −0.0117672820980625 | ||
| 0.128019358635212 | ||
| −0.0429896134897322 | ||
| 0.103528931695373 | ||
| 0.950921179229178 |
| Wavelength | Value | Wavelength | Value | Wavelength | Value |
|---|---|---|---|---|---|
| 350 | 0.990 | 505 | 1.018 | 655 | 0.992 |
| 355 | 0.990 | 510 | 1.013 | 660 | 0.993 |
| 360 | 0.992 | 515 | 1.009 | 665 | 0.998 |
| 365 | 0.992 | 520 | 1.005 | 670 | 1.000 |
| 370 | 0.992 | 525 | 1.002 | 675 | 1.001 |
| 375 | 0.995 | 530 | 0.999 | 680 | 1.000 |
| 380 | 0.997 | 535 | 0.996 | 685 | 0.995 |
| 385 | 0.997 | 540 | 0.995 | 690 | 0.994 |
| 390 | 0.998 | 545 | 0.992 | 695 | 0.993 |
| 395 | 1.000 | 550 | 0.989 | 700 | 0.994 |
| 400 | 1.000 | 555 | 0.987 | 705 | 0.994 |
| 405 | 1.000 | 560 | 0.985 | 710 | 0.996 |
| 410 | 1.002 | 565 | 0.982 | 715 | 0.997 |
| 415 | 1.003 | 570 | 0.981 | 720 | 0.999 |
| 420 | 1.006 | 575 | 0.982 | 725 | 1.000 |
| 425 | 1.008 | 580 | 0.983 | 730 | 1.000 |
| 430 | 1.010 | 585 | 0.984 | 735 | 1.000 |
| 435 | 1.013 | 590 | 0.986 | 740 | 0.999 |
| 440 | 1.016 | 595 | 0.987 | 745 | 0.999 |
| 445 | 1.020 | 600 | 0.988 | 750 | 0.999 |
| 450 | 1.023 | 605 | 0.988 | 755 | 0.999 |
| 455 | 1.024 | 610 | 0.989 | 760 | 0.999 |
| 460 | 1.025 | 615 | 0.989 | 765 | 0.999 |
| 465 | 1.025 | 620 | 0.989 | 770 | 0.999 |
| 470 | 1.026 | 625 | 0.990 | 775 | 1.000 |
| 475 | 1.026 | 630 | 0.990 | 780 | 1.000 |
| 480 | 1.026 | 635 | 0.990 | 785 | 1.001 |
| 485 | 1.026 | 640 | 0.990 | 790 | 1.002 |
| 490 | 1.026 | 645 | 0.990 | 795 | 1.002 |
| 495 | 1.024 | 650 | 0.990 | 800 | 1.002 |
| 500 | 1.022 |
References
- Gordon, H.R. Inverse methods in hydrologic optics. Oceanologia 2002, 44, 9–58. [Google Scholar]
- Zaneveld, J.R.V.; Twardowski, M.S.; Lewis, M.; Barnard, A. Radiative transfer and remote sensing. In Remote Sensing of Coastal Aquatic Waters; Miller, R., Del-Castillo, C., McKee, B., Eds.; Springer: Dordrecht, The Netherlands, 2005; pp. 1–20. [Google Scholar]
- Twardowski, M.; Lewis, M.; Barnard, A.; Zaneveld, J.R.V. In-water instrumentation and platforms for ocean color remote sensing applications. In Remote Sensing of Coastal Aquatic Waters; Miller, R., Del-Castillo, C., McKee, B., Eds.; Springer: Dordrecht, The Netherlands, 2005; pp. 69–100. [Google Scholar]
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic Press: San Diego, CA, USA, 1994; 592p. [Google Scholar]
- Morel, A.; Gentili, B. Diffuse reflectance of oceanic waters. II. Bidirectional aspects. Appl. Opt. 1993, 32, 6864–6879. [Google Scholar] [CrossRef] [PubMed]
- Morel, A.; Gentili, B. Diffuse reflectance of oceanic waters. III. Implication of bidirectionality for the remote-sensing problem. Appl. Opt. 1996, 35, 4850. [Google Scholar] [CrossRef] [PubMed]
- Morel, A.; Antoine, D.; Gentili, B. Bidirectional reflectance of oceanic waters: Accounting for Raman emission and varying particle phase function. Appl. Opt. 2002, 41, 6289–6306. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Li, W.; Gatebe, C.K.; Stamnes, K. Neural network method to correct bidirectional effects in water leaving radiance. Appl. Opt. 2016, 55, 10–21. [Google Scholar] [CrossRef] [PubMed]
- Gordon, H.; Brown, O.B.; Evans, R.H.; Brown, J.W.; Smith, R.C.; Baker, K.S.; Clark, D.K. A semianalytic radiance model of ocean color. J. Geophys. Res. 1988, 93, 10909–10924. [Google Scholar] [CrossRef]
- Park, Y.-J.; Ruddick, K. Model of remote sensing reflectance including bidirectional effects for case 1 and case 2 waters. Appl. Opt. 2005, 44, 1236–1249. [Google Scholar] [CrossRef]
- Lee, Z.-P.; Du, K.-P.; Voss, K.J.; Zibordi, G.; Lubac, B.; Arnone, R.; Weidemann, A. An inherent optical property centered approach to correct the angular effects in water-leaving radiance. Appl. Opt. 2011, 50, 3155–3167. [Google Scholar] [CrossRef]
- Hlaing, S.; Gilerson, A.; Harmel, T.; Tonizzo, A.; Weidemann, A.; Arnone, R.; Ahmed, S. Assessment of a bidirectional reflectance distribution correction of above-water and satellite water-leaving radiance in coastal waters. Appl. Opt. 2012, 51, 220–237. [Google Scholar] [CrossRef]
- Werdell, J.; McKinna, L.I.W.; Boss, E.; Ackleson, S.G.; Craig, S.E.; Gregg, W.W.; Lee, Z.-P.; Maritorena, S.; Roesler, C.S.; Rousseaux, C.S.; et al. An overview of approaches and challenges for retrieving marine inherent optical properties from ocean color remote sensing. Prog. Oceanogr. 2018, 160, 186–212. [Google Scholar] [CrossRef]
- Morel, A. In-water and remote measurements of ocean color. Bound.-Lay. Meteorl. 1980, 18, 177–201. [Google Scholar] [CrossRef]
- Mobley, C.D.; Werdell, J.; Franz, B.; Ahmad, Z.; Bailey, S. Atmospheric Correction for Satellite Ocean Color Radiometry; NASA Report NASA/TM–2016-217551; NASA: Washington, DC, USA, 2016; 73p.
- Werdell, P.J.; Franz, B.A.; Bailey, S.W.; Feldman, G.C.; Boss, E.; Brando, V.E.; Dowell, M.; Hirata, T.; Lavender, S.J.; Lee, Z.-P.; et al. Generalized ocean color inversion model for retrieving marine inherent optical properties. Appl. Opt. 2013, 52, 2019–2037. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Voss, K.; Morel, A. Bidirectional reflectance function for oceanic waters with varying chlorophyll concentrations: Measurements versus predictions. Limnol. Oceanogr. 2005, 50, 698–705. [Google Scholar] [CrossRef] [Green Version]
- Voss, K.J.; Morel, A.; Antoine, D. Detailed validation of the bidirectional effect in various Case 1 waters for application to ocean color imagery. Biogeosciences 2007, 4, 781–789. [Google Scholar] [CrossRef] [Green Version]
- Gleason, A.; Voss, K.; Gordon, H.R.; Twardowski, M.; Sullivan, J.; Trees, C.; Weidemann, A.; Berthon, J.-F.; Clark, D.; Lee, Z.-P. Detailed validation of ocean color bidirectional effects in various Case I and Case II waters. Opt. Express 2012, 20, 7630–7645. [Google Scholar] [CrossRef]
- He, S.; Zhang, X.; Xiong, Y.; Gray, D. A bidirectional subsurface remote sensing reflectance model explicitly accounting for particle backscattering shapes. J. Geophys. Res. Oceans 2017, 122, 8614–8626. [Google Scholar] [CrossRef]
- Talone, M.; Zibordi, G.; Lee, Z.-P. Correction for the non-nadir viewing geometry of AERONET-OC above water radiometry data: An estimate of uncertainties. Opt. Express 2018, 26, A541–A561. [Google Scholar] [CrossRef] [PubMed]
- Hirata, T.; Hardman-Mountford, N.; Aiken, J.; Fishwick, J. Relationship between the distribution function of ocean nadir radiance and inherent optical properties for oceanic waters. Appl. Opt. 2009, 48, 3129–3138. [Google Scholar] [CrossRef] [PubMed]
- Gordon, H.R. Sensitivity of radiative transfer to small-angle scattering in the ocean: Quantitative assessment. Appl. Opt. 1993, 32, 7505–7511. [Google Scholar] [CrossRef] [PubMed]
- Mishchenko, M.I.; Travis, L.D.; Lacis, A.A. Scattering, Absorption, and Emission of Light by Small Particles; Cambridge University Press: Cambridge, UK, 2002; pp. 74–82. [Google Scholar]
- Hair, J.; Hostetler, C.; Hu, Y.; Behrenfeld, M.; Butler, C.F.; Harper, D.B.; Hare, R.; Berkoff, R.; Cook, A.; Collins, J.; et al. Combined Atmospheric and Ocean Profiling from an Airborne High Spectral Resolution Lidar. Eur. Phys. J. Conf. 2016, 119, 22001. [Google Scholar] [CrossRef] [Green Version]
- Sullivan, J.M.; Twardowski, M.S. Angular shape of the volume scattering function in the backward direction. Appl. Opt. 2009, 48, 6811–6819. [Google Scholar] [CrossRef] [PubMed]
- Zaneveld, J.R.V. Remotely sensed reflectance and its dependence on vertical structure: A theoretical derivation. Appl. Opt. 1982, 21, 4146–4150. [Google Scholar] [PubMed]
- Zaneveld, J.R.V. A theoretical derivation of the dependence of the remotely sensed reflectance on the inherent optical properties. J. Geophys. Res. 1995, 100, 13135–13142. [Google Scholar] [CrossRef]
- Tonizzo, A.; Twardowski, M.; McLean, S.; Voss, K.; Lewis, M.; Trees, C. Closure and uncertainty assessment for ocean color reflectance using measured volume scattering functions and reflective tube absorption coefficients with novel correction for scattering. Appl. Opt. 2017, 56, 130–146. [Google Scholar] [CrossRef]
- Wolanin, A.; Rozanov, V.; Dinter, T.; Bracher, A. Detecting CDOM Fluorescence Using High Spectrally Resolved Satellite Data: A Model Study. In Towards an Interdisciplinary Approach in Earth System Science: Advances of a Helmholtz Graduate Research School; Springer International Publishing: Cham, Switzerland, 2015; pp. 109–121. [Google Scholar] [Green Version]
- Zhai, P.W.; Hu, Y.; Winker, D.M.; Franz, B.A.; Boss, E. Contribution of Raman scattering to polarized radiation field in ocean waters. Opt. Express 2015, 23, 23582–23596. [Google Scholar] [CrossRef]
- Rozanov, V.; Dinter, T.; Rozanov, A.; Wolanin, A.; Bracher, A.; Burrows, J. Radiative transfer modeling through terrestrial atmosphere and ocean accounting for inelastic processes: Software package SCIATRAN. J. Quant. Spectrosc. Radiat. Transf. 2017, 194, 65–85. [Google Scholar] [CrossRef] [Green Version]
- Zhai, P.W.; Hu, Y.; Winker, D.M.; Franz, B.A.; Werdell, J.; Boss, E. Vector radiative transfer model for coupled atmosphere and ocean systems including inelastic sources in ocean waters. Opt. Express 2017, 25, A223–A239. [Google Scholar] [CrossRef]
- Weidemann, A.; Stavn, R.; Zaneveld, J.R.V.; Wilcox, M.R. Error in predicting hydrosol backscattering from remotely sensed reflectance. J. Geophys. Res. 1995, 100, 163–177. [Google Scholar] [CrossRef]
- Berthon, J.-F.; Shybanov, E.; Lee, M.; Zibordi, G. Measurements and modeling of the volume scattering function in the coastal northern Adriatic Sea. Appl. Opt. 2007, 46, 5189–5203. [Google Scholar] [CrossRef]
- Twardowski, M.; Zhang, X.; Vagle, S.; Sullivan, J.; Freeman, S.; Czerski, H.; You, Y.; Bi, L.; Kattawar, G. The optical volume scattering function in a surf zone inverted to derive sediment and bubble particle subpopulations. J. Geophys. Res. 2012, 117, C00H17. [Google Scholar] [CrossRef]
- Lee, M.; Korchemkina, E.N. Chapter 4: Volume scattering function of seawater. In Springer Series in Light Scattering; Kokhanovsky, A., Ed.; Springer International Publishing: New York, NY, USA, 2017; pp. 151–195. [Google Scholar]
- Voss, K.; Austin, R. Beam attenuation measurement error due to small angle scattering acceptance. J. Atmos. Ocean. Technol. 1993, 10, 113–121. [Google Scholar] [CrossRef]
- Boss, E.; Slade, W.H.; Behrenfeld, M.; Dall’Olmo, G. Acceptance angle effects on the beam attenuation in the ocean. Opt. Express 2009, 17, 1535–1550. [Google Scholar] [CrossRef] [PubMed]
- Twardowski, M.; Tonizzo, A. Scattering and absorption effects on asymptotic light fields in seawater. Opt. Express 2017, 25, 18122–18130. [Google Scholar] [CrossRef] [PubMed]
- Twardowski, M.S.; Boss, E.; Macdonald, J.B.; Pegau, W.S.; Barnard, A.H.; Zaneveld, J.R.V. A model for estimating bulk refractive index from the optical backscattering ratio and the implications for understanding particle composition in Case I and Case II waters. J. Geophys. Res. 2001, 106, 14129–14142. [Google Scholar] [CrossRef]
- Prieur, L.; Morel, A. Etude theorique du regime asymptotique: Relations entre characteristiques optiques et coefficient d’extinction relatif a la penetration de la lumibr, e du jour. Cah. Oceanogr. 1971, 23, 35–48. [Google Scholar]
- Berwald, J.; Stramski, D.; Mobley, C.D.; Kiefer, D.A. Influences of absorption and scattering on vertical changes in the average cosine of the underwater light field. Limnol. Oceanogr. 1995, 40, 1347–1357. [Google Scholar] [CrossRef] [Green Version]
- Fournier, G.; Forand, F. Analytic phase function for ocean water. Ocean Opt. XII 1994, 2558, 194–201. [Google Scholar]
- Jonasz, M.; Fournier, G. Light Scattering by Particles in Water; Academic Press: Amsterdam, The Netherlands, 2007; 704p. [Google Scholar]
- IOCCG. Remote Sensing of Inherent Optical Properties: Fundamentals, Tests of Algorithms, and Applications. In Reports of the International Ocean-Colour Coordinating Group, No. 5; Lee, Z.-P., Ed.; IOCCG: Dartmouth, NS, Canada, 2006; 123p. [Google Scholar]
- Twardowski, M.S.; Sullivan, J.M.; Donaghay, P.L.; Zaneveld, J.R.V. Microscale quantification of the absorption by dissolved and particulate material in coastal waters with an ac-9. J. Atmos. Ocean. Technol. 1999, 16, 691–707. [Google Scholar] [CrossRef]
- Sullivan, J.; Twardowski, M.; Zaneveld, J.R.V.; Moore, C. Measuring optical backscattering in water. In Light Scattering Reviews 7: Radiative Transfer and Optical Properties of Atmosphere and Underlying Surface; Kokhanovsky, A., Ed.; Springer Praxis Books: New York, NY, USA; pp. 189–224. [CrossRef]
- Stockley, N.D.; Rottgers, R.; McKee, D.; Lefering, I.; Sullivan, J.M.; Twardowski, M.S. Assessing uncertainties in scattering correction algorithms for reflective tube absorption measurements made with a WET Labs ac-9. Opt. Express 2017, 25, A1139–A1153. [Google Scholar] [CrossRef]
- Gordon, H.R.; Brown, O.B.; Jacobs, M.M. Computed relationships between the inherent and apparent optical properties of a flat homogeneous ocean. Appl. Opt. 1975, 14, 417–427. [Google Scholar] [CrossRef] [PubMed]
- Twardowski, M.S.; Claustre, H.; Freeman, S.A.; Stramski, D.; Huot, Y. Optical backscattering properties of the “clearest” natural waters. Biogeosciences 2007, 4, 1041–1058. [Google Scholar] [CrossRef]
- Zhang, X.D.; Hu, L.B.; He, M.-X. Scattering by pure seawater: Effect of salinity. Opt. Express 2009, 17, 5698–5710. [Google Scholar] [CrossRef] [PubMed]
- Twardowski, M.; Jamet, C.; Loisel, H. Analytical Model to Derive Suspended Particulate Matter Concentration in Natural Waters by Inversion of Optical Attenuation and Backscattering. Proc. SPIE Ocean Sens. Monit. X 2018. [Google Scholar] [CrossRef]
- Boss, E.; Pegau, W.S.; Lee, M.; Twardowski, M.S.; Shybanov, E.; Korotaev, G.; Baratange, F. The particulate backscattering ratio at LEO 15 and its use to study particles composition and distribution. J. Geophys. Res. 2004, 109, C01014. [Google Scholar] [CrossRef]
- Sullivan, J.M.; Twardowski, M.S.; Donaghay, P.L.; Freeman, S.A. Using scattering characteristics to discriminate particle types in US coastal waters. Appl. Opt. 2005, 44, 1667–1680. [Google Scholar] [CrossRef] [PubMed]
- Stramski, D.; Reynolds, R.A.; Babin, M.; Kaczmarek, S.; Lewis, M.R.; Röttgers, R.; Sciandra, A.; Stramska, M.; Twardowski, M.S.; Franz, B.A.; et al. Relationships between the surface concentration of particulate organic carbon and optical properties in the eastern South Pacific and eastern Atlantic Oceans. Biogeosciences 2008, 5, 171–201. [Google Scholar] [CrossRef] [Green Version]
- Morel, A.; Prieur, L. Analyse spectrale des coefficients d’attenuation diffuse, de retrodiffusion pour diverses regions marines. Cent. Rech. Oceanogr. 1975, 17, 1–157. [Google Scholar]
- Gregg, W.; Carder, K. A simple spectral solar irradiance model for cloudless maritime atmospheres. Limnol. Oceanogr. 1990, 35, 1657–1675. [Google Scholar] [CrossRef] [Green Version]
- Loisel, H.; Stramski, D. Estimation of the inherent optical properties of natural waters from the irradiance attenuation coefficient and reflectance in the presence of Raman scattering. Appl. Opt. 2000, 39, 3001–3011. [Google Scholar] [CrossRef]
- Westberry, T.K.; Boss, W.; Lee, Z.-P. Influence of Raman scattering on ocean color inversion models. Appl. Opt. 2013, 52, 5552–5561. [Google Scholar] [CrossRef]
- Pope, R.M.; Fry, E. Absorption spectrum (380–700 nm) of pure water. II. Integrating cavity measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef]
- Ciotti, A.M.; Lewis, M.R.; Cullen, J.J. Assessment of the relationships between dominant cell size in natural phytoplankton communities and the spectral shape of the absorption coefficient. Limnol. Oceanogr. 2002, 47, 404–417. [Google Scholar] [CrossRef] [Green Version]
- Roesler, C.S.; Perry, M.J. In situ phytoplankton absorption, fluorescence emission, and particulate backscattering spectra determined from reflectance. J. Geophys. Res. 1995, 100, 13279–13294. [Google Scholar] [CrossRef]
- Twardowski, M.S.; Boss, E.; Sullivan, J.M.; Donaghay, P.L. Modeling the spectral shape of absorbing chromophoric dissolved organic matter. Mar. Chem. 2004, 89, 69–88. [Google Scholar] [CrossRef]
- Loisel, H.; Morel, A. Light scattering and chlorophyll concentration in case 1 waters: A reexamination. Limnol. Oceanogr. 1998, 43, 847–858. [Google Scholar] [CrossRef] [Green Version]
- Morel, A. Are the empirical relationships describing the bio-optical properties of case 1 waters consistent and internally compatible? J. Geophys. Res. 2009, 114, C01016. [Google Scholar] [CrossRef]
- Mobley, C.D.; Sundman, L.K.; Boss, E. Phase function effects on oceanic light fields. Appl. Opt. 2002, 41, 1035–1050. [Google Scholar] [CrossRef] [PubMed]
- Voss, K.J.; McLean, S.; Lewis, M.; Johnson, C.; Flora, S.; Feinholz, M.; Yarbrough, M.; Trees, C.; Twardowski, M.; Clark, D. An example crossover experiment for testing new vicarious calibration techniques for satellite ocean color radiometry. J. Atmos. Ocean. Technol. 2010, 27, 1747–1759. [Google Scholar] [CrossRef]
- Zaneveld, J.R.V.; Barnard, A.H.; Boss, E. A theoretical derivation of the depth average of remotely sensed optical parameters. Opt. Express 2005, 13, 9052–9061. [Google Scholar] [CrossRef]
- Gordon, H.R.; Clark, D.K. Remote sensing optical properties of a stratified ocean: An improved interpretation. Appl. Opt. 1980, 19, 3428–3430. [Google Scholar] [CrossRef]
- Gordon, H.R. Dependence of the diffuse reflectance of natural waters on the sun angle. Limnol. Oceanogr. 1989, 34, 1484. [Google Scholar] [CrossRef]
- Kirk, J.T.O. Estimation of the absorption and scattering coefficients of natural waters by the use of underwater irradiance measurements. Appl. Opt. 1994, 33, 3276–3278. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.-P.; Du, K.-P.; Arnone, R. A model for the diffuse attenuation coefficient of downwelling irradiance. J. Geophys. Res. 2005, 110, C02016. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model. Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Brewin, R.J.W. The Ocean Colour Climate Change Initiative: III. A round-robin comparison on in-water bio-optical algorithms. Remote Sens. Environ. 2013. [Google Scholar] [CrossRef]
- Hoge, F.; Lyon, P.E.; Mobley, C.D.; Sundman, L.K. Radiative transfer equation inversion: Theory and shape factor models for retrieval of oceanic inherent optical properties. J. Geophys. Res. 2003, 108, 3386. [Google Scholar] [CrossRef]
- Agrawal, Y.; Mikkleson, O. Empirical forward scattering phase functions from 0.08 to 16 deg. for randomly shaped terrigenous 1-21 μm sediment grains. Opt. Express 2009, 17, 8805–14. [Google Scholar] [CrossRef] [PubMed]
- Nardelli, S.; Twardowski, M.S. Improving assessments of chlorophyll concentration from in situ optical measurements. Opt. Express 2016, 24, A1374–A1389. [Google Scholar] [CrossRef] [PubMed]
- Petzold, T.J. Volume Scattering Functions for Selected Ocean Waters, Report 72–78; Scripps Institution of Oceanography: La Jolla, CA, USA, 1972. [Google Scholar]
- Li, L.; Stramski, D.; Reynolds, R.A. Effects of inelastic radiative processes on the determination of water-leaving spectral radiance from extrapolation of underwater near-surface measurements. Appl. Opt. 2016, 55, 7050–7067. [Google Scholar] [CrossRef]
- Voss, K.; Gordon, H.; Flora, S.; Johnson, B.C.; Yarbrough, M.; Feinholz, M.; Houlihan, T. A method to extrapolate the diffuse upwelling radiance attenuation coefficient to the surface as applied to the Marine Optical Buoy (MOBY). J. Atmos. Ocean. Technol. 2017, 34, 1423–1432. [Google Scholar] [CrossRef]
- Gordon, H.; Ding, K. Self-shading of in-water optical instruments. Limnol. Oceanogr. 1992, 37, 491–500. [Google Scholar] [CrossRef] [Green Version]
- Leathers, R.A.; Downes, T.V.; Mobley, C.D. Self-shading correction for oceanographic upwelling radiometers. Opt. Express 2004, 12, 4709–4718. [Google Scholar] [CrossRef] [PubMed]
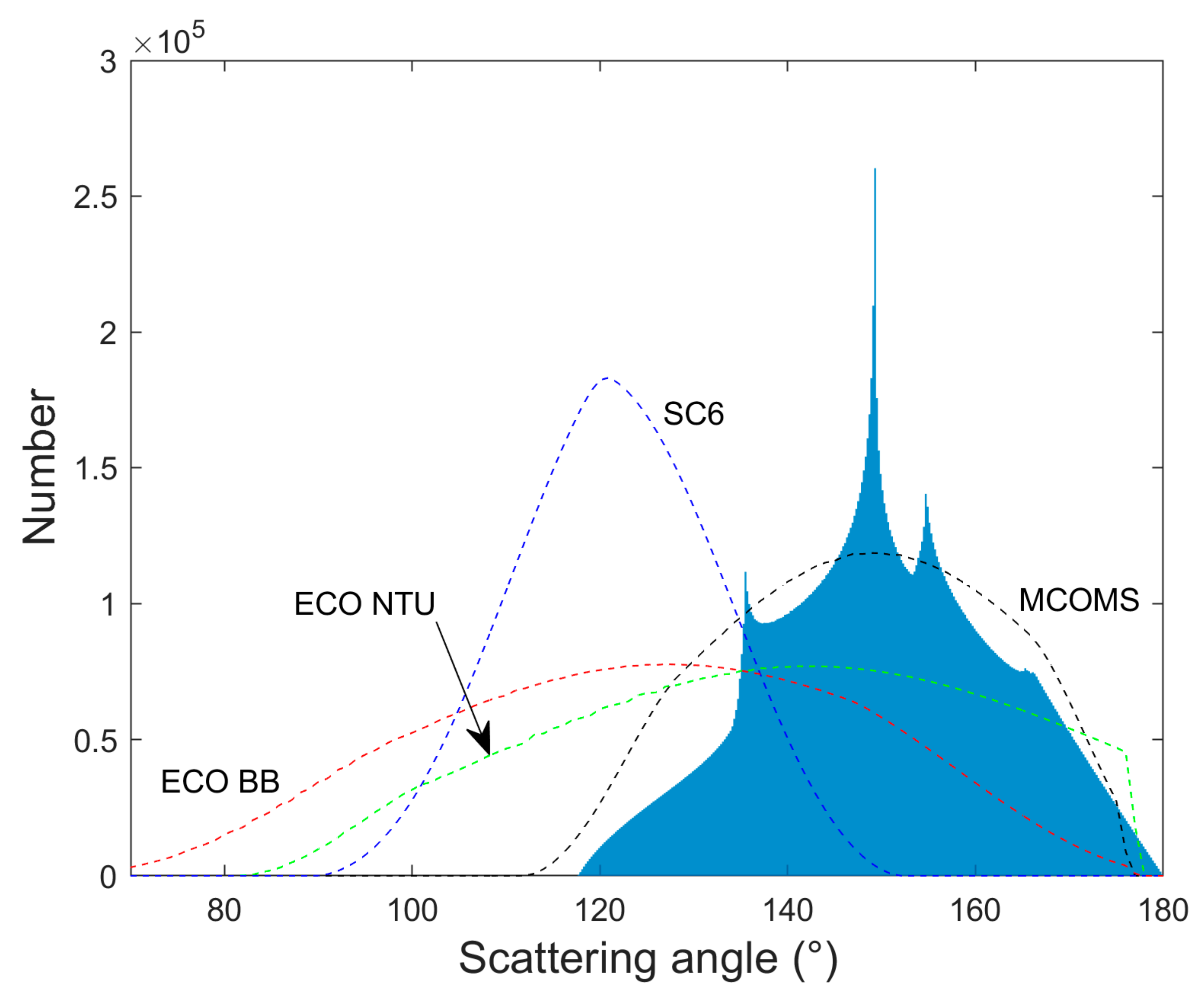
- Zhang, X.; Fournier, G.R.; Gray, D.J. Interpretation of scattering by oceanic particles around 120 degrees and its implication in ocean color studies. Opt. Express 2017, 25, A191–A199. [Google Scholar] [CrossRef] [PubMed]
- Lotsberg, J.K.; Marken, E.; Stamnes, J.; Erga, S.R.; Aursland, K.; Olseng, C. Laboratory measurements of light scattering from marine particles. Limnol. Oceanogr. Methods 2007, 5, 34–40. [Google Scholar] [CrossRef] [Green Version]
- Tan, H.; Doerffer, R.; Oishi, T.; Tanaka, A. A new approach to measure the volume scattering function. Opt. Express 2013, 21, 18697–18711. [Google Scholar] [CrossRef] [PubMed]
- Harmel, T.; Hieronymi, M.; Slade, W.; Röttgers, R.; Roullier, F.; Chami, M. Laboratory experiments for intercomparison of three volume scattering meters to measure angular scattering properties of hydrosols. Opt. Express 2016, 24, A234–A256. [Google Scholar] [CrossRef] [PubMed]
- Tan, H.; Oishi, T.; Tanaka, A.; Doerffer, R.; Tan, Y. Chlorophyll-a specific volume scattering function of phytoplankton. Opt. Express 2017, 25, A564–A573. [Google Scholar] [CrossRef] [PubMed]
- Volten, H.; de Haan, J.F.; Hovenier, J.W.; Schreurs, R.; Vassen, W.; Dekker, A.G.; Hoogenboom, H.J.; Charlton, F.; Wouts, R. Laboratory measurements of angular distributions of light scattered by phytoplankton and silt. Limnol. Oceanogr. 1998, 43, 1180–1197. [Google Scholar] [CrossRef] [Green Version]
- Loisel, H.; Morel, A. Non-isotropy of the upward radiance field in typical coastal (Case 2) waters. Int. J. Remote Sens. 2001, 22, 275–295. [Google Scholar] [CrossRef]
- Xiong, Y.; Zhang, X.; He, S.; Gray, D.J. Re-examining the effect of particle phase functions on the remote-sensing reflectance. Appl. Opt. 2017, 56, 6881–6888. [Google Scholar] [CrossRef]
- Hostetler, C.; Behrenfeld, M.J.; Hu, Y.; Hair, J.W.; Schulien, J.A. Spaceborne lidar in the study of marine systems. Annu. Rev. Mar. Sci. 2018, 10, 121–147. [Google Scholar] [CrossRef]
- Dayou, J.; Chang, J.H.W.; Sentian, J. Ground-Based Aerosol Optical Depth Measurement Using Sunphotometers; Springer: Singapore, 2014; pp. 9–30. [Google Scholar]
- The NASA PACE Mission. Available online: https://pace.oceansciences.org/mission.htm (accessed on 16 June 2018).
- Boss, E.; Remer, L.A. A novel approach to a satellite mission’s science team. Eos 2018, 99. [Google Scholar] [CrossRef]
- Bracher, A.; Bouman, H.A.; Brewin, R.J.W.; Bricaud, A.; Brotas, V.; Ciotti, A.M.; Clementson, L.; Devred, E.; Di Cicco, A.; Dutkiewicz, S.; et al. Obtaining phytoplankton diversity from ocean color: A scientific roadmap for future development. Front. Mar. Sci. 2017, 4. [Google Scholar] [CrossRef]
- Vandermeulen, R.A.; Mannino, A.; Neeley, A.; Werdell, J.; Arnone, R. Determining the optical spectral sampling frequency and uncertainty thresholds for hyperspectral remote sensing of ocean color. Opt. Express 2017, 25, A785–A797. [Google Scholar] [CrossRef] [PubMed]






| Approach | βp(ψ)/bbp Input | Input | %δabs | |
|---|---|---|---|---|
| SORTIE and OCVAL (23 Stations) 1 | NOMAD (80 Stations) | |||
| Full RT 2 | directly measured | N/A | 17 | nd 4 |
| Full RT 2 | Fournier-Forand 3 | measured | 20 | nd 4 |
| ZTT | directly measured | measured | 17 | nd 4 |
| ZTT | Fournier-Forand 3 | measured | 19 | 25 |
| ZTT | Pbb,ST(ψ) | measured | 16 | 20 |
| ZTT | Pbb,ST(ψ) | 0.005 | 18 | 22 |
| ZTT | Pbb,ST(ψ) | 0.006 | 17 | 23 |
| ZTT | Pbb,ST(ψ) | 0.008 | 18 | 25 |
| ZTT | Pbb,ST(ψ) | 0.010 | 19 | 27 |
| ZTT | Pbb,ST(ψ) | 0.015 | 22 | 29 |
| ZTT | Large and small population phase functions with of 0.19% and 1.4%, blended according to [Chl] 5 | measured | 23 | 26 |
| Morel et al. [7] (M02) | Large and small population phase functions with of 0.19% and 1.4%, blended according to [Chl] 5 | N/A | 21 | 25 |
| Lee et al. [11] (L11) | Blend of Petzold6 average and 1% Fournier-Forand 3 | N/A | 21 | 26 |
| Approach | βp (ψ)/bbp Input | Input | λ (nm) | %δabs | |
|---|---|---|---|---|---|
| SORTIE and OCVAL (23 Stations) | NOMAD (80 Stations) | ||||
| ZTT | Pbb,ST(ψ) | measured | 412 (410) | 20 | 17 |
| 440 | 16 | 20 | |||
| 488 (490) | 16 | 20 | |||
| 510 | 19 | 19 | |||
| 532 | 13 | - | |||
| 555 | 14 | 23 | |||
| 650 | 13 | - | |||
| 665 | - | 63 | |||
| ZTT | Pbb,ST(ψ) | 0.006 | 412 (410) | 20 | 20 |
| 440 | 16 | 23 | |||
| 488 (490) | 19 | 23 | |||
| 510 | 13 | 25 | |||
| 532 | 14 | - | |||
| 555 | 13 | 26 | |||
| 650 | 22 | - | |||
| 665 | - | 63 | |||
| Morel et al. [7] (M02) | Large and small population phase functions with of 0.19% and 1.4%, blended according to [Chl] | N/A | 412 (410) | 17 | 22 |
| 440 | 14 | 25 | |||
| 488 (490) | 16 | 25 | |||
| 510 | 18 | 26 | |||
| 532 | 22 | - | |||
| 555 | 38 | 21 | |||
| 650 | 17 | - | |||
| 665 | - | 71 | |||
| Lee et al. [11] (L11) | Blend of Petzold average and 1% Fournier-Forand | N/A | 412 (410) | 22 | 22 |
| 440 | 21 | 26 | |||
| 488 (490) | 24 | 27 | |||
| 510 | 21 | 27 | |||
| 532 | 20 | - | |||
| 555 | 19 | 24 | |||
| 650 | 26 | - | |||
| 665 | - | 66 | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Twardowski, M.; Tonizzo, A. Ocean Color Analytical Model Explicitly Dependent on the Volume Scattering Function. Appl. Sci. 2018, 8, 2684. https://doi.org/10.3390/app8122684
Twardowski M, Tonizzo A. Ocean Color Analytical Model Explicitly Dependent on the Volume Scattering Function. Applied Sciences. 2018; 8(12):2684. https://doi.org/10.3390/app8122684
Chicago/Turabian StyleTwardowski, Michael, and Alberto Tonizzo. 2018. "Ocean Color Analytical Model Explicitly Dependent on the Volume Scattering Function" Applied Sciences 8, no. 12: 2684. https://doi.org/10.3390/app8122684
APA StyleTwardowski, M., & Tonizzo, A. (2018). Ocean Color Analytical Model Explicitly Dependent on the Volume Scattering Function. Applied Sciences, 8(12), 2684. https://doi.org/10.3390/app8122684




