Retinal Vessels Segmentation Techniques and Algorithms: A Survey

Abstract

Retinal vessels identification and localization aim to separate the different retinal vasculature structure tissues, either wide or narrow ones, from the fundus image background and other retinal anatomical structures such as optic disc, macula, and abnormal lesions. Retinal vessels identification studies are attracting more and more attention in recent years due to non-invasive fundus imaging and the crucial information contained in vasculature structure which is helpful for the detection and diagnosis of a variety of retinal pathologies included but not limited to: Diabetic Retinopathy (DR), glaucoma, hypertension, and Age-related Macular Degeneration (AMD). With the development of almost two decades, the innovative approaches applying computer-aided techniques for segmenting retinal vessels are becoming more and more crucial and coming closer to routine clinical applications. The purpose of this paper is to provide a comprehensive overview for retinal vessels segmentation techniques. Firstly, a brief introduction to retinal fundus photography and imaging modalities of retinal images is given. Then, the preprocessing operations and the state of the art methods of retinal vessels identification are introduced. Moreover, the evaluation and validation of the results of retinal vessels segmentation are discussed. Finally, an objective assessment is presented and future developments and trends are addressed for retinal vessels identification techniques.

1. Introduction

Retinal vasculature structure implicates important information helps the ophthalmologist in detecting and diagnosing a variety of retinal pathology such as Retinopathy of Prematurity (RoP), diabetic retinopathy, glaucoma, hypertension, and age-related macular degeneration or in diagnosis of diseases related to brain and heart stocks, which are associated with the abnormal variations in retinal vascular structure. Therefore, changes in retina’s arterioles and venules morphology have a principal diagnostic value.

In general, vessels (vessels structure-like) segmentation occupy a remarkable place in medical image segmentation field [1,2,3,4]; retinal vessels segmentation belongs to this category where a broad variety of algorithms and methodologies have been developed and implemented for the sake of automatic identification, localization and extraction of retinal vasculature structures [5,6,7,8,9,10]. In this paper, we have presented a review that covers and categorizes early and recent literature methodologies and techniques, with the major focus on the detection and segmentation of retinal vasculature structures in two-dimensional retinal fundus images. In addition, our review covers the theoretical basis behind each segmentation category as well as the associated advantages and limitations.

The remainder of this paper is organized as follows. Section 2 describes the different types of retinal fundus imaging. The different challenges that faced by researcher during retinal images segmentation are elaborated in Section 3. Detailed description of different categories of vessel segmentation methodologies and algorithms along with theoretical framework is given in Section 4. Finally, Section 5 summarizes the discussion and conclusions of this work.

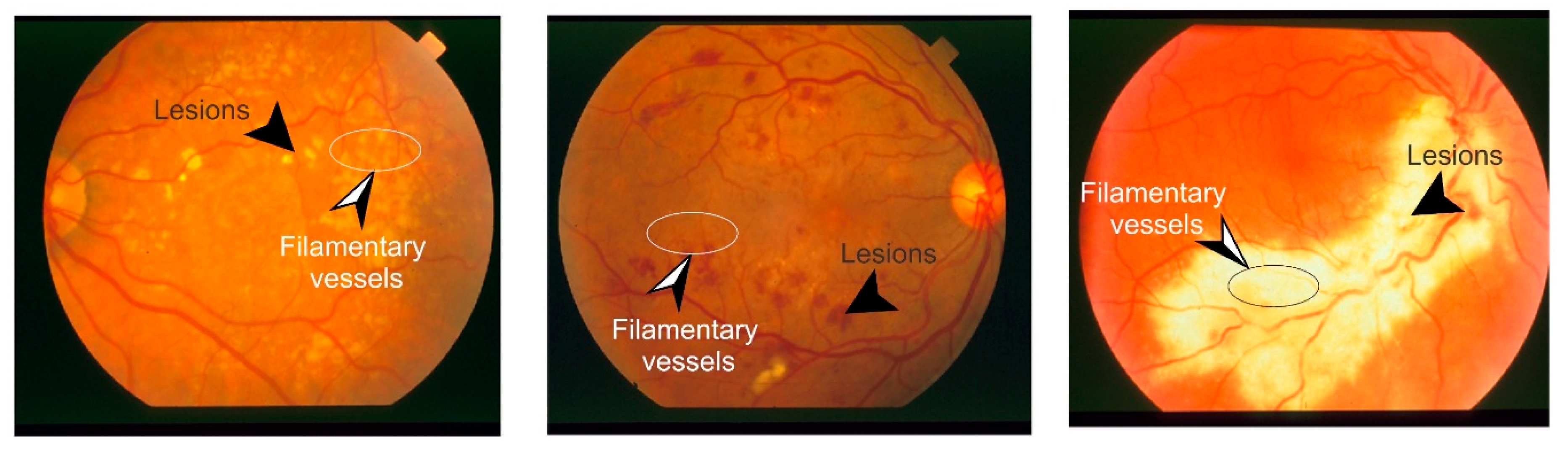
2. Retinal Fundus Imaging

Retina photography is typically conducted via an optical apparatus called fundus camera, as shown in Figure 1. Reference [11] fundus camera can be viewed as a low power microscope that specializes in retina fundus imaging, where the retina is illuminated and imaged via the attached camera. In particular, fundus camera is designed to capture an image for the interior surface of human eye, which is composed of major parts, including macula, optic disk, retina and posterior pole [12].

Fundus photography can be viewed as a sort of documentation process for the retinal interior structure and retinal neurosensory tissues. The retinal neurosensory tissues convert the optical images reflection, that we see, into electrical signals in the form of pulses sent to our brain where it decoded and understood. Retina photography can be conducted based on the idea that the eye pupil is utilized as both an entrance and exit for the illuminating and imaging light rays that are used by the fundus camera. During the fundus photography, patients’ foreheads are placed against the bar and their chins placed in the chin rest, as shown in Figure 1. After the oculist aligns the fundus camera, the camera shutter is released so a flash light is fired and a two-dimensional picture for retina fundus has been taken [13], as anatomically illustrated in Figure 2.

As shown in Figure 2, the fundus of the human eye is the back portion of the interior of the eye ball. The optic nerve resides at the center of retina, which can be seen as a white area of circular to oval shape and measuring about $3\times 3$ mm across diameter. The major blood vessels of the retina radiate from the center of the area of optic nerve and then radiate and branched to fill the entire area excepting the fovea zone, which is a blood-vessel free reddish spot with an oval-shaped that lies directly to the left of the optic disc and resides in the center of an area that is known by ophthalmologists as the “macula” region [14]. In General, the photographic process involves grasping the light that reflected off the subject under consideration. In our case, the subject is the fundus of retina. Since the internal room of the eye has no light source of its own, in the retina photography, we need to flash or shine a light into eye room to capture a good photograph. The ocular fundus imaging has three major photography modes, as elaborated in Figure 3:

• Full-color Imaging
• Monochromatic (Filtered) Imaging
• Fluorescence Angiogram

In the case of full-color photography mode, no light-filtration is used and it is totally non-invasive contrary to other modes of fundus imaging. The resultant retina fundus image is a two-dimensional full color image, as illustrated in Figure 3a. On the other hand, if the fundus is imaged via a monochromatic filter or via particular colored illumination, then the fundus photography is called “monochromatic”, as shown in Figure 3b. This type of fundus photography is built based on the idea that the visibility of different structures in a retinal image is enhanced if the spectral range of illumination is changed correspondingly. In other words, instead of using white light of a broad scale of wavelengths, we use a light of a specified wavelength that corresponds to a specific color, for example, a red object in an image would appear lighter if the image is taken through a red filter and it would appear darker if it is taken through green filter. As the white light can be divided into red, green and blue lights, the ocular fundus can be photographed via one of these gradient lights where each light has the capability to enhance the visibility of specific retinal anatomical structures based on their colors. For example, blue filter (filter with blue light) enhances the visibility of the interior layers of retina, which in full-color photo (taken by white light) appears almost transparent. On the other hand, we can get the best overall view of retina fundus and the most enhanced contrast if we use the green filter. Moreover, green filters have the capability to enhance the visibility of common lesions such as exudates, hemorrhage and drusen.

Another alternative to monochromatic filters is to split the full-color fundus image into its basic components, namely, red, green and blue. It operates similar to colored filters, except we lose the resolution, and is adopted in a variety of retinal vessel identification approaches in the stage of image preprocessing framework [15].

Fundus angiography is the most invasive fundus imaging, and involves injecting a tiny amount of fluorescein dye into a vein of patient’s arm; the dye makes its way to the main blood stream leading to retina vessels, and then the retina fundus is photographed. Originally, the word “angiography” is derived from the Greek words Angeion, which means “vessels”, and “graphien”, which means to record or to write. Once the sodium-fluorescein has been injected, and reaches retina, the retina fundus is illuminated with a blue light, and then is flashed in a yellow-green color. Later, specialized filters in the fundus camera allow the fluorescent light to be imaged, leading to high contrast (grey-scaled) retinal vascular structure images, as shown in Figure 3c [16]. Retina angiography is considered the photography mode that highly revolutionized the ophthalmologists’ ability to understand both retina physiology and pathology. Moreover, it is used in the process of diagnosing and treating choroidal diseases [16]. However, this mode is considered the most invasive one, due to injecting dyes in the human veins directly. Thus, as recently reported, it is important to consider the potential risk associated with using such mode of retina fundus photography, especially for neonatal people [17].

3. Retinal Image Processing

The oculists scan the retina of patients using fundus camera with high resolution. Accordingly, the situation of retina blood vessels is probed to diagnose retinal diseases. In many cases, it is found that the retinal vascular structure has low contrast with regard to their background. Thus, the diagnosis of retinal diseases becomes a hard task, and applying a suitable image segmentation technique becomes a must for highly accurate retinal vascular structure detection, since it leads to accurate diagnosis. Retina vessel identification and extraction faces many challenges that may be outlined as follows. Firstly, the retinal vessels’ widths take a wide range of color intensity range from less than one pixel up to more than five pixels in the retinal image, as shown in Figure 4, which requires an identification technique with high flexibility.

To elaborate this challenge, a snippet of MATLAB^® code has been developed for sake of grey levels substitution in retinal image; the different grey levels of a raw retinal image have been replaced by color ones, as shown in Figure 5. It can be noted that many retinal vessels, either large or tiny ones, take the same background color intensities. This reveals the broad range of colors that may be taken by the retinal vasculature structure, making the identification process more complicated rather than that found in other identification problems.

This challenge opens the room for a field of research specialized in detecting and segmenting thin (filamentary) retinal vascular structures, as in [18,19,20,21,22,23,24,25]. Secondly, Vessels identification in pathological retinal images faces a tension between accurate vascular structure extraction and false responses near pathologies (such as hard and soft exudates, hemorrhages, microaneuryms and cotton wool spots) and other nonvascular structures (such as optic disc and fovea region). The retinal blood vasculature is a tree-like structure that disperses across the fundus image surface including pathologies. Thin and filamentary retinal vessels melt in the retinal abnormal regions burden the task of accurate vessel segmentation, as shown in Figure 6.

In summary, retinal vascular structure, inside either normal or abnormal retina images, has low contrast with respect to the retinal background. Conversely, other retinal anatomical structures have high contrast to other background tissues but with indistinct features in comparison with abnormal structures; optic disc and exudates lesions represent typical examples. All these challenges, in terms of medical image processing, make the classical segmentation techniques such as Sobel operators [26], Prewitt operators [27], gradient operators [28], and Robert and Krish differential operations [29] inefficient and inaccurate. Consequently, various algorithms and methodologies have been developed and implemented for sake of automatic identification, localization and extraction of retinal anatomical structures and can be broadly divided into rule-based and machine learning techniques, as elaborated in Section 4.

4. Retinal Vessels Segmentation Techniques

Generally, regarding segmentation issue, there exist as many methods and algorithms as there are specific cases and situations. Among them, segmentation tools used for medical purposes in general, and for retinal anatomical structures segmentation in particular. All retinal vessel segmentation methods share common stages: pre-processing stage, processing stage and post-processing stage. In this review, we have categorized the covered papers based on the algorithm or technique used in the processing stage, yielding six major categories: (1) kernel-based techniques; (2) vessel-tracking; (3) mathematical morphology-based; (4) multi-scale; (5) model-based; (6) adaptive local thresholding; and (7) machine learning. These categories are also grouped into two major classifications: Rule-based or Machine learning, as shown in Figure 7 and categorized in

Table 1. Categorization of retinal vessel segmentation techniques.

Method	Year	Image Processing Technique	Performance Metric	Validation Dataset	Technique Category
Chaudhuri et al. [48]	1989	Two-dimensional Gaussian matched filter	-	-	Kernel-based
Chanwimaluang and Fan [49]	2003	Gaussian matched filter + entropy adaptive thresholding	-	STARE
Al-Rawi et al. [50]	2007	Gaussian matched filter with modified parameters	ROC 1	DRIVE
Villalobos-Castaldi et al. [51]	2010	Gaussian matched filter + entropy adaptive thresholding	Acc 2, Sp 3, Se 4	DRIVE
Zhang et al. [52]	2010	Two kernels: Gaussian + FDOG 5	Acc, FPR 6	DRIVE, STARE
Zhu and Schaefer [53]	2011	Piece-wise Gaussian scaled model	-	-
Kaur and Sinha [54]	2012	Filter Kernel: Gabor filter	ROC	DRIVE, STARE
Odstrcilik et al. [47]	2013	Improved t-dimensional Gaussian matched filter.	Acc, Sp, Se	DRIVE, STARE
Zolfagharnasab et al. [55]	2014	Filter kernel: Caushy Probability Density Function	Acc, FPR	DRIVE
Singh et al. [56]	2015	Modified Gaussian matched filter + Entropy thresholding	Acc, Sp, Se	DRIVE
Kumar et al. [57]	2016	Filter Kernel: Laplacian of Gaussian	Acc, Sp, Se	DRIVE, STARE
Singh and Strivastava [58]	2016	Filter kernel: Gumbel Probability Density Function.	Acc, ROC	DRIVE, STARE
Chutatape et al. [59]	1998	Vessel tracking by Kalman filter and matched Gaussian	-	-	Vessel tracking
Sofka and Stewar [60]	2006	Vessel tracking by matched filter responses + confidence	(1-Precision)	DRIVE, STARE
		measures + vessel boundaries measure.	versus Recall curve
Adel et al. [61]	2009	Bayesian vessel tracking.	SMF 7	Simulated
				Dataset + 20
				Images at
				Marseille
				University
Wu et al. [62]	2007	Vessel tracking by matched filters + Hessian matrix.	Se, FPR	DRIVE, STARE
Yedidya and Hartley [63]	2008	Vessel tracking by Kalman filter.	TPR 8, FNR 9	DRIVE
Yin et al. [64]	2010	Statistical-based vessel tracing	TPR, FPR	DRIVE
Li et al. [65]	2013	Vessel tracking by Bayesian theory.	-	-
De et al. [23]	2016	Vessel tracking using mathematical graph theory.	GFPR 10	DRIVE, STARE
Budai et al. [66]	2010	Gaussian pyramid multi-scaling.	Acc, Sp, Se	DRIVE, STARE	Multi-scale
Moghimirad et al. [67]	2010	Multi-scale based on weighted medialness function.	ROC, Acc	DRIVE, STARE
Abdallah et al. [68]	2011	Multi-scale based on Anisotropic diffusion.	ROC	STARE
Rattathanapad et al. [69]	2012	Multi-scale based on line primitives.	FPR	DRIVE
Kundu and Chatterjee [70]	2012	Morphological Angular Scale-space	MSE 11	DRIVE	Morphological
					Based
Frucci et al. [71]	2014	Watershed transform + Contrast and directional Maps.	Acc, Precision	DRIVE
Jiang et al. [72]	2017	Global thresholding based on morphological operations.	Acc, Execution time	DRIVE, STARE
Dizdaro et al. [73]	2012	Level set in terms of initialization and edge detection.	Acc, Sp, Se	DRIVE	Deformable Model
				Proposed Dataset
Jin et al. [74].	2015	Snakes contours	Acc, Sp, Se	DRIVE
Zhao et al. [31].	2015	Infinite perimeter active contour with hybrid region terms.	Acc, Sp, Se	DRIVE, STARE
Gong et al. [75]	2015	Level set without using local region area.	Acc, Sp, Se	DRIVE
Jiang and Mojon [76]	2003	Knowledge-guided local adaptive thresholding	TPR, FPR	STARE	Adaptive Local
			Filter response		Thresholding
			analysis
Akram et al. [77]	2009	Statistical-based adaptive thresholding.	Acc, ROC	DRIVE
Christodoulidis et al. [78]	2016	Local adaptive thresholding based on multi-scale tensor	Acc, Sp, Se	Erlangen Dataset
		voting
Nekovei and Ying [79]	1995	Back propagation ANN 12	Se	-	Machine Learning
Salem et al. [80]	2006	K-nearest neighbors (KNN)	Se, Sp	STARE
Xie and Nie [81]	2013	Genetic Algorithm + Fuzzy c-means	-	DRIVE
Akhavan and Faez [82]	2014	Vessel Tracking + Fuzzy c-means	Acc	DRIVE, STARE
Emary et al. [83]	2014	Possibilistic version of fuzzy c-means	Acc, Sp, Se	DRIVE, STARE
		Optimized with Cuckoo search algorithm
Maji et al. [84]	2015	Hybrid framework of deep ANNS and
Gu and Cheng [22]	2015	Iterative Latent classification tree	Acc	DRIVE, STARE
Sharma and Wasson [85]	2015	Fuzzy Logic	Acc	DRIVE
		Ensemble Learning.	Acc	DRIVE
Roy et al. [86]	2016	Denoised stacked auto-encoder ANN	ROC	DRIVE, STARE
Lahiri et al. [87]	2016	Ensemble of two parallel levels of	Acc	DRIVE
		Stacked denoised auto-encoder ANNS
Maji et al. [88]	2016	Ensemble of 12 convolutional ANNs	Acc	DRIVE
Maninis et al. [24]	2016	Deep Convolutional ANNs.	Area under	DRIVE, STARE
			Recall-Precision
			Curve
Liskowski et al. [89]	2016	Deep ANNs	ROC, Acc	DRIVE, STARE
				CHASE [90]
Dasgupta and Singh [91]	2016	Convolutional ANNs	ROC, Se, Acc, Sp	DRIVE

¹ ROC: Receiver Operating Characteristics; ² Acc: Accuracy; ³ Sp: Specificity; ⁴ Se: Sensitivity; ⁵ FDOG: First-order Derivative of Gaussian; ⁶ FPR: False Positive Rate; ⁷ SMF: Segmentation Matching Factor; ⁸ TPR: True Negative Rate; ⁹ FNR: False Negative Rate; ¹⁰ GFPR: Geometric False Positive Rate; ¹¹ MSE: Means Square Error; ¹² ANN: Artificial Neural Network.

.

The category of rule-based techniques follows specific rules in an algorithmic framework, whereas machine learning ones utilize a pre-segmented retinal image (ground truth or gold standard) to form a labeled dataset that can be used in training process. However, any non-image processing specialist, when faced with an image analysis problem, readily apprehends that a one image transformation or a stand-alone image processing technique usually fails. Therefore, Figure 7 depicts this fact, where nested lobes stand for the Hybrid Nature of these techniques. Most image analysis problems are very complicated, especially medical ones, and can be solved in high performance by a hybrid combination of many elementary transformations and techniques. These reasons give arise to the utilization of hybrid techniques in retinal vessels segmentation problems, as proposed in [30,31,32,33,34,35,36].

The capability of retinal segmentation algorithm to extract the retinal vasculature structure is evaluated by many metrics. The most common ones are: average True Positive Rate (TPR), average False Positive Rate (FPR), average Sensitivity (recall, TPR), average Specificity (1-FPR), average Accuracy, and average Precision. Sensitivity and specificity represent the most widely used metrics in medical research; the higher the specificity and sensitivity values, the better diagnosis. The sensitivity reflects the capability of the algorithm to detect the vessels’ pixels, whereas the specificity determines the ability of the algorithm to detect non-vessel pixels. Sensitivity and Specificity represent the features of the algorithm and are associated with the accuracy metric in many medical image processing fields, including retinal vessel segmentation [37], as given by the following equations [38]:

$$Sensitivity \left(Recall\right)=TP/\left(TP+FN\right)$$

(1)

$$Specificity=TN/\left(TN+FP\right)$$

(2)

$$Accuracy=\left(TP+TN\right)/\left(TP+FN+FP+TN\right)$$

(3)

$$Precision=TP/\left(TP+FP\right)$$

(4)

where TP is True Positives, FP is False Positives, FN is False Negatives, and TN is True Negatives.

On the other hand, many papers use the area under the Receiver Operating Characteristic (ROC) curve [39,40] to evaluate their works, especially for methods that highly depend on specific parameters during the segmentation execution. ROC curve is a non-linear function between TPR and FPR values. Optimal area under ROC is 1 for an optimal performance.

Most of retinal vessels segmentation techniques and algorithms use the most popular datasets in this field: (1) Digital Retinal Image for Vessel Extraction (DRIVE) [41,42]; and (2) Structuring Analysis of the Retina (STARE) [43]. Both datasets are well-considered and popular in the field of retinal vessels segmentation to the extent that almost every research performance involving vessels segmentation is evaluated via these datasets. The popularity of these datasets is due to the good resolution of the retinal fundus images and to the availability of manually labeled ground truth images prepared by two experts. The DRIVE dataset, consisting of 40 retinal images, is evenly divided into a training set and a test set, whereas the STARE dataset consists of 20 images, 10 of which are normal retinal images and the other 10 images are abnormal ones. Nevertheless, many researchers use other less common datasets for validation and performance evaluation, such as: Automated Retinal Image Analyzer (ARIA) dataset [44], DIAbietes RETina Data Base (DIARETDB) dataset [37], Methods for Evaluating Segmentation and Indexing techniques Dedicated to Retinal (Messidor) dataset [45,46], and High Resolution Fundus (HRF) [47].

4.1. Kernel-Based Techniques

This type of retinal vessels segmentation depends on the intensities distribution of vessel pixels to build a filter kernel, which, in turn, can detect the retinal vasculature structure boundaries. The kernel can either follow a pre-specified form based on the cross-section profile of retinal vessel, or it can be deformable according to vessels boundaries especially when they lie in or in neighbor of hemorrhages and microaneuryms lesions. Most often, kernel-based approaches are used as preprocessing image enhancement step for other retinal vessels segmentation methodologies, since it enhances the map for vessels boundaries. The profile-based kernels use one of various models that have been proposed and implemented in retinal vessels profiling that are built based on the idea that intensity distribution of retinal vessel can describe retinal vessels characteristics which can be turned into maps for vessels detection. The basic idea of kernel-based techniques (also called matched filtering-based) techniques is to compare the pixels’ intensity variations along with the cross-section profile of the retinal vessel with a prefigured template works as a kernel. Therefore, most typical matched filter-based techniques detect retinal vessels by applying a matched filter kernel on the original grey retinal image followed by a thresholding step.

Retinal vessel profiling has many applications in the fields of vascular width measurement [92] or in the field of vessels type classification [93]. In the case of vessels detection and extraction, it is used to create the map for process of detection, which paves the way for vessels extraction through region growing or filtering based approaches. Generally speaking, retinal vascular matched kernels can fall in one of two major categories: Gaussian shaped or non-Gaussian shaped [94].

Early work in this direction was performed by Chaudhuri et al. [48], who observed the high similarity of the intensity variations of the cross-section profile of the retinal image with a Gaussian function, as illustrated in Figure 8.

Since Chaudhuri et al. [48] published his well-known paper that stated the cross section profile of retinal vascular structure has approximate Gaussian shape, matched filters with Gaussian kernels have emerged, and were later reported in the literature for retinal vessel tree detection. According to the fact that the cross section of retinal vessels can be modeled as a Gaussian function, a series of Gaussian shaped filters (different in Gaussian parameters values µ and σ) can be used to match different vessel sizes simply and efficiently. However, matched filters have strong response to both vessels and non-vessels structures, such as red lesions and bright blobs, which results in degradation in the performance in terms of false detection rate. Three important aspects should be taken into consideration through designing a matched filter kernel: (1) limited curvature of retina vascular structure, where the curvature of vessel segments can be approximated by bell-shape piecewise linear segments; (2) vessels’ width, as the width of the retinal vessels decreases in a gradual way when one moves from optical disk towards Fovea region, as shown in Figure 2; and (3) accurate cross-section profile of pixel intensities distribution of the retinal blood vessels [58].

The same idea of Chaudhuri et al. [48] was followed and re-implemented by [56] via DRIVE dataset. The regenerated segmentation results have reported an average accuracy of 0.9387, and 0.9647 and 0.6721 for average specificity and average sensitivity, respectively. Zhu and Schaefer [53] proposed a profile kernel-based algorithm for retinal vessel extraction based on profiling the cross-section of retinal vessels using piece-wise Gaussian scaled model. Once the profile has been modeled, a phase alignment function based on data obtained from oriented log-Gabor wavelet was applied. After boundary area map of retinal vascular structure has been produced, cross-sections were extracted by following an approach was proposed by same author in [95].

A notable vessel extraction performance has been achieved by Villalobos-Castaldi et al. [51], where matched filter in a conjugation with entropy-based adaptive thresholding algorithm was employed. The methodology was applied on DRIVE dataset where it used matched filter in sake of piecewise linear segments enhancement of the retina vascular structure. Later, a co-occurrence matrix [96] that records the number of transitions between all pairs of grey-retinal levels was captured where the grey-level changes were depicted. Then, the entropy of the image grey levels distribution was exploited through second-entropy thresholding to segment the background pixels from the foreground (vessels) ones. The time consumed in the process of obtaining vascular structures approximated 3 s, and high detection accuracy was achieved, up to 0.9759, as well as sensitivity and specificity of 0.9648 and 0.9480, respectively.

Compared to the performance achieved in [51], Chanwimaluang and Fan [49] followed same procedure that was proposed in [51] to extract both the retinal vessel and the optic disk using STARE dataset. However, the time consumed approximated 2.5 min per retina image; most of it was consumed in matched filtering and local entropy thresholding steps. Moreover, it required post-processing steps that were not required by [51] including long filtering stages for isolated pixel removal. Then, filtering steps were followed by morphological thinning used to identify the retinal vascular intersection/crossovers. on the other hand, the optic disk identification proceeded into two major stages: (1) optic disk center identification through maximum local variance detection; and (2) optic disk boundary identification through snake active contour. Even though the same methodology steps have been followed by both [51,49], they are extremely different in terms of achieved performance.

Singh et al. [56] have noted the important effect of Gaussian kernel parameters on the subsequent image processing stages. Singh et al. [56] followed same procedure that was proposed in [51,49] as well. However, the parameters of Gaussian function have been modified in a way that enhances the overall performance, which reached up to 0.9459 for accuracy, and 0.9721 and 0.6735 for specificity and sensitivity, respectively, using DRIVE dataset in comparison with average ROC area of 0.9352 reported by Al-Rawi et al. [50] applied on DRIVE dataset, where they used a different set of modifications for Gaussian-kernel parameters.

On the same procedure that have been reported in [51,56,49], Kaur and Sinha [54] employed Gabor filter instead of Gaussian one in the early stages of vessel extraction. The enhanced vessels were obtained via banks of 12 different oriented Gabor filters in range of 0 to 170 degree. Gabor-filter based approach outperforms the Gaussian one in terms of both area under ROC curve and in terms of specificity. The overall achieved sensitivity is less than that achieved by [56,51]. The performance of [56,51] was evaluated via DRIVE dataset, whereas the performance of [56] was evaluated on both DRIVE and the challengeable (pathologies bearing) STARE dataset, where it showed a high specificity of 96% in the presence of lesions in abnormal retinal images.

Based on the fact that retinal vessels have symmetric Gaussian cross-section profile, while the cross-section profile for the non-vessels is asymmetric, two matched filters, one constructed with symmetric Gaussian (zero-mean) kernel and the other with first-Order Derivative Of Gaussian (FDOG) kernel, were applied to retina images by Zhang et al. [52]. The response of matched filter that has Gaussian kernel was used to detect vessels, while the local mean of the response of first-order derivative of Gaussian kernel was used to establish and adjust a “dynamic threshold”, which, in turn, was used in the thresholding phase that followed the matched filter phase. The proposed technique exploits the difference between FDOG kernel responses for both vessels and non-vessels regions (such as bright blobs, lesions, and optic disk) to vary thresholding level according to local mean signal. The experimental results, obtained via both DRIVE and STARE datasets, demonstrated that applying hybrid matched filtering kernels can reduce the false detection dramatically to less than 0.05 compared to that inherently generated with Gaussian kernel, even for thin vessels, with average accuracy of 0.9510 for normal cases retina images and 0.9439 for pathological ones.

According to techniques reported and discussed above, most conventional matched filters-based approaches enhance the performance of matched filter-based methodology by enhancing the performance of the thresholding techniques rather than improving the matched filter kernel itself. Zolfagharnasab et al. [55], on the other hand, replaced the Gaussian kernel of matched filter by Caushy Probability Density Function (CPDF), and reported an overall accuracy of 0.9170 with 3.5% false positive rate via DRIVE dataset.

The inherent zero-crossing property of Laplacian of Gaussian (LoG) filter was exploited in an algorithm proposed by Kumar et al. [57] where two-dimensional matched filters with LoG kernel functions are applied to fundus retinal images to detect retinal vasculature structure which are firstly enhanced by Contrast Limited Adaptive Histogram Equalization (CLAHE) method. The proposed algorithm achieved average accuracy of 0.9626, and sensitivity and specificity of 0.7006 and 0.9871 via DRIVE dataset, respectively, and average accuracy of 0.9637, and 0.7675 and 0.9799 for sensitivity and specificity, respectively, via STARE dataset in comparison with average accuracy of 0.9340 and 0.7060 and 0.9693 for sensitivity and specificity respectively on DRIVE dataset achieved by Odstrcilik et al. [47] using improved two dimensional matched filter with two-dimensional Gaussian kernel. The method was applied on STARE dataset as well, where it has achieved an overall accuracy of 0.9341, and 0.7847 and 0.9512 for sensitivity and specificity, respectively.

As a novel matched filter kernel improvement, Singh and Strivastava [58] suggested the Gumbel PDF as a kernel function, where they noted the slight skewness of vessel-cross section profile, which most approximates Gumble PDF with respect to Gaussian and Caushy PDF functions proposed in [48,50]. In the thresholding phase, entropy-based optimal thresholding was used in a companion of length filtering as post-processing step to remove isolated pixels. The proposed technique showed an improved performance in terms of average detection accuracy of 0.9522 for DRIVE dataset and 0.9270 for STARE dataset, and the value of area under ROC curve was 0.9287 and 0.9140 for DRIVE and STARE datasets, respectively.

Since the performance metrics used in reported papers are not common, Figure 9 and Figure 10 illustrate graphical comparisons between some of the reviewed kernel-based methodologies for DRIVE and STARE datasets based on accuracy, sensitivity and specificity metrics.

4.2. Vessel Tracking/Tracing Techniques

The heart of vessel tracking algorithms is to trace the ridges of retina fundus image based on a set of starting points. Graphical representation of ridges of retina image can be noticed in Figure 11. Any tracking algorithm involves seeds selection as a preliminary step, where seeds can be defined either manually or automatically. The ridges of vessels are detected by inspecting zero-crossing of the gradient and curvature. However, “clean-limbed” ridges detection need a pre-processing phase involves complicated steps of vessel enhancement for all vessels sizes and orientations. Consequently, one of the major drawbacks of vessel tracking is the extreme dependency on the pre-processing steps that proceed the phase of tracing.

In tracing techniques, it is not an essence for seed points (starting points of tracking process) to be located at the center of retinal vessels, Chutatape et al. [59], for instance, have extracted seed points from the circumference of the optic disc, then the centers of vessels were traced using an extended Kalman filter. A semi-ellipse was defined around the optic disk as a searching region for starting points of vascular structure, which was later used by [65]. As the candidate pixels locations for next vessel edge points were selected on the semi-ellipse, vessel tracking took place based on Bayesian theory.

Wu et al. [62] proposed a vessel tracking methodology for retinal vasculature structure extraction that combines Hessian and matched filters and an idea of exploiting the edge information at the vessels parallel boundaries, which as first proposed by Sofka and Stewar [60] for retinal vessels extraction. Once the contrast between vessels and other retina tissues are enhanced and the information of sizes and the orientations of enhanced vessels are available, the ridges are used to trace vessels via their center lines along ridge seeds that were selected automatically. The tracking performance was tested via DRIVE dataset, where 84.4% of retinal vasculature skeleton was successfully detected with 19.3% false positive rate, and the majority of false tracked vessels were the small ones that the researchers considered a subject of further ongoing research.

In contrast to [62], Yedidya and Hartley [63] proposed a tracking methodology trace the retinal vessels centers through Kalman filter, where it has the capability to detect both wide and thin vessels, even in noisy retinal images, by defining a linear model. The proposed model proceeds into four stages. Firstly, a set of seed points all over the image were found by convolving the whole retina image with a set of matched filters at different scales and orientations in aim of finding at least one seed point at each vessel, which, in turn, remove the need to follow all branches. Secondly, Kalman filter was used to trace blood vessels’ centers starting from seed points found in the first stage. Thirdly, tracing process ceases once the probability of vessel tracing is small for a number of back-to-back moves or once tracing hit previously segmented vessel. Fourthly, the segmentation results are traced in the case of tracking failure in less than minimum number of steps. The proposed tracking methodology managed to detect retinal vessels with true positive rate reaching up to 85.9% and false negative of 8.1% via DRIVE dataset.

Making use of mathematical graph theory, De et al. [23] designed a novel technique to extract the filamentary retinal structure. Their technique was built based on connecting the tracing problem and the digraph matrix-forest theorem in algebraic graph theory with a primary goal to address the vessel cross-over issue. The proposed technique is composed of two main stages. (1) Segmentation step: The main skeleton of the retinal vasculature structure is extracted; (2) Tracing step: The first step is used to construct the digraph representation, which enables tracing task to cast as digraph-based label propagation using Matrix-forest theorem. The proposed technique was used for both retinal and neural tracing where the empirical evaluation of the proposed technique showed high achievable performance in both cases.

Yin et al. [64] presented a statistical based tracking method as an improved version of a work suggested by [61]. This method detects edge points iteratively based on a Bayesian approach using local grey levels statistics and continuity properties of blood vessels. Then, it combines the grey level profile and vessel geometric properties for sake of both accuracy improvement and tracking robustness. Experiments on both synthetic and real retinal images (DRIVE dataset) showed promising results, where the true positive rate was 0.73 and the false positive rate was 0.039. However, due to relatively low attained detection rate (TPR), a deeper evaluation on retinal images is needed to make the proposed method widely usable for vessel detection technique.

4.3. Mathematical Morphology-Based Techniques

Originally, mathematical morphology belongs to set theory of mathematics science, where it is considered an application of lattice theory to spatial structures. Mathematical morphology concerns the shapes that exists inside the image frame instead of pixels’ intensities. That means it ignores the details that regard image content where the pixel intensities are viewed as topographical highs, as shown in Figure 12. Typically, mathematical morphology was used in binary images, and then it extended to grey and colored ones, as a general processing framework, through morphological operators. In terms of mathematical morphology, the image $I$ is represented as a set $I\subseteq {\Re }^2$, where foreground pixels are the members that belong to $I$, whereas the background ones belong to the complement $I^c.$ The image $I$ undergoes a transformation by another set known as structuring element. Typically, the morphological operations can be applied to binary images and then can be extended to grey images. Morphological operations can be divided into: erosion, dilation, opening and closing operations. Erosion operation is used to lessen the objects in the image, whereas the dilation one is used to boost them. Morphological openings are used to remove unwanted structures in the image by applying an erosion followed by a dilation, whereas, in the case of morphological closing, some of structures in image are filled or merged by applying dilation operation followed by erosion one.

In aim of retinal vessel segmentation, a Morphological Angular Scale-Space (MASS) technique was proposed by [70]. The basic idea of the proposed technique was to rotate a varying length (multiscale) linear structuring element at different angles to determine the connected components and assure the connectivity across vessels where the scale-space is created through the variation in the length of linear structuring elements. Gradual evolution to higher scales lessens the non-vessel like elements out of the processed retinal image, where the extracted information from lower scales is used to build the retinal image of higher scales. At a certain scale (determined by authors experimentally), and using a vessel-ness measure proposed by [97], the method reported a lowest mean square error value of 0.0363, which was averaged over 50 retinal images taken from DRIVE dataset.

In addition to morphological operations, morphological tools are used in retinal vessel segmentation tasks including: gradient, watershed transform, top-hat transform, distance function and geodesic distance. Watershed transform was developed in the framework of mathematical morphology by Digabel and Lantu´ejoul [98]. The principal idea underlying this method was inspired from geography when a landscape is flooded by water, then watersheds appear as dividing lines of the domains of rain falling over the entire region [99]. A watershed-based segmentation algorithm was used by Frucci et al. [71] to segment retinal vasculature structure. The proposed algorithm combines watershed transform and both contrast and directional information extracted from retinal image. First, watershed transform was used to segment the image into multi-regions. Then, a unique grey-level value was assigned to each single region. A contrast value was computed for each region through calculating the difference in grey-level with respect to its adjacent regions. A $9\times 9$ window was applied to each pixel to attain the directional map composed of 16 directions. The standard deviation of pixels’ grey levels is aligned along these directions. Then, based on the occurrences of directions within watershed region, pixels locating in same region are assigned same direction. Once the contrast and directional maps had been obtained for each watershed region, a precursory segmentation of retinal vascular structure was acquired where the regions with highest contrast (positive difference) were most likely considered as non-vessel regions. Otherwise, they were considered as vessel ones. The proposed algorithm, developed using DRIVE dataset, and achieved a detection precision of 77% and accuracy of 95%.

Jiang et al. [72] presented a novel work to extract the retinal vasculature structure, by using global thresholding based on morphological operations. The proposed system was tested via DRIVE and STARE datasets, and achieved an average accuracy of 95.88% for single dataset test and 95.27% for the cross-dataset test. In terms of time and computational complexity, the system has been designed to minimize the computing complexity, and processes multiple independent procedures in parallel, thus having an execution time of 1.677 s per each retinal image on CPU platform.

4.4. Multi-Scale Techniques

The core idea behind the multi-scale representation is to represent the image at multiple scales (levels) where the data contained in a given image are embedded into one-parameter family of derived images at multiple scales [100], as shown in Figure 13. This representation is constructed provided that the structures at coarse scales (levels) are the simplified versions of the corresponding structures at fine scales by convoluting with smoothing kernels. The only possible smoothing kernels that meet the linearity and spatial shift invariance are Gaussian and its derivatives kernels that have increasing widths (scales $\sigma$) [101].

Originally, the scale-space is the framework of the multi-scale image representation [102]; two widely-used types of multi-scale representation are: pyramid [103,104], and Quad-tree [105]. Most retinal vessels segmentation methodologies are built based on the pyramid multi-scale type, where the grey-level data are represented in such a way that combines sampling operations with successive smoothing steps conducted by Gaussian kernels with different scales gives rise to a response that is represented by 2D Hessian matrix [106]. The eigen values of Hessian matrix determine the vessel-likeness which, in turn, result in retinal vasculature structure enhancement. Hessian matrix processing through eigen values analysis aims to obtain the principal directions of vessels where the decomposition of local second order structures in retinal image can be performed in order to attain the direction of the smallest curvature along the retinal vessels [107]. The retinal image size decreases exponentially with scale level, as illustrated in Figure 13, and, as a consequent, the amount of required computation too. However, it shows weakness in extracting fixed-size structures such as optic disc and non-uniform structures such as retinal lesions. Thus, multiscale approaches can be best suited for structures that have varying width and length (coarse and fine) in the same image.

A typical multi-scale based technique for retinal vessel segmentation was proposed by Budai et al. [66]. The proposed technique composed of three major phases: (1) Gaussian pyramid generation; (2) neighborhood analysis; and (3) images fusion. After the green channel of raw retinal image was extracted, Gaussian pyramid of resolution hierarchy was generated. The hierarchy is composed of three levels (level 0, level 1, and level 2, as shown in Figure 13). The original retinal image (green channel) has the highest resolution (level 0), and the width and height of image begin reducing as we move towards further levels (fine to coarse levels).

In the second phase, for each level, a $3\times 3$ neighborhood window analysis for each pixel was analyzed by calculating Hessian matrix followed by calculation of a couple of eigenvalues ${\lambda }_l \mathrm{and}{\lambda }_h$ of Hessian matrix which reflect the scale of lowest curvature ${\lambda }_l$ and the highest one ${\lambda }_h$ in the neighborhood window of the target pixel. Then, the ratio of these values was used to calculate a vessel likeness measure $P_{vessel}=1-\frac{{\lambda }_l}{{\lambda }_h}$; the value of $P_{vessel}$ determines whether target pixel belongs to vessel tree or not. If $P_{vessel}$ value is close to one, it means it is most likely a vessel pixel since ${\lambda }_l\mathrm{and}{\lambda }_h$ are similar to each other. This analysis was applied to each pixel at every scale (level). At the final stage, segmentation results from different levels were undergone binarization using two hysteresis thresholds, then they merged together using pixel-wise OR operation, which yielded the final segmented image. The methodology has achieved an accuracy, specificity, and sensitivity of 93.8%, 97.5% and 65.1% on STARE dataset, and 94.9%, 96.8% and 75.9% on the DRIVE dataset, respectively.

Abdallah et al. [68] proposed a two-step multi-scale retinal vessel detection algorithm. As a first step, the noise-corrupted retinal image (grey layer) was denoised against the additive Gaussian noise by applying a flux based anisotropic diffusion technique; a multi-scale response of multi-level resolution of retinal image was computed. Then, as a second step, a vessel model was established in order to analyze the eigenvalues and the eigenvectors of Hessian matrix for each scale. The final result of multi-level analysis represents the pixel-wise maximum of the results obtained over all scales. The proposed algorithm reported area under ROC curve of 0.94514 on STARE dataset.

Rattathanapad et al. [69] presented an algorithm to segment the blood vessel in retinal images based on multilevel line detection and connection of line primitives. Multilevel line detection is used for extracting the retinal vessels at multiple values of Gaussian smoothing parameters. Then, the line primitives that extracted at different scales were merged into one single vessel extraction result. The proposed algorithm was validated using DRIVE dataset where it proved the capability to detect most of the major part of vessel skeleton with false positives.

A new approach based on a multi-scale method for segmentation of retinal vessel was proposed by Moghimirad et al. [67] where it used weighted Medialness function along with the eigenvalues of the Hessian matrix. The proposed approach consists of two phases. In the first phase, the medial axis of retinal vessels was extracted using a two-dimensional Medialness function in multiple scales and sum of smoothed eigenvalues of the image. The second phase is for vessel reconstruction where centerline of vessels was extracted and radius of vessels was estimated simultaneously to obtain the final segmented results. The proposed approach was validated using DRIVE and STARE datasets where it showed high performance in terms of accuracy and area under the ROC curve where it has achieved accuracy of 0.9659 with area under ROC of 0.9580 via DRIVE dataset and accuracy of 0.9756 with area under ROC curve of 0.9678.

4.5. Model-Based Techniques

The concept of deformable model is used to describe a set of computer vision techniques and algorithms that abstractly model the variability of a certain class of objects in an image (vessels in retina image). The most basic versions of these algorithms concern shape variations modeling, where the shape is represented as flexible curve or surface, and is then deformed to match specific instance of the object class [108]. The deformation is not an arbitrary process, rather it is performed based on two powerful theories, Energy Minimization and Curve Evolution, which have roots in physics, geometry and approximation theories [109]. Deformable models can be divided into two main categories: parametric and geometric ones [110].

4.5.1. Parametric Deformable Models

Parametric deformable modeling, also called snakes or active contours, are parametrized curves that depend inherently on particular parameters to be created. The major goal of active contour modeling is to segment objects in retinal images by fitting the curve to objects’ boundaries in the image. It is called dynamic contour modeling since it initialized at a place in the neighborhood of target object, then the model can evolve dynamically to fit the shape of object by an iterative adaption. The major idea of snakes is to represent a curve via parametric curve; however, since it depends on a parameter to control the movement of curves (when slithering as snakes) during fitting process, it is rigid topologically, namely, it does not have the flexibility required to represent objects composed of a variable number of independent parts [108]. Moreover, another widely-recognized issue associated with snake-based segmentation technique is the incapability of snakes to converge to the correct vessel edges in the presence of high level noise or if the vessels were “empty” or have relatively low contrast levels [74].

A novel segmentation algorithm built on snake contours was developed by Jin et al. [74]. The proposed technique consists of three major steps: (1) First, parameter initialization technique based on Hessian feature boundaries, where the Hessian feature was used to extract all darker linear structures in retinal image, and then, the retinal image was divided into (N) segmentation regions (R), based on the seeds of extracted linear structure; (2) Second, each segmentation region R was represented as image through utilizing pixels’ average intensity influence, and then, the snake energy function was constructed on this image representation to realize the snake’s locations from the neighborhood of vessel edges to real ones; (3) Finally, as all model-based methodologies end, a region growing technique was used r to get the final vessels’ area, and then, the grown area was post-processed via context feature. The proposed methodology, validated on DRIVE dataset, reported a competitive performance, reaching up to 95.21% (accuracy), 75.08% (sensitivity), and 96.56% (specificity).

An efficient and effective infinite perimeter active contour model with hybrid region terms for vessel segmentation was proposed by Zhao et al. [31]. The proposed model used hybrid region information of the retinal image, such as the combination of intensity information and local phase based enhancement map. For its superiority, the local phase based enhancement map was used to preserve vessel edges, whereas the given information of image intensity guaranteed a correct feature segmentation. The proposed method was applied to DRIVE and STARE datasets where the methodology achieved sensitivity, specificity and accuracy of 0.780, 0.978 and 0.956, respectively, on STARE, whereas, for DRIVE, the measures are reported to be 0.7420, 0.9820 and 0.9540, respectively.

4.5.2. Geometric Deformable Models

Fast Marching methods and level sets methods are considered numerical techniques devised to track the propagating interfaces, the starting point for geometric deformable methods comes from the evolution analysis of the curves and surfaces, considered interfaces, and was first proposed by the mathematician, Sethian [111,112]. Afterwards, Caselles et al. [110] suggested representing the curve depending on Euclidian distance rather than parameters-dependency by representing a curve as a level set, which means the contour is represented as zero-level set of an auxiliary distance function $\varnothing$. Level sets theory paved the way to represent contours in flexible manner, where it can join or break apart without the need of reparameterization.

Gong et al. [75] used a novel level set technique does not need level set function initialization, by using local region area descriptor. The proposed technique involves two major steps: (1) a contour C is found, and then used to divide the entire retinal image into several parts based on whether the pixel position is inside the contoured area or not; and (2) a clustering algorithm is applied on the sub-regions that result from the first step, which, in turn, yield local cluster value, namely, a new region information used to redefine an energy functional in the first step until the algorithm converges. The second step represents key contribution of this paper, since it eliminates the effect of inhomogeneity of retinal image pixels’ intensities. Moreover, it gives more information about the local intensity information at level of image pixel, which eliminates the need for level set function re-initialization, considered a major drawback of level sets-based techniques. The proposed technique was tested on DRIVE dataset and an accuracy of 0.9360, sensitivity of 0.7078 and specificity of 0.9699 are reported.

A novel modification to level set based retinal vessels segmentation was presented by Dizdaro et al. [73] in terms of initialization and edge detection phases, which are needed as a pre-requirement for level set based techniques. In the initialization phase, the seed points were determined by sampling centerlines of vessels based on ridge identification, and then accurate boundaries of the retinal vessel tree are determined through phase map built based on ridge detection technique. The proposed algorithm was tested on both DRIVE dataset and a dataset created by paper’s authors. The algorithm achieved values of 0.9412, 0.9743, and 0.7181 for accuracy, specificity and sensitivity, respectively, for DRIVE, and 0.9453, 0.9640 and 0.6130, respectively, on the proposed dataset. As a conclusion, both deformable models, either parametric or geometric, share a common problem: both require, as essential step, a set of seed points that are determined either manually or automatically.

4.6. Adaptive Local Thresholding Techniques

Thresholding is considered one of the most well-known, plain and direct methodologies to image segmentation in general and to medical image segmentation in particular. Whereas the objects arrangement in the natural scene images looks relatively undistinguishable, the arrangement of objects including the organs and tissues in the medical image is usually more discernible. Therefore, thresholding segmentation techniques are used extensively in the research that involves the medical image segmentation, where different tissues and organs are represented in different grey levels. Typically, thresholding techniques, in their basic framework, search for a global value (level) that optimally maximizes the separation between different classes (different tissues in our case) in the image. The effectiveness of thresholding with a global level manifests if the objects in the image under consideration have well-defined areas and if the grey levels can be congregated around values with minimum interference.

Uneven illumination, inferior quality of source material, camera artifacts/distortions, and anatomical objects with multi-classes and hybrid features make the global thresholding for the entire retinal image a major source for segmentation errors. Moreover, since retinal image shows soft transition between different grey levels, uneven illumination or noise distortions, the principal segmentation errors begin to appear due to pixel-wise approach that adopted by global thresholding, namely, the pixels that have same grey levels (pixel intensity) will be segmented into the same anatomical object, which is considered a long-standing issue of global thresholding with a single hard value. To resolve these issues, region-wise thresholding methodologies have been suggested for case of retinal vessels identification, developed and implemented via different techniques which can be classified into three major categories: statistical, knowledge-based and fuzzy-based adaptive thresholding, as shown in Figure 14.

A novel work by Christodoulidis et al. [78] focused on segmenting small thin vessels through Multi Scale Tensor Voting (MTVF) scheme, based on the fact that small vessels represent nearly 10% of the total surface of vascular network [42] which, in turn, represents the framework of statistical-based adaptive thresholding. The proposed technique consists of four major stages: pre-processing; multiscale line detecting vessel enhancement; adaptive thresholding and MTVF processing; and post-processing stage. In the pre-processing stage, the green channel of raw retina image was extracted. Then, image contrast was enhanced by applying a contrast correction approach proposed by [113]. Dual-tree complex wavelet transform [114] was used to remove noise. Following the pre-processing stage, retinal vessels were enhanced via multi-scale line detection approach proposed by [115]. The output of multi-scale line detector was fed into adaptive thresholding processer to isolate vessels. To obtain various levels of adaptive thresholding, authors have fitted the histogram of MSLD response to a simple Gaussian function and modified the optimum global threshold [116] by varying the distance from the mean of Gaussian function through following equation:

$$T=\left|{\mu }_{Gaussian}\right|+\alpha \left|{\sigma }_{Gaussian}\right|$$

(5)

where ${\mu }_{Gaussian}$ and ${\sigma }_{Gaussian}$ are the mean and standard deviation of the fitted Gaussian function, respectively. Then, various thresholds revealed through experimentally changing $\alpha$ parameter, which is considered the heart of adaptive thresholding. Once the adaptive thresholding step has been performed, many smaller vessels separate. Thus, a multi-scale tensor voting framework inspired by [117,118] has been used to reconnect them. In summary, adaptive thresholding was used to extract large- and medium-sized retinal vessels, while MTVF was used to extract the smallest ones. Finally, as a post-processing step, morphological cleaning was used to remove the non-vasculature components remaining after applying adaptive thresholding. The proposed methodology was tested on a recently available Erlangen dataset [47], where it achieved average accuracy of 94.79%, and 85.06% and 95.82% for sensitivity and specificity, respectively.

Akram et al. [77] used adaptive thresholding technique to locate and extract retinal vessels automatically. The statistical-based adaptive thresholding was used to create the binary vascular mask by selecting points that isolate vessels from the rest of image. The proposed method has two major phases: pre-processing and adaptive thresholding phases. In the first phase, the monochromatic RGB retinal image was fed into Gabor wavelet filter for vasculature pattern enhancement, specifically for thin and less visible vessels, based on an image analysis technique proposed by [119]. The yielded enhanced retinal image has maximum grey values occur for background whereas pixels belong to vessels have a slightly greater intensity values rather than that belong to background. The proposed technique has been tested using DRIVE dataset, where it achieved an average accuracy of 0.9469 with area under ROC curve approximate value of 0.963.

A knowledge-guided local adaptive thresholding was proposed by Jiang and Mojon [76] where a verification-based multi-thresholding probing scheme was used. In its most basic form, given a binary image $I_{binary}$ results from thresholding process at a threshold level $T$, a classification procedure is used to decide if any region in $I_{binary}$ can be defined as an object. The operation is carried out on a series of different thresholds. The final image segmentation is set by combining different results of different thresholds. In summary, the objects hypotheses in an image are generated by binarization via some hypothetic thresholds, and then, according to a particular classification procedure, the object is accepted or rejected. The classification procedure represents the core of this proposed algorithm, where any piece of information related to object under consideration is incorporated, such as shape, color intensity and contrast. This is why it is called knowledge-guided technique, since, during segmentation, thresholding levels varying according to the knowledge available about the target object.

4.7. Machine Learning Techniques

While pattern recognition has its roots in engineering, machine learning was developed in computer science [120]. Pattern recognition has become a more well-known and active research field since the 1960s [121], and has undergone considerable development for many years, which yields a variety of paradigms and methods that have important applicability in many fields; retinal vascular structure is such a one. Machine learning algorithms are typically divided into three major categories: supervised, unsupervised and reinforcement learning. This categorization is mostly based on the availability of responses $y$ for input data $x$. Supervised learning addresses the problems where, for each input $x$, there is a corresponding observed output $y$, whereas, in the case of the latter two categories, this correspondence cannot be found due to the lack of data. Unsupervised learning explores interesting patterns in the input data without a need for explicit supervision [122]. Reinforcement learning assumes that the dynamics of the system under consideration follows a particular class of model [123].

A back propagation artificial neural network vessel classifier was designed by Nekovei and Ying [79] to identify the blood vasculature structure in angiogram images. The proposed technique uses the raw grey-intensity values of pixels instead of feature extraction. Each pixel in the image is processed by creating a window around it that covers number of pixels, and then, the raw grey intensities of these pixels are fed into the neural network as input. To cover the entire image, a process of sliding windows, pixel by pixel, takes place. Training dataset consists of manually selected patch samples of angiogram, where the distribution of vessel and background pixels is kept roughly equal to prevent neural network biasing towards background pixels’ classification. The proposed method avoids the complexity of feature extraction. Besides, the method achieved vessel detection performance of 92% on angiograms.

Transfer learning and domain adaptation [124] has been investigated in the field of retinal vessels segmentation by [86], where a denoised stacked auto-encoder neural network was trained with ample labeled mini-patches of retinal images taken from DRIVE dataset. DRIVE dataset represents the source domain where the auto-encoder was adapted to deploy on STARE dataset which represent target domain. The stacked auto encoder consists of two encoding layers with 400 and 100 nodes per layer, respectively, and is followed by a SoftMax regression layer. Due to power of knowledge transfer, the proposed technique exhibited an accelerated learning performance with area under ROC curve of 0.92.

For an exhaustive detection of fine retinal vessels, Maji et al. [84] designed a hybrid framework of deep and ensemble learning, where a Deep Neural Network (DNN) was used for unsupervised learning of vesselness via denoising auto-encoder, utilizing sparse trained retinal vascular patches. The learned representation of retinal vasculature patches was used as weights in the deep neural network, and the response of deep neural network was used in supervised learning process with a random forest for sake of vasculature tissues identification. The high capability of denoising auto encoder to learn feature representation was furiously exploited. The method was trained and tested via DRIVE dataset. Although the achieved average accuracy was 0.9327, it is considered marginally weak in contrast with state of the art approaches; the performance consistency of the method and the ability to identify both coarse and fine retinal vascular structures are considered its unique ambience.

Invigorated by the success of [84,86], Lahiri et al. [87] presented an ensemble of two parallel levels of stacked denoised auto-encoder networks. Each kernel is accountable for distinguishing a particular orientation of vessel. First level of the ensemble is composed by training (n) parallel stacked denoised autoencoders that have the same architecture, whereas second level is implemented by parallel training of two stacked denoised autoencoders, and the final architecture was fine-tuned until a satisfied accuracy was achieved. The decisions of individual members of the ensemble are combined by a simple SoftMax classifier. The method proves to be reliable and consistent in addition to high average detection accuracy that reached up to 0.953.

Contemporaneous research proposed by Maji et al. [88] uses deep neural network technique ensemble of twelve convolutional neural networks to distinguish vessel pixels from non-vessel ones. Each convolutional neural network has three convolutional layers; each one was trained separately using a set of 60,000 randomly selected $31\times 31\times 31$-sized patches taken from 20 raw color retinal images of DRIVE dataset. At the time of deduction, the probabilities of vesselness were produced by each convolutional network in a separate manner. Then, the individual responses were averaged to form the final vesselness probability of each pixel. Although the method did not achieve the highest detection accuracy (0.9470) among other methods, it exhibited superior performance in terms of learning vessel presentation from data because multiple experts represented by ensemble of conventional networks are more powerful and accurate than one neural network.

Detecting and restoring small foreground retinal filamentary structure was handled by Gu and Cheng [22] using an iterative two-step approach built based on Latent Classification Tree (LCT) model. After the confidence map has been constructed, a sufficiently high thresholding was placed on it, yielding a partially segmented image containing the main (thick and long) vessels. Using latent classification tree, the remaining low confidence map (filamentary filaments) was obtained. The filamentary structure was re-connected to main filaments (large vessels) via novel matting and completion field technique. These steps were performed iteratively until the whole retina surface was scanned. The proposed method achieved high detection accuracy, up to 97.32% for DRIVE dataset and 97.72% for STARE dataset, which is considered an expected result due to the noticeable degradation in the false positives produced by false detection of fine retinal filaments. The proposed method achieved encouraging performance, and also has a broad range of applications in fields other than retinal vessels extraction such as 3D magnetic resonance angiography and neural tracing.

A fast and accurate automated segmentation method for retinal and optic disc structures was proposed by Maninis et al. [24]. Their method uses deep Conventional Neural Networks (CNNs) as supervised segmentation methods. As all neural networks, the layers of CNN were trained in a specialized manner to address both retrial and optic disc segmentation. The proposed method was validated using DRIVE and STARE dataset for retinal vessel segmentation task where the area under recall–precision curve reached up to 0.822 for DRIVE dataset and 0.831 for STARE dataset. In context of CNN-based approaches, remarkable performances have been achieved by Liskowski et al. [89] with supremum area under curve (AUC) of 0.99 and accuracy of 95.33%, while AUC of 0.974 was achieved by Dasgupta and Singh [91] for automated retinal vessel segmentation.

A novel enhancement applied on the classic K-nearest neighbor (KNN) clustering algorithm for retinal vessel segmentation has been demonstrated by Salem et al. [80]. Each pixel was represented by a feature vector composed of green channel intensity, local maxima of the gradient magnitude and the local maxima of the largest eigenvalue. Based on these features, image pixels were clustered using the modified version of KNN without using training set. The segmentation algorithm was evaluated on the STARE dataset resulting in an average sensitivity and specificity of 77% and 90%, respectively, for three feature vectors, and 76% and 93%, respectively, using only one feature (maximum eigenvalue) vector.

A fuzzy-based retinal vessel segmentation methodology proposed by Sharma and Wasson [85] used the difference between low-pass filtered and high-pass filtered version of retinal image as input for fuzzy-logic based processing. The fuzzy logic consists of different sets of fuzzy rules; each fuzzy rule was built based on different thresholding values. Thresholding values were used to select and discard pixel values according to fuzzy rules, which, in turn, led to vessel extraction. The methodology attained an average accuracy of 95% on DRIVE dataset.

A two-stage combination between vessel tracking and fuzzy logic techniques was proposed by Akhavan and Faez [82]. In the first stage, the centerlines of enhanced retinal image were detected, while retinal vessels were filled using Fuzzy C-Means (FCM) clustering technique in the second stage. The final segmented result was obtained by combining centerlines images with fuzzy segmented images. Centerlines are used as initial points for a FCM-based region growing algorithm. The evaluation of the technique resulted in an average accuracy of 72.52% on DRIVE dataset and 77.66% on STARE dataset.

A novel scheme based on combination of genetic algorithm and fuzzy c-means clustering algorithm was proposed by Xie and Nie [81]. In pre-processing stage, the green channel of raw retinal image was extracted and enhanced by histogram equalization. Then, the retinal image was divided into two major layers: texture layer and smooth layer. Texture layer was directly fed as input to the processing stage due to the amount of information that contains. The features, containing data obtained in the first stage, were clustered via fuzzy c-means algorithm in conjunction with genetic algorithm, where, firstly, the genetic algorithm is used to obtain the approximate solution of the global optimal solution; and, secondly, the approximate solution was used as initial value of the fuzzy c-means algorithm. Genetic algorithm eases and enhances the duty of fuzzy c-means in finding the optimal solution without falling into issue of local detection of optimal solutions.

To overcome the issues related to the objective function of the classic fuzzy c-means classifier, Emary et al. [83] utilized the possibilistic version of fuzzy c-means algorithm optimized by Cuckoo search algorithm. They used the new clustering methods, possibilistic c-means proposed by [125] and possibilistic fuzzy c-means proposed by [126]m to establish an optimal version of fuzzy c-means that were used accordingly for retinal vessels segmentation. The optimality of the proposed method was examined by the heuristic search algorithm Cuckoo Search (CS). The evaluation on the STARE dataset indicated an average accuracy, specificity and sensitivity of 0.94478, 0.987 and 0.586, respectively, whereas, for DRIVE dataset, the measures were 0.938, 0.984 and 0.628, respectively.

5. Discussion and Conclusions

The existing retinal blood vessel segmentation methodologies are categorized, and described in the last section. We discussed various techniques used in these methodologies for the segmentation of blood vessels in retinal image and compare performance result of the methods. These methodologies were evaluated using publicly available datasets. Various retinal vessels segmentation methodologies follow similar procedures: each methodology initiates by pre-processing step, where the green layer (or grey) is extracted from the raw color retinal image, and then the contrast of the image is enhanced. Processing step represents the heart of algorithm, where the different techniques categorized in last section are used. Finally, in the post-processing step, the initial segmented image undergoes steps of smoothing and edge preserving and enhancement.

Regarding retinal segmentation categories shown in Figure 7, there is neither a best technique or algorithm to face all performance metrics in high segmentation achievement, nor a best mathematical scheme to do so. Deciding whether the methodology is best depends on a set of factors including: (1) Achieved accuracy, which in turn, depends on the achieved specificity and sensitivity, where segmentation is considered the best if it achieves the highest possible sensitivity value (or shows low false detection to other retinal structures), while also maintaining the specificity at optimal level. On the other hand, the optimality of the method increases as detection capability of the method records high performance in pathological retinal images; (2) Time and computational complexity: The time and computational power required by the methods tend to be low, as the accuracy has increased tendency on the condition that high performance of high accuracy has achieved; (3) Robustness: The method is considered to be best if it shows robustness against method parameters variation.

The accurate detection and segmentation of the retinal vascular structure forms the backbone of a variety of automated computer aided systems for screening and diagnosis of ophthalmologic and cardiovascular diseases. Even though many promising methodologies have been developed and implemented, there is still room for research improvement in blood vessel segmentation methodologies, especially for noisy and pathological retinal images outside the limited number of retinal images available in public datasets. In real-life applications, retinal vessels segmentation systems will not replace the experts’ role in diagnosis; rather, they will enhance the diagnosis accuracy and reduce the workload of the ophthalmologists. Therefore, large volume of patients’ images can be processed with high diagnosis accuracy and comparable time.