Robust Sampling Frequency Offset Estimation for OFDM over Frequency Selective Fading Channels

Abstract

Digital radio mondiale (DRM) is a terrestrial radio broadcasting standard to replace existing analogue AM and FM broadcasting, which is based on an orthogonal frequency division multiplexing (OFDM) technique. This paper focuses on the issue of estimating a sampling frequency offset (SFO) in OFDM-based broadcasting systems under frequency selective fading channels. In order to design a robust SFO estimation scheme and to benchmark its performance, the performance of the various conventional SFO estimation schemes is discussed and some improvements on the conventional estimation algorithms are highlighted. The simulation results show that such a design enhances the robustness of the proposed scheme against frequency selective fading.

1. Introduction

Orthogonal frequency division multiplexing (OFDM) has been widely used due to its high data rate and robustness regarding multipath fading distortions. OFDM has proven to be very effective in broadcast systems, such as digital multimedia broadcasting (DMB), digital radio mondiale (DRM), and terrestrial digital video broadcasting (DVB-T) [1,2,3]. Recently, a new second generation terrestrial digital video broadcasting (DVB-T2) standard has been defined to provide high definition television (HDTV) and high rate services [4]. In order to effectively offer HDTV services, the DVB-T2 standard adopts a multiple-input single-output (MISO) antenna mode. OFDM has also been adopted by numerous wireless transmission standards such as long term evolution (LTE) and wireless local area network (WLAN) [5,6], which adopt the multiple-input multiple-output (MIMO) technique as the key technology to cope with increasing transmission reliability without any additional wireless bandwidth. There has been explosive adoption of MIMO technology in the wireless environment to improve the performance of antennas and transceivers [7,8,9].

DRM has been developed to replace the current analog radio transmission in all the frequency bands, the AM broadcast bands below 30 MHz as well as above 30 MHz up to and including VHF band III [2]. Because the DRM system utilizes OFDM modulation, the frequency synchronization plays a crucial role in improving the performance of the OFDM receiver. In particular, the carrier frequency offset (CFO) and sampling frequency offset (SFO) will damage the performance of an OFDM system. If not properly estimated and compensated, the frequency error may limit the performance of an OFDM system. Therefore, time and frequency synchronization has been one of the major concerns of the OFDM-based DRM system [10,11,12,13,14,15,16]. Several schemes have been proposed in literature to estimate the SFO in frequency domain in the DRM system [12,13,14,15,16]. They are based on frequency reference cell (FRC) and gain reference cell (GRC), and work for all DRM operation modes. Although they are proposed for general channel conditions, its performance is strongly influenced by frequency selective fading distortions. Therefore, there is still room for a better estimation scheme that is robust to the fading distortion and not computationally demanding. In addition, a complete performance analysis, especially one that includes mean square error (MSE) derivation, has not been done.

This paper considers the issue of the SFO estimation in the OFDM-based DRM system, focusing on improving the robustness of SFO estimation in the presence of the frequency selective fading and designing its receiver structure. Firstly, we present the MSE analysis of the conventional estimation schemes that can be applied in the DRM system. Then, a robust estimation scheme to the frequency selective fading is proposed. The MSE of the proposed estimator is numerically calculated. Finally, the effectiveness of the proposed estimation scheme is analyzed and verified through numerical simulations.

This paper is organized as follows: Section 2 introduces the signal model and problem definition. In Section 3, we briefly introduce the conventional SFO estimation algorithms suitable for DRM systems. An improved unbiased SFO estimation method is proposed and its performance is numerically derived in Section 4. In Section 5, simulation results verifying the MSE analysis and the usefulness of the proposed scheme are presented. Section 6 concludes this paper.

2. Signal Model

We assume a baseband OFDM system with N subcarriers and $N_g$ cyclic prefix (CP) samples. A transmission signal is modulated by using the inverse fast Fourier transform (IFFT) on the transmitter side and the last $N_g$ IFFT samples are appended at the beginning to form the guard interval (GI). OFDM is highly sensitive to frequency offset and timing mismatch, so the synchronization problem between the transmitter and the receiver is of paramount importance to OFDM. Synchronization algorithms can, in general, be divided into pre-FFT and post-FFT classes. The goal of pre-FFT processing is to obtain the initial timing and fractional CFO based on GI correlation. In the post-FFT stage, residual CFO, SFO, and integer CFO are estimated by using the periodic nature of pilots. Since the focus here is the estimation of SFO, it is assumed that the symbol timing mismatch has been perfectly recovered at the receiver and coarse CFO acquisition has been successfully applied at the beginning of the reception of OFDM frame. For this purpose, many schemes are currently available in the literature [17,18,19]. During the data section, therefore, relatively small SFO and residual CFO will be present.

At the receiver, the l-th received OFDM symbol at the k-th subcarrier after FFT demodulation is given in [20,21]

$$\begin{array}{cc}\hfill R_l\left(k\right)& =\alpha \left(\varphi \left(k\right)\right)H_l\left(k\right)X_l\left(k\right)e^{j2\pi \varphi \left(k\right)(l{N}_u+N_g)/N}{e}^{j\pi (N-1)\varphi \left(k\right)/N}+I_l\left(k\right)+Z_l\left(k\right),0\le k<N\hfill \end{array}$$

(1)

where $\alpha \left(\varphi \right(k\left)\right)$ is the attenuation of the subcarriers magnitudes due to the frequency offset, $N_u=N+N_g$, $H_l\left(k\right)$ is the zero-mean channel’s frequency response with variance ${\sigma }_H^2$, $Z_l\left(k\right)$ is a zero-mean complex Gaussian noise with variance ${\sigma }_Z^2$ during the l-th symbol period, and $I_l\left(k\right)$ is the inter-carrier interference (ICI) term introduced by frequency offsets. In (1), $\alpha \left(\varphi \right(k\left)\right)$ and $I_l\left(k\right)$ are given by

$$\alpha \left(\varphi \left(k\right)\right)=\frac{sin\left(\pi \right(\varphi \left(k\right))}{Nsin\left(\pi \varphi \right(k)/N)}$$

(2)

and

$$\begin{array}{cc}\hfill I_l\left(k\right)& =\sum _{n=0,n\ne k}^{N-1}{H}_l\left(n\right)X_l\left(n\right)e^{j2\pi \varphi \left(n\right)(l{N}_u+N_g)/N}\frac{sin\left(\pi \right(\varphi \left(n\right)+n-k\left)\right)}{Nsin\left(\pi \right(\varphi \left(n\right)+n-k)/N)}{e}^{j\pi (N-1)\left(\varphi \right(n)+n-k)N}\hfill \end{array}$$

(3)

where $\varphi \left(k\right)$ is formed with CFO ${\Delta }_f$ and SFO ${\Delta }_s$. The former is the same for all subcarriers, while the latter occurs linearly according to the subcarrier index k, i.e., $\varphi \left(k\right)={\Delta }_f+k{\Delta }_s$. Here, ${\Delta }_f$ and ${\Delta }_s$ denote the normalized CFO and SFO by the sampling rate, respectively. Since CFO and SFO are small during the data section of the frame, we approximate $\alpha \left(\varphi \right(k\left)\right)\approx 1$ and the ICI term is negligible compared to the additive noise $Z_l\left(k\right)$ for medium SNR conditions [21]. In this paper, however, its impact on the system performance will be addressed. From [22], $I_l\left(k\right)$ may be handled as Gaussian noise with zero mean and variance ${\sigma }_I^2$.

In the DRM standard, three FRCs are embedded for frequency tracking in subcarriers $\{k_1,k_2,k_3\}$, which are fixed for all DRM modes in Hz and are transmitted at a boosted power level of $E_X={|X_l\left(k\right)|}^2=2$. Denote $k_m$ the subcarrier index of the m-th FRC, where $m\in \{1,2,3\}$. For subsequent symbols, the l-th pilot symbol $X_l\left(k_m\right)$ is derived from the first pilot symbol in the frame denoted by $X_{l_1}\left(k_m\right)$ as follows $X_l\left(k_m\right)=d_l\left(k_m\right)X_{l_1}\left(k_m\right)$, where $d_l\left(k_m\right)\in \{1,-1\}$. In [2], the phases of FRCs are chosen to ensure the tones are continuous: (1) $d_l\left(k_m\right)=1$ for all l’s and m’s (modes A, B, C, and $k_3$ only of mode D), and for even values of l ($k_1$ and $k_2$ of mode D) (2) $d_l\left(k_m\right)=-1$ for odd values of l ($k_1$ and $k_2$ of mode D). The GRCs are used mainly to get a proper estimate of the channel transfer function, which are spread equally in time and frequency directions. The GRCs are also used to track the frequency errors.

3. Conventional Estimation Scheme

In this section, we briefly revisit the conventional SFO estimation algorithms used n the DRM system [12,13,14] and focus on the MSE performance of the considered estimation schemes. In [12,13], the differential relation among FRCs is used, while [14] exploits two adjacent OFDM blocks where the sets of pilot subcarriers are located symmetrically and distributed equally around the DC carrier. In order to benchmark the proposed estimation scheme, a robust estimation algorithm which archives frequency estimates in closed-form [22] can be applied to the DRM system.

3.1. Conventional Scheme A

The method in [12] is designed for real-time implementation in a DRM receiver, which utilizes the difference between two adjacent FRCs. In this scheme, the SFO is estimated in the form of

$${\widehat{\Delta }}_s=\frac{N}{4\pi D{N}_u}\sum _{m=2}^3\frac{\arg \left\{{\widehat{R}}_l\left(k_m\right)\right\}-\arg \left\{{\widehat{R}}_l\left(k_1\right)\right\}}{k_m-k_1}$$

(4)

with

$${\widehat{R}}_l\left(k_m\right)=b_l\left(k_m\right)R_l^{\ast }\left(k_m\right)R_{l+D}\left(k_m\right)$$

(5)

where ${(·)}^{\ast }$ is the complex conjugate operation, $\arg \left\{x\right\}$ represents the argument of a complex number x, D is the distance between two pilot symbols selected for the parameter estimation, and $b_l\left(k_m\right)=d_l\left(k_m\right)/d_{l+D}\left(k_m\right)$ is introduced to remove the polarity of the temporal correlation. In order to cope with the effects of noise when it is encountered with a relatively small difference of the rotated phases between two adjacent symbols, D-symbol delay estimation is employed in (5). By using D-symbol delay estimation, the MSE of (4) can be calculated by [13]

$$\begin{array}{cc}\hfill E\left[|{\widehat{\Delta }}_s-{\Delta }_s{|}^2\right]& \approx \left(\frac{1}{\gamma }+\frac{1}{2{\gamma }^2}\right)\frac{N^2}{8{\pi }^2{D}^2{N}_u^2}\left[\frac{1}{(k_2-k_1)(k_3-k_1)}+\sum _{m=2}^3\frac{1}{{(k_m-k_1)}^2}\right]\hfill \end{array}$$

(6)

where $\gamma =E_X/{\sigma }_Z^2$ stands for the signal-to-noise ratio (SNR).

3.2. Conventional Scheme B

The second conventional method [13] uses the differential relation among pilot subcarrier indexes specified in the DRM standard, i.e., $k_2-k_1=2(k_3-k_2)$ and $k_3-k_1=3(k_3-k_2)$. Denote $x^Q$ be the imaginary term of x. By using D-symbol delay estimation, the resulting expression leads to

$${\widehat{\Delta }}_s=\frac{N}{4\pi D{N}_u(k_3-k_2)}\arg \left\{\sum _{m=1}^3\sum _{\underset{n<m}{n=1}}^3{\widehat{R}}_l\left(k_m\right){\widehat{R}}_l^{\ast }\left(k_n\right)\right\}$$

(7)

with

$$\begin{array}{cc}\hfill \sum _{m=1}^3\sum _{\underset{n<m}{n=1}}^3{\widehat{R}}_l\left(k_m\right){\widehat{R}}_l^{\ast }\left(k_n\right)& \approx 3{\left(E_X\right)}^2{e}^{j4\pi (k_3-k_2){\Delta }_{s}D{N}_u/N}+\sum _{m=1}^3\sum _{\underset{n<m}{n=1}}^3{Z}_l(k_m,k_n)\hfill \end{array}$$

(8)

where $Z_l(k_m,k_n)$ is the appropriate noise contribution. By using the high SNR approximation, the variance of the estimate is

$$\begin{array}{cc}\hfill E\left[|{\widehat{\Delta }}_s-{\Delta }_s{|}^2\right]& \approx {\left(\frac{N}{12\pi (k_3-k_2)E_X^{2}D{N}_u}\right)}^{2}E\left[{\left|\sum _{m=1}^3\sum _{\underset{n<m}{n=1}}^3{\left\{Z_l(k_m,k_n)e^{-j\upsilon }\right\}}^Q\right|}^2\right]\hfill \end{array}$$

(9)

where $\upsilon =4\pi (k_3-k_2){\Delta }_{s}D{N}_u/N$. The MSE has the form after some simple computations [13]

$$\begin{array}{cc}\hfill E\left[|{\widehat{\Delta }}_s-{\Delta }_s{|}^2\right]& \approx \frac{N^2}{144{\pi }^2{D}^2{N}_u^2{(k_3-k_2)}^2}\left(\frac{1}{\gamma }+\frac{1}{2{\gamma }^2}\right)\left[8+3\left(\frac{1}{\gamma }+\frac{1}{2{\gamma }^2}\right)\right]\hfill \end{array}$$

(10)

3.3. Conventional Scheme C

Since (4) and (7) are based on the limited FRCs, the basic concept reported in [22,23] can be straightforwardly extended to the DRM system for further enhancing the estimation performance, which uses the GRC as the pilot symbol [14]. Depending on DRM robustness mode and OFDM symbol index l, GRC pattern is repeated in the frequency and time directions. Without the loss of generality, the GRCs with length $N_p$ are assumed to be either uniformly or symmetrically inserted at the subcarrier positions $\{-k_{N_p/2},-k_{N_p/2-1},\cdots ,-k_1,k_1,k_2,\cdots ,k_{N_p/2}\}$. Denote ${\mathsf{\Lambda }}_{l,1}$ and ${\mathsf{\Lambda }}_{l,2}$ the temporal correlations for the first and the second half of pilots around DC, respectively.

For the simple description, we assume that $H_l\left(k\right)\approx H_{l+D_t}\left(k\right)$. By using the structure of the post-FFT pilot-aided estimator [22,23], the temporal correlation between two pilot symbols is of the form

$$\begin{array}{ccc}\hfill {\mathsf{\Lambda }}_{l,i}& =& \sum _{m=1}^{N_p/2}{b}_l\left({(-1)}^i{k}_m\right)R_l^{\ast }\left({(-1)}^i{k}_m\right)R_{l+D_t}\left({(-1)}^i{k}_m\right)\hfill \\ & \approx & \sum _{i=1}^{N_p/2}{|H_l\left({(-1)}^i{k}_m\right)|}^2{E}_X{e}^{j2\pi \varphi \left({(-1)}^i{k}_m\right)D_t{N}_u/N}+\sum _{m=1}^{N_p/2}{b}_l\left({(-1)}^i{k}_m\right){\tilde{I}}_l\left({(-1)}^i{k}_m\right)\hfill \\ & & +\sum _{m=1}^{N_p/2}{b}_l\left({(-1)}^i{k}_m\right){\tilde{Z}}_l\left({(-1)}^i{k}_m\right),i=1,2\hfill \end{array}$$

(11)

where $D_t$ is the distance between the two consecutive GRCs in time direction, ${\tilde{I}}_l\left(k\right)$ denotes the combined ICI contribution given by

$$\begin{array}{cc}\hfill {\tilde{I}}_l\left(k\right)& =H_l^{\ast }\left(k\right)X_l^{\ast }\left(k\right)I_{l+D_t}\left(k\right)e^{-j2\pi \varphi \left(k\right)((l+D_t)N_u+N_g)/N}+I_{l+D_t}\left(k\right)Z_l^{\ast }\left(k\right)\hfill \\ & +H_{l+D_t}\left(k\right)X_{l+D_t}\left(k\right)I_l^{\ast }\left(k\right)e^{j2\pi \varphi \left(k\right)(l{N}_u+N_g)/N}+I_l^{\ast }\left(k\right)Z_{l+D_t}^{\ast }\left(k\right)+I_{l+D_t}\left(k\right)I_l^{\ast }\left(k\right)\hfill \end{array}$$

(12)

and ${\tilde{Z}}_l\left(k\right)$ stands for the AWGN defined as

$$\begin{array}{ccc}\hfill {\tilde{Z}}_l\left(k\right)& =& H_l^{\ast }\left(k\right)X_l^{\ast }\left(k\right)Z_{l+D_t}\left(k\right)e^{-j2\pi \varphi \left(k\right)((l+D_t)N_u+N_g)/N}\hfill \\ & & +H_{l+D_t}\left(k\right)X_{l+D_t}\left(k\right)Z_l^{\ast }\left(k\right)e^{j2\pi \varphi \left(k\right)(l{N}_u+N_g)/N}+Z_{l+D_t}\left(k\right)Z_l^{\ast }\left(k\right)\hfill \end{array}$$

(13)

Then, the estimate of ${\Delta }_s$ takes the expression

$${\widehat{\Delta }}_s=\frac{N}{2\pi N_u{D}_t}\frac{\arg \left\{{\mathsf{\Lambda }}_{l,2}\right\}-\arg \left\{{\mathsf{\Lambda }}_{l,1}\right\}}{k_{N_p/2}+k_1}$$

(14)

In [23], it has been proved that the estimation scheme (14) is asymptotically unbiased in AWGN channel. In this case, the MSE of (14) is expressed as

$$E\left[|{\widehat{\Delta }}_s-{\Delta }_s{|}^2\right]=\frac{N^2}{{\pi }^2{N}_u^2{(k_{N_p/2}+k_1)}^2{D}_t^2{N}_p}\left(\frac{1}{\gamma }+\frac{1}{2{\gamma }^2}\right)$$

(15)

As discussed in [22,23], the condition of small SFO and less frequency selectivity ensures the unbiasedness of (14). To overcome this drawback, the robust SFO estimation scheme to the presence of the CFO along with frequency selectivity will be suggested in the following section.

3.4. Conventional Scheme D

In [22], the g-lag correlation is adopted to estimate frequency errors $\varphi \left(k\right)={\Delta }_f+k{\Delta }_s$. A SFO estimate is get upon observation of $N_s$ OFDM blocks with indices $l=1,2,\cdots ,N_s$. Based on the $N_s$ observed OFDM blocks, the g-lag correlation is defined as

$${\Omega }_g\left(k\right)=\sum _{l=g+1}^{N_s}{R}_l\left(k\right)R_{l-g}^{\ast }\left(k\right),1\le g\le N_s$$

(16)

By using the g-lag correlations, an estimate of $\varphi \left(k\right)$ can be obtained as

$$\widehat{\varphi }\left(k\right)=\frac{N}{2\pi N_u}\sum _{g=1}^{N_s/2}p\left(g\right)\arg \left\{{\Omega }_g\left(k\right){\Omega }_{g-1}^{\ast }\left(k\right)\right\}$$

(17)

where $\left\{p\right(g\left)\right\}$ denotes the scaling coefficients [22]. Finally, the quantity $\widehat{\varphi }\left(k\right)$ is now used to get estimate of ${\Delta }_s$ as follows

$${\widehat{\Delta }}_s=\frac{J\left(1\right)Q\left(2\right)-J\left(2\right)Q\left(1\right)}{J\left(1\right)J\left(3\right)-J^2\left(2\right)}$$

(18)

where

$$\begin{array}{cc}\hfill J\left(n\right)=\frac{1}{N_p}\sum _{m=1}^{N_p/2}& \{{\left(k_m\right)}^{n-1}|H_l\left(k_m\right){|}^2+{(-k_m)}^{n-1}{|H_l(-k_m)|}^2\}\hfill \end{array}$$

(19)

and

$$\begin{array}{cc}\hfill Q\left(n\right)=\frac{1}{N_p}\sum _{m=1}^{N_p/2}& \{{\left(k_m\right)}^{n-1}|H_l\left(k_m\right){|}^2\widehat{\varphi }\left(k_m\right)+{(-k_m)}^{n-1}{|H_l(-k_m)|}^2\widehat{\varphi }(-k_m)\}\hfill \end{array}$$

(20)

These quantities (19) and (20) rely on the channel coefficients $|H_l{\left(k\right)|}^2$. Since the GRC pattern is periodical every $D_t+1$ OFDM symbol in time direction, (18) can not be directly applied to the DRM system. In the sequel, we assume that (18) uses the pilot symbols inserted into every OFDM symbol.

4. Proposed Estimation Scheme for DRM with Frequency Selective Fading

In this section, a pilot-assisted SFO estimation algorithm is proposed with an improved accuracy in the presence of frequency selectivity. With the use of GRCs, a simple way of designing an unbiased estimation scheme is designed and its estimation performance is analytically derived. As reported in [22,23], (14) is approximately unbiased in the case of frequency selective slowly fading channels when a small SFO is encountered. In addition, the unbiasedness of (14) is guaranteed if the pilot subcarriers are located symmetrically and distributed uniformly around the DC carrier. Unfortunately, the preliminary condition is not valid for DRM mode C and only one GRC pattern to meet this condition is existed for other DRM modes. To solve this problem, we derive a robust unbiased SFO estimation method, which has no restriction to pilot patterns. In contrast to the conventional schemes, the proposed scheme uses two-step correlation, namely temporal correlation and frequential correlation, which are adopted to remove the need of channel state information (CSI) and get an unbiased estimate in the presence of frequency selective fading, respectively.

In the first step, we consider the temporal correlation as similarly used in the conventional scheme (14) to offset the unknown channel $H_l\left(k\right)$. Without the loss of generality, in the following derivation we assume that $H_l\left(k\right)\approx H_{l+D_t}\left(k\right)$, which leads to

$$\begin{array}{c}\hfill {\widehat{R}}_l\left(k\right)={|H_l\left(k\right)|}^2{E}_X{e}^{j2\pi \varphi \left(k\right)D_t{N}_u/N}+{\tilde{I}}_l\left(k\right)+{\tilde{Z}}_l\left(k\right)\end{array}$$

(21)

where $E_X={|X_l\left(k\right)|}^2$ is the pilot symbol energy. For the simple description, we omit the parameter $b_l\left(k\right)\in \{1,-1\}$, assuming that its polarity is compensated at the receiver. In the next step, the frequential correlation is adopted to obtain an unbiased SFO estimation in a severe frequency selective fading channel. The frequential correlation is performed on two pilot subcarriers spaced $k_m+k_{N_p/2+1-m}(m=1,2,\cdots ,N_p/2)$ subcarrier apart, which is defined by

$$\begin{array}{ccc}\hfill {\widehat{R}}_l\left(k_m\right){\widehat{R}}_l^{\ast }(-k_{N_p/2+1-m})& =& |H_l\left(k_m\right){|}^2{|H_l(-k_{N_p/2+1-m})|}^2{E}_X^2{e}^{j2\pi (k_m+k_{N_p/2+1-m}){\Delta }_s{D}_t{N}_u/N}\hfill \\ & & +{\mathcal{I}}_l\left(k_m\right)+{\mathcal{Z}}_l\left(k_m\right)\hfill \end{array}$$

(22)

where ${\mathcal{I}}_l\left(k_m\right)$ is the ICI contribution given by

$$\begin{array}{ccc}\hfill {\mathcal{I}}_l\left(k_m\right)& =& |H_l\left(k_m\right){|}^2{E}_X{\tilde{I}}_l^{\ast }(-k_{N_p/2+1-m})e^{j2\pi \varphi \left(k_m\right)D_t{N}_u/N}+{\tilde{Z}}_l\left(k_m\right){\tilde{I}}_l^{\ast }(-k_{N_p/2+1-m})\hfill \\ & & +|H_l(-k_{N_p/2+1-m}){|}^2{E}_X{\tilde{I}}_l\left(k_m\right)e^{-j2\pi \varphi (-k_{N_p/2+1-m})D_t{N}_u/N}\hfill \\ & & +{\tilde{Z}}_l^{\ast }(-k_{N_p/2+1-m}){\tilde{I}}_l\left(k_m\right)+{\tilde{I}}_l\left(k_m\right){\tilde{I}}_l^{\ast }(-k_{N_p/2+1-m})\hfill \end{array}$$

(23)

and ${\mathcal{Z}}_l\left(k_m\right)$ is the AWGN contribution given by

$$\begin{array}{ccc}\hfill {\mathcal{Z}}_l\left(k_m\right)& =& |H_l\left(k_m\right){|}^2{E}_X{\tilde{Z}}_l^{\ast }(-k_{N_p/2+1-m})e^{j2\pi \varphi \left(k_m\right)D_t{N}_u/N}\hfill \\ & & +|H_l(-k_{N_p/2+1-m}){|}^2{E}_X{\tilde{Z}}_l\left(k_m\right)e^{-j2\pi \varphi (-k_{N_p/2+1-m})D_t{N}_u/N}+{\tilde{Z}}_l\left(k_m\right){\tilde{Z}}_l^{\ast }(-k_{N_p/2+1-m})\hfill \end{array}$$

(24)

Since $E\left[{\mathcal{Z}}_l\left(k\right)\right]=E\left[{\mathcal{I}}_l\left(k\right)\right]=0$, we eventually establish an estimate for ${\Delta }_s$ as

$${\widehat{\Delta }}_s=\frac{N}{2\pi D_t{N}_u}\frac{{\displaystyle \sum _{m=1}^{N_p/2}\arg \left\{{\widehat{R}}_l\left(k_m\right){\widehat{R}}_l^{\ast }(-k_{N_p/2+1-m})\right\}}}{{\displaystyle \sum _{m=1}^{N_p/2}\left\{k_m+k_{N_p/2+1-m}\right\}}}$$

(25)

We compute hereafter the MSE of the estimation scheme (25) when the SNR is assumed to be high. Denote $m_{\upsilon }=2\pi {\Delta }_s{D}_t(k_m+k_{N_p/2+1-m})N_u/N$. In the case of DRM channel model 1 [2], which corresponds to AWGN channel, one can write the correlation metric as

$$\begin{array}{c}{\widehat{R}}_l\left(k_m\right){\widehat{R}}_l^{\ast }(-k_{N_p/2+1-m})=E_X^2{e}^{j2\pi D_t\left(k_m+k_{N_p/2+1-m}\right){\Delta }_s{N}_u/N}\left[1+\frac{\left\{{\mathcal{I}}_l\left(k_m\right)+{\mathcal{Z}}_l\left(k_m\right)\right\}{e}^{-j{m}_{\upsilon }}}{E_X^2}\right]\hfill \end{array}$$

(26)

whose argument can be factorized as

$$\begin{array}{ccc}\hfill \arg \left\{{\widehat{R}}_l\left(k_m\right){\widehat{R}}_l^{\ast }(-k_{N_p/2+1-m})\right\}& =& 2\pi D_t{\Delta }_s{N}_u/N\left\{k_m+k_{N_p/2+1-m}\right\}\hfill \\ & & +{\tan }^{-1}\left\{\frac{{\left[\left\{{\mathcal{I}}_l\left(k_m\right)+{\mathcal{Z}}_l\left(k_m\right)\right\}{e}^{-j{m}_{\upsilon }}\right]}^Q}{E_X^2}\right\}\hfill \\ & & =2\pi D_t{\widehat{\Delta }}_s{N}_u/N\left\{k_m+k_{N_p/2+1-m}\right\}\hfill \end{array}$$

(27)

Since the pilots are transmitted at a boosted power level, it is very likely that $|{\left[\left\{{\mathcal{I}}_l\left(k_m\right)+{\mathcal{Z}}_l\left(k_m\right)\right\}{e}^{-j{m}_{\upsilon }}\right]}^Q|\ll E_X^2$ when SNR is high [24], hence the arctangent in (27) can be approximated to get

$$\begin{array}{c}{\tan }^{-1}\left\{\frac{{\left[\left\{{\mathcal{I}}_l\left(k_m\right)+{\mathcal{Z}}_l\left(k_m\right)\right\}{e}^{-j{m}_{\upsilon }}\right]}^Q}{E_X^2}\right\}\approx \frac{{\left[\left\{{\mathcal{I}}_l\left(k_m\right)+{\mathcal{Z}}_l\left(k_m\right)\right\}{e}^{-j{m}_{\upsilon }}\right]}^Q}{E_X^2}\hfill \end{array}$$

(28)

It is easily shown from (27) and (28) that we obtain

$$\begin{array}{c}2\pi D_t({\widehat{\Delta }}_s-{\Delta }_s)N_u/N\approx \frac{{\displaystyle \sum _{m=1}^{N_p/2}\frac{{\left[\left\{{\mathcal{I}}_l\left(k_m\right)+{\mathcal{Z}}_l\left(k_m\right)\right\}{e}^{-j{m}_{\upsilon }}\right]}^Q}{E_X^2}}}{{\displaystyle \sum _{m=1}^{N_p/2}\left\{k_m+k_{N_p/2+1-m}\right\}}}\hfill \end{array}$$

(29)

Since $E\left[\left\{{\mathcal{I}}_l\left(k_m\right)+{\mathcal{Z}}_l\left(k_m\right)\right\}{e}^{-j{m}_{\upsilon }}\right]=0$, we arrive at

$$\begin{array}{c}E\left[|{\widehat{\Delta }}_s-{\Delta }_s{|}^2\right]\approx {\left(\frac{N}{2\pi D_t{N}_u}\right)}^2\frac{{\displaystyle \sum _{m=1}^{N_p/2}\frac{E\left[{\left|{\left[\left\{{\mathcal{I}}_l\left(k_m\right)+{\mathcal{Z}}_l\left(k_m\right)\right\}{e}^{-j{m}_{\upsilon }}\right]}^Q\right|}^2\right]}{E_X^4}}}{{\left({\displaystyle \sum _{m=1}^{N_p/2}\left\{k_m+k_{N_p/2+1-m}\right\}}\right)}^2}\hfill \end{array}$$

(30)

A close observation of (23) and (24) reveals that the variance of the denominator in (30) is calculated by

$$\begin{array}{cc}\hfill \frac{E\left[{\left|{\left[\left\{{\mathcal{I}}_l\left(k_m\right)+{\mathcal{Z}}_l\left(k_m\right)\right\}{e}^{-j{m}_{\upsilon }}\right]}^Q\right|}^2\right]}{E_X^4}=& \left(\frac{{\sigma }_Z^2}{E_X}+\frac{{\sigma }_Z^4}{2E_X^2}\right)\left[1+\frac{1}{4}\left(\frac{{\sigma }_Z^2}{E_X}+\frac{{\sigma }_Z^4}{2E_X^2}\right)\right]\hfill \\ & +\frac{{\sigma }_I^2}{E_X}\left(1+\frac{{\sigma }_Z^2}{E_X}\right)\left(1+\frac{{\sigma }_Z^2}{E_X}+\frac{{\sigma }_Z^4}{2E_X^2}\right)\hfill \end{array}$$

(31)

Substituting (31) to (30), the MSE expression of (25) can be calculated by

$$\begin{array}{cc}\hfill E\left[|{\widehat{\Delta }}_s-{\Delta }_s{|}^2\right]=& \frac{N^2{N}_p}{2{\pi }^2{D}_t^2{N}_u^2{\mathcal{K}}^2}\left(\frac{1}{\gamma }+\frac{1}{2{\gamma }^2}\right)\left[1+\frac{1}{4}\left(\frac{1}{\gamma }+\frac{1}{2{\gamma }^2}\right)\right]\hfill \\ & +\frac{N^2{N}_p}{2{\pi }^2{D}_t^2{N}_u^2{\mathcal{K}}^2}\frac{{\sigma }_I^2}{E_X}\left(1+\frac{1}{\gamma }\right)\left(1+\frac{1}{\gamma }+\frac{1}{2{\gamma }^2}\right)\hfill \end{array}$$

(32)

where

$$\mathcal{K}=\sum _{m=1}^{N_p/2}\left\{k_m+k_{N_p/2+1-m}\right\}$$

(33)

In the case of the uniform distribution of pilot tones, one can see that

$$\begin{array}{cc}\hfill k_1+k_{N_p/2}& =k_2+k_{N_p/2-1}=\cdots =k_{N_p/2-1}+k_2=k_{N_p/2}+k_1\hfill \end{array}$$

(34)

which results in

$$\mathcal{K}=\left(k_1+k_{N_p/2}\right)N_p/2$$

(35)

It is worthwhile to note that all GRC patterns defined in each DRM mode satisfy (34) because the GRC is uniformly distributed in the DRM specification.

5. Simulation Results and Discussions

In order to verify the correctness of the MSE analysis as well as the effectiveness of the proposed estimation scheme, the simulations are conducted on DRM systems, taking into account different DRM robustness modes, whose main parameters are summarized in Table 1. To make a fair comparison, $D=D_t$ is chosen for the conventional and proposed schemes. To show the performance, we consider the six channel models (CMs) provided in the DRM standard [2], which are listed in Table 2. In order to focus on the effect of SFO on the MSE performance of the DRM receiver in the presence of the frequency selectivity of the channel, the mobile speed is not included in the considered CMs.

Table 1. Main parameters in Digital Radio Mondiale (DRM) modes.

	Mode A	Mode B	Mode C	Mode D
N	288	256	176	112
$N_g$	32	64	64	88
$N_p$	12	34	36	28
$D_t$	5	3	2	3

Table 2. Main parameters in DRM channel models.

	CM1	CM2	CM3	CM4	CM5	CM6
Number of path	1	2	4	2	2	4
Maximum delay spread (ms)	0	1	2.2	2	4	6
Maximum Doppler spread (Hz)	0	0.1	2	1	2	7.2

Firstly, the complexity comparison of the proposed scheme (25) to the conventional schemes in (14) and (18) is discussed in terms of the number of real floating point operations (flops) needed to complete one-shot estimation. A complex multiplication and a complex addition count six and two flops, respectively [25]. For fair comparison, we consider only the GRC-based estimation schemes. We assume that the CSI has already been estimated at the receiver so that the complexity analysis in the conventional scheme D is presented for the case of known CSI. Since $b_l\left(k\right)\in \{1,-1\}$ does not require actual multiplication, its calculation to obtain ${\widehat{R}}_l\left(k\right)$ is not included in the complexity comparison. Table 3 lists the computational complexity between the conventional and proposed estimation schemes. For each one-shot estimate, the total number of flops of the conventional scheme C is $8N_p-2$, while the conventional scheme D consumes $N_p(12N_s^2-13N_s+98)/2+7$ flops. On the other hand, the total flops needed to obtain (25) in the proposed scheme is $19N_p/2$.

Table 3. Complexity of the conventional and proposed schemes.

Scheme	Complex Multiplication	Complex Addition	Real Multiplication	Real Addition
(14)	$N_p$	$N_p-2$	1	1
(18)	$N_p(3N_s^2/4-N_s/2+6)$	$N_p(3N_s^2/4-2N_s+1)$	$7N_p+10$	$N_p(N_s/2+4)-3$
(25)	$3N_p/2$	-	1	$N_p/2-1$

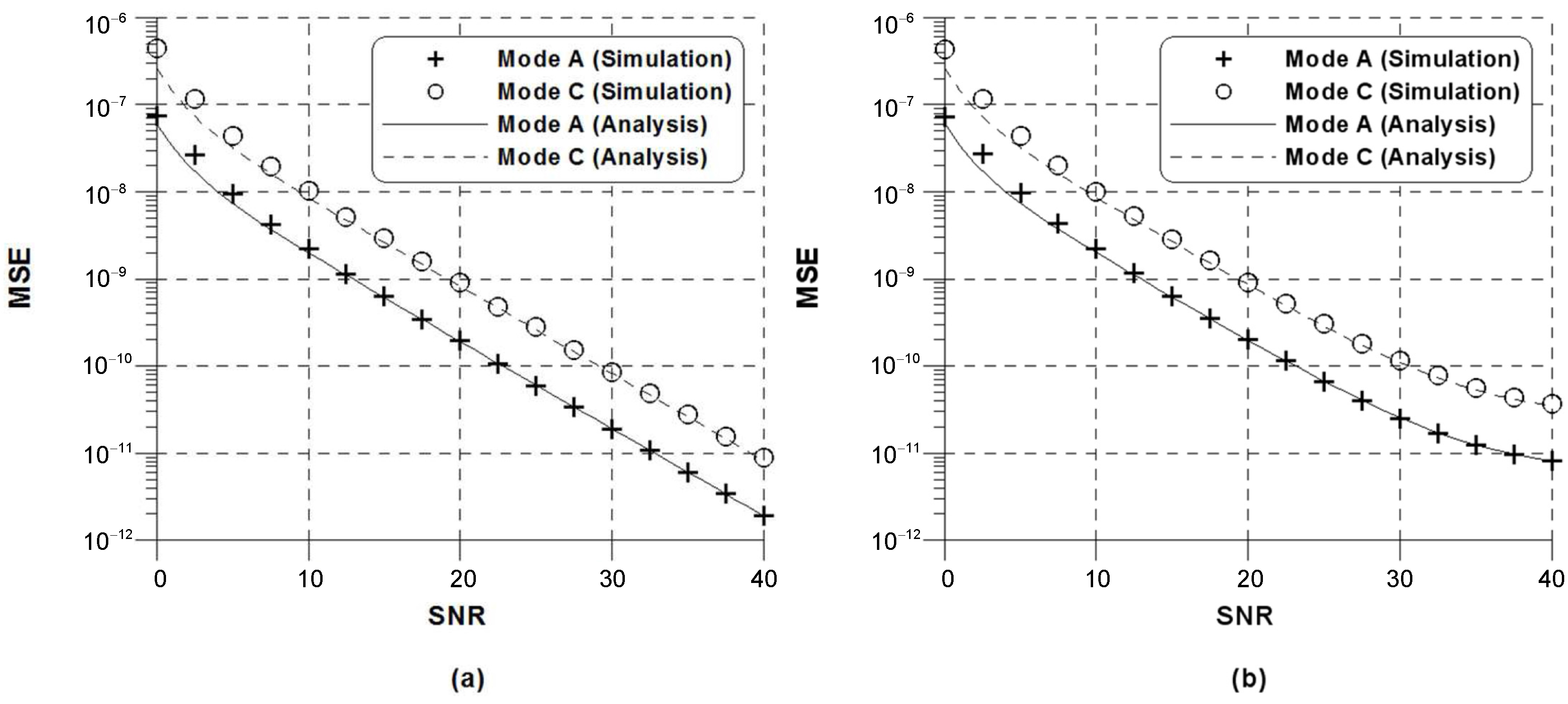
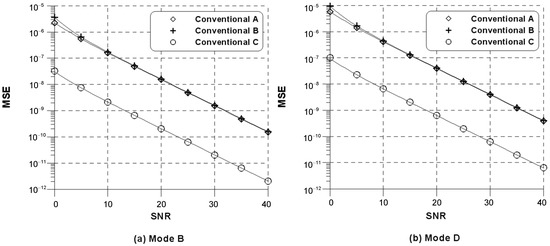
The MSE of the conventional estimation schemes in DRM channel model 1 (CM1) is shown in Figure 1 according to DRM robustness modes. The CM1 corresponds to AWGN channel. In this example, DRM modes B and D are considered, ${\Delta }_f={10}^{-2}$, and ${\Delta }_s=50$ ppm. First of all, one can see that the analytical curves in (6), (10), and (15) are shown to be close to the simulated curves. Note that the estimation scheme (14) can be generalized only to uniformly distributed pilot tones in the frequency domain, whereas (7) is valid for a specifically designed pilot symbol in the DRM. On the other hand, the estimation scheme (4) has no restriction to pilots, thereby can be generalized to arbitrary pilot configurations as similarly done in [21].

Figure 1. Mean square error (MSE) of the conventional frequency estimators in channel model (CM)1: (1) lines-analysis; (2) symbols-simulation.

The MSE of the proposed estimator in CM1 is reported in Figure 2 for ${\Delta }_s=50$ ppm. It is evident that the analytic curves in (32) are parallel to the simulated curves in CM1. It can be observed that the MSE of the proposed estimator is unbiased for relatively small ${\Delta }_f$. With the increase in ${\Delta }_f$, however, this does not hold at high SNR conditions, because the ICI is no longer negligible. For typical values of ${\Delta }_s$ and ${\Delta }_f$, therefore, the ICI is negligible in comparison with the Gaussian noise under medium SNR conditions. It is also found that the DRM system is shown to contain sufficient information to perform synchronization. Interestingly, the different estimation performance can be observed according to the robustness mode-specific parameter as shown in Table 1. It is interesting to note that the proposed scheme (25) has no restriction to pilots similarly to (4).

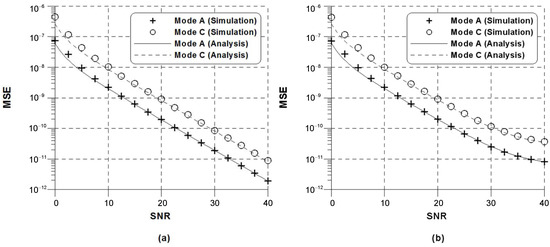
Figure 2. MSE of the proposed frequency estimator in CM1: (a) ${\Delta }_f={10}^{-2}$; (b) ${\Delta }_f=3\times {10}^{-2}$.

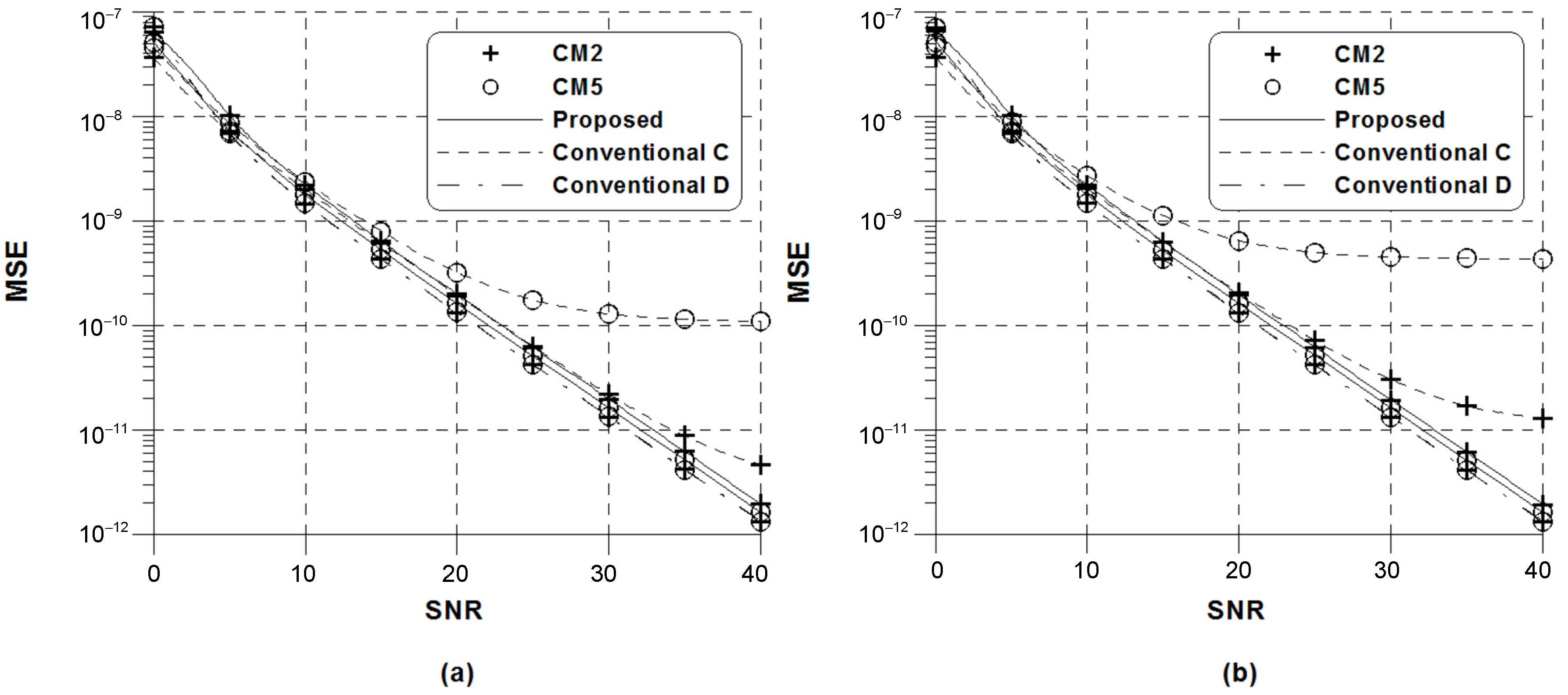
Figure 3 presents the comparison of MSE between the conventional scheme (14) and the proposed scheme when DRM mode A is used and ${\Delta }_f={10}^{-2}$. For the sake of fairness, $N_s=D_t+1$ is chosen for the conventional scheme (18), which uses the pilot symbols inserted into every OFDM symbol. In order to compute (19) and (20), a perfect knowledge of the CSI is assumed in the conventional scheme D. From the figure, it is observed that a slight performance degradation of the proposed scheme relative to the conventional scheme C in low SNR regions is observed, which is due to the SNR loss induced by the squaring of the complex conjugate operation in (22). As reported in [22,23], the conventional scheme C exhibits a non-negligible bias with an increase in SNR, which stems from the fact that its performance strongly is affected by the frequency selectivity of the channel and the value of SFO. Conversely, the performance of the proposed estimation scheme and the conventional scheme D is almost independent of the increased frequency selectivity and SFO. For a relatively small values of ${\Delta }_s$ and ${\Delta }_f$, therefore, we conclude that the proposed SFO estimation scheme and the conventional scheme D are shown to be unbiased in the presence of the frequency selectivity. Under the assumption of perfect CSI, the MSE of the conventional scheme D is better than that of the proposed method at the cost of computational burdens. It can be seen that the number of flops used in the proposed estimation scheme is decreased by approximately 96% when compared with that used in the conventional scheme D.

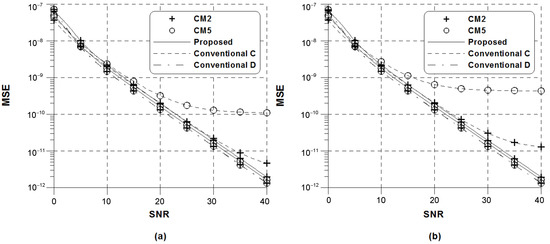
Figure 3. MSE of the conventional and proposed frequency estimators in DRM mode A: (a) ${\Delta }_s=50$ ppm; (b) ${\Delta }_s=100$ ppm.

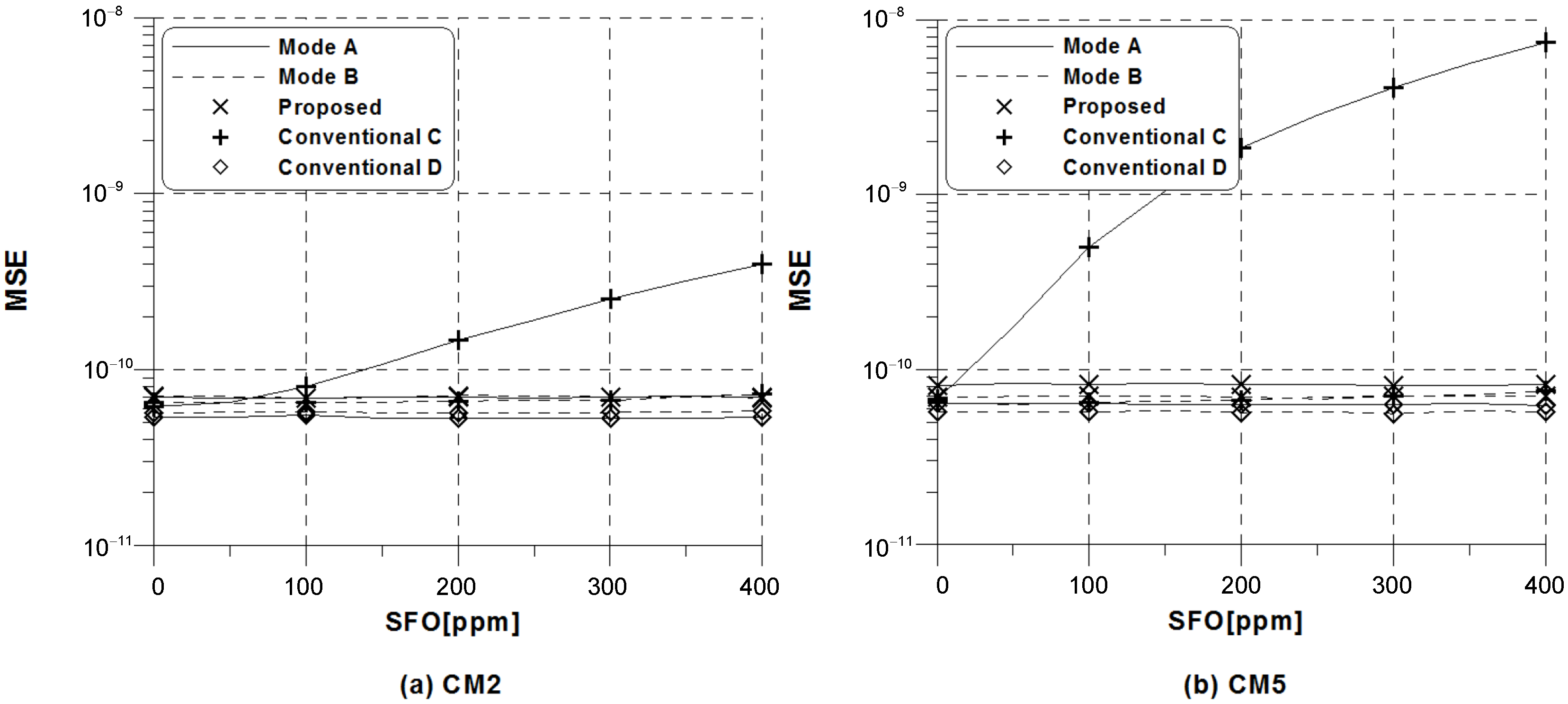
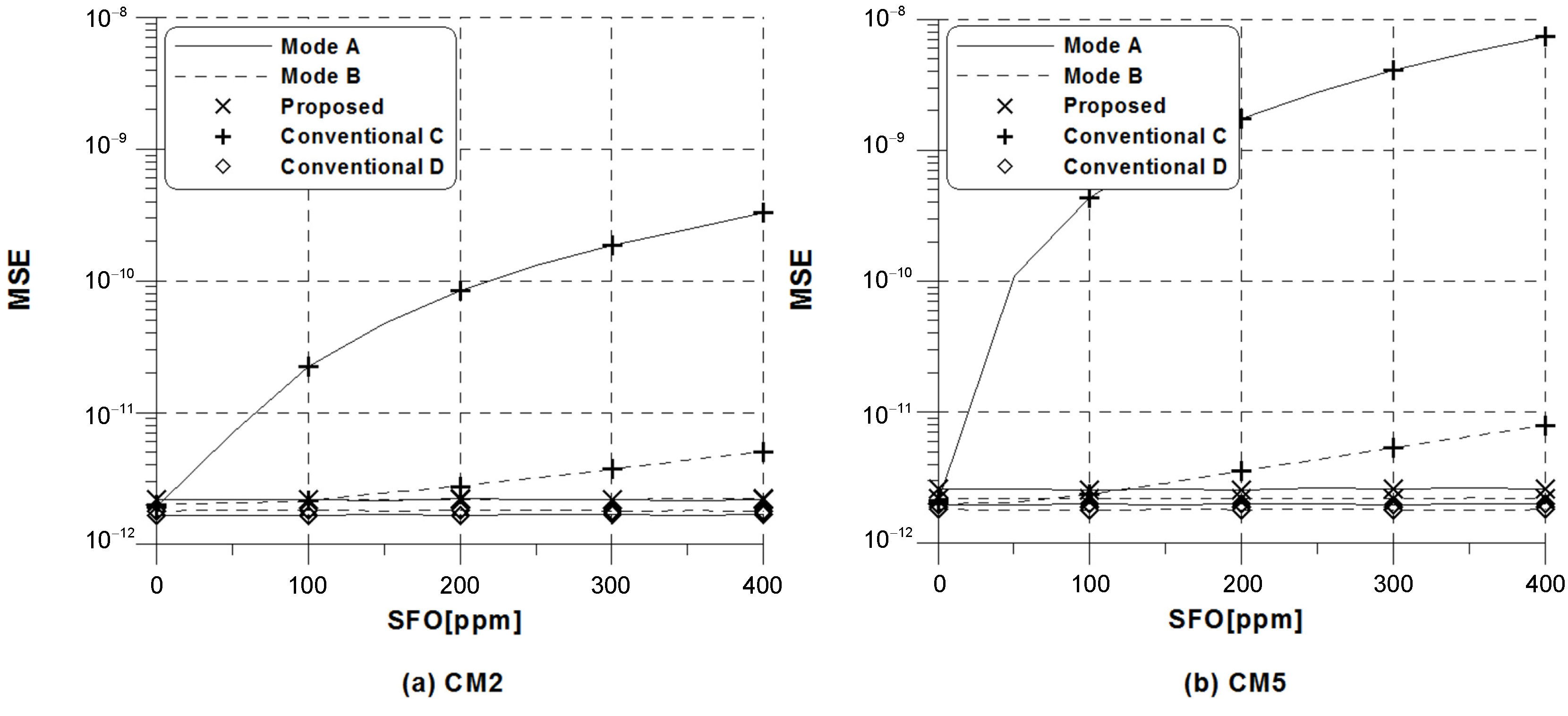
In Figure 4 and Figure 5, we compare MSE performance of the proposed scheme with the conventional schemes (14) and (18) under the same conditions as in Figure 3 when $SNR=25$ dB and $SNR=40$ dB, respectively. It is observed that the MSE of the conventional method C heavily depends on the amount of SFO, whereas the proposed scheme and the conventional scheme D exhibit a remarkable robustness against the SFO. Notably, we find that the amount of dependence on SFO in the conventional scheme C is different according to the DRM modes, which is inversely proportional to the ratio $N_g/N$. This primarily comes from the fact that the conventional estimation scheme C experiences substantially less frequency selectivity as the ratio $N_g/N$ grows. Since SFO estimation is the focus here, the mobile speed is not taken into account. The DRM standard provides four different modes to cope with various transmission channel like delay spread and Doppler spread. In the case of analyzing the robustness of DRM modes against Doppler spread, the effect of mobile speed should be considered. As discussed in Figure 3, the MSE of the proposed scheme is slightly worse than that of the conventional scheme D, because the proposed scheme uses only two pilot symbols based on $D_t$-symbol delay estimation. If the estimated CSI is used in the conventional scheme D, the performance degradation at low SNR regions can be observed due to channel estimation error, while the performance gap between the ideal and estimated cases is expected to be negligible with the increase in SNR. As for the conventional estimation scheme C and the proposed estimation scheme, they do not require any CSI.

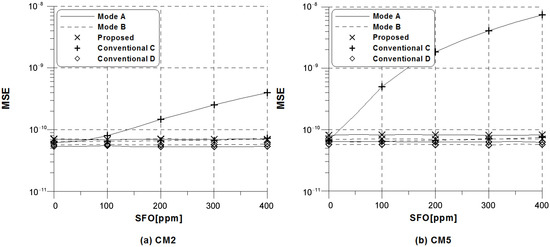
Figure 4. MSE of the conventional and proposed frequency estimators versus sampling frequency offset (SFO) for DRM modes A and B when signal-to-noise ratio (SNR) = 25 dB.

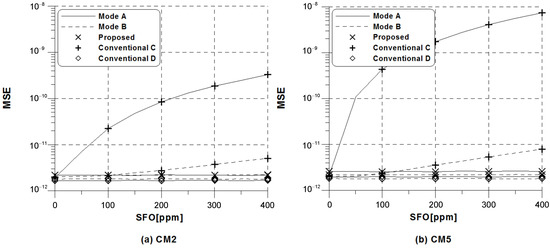
Figure 5. MSE of the conventional and proposed frequency estimators versus SFO for DRM modes A and B when SNR = 40 dB.

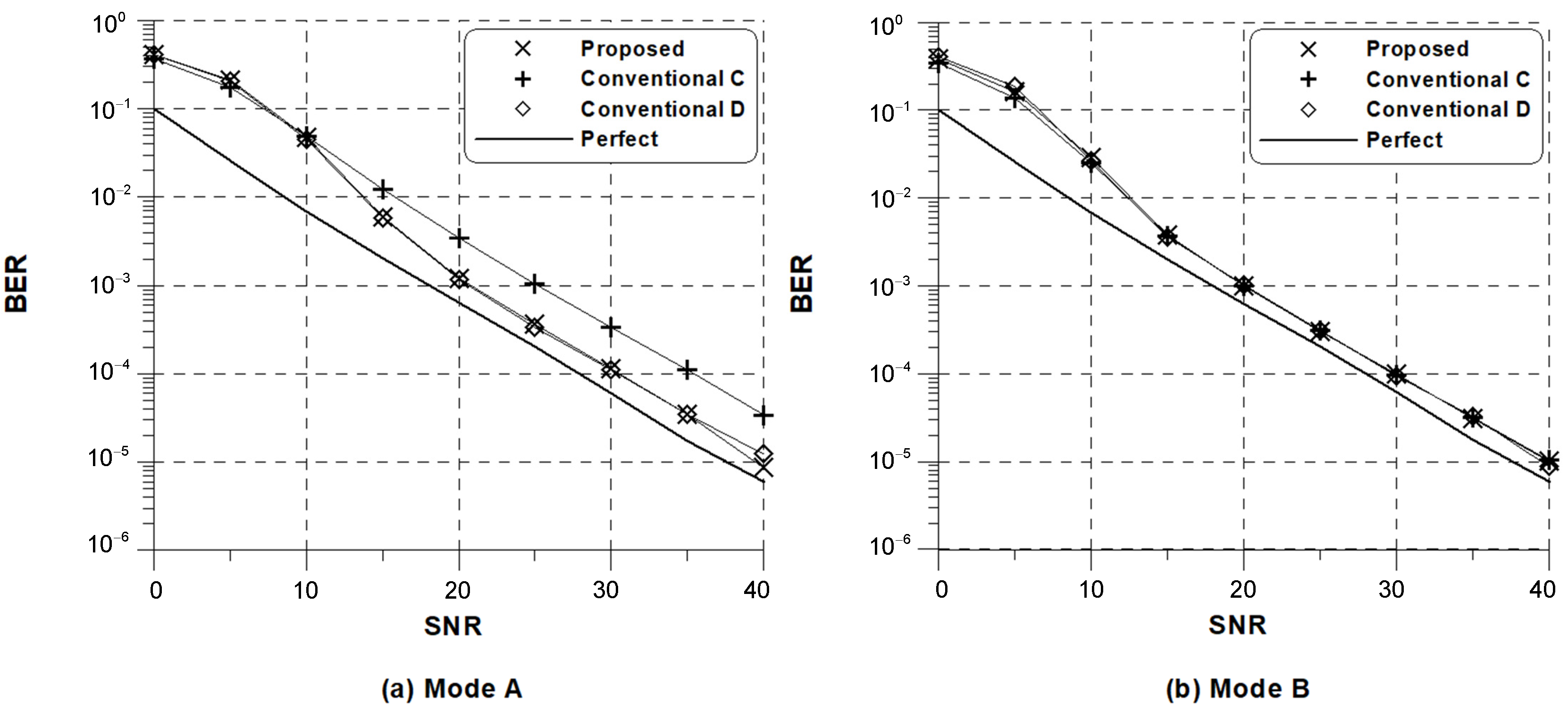
Figure 6 depicts the uncoded bit error rate (BER) obtained with the adoption of the conventional and proposed estimators followed by a one-tap frequency domain equalizer with perfect knowledge of CSI when ${\Delta }_f={10}^{-2}$, ${\Delta }_s=200$ ppm, and CM5 is used. As a benchmark, the performance is compared with that of the perfectly synchronized DRM system. Here, the received OFDM symbols are directly compensated soon after SFO is estimated every $D_t+1$ symbol periods. One can observe a substantial performance gap between the BER with perfect synchronization and the BER with estimated SFO for all estimation schemes especially at low SNR values. As reported in Figure 3, a slight performance degradation of the proposed scheme at low SNR is also inherent in the case of BER. On the other hand, the fact that no irreducible floor is visible indicates that the proposed estimation scheme is capable of effectively mitigating the ICI induced by frequency errors with a reduced computational complexity.

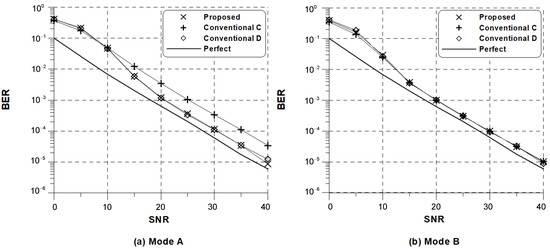
Figure 6. Bit error rate (BER) performance of the conventional and proposed frequency estimators in CM5.

6. Conclusions

In this paper, the problem of SFO estimation for the DRM system has been discussed, aiming at improving the robustness of SFO estimation in the presence of the frequency selective fading and designing its simple receiver structure. For verification of the SFO estimation schemes, the MSE expression of the conventional and proposed schemes was theoretically derived. We have demonstrated that the MSE analysis is fairly accurate, and the proposed estimation algorithm is shown to be not only robust but also unbiased in the presence of frequency selectivity of the channel.