Smart Control System to Optimize Time of Use in a Solar-Assisted Air-Conditioning by Ejector for Residential Sector

Abstract

The present work provides a series of theoretical improvements of a control strategy in order to optimize the time of use of solar air-conditioning by an ejector distributed in multiple solar collectors of vacuum tubes for the residential sector, which will allow us to reduce carbon-dioxide emissions, costs and electrical energy consumption. In a solar ejector cooling system, the instability of the solar source of energy causes an operational conflict between the solar thermal system and ejector cooling cycle. A fuzzy control structure for the supervisory ejector cycle and multi-collector control system is developed: the first control is applied to control the mass flow of the generator and the evaporator for different cooling capacities (3, 3.5, 4, 4.5 and 5 kW) and set a temperature reference according to the operating conditions; the second is applied to keep a constant temperature power source that feeds the low-grade ejector cooling cycle using R134aas refrigerant. For the present work, the temperature of the generator oscillates between 65 °C and 90 °C, a condenser temperature of 30 °C and an evaporator temperature of 10 °C. For the purpose of optimization, there are different levels of performance for time of use: the Mode 0 (economic) gives a performance of 17.55 h, Mode 5 (maximum cooling power) 14.86 h and variable mode (variable mode of capacities) 16.25 h, on average. Simulations are done in MATLAB-Simulink applying fuzzy logic for a mathematical model of the thermal balance. They are compared with two different types of solar radiation: real radiation and disturbed radiation.

1. Introduction

Mechanical vapor compression consumes exorbitant amounts of high-grade energy [1,2]. The high consumption of nonrenewable energy from fossil fuels, such as gas and oil, is a part of the remarkable deterioration of the planet, resulting in an increased temperature and higher rates of carbon-dioxide emissions (CO₂) [3,4,5]. Refrigeration and air-conditioning in buildings are among the reported highest consumers of energy, accounting for approximately 17% of the world’s electricity consumption [6,7,8]. In order to reduce electricity consumption of air-conditioning, a solution would be the use of solar energy [9,10]. In Mexico, more than 70% of the territory has Global Horizontal Irradiation (GHI) values greater than 4.5 kWh/m². By taking advantage of this resource, interior comfort conditions will be enhanced with the use of solar-air-conditioning [9].

Solar thermally-driven heating systems work by thermal applications to absorb solar energy [11,12,13]. Solar collectors are used in this process to achieve a cooling task; however, usually, an auxiliary heater is needed to provide the required energy. The efficiency of a solar refrigeration system depends on the collector type, solar radiation intensity and the system operating conditions. When refrigeration systems operate at temperatures between 80 °C and 100 °C, a single glazed flat plate-type collector with a selective surface is recommended [14]. The vacuum tube [15] and parabolic solar concentrating collector [16] can provide higher thermal efficiencies at higher operating temperatures.

The cooling cycles operate by means of absorption, adsorption, Rankine, solar desiccant cooling cycles [17,18,19,20] and the ejector refrigeration system [21]. Desiccant cooling systems are used as isolated or as hybrid systems [22]. Absorption solar refrigeration systems commonly use ammonia-water as working fluids, which require high temperatures in the generator, provided by parabolic cylindrical collectors. Its use is mainly in refrigeration for food preservation and very little for air-conditioning systems. It is confirmed that absorption refrigeration systems that employ vacuum tube solar collectors are more efficient than those that use flat solar collectors [23]. The absorption refrigeration system uses a process of chemical absorption; therefore, its design is complicated. In addition, the high installation cost delays its application in solar cooling systems [24].

Ejection cooling is a system in which the refrigeration effect is produced through a phase change and which is analyzed in this work. In the ejection systems, the compression that the refrigerating fluid must suffer to produce cooling does not take place in a compressor as in the absorption systems. The pressure of the fluid is increased by an exchange of kinetic energy in an ejector. This method of compression does not involve moving parts and therefore does not consume energy. However, the compressor of the ideal vapor-compression refrigerator cycle is a substitute for an ejector and a pump (at least one). Ejector cooling is one of the most promising technologies because of its relative simplicity and low capital cost when compared with other heat-driven refrigeration systems such as vapor absorption [25]. The relatively low cost of the ejector in the air-conditioning system makes it possible to be used in the residential sector, and it can be used as an environmentally-friendly refrigerator operating with a low boiling point [24]. Cooling cycles per ejector are trithermic; the exchange heat comes from three different temperatures: evaporator, in which the heat is collected from the cold area; generator, which has the hottest temperatures from solar collectors; and condenser, which releases energy to the environment [26]. However, in solar ejector cooling systems, the instability of solar power and the thermal refrigeration cycle requires great complexity to operate and control the complete cycle. This work proposes a system of control integrated with an optimization system to improve this.

The main idea of the present work is to develop an intelligent control system for better use of multiple solar collectors of vacuum tubes for solar air-conditioning applications by an ejector. This system requires a constant temperature source of energy for the process, which should be independent of weather conditions and shade. This controller follows a temperature reference, which is fixed by another governor control, with the objective of optimizing the use of time, taking into account the operation of the ejector-based refrigeration cycle, which will take advantage of the physical resources and will minimize the costs of operation and maintenance. These systems are difficult to control due to certain factors such as the nonlinear solar thermal characteristic and perturbations, in which the system is subjected to energy and the changes that arise in the dynamics of the process over time and optimal operating conditions of the refrigeration cycle. The results obtained contribute to those achieved by the classical control methods. We develop an intelligent control system based on fuzzy logic, for the synthesis of a nonlinear dynamic system model integrated with the operation of a refrigeration cycle. This research is the basis for future studies; however, the efficiency of the ejector cooling system should be further improved to compete with the absorption system [24].

The outline of this paper is as follows. Section 2 presents an overview of related works, such as other performance and comparative studies. In Section 3, a description of a solar air-conditioning system, with different constituent elements, is presented. Section 4 discusses and analyzes a fuzzy control structure to operate and control the complete refrigeration cycle. In Section 5, a performance analysis to optimize the refrigeration cycle is presented; at the same time, the validation results and discussions of the simulation are carried out. Section 6 concludes this study.

2. Related Works

In this paper, we address various aspects to optimize the time of use for an ejector cooling cycle using an intelligent control, which includes aspects such as control of multiple vacuum tube solar collectors, thermal cooling cycle analysis, control of temperature energy source, in spite of unknown dynamics and perturbations, and selection of functioning modes by end users with the same controller. To meet these requirements, the main focus is the optimization of an intelligent control system for a better time of use in a solar-assisted air-conditioning by an ejector. In this section, we provide a discussion of the related literature.

A control strategy to improve the partial load performance of the solar air-conditioning system was applied by [27,28]; due to the nocturnal unavailability of solar energy, studies have been carried out to improve the performance of solar air-conditioning by means of thermal storage. Advanced automation and control for buildings are possible in order to lower the consumption of energy, where improved control strategies of building systems have shown a decrease of overall energy consumption [29]. In [30], the authors present a method of designing a nonlinear predictive controller based on the Takagi–Sugeno fuzzy model, using the internal model control scheme to compensate for disturbances and modeling errors; the algorithm is applied to temperature control in an air-conditioning system. Hot water at 65 °C is supplied to the coil, which exchanges the heat between the hot water and the surrounding air. A model-based predictive control of a solar thermal system consisting of a flat plate solar collector and heat exchanger was described in [29].

The aim is to control the temperature at the outputs of the heat exchanger in the solar circuit, as well as the storage circuit using a model-based predictive control, where the desired set-points for the temperature should be achieved predictively consuming the minimum energy, whereas variations such as solar radiation, ambient temperature, etc., should be rejected. The vector $u\left(K\right)$ contains the mass flow rates used as the control variables for temperature control. The optimization routine was implemented using the MATLAB optimization toolbox. The model predictive controller shows a behavior with a much lower demand on control energy compared with the PI controller and good performance with regards to disturbance rejections. According to [31], a predictive control for solar absorption cooling systems has the objective of optimizing the use of the solar energy, in order to ensure the cooling requirement of the building; a relaxation technique also is proposed to solve the nonlinear hybrid problem. The aim is to optimize the energy consumption, comfort and lifetime of the system by better interactions, in order to define the temperature profile in the building and the hot water consumption flow rate.

In [32], a sliding mode predictive control is presented in a way that is combined with model-based predictive control; mixing both control techniques results in a new predictive control with better robustness properties, producing disturbances by changes in solar irradiation and the solar collector’s inlet temperature. It consists of a solar field that produces hot water with an absorption machine, achieving a cooling power of 35 kW. Its output temperature can be controlled by adjusting the water flow inside the solar field by manipulating the B1 pump speed. Pursuant to [33], the employment of a model-based predictive control algorithm for the energy-efficient temperature control of a solar-thermal system consists of a solar collector and heat exchanger; the model predictive control strategy showed good performance with regards to disturbance rejections.

In [34], a supervisory control is implemented in a solar air-conditioning plant, where the control goal was to match the cooling demand and, at the same time, minimize the gas heater contribution to the absorption chiller heat input, thus showing the importance of the system models for the robustness of this control. According to [35], a modeling and control strategy for a novel HVAC system is presented in a way that considers temperature, humidity ratio and CO₂ concentration; the HVAC system is Multi-Input Multi-Output (MIMO); thus, a dynamic extension algorithm can be employed, and a feedback linearization technique is applied. A Linear-Quadratic Regulator (LQR) is designed to optimize control performance and to stabilize the proposed HVAC system.

All of these works propose control solutions with additional systems that supply energy, mainly with an auxiliary generator. On the other hand, the technique based on ejector cooling is not generally considered; in this work, we have presented the advantages of using the ejector for use in air-conditioning systems in residential areas. In this paper, we propose a control model, which according to different parameters such as operation modes set by end users, solar radiation disturbances and optimal conditions of operation of the ejector cooling cycle, sets the reference temperature of storage tank and references in the mass flows of operation for the generator and evaporator, thus optimizing the time of use of air-conditioning operated by the ejector without the need of energy supply by an alternate source.

Recent studies on the temperature required for the ejection cooling cycle are mentioned in this work. In [36], the authors report a maximum cooling capacity and COP using a generator temperature of 90 °C and 92.8 °C. According to [37], an experimental investigation on ejector cooling at low temperature is realized by obtaining a COP of 0.42 at a generator temperature of 74 °C, evaporator temperature of 10 °C and a critical condenser temperature of 29 °C. A cooling capacity of 1080 W was obtained for an area of 9.2 m² of single-glazed selective-type collectors in a horizontal position. In [38], the ejector performance using R141brefrigerant with thermal storage for solar air-conditioning is presented. A COP average of 0.265 is given for an area of 10 m² of an evacuated solar collector at a generator temperature of 84 °C, condenser temperature of 28 °C and evaporator temperature of 8 °C for a cooling capacity of 3.5 kW.

According to [24], a solar ejector cooling system is developed using R141b refrigerant; a COP of 0.5 is obtained experimentally for a single-stage ejector cooling system at a $T_g$ of 90 °C, $T_c$ of 28 °C and $T_e$ of 8 °C, covering a cooling capacity of 10.5 kW for a solar flat-plate collector area of 68 m². As presented in [39], an acceptable coefficient of performance is one for which generator temperatures should not fall below 90 °C, evaporator temperatures below 10 °C and condenser temperatures be over 35 °C; the COP was 0.13 for an evacuated tube area of 50 m², which can provide a cooling capacity of 3.5 kW; $T_e$ below 10 °C resulted in poor system performance. In [40], an ejector cooling system using water as a working fluid is not suitable for low evaporator temperatures; the COP ejector decreases rapidly as the $T_c$ increases. The results indicated that both COP and system efficiency increased with generator temperature. According to [41], R141b is used as a working fluid to verify the theoretical results.

As for thermal analysis in the previous works, the biggest difference with our work is to maintain a low operating range in the generator temperature, which oscillates between 65 °C and 90 °C; the condenser temperature is 30 °C, and the evaporator temperature is 10 °C.

3. Description of the Solar Air-Conditioning Plant

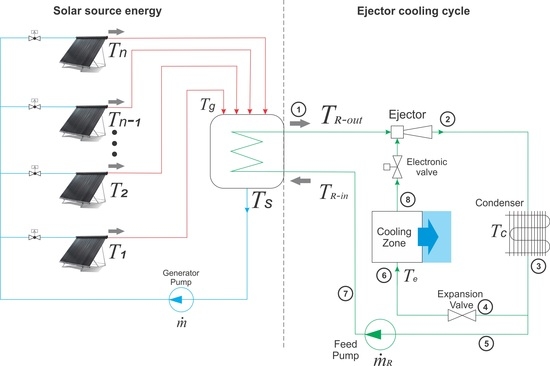
The solar air-conditioning system consists of two parts, the energy source and the ejector cooling cycle, and the structure of the solar thermal system is shown in Figure 1 with its respective controlled variables. In the first, a mathematical model is presented to describe the solar thermal system of vacuum tubes; the interest is to build a mathematical model that is able to scale and integrate with the refrigeration cycle and additionally contribute with rapid prototyping to optimize the time of use of the air-conditioning, thus integrating all aspects related to the intelligent control system. The second consists of the cooling cycle, in which a series of theoretical analyses was carried out to verify at which points of the generator temperature the ejector can operate; according to the different cooling capacities in which it operates, it will have a respective amount of mass flow $\dot{m}$.

The dynamic system of the solar source energy is represented by the variable to be controlled, which is the mass flow $\dot{m}$ in each solar collector; this will provide the constant energy source. The present model allows us to study the effect that the manipulated variable of closed-loop control $\dot{m}$ and the perturbations (solar radiation) have on the variable of interest $T_g$. The fuzzy controller aims to control the input temperature to the generator $T_g$ to be constant, where $T_1,T_2,\dots T_n$ are the temperatures of each solar collector. The analysis applies to four solar collectors with 30 vacuum tubes for each one, a tank dimensioned to a capacity of 180 liters, an evaporator temperature of 10 °C and a condenser temperature of 30 °C. However, this model can be variable, depending on the required cooling capacities.

The ejector cooling cycle operates using low-grade thermal energy produced in the heat exchanger, as mentioned earlier in the solar energy source section. The cycle function is such that the portion of the expenditure being driven through the generator undergoes a direct thermodynamic cycle, which allows the rest of the mass flow of the refrigerant to complete the inverse thermodynamic cycle of a refrigeration machine. Pressurization starts from the conversion of kinetic energy into enthalpy by means of a diffuser; thus, it is necessary to induce kinetic energy to the refrigerant flow, which is a process that takes advantage of the Venturi effect provided by an ejector (nozzle-inductor-diffuser set) [26]. The main disadvantages of this system are its low Coefficient Of Performance (COP), which varies in the range of (0.1–0.4), and its operation must be around critical points; otherwise, its COP deteriorates rapidly [42]. The present research does not model the thermal performance of the ejector cooling cycle; instead of that characteristic temperature, flow rates and COP of the ejector cycle obtained from different authors are used (values are shown in

Table 1. Low operating temperatures of an ejector.

${\mathit{T}}_{\mathit{g}}$ (°C)	${\mathit{T}}_{\mathit{c}}$ (°C)	${\mathit{T}}_{\mathit{e}}$ (°C)	kW	Working Fluid	COP	Reference
50–60	26.5–38.5	8–16	1.8–3	R134a	0.3–0.48	[43]
65–85	25–40	6–10	-	R134a	0.355	[44]
60–85	25	−5–5	-	R717	0.06–0.34	[45]
40–70	15–40	10–15	0.5–1.1	water	0.1–1.2	[46]
65–90	26–38	2–13	0.5	R134a	0.09–0.16	[47]

).

A COP of 0.48 will be used in this work according to experimental studies of the refrigeration cycle by ejector with R134a refrigerant [43]. R134a gives better performance and a higher critical entrainment ratio in comparison with other refrigerants, which will be used for the present research [48]. The present investigation is carried out to cool approximately an area of 20–25 m² in different cooling capacities. The properties of the refrigeration cycle are listed according to Figure 1.

Table 2. Cooling cycle properties.

Number	Temperature(°C)	Enthalpy (kJ/kg)	Pressure (MPa)	Phase Status
1	65	279.64	1.891	Saturated vapor
3, 4, 5	30	93.58	0.77064	Saturated liquid
6	10	h6 = h4 = h3	0.41489	Liquid-vapor
7	30.7	94.5235	p7 = p1	Subcooled liquid
8	10	256.16	p8 = p6	Saturated liquid

shows the temperatures at each point of the operation of the refrigeration cycle, with its respective pressure, enthalpy and phase state. The data were obtained from thermodynamic tables of the R134a refrigerant [49].

4. Fuzzy Control Structure for Supervisory Ejector Cycle and Multi-Solar Collector Systems

Solar air-conditioning systems require optimal operating conditions to secure the highly demanding indoor temperature. This section describes the implemented fuzzy control. The nonlinearities, imprecisions, variations, more than one control and the manipulated variables presented in this plant make the controller design a nontrivial task.

Fuzzy logic has the ability to transform vague information and expert knowledge into numerical computable data, thus allowing control of plants with the aforementioned characteristics. In this section, we describe the implemented fuzzy control. The control structure is represented in two layers, as shown in Figure 2. Layer 1 is the fuzzy control of the solar collector system; the aim of Layer 1 is to control the temperature at the outputs of the heat exchanger in the solar circuit, as well as storage circuit using model-based fuzzy logic control. Layer 2 is the supervisory fuzzy control of the ejector cooling cycle, which according to different parameters such as operation modes, solar radiation disturbances and optimal conditions of operation of the ejector cooling cycle, sets the reference temperature of storage tank and the references in the mass flows of operation for the generator and evaporator. The supervisory or governor controller uses Servo-Pumps (SP) and Servo-Electronic-Valves (SEEV) as actuators for the evaporator and generator flow.

4.1. Layer 1: Fuzzy Control of Solar Collector System

Two sets of sensor inputs are presented in Figure 3: temperature sensor of the solar collectors $T_c$ and temperature sensor of tank $T_s$. A controller output is distributed to regulate the mass flow $\dot{m}$ to the manifolds. The control problem in a tank with an energy supply from the solar collectors is to keep the outlet temperature near a desired set-point. This reference is set by operating conditions imposed by supervisory control, which are fixed by the different modes of operation defined by the operator or end user and the climatic conditions of the moment. Moreover, the plant is a nonlinear solar thermal system exposed to disturbances, such as inlet temperature changes, variations in ambient temperature and changes in solar radiation. All these characteristics make it difficult to control and maintain the performance and reliability of nonlinear solar thermal plants.

For the controller design, a mathematical model is created by performing an energy balance in each solar collector and in the generator. Equation (1) shows the output temperature $T_S$ of the generator with regard to time [50]. This dynamic equation is maintained as a function of the working fluid mass flow $\dot{m}$ of each solar collector, considering constant properties as the density ${\rho }_f$ = 998.2 kg/m³, specific heat $C_{pf}$ = 4182 j/kg K and the tank volume ${\forall }_T$ = 0.180 m³. This equation also considers the energy requirements of the refrigeration cycle, $T_{R_{out}}$, which use R134a as the refrigerant fluid with a mass flow of ${\dot{m}}_R$ = 0.0567 kg/s and specific heat of $C_{PR}$ = 1443 j/kg K:

$$\begin{array}{c}\frac{d{T}_s}{dt}={\displaystyle \frac{{\dot{m}}_1{T}_1+{\dot{m}}_2{T}_2\dots {\dot{m}}_n{T}_n}{P_f{\forall }_T}}-{\displaystyle \frac{\left({\dot{m}}_1+{\dot{m}}_2\dots {\dot{m}}_n\right)T_S}{P_f{\forall }_T}}-{\displaystyle \frac{{\dot{m}}_R{C}_{PR}}{P_f{\forall }_T{C}_{pf}}}\left(T_{R_{out}}-T_{R_{in}}\right).\end{array}$$

(1)

To provide the thermal energy to the generator, an arrangement of vacuum tube solar collectors is required. These collectors consist of a heat pipe inside a vacuum-sealed tube and have shown that the combination of a selective surface and an effective convection suppressor can lead to good performance at high temperatures. The vacuum envelope reduces convection and conduction losses, so that the collectors can run at higher temperatures than the flat plate [51].

For the analysis, the solar collectors are divided into two thermal systems: the vacuum tubes and the storage tank. Equation (2) expresses the energy balance of the storage tank, taking into account that the tank walls are adiabatic, where $T_S$ represents the output temperature of the generator, $T_T$ is the output temperature of the tank, $T_a$ is the temperature of the vacuum tubes, N is the total number of vacuum tubes in each solar collector, (${\dot{m}}_{conv}$) is the natural convection mass flow rate and $M_t$ = 292.6345 kg, which is the mass of water in the tank:

$$\begin{array}{c}\frac{d{T}_T}{dt}=\left[\left(\dot{m}\left(T_S-T_T\right)\right)+\left(N·{\dot{m}}_{conv}\left(T_a-T_T\right)\right)\right]\frac{1}{M_t}.\end{array}$$

(2)

The differential Equation (3) shows the energy balance of water inside the tubes, considering heat losses by radiation to the atmosphere. For simulation purposes, two types of solar radiation $G_t$ are compared: the first reaches 900 kW/m², which is obtained from real data in seconds of a solar radiation of a normal sunny day of the state of Colima (Pacific center zone of the Mexican Republic), and the second, which is considered as perturbation by its low solar radiation of 500 kW/m² and is realized by means of a sinusoidal equation, as represented in Equation (4):

$$\begin{array}{c}\frac{d{T}_a}{dt}=\left[\left(G\left(t\right)\left(\tau \alpha \right)A_{pint}\right)+\left({\dot{m}}_{conv}{C}_{pf}\left(T_T-T_a\right)\right)-\left(\sigma {\epsilon }_{gp}{A}_{pint}\left({T_a}^4-T_{sky}\right)\right)\right]\frac{1}{C_f},\end{array}$$

(3)

$$\begin{array}{c}{G}_t=\frac{500}{2}\times (sin(\Omega \times t)+abs(sin(\Omega \times t)))\end{array}$$

(4)

The input variables for the fuzzy controller are the error defined as the difference between the desired value of temperature in tank ($T_{ref}$) and the actual value $T_s$, while $d{T}_s/dt$ act as the derivative of temperature $T_s$ and $T_c$ is the temperature in the solar collectors and allows one to know the behavior of solar radiation at all times.

The following six fuzzy sets, L (Large), M (Medium), H (High), NH (High Negative), Zero (Zero) and PH (High Positive), represented as triangular and trapezoidal functions of the membership degrees, are defined for each of the input variables. Output temperature in collectors, derivative temperature and temperature error in the tank are quantified according to the memberships in the fuzzy sets, as shown in Figure 4. Figure 4a shows the input for collector temperature and uses the following fuzzy sets: L (Large), M (Medium) and H (High). Figure 4b shows the input for derivative temperature in the storage tank, NH (High Negative), zero (Zero) and PH (High Positive), and Figure 4b is the input for storage tank temperature: NH (high negative), Z (Zero) and PH (High Positive). Finally, Figure 5 shows the output fuzzy set membership function for flow reference in each collector, using the following fuzzy set: Zero (Zero), P (Positive) and G (Good).

4.2. Layer 2: Supervisory Fuzzy Control of Ejector Cooling Cycle

Layer 2 is a supervisory controller, which will be controlled according to the different modes of operation implemented. This layer will be subject to the temperature variable of the solar collectors $T_{col}$, which will be a function of the disturbances of solar radiation G. Depending on $T_{col}$ and G, a reference in the generator mass flow ${\dot{m}}_g$ and the evaporator mass flow ${\dot{m}}_e$ are given. The temperature reference $T_{ref}$ Layer 2 is connected to Layer 1. A supervisory or governor controller uses Servo-Pumps (SP) and Servo-Electronic-Valves (SEEV) as actuators for the evaporator and generator flow. The operating modes are defined as an input to the system, according to the conditions of use that the operator or end user requires. The operating modes are defined continuously from 0–5. Mode 0 represents the highest energy consumption savings, and Mode 5 has the highest power consumption, but higher cooling power. The operator or end user according to his or her needs defines the mode of operation; however, the supervisory or optimization layer, based on additional operating conditions such as disturbances and climatic conditions, defines optimal references for a longer time of use of solar air-conditioning.

The supervisory controller treats a set of information to optimize the operating conditions of the complete cooling cycle. The temperature in solar collectors, temperature variation in solar collectors and temperature in tank storage and operation modes are the inputs to the multiple input and multiple output plant. Temperature and its variation in solar collectors give the solar energy currently available. The controller outputs are the reference temperature for the tank (reference for Layer 1), mass flow references for the servo-pump controlling the flow of the generator and the servo-valve controlling the flow of the evaporator, to make the ejector operate at a critical or noncritical double-choking condition obtain better performance or effective time of use of the air-conditioning system.

For the control simulations, the temperature conditions set $T_g$ was 10 °C higher than the coolant outlet temperature [24], $T_{R_{out}}$ = $T_g$ − 10 °C; the coolant inlet temperature $T_{R_{in}}$= 30.7 °C, the condenser temperature $T_c$ = 30 °C and the evaporator temperature $T_e$ = 10 °C. For the present investigation, the temperature range of the generator is defined as 55–90 °C, in relation to Table 1, to determine the operating points of the ejector.

Figure 6 shows the entrainment ratio with respect to the different temperatures of the generator, where, at 75 °C, the optimum operating point is located, according to our objective to optimize the air-conditioning use time; 65 °C is defined as the minimum temperature of the generator at which the ejector can operate, considering there is a loss of 10 °C. The behavior of the entrainment ratio at different condenser temperatures is presented in Figure 7; it can be appreciated that the condenser temperature must be maintained at 30 °C, due to the generator’s minimum temperature of 65 °C, which depends on an entrainment ratio of 0.54654, according to Figure 6.

Equation (5) determines the thermal load ($Q_R$) required for the cooling area. According to our objective, which is to optimize the use of the refrigeration cycle, different cooling capacities, e.g., 3.0, 3.5, 4.0, 4.5 and 5 kW, are maintained for our analysis. Equation (5) helps us to calculate the necessary energy and mass flow to operate the ejector refrigeration cycle for different cooling capacities:

$$Q_R={\dot{m}}_e(h_8-h_6).$$

(5)

For the development of the control strategy, it is necessary to calculate the mass flow rate of the evaporator and the generator for different powers. In relation to the analysis performed for the five cooling capacities, obtained according to Figure 8, the mass flow rates of the evaporator will remain constant in each cooling capacity, according to the temperature limit of the generator. For the generator mass flow, Figure 9 shows that the flow varies in each of the different cooling capacities.

To facilitate the control strategy, we proceed to calculate the average mass flow of the evaporator and the generator with the five cooling powers. Figure 10 and

Table 3. Average of ${\dot{m}}_e$ and ${\dot{m}}_g$ for different cooling powers.

Cooling Power (kW)	${\dot{\mathit{m}}}_{\mathit{e}}$ (kg/s)	${\dot{\mathit{m}}}_{\mathit{g}}$ (kg/s)
3	0.01845	0.03382
3.5	0.02153	0.03946
4	0.02460	0.04510
4.5	0.02768	0.05073
5	0.03075	0.05637

show the linkage of the mass flows.

The operation modes are determined by the end user. Mode 0 means economical use in energy; according to the analysis made in the previous section, the reference for the tank temperature control system should be low, and the outputs of references in flow generator and evaporator also should be moderately low, but within the limits that have been set for the ejector cooling cycle to work. In contrast, Mode 5 must set the reference temperature for the tank control to the maximum permissible by the previous analysis performed.

Figure 11 shows the input variables for the fuzzy governor controller; this variable is the actual value $T_c$, while $d{T}_c/dt$ act as the derivative of temperature $T_c$ in the solar collectors and allow one to know the behavior of solar radiation at all times. Finally, in Figure 12 are shown the governor outputs ${\dot{m}}_g$ and reference temperature for fuzzy control of the solar collector.

The following fifteen fuzzy sets: LL (Low Low), L (Low), M (Medium), H (High), HH (High High), NH (High Negative), NM (Medium Negative), Z (Zero), P (Positive), PH (High Positive), $M_1$ (Mode 1), $M_2$ (Mode 2), $M_3$ (Mode 3), $M_4$ (Mode 4) and $M_5$ (Mode 5), represented as triangular and trapezoidal functions of the membership degrees, are defined for each of the input variables; see Figure 11. Output fuzzy set membership function for generator mass flow and input temperature reference to fuzzy control of solar collector, respectively, use the following fuzzy sets: $M{g}_1$ (Generator Mass Flow 1), $M{g}_2$ (Generator Mass Flow 2), $M{g}_3$ (Generator Mass Flow 3), $M{g}_4$ (Generator Mass Flow 4), and $M{g}_5$ (Generator Mass Flow 5) and output temperature set reference for fuzzy control of solar collector: LL (Low Low), L (Low), M (Medium), H (High) and HH (High High); see Figure 12.

5. Evaluation, Results and Discussion

In this work, we are interested in the performance analysis of multiple control of driven-solar collector systems for a solar-ejector air-conditioning system. The main idea is to optimize the refrigeration cycle in a solar air-conditioning system, using a single controller, optimizing physical resources and minimizing operating and maintenance costs. One of the main reasons is to offer greater scalability, thus facilitating different operation points in an ejector-based refrigeration cycle, without the need for reconfiguring the system, while maintaining functional restrictions in the system.

The priority is to increase the times of use of a solar air-conditioning system, facilitating their implementation, maintenance and easy development. In this context, a control structure based on a system of supervision or a governor and a system of regulations based on fuzzy logic have been implemented. The simulation time considered for the performance analysis of the system is a day, taking into account that this time is enough to carry out a full solar air-conditioning system procedures. In subsequent analyses, the time (86,400 s) used for the simulation also allows us to appreciate the behavior of the control and the entire system as a whole against perturbations.

The simulations are performed for two types of solar radiation, the first with real solar radiation and the second with a low radiation of 500 kW/m². The first is executed with real solar radiation of a normal day of the state of Colima in seconds, which starts from 7:00 a.m. and ends around 5:30 p.m. (winter time), as shown in Figure 13a,b. To show the behavior of the implemented control system and the optimization of cooling time, three simulations with different modes of operation of the air-conditioner are analyzed; the first mode of operation called Mode 0 is the most economical; the second mode of operation called Mode 5 is the least economical, but has higher cooling power; and finally, a variable mode is realized, whose capacities of refrigeration vary according to the solar radiation.

5.1. Real Solar Radiation

The first test is for Mode 0, according to Figure 14a; the collector reaches a temperature higher than 110 °C, and the reference is kept constant at a low temperature of 68 °C, which allows us to have a greater use of cooling, but with low power. On the other hand, Mode 5 is shown in Figure 14b, reaching a collector temperature of 110 °C; due to the user’s needs for more cooling power, a higher reference temperature of 75 °C is required, which leads to decreasing the use time. For Modes 0 and 5, the cooling capacities are shown in Figure 15. For Mode 0, a capacity of 3 kW is needed, which remains in the lowest capacity because it is the most economical system. For Mode 5, its cooling capacity is 5 kW because it is the mode that requires more power. The mass flow of the generator and evaporator for Modes 0 and 5 are shown in

Table 4. Comparison of the economic mode and the maximum mode for a radiation of 900 kW/m².

Mode of Use	Power (kW)	Mass Flow ${\dot{\mathit{m}}}_{\mathit{g}}$ (kg/s)	Mass Flow ${\dot{\mathit{m}}}_{\mathit{e}}$ (kg/s)	Time (h)
Economic mode (Mode 0)	3	0.035	0.018	17.55
Maximum mode (Mode 5)	5	0.0548–0.0553	0.0299–0.0301	14.85

and Figure 16.

The last mode of operation, called variable mode, reaches a collector temperature of 112 °C, and the reference varies at three different temperatures: starting with 68 °C, after 5 h, it reaches 70 °C; passing 1.38 h, it reaches 75 °C; after 14 h, the reference temperature drops from 75–70 °C; after 2 h, the reference drops back from 70–68 °C. This is the behavior of variable mode, which is regulated according to the solar radiation, as shown in Figure 14c.

Figure 17a shows a simulation with different modes of operation varying in time, which is a situation dependent on the operator of the solar air-conditioning system. The variation of variable mode is shown in Figure 17a, where the modes operate from 0–5. The controller optimizes the time of use according to the climatic conditions and solar radiation. Different powers and mass flows are visualized in Figure 17c and

Table 5. Different modes of operation varying in time for radiation of 900 kW/m².

Time (h)	Mode	Power (kW)	Mass Flow ${\dot{\mathit{m}}}_{\mathit{g}}$ (kg/s)	Mass Flow ${\dot{\mathit{m}}}_{\mathit{e}}$ (kg/s)
0	0	3.075–3.11	0.0347–0.035	0.0189–0.0191
1.5	1	3.245–3.287	0.0365–0.037	0.0199–0.0202
1.8	2	4.2388	0.0478	0.0261
2.3	3	4.87–4.905	0.0549–0.0552	0.0299–0.0301
4.9	5	4.87–4.905	0.0549–0.0552	0.0299–0.0301
4.3	3	4.87–4.905	0.0549–0.0552	0.0299–0.0301
4.9	2	4.2388	0.0478	0.0261
5.8	1	3.245–3.287	0.0365–0.037	0.0199–0.0202
6.8	0	3.075–3.11	0.0347–0.035	0.0189–0.0191

.

The results obtained according to Figure 18 show a comparison of the three different modes of use with respect to the real solar radiation. In variable mode, a usage time of 16.25 h is obtained. Mode 0 (economical) will maintain a time of use of 17.55 h, but at the lowest cooling power of 3 kW. Finally, Mode 5 (greater power) is maintained at a time of use of 14.86 h with the maximum cooling power of 5 kW. This mode is the one that has the least time of use.

5.2. Disturbed Radiation

A series of simulations is performed to analyze different modes of operation with a solar radiation of 500 kW/ m² considered as low radiation, which starts from 7:00 a.m. and ends around 7:00 p.m., as shown in Figure 13b.

The first simulation test with a perturbed radiation is for Mode 0; according to Figure 19a, the collector reaches an approximate temperature of 85 °C, and the reference temperature ${Ts}_{\left(ref\right)}$ is kept constant at 68 °C. On the other hand, Mode 5, as shown in Figure 19b, reaches a collector temperature of over 80 °C with a reference temperature ${Ts}_{\left(ref\right)}$ of 75 °C required. The variable mode reaches a collector temperature of 85 °C, and the reference varies at two different temperatures, starting with 68 °C; after 7.5 h, it reaches 70 °C; passing 4.5 h, the reference temperature drops from 70–68 °C; during 8.7 h, it says constant until the day is over. This is the behavior of variable mode, as shown in Figure 19c.

For Modes 0 and 5, the cooling capacities are shown in Figure 20. For Mode 0, a capacity of 3 kW is needed. For Mode 5, its cooling capacity is 5 kw. The variable mode is shown in Figure 21; the modes operate from 0–2, as shown in Figure 21a. The power varies according to the solar radiation, as shown in Figure 21b.

The mass flow of the generator and evaporator for Modes 0 and 5 is shown in

Table 6. Comparison of the economic mode and the maximum mode for a radiation of 500 kW/m².

Mode of Use	Power (kW)	Mass Flow ${\dot{\mathit{m}}}_{\mathit{g}}$ (kg/s)	Mass Flow ${\dot{\mathit{m}}}_{\mathit{e}}$ (kg/s)	Time (h)
Economic mode (Mode 0)	3	0.035	0.018	11.93
Maximum mode (Mode 5)	5	0.0548–0.0553	0.0299–0.0301	9.5

and Figure 22. For variable mode, different powers and mass flows are visualized in

Table 7. Behavior of the variable mode for a radiation of 500 kW/m².

Time (h)	Mode	Power (kW)	Mass Flow ${\dot{\mathit{m}}}_{\mathit{g}}$ (kg/s)	Mass Flow ${\dot{\mathit{m}}}_{\mathit{e}}$ (kg/s)
0	0	3.075–3.108	0.0347–0.035	0.0189–0.0191
1.9	1	3.245–3.265	0.0365–0.037	0.0199–0.0202
2.7	2	4.2388	0.0478	0.0261
4.3	1	3.245–3.2655	0.0365–0.0368	0.0199–0.0201
5.4	0	3.075–3.108	0.0347–0.035	0.0189–0.0191

; Figure 21c shows the behavior of the evaporator and generator flow for variable mode, which is perceived to have the same behavior and operating times, but with different flows.

Finally, a comparison is made for the three modes of use with a solar radiation of 500 kW/m² according to Figure 23. In variable mode, it is obtained with a use time of 11.5 h. Mode 0 (economical) maintain a time of use of 11.93 h at the lowest cooling power of 3 kW. Mode 5 (greater power) is maintained with a use time of 9.5 h; with the maximum cooling power of 5 kW, the use time is the lowest compared with the two previous modes.

6. Conclusions

The analysis and design of a control system that optimizes the time of use in a solar-assisted air-conditioning system were accomplished in this work. The main objective is to optimize the refrigeration cycle by an ejector for a solar air-conditioning system, using a single controller, optimizing physical resources and minimizing operating and maintenance costs. The priority is to increase the time of use of a solar air-conditioning system, thus facilitating its implementation, maintenance and easy development.

A control structure based on two layers was designed. The first layer implements a temperature- control system of a storage tank, which follows a reference defined by a supervisory control layer. The second layer is supervisory control and optimization, which automatically generates a series of references for better performance of the air-conditioning. These references take into account solar-power supply conditions, user-defined modes of operation and disturbances of the system, thus optimizing the cost function based on the longest possible time of use. The advantage of this concept is being able to perform the optimization easily for a set of operation modes in the same refrigeration cycle controlled by the same controller, in spite of unknown dynamics and perturbations. Three simulations with different modes of operation are analyzed; the first mode of operation, called Mode 0, is the most economical; the second mode of operation, called Mode 5, is the least economical, but has higher cooling power; and lastly, variable mode is performed, in which cooling capacity depends on the selection of functioning modes by the end users.

The simulations show that a fuzzy governor control can be optimized to obtain better performance in terms of time of use of a solar thermal system for residential applications. The operating tests prove that a time of use of approximately 17.55 h can be obtained in an optimized mode of operation in power economy. However, without an optimized control system and at the same conditions of functionality, solar air-conditioning would only work approximately for 14.85 h, in the case of a single point of operation, for which it was designed. Fuzzy intelligent controls and optimization systems were compared for a typical operating day, with real and simulated solar radiation, showing that it is possible to improve the performance and reliability of nonlinear solar thermal systems in several ways:

• Greater scalability, facilitating different operation points in an ejector-based refrigeration cycle, without the need for reconfiguring the system.
• Increased usage time of a solar air-conditioning system, thus facilitating their implementation, maintenance and easy development.
• Different tests show that the intelligent optimization and control systems are self-adapting to the end user requirements, disturbances and climatic conditions.
• Less human supervision required.
• No need to use electrical installations for the operation and use of solar air-conditioning.
• Lower cost of implementation, maintenance and nonrenewable energy consumption.

Finally, the tests performed demonstrate that the designed control structure optimizes the time of use before different conditions, the selection of functioning modes by end users, disturbances and solar radiation.