Recent Progress on Aberration Compensation and Coherent Noise Suppression in Digital Holography
Abstract
:1. Introduction
2. Basic Principle of DHM
3. Tilt Phase Error Compensation
4. Phase Aberration Compensation
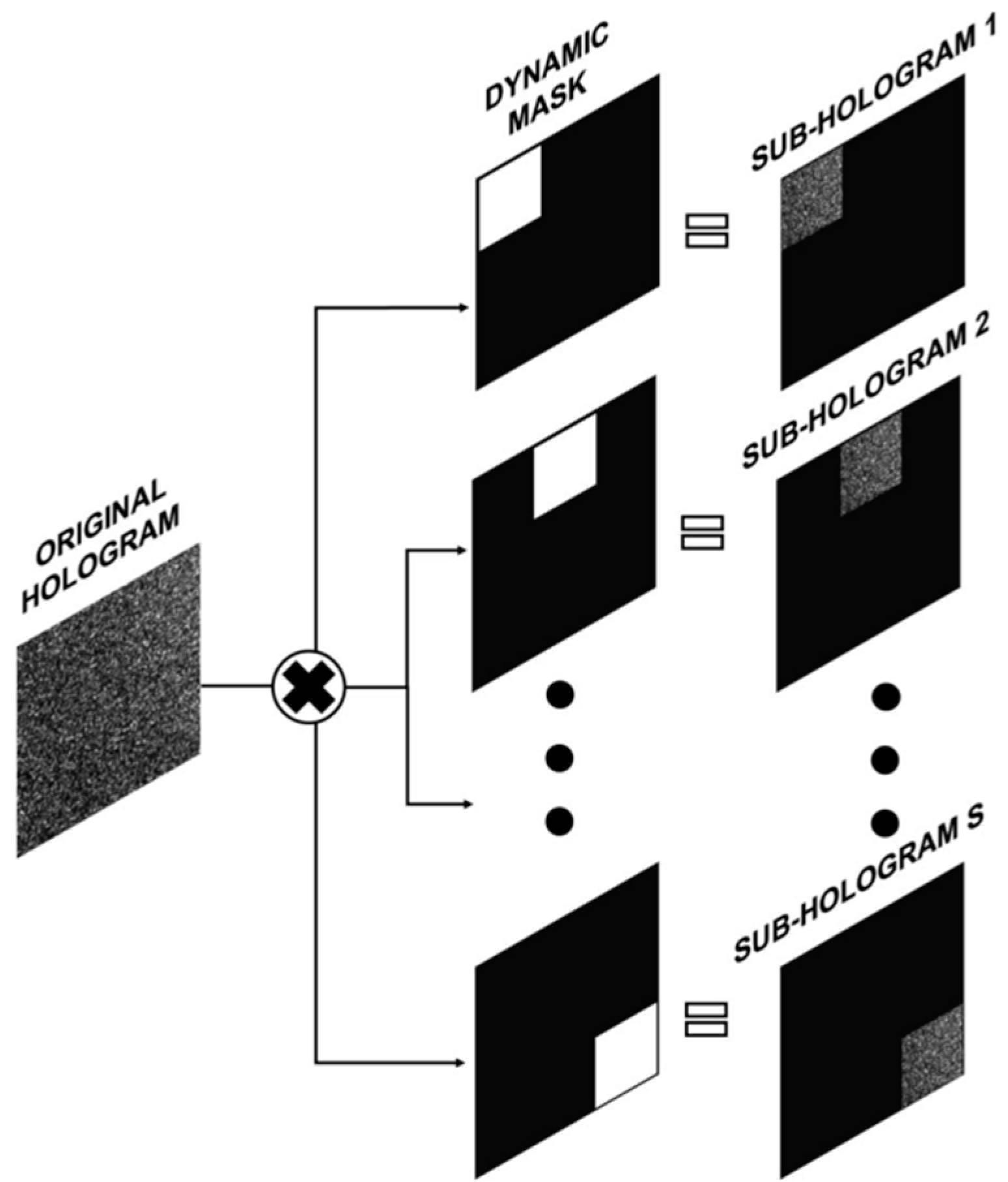
5. Coherent Noise Suppression
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yamaguchi, I.; Zhang, T. Phase-shifting digital holography. Opt. Lett. 1997, 22, 1268–1270. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Yamaguchi, I. Three-dimensional microscopy with phase-shifting digital holography. Opt. Lett. 1998, 23, 1221–1223. [Google Scholar] [CrossRef] [PubMed]
- Takaki, Y.; Kawai, H.; Ohzu, H. Hybrid holographic microscopy free of conjugate and zero-order images. Appl. Opt. 1999, 38, 4990–4996. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.K. Wavelength-scanning digital interference holography for optical section imaging. Opt. Lett. 1999, 24, 1693–1695. [Google Scholar] [CrossRef] [PubMed]
- Cuche, E.; Marquet, P.; Depeursinge, C. Simultaneous amplitude-contrast and quantitative phase-contrast microscopy by numerical reconstruction of Fresnel off-axis holograms. Appl. Opt. 1999, 38, 467–494. [Google Scholar] [CrossRef]
- Cuche, E.; Bevilacqua, F.; Depeursinge, C. Digital holography for quantitative phase-contrast imaging. Opt. Lett. 1999, 24, 291–293. [Google Scholar] [CrossRef] [PubMed]
- Schnars, U.; Jüptner, W.P.O. Digital recording and numerical reconstruction of holograms. Meas. Sci. Technol. 2002, 13, R85–R101. [Google Scholar] [CrossRef]
- Schnars, U.; Jüptner, W. Direct recording of holograms by a CCD target and numerical reconstruction. Appl. Opt. 1994, 33, 179–181. [Google Scholar] [CrossRef] [PubMed]
- Schnars, U.; Kreis, T.M.; Jueptner, W.P. Digital recording and numerical reconstruction of holograms: Reduction of the spatial frequency spectrum. Opt. Eng. 1996, 35, 977–982. [Google Scholar] [CrossRef]
- Yamaguchi, I.; Kato, J.-I.; Ohta, S.; Mizuno, J. Image formation in phase-shifting digital holography and applications to microscopy. Appl. Opt. 2001, 40, 6177–6186. [Google Scholar] [CrossRef] [PubMed]
- Nicola, S.D.; Finizio, A.; Pierattini, G.; Ferraro, P.; Alfieri, D. Angular spectrum method with correction of anamorphism for numerical reconstruction of digital holograms on tilted planes. Opt. Express 2005, 13, 9935–9940. [Google Scholar] [CrossRef] [PubMed]
- Weng, J.W.; Zhong, J.G.; Hu, C.Y. Digital reconstruction of fresnel hologram with a ridge of gabor wavelet transform. Acta Opt. Sin. 2009, 29, 2109–2114. [Google Scholar] [CrossRef]
- Smith, D.R.; Winters, D.G.; Schlup, P.; Bartels, R.A. Hilbert reconstruction of phase-shifted second-harmonic holographic images. Opt. Lett. 2012, 37, 2052–2054. [Google Scholar] [CrossRef] [PubMed]
- Chaab, O.; Bouamama, L.; Simoens, S. An adaptive anisotropic magnification algorithm of numerical reconstructed holographic image via a cascaded fresnel transform. Opt. Commun. 2013, 291, 61–69. [Google Scholar] [CrossRef]
- Kreis, T.M.; Jueptner, W.P.O. Suppression of the dc term in digital holography. Opt. Eng. 1997, 36, 2357–2360. [Google Scholar] [CrossRef]
- Cuche, E.; Marquet, P.; Depeursinge, C. Spatial filtering for zero-order and twin-image elimination in digital off-axis holography. Appl. Opt. 2000, 39, 4070–4075. [Google Scholar] [CrossRef] [PubMed]
- Pavillon, N.; Seelamantula, C.S.; Kühn, J.; Unser, M.; Depeursinge, C. Suppression of the zero-order term in off-axis digital holography through nonlinear filtering. Appl. Opt. 2009, 48, 186–195. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.-L.; Lin, C.-Y.; Kuo, M.-K.; Chang, C.-C. Numerical suppression of zero-order image in digital holography. Opt. Express 2007, 15, 8851–8856. [Google Scholar] [CrossRef] [PubMed]
- Weng, J.W.; Zhong, J.G.; Hu, C.Y. Automatic spatial filtering to obtain the virtual image term in digital holographic microscopy. Appl. Opt. 2010, 49, 189–195. [Google Scholar] [CrossRef] [PubMed]
- Pavillon, N.; Arfire, C.; Bergoënd, I.; Depeursinge, C. Iterative method for zero-order suppression in off-axis digital holography. Opt. Express 2010, 18, 15318–15331. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Deng, L.; Yang, Y.; Zhai, H.; Ge, Q. Numerical iterative approach for zero-order term elimination in off-axis digital holography. Opt. Express 2013, 21, 28314–28324. [Google Scholar] [CrossRef] [PubMed]
- Ferraro, P.; Nicola, S.D.; Finizio, A.; Coppola, G.; Grilli, S.; Magro, C.; Pierattini, G. Compensation of the inherent wave front curvature in digital holographic coherent microscopy for quantitative phase-contrast imaging. Appl. Opt. 2003, 42, 1938–1946. [Google Scholar] [CrossRef] [PubMed]
- Colomb, T.; Montfort, F.; Kühn, J.; Aspert, N.; Chche, E.; Marian, A.; Charrière, F.; Bourquin, S.; Marquet, P.; Depeursinge, C. Numerical parametric lens for shifting, magnification, and complete aberration compensation in digital holographic microscopy. J. Opt. Soc. Am. A 2006, 23, 3177–3190. [Google Scholar] [CrossRef]
- Di, J.L.; Zhao, J.L.; Sun, W.W.; Jiang, H.Z.; Yan, X.B. Phase aberration compensation of digital holographic microscopy based on least squares surface fitting. Opt. Commun. 2009, 282, 3873–3877. [Google Scholar] [CrossRef]
- Qu, W.J.; Choo, C.O.; Singh, V.R.; Yu, Y.J.; Asundi, A. Quasi-physical phase compensation in digital holographic microscopy. J. Opt. Soc. Am. A 2009, 26, 2005–2011. [Google Scholar] [CrossRef]
- Qu, W.J.; Choo, C.O.; Yu, Y.J.; Asundi, A. Microlens characterization by digital holographic microscopy with physical spherical phase compensation. Appl. Opt. 2010, 49, 6448–6454. [Google Scholar]
- Qu, W.J.; Choo, C.O.; Yu, Y.J.; Singh, V.R.; Asundi, A. Physical phase compensation in digital holographic microscopy. In Proceedings of the Fourth International Conference on Experimental Mechanics, Singapore, 18–20 November 2009; SPIE: Bellingham, WA, USA, 2010. [Google Scholar]
- Sánchez-Ortiga, E.; Ferraro, P.; Martínez-Corral, M.; Saavedra, G.; Doblas, A. Digital holographic microscopy with pure-optical spherical phase compensation. J. Opt. Soc. Am. A 2011, 28, 1410–1417. [Google Scholar] [CrossRef] [PubMed]
- Qu, W.J.; Choo, C.O.; Lewis, T.R. Physical spherical phase compensation in reflection digital holographic microscopy. Opt. Lasers Eng. 2012, 50, 563–567. [Google Scholar]
- Doblas, A.; Sánchez-Ortiga, E.; Martínez-Corral, M.; Saavedra, G.; Andrés, P.; Garcia-Sucerquia, J. Shift-variant digital holographic microscopy: Inaccuracies in quantitative phase imaging. Opt. Lett. 2013, 38, 1352–1354. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Sucerquia, J. Reduction of speckle noise in digital holography by using digital image processing. Optik 2005, 116, 44–48. [Google Scholar] [CrossRef]
- Guo, R.L.; Yao, B.L.; Gao, P.; Min, J.W.; Zhou, M.L.; Han, J.; Yu, X.; Yu, X.H.; Lei, M.; Yan, S.H.; et al. Off-axis digital holographic microscopy with LED illumination based on polarization filtering. Appl. Opt. 2013, 52, 8233–8238. [Google Scholar] [CrossRef] [PubMed]
- Nomura, T.; Okamura, M.; Nitanai, E.; Numata, T. Image quality improvement of digital holography by superposition of reconstructed images obtained by multiple wavelengths. Appl. Opt. 2008, 47, 38–43. [Google Scholar] [CrossRef]
- Park, Y.; Choi, W.; Yaqoob, Z.; Dasari, R.; Badizadegan, K.; Feld, M.S. Speckle-field digital holographic microscopy. Opt. Express 2009, 17, 12285–12292. [Google Scholar] [CrossRef] [PubMed]
- Rong, L.; Xiao, W.; Pan, F.; Liu, S.; Li, R. Speckle noise reduction in digital holography by use of multiple polarization holograms. Chin. Opt. Lett. 2010, 8, 653–655. [Google Scholar] [CrossRef]
- Abdelsalam, D.G.; Kim, D. Coherent noise suppression in digital holography based on flat fielding with apodized apertures. Opt. Express 2011, 19, 17951–17959. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Meng, P.; Wang, D.; Rong, L.; Panezai, S. Speckle noise suppression in digital holography by angular diversity with phase-only spatial light modulator. Opt. Express 2013, 21, 19568–19578. [Google Scholar] [CrossRef] [PubMed]
- Uzan, A.; Rivenson, Y.; Stern, A. Speckle denoising in digital holography by nonlocal means filtering. Appl. Opt. 2013, 52, 195–200. [Google Scholar] [CrossRef] [PubMed]
- Di, J.L.; Zhao, J.L.; Jiang, H.Z.; Zhang, P.; Fan, Q.; Sun, W.W. High resolution digital holographic microscopy with a wide field of view based on a synthetic aperture technique and use of linear CCD scanning. Appl. Opt. 2008, 47, 5654–5659. [Google Scholar] [CrossRef] [PubMed]
- Paturzo, M.; Ferraro, P. Correct self-assembling of spatial frequencies in super-resolution synthetic aperture digital holography. Opt. Lett. 2009, 34, 3650–3652. [Google Scholar] [CrossRef] [PubMed]
- Claus, D. High resolution digital holographic synthetic aperture applied to deformation measurement and extended depth of field method. Appl. Opt. 2010, 49, 3187–3198. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.Z.; Zhao, J.L.; Di, J.L. Numerical correction of splicing dislocation between sub-holograms in synthetic aperture digital holography using convolution approach. Chin. Opt. Lett. 2012, 10, 22–24. [Google Scholar]
- Thurman, S.T.; Bratcher, A. Multiplexed synthetic-aperture digital holography. Appl. Opt. 2015, 54, 559–568. [Google Scholar] [CrossRef]
- Ma, J.; Yuan, C.J.; Situ, G.H. Resolution enhancement in digital holographic microscopy with structured illumination. Chin. Opt. Lett. 2013, 11, 28–32. [Google Scholar]
- Gao, P.; Pedrini, G.; Osten, W. Structured illumination for resolution enhancement and autofocusing in digital holographic microscopy. Opt. Lett. 2013, 38, 1328–1330. [Google Scholar] [CrossRef] [PubMed]
- Sánchezortiga, E.; Martínezcorral, M.; Saavedra, G.; Garciasucerquia, J. Enhancing spatial resolution in digital holographic microscopy by biprism structured illumination. Opt. Lett. 2014, 39, 2086–2089. [Google Scholar] [CrossRef] [PubMed]
- Yuan, C.J.; Feng, S.T.; Nie, S.P. Digital holographic microscopy by using structured illumination. Chin. Opt. Lett. 2016, 43, 0609003. [Google Scholar] [CrossRef]
- Ghiglia, D.C.; Romero, L.A. Robust two-dimensional weighted and unweighted phase unwrapping that uses fast transforms and iterative methods. J. Opt. Soc. Am. A 1994, 11, 107–117. [Google Scholar] [CrossRef]
- Kerr, D.; Kaufmann, G.H.; Galizzi, G.E. Unwrapping of interferometric phase-fringe maps by the discrete cosine transform. Appl. Opt. 1996, 35, 810–816. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Xiao, W.; Pan, F.; Wang, F.; Cong, L. Complex-amplitude-based phase unwrapping method for digital holographic microscopy. Opt. Lasers Eng. 2012, 50, 322–327. [Google Scholar] [CrossRef]
- Nicola, S.D.; Finizio, A.; Pierattini, G.; Alfieri, D.; Grilli, S.; Sansone, L.; Ferraro, P. Recovering correct phase information in multiwavelength digital holographic microscopy by compensation for chromatic aberrations. Opt. Lett. 2005, 30, 2706–2708. [Google Scholar] [CrossRef] [PubMed]
- Mann, C.J.; Bingham, P.R.; Paquit, V.C.; Tobin, K.W. Quantitative phase imaging by three-wavelength digital holography. Opt. Express 2008, 16, 9753–9764. [Google Scholar] [CrossRef] [PubMed]
- Upputuri, P.K.; Mohan, N.K.; Kothiyal, M.P. Measurement of discontinuous surfaces using multiple-wavelength interferometry. Opt. Eng. 2009, 48, 705–709. [Google Scholar] [CrossRef]
- Goodman, J.W. Introduction to Fourier Optics, 3rd ed.; Chinese Edition; Publishing House of Electronics Industry: Beijing, China, 2011; p. 72. ISBN 978-7-121-13279-7. [Google Scholar]
- Liu, Y.; Wang, Z.; Li, J.S.; Gao, J.M.; Huang, J.H. Phase based method for location of the centers of side bands in spatial frequency domain in off-axis digital holographic microcopy. Opt. Lasers Eng. 2016, 86, 115–124. [Google Scholar] [CrossRef]
- Cho, H.-J.; Kim, D.-C.; Yu, Y.-H.; Shin, S.; Jung, W. Tilt aberration compensation using interference patterns in digital holography. J. Opt. Soc. Korea 2009, 13, 451–455. [Google Scholar] [CrossRef]
- Takeda, M. Fourier fringe analysis and its application to metrology of extreme physical phenomena: A review. Appl. Opt. 2013, 52, 20–29. [Google Scholar] [CrossRef] [PubMed]
- Takeda, M.; Ina, H.; Kobayashi, S. Fourier-transform method of fringe-pattern analysis for computer-basedtopography and interferometry. J. Opt. Soc. Am. 1982, 72, 156–160. [Google Scholar] [CrossRef]
- Cui, H.K.; Wang, D.Y.; Wang, Y.X.; Zhao, J.; Zhang, Y.Z. Phase aberration compensation by spectrum centering in digital holographic microscopy. Opt. Commun. 2011, 284, 4152–4155. [Google Scholar] [CrossRef]
- Colomb, T.; Cuche, E.; Charrière, F.; Kühn, J.; Aspert, N.; Montfort, F.; Marquet, P.; Depeursinge, C. Automatic procedure for aberration compensation in digital holographic microscopy and applications to specimen shape compensation. Appl. Opt. 2006, 45, 851–863. [Google Scholar] [CrossRef] [PubMed]
- Fan, Q.; Yang, H.R.; Li, G.P.; Zhao, J.L. Suppressing carrier removal error in the Fourier transform method for interferogram analysis. J. Opt. 2010, 12, 115401. [Google Scholar] [CrossRef]
- Du, Y.Z.; Feng, G.Y.; Li, H.R.; Zhou, S.H. Accurate carrier-removal technique based on zero padding in fourier transform method for carrier interferogram analysis. Optik 2014, 125, 1056–1061. [Google Scholar] [CrossRef]
- Zhou, W.J.; Yu, Y.J.; Asundi, A. Study on aberration suppressing methods in digital micro-holography. Opt. Lasers Eng. 2009, 47, 264–270. [Google Scholar] [CrossRef]
- Mann, C.J.; Yu, L.F.; Lo, C.-M.; Kim, M.K. High-resolution quantitative phase-contrast microscopy by digital holography. Opt. Express 2005, 13, 8693–8698. [Google Scholar] [CrossRef] [PubMed]
- Choi, I.; Lee, K.; Park, Y. Compensation of aberration in quantitative phase imaging using lateral shifting and spiral phase integration. Opt. Express 2017, 25, 30771–30779. [Google Scholar] [CrossRef] [PubMed]
- Kühn, J.; Charrière, F.; Colomb, T.; Cuche, E.; Montfort, F.; Emery, Y.; Marquet, P.; Depeursinge, C. Axial sub-nanometer accuracy in digital holographic microscopy. Meas. Sci. Technol. 2008, 19, 184–187. [Google Scholar] [CrossRef]
- Colomb, T.; Kühn, J.; Charrière, F.; Depeursinge, C.; Marquet, P.; Aspert, N. Total aberrations compensation in digital holographic microscopy with a reference conjugated hologram. Opt. Express 2006, 14, 4300–4306. [Google Scholar] [CrossRef] [PubMed]
- Coppola, G.; Caprio, G.D.; Gioffré, M.; Puglisi, R.; Balduzzi, D.; Galli, A.; Miccio, L.; Paturzo, M.; Grilli, S.; Finizio, A.; et al. Digital self-referencing quantitative phase microscopy by wavefront folding in holographic image reconstruction. Opt. Lett. 2010, 35, 3390–3392. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.Z.; Wang, D.Y.; Wang, Y.X.; Tao, S.Q. Automatic compensation of total phase aberrations in digital holographic biological imaging. Chin. Opt. Lett. 2011, 28, 114209. [Google Scholar] [CrossRef]
- Min, J.W.; Yao, B.L.; Gao, P.; Ma, B.H.; Yan, S.H.; Peng, F.; Zheng, J.J.; Ye, T.; Rupp, R. Wave-front curvature compensation of polarization phase-shifting digital holography. Optik 2012, 123, 1525–1529. [Google Scholar] [CrossRef]
- Miccio, L.; Alfieri, D.; Grilli, S.; Ferraro, P. Direct full compensation of the aberrations in quantitative phase microscopy of thin objects by a single digital hologram. Appl. Phys. Lett. 2007, 90, 041104. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z.; Li, J.S.; Gao, J.M.; Huang, J.H. Total aberrations compensation for misalignment of telecentric arrangement in digital holographic microscopy. Opt. Eng. 2014, 53, 112307. [Google Scholar] [CrossRef]
- Seo, K.W.; Choi, Y.S.; Seo, E.S.; Lee, S.J. Aberration compensation for objective phase curvature in phase holographic microscopy. Opt. Lett. 2012, 37, 4976–4978. [Google Scholar] [CrossRef] [PubMed]
- Zuo, C.; Chen, Q.; Qu, W.J.; Asundi, A. Phase aberration compensation in digital holographic microscopy based on principal component analysis. Opt. Lett. 2013, 38, 1724–1726. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.S.; Chen, Q.; Zhang, Y.Z.; Zuo, C. Optimal principal component analysis-based numerical phase aberration compensation method for digital holography. Opt. Lett. 2016, 41, 1293–1296. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.; Bui, V.; Lam, V.; Raub, C.B.; Chang, L.-C.; Nehmetallah, G. Automatic phase aberration compensation for digital holographic microscopy based on deep learning background detection. Opt. Express 2017, 25, 15043–15057. [Google Scholar] [CrossRef] [PubMed]
- Dubois, F.; Requena, M.L.; Minetti, C.; Monnom, O.; Lstasse, E. Partial spatial coherence effects in digital holographic microscopy with a laser source. Appl. Opt. 2004, 43, 1131–1139. [Google Scholar] [CrossRef] [PubMed]
- Dubois, F.; Callens, N.; Yourassowsky, C.; Hoyos, M.; Kurowski, P.; Monnom, O. Digital holographic microscopy with reduced spatial coherence for three-dimensional particle flow analysis. Appl. Opt. 2006, 45, 864–871. [Google Scholar] [CrossRef] [PubMed]
- Alexandrov, S.A.; Hillman, T.R.; Gutzler, T.; Sampson, D.D. Synthetic Aperture Fourier Holographic Optical Microscopy. Phys. Rev. Lett. 2006, 97, 168102. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.; Kim, H.-D.; Kim, K.; Kim, Y.; Hillman, T.R.; Min, B.; Park, Y. Synthetic Fourier transform light scattering. Opt. Express 2013, 21, 22453–22463. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.; Yang, T.D.; Lee, K.J.; Choi, W. Full-field and single-shot quantitative phase microscopy using dynamic speckle illumination. Opt. Lett. 2011, 36, 2465–2467. [Google Scholar] [CrossRef] [PubMed]
- Farrokhi, H.; Boonruangkan, J.; Chun, B.J.; Rohith, T.M.; Mishra, A.; Toh, H.T.; Yoon, H.S.; Kim, Y.-J. Speckle reduction in quantitative phase imaging by generating spatially incoherent laser field at electroactive optical diffusers. Opt. Express 2017, 25, 10791–10800. [Google Scholar] [CrossRef] [PubMed]
- Massatsch, P.; Charrière, F.; Cuche, E.; Marquet, P.; Depeursinge, C.D. Time-domain optical coherence tomography with digital holographic microscopy. Appl. Opt. 2005, 44, 1806–1812. [Google Scholar] [CrossRef] [PubMed]
- Shin, S.; Kim, Y.; Lee, K.; Kim, K.; Kim, Y.-J.; Park, H.; Park, Y. Common-path diffraction optical tomography with a low-coherence illumination for reducing speckle noise. In Proceedings of the Quantitative Phase Imaging, San Francisco, CA, USA, 7–12 February 2015; Volume 9336. [Google Scholar]
- Ding, H.; Popescu, G. Instantaneous spatial light interference microscopy. Opt. Express 2010, 18, 1569–1575. [Google Scholar] [CrossRef] [PubMed]
- Bhaduri, B.; Pham, H.; Mir, M.; Popescu, G. Diffraction phase microscopy with white light. Opt. Lett. 2012, 37, 1094–1096. [Google Scholar] [CrossRef] [PubMed]
- Bhaduri, B.; Tangella, K.; Popescu, G. Fourier phase microscopy with white light. Biomed. Opt Express 2013, 4, 1434–1441. [Google Scholar] [CrossRef] [PubMed]
- León-Rodríguez, M.; Rodríguez-Vera, R.; Rayas, J.A.; Calixto, S. High topographical accuracy by optical shot noise reduction in digital holographic microscopy. J. Opt. Soc. Am. A 2012, 29, 498–506. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Sucerquia, J. Noise reduction in digital lensless holographic microscopy by engineering the light from a light-emitting diode. Appl. Opt. 2013, 52, 232–239. [Google Scholar] [CrossRef] [PubMed]
- Agour, M.; Klattenhoff, R.; Falldorf, C.; Bergmann, R.B. Speckle noise reduction in single-shot holographic two-wavelength contouring. In Proceedings of the Holography: Advances and Modern Trends V, Prague, Czech Republic, 24–27 April 2017; Volume 10233. [Google Scholar]
- Poon, T.-C.; Korpel, A. Optical transfer function of an acousto-optic heterodyning image processor. Opt. Lett. 1979, 4, 317–319. [Google Scholar] [CrossRef] [PubMed]
- Ou, H.; Poon, T.-C.; Wong, K.K.Y.; Lam, E.Y. Enhanced depth resolution in optical scanning holography using a configurable pupil. Photonics Res. 2014, 2, 64–70. [Google Scholar] [CrossRef]
- Liu, J.-P.; Luo, D.-Z.; Lu, S.-H. Spatial-temporal demodulation technique for heterodyne optical scanning holography. Opt. Lasers Eng. 2015, 68, 42–49. [Google Scholar] [CrossRef]
- Chen, N.; Ren, Z.; Ou, H.; Lam, E.Y. Resolution enhancement of optical scanning holography with a spiral modulated point spread function. Photonics Res. 2016, 4, 1–6. [Google Scholar] [CrossRef]
- Rosen, J.; Brooker, G. Digital spatially incoherent Fresnel holography. Opt. Lett. 2007, 32, 912–914. [Google Scholar] [CrossRef] [PubMed]
- Bouchal, P.; Kapitán, J.; Chmelík, R.; Bouchal, Z. Point spread function and two-point resolution in Fresnel incoherent correlation holography. Opt. Express 2011, 19, 15603–15620. [Google Scholar] [CrossRef] [PubMed]
- Kelner, R.; Rosen, J.; Brooker, G. Enhanced resolution in Fourier incoherent single channel holography (FISCH) with reduced optical path difference. Opt. Express 2013, 21, 20131–20144. [Google Scholar] [CrossRef] [PubMed]
- Vijayakumar, A.; Kashter, Y.; Kelner, R.; Rosen, J. Coded aperture correlation holography—A new type of incoherent digital holograms. Opt. Express 2016, 24, 12430–12441. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.-P.; Tahara, T.; Hayasaki, Y.; Poon, T.-C. Incoherent digital holography: A review. Appl. Sci. 2018, 8, 143. [Google Scholar] [CrossRef]
- Quan, C.; Tay, C.J. Speckle noise reduction in digital holography by multiple holograms. Opt. Eng. 2007, 46, 115801. [Google Scholar] [CrossRef]
- Xiao, W.; Zhang, J.; Rong, L.; Pan, F.; Liu, S.; Wang, F.J.; He, A.X. Improvement of speckle noise suppression in digital holography by rotating linear polarization state. Chin. Opt. Lett. 2011, 9, 36–38. [Google Scholar]
- Garcia-Sucerquia, J.; Ramírez, J.H.; Castaneda, R. Incoherent recovering of the spatial resolution in digital holography. Opt. Commun. 2006, 260, 62–67. [Google Scholar] [CrossRef]
- Kubota, S.; Goodman, J.W. Very efficient speckle contrast reduction realized by moving diffuser device. Appl. Opt. 2010, 49, 4385–4391. [Google Scholar] [CrossRef] [PubMed]
- Pan, F.; Xiao, W.; Liu, S.; Wang, F.J.; Rong, L.; Li, R. Coherent noise reduction in digital holographic phase contrast microscopy by slightly shifting object. Opt. Express 2011, 19, 3862–3869. [Google Scholar] [CrossRef] [PubMed]
- Baumbach, T.; Kolenovic, E.; Kebbel, V.; Jüptner, W. Improvement of accuracy in digital holography by use of multiple holograms. Appl. Opt. 2006, 45, 6077–6085. [Google Scholar] [CrossRef] [PubMed]
- Pan, F.; Xiao, W.; Liu, S.; Rong, L. Coherent noise reduction in digital holographic microscopy by laterally shifting camera. Opt. Commun. 2013, 292, 68–72. [Google Scholar] [CrossRef]
- Herrera-Ramirez, J.; Hincapie-Zuluaga, D.A.; Garcia-Sucerquia, J. Speckle noise reduction in digital holography by slightly rotating the object. Opt. Eng. 2016, 55, 121714. [Google Scholar] [CrossRef]
- Sharma, A.; Sheoran, G.; Jaffery, Z.A.; Moinuddin. Improvement of signal-to-noise ratio in digital holography using wavelet transform. Opt. Lasers Eng. 2008, 46, 42–47. [Google Scholar] [CrossRef]
- Cai, X.O. Reduction of speckle noise in the reconstructed image of digital holography. Optik 2010, 121, 394–399. [Google Scholar] [CrossRef]
- Maycock, J.; Hennelly, B.M.; Mcdonald, J.B.; Frauel, Y.; Castro, A.; Javidi, B.; Naughton, T.J. Reduction of speckle in digital holography by discrete fourier filtering. J. Opt. Soc. Am. A 2007, 24, 1617–1622. [Google Scholar] [CrossRef]
- Abolhassani, M.; Rostami, Y. Speckle noise reduction by division and digital processing of a hologram. Optik 2012, 123, 937–939. [Google Scholar] [CrossRef]
- Leportier, T.; Park, M.-C. Filter for speckle noise reduction based on compressive sensing. Opt. Eng. 2016, 55, 121724. [Google Scholar] [CrossRef]
- Morimoto, Y.; Matui, T.; Fujigaki, M.; Kawagishi, N. Subnanometer displacement measurement by averaging of phase difference in windowed digital holographic interferometry. Opt. Eng. 2007, 46, 025603. [Google Scholar] [CrossRef]
- Hincapie, D.; Herrera-Ramírez, J.; Garcia-Sucerquia, J. Single-shot speckle reduction in numerical reconstruction of digitally recorded holograms. Opt. Lett. 2015, 40, 1623–1626. [Google Scholar] [CrossRef] [PubMed]
- Fukuoka, T.; Mori, Y.; Nomura, T. Speckle reduction by spatial-domain mask in digital holography. J. Disp. Technol. 2016, 12, 315–322. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z.; Huang, J.H.; Gao, J.M.; Li, J.S.; Zhang, Y.; Li, X.M. Coherent noise reduction of reconstruction of digital holographic microscopy using a laterally shifting hologram aperture. Opt. Eng. 2016, 55, 121725. [Google Scholar] [CrossRef]







| Method | Advantage | Limitation |
|---|---|---|
| Double exposure method [22,63,65] | Compensating aberrations in optical components | Recording two holograms |
| Two MOs compensation method in two branches [25,26,29,64] | Compensating quadratic phase aberration | Precisely adjusting the distance between MO and CCD |
| Compensation method in telecentric arrangement [28,30] | Compensating quadratic phase aberration | precise adjustment of the distance between MO and collimated lens |
| Phase mask method [22,26,60] | Compensating aberrations set by mask | Requiring the sample-free blank region |
| Surface fitting method for a blank area [23,60,70] | Compensating aberrations set by polynomials | Requiring identical distortion in the total phase |
| Surface fitting method for a total reconstructed phase [69,71,72] | Compensating aberrations set by polynomials | Affection by sample’s topographic distribution |
| Reference conjugated hologram method [66,67,68] | Compensating aberrations set by polynomials | Requiring the sample-free blank region |
| Method | Advantage | Limitation |
|---|---|---|
| Low spatial or temporal coherent source method [77,78,79,80,81,82,83,84,85,86,87,88,89,90] | Recording one hologram | Increasing the adjustment difficulty of light configuration |
| OSH method [91,92,93,94] | Higher signal-to-noise ratio | Complicated setup and slower recording speed |
| FINCH method [95,96,97,98] | Higher signal-to-noise ratio and dynamic measurement | Larger bias buildup for complicated objects |
| Multiplexing holograms method [33,35,100,101,102,103,104,105,106,107] | Uncorrelated holograms obtained by different ways | Recording multiple holograms |
| Digital processing method [31,108,109,110,111,112,113,114,115,116] | Recording one hologram | Loss of spatial resolution |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Wang, Z.; Huang, J. Recent Progress on Aberration Compensation and Coherent Noise Suppression in Digital Holography. Appl. Sci. 2018, 8, 444. https://doi.org/10.3390/app8030444
Liu Y, Wang Z, Huang J. Recent Progress on Aberration Compensation and Coherent Noise Suppression in Digital Holography. Applied Sciences. 2018; 8(3):444. https://doi.org/10.3390/app8030444
Chicago/Turabian StyleLiu, Yun, Zhao Wang, and Junhui Huang. 2018. "Recent Progress on Aberration Compensation and Coherent Noise Suppression in Digital Holography" Applied Sciences 8, no. 3: 444. https://doi.org/10.3390/app8030444
APA StyleLiu, Y., Wang, Z., & Huang, J. (2018). Recent Progress on Aberration Compensation and Coherent Noise Suppression in Digital Holography. Applied Sciences, 8(3), 444. https://doi.org/10.3390/app8030444






