Energy Management Strategy for Rural Communities’ DC Micro Grid Power System Structure with Maximum Penetration of Renewable Energy Sources
Abstract
:1. Introduction
2. Power System Network
Proposed DC Microgrid Architecture for Rural Communities
3. Mathematical Modeling of ProposedDC Architecture
3.1. Mathematical Modeling of Solar Power
System Modeling
3.2. Mathematical Modeling of Wind Power
3.3. Mathematical Modeling of Fuel Cell Power
- Idealized modeling;
- Uniform circulated gases;
- Constant pressure in the flow channel;
- Cell parameters are represented together to form stack parameters;
- The output voltage of the single fuel cell can be represented as
3.4. Mathematical Modeling of the Battery
4. Energy Management Strategy
- = power generated by PV (kW);
- = power generated by Wind (kW);
- = power generated by Fuel cell (kW);
- = Domestic load (kW);
- = Agriculture vehicle load (kW);
- = Priority load (kW).
5. Simulation Study and Results
5.1. Simulation Results
- Generation equal to load (PG = PL);
- Generation greater than load (PG > PL);
- Generation less than load (PG < PL).
5.2. Generation Equal to Load (PG = PL)
5.3. Generation Greater Than Load (PG > PL)
5.4. Generation Greater Than Load (PG < PL)
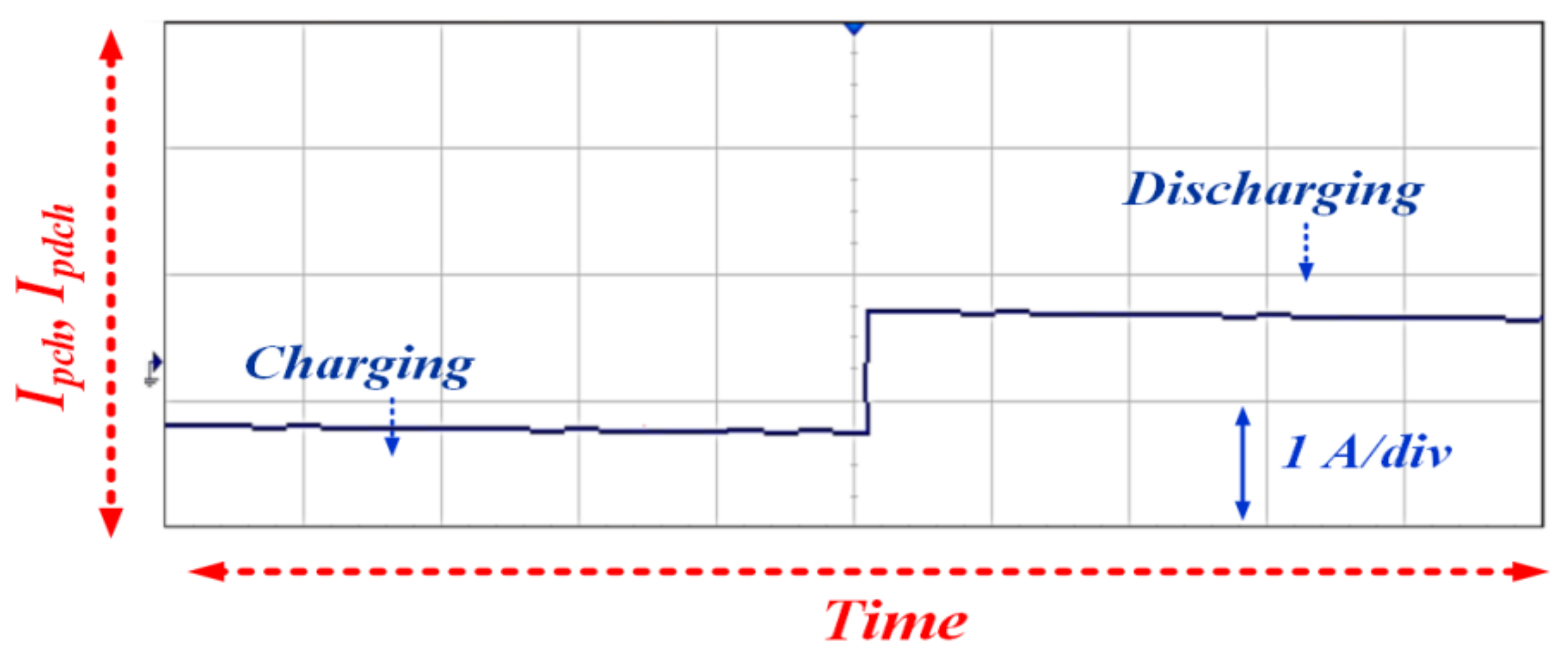
6. Experimental Analysis
7. Conclusions
Author Contributions
Conflicts of Interest
References
- Bloomberg New Energy Finance. The Future of Energy 2012 Results Book; Bloomberg New Energy Finance: New York, NY, USA, 2012. [Google Scholar]
- International Energy Agency World Energy Investment. Available online: https://www.iea.org/media/publications/investment/WEI2017Launch_forWEB.pdf (accessed on 10 April 2017).
- Anand, S.; Fernandes, B.G. Steady state performance analysis for load sharing in DC distributed generation system. In Proceedings of the 2011 10th International Conference on Environment and Electrical Engineering (EEEIC), Rome, Italy, 8–11 May 2011; pp. 1–4. [Google Scholar]
- Gao, L.; Liu, Y.; Ren, H.; Guerrero, J.M. A DC Microgrid Coordinated Control Strategy Based on Integrator Current-Sharing. Energies 2017, 10, 1116. [Google Scholar] [CrossRef]
- Patterson, B.T. Dc, come home: Dc microgrids and the birth of the ‘enernet’. IEEE Power Energy Mag. 2012, 10, 60–69. [Google Scholar] [CrossRef]
- Ali, A.; Padmanaban, S.; Twala, B.; Marwala, T. Electric Power Grids Distribution Generation System for Optimal Location and Sizing—A Case Study Investigation by Various Optimization Algorithms. Energies 2017, 10, 960. [Google Scholar] [CrossRef]
- Liu, X.; Wang, P.; Loh, P.C. A hybrid AC/DC microgrid and its coordination control. IEEE Trans. Smart Grid 2011, 2, 278–286. [Google Scholar] [CrossRef]
- Sechilariu, M.; Wang, B.C.; Locment, F. Supervision control for optimal energy cost management in DC microgrid: Design and simulation. Int. J. Electr. Power Energy Syst. 2014, 58, 140–149. [Google Scholar] [CrossRef]
- Hossain, E.; Perez, R.; Padmanaban, S.; Mihet-Popa, L.; Blaabjerg, F.; Ramachandaramurthy, V.K. Sliding Mode Controller and Lyapunov Redesign Controller to Improve Microgrid Stability: A Comparative Analysis with CPL Power Variation. Energies 2017, 10, 1959. [Google Scholar] [CrossRef]
- Subramani, G.; Ramachandaramurthy, V.K.; Padmanaban, S.; Mihet-Popa, L.; Blaabjerg, F.; Guerrero, J.M. Grid-Tied Photovoltaic and Battery Storage Systems with Malaysian Electricity Tariff—A Review on Maximum Demand Shaving. Energies 2017, 10, 1884. [Google Scholar] [CrossRef]
- Tan, K.M.; Ramachandaramurthy, V.K.; Yong, J.Y.; Padmanaban, S.; Mihet-Popa, L.; Blaabjerg, F. Minimization of Load Variance in Power Grids—Investigation on Optimal Vehicle-to-Grid Scheduling. Energies 2017, 10, 1880. [Google Scholar] [CrossRef]
- Sen, R.; Bhattacharyya, S.C. Off-grid electricity generation with renewable energy technologies in India: An application of HOMER. Renew. Energy 2014, 62, 388–398. [Google Scholar] [CrossRef]
- AL-Nussairi, M.K.; Bayindir, R.; Padmanaban, S.; Mihet-Popa, L.; Siano, P. Constant Power Loads (CPL) with Microgrids: Problem Definition, Stability Analysis and Compensation Techniques. Energies 2017, 10, 1656. [Google Scholar] [CrossRef]
- Ganesan, S.; Padmanaban, S.; Varadarajan, R.; Subramaniam, U.; Mihet-Popa, L. Study and Analysis of an Intelligent Microgrid Energy Management Solution with Distributed Energy Sources. Energies 2017, 10, 1419. [Google Scholar] [CrossRef]
- Song, M.; Chen, K.; Zhang, X.; Wang, J. Optimization of wind turbine micro-siting for reducing the sensitivity of power generation to wind direction. Renew. Energy 2016, 85, 57–65. [Google Scholar] [CrossRef]
- Dixon, C.; Reynolds, S.; Rodley, D. Micro/small wind turbine power control for electrolysis applications. Renew. Energy 2016, 87, 182–192. [Google Scholar] [CrossRef]
- Macedo, W.N.; Monteiro, L.G.; Corgozinho, I.M.; Macêdo, E.N.; Rendeiro, G.; Braga, W.; Bacha, L. Biomass based microturbine system for electricity generation for isolated communities in amazon region. Renew. Energy 2016, 91, 323–333. [Google Scholar] [CrossRef]
- Chokkalingam, B.; Padmanaban, S.; Siano, P.; Krishnamoorthy, R.; Selvaraj, R. Real-Time Forecasting of EV Charging Station Scheduling for Smart Energy Systems. Energies 2017, 10, 377. [Google Scholar] [CrossRef]
- Bonfiglio, A.; Brignone, M.; Invernizzi, M.; Labella, A.; Mestriner, D.; Procopio, R. A Simplified Microgrid Model for the Validation of Islanded Control Logics. Energies 2017, 10, 1141. [Google Scholar] [CrossRef]
- Long, B.; Jeong, T.W.; Deuk Lee, J.; Jung, Y.C.; Chong, K.T. Energy management of a hybrid AC–DC micro-grid based on a battery testing system. Energies 2015, 8, 1181–1194. [Google Scholar] [CrossRef]
- Martin-Martínez, F.; Sánchez-Miralles, A.; Rivier, M. A literature review of Microgrids: A functional layer based classification. Renew. Sustain. Energy Rev. 2016, 62, 1133–1153. [Google Scholar] [CrossRef]
- Shahzad, M.K.; Zahid, A.; Ur Rashid, T.; Rehan, M.A.; Ali, M.; Ahmad, M. Techno-economic feasibility analysis of a solar-biomass off grid system for the electrification of remote rural areas in Pakistan using HOMER software. Renew. Energy 2017, 106, 264–273. [Google Scholar] [CrossRef]
- Olatomiwa, L.; Mekhilef, S.; Ismail, M.S.; Moghavvemi, M. Energy management strategies in hybrid renewable energy systems: A review. Renew. Sustain. Energy Rev. 2016, 62, 821–835. [Google Scholar] [CrossRef]
- Mandelli, S.; Barbieri, J.; Mereu, R.; Colombo, E. Off-grid systems for rural electrification in developing countries: Definitions, classification and a comprehensive literature review. Renew. Sustain. Energy Rev. 2016, 58, 1621–1646. [Google Scholar] [CrossRef]
- Hosseini, S.A.; Abyaneh, H.A.; Sadeghi, S.H.H.; Razavi, F.; Nasiri, A. An overview of microgrid protection methods and the factors involved. Renew. Sustain. Energy Rev. 2016, 64, 174–186. [Google Scholar] [CrossRef]
- Jing, W.; Lai, C.H.; Wong, S.H.W.; Wong, M.L.D. Battery-supercapacitor hybrid energy storage system in standalone DC microgrids: A review. IET Renew. Power Gener. 2016, 11, 461–469. [Google Scholar] [CrossRef]
- Kinhekar, N.; Padhy, N.P.; Li, F.; Gupta, H.O. Utility oriented demand side management using smart AC and micro DC grid cooperative. IEEE Trans. Power Syst. 2016, 31, 1151–1160. [Google Scholar] [CrossRef]
- Gabbar, H.A.; Othman, A.M. Performance optimisation for novel green plug-energy economizer in micro-grids based on recent heuristic algorithm. IET Gener. Transm. Distrib. 2016, 10, 678–687. [Google Scholar] [CrossRef]
- Ackermann, T.; Cherevatskiy, S.; Brown, T.; Eriksson, R.; Samadi, A.; Ghandhari, M.; Söder, L.; Lindenberger, D.; Jägemann, C.; Hagspiel, S.; et al. Smart Modeling of Optimal Integration of High Penetration of PV-SMOOTH PV. Available online: http://smooth-pv.info/doc/SmoothPV_Final_Report_Part1.pdf. (accessed on 19 January 2018).
- Arboleya, P.; Gonzalez-Moran, C.; Coto, M.; Falvo, M.C.; Martirano, L.; Sbordone, D.; Bertini, I.; Di Pietra, B. Efficient energy management in smart micro-grids: ZERO grid impact buildings. IEEE Trans. Smart Grid 2015, 6, 1055–1063. [Google Scholar] [CrossRef]
- Chub, A.; Husev, O.; Blinov, A.; Vinnikov, D. Novel Isolated Power Conditioning Unit for Micro Wind Turbine Applications. IEEE Trans. Ind. Electron. 2017, 64, 5984–5993. [Google Scholar] [CrossRef]
- RRahman, S.A.; Varma, R.K.; Vanderheide, T. Generalised model of a photovoltaic panel. IET Renew. Power Gener. 2014, 8, 217–229. [Google Scholar] [CrossRef]
- Silva, E.A.; Bradaschia, F.; Cavalcanti, M.C.; Nascimento, A.J. Nascimento. Parameter estimation method to improve the accuracy of photovoltaic electrical model. IEEE J. Photovolt. 2016, 6, 278–285. [Google Scholar] [CrossRef]
- Bhayo, M.A.; Yatim, A.H.M.; Khokhar, S.; Aziz, M.J.A.; Idris, N.R.N. Modeling of Wind Turbine Simulator for analysis of the wind energy conversion system using MATLAB/Simulink. In Proceedings of the IEEE Conference on Energy Conversion (CENCON), Johor Bahrum, Malaysia, 19–20 October 2015; pp. 122–127. [Google Scholar]
- Breaz, E.; Gao, F.; Blunier, B.; Tirnovan, R. Mathematical modeling of proton exchange membrane fuel cell with integrated humidifier for mobile applications. In Proceedings of the IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 18–20 June 2012; pp. 1–6. [Google Scholar]
- Mihet-Popa, L.; Boldea, I. Dynamics of control strategies for wind turbine applications. In Proceedings of the 10th International Conference on Optimisation of Electrical and Electronic Equipment, OPTIM 2006, Poiana Brasov, Romania, 18−19 May 2006; pp. 199–206. [Google Scholar]
- Yu, S.Y.; Kim, H.J.; Kim, J.H.; Han, B.M. SoC-based output voltage control for BESS with a lithium-ion battery in a stand-alone DC microgrid. Energies 2016, 9, 924. [Google Scholar] [CrossRef]
- Zhou, N.; Liu, N.; Zhang, J.; Lei, J. Multi-Objective optimal sizing for BATTERY Storage of PV-based microgrid with demand response. Energies 2016, 9, 591. [Google Scholar] [CrossRef]
- Mihet-Popa, L.; Camacho, O.M.F.; Norgard, P.B. Charging and discharging tests for obtaining an accurate dynamic electro-thermal model of high power lithium-ion pack system for hybrid and EV applications. In Proceedings of the IEEE PES Power Tech Conference, Grenoble, France, 16−20 June 2013. [Google Scholar]
- Camacho, O.M.F.; Mihet-Popa, L. Fast Charging and Smart Charging Tests for Electric Vehicles Batteries using Renewable Energy. Oil Gas Sci. Technol. 2016, 71, 13. [Google Scholar] [CrossRef]

















| Description | Specification |
|---|---|
| Wind generator | 5 kW, 220 V |
| PV | 5 kW, 220 V |
| Fuel Cell | 5 kW, 220 V |
| DC bus voltage | 220 V |
| DC-DC converter | 220 V |
| Dynamic Load | 5 kW |
| Motor load | 2.5 kW to 5 kW |
| Battery | 220 V battery/150 Ah |
| Time | Power Generated by Renewable Energy Source | Diesel Power | Total Generated Power | Commercial Battery | Priority Load Battery | Priority Load | Domestic Loads | Agricultural Loads | Total Loads | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ppv (kW) | Wind (kW) | Fuel (kW) | Diesel (kW) | Pg (kW) | Charge (kW/h) | Discharge (kW/h) | Charge (kW/h) | Discharge (kW/h) | Load (kW) | Pd1 (kW) | Pd2 (kW) | Pag1 (kW) | Pag2 (kW) | PL (kW) | |
| 6 a.m.–7 a.m. | 1 | 3 | 5 | 4 | 9 | 0 | 0 | −2 | 0 | 2 | 3 | 2 | 4 | 4 | 15 |
| 7 a.m.–8 a.m. | 3 | 4 | 4 | 0 | 11 | −1 | 0 | −2 | 0 | 2 | 2 | 2 | 2 | 2 | 10 |
| 8 a.m.–9 a.m. | 4 | 5 | 4 | 0 | 13 | −1 | 0 | −2 | 0 | 2 | 1 | 2 | 4 | 3 | 12 |
| 9 a.m.–10 a.m. | 3 | 5 | 4 | 0 | 12 | 0 | 0 | −2 | 0 | 2 | 4 | 0 | 3 | 3 | 12 |
| 10 a.m.–12 p.m. | 5 | 4 | 5 | 0 | 14 | −2 | 0 | −2 | 0 | 2 | 2 | 2 | 3 | 3 | 12 |
| 12 p.m.–2 p.m. | 5 | 5 | 5 | 0 | 15 | −7 | 0 | −2 | 0 | 2 | 2 | 1 | 3 | 0 | 8 |
| 2 p.m.–3 p.m. | 4 | 2 | 3 | 0 | 9 | 0 | 3 | −2 | 0 | 1 | 2 | 3 | 3 | 3 | 12 |
| 3 p.m.–4 p.m. | 5 | 4 | 4 | 0 | 13 | 0 | 0 | −1 | 0 | 1 | 4 | 1 | 4 | 3 | 13 |
| 4 p.m.–6 p.m. | 3 | 5 | 3 | 0 | 11 | −9 | 0 | 1 | 3 | −3 | 1 | 1 | 1 | 1 | 4 |
| 6 p.m.–8 p.m. | 1 | 2 | 4 | 0 | 7 | 0 | 4 | 2 | 3 | −3 | 4 | 3 | 2 | 2 | 11 |
| 8 p.m.–12 a.m. | 0 | 4 | 5 | 0 | 9 | 0 | 1 | 2 | 3 | −3 | 1 | 3 | 2 | 4 | 10 |
| 12 a.m.–4 a.m. | 0 | 4 | 5 | 0 | 9 | −4 | 0 | 2 | 3 | −3 | 3 | 2 | 0 | 0 | 5 |
| 4 a.m.–6 a.m. | 0 | 0 | 2 | 0 | 2 | 0 | 9 | 2 | 3 | −3 | 2 | 2 | 5 | 2 | 11 |
| PG | PL | PPriority | PCom | PDiesel | Cases | Remarks | |
|---|---|---|---|---|---|---|---|
| 1 | PG = PL | ✓ | ✓ | ✓ | × | 1 | The power from renewable source is enough to supply the load without storage unit and diesel generator. |
| 2 | PG > PL | ✓ | ✓ | ✓ | × | 2,3,4 | The load will be supplied and additionally the batteries will charge with the surplus power |
| 3 | PG < PL | ✓ | ✓ | ✓ | ✓ | 5,6,7 | The load is supplied by the combination of diesel generator, available power, and battery. |
| PV | Wind | Fuel Cell | |||
|---|---|---|---|---|---|
| Centsys Solar 250 W | SIKCO Wind 1000 | Horizon 500 W PEM Fuel Cell | |||
| PV Modules | Specification | Wind | Specification | Fuel Cell | Specification |
| Maximum capacity | 250 W | Type of Turbine | Horizontal Axis Downwind Turbine | Rated capacity | 500 W |
| Tolerance | ±3% | voltage | 12 V DC | Rated voltage | 14.4 V |
| Open circuit voltage | 37.8 V | Rated Wind Speed | 5 m/s | Valve Voltage | 12 V |
| Short circuit current | 7.94 A | Rated Power | 300 W | Blower range | 12 V |
| Module efficiency | 15.3% | Rated rpm | 300 | Reactants | Hydrogen and Air |
| Solar cell efficiency | 17.2% | Cut-in wind speed | 2 m/s | Ambient Temperature | 5–30 °C (41–86 °F) |
| Maximum voltage (Vm) | 31.5 V | Cut-out wind speed | 15 m/s | Max Stack Temperature | 65 °C (149 °F) |
| Maximum current (Im) | 7.94 A | Blade length | 600 mm | Gas Pressure | 0.45–0.55 Bar |
| Nominal Temperature | 42 °C (±2 °C) | blades | 6 | Stack Size | 268 mm × 130 mm × 122.5 mm (10.5″ × 5.1″ × 4.8″) |
| Dimensions | 1650 mm × 992 m × 40 mm | Noise Level | <20 dB | Efficiency of System | 40% at 14.4 V |
| Parameters | Specification |
|---|---|
| DC bus voltage | 24 V |
| Capacityof wind generator | 200 W |
| Capacity of PV panel | 200 W |
| Capacity of fuel cell power | 100 W |
| Battery type | Tall tubular C10 |
| Battery capacity | 14 Ah/12 V |
| DC-DC converter | 24 V/220 V |
| Lamp loads | 500 W |
| Load bus | 220 V |
| Diesel generator | 500 W |
| Maximum current | 3 A |
| Time | PV Power (W) | Wind Power (W) | Fuel Cell Power (W) | Generated Power (W) | Loads (W) | Batteries | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Priority Load | Commercial Loads | Net Loads | Priority Load Battery | Commercial Load Battery | |||||||||||
| P(W) | I(A) | P(W) | I(A) | P(W) | I(A) | P(W) | I(A) | P(W) | I(A) | P(W) | I(A) | ||||
| 7 a.m.–8 a.m. | 100 | 170 | 100 | 370 | 1.68 | 100 | 0.5 | 150 | 0.7 | 250 | 1.2 | −100 | −0.5 | −120 | −0.7 |
| 9 a.m.–10 a.m. | 200 | 140 | 100 | 440 | 2 | 100 | 0.5 | 340 | 1.5 | 440 | 2.0 | −100 | −0.5 | 0 | 0 |
| 8 p.m.–12 a.m. | 0 | 150 | 100 | 250 | 1.13 | 100 | 0.5 | 250 | 1.1 | 350 | 1.6 | 100 | 0.5 | 100 | 0.45 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gunasekaran, M.; Mohamed Ismail, H.; Chokkalingam, B.; Mihet-Popa, L.; Padmanaban, S. Energy Management Strategy for Rural Communities’ DC Micro Grid Power System Structure with Maximum Penetration of Renewable Energy Sources. Appl. Sci. 2018, 8, 585. https://doi.org/10.3390/app8040585
Gunasekaran M, Mohamed Ismail H, Chokkalingam B, Mihet-Popa L, Padmanaban S. Energy Management Strategy for Rural Communities’ DC Micro Grid Power System Structure with Maximum Penetration of Renewable Energy Sources. Applied Sciences. 2018; 8(4):585. https://doi.org/10.3390/app8040585
Chicago/Turabian StyleGunasekaran, Maheswaran, Hidayathullah Mohamed Ismail, Bharatiraja Chokkalingam, Lucian Mihet-Popa, and Sanjeevikumar Padmanaban. 2018. "Energy Management Strategy for Rural Communities’ DC Micro Grid Power System Structure with Maximum Penetration of Renewable Energy Sources" Applied Sciences 8, no. 4: 585. https://doi.org/10.3390/app8040585
APA StyleGunasekaran, M., Mohamed Ismail, H., Chokkalingam, B., Mihet-Popa, L., & Padmanaban, S. (2018). Energy Management Strategy for Rural Communities’ DC Micro Grid Power System Structure with Maximum Penetration of Renewable Energy Sources. Applied Sciences, 8(4), 585. https://doi.org/10.3390/app8040585








