Reconstruct Recurrent Neural Networks via Flexible Sub-Models for Time Series Classification
Abstract
:1. Introduction
2. Problem Description
2.1. RNNs Structure
2.2. Classification by RNNs
2.3. Gradient Problem
3. Proposed BICORN-RNN
3.1. Random Mapping Input Space
3.2. Convolutional Rearrange
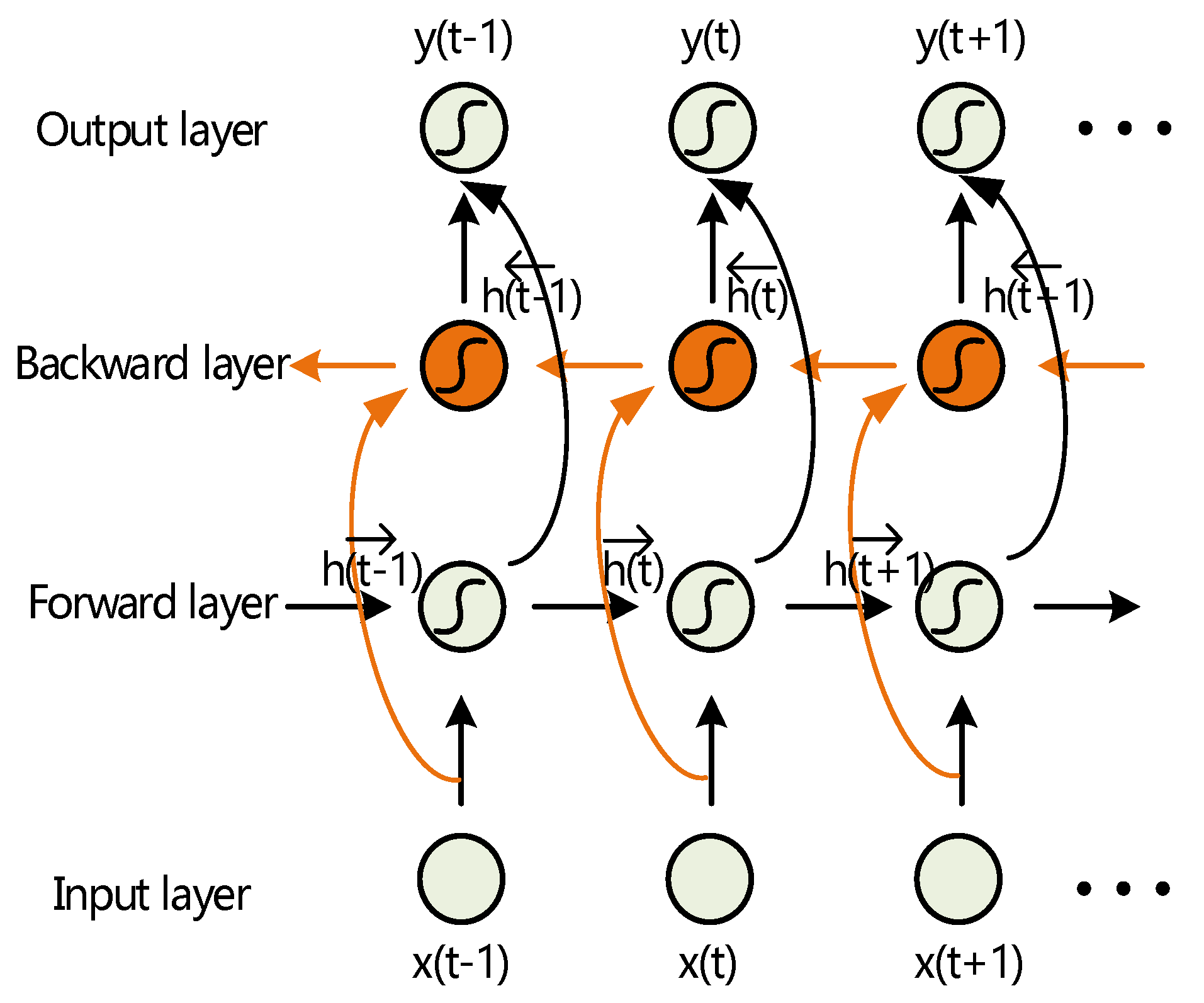
3.3. Bidirectional Transmission
3.4. BICORN-RNNs Structure
4. Experiments
4.1. Experiments on Benchmark Datasets
4.1.1. Experiments Description
4.1.2. Results and Discussion
4.2. Experiments about Influencing Factors
4.2.1. Experiments Description
4.2.2. Results regarding SNR and Discussion
4.2.3. Results on Segmented Length and Discussion
4.2.4. Results regarding Data Missing and Discussion
4.2.5. Result regarding Overlapping and Discussion
4.3. Result about Synthetical Dataset and Discussion
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Graves, A.; Beringer, N.; Schmidhuber, J. Rapid Retraining on Speech Data with LSTM Recurrent Networks; Technical Report; Instituto Dalle Molle di Studi Sull’ Intelligenza Artificiale: Manno, Switzerland, 2005. [Google Scholar]
- Mao, Y.; Chen, W.; Chen, Y.; Lu, C.; Kollef, M.; Bailey, T. An integrated data mining approach to real-time clinical monitoring and deterioration warning. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, 12–16 August 2012; pp. 1140–1148. [Google Scholar]
- Maharaj, E.A.; Alonso, A.M. Discriminant analysis of multivariate time series: Application to diagnosis based on ECG signals. Comput. Stat. Data Anal. 2014, 70, 67–87. [Google Scholar] [CrossRef]
- Daigo, K.; Tomoharu, N. Stock prediction using multiple time series of stock prices and news articles. In Proceedings of the 2012 IEEE Symposium on Computers & Informatics (ISCI), Penang, Malaysia, 18–20 March 2012; pp. 11–16. [Google Scholar]
- Karim, F.; Majumdar, S.; Darabi, H.; Chen, S. LSTM Fully Convolutional Networks for Time Series Classification. IEEE Access 2017, 6, 1662–1669. [Google Scholar] [CrossRef]
- Ding, H.; Trajcevski, G.; Scheuermann, P.; Wang, X.; Keogh, E. Querying and mining of time series data: Experimental comparison of representations and distance measures. Proc. Vldb Endow. 2008, 1, 1542–1552. [Google Scholar] [CrossRef]
- Wang, X.; Mueen, A.; Ding, H.; Trajcevski, G.; Scheuermann, P.; Keogh, E. Experimental comparison of representation methods and distance measures for time series data. Data Min. Knowl. Discov. 2013, 26, 275–309. [Google Scholar] [CrossRef]
- Oehmcke, S.; Zielinski, O.; Kramer, O. kNN ensembles with penalized DTW for multivariate time series imputation. In Proceedings of the 2016 International Joint Conference on Neural Networks, Vancouver, BC, Canada, 24–29 July 2016; pp. 2774–2781. [Google Scholar]
- Faloutsos, C.; Ranganathan, M.; Manolopoulos, Y. Fast subsequence matching in time-series databases. In Proceedings of the 1994 ACM SIGMOD International Conference on Management of Data, Minneapolis, MN, USA, 24–27 May 1994; pp. 419–429. [Google Scholar]
- Berndt, D.; Clihord, J. Using Dynamic Time Warping to Find Patterns in Sequences. In Proceedings of the 3rd International Conference on Knowledge Discovery and Data Mining, Seattle, WA, USA, 31 July–1 August 1994; pp. 359–370. [Google Scholar]
- Keogh, E.J.; Rakthanmanon, T. Fast Shapelets: A Scalable Algorithm for Discovering Time Series Shapelets. In Proceedings of the 2013 SIAM International Conference on Data Mining, Austin, TX, USA, 2–4 May 2013. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ye, L.; Keogh, E. Time Series Shapelets: A Novel Technique that Allows Accurate, Interpretable and Fast Classification. Data Min. Knowl. Discov. 2011, 22, 149–182. [Google Scholar] [CrossRef]
- Ye, L.; Keogh, E. Time series shapelets: A new primitive for data mining. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, 28 June–1 July 2009; pp. 947–956. [Google Scholar]
- Hinton, G.E. Learning multiple layers of representation. Trends Cogn. Sci. 2007, 11, 428–434. [Google Scholar] [CrossRef] [PubMed]
- WöHler, C.; Anlauf, J.K. An adaptable time-delay neural-network algorithm for image sequence analysis. IEEE Trans. Neural Netw. 1999, 10, 1531–1536. [Google Scholar] [CrossRef] [PubMed]
- Elman, J.L. Finding Structure in Time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the International Conference on International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 1310–1318. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the International Conference on International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Gers, F.A.; Schraudolph, N.N.; Schmidhuber, J. Learning precise timing with LSTM recurrent networks. J. Mach. Learn. Res. 2003, 3, 115–143. [Google Scholar]
- Mehdiyev, N.; Lahann, J.; Emrich, A.; Enke, D.; Fettke, P.; Loos, P. Time Series Classification using Deep Learning for Process Planning: A Case from the Process Industry. Procedia Comput. Sci. 2017, 114, 242–249. [Google Scholar] [CrossRef]
- Achanta, S.; Alluri, K.R.; Gangashetty, S.V. Statistical Parametric Speech Synthesis Using Bottleneck Representation from Sequence Auto-encoder. arXiv, 2016; arXiv:1606.05844. [Google Scholar]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 2002, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.M.; Sattar, M.A.; Amin, M.F.; Murase, K. A New Adaptive Strategy for Pruning and Adding Hidden Neurons during Training Artificial Neural Networks. In International Conference on Intelligent Data Engineering and Automated Learning; Springer: Berlin/Heidelberg, Germany, 2008; pp. 40–48. [Google Scholar]
- Panchal, G.; Ganatra, A.; Kosta, Y.P.; Panchal, D. Behaviour analysis of multilayer perceptrons with multiple hidden neurons and hidden layers. Int. J. Comput. Theory Eng. 2011, 3, 332–337. [Google Scholar] [CrossRef]
- Shore, J.E.; Johnson, R.W. Properties of cross-entropy minimization. IEEE Trans. Inf. Theory 1981, 27, 472–482. [Google Scholar] [CrossRef]
- Bridle, J.S. Probabilistic Interpretation of Feedforward Classification Network Outputs, with Relationships to Statistical Pattern Recognition. In Neurocomputing; Springer: Berlin/Heidelberg, Germany, 1990; pp. 227–236. [Google Scholar]
- Martens, J.; Sutskever, I. Learning recurrent neural networks with hessian-free optimization. In Proceedings of the International Conference on International Conference on Machine Learning, Bellevue, WA, USA, 28 June–2 July 2011; pp. 1033–1040. [Google Scholar]
- Zhang, N.; Behera, P.K. Solar radiation prediction based on recurrent neural networks trained by Levenberg-Marquardt backpropagation learning algorithm. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Washington, DC, USA, 16–20 January 2012; IEEE Computer Society: Washington, DC, USA, 2012; pp. 1–7. [Google Scholar]
- Rumelhart, D.; Mcclelland, J. Learning Internal Representations by Error Propagation. In Neurocomputing: Foundations of Research; MIT Press: Cambridge, MA, USA, 1988; pp. 318–362. [Google Scholar]
- Hüsken, M.; Stagge, P. Recurrent neural networks for time series classification. Neurocomputing 2003, 50, 223–235. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arxiv, 2014; arXiv:1412.3555. [Google Scholar]
- Vesanto, J.; Alhoniemi, E. Clustering of the self-organizing map. IEEE Trans. Neural Netw. 2000, 11, 586–600. [Google Scholar] [CrossRef] [PubMed]
- Vinyals, O.; Jia, Y.; Deng, L.; Darrell, T. Learning with recursive perceptual representations. In Proceedings of the Advances in Neural Information Processing Systems 25 (NIPS), Lake Tahoe, NV, USA, 3–6 December 2012. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 37, 1904–1916. [Google Scholar] [CrossRef] [PubMed]
- Lecun, Y.; Bengio, Y. Convolutional networks for images, speech, and time series. In The Handbook of Brain Theory and Neural Networks; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Lin, S.; Runger, G.C. GCRNN: Group-Constrained Convolutional Recurrent Neural Network. IEEE Trans. Neural Netw. Learn. Syst. 2017, 1–10. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Baldi, P.; Brunak, S.; Frasconi, P.; Pollastri, G.; Soda, G. Bidirectional Dynamics for Protein Secondary Structure Prediction. Seq. Learn. Paradig. Algorithms Appl. 2000, 21, 99–120. [Google Scholar]
- Schuster, M. On Supervised Learning from Sequential Data with Applications for Speech Recognition. Ph.D. Thesis, Nara Institute of Science and Technology, Ikoma, Japan, 15 February 1999. [Google Scholar]
- Ibeyli, E.D. Recurrent neural networks employing Lyapunov exponents for analysis of ECG signals. Expert Syst. Appl. 2010, 37, 1192–1199. [Google Scholar]
- Chen, Y.; Keogh, E.; Hu, B.; Begum, N.; Bagnall, A.; Mueen, A.; Batista, G. The UCR Time Series Classification Archive. 2015. Available online: www.cs.ucr.edu/~eamonn/time_series_data/ (accessed on 18 April 2015).
- Chen, K.; Kvasnicka, V.; Kanen, P.C.; Haykin, S. Feedforward Neural Network Methodology. IEEE Trans. Neural Netw. 2001, 12, 647–648. [Google Scholar] [CrossRef]
- Bagnall, A.; Lines, J.; Hills, J.; Bostrom, A. Time-Series Classification with COTE: The Collective of Transformation-Based Ensembles. IEEE Trans. Knowl. Data Eng. 2015, 27, 2522–2535. [Google Scholar] [CrossRef]
- Schafer, P. Scalable time series classification. Data Min. Knowl. Discov. 2016, 30, 1273–1298. [Google Scholar] [CrossRef]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Demsar, J. Statistical Comparisons of Classifiers over Multiple Data Sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- Gandhi, A. Content-based Image Retrieval: Plant Species Identification. Master’s Thesis, Oregon State University, Corvallis, OR, USA, 2011. [Google Scholar]
- Landgrebe, T.C.W.; Duin, R.P.W. Efficient Multiclass ROC Approximation by Decomposition via Confusion Matrix Perturbation Analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 810–822. [Google Scholar] [CrossRef] [PubMed]













| Methods | 1~(t-1) time-steps | (t-N-1)~(t-1) time-steps | 1~(t-1) time-steps (sampled at M) |
|---|---|---|---|
| Times of indexes |
| Dataset | Distance-Based | Feature-Based | ANN-Based | |||||
|---|---|---|---|---|---|---|---|---|
| 1NN-ED | 1NN-DTW | Shapelets | Features-RF | FNNs | RNNs | LSTM | BICORN-RNNs | |
| 50Words | 0.369(3) | 0.310(1) | 0.489(6) | 0.333(2) | 0.677(8) | 0.641(7) | 0.425(5) | 0.408(4) |
| ChlorineCon | 0.352(7) | 0.350(6) | 0.417(8) | 0.272(5) | 0.209(3) | 0.174(2) | 0.213(4) | 0.165(1) |
| ECG | 0.232(8) | 0.203(7) | 0.004(1) | 0.158(5) | 0.160(6) | 0.146(4) | 0.120(3) | 0.097(2) |
| Fish | 0.217(6) | 0.177(3) | 0.197(4) | 0.157(2) | 0.302(8) | 0.253(7) | 0.208(5) | 0.154(1) |
| MoteStrain | 0.121(4) | 0.165(5) | 0.217(8) | 0.103(2) | 0.194(7) | 0.188(6) | 0.101(1) | 0.114(3) |
| OliveOil | 0.133(3) | 0.167(5) | 0.213(7) | 0.093(1) | 0.302(8) | 0.150(4) | 0.211(6) | 0.102(2) |
| Lightning7 | 0.425(6) | 0.274(1) | 0.403(4) | 0.295(2) | 0.552(8) | 0.545(7) | 0.386(3) | 0.412(5) |
| SwedishLeaf | 0.213(5) | 0.208(4) | 0.269(8) | 0.088(2) | 0.259(7) | 0.248(6) | 0.103(3) | 0.087(1) |
| Symbols | 0.100(7) | 0.050(3) | 0.068(4) | 0.138(8) | 0.091(6) | 0.083(5) | 0.042(2) | 0.023(1) |
| SyntheticControl | 0.120(6) | 0.007(1) | 0.081(4) | 0.017(2) | 0.139(7) | 0.097(5) | 0.156(8) | 0.024(3) |
| Best | 0 | 3 | 1 | 1 | 0 | 0 | 1 | 4 |
| Better-3 | 2 | 5 | 1 | 7 | 1 | 1 | 5 | 8 |
| Mean-ranking | 5.5 | 3.6 | 5.4 | 3.1 | 6.8 | 5.3 | 4.0 | 2.3 |
| Experiments | SNR (dB) | Length (Time-Steps) | Missing Ratio (%) | Overlapping Ratio (%) |
|---|---|---|---|---|
| 4.2.2 | Range: 0~30 Step: 2 | 20 | 0 | 0 |
| 4.2.3 | 20 | Range: 5~100 Step: 5 | 0 | 0 |
| 4.2.4 | 20 | 20 | Range: 0~50 Step: 2 | 0 |
| 4.2.5 | 20 | 20 | 0 | Range: 0~100 Step: 5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Chang, Q.; Lu, H.; Liu, J. Reconstruct Recurrent Neural Networks via Flexible Sub-Models for Time Series Classification. Appl. Sci. 2018, 8, 630. https://doi.org/10.3390/app8040630
Ma Y, Chang Q, Lu H, Liu J. Reconstruct Recurrent Neural Networks via Flexible Sub-Models for Time Series Classification. Applied Sciences. 2018; 8(4):630. https://doi.org/10.3390/app8040630
Chicago/Turabian StyleMa, Ye, Qing Chang, Huanzhang Lu, and Junliang Liu. 2018. "Reconstruct Recurrent Neural Networks via Flexible Sub-Models for Time Series Classification" Applied Sciences 8, no. 4: 630. https://doi.org/10.3390/app8040630
APA StyleMa, Y., Chang, Q., Lu, H., & Liu, J. (2018). Reconstruct Recurrent Neural Networks via Flexible Sub-Models for Time Series Classification. Applied Sciences, 8(4), 630. https://doi.org/10.3390/app8040630





