Development of Proportional Pressure Control Valve for Hydraulic Braking Actuator of Automobile ABS
Abstract
:1. Introduction
- (1)
- When encountering an obstacle or any road conditions, it can be actuated by the steering wheel to obtain suitable tracking performance.
- (2)
- It can avoid excessive braking effects that can cause uncontrolled steering (if the front wheels are locked) or drifting (if the rear wheels are locked)
- (3)
- The electronic control braking effects can shorten the stopping distance.
- (1)
- Firstly, using electromagnetic theory and mathematical calculations, parameters of the new cone proportional electromagnet were analyzed, and then the electromagnet force using a simulation program was estimated.
- (2)
- Secondly, according to the configuration design (post-analysis), the production and electromagnet force test were completed.
- (3)
- Thirdly, the proportional valve was tested, and its relief pressure control capability for ABS control applications of the PEHB actuator was confirmed.
2. Analysis of Proportional Solenoid Force
2.1. Permeance of Air Gaps
2.2. Permeability of Air of the Proportional Electromagnet
2.3. Equivalent Permeance of Air Gaps
2.4. Permeance of Metal Zone Calculation
2.5. Solenoid Force of Proportional Electromagnet
3. Design and Simulation of Solenoid Force
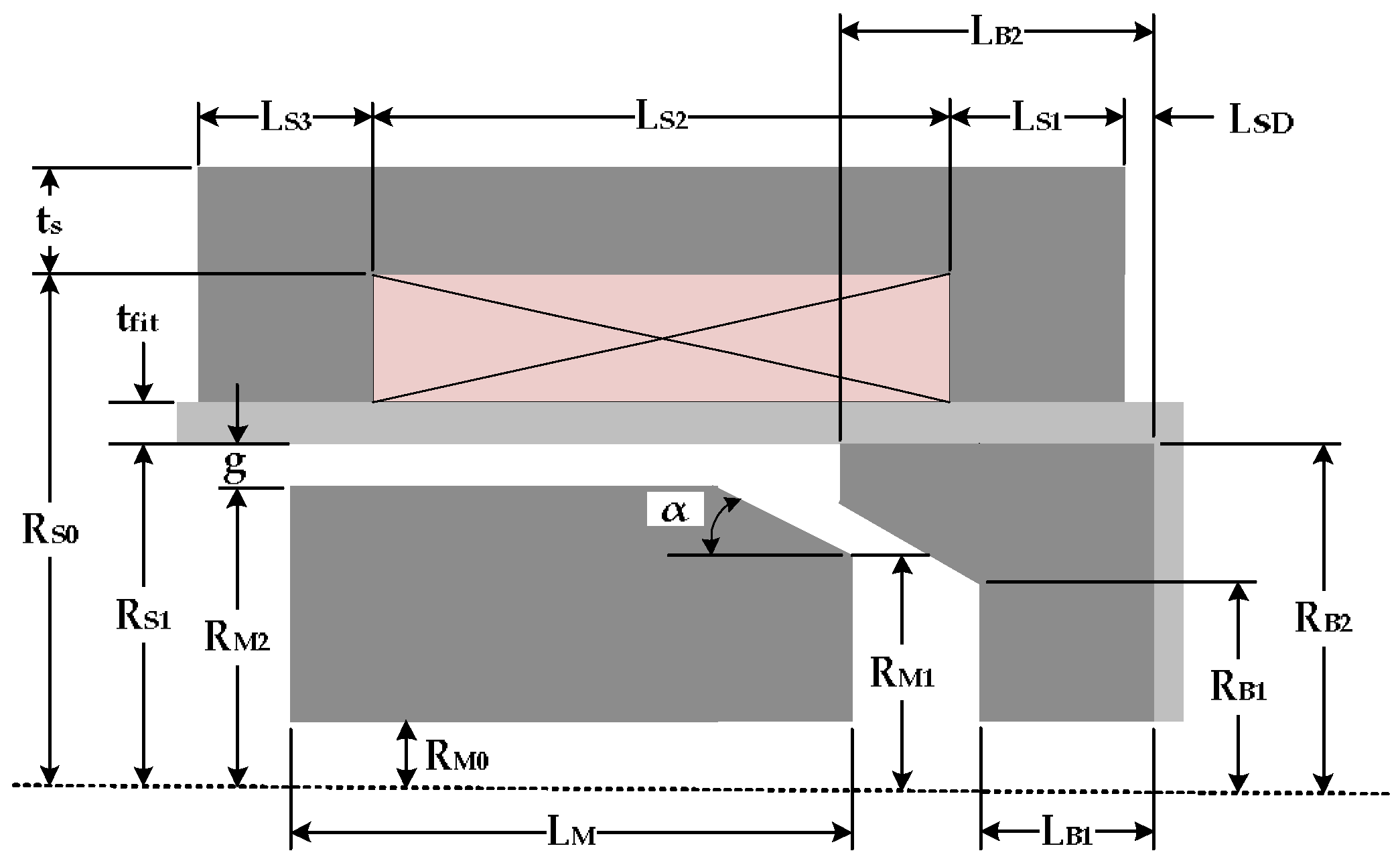
3.1. Configuration Parameter Design
3.1.1. Base Flange
3.1.2. Taper Angle
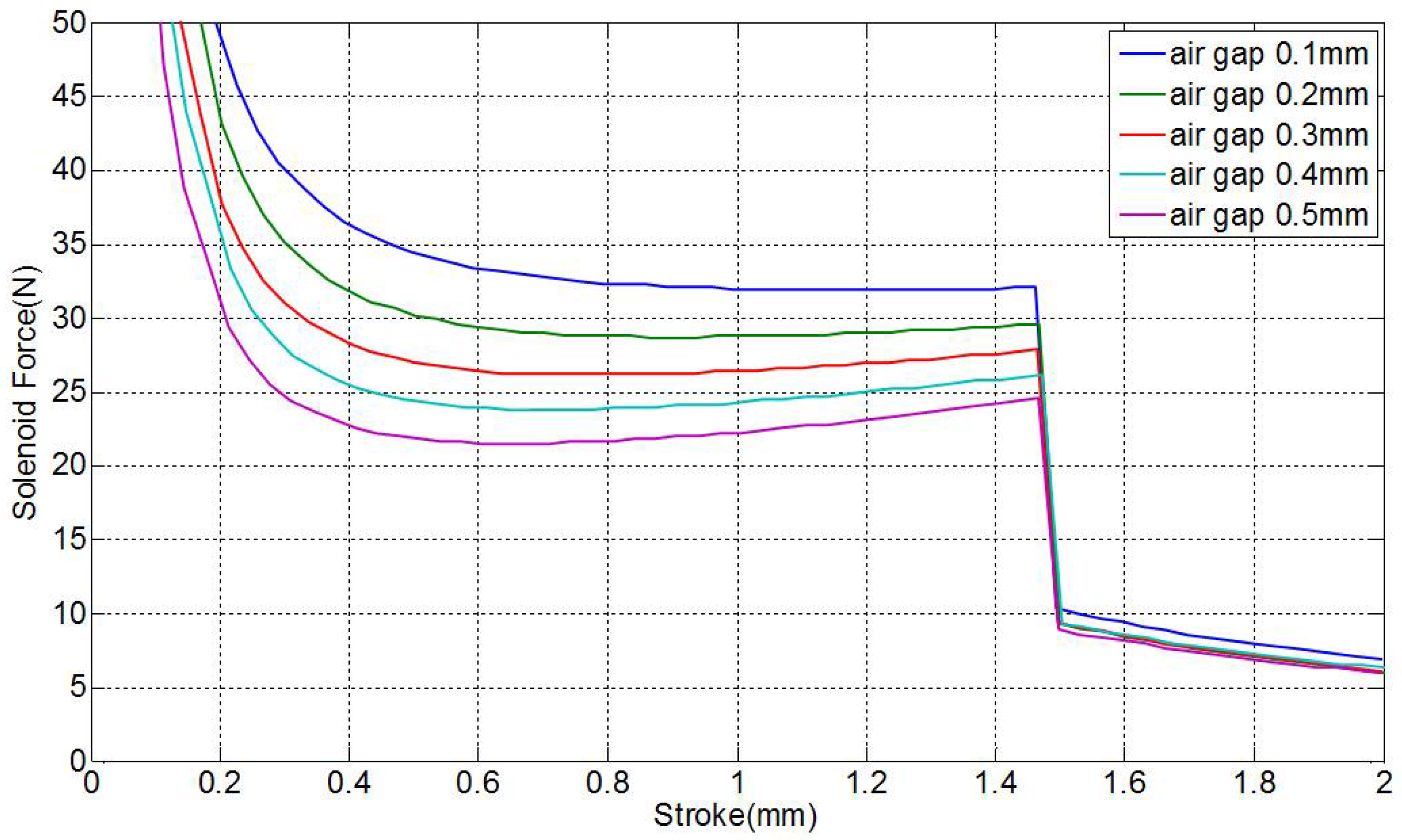
3.1.3. Air Gap
3.1.4. Parameter Design Results
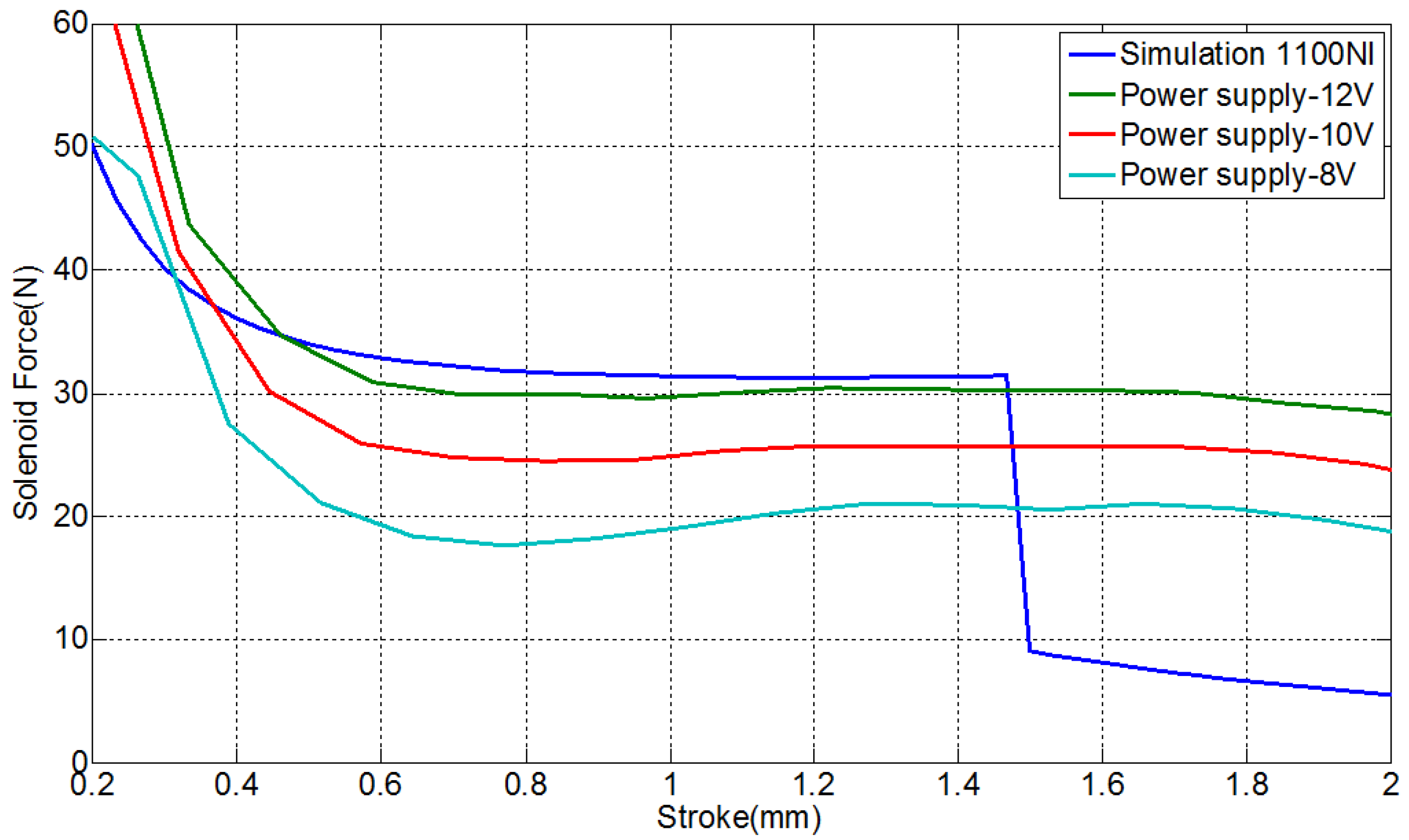
3.2. Simulation and Test Results of Armature Force
4. Design and Test of Proportional Valve
4.1. Design of the Proportional Valve Body
4.2. Single Proportional Valve Test
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Aksjonov, A.; Augsburg, K.; Vodovozov, V. Design and Simulation of the Robust ABS and ESP Fuzzy Logic Controller on the Complex Braking Maneuvers. Appl. Sci. 2016, 6, 382. [Google Scholar] [CrossRef]
- Ivanov, V.; Savitski, D.; Augsburg, K.; Barber, P.; Knauder, B.; Zehetner, J. Wheel slip control for all-wheel drive electric vehicle with compensation of road disturbances. J. Terramech. 2015, 61, 1–10. [Google Scholar] [CrossRef]
- Mirzaei, M.; Mirzaeinejad, H. Optimal design of a non-linear controller for anti-lock braking system. Transp. Res. Part C 2012, 24, 19–35. [Google Scholar] [CrossRef]
- Mirzaeinejad, H.; Mirzaei, M. A novel method for non-linear control of wheel slip in anti-lock braking systems. Control Eng. Pract. 2010, 18, 918–926. [Google Scholar] [CrossRef]
- Wang, B.; Huang, X.; Wang, J.; Guo, X.; Zhu, X. A robust wheel slip ratio control design combining hydraulic and regenerative braking systems for in-wheel-motors-driven electric Vehicles. J. Frankl. Inst. 2015, 352, 577–602. [Google Scholar] [CrossRef]
- Wu, M.C.; Shih, M.C. Simulated and experimental study of hydraulic anti-lock braking system using sliding-mode PWM control. Mechatronics 2003, 13, 331–351. [Google Scholar] [CrossRef]
- Qiuetal, Y.; Liang, X.; Dai, Z. Backstepping dynamic surface control for an anti-skid braking system. Control Eng. Pract. 2015, 42, 140–152. [Google Scholar]
- Tanelli, M.; Sartori, R.; Savaresi, S.M. Combining Slip and Deceleration Control for Brake-by-wire Control Systems: A Sliding-mode Approach. Eur. J. Control 2007, 6, 593–611. [Google Scholar] [CrossRef]
- Lv, C.; Zhang, J.; Li, Y.; Yuan, Y. Novel control algorithm of braking energy regeneration system for an electric vehicle during safety-critical driving maneuvers. Energy Convers. Manag. 2015, 106, 520–529. [Google Scholar] [CrossRef]
- Patra, N.; Datta, K. Observer based road-tire friction estimation for slip control of braking system. Procedia Eng. 2012, 38, 1566–1574. [Google Scholar] [CrossRef]
- Bhandari, R.; Patil, S.; Singh, R.K. Surface prediction and control algorithms for anti-lock brake system. Transp. Res. Part C 2012, 21, 181–195. [Google Scholar] [CrossRef]
- Choa, J.R.; Choia, J.H.; Yoo, W.S.; Kim, G.J.; Woo, J.S. Estimation of dry road braking distance considering frictional energy of patterned tires. Finite Elem. Anal. Des. 2006, 42, 1248–1257. [Google Scholar] [CrossRef]
- Chen, C.P.; Tung, C.; Chen, C.A. A Proportional Electro-Hydraulic Breaking Control Valve, Taiwan, 2010. Patent No. I320374, 11 February 2010. [Google Scholar]
- Lee, C.O.; Song, C.S. Analysis of the solenoid of a hydraulic proportional compound valve. In Proceedings of the 35th National Conference on Fluid, Chicago, IL, USA, 13–15 November 1979. [Google Scholar]
- Chen, Y.N.; Kuo, W.H. Analysis and Design of Proportional Pressure Control Valve. Master’s Thesis, National Taiwan University, Taipei, Taiwan, 1987. [Google Scholar]
- Chen, C.A.; Tung, C.; Chen, C.P. The Proportional Solenoid Module for a Hydraulic System, Taiwan, 2015. Patent No. I474350, 21 February 2015. [Google Scholar]
- Merritt, H.E. Hydraulic Control Systems, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1985; pp. 76–113. [Google Scholar]



















| Flux Path Model | Mean Path Length | Permeance () |
|---|---|---|
| I | ||
| II | ||
| III | ||
| IV | ||
| V | ||
| VI |
| Permeance | Mean Path Area | Mean Path Length () | Equation () |
|---|---|---|---|
| — | |||
| — | |||
| — | |||
| — | — | ||
| — |
| Mean Path Area () | Mean Path Length () | ||
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 |
| Feature | Location (Figure 8) | Design Size | Thrust (N) | Size V.S. Thrust | |
|---|---|---|---|---|---|
| Parameter | |||||
| base flange | 1.5 mm | 31 | Size ↑, Thrust ↓ | ||
| taper angle | α | 70 | 31 | Angle ↑, Thrust ↑ | |
| guide tube | 0.35 mm | 31 | Size ↑, Thrust ↓ | ||
| air gap | 0.1 mm | 32 | Size ↑, Thrust ↓ | ||
| armature diameter | 6.8 mm | 32 | Size ↑, Thrust ↑ | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.-P.; Chiang, M.-H. Development of Proportional Pressure Control Valve for Hydraulic Braking Actuator of Automobile ABS. Appl. Sci. 2018, 8, 639. https://doi.org/10.3390/app8040639
Chen C-P, Chiang M-H. Development of Proportional Pressure Control Valve for Hydraulic Braking Actuator of Automobile ABS. Applied Sciences. 2018; 8(4):639. https://doi.org/10.3390/app8040639
Chicago/Turabian StyleChen, Che-Pin, and Mao-Hsiung Chiang. 2018. "Development of Proportional Pressure Control Valve for Hydraulic Braking Actuator of Automobile ABS" Applied Sciences 8, no. 4: 639. https://doi.org/10.3390/app8040639
APA StyleChen, C.-P., & Chiang, M.-H. (2018). Development of Proportional Pressure Control Valve for Hydraulic Braking Actuator of Automobile ABS. Applied Sciences, 8(4), 639. https://doi.org/10.3390/app8040639




