A Review of MEMS Scale Piezoelectric Energy Harvester
Abstract
:1. Introduction
2. Research Progress of PEH
2.1. General Model of Energy Harvester
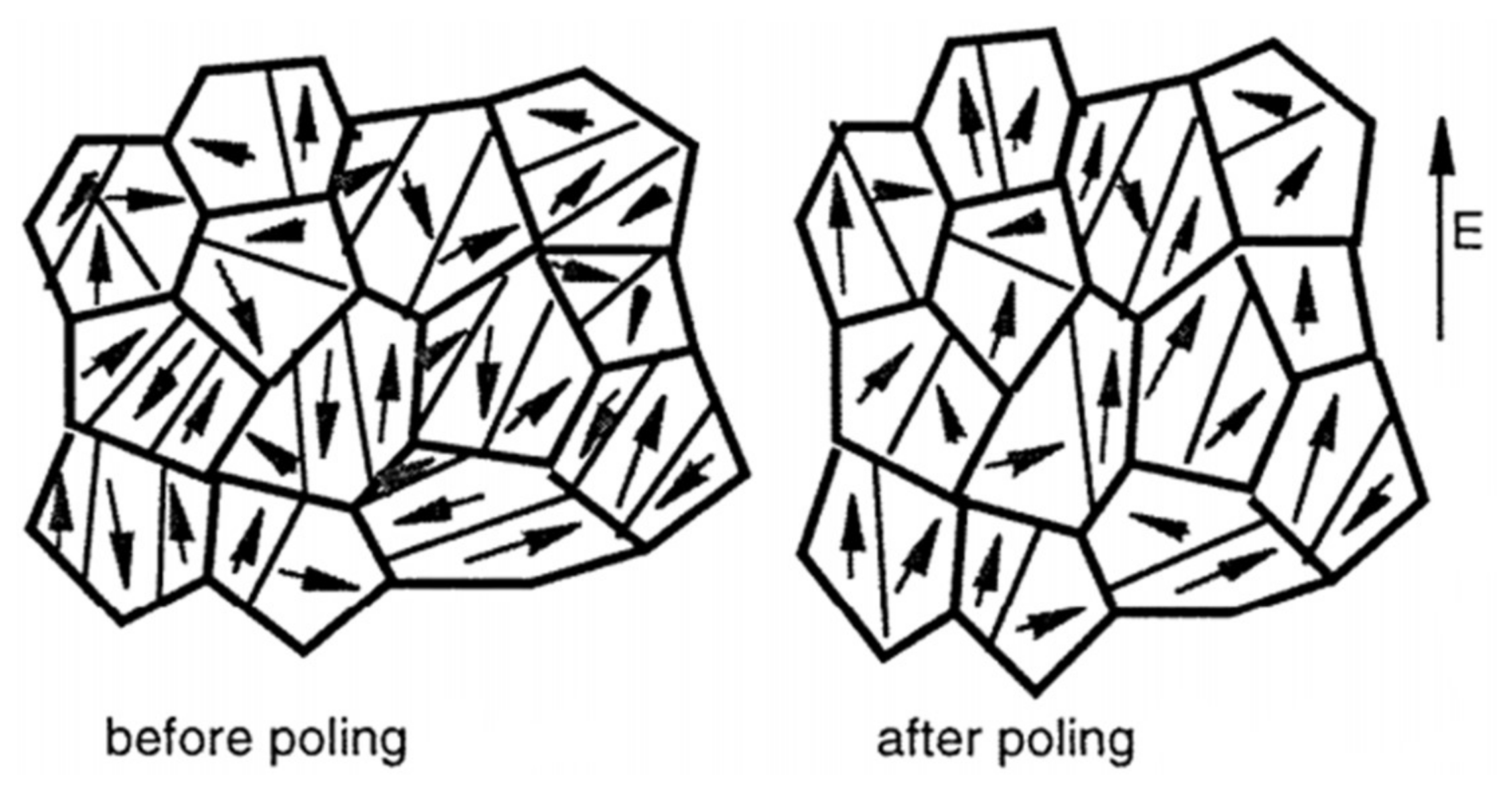
2.2. Research Progress of Piezoelectric Materials
2.3. Research and Improvement of Piezoelectric Modes
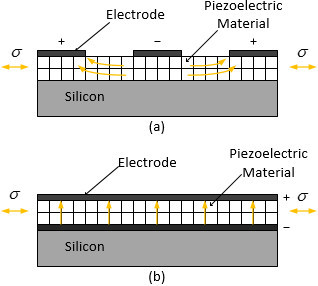
2.3.1. Piezoelectric Energy Harvesters in d31 and d33 Mode
2.3.2. Piezoelectric Energy Harvester in d15 Mode
2.4. Optimization of Energy Harvesters’ Structure
2.4.1. Adjusting the Resonant Frequency
2.4.2. Frequency Up-Converting
2.4.3. Broadening the Frequency Bandwidth of the PEH
2.4.4. Impedance Matching for the PEH
3. Analysis and Summaries
4. Prospect
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Puccinelli, D.; Haenggi, M. Wireless sensor networks: Applications and challenges of ubiquitous sensing. IEEE Circuits Syst. Mag. 2005, 5, 19–31. [Google Scholar] [CrossRef]
- Rault, T.; Bouabdallah, A.; Challal, Y.; Marin, F. A survey of energy-efficient context recognition systems using wearable sensors for healthcare applications. Pervasive Mob. Comput. 2017, 37, 23–44. [Google Scholar] [CrossRef]
- Park, G.; Farrar, C.R.; Todd, M.D.; Hodgkiss, W.; Rosing, T. Energy harvesting for structural health monitoring sensor networks. J. Infrastruct. Syst. 2007, 14, 64–79. [Google Scholar] [CrossRef]
- Brownfield, M.I.; Mehrjoo, K.; Fayez, A.S.; Iv, N.J.D. Wireless sensor network energy-adaptive MAC protocol. In Proceedings of the 3rd IEEE Consumer Communications and Networking Conference (CCNC), Las Vegas, NV, USA, 8–10 January 2006; pp. 778–782. [Google Scholar]
- Rashid, B.; Rehmani, M.H. Applications of wireless sensor networks for urban areas: A survey. J. Netw. Comput. Appl. 2016, 60, 192–219. [Google Scholar] [CrossRef]
- Vullers, R.J.M.; Van Schaijk, R.; Visser, H.J.; Penders, J.; Van Hoof, C. Energy harvesting for autonomous wireless sensor networks. IEEE Solid-State Circuits Mag. 2010, 2, 29–38. [Google Scholar] [CrossRef]
- Mateu, L.; Moll, F. Review of energy harvesting techniques and applications for microelectronics. In VLSI Circuits and Systems II, Pts 1 and 2; Lopez, J.F., Fernandez, F.V., LopezVillegas, J.M., DelaRosa, J.M., Eds.; Spie-Int Soc Optical Engineering: Bellingham, WA, USA, 2005; Volume 5837, pp. 359–373. [Google Scholar]
- Hu, Y.; Wang, Z.L. Recent progress in piezoelectric nanogenerators as a sustainable power source in self-powered systems and active sensors. Nano Energy 2015, 14, 3–14. [Google Scholar] [CrossRef]
- Naifar, S.; Bradai, S.; Viehweger, C.; Kanoun, O. Survey of electromagnetic and magnetoelectric vibration energy harvesters for low frequency excitation. Measurement 2017, 106, 251–263. [Google Scholar] [CrossRef]
- Remick, K.; Quinn, D.D.; McFarland, D.M.; Bergman, L.; Vakakis, A. High-frequency vibration energy harvesting from impulsive excitation utilizing intentional dynamic instability caused by strong nonlinearity. J. Sound Vib. 2016, 370, 259–279. [Google Scholar] [CrossRef]
- Tian, W.C.; Chen, Z.Q.; Cao, Y.R. Analysis and test of a new mems micro-actuator. Microsyst. Technol. 2016, 22, 943–952. [Google Scholar] [CrossRef]
- Tvedt, L.G.W.; Nguyen, D.S.; Halvorsen, E. Nonlinear behavior of an electrostatic energy harvester under wide- and narrowband excitation. J. Microelectromech. Syst. 2010, 19, 305–316. [Google Scholar] [CrossRef]
- Pillatsch, P.; Xiao, B.L.; Shashoua, N.; Gramling, H.M.; Yeatman, E.M.; Wright, P.K. Degradation of bimorph piezoelectric bending beams in energy harvesting applications. Smart Mater. Struct. 2017, 26, 035046. [Google Scholar] [CrossRef]
- El-Sayed, A.R.; Tai, K.; Biglarbegian, M.; Mahmud, S.; IEEE. A survey on recent energy harvesting mechanisms. In Proceedings of the 2016 IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), Vancouver, BC, Canada, 15–18 May 2016; IEEE: New York, NY, USA, 2016. [Google Scholar]
- Kholkin, A.; Amdursky, N.; Bdikin, I.; Gazit, E.; Rosenman, G. Strong piezoelectricity in bioinspired peptide nanotubes. ACS Nano 2010, 4, 610–614. [Google Scholar] [CrossRef] [PubMed]
- Malakooti, M.H.; Patterson, B.A.; Hwang, H.S.; Sodano, H.A. Zno nanowire interfaces for high strength multifunctional composites with embedded energy harvesting. Energy Environ. Sci. 2016, 9, 634–643. [Google Scholar] [CrossRef]
- Wang, Z.L. Triboelectric nanogenerators as new energy technology for self-powered systems and as active mechanical and chemical sensors. ACS Nano 2013, 7, 9533–9557. [Google Scholar] [CrossRef] [PubMed]
- Gasnier, P.; Willemin, J.; Chaillout, J.J.; Condemine, C.; Despesse, G.; Boisseau, S.; Gouvernet, G.; Barla, C. Power conversion and integrated circuit architecture for high voltage piezoelectric energy harvesting. Proccedings of the 2012 IEEE 10th International New Circuits and Systems Conference (NEWCAS), Montreal, QC, Canada, 17–20 June 2012; pp. 377–380. [Google Scholar]
- Tian, W.C.; Chen, Z.Q. Analysis of a double-phase regulation and an ultra wideband tunable micro electromechanical system resonator. In Proceedings of the 2015 16th International Conference on Electronic Packaging Technology (ICEPT), Changsha, China, 11–14 August 2015; pp. 1149–1153. [Google Scholar]
- Hosseinloo, A.H.; Turitsyn, K. Non-resonant energy harvesting via an adaptive bistable potential. Smart Mater. Struct. 2016, 25, 015010. [Google Scholar] [CrossRef]
- Andò, B.; Baglio, S.; Bulsara, A.R.; Marletta, V.; Pistorio, A. Investigation of a nonlinear energy harvester. IEEE Trans. Instrum. Meas. 2017, 66, 1067–1075. [Google Scholar] [CrossRef]
- Iannacci, J.; Sordo, G.; Serra, E.; Schmid, U. The mems four-leaf clover wideband vibration energy harvesting device: Design concept and experimental verification. Microsyst. Technol. 2016, 22, 1865–1881. [Google Scholar] [CrossRef]
- Sodano, H.A.; Park, G.; Inman, D.J. Estimation of electric charge output for piezoelectric energy harvesting. Strain 2004, 40, 49–58. [Google Scholar] [CrossRef]
- Williams, C.; Yates, R.B. Analysis of a micro-electric generator for microsystems. Sens. Actuator A Phys. 1996, 52, 8–11. [Google Scholar] [CrossRef]
- Roundy, S.; Wright, P.K.; Rabaey, J. A study of low level vibrations as a power source for wireless sensor nodes. Comput. Commun. 2003, 26, 1131–1144. [Google Scholar] [CrossRef]
- Koptsik, V.A.; Rez, I.S. From the history of physics: Pierre curie’s works in the field of crystal physics (on the one-hundredth anniversary of the discovery of the piezoelectric effect). Sov. Phys. Uspekhi 1981, 24, 426. [Google Scholar] [CrossRef]
- Damjanovic, D. Ferroelectric, dielectric and piezoelectric properties of ferroelectric thin films and ceramics. Rep. Prog. Phys. 1998, 61, 1267–1324. [Google Scholar] [CrossRef]
- Bernstein, J.J.; Bottari, J.; Houston, K.; Kirkos, G.; Miller, R.; Xu, B.; Ye, Y.; Cross, L.E. Advanced mems ferroelectric ultrasound 2D arrays. In Proceedings of the 1999 IEEE Ultrasonics Symposium, Caesars Tahoe, NV, USA, 17–20 October 1999; Schneider, S.C., Levy, M., McAvoy, B.R., Eds.; IEEE: New York, NY, USA, 1999; pp. 1145–1153. [Google Scholar]
- Tressler, J.F.; Alkoy, S.; Newnham, R.E. Piezoelectric sensors and sensor materials. J. Electroceram. 1998, 2, 257–272. [Google Scholar] [CrossRef]
- Kawai, H. The piezoelectricity of poly (vinylidene fluoride). Jpn. J. Appl. Phys. 1969, 8, 975. [Google Scholar] [CrossRef]
- Zeng, W.; Tao, X.M.; Chen, S.; Shang, S.M.; Chan, H.L.W.; Choy, S.H. Highly durable all-fiber nanogenerator for mechanical energy harvesting. Energy Environ. Sci. 2013, 6, 2631–2638. [Google Scholar] [CrossRef]
- Soin, N.; Shah, T.H.; Anand, S.C.; Geng, J.F.; Pornwannachai, W.; Mandal, P.; Reid, D.; Sharma, S.; Hadimani, R.L.; Bayramol, D.V.; et al. Novel “3-D spacer” all fibre piezoelectric textiles for energy harvesting applications. Energy Environ. Sci. 2014, 7, 1670–1679. [Google Scholar] [CrossRef]
- Takenaka, T.; Okuda, T.; Takegahara, K. Lead-free piezoelectric ceramics based on (Bi1/2Na1/2)TiO3-NaNbO3. Ferroelectrics 1997, 196, 175–178. [Google Scholar] [CrossRef]
- Guo, Y.; Kakimoto, K.I.; Ohsato, H. (Na0.5K0.5)NbO3–LiTaO3 lead-free piezoelectric ceramics. Mater. Lett. 2005, 59, 241–244. [Google Scholar] [CrossRef]
- Li, J.F.; Wang, K.; Zhang, B.P.; Zhang, L.M. Ferroelectric and piezoelectric properties of fine-grained Na0.5K0.5NbO3 lead-free piezoelectric ceramics prepared by spark plasma sintering. J. Am. Ceram. Soc. 2006, 89, 706–709. [Google Scholar] [CrossRef]
- Lin, D.; Xiao, D.; Zhu, J.; Yu, P. Piezoelectric and ferroelectric properties of [Bi0.5(Na1−x−yKxLiy)0.5]TiO3 lead-free piezoelectric ceramics. Appl. Phys. Lett. 2006, 88, 062901. [Google Scholar] [CrossRef]
- Lin, Y.; Zhang, L.; Yu, J. Piezoelectric and ferroelectric property in Mn-doped 0.69BiFeO3–0.04Bi(Zn1/2Ti1/2)O3–0.27BaTiO3 lead-free piezoceramics. J. Mater. Sci.-Mater. Electron. 2016, 27, 1955–1965. [Google Scholar] [CrossRef]
- Cheng, C.M.; Pei, C.H.; Chen, M.L.; Chen, K.H. The inferences of ZnO additions for LKNNT lead-free piezoelectric ceramics. Integr. Ferroelectr. 2016, 168, 61–68. [Google Scholar] [CrossRef]
- Shi, J.; Tian, W.; Liu, X.; Fan, H. Electric-field induced phase transition and fatigue behaviors of (Bi0.5+x/2Na0.5−x/2)0.94Ba0.06Ti1−xFexO3 ferroelectrics. J. Am. Ceram. Soc. 2017, 100, 1080–1090. [Google Scholar] [CrossRef]
- Koruza, J.; Rojas, V.; Molina-Luna, L.; Kunz, U.; Duerrschnabel, M.; Kleebe, H.J.; Acosta, M. Formation of the core–shell microstructure in lead-free Bi1/2Na1/2TiO3-SrTiO3 piezoceramics and its influence on the electromechanical properties. J. Eur. Ceram. Soc. 2016, 36, 1009–1016. [Google Scholar] [CrossRef]
- Martins, P.; Lopes, A.C.; Lanceros-Mendez, S. Electroactive phases of poly(vinylidene fluoride): Determination, processing and applications. Prog. Polym. Sci. 2014, 39, 683–706. [Google Scholar] [CrossRef]
- Kornphom, C.; Vittayakorn, N.; Bongkarn, T. Lead-free piezoelectric ceramics based on (1 − x)BNKLLT–xBCTZ binary solid solutions synthesized by the solid-state combustion technique. J. Mater. Sci. 2016, 51, 4142–4149. [Google Scholar] [CrossRef]
- Machado, R.; Santos, V.B.D.; Ochoa, D.A.; Cerdeiras, E.; Mestres, L.; García, J.E. Elastic, dielectric and electromechanical properties of (Bi0.5Na0.5)TiO3-BaTiO3 piezoceramics at the morphotropic phase boundary region. J. Alloys Compd. 2017, 690, 568–574. [Google Scholar] [CrossRef]
- Weng, C.-M.; Tsai, C.-C.; Hong, C.-S.; Sheen, J.; Chu, S.-Y.; Tang, J.-F.; Zou, Y.-H. Effects of LiNbO3-doping on properties of (Na0.535K0.48)NbO3 piezoelectric ceramics with high electromechanical coupling coefficient for application in surface acoustic wave devices. Ceram. Int. 2017, 43, 11324–11330. [Google Scholar] [CrossRef]
- Chen, Y.; Xue, D.; Chen, Z.; Jiang, X.; Gou, J.; Liu, G.; Liu, X.; Xu, Z. Lithium-modified (K0.5Na0.5)NbO3–BiAlO3 lead-free piezoelectric ceramics with high curie temperature. Ceram. Int. 2017, 43, 634–640. [Google Scholar] [CrossRef]
- Chhabra, P.; Sharma, A.; Krishna, N.P.V. Fabrication and characterisation of bulk micromachined zno energy transducer with interdigitated electrodes. Microsyst. Technol. 2016, 22, 1055–1066. [Google Scholar] [CrossRef]
- Deng, L.; Wen, Z.; Zhao, X.; Yuan, C.; Luo, G.; Mo, J. High voltage output mems vibration energy harvester in d31 mode with pzt thin film. J. Microelectromech. Syst. 2014, 23, 855–861. [Google Scholar] [CrossRef]
- Kulkarni, V.; Ben-Mrad, R.; Prasad, S.E. A torsion based shear mode piezoelectric energy harvester for wireless sensor modules. In Proceedings of the ASME 2014 International Mechanical Engineering Congress and Exposition, Montreal, QC, Canada, 14–20 November 2014; p. V04BT04A053. [Google Scholar]
- Sherman, C.H.; Butler, J.L. Transducers and arrays for underwater sound. J. Acoust. Soc. Am. 2008, 124, 1385. [Google Scholar]
- Kim, S.B.; Park, H.; Kim, S.H.; Wikle, H.C.; Park, J.H.; Kim, D.J. Comparison of mems pzt cantilevers based on d31 and d33 modes for vibration energy harvesting. J. Microelectromech. Syst. 2013, 22, 26–33. [Google Scholar] [CrossRef]
- Bowen, C.R.; Nelson, L.J.; Stevens, R.; Cain, M.G.; Stewart, M. Optimisation of interdigitated electrodes for piezoelectric actuators and active fibre composites. J. Electroceram. 2006, 16, 263–269. [Google Scholar] [CrossRef]
- Chidambaram, N.; Mazzalai, A.; Balma, D.; Muralt, P. Comparison of lead zirconate titanate thin films for microelectromechanical energy harvester with interdigitated and parallel plate electrodes. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 1564. [Google Scholar] [CrossRef] [PubMed]
- Gevorgian, S.S.; Martinsson, T.; Linner, P.L.J.; Kollberg, E.L. Cad models for multilayered substrate interdigital capacitors. IEEE Trans. Microw. Theory Tech. 1996, 44, 896–904. [Google Scholar] [CrossRef]
- Yang, S.; Dong, W.; Wang, D.; Yin, X. Study of complete interdigital electrode d33 mode piezoelectric cantilever energy harvester. Transducer Microsyst. Technol. 2015, 34, 52–55. [Google Scholar]
- Cho, H.; Park, J.; Park, J.Y. Micro-fabricated flexible pzt cantilever using d33 mode for energy harvesting. Micro Nano Syst. Lett. 2017, 5, 20. [Google Scholar] [CrossRef]
- Kim, H.; Tadesse, Y.; Priya, S. Piezoelectric energy harvesting. In Energy Harvesting Technologies; Priya, S., Inman, D.J., Eds.; Springer: Boston, MA, USA, 2009; pp. 3–39. [Google Scholar]
- Malakooti, M.H.; Sodano, H.A. Shear mode energy harvesting of piezoelectric sandwich beam. In Active and Passive Smart Structures and Integrated Systems 2013; Sodano, H.A., Ed.; Spie-Int Soc Optical Engineering: Bellingham, WA, USA, 2013; Volume 8688. [Google Scholar]
- Malakooti, M.H.; Sodano, H.A. Piezoelectric energy harvesting through shear mode operation. Smart Mater. Struct. 2015, 24, 055005. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Najar, F.; Nayfeh, A.H.; Ben Ayed, S. An energy harvester using piezoelectric cantilever beams undergoing coupled bending-torsion vibrations. Smart Mater. Struct. 2011, 20, 115007. [Google Scholar] [CrossRef]
- Gao, S.; Zhang, G.; Jin, L.; Li, P.; Liu, H. Study on characteristics of the piezoelectric energy-harvesting from the torsional vibration of thin-walled cantilever beams. Microsyst. Technol. 2017, 23, 5455–5465. [Google Scholar] [CrossRef]
- Kulkarni, V.; Ben-Mrad, R.; Prasad, S.E.; Nemana, S. A shear-mode energy harvesting device based on torsional stresses. IEEE/ASME Trans. Mechatron. 2014, 19, 801–807. [Google Scholar] [CrossRef]
- Ferrari, M.; Ferrari, V.; Guizzetti, M.; Andò, B.; Baglio, S.; Trigona, C. Improved energy harvesting from wideband vibrations by nonlinear piezoelectric converters. Sens. Actuator A Phys. 2010, 162, 425–431. [Google Scholar] [CrossRef]
- Liu, H.; Lee, C.; Kobayashi, T.; Tay, C.J.; Quan, C. A new S-shaped MEMS PZT cantilever for energy harvesting from low frequency vibrations below 30 Hz. Microsyst. Technol. 2012, 18, 497–506. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, J.; Takei, R.; Makimoto, N.; Itoh, T.; Kobayashi, T. S-shape spring sensor: Sensing specific low-frequency vibration by energy harvesting. Rev. Sci. Instrum. 2016, 87, 085005. [Google Scholar] [CrossRef] [PubMed]
- Karami, M.A.; Inman, D.J. Electromechanical modeling of the low-frequency zigzag micro-energy harvester. J. Intell. Mater. Syst. Struct. 2011, 22, 271–282. [Google Scholar] [CrossRef]
- Kim, I.H.; Jin, S.S.; Jang, S.J.; Jung, H.J. A performance-enhanced energy harvester for low frequency vibration utilizing a corrugated cantilevered beam. Smart Mater. Struct. 2014, 23, 623–626. [Google Scholar] [CrossRef]
- Kulah, H.; Najafi, K. Energy scavenging from low-frequency vibrations by using frequency up-conversion for wireless sensor applications. IEEE Sens. J. 2008, 8, 261–268. [Google Scholar] [CrossRef]
- Chen, S.; Ma, L.; Chen, T.; Liu, H.; Sun, L.; Wang, J. Modeling and verification of a piezoelectric frequency-up-conversion energy harvesting system. Microsyst. Technol. 2017, 23, 2459–2466. [Google Scholar] [CrossRef]
- Kwon, D.S.; Ko, H.J.; Kim, J. Piezoelectric and electromagnetic hybrid energy harvester using two cantilevers for frequency up-conversion. In Proceedings of the IEEE International Conference on MICRO Electro Mechanical Systems, Las Vegas, NV, USA, 22–26 January 2017. [Google Scholar]
- Halim, M.A.; Park, J.Y. A non-resonant, frequency up-converted electromagnetic energy harvester from human-body-induced vibration for hand-held smart system applications. J. Appl. Phys. 2014, 115, 094901. [Google Scholar] [CrossRef]
- Halim, M.A.; Park, J.Y. Piezoelectric energy harvester using impact-driven flexible side-walls for human-limb motion. Microsyst. Technol. 2018, 24, 2099–2107. [Google Scholar] [CrossRef]
- Jeong, S.W.; Yoo, H.H. Bi-stable cantilevered piezoelectric energy harvester using springs. In Proceedings of the 23rd International Congress on Sound and Vibration: From Ancient to Modern Acoustics, Athens, Greece, 10–14 July 2016; Vogiatzis, K., Kouroussis, G., Crocker, M., Pawelczyk, M., Eds.; International Institute Acoustics & Vibration: Auburn, AL, USA, 2016. [Google Scholar]
- Braghin, F.; Mehdipour, I.; Lecis, N.; Galassi, C. Periodic substructure for multi-frequency energy harvesting with single piezoelectric patch. In Active and Passive Smart Structures and Integrated Systems 2016; Park, G., Ed.; Spie-Int Soc Optical Engineering: Bellingham, WA, USA, 2016; Volume 9799. [Google Scholar]
- Yang, W.; Towfighian, S. A hybrid nonlinear vibration energy harvester. Mech. Syst. Signal Process. 2017, 90, 317–333. [Google Scholar] [CrossRef]
- Wang, X.; Chen, C.; Wang, N.; San, H.; Yu, Y.; Halvorsen, E.; Chen, X. A frequency and bandwidth tunable piezoelectric vibration energy harvester using multiple nonlinear techniques. Appl. Energy 2017, 190, 368–375. [Google Scholar] [CrossRef]
- Bao, M.; Yang, H. Squeeze film air damping in mems. Sens. Actuator A Phys. 2007, 136, 3–27. [Google Scholar] [CrossRef]
- Schmidt, V.H. Theoretical electrical power output per unit voume of PVF2 and mechanical-to-electrical conversion efficiency as functions of frequency. In Proceedings of the 6th IEEE International Symposium on Applications of Ferroelectrics, Bethlehem, PA, USA, 8–11 June 1986; pp. 538–542. [Google Scholar]
- Le, T.T.; Han, J.F.; von Jouanne, A.; Mayaram, K.; Fiez, T.S. Piezoelectric micro-power generation interface circuits. IEEE J. Solid-State Circuits 2006, 41, 1411–1420. [Google Scholar] [CrossRef]
- Woo, M.S.; Ahn, J.H.; Eom, J.H.; Hwang, W.S.; Kim, J.H.; Yang, C.H.; Song, G.J.; Hong, S.D.; Jhun, J.P.; Sung, T.H. Study on increasing output current of piezoelectric energy harvester by fabrication of multilayer thick film. Sens. Actuator A Phys. 2018, 269, 524–534. [Google Scholar] [CrossRef]











| Materials | d31 (pC/N) | d33 (pC/N) | Kp (%) | ɛr | TCurie (°C) | Reference |
|---|---|---|---|---|---|---|
| PZT-2 | −60.2 | 152 | 47 | - | 370 | |
| PZT-4 | −123 | 289 | 58 | - | 328 | |
| PZT-5A | −171 | 374 | 60 | - | 365 | |
| PZT-5H | −274 | 593 | 65 | - | 193 | |
| PZT-8 | −37 | 225 | 51 | - | 300 | |
| (Na0.5K0.5)NbO3-LiTaO3 | - | 200 | 36 | 570 | - | [34] |
| (Na0.5K0.5)NbO3 | - | 148 | 38.9 | 606 | 395 | [35] |
| [Bi0.5(Na1−x−yKxLiy)0.5]TiO3 | - | 231 | 41.0 | 1190 | - | [36] |
| 0.69BiFeO–0.04Bi(ZnTi)O–0.27BaTiO (MoOdoped) | - | 145 | 41.0 | - | 510 | [37] |
| Li0.058(K0.480Na0.535)0.966(Nb0.9Ta0.1)O3(ZnO doped) | - | 272 | 44 | 5081 | 395 | [38] |
| Bi0.5(Na0.68K0.22Li0.1)0.5TiO3 ((Ba0.90Ca0.10)(Ti0.85Zr0.15)O3 doped) | - | 295 | - | 2720 | - | [42] |
| (Bi0.5Na0.5)TiO3(BaTiO3doped) | 37 | 180 | - | 1557 | - | [43] |
| ((Na0.535K0.48)NbO3(LiNbO3 doped) | 150 | 50 | 5500 | 470 | [44] | |
| 0.995(K0.5Na0.5)1−xLixNbO3–0.005BiAlO3 | 182 | 37.5 | 5000 | 450 | [45] | |
| PVDF | 8~22 | −24~−34 | - | - | - | |
| P(VDF-TrFE) | 12 | −38 | - | - | - | |
| P(VDF-HFP) | 30 | −24 | - | - | - | |
| P(VDF-CTFE) | - | −140 | - | - | - |
| Structure | Max Power | Max Voltage | Bandwidth (Hz) | Frequency (Hz) | Excitation Acceleration (g) | Reference |
|---|---|---|---|---|---|---|
| S-shaped cantilever | 1.117 nW | 42.1mV | - | 27.4 | 0.06 | [63] |
| Wavy cantilever | - | 91.8V/g | - | 6.0 | 0.1 | [66] |
| Flexible sidewall | 175 µW | - | - | 4.96 | 2 | [71] |
| S-shaped cantilever with a stopper | 2.8nW/g2 (np) | 16 mV | 10.1 | 23.5–33.6 | 0.3 | [63] |
| Cantilever attached to the spring | 2.5 mW | 15 V | 6 | 1–7 | 0.3 | [72] |
| Cantilevers with three intrinsic frequencies | - | - | - | 41.31 56.85 79.78 | - | [73] |
| Parallel-plate | - | 0.733 V | 100 | 250–350 | 1.5 | [75] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, W.; Ling, Z.; Yu, W.; Shi, J. A Review of MEMS Scale Piezoelectric Energy Harvester. Appl. Sci. 2018, 8, 645. https://doi.org/10.3390/app8040645
Tian W, Ling Z, Yu W, Shi J. A Review of MEMS Scale Piezoelectric Energy Harvester. Applied Sciences. 2018; 8(4):645. https://doi.org/10.3390/app8040645
Chicago/Turabian StyleTian, Wenchao, Zongyu Ling, Wenbo Yu, and Jing Shi. 2018. "A Review of MEMS Scale Piezoelectric Energy Harvester" Applied Sciences 8, no. 4: 645. https://doi.org/10.3390/app8040645
APA StyleTian, W., Ling, Z., Yu, W., & Shi, J. (2018). A Review of MEMS Scale Piezoelectric Energy Harvester. Applied Sciences, 8(4), 645. https://doi.org/10.3390/app8040645