On the Statistical Characterization of Lightning-Induced Voltages
Abstract
:1. Introduction
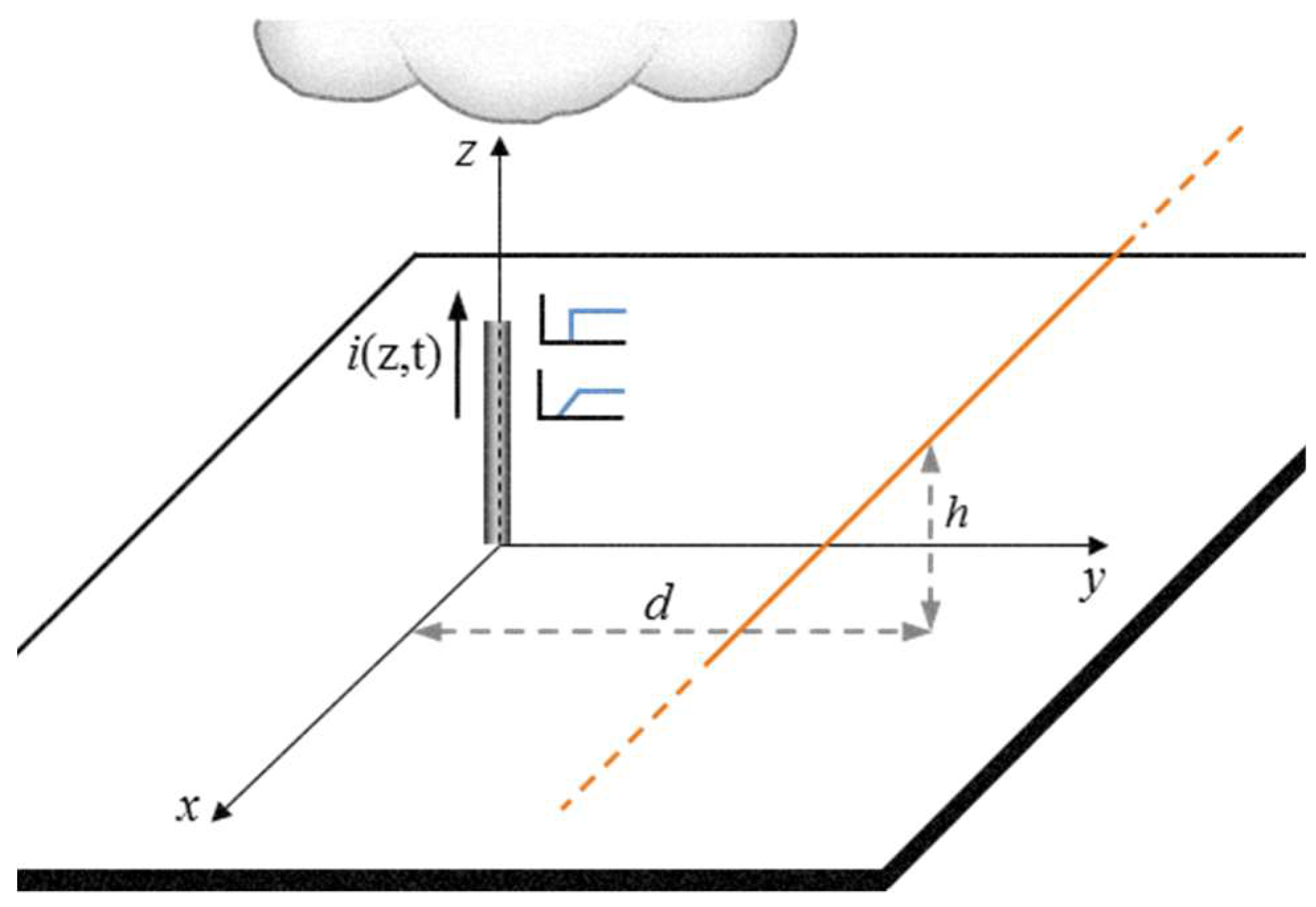
2. Lightning-Induced Voltage: AESs
2.1. Step-Funcion Current
2.2. Linearly-Rising Current
2.3. Finite Conductivity Ground Effects and Countermeasures to Mitigate the Induced Overvoltages
3. Statistical Characterization of the Lightning Parameters
- –
- the current peak and the distance in the case of the step-function current, and
- –
- the above two variables along with front time , which is provided in terms of T-10 ( = T-10/0.8) [10], in the case of the linearly-rising current.
4. Numerical Applications
4.1. Step-Function Current
4.2. Linearly-Rising Current
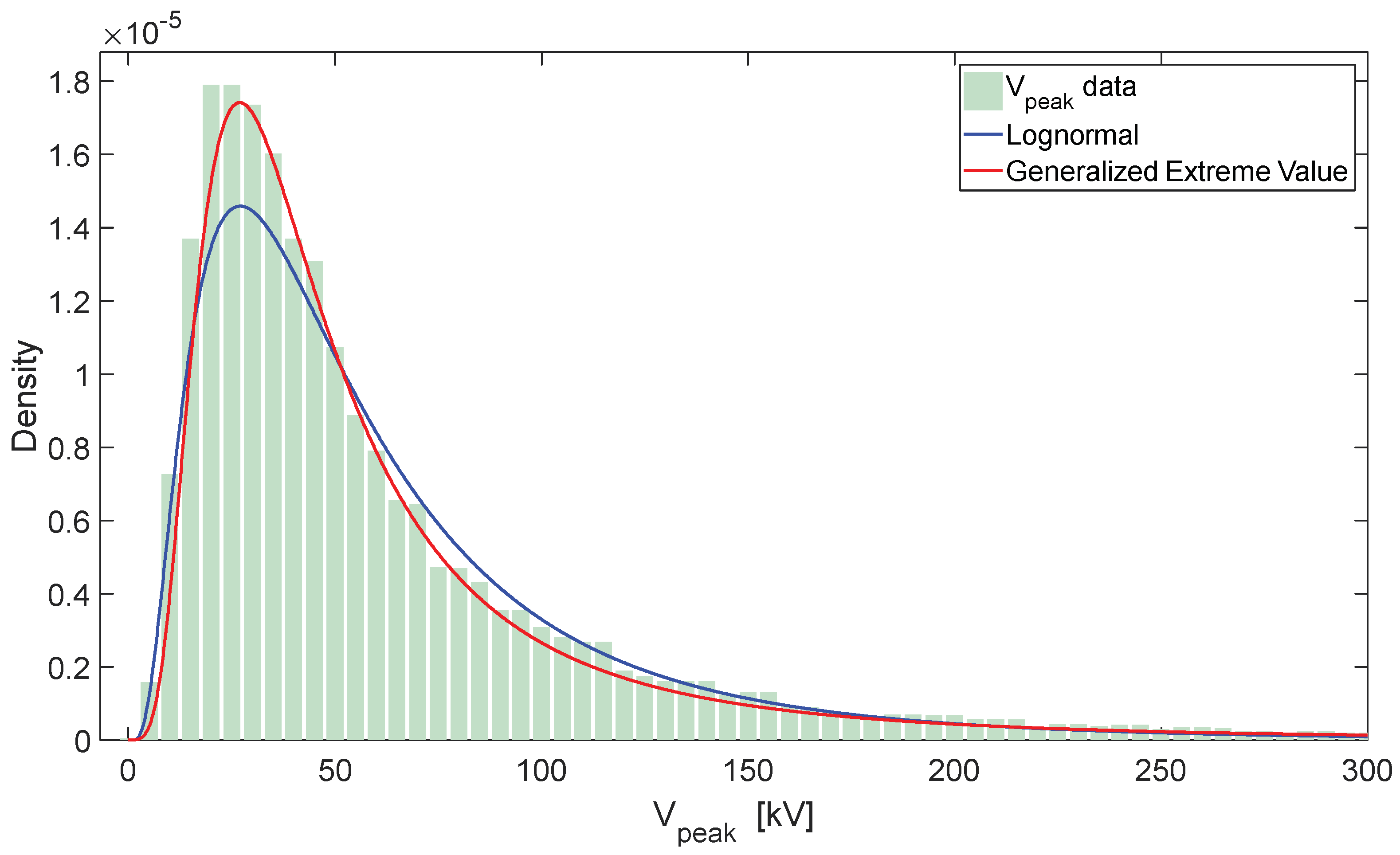
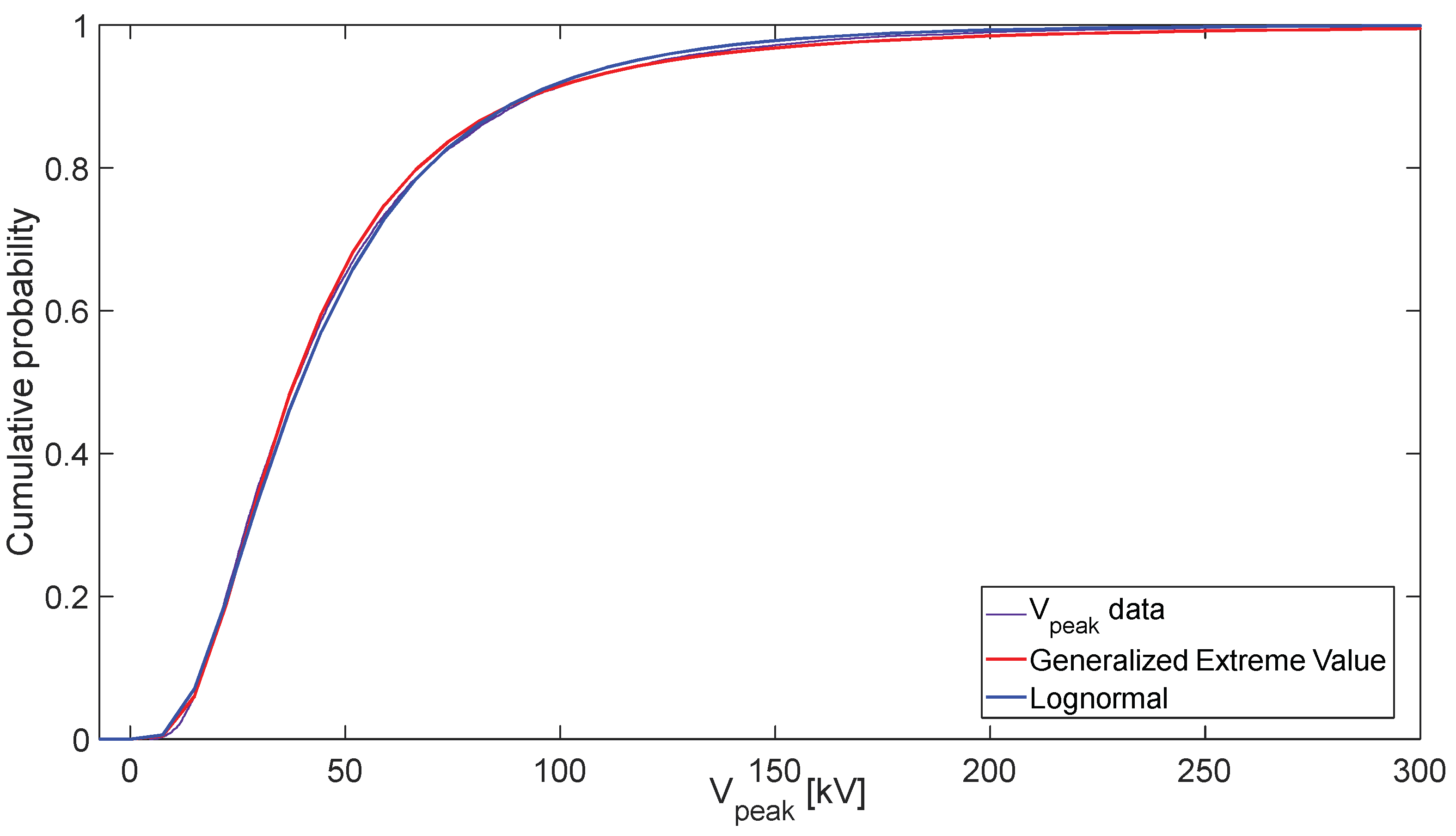
4.3. Comparison with Experimental Data
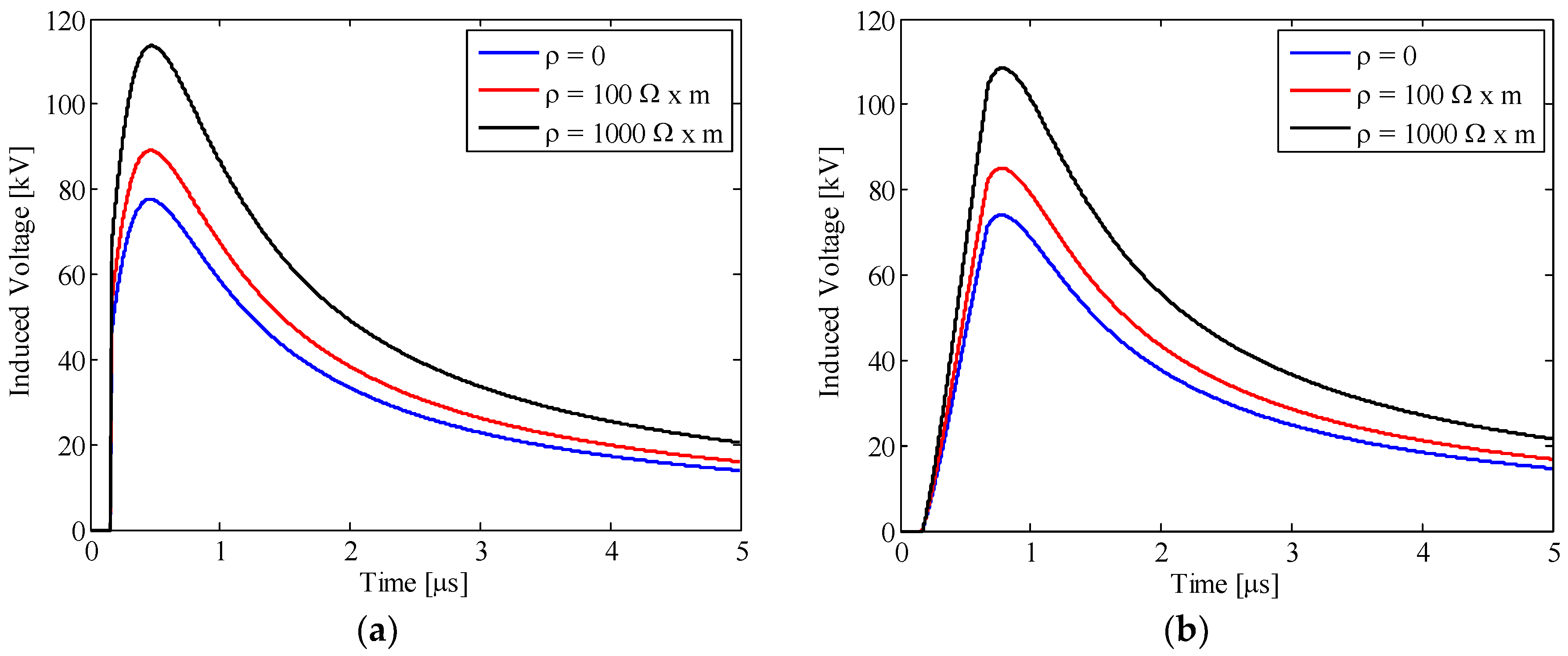
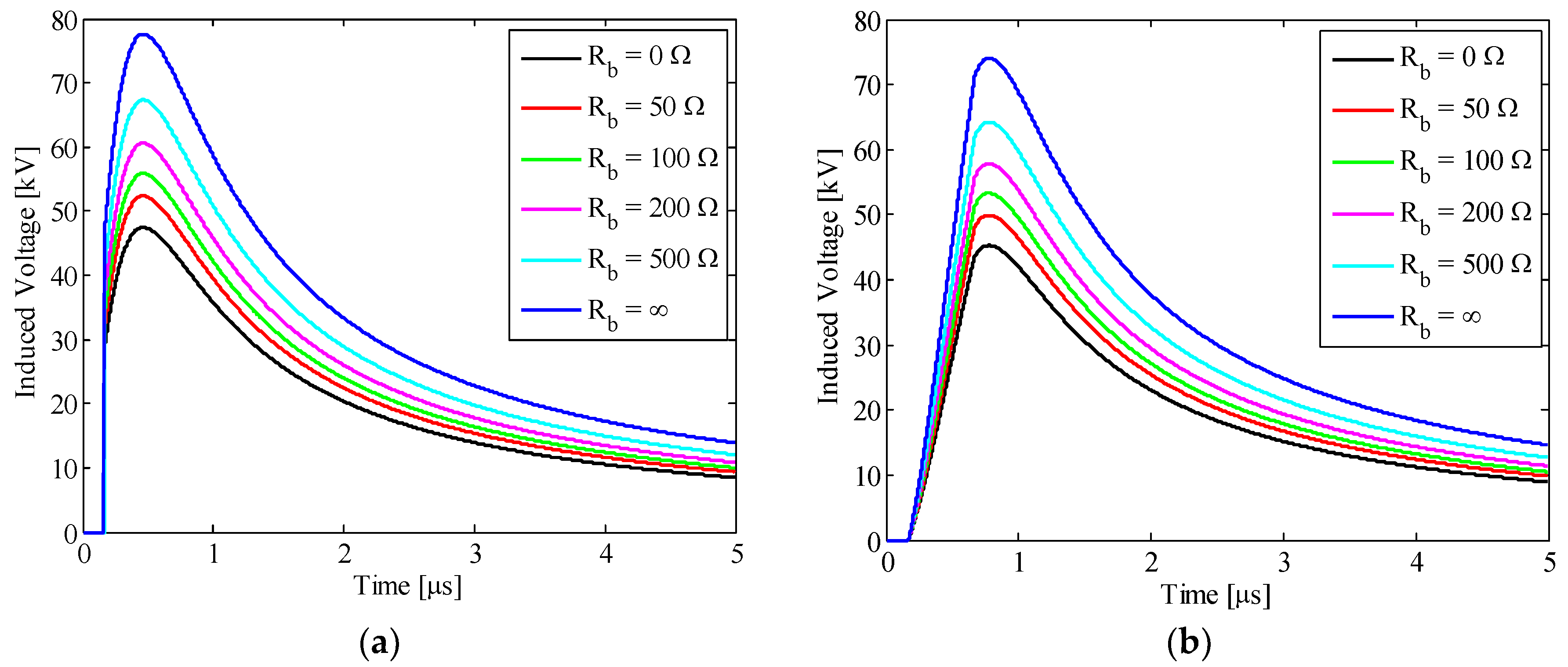
4.4. Effect of the Countermeasures to Mitigate the Induced Overvoltages
4.5. Discussions of the Results
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Zaini, N.H.; Ab Kadir, M.Z.A.; Mohd Radzi, M.A.; Izadi, M.; Azis, N.; Ahmad, N.I.; Nasir, M.S.M. Lightning surge analysis on a large scale grid-connected solar photovoltaic system. Energies 2017, 10, 2149. [Google Scholar] [CrossRef]
- Shaban, M.; Salam, M.A.; Ang, S.P.; Voon, W. Induced sheath voltage in power cables: A review. Renew. Sustain. Energy Rev. 2016, 62, 1236–1251. [Google Scholar] [CrossRef]
- Becerra, M.; Long, M.; Schulz, W.; Thottappillil, R. On the estimation of the lightning incidence to offshore wind farms. Electr. Power Syst. Res. 2018, 157, 211–226. [Google Scholar] [CrossRef]
- Sarajcev, P.; Vasilj, J.; Jakus, D. Monte–Carlo analysis of wind farm lightning-surge transients aided by LINET lightning-detection network data. Renew. Energy 2016, 99, 501–513. [Google Scholar] [CrossRef]
- Anderson, R.B.; Eriksson, A.J. Lightning parameters for engineering applications. Electra 1980, 69, 65–102. [Google Scholar]
- Lightning and Insulator Subcommittee of the T&D Committee. Parameters of lightning strokes: A review. IEEE Trans. Power Deliv. 2005, 20, 346–358. [Google Scholar] [CrossRef]
- Fisher, R.J.; Schnetzer, G.H.; Thottappillil, R.; Rakov, V.A.; Uman, M.A.; Goldberg, J.D. Parameters of triggered-lightning flashes in Florida and Alabama. J. Geophys. Res. 1993, 98, 22887–22902. [Google Scholar] [CrossRef]
- Berger, K.; Anderson, R.B.; Kroninger, H. Parameters of lightning flashes. Electra 1975, 41, 23–37. [Google Scholar]
- Andreotti, A.; Mottola, F.; Pagano, M.; Verolino, L. Lightning induced voltages on power lines: A new statistical approach. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM 2008), Ischia, Italy, 11–13 June 2008; pp. 445–451. [Google Scholar] [CrossRef]
- IEEE Guide for Improving the Lightning Performance of Electric Power Overhead Distribution Lines; IEEE Standard 1410; IEEE Power Engineering Society: Piscataway, NJ, USA, 2004. [CrossRef]
- Rusck, S. Induced lightning overvoltages on power transmission lines with special reference to the overvoltage protection of low-voltage networks. Trans. R. Inst. Technol. 1958, 120, 1–118. [Google Scholar]
- Bendato, I.; Brignone, M.; Delfino, F.; Procopio, R.; Rachidi, F. A methodology to reduce the computational effort in the evaluation of the lightning performance of distribution networks. Atmosphere 2016, 7, 147. [Google Scholar] [CrossRef]
- Andreotti, A.; Assante, D.; Mottola, F.; Verolino, L. An exact closed-form solution for lightning-induced overvoltages calculations. IEEE Trans. Power Deliv. 2009, 24, 1328–1343. [Google Scholar] [CrossRef]
- Andreotti, A.; Pierno, A.; Rakov, V.A.; Verolino, L. Analytical formulations for lightning-induced voltage calculations. IEEE Trans. Electromagn. Compat. 2013, 55, 109–123. [Google Scholar] [CrossRef]
- Andreotti, A.; Rakov, V.A.; Verolino, L. Exact and approximate solutions for lightning-induced voltage calculations. IEEE Trans. Electromagn. Compat. 2018. [Google Scholar] [CrossRef]
- Yokoyama, S. Calculation of lightning-induced voltages on overhead multiconductor systems. IEEE Trans. Power Appar. Syst. 1984, 103, 100–108. [Google Scholar] [CrossRef]
- Yokoyama, S. Experimental analysis of earth wires for induced lightning surges. IEE Proc. C Gener. Transm. Distrib. 1980, 127, 33–40. [Google Scholar] [CrossRef]
- Piantini, A. Lightning protection of low-voltage networks. In Lightning Protection; Cooray, V., Ed.; The Institution of Engineering and Technology: London, UK, 2010; pp. 553–634. ISBN 9780863417443. [Google Scholar]
- Darveniza, M. A practical extension of Rusck’s formula for maximum lightning-induced voltages that accounts for ground resistivity. IEEE Trans. Power Deliv. 2007, 22, 605–612. [Google Scholar] [CrossRef]
- Rachidi, F.; Nucci, C.A.; Ianoz, M.; Mazzetti, C. Response of multiconductor power lines to nearby lightning return stroke electromagnetic fields. IEEE Trans. Power Deliv. 1997, 12, 1404–1411. [Google Scholar] [CrossRef]
- Le Cam, L. Maximum likelihood: An introduction. Int. Stat. Rev 1990, 58, 153–171. [Google Scholar] [CrossRef]
- Carta, J.A.; Ramirez, P.; Velazquez, S. Influence of the level of fit of a density probability function to wind-speed data on the WECS mean power output estimation. Energy Convers. Manag. 2008, 49, 2647–2655. [Google Scholar] [CrossRef]
- Master, M.J.; Uman, M.A.; Beasley, W.; Darveniza, M. Lightning induced voltages on power lines: Experiment. IEEE Trans. Power Appar. Syst. 1984, PAS-103, 2519–2529. [Google Scholar] [CrossRef]
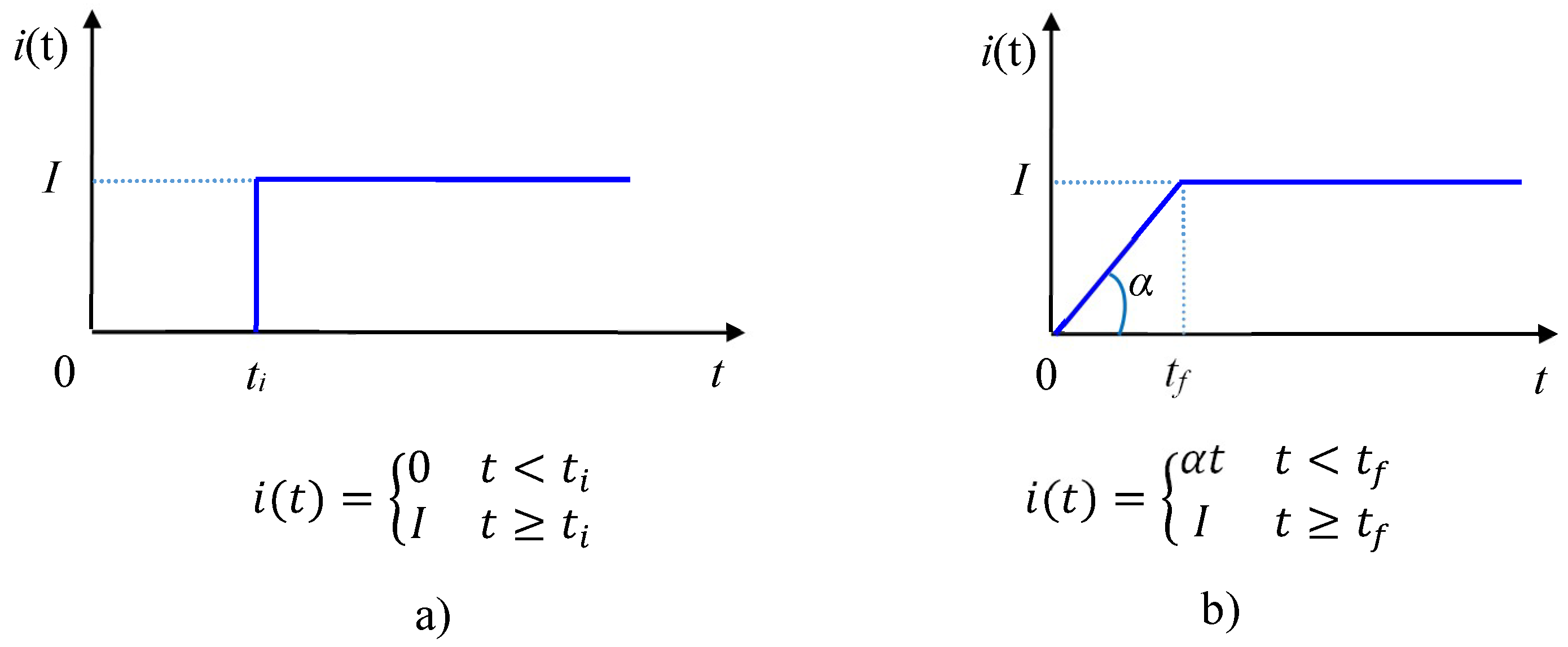










| Variable | Distribution | Density Functions | Parameters | Parameter’s Values |
|---|---|---|---|---|
| Uniform | lower endpoint (minimum) upper endpoint (maximum) | |||
| Lognormal | mean and variance with and the mean and standard deviation, of the associated normal distribution. | = 3.44 = 0.48 | ||
| T-10 | Lognormal | mean and variance with and the mean and standard deviation of the associated normal distribution. | = 1.5 = 0.58 |
| Fitting Distribution Generalized Extreme Value | ||||
|---|---|---|---|---|
| Log Likelihood | Det. Coeff. | k | ||
| −119,149 | 0.9989 | 0.4865 | 23,409.2 | 35,382.7 |
| Fitting Distribution Lognormal | ||||
| Log Likelihood | Det. Coeff. | 1 | 1 | |
| −119,223 | 0.9940 | - | 0.7579 | 10.7806 |
| Fitting Distribution Generalized Extreme Value | ||||
|---|---|---|---|---|
| Log Likelihood | Det. Coeff. | k | ||
| −115,898 | 0.9990 | 0.340768 | 18348 | 30962.5 |
| Fitting Distribution Lognormal | ||||
| Log Likelihood | Det. Coeff. | 1 | 1 | |
| −115,897 | 0.9984 | 0.660467 | 10.5856 | |
| Fitting Distribution Generalized Extreme Value | ||||
|---|---|---|---|---|
| Log Likelihood | Det. Coeff. | k | ||
| −114,827 | 0.9993 | 0.489427 | 15,166.9 | 23,092.8 |
| Fitting Distribution Lognormal | ||||
| Log Likelihood | Det. Coeff. | 1 | 1 | |
| −114,941 | 0.9945 | 0.756103 | 10.3548 | |
| Fitting Distribution Generalized Extreme Value | ||||
|---|---|---|---|---|
| Log Likelihood | Det. Coeff. | k | ||
| −111,639 | 0.9992 | 0.339906 | 11,990.6 | 20,166.9 |
| Fitting Distribution Lognormal | ||||
| Log Likelihood | Det. Coeff. | 1 | 1 | |
| −111,631 | 0.9986 | 0.662053 | 10.1567 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andreotti, A.; Mottola, F.; Pierno, A.; Proto, D. On the Statistical Characterization of Lightning-Induced Voltages. Appl. Sci. 2018, 8, 651. https://doi.org/10.3390/app8040651
Andreotti A, Mottola F, Pierno A, Proto D. On the Statistical Characterization of Lightning-Induced Voltages. Applied Sciences. 2018; 8(4):651. https://doi.org/10.3390/app8040651
Chicago/Turabian StyleAndreotti, Amedeo, Fabio Mottola, Antonio Pierno, and Daniela Proto. 2018. "On the Statistical Characterization of Lightning-Induced Voltages" Applied Sciences 8, no. 4: 651. https://doi.org/10.3390/app8040651
APA StyleAndreotti, A., Mottola, F., Pierno, A., & Proto, D. (2018). On the Statistical Characterization of Lightning-Induced Voltages. Applied Sciences, 8(4), 651. https://doi.org/10.3390/app8040651







