An Effective Directional Residual Interpolation Algorithm for Color Image Demosaicking
Abstract
:1. Introduction
2. Related Work
2.1. The Outline of MLRI
- Step 1.
- The G pixel values are calculated through residuals at the location of R and B pixels from horizontal and vertical directions. R and B pixel values also are calculated at the location of G pixels. The calculation of the residuals replaces the calculation of the color difference in Adams and Hamilton’s interpolation equation [15].
- Step 2.
- MLRI calculates both horizontal and vertical color difference estimations based on Step 1 at each pixel, then MLRI combines and smooths the color difference estimations.
- Step 3.
- The color difference estimations are added to the observed R or B pixel values. It aims to interpolate G pixel values.
2.2. Guided Filter
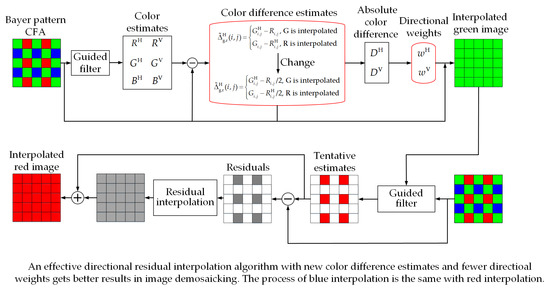
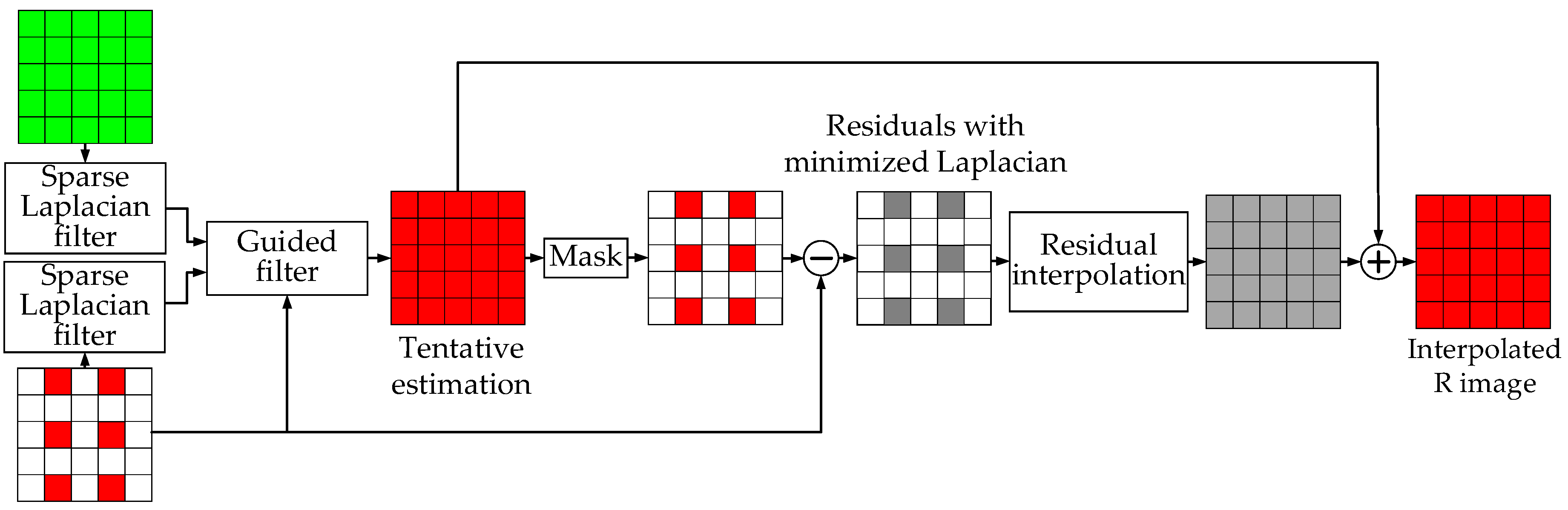
3. The Proposed Demosaicking Algorithm
- Step 1.
- Step 2.
- The horizontal and vertical color difference estimations are calculated, and we can generate the horizontal and vertical weights at each pixel.
- Step 3.
- To get color difference, the horizontal and vertical color difference estimations are combined and smoothed by two directional weights. As a result, the G pixel values at the location of R and B pixels are generated by adding final color difference to the observed R or B pixel values.
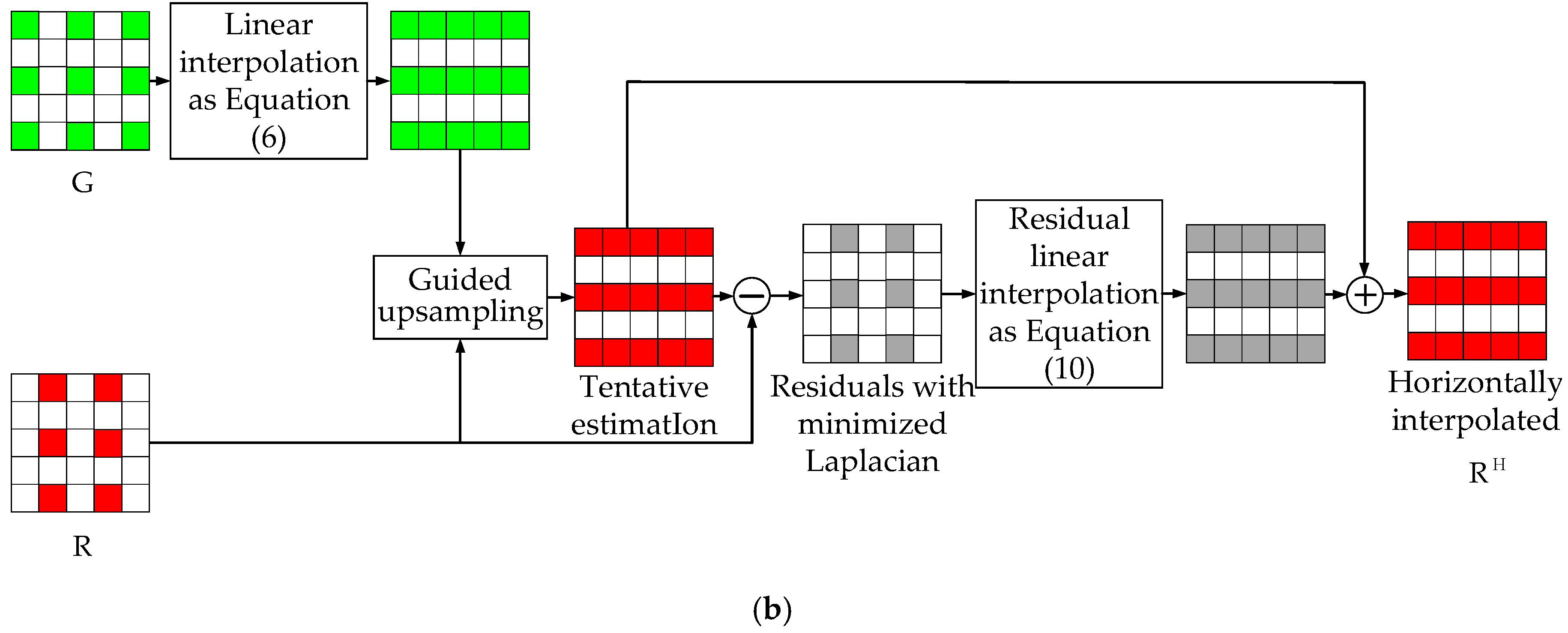
3.1. The Calculation Process of Directionaly Estimated Pixel Value
3.2. The Calculation Process of Directional Weights
3.3. The Calculation Process of Estimated Pixel Values
4. Experimental Results
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Gunturk, B.K.; Glotzbach, J.; Altunbasak, Y.; Schafer, R.W.; Mersereau, R.M. Demosaicking: Color filter array interpolation. IEEE Signal Process. Mag. 2005, 22, 44–54. [Google Scholar] [CrossRef]
- Bayer, B.E. Color Imaging Array. U.S. Patent 3,971,065, 20 July 1976. [Google Scholar]
- Adams, J.E. Interactions between color plane interpolation and other image processing functions in electronic photography. In Proceedings of the SPIE—Cameras and Systems for Electronic Photography and Scientific Imaging, San Jose, CA, USA, 8–9 February 1995; Volume 2416, pp. 144–151. [Google Scholar]
- Longère, P.; Zhang, X.; Delahunt, P.B.; Brainard, D.H. Perceptual assessment of demosaicing algorithm performance. Proc. IEEE 2002, 90, 123–132. [Google Scholar] [CrossRef]
- Yu, W. Colour demosaicking method using adaptive cubic convolution interpolation with sequential averaging. IEE Proc. Vis. Image Signal Process. 2006, 153, 666–676. [Google Scholar] [CrossRef]
- Malvar, H.S.; He, L.W.; Cutler, R. High-quality linear interpolation for demosaicing of Bayer-patterned color images. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Montreal, QC, Canada, 17–21 May 2004; Volume 3, pp. 485–488. [Google Scholar]
- Yu, T.; Hu, W.; Xue, W.; Zhang, W. Colour image demosaicking via joint intra and inter channel information. Electron. Lett. 2016, 52, 605–607. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Y.; Wang, J.; Hao, P. Universal demosaicking of color filter arrays. IEEE Trans. Image Process. 2016, 25, 5173–5186. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Wu, X. Color demosaicking via directional linear minimum mean square-error estimation. IEEE Trans. Image Process. 2005, 14, 2167–2178. [Google Scholar] [CrossRef] [PubMed]
- Wachira, K.; Mwangi, E. A multi-variate weighted interpolation technique with local polling for Bayer CFA demosaicking. In Proceedings of the 1st International Conference on Information and Communication Technology Research, Abu Dhabi, UAE, 17–19 May 2015; pp. 76–79. [Google Scholar]
- Shi, J.; Wang, C.; Zhang, S. Region-adaptive demosaicking with weighted values of multidirectional information. J. Commun. 2014, 9, 930–936. [Google Scholar] [CrossRef]
- Chen, W.J.; Chang, P.Y. Effective demosaicking algorithm based on edge property for color filter arrays. Digit. Signal Process. 2012, 22, 163–169. [Google Scholar] [CrossRef]
- Pekkucuksen, I.; Altunbasak, Y. Edge strength filter based color filter array interpolation. IEEE Trans. Image Process. 2012, 21, 393–397. [Google Scholar] [CrossRef] [PubMed]
- Tsai, C.Y.; Song, K.T. A new edge-adaptive demosaicing algorithm for color filter arrays. Image Vis. Comput. 2007, 25, 1495–1508. [Google Scholar] [CrossRef]
- Adams, J.E.; Hamilton, J.F. Adaptive Color Plan Interpolation in Single Sensor Color Electronic Camera. U.S. Patent 5,629,734, 13 May 1997. [Google Scholar]
- Pekkucuksen, I.; Altunbasak, Y. Gradient based threshold free color filter array interpolation. In Proceedings of the 17th IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 137–140. [Google Scholar]
- Pekkucuksen, I.; Altunbasak, Y. Multiscale gradients-based color filter array interpolation. IEEE Trans. Image Process. 2013, 22, 157–165. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Jeon, G.; Jeong, J. Voting-based directional interpolation method and its application to still color image demosaicking. IEEE Trans. Circuits Syst. Video Technol. 2014, 24, 255–262. [Google Scholar] [CrossRef]
- Kiku, D.; Monno, Y.; Tanaka, M.; Okutomi, M. Residual interpolation for color image demosaicking. In Proceedings of the 20th IEEE International Conference on Image Processing, Melbourne, Australia, 15–18 September 2013; pp. 2304–2308. [Google Scholar]
- Kiku, D.; Monno, Y.; Tanaka, M.; Okutomi, M. Beyond color difference: Residual interpolation for color image demosaicking. IEEE Trans. Image Process. 2016, 25, 1288–1300. [Google Scholar] [CrossRef] [PubMed]
- Kiku, D.; Monno, Y.; Tanaka, M.; Okutomi, M. Minimized-Laplacian residual interpolation for color image demosaicking. In Proceedings of the SPIE—IS and T Electronic Imaging—Digital Photography X, San Francisco, CA, USA, 3–5 February 2014; Volume 9023, pp. 1–8. [Google Scholar]
- Ye, W.; Ma, K.K. Color image demosaicing using iterative residual interpolation. IEEE Trans. Image Process. 2015, 24, 5879–5891. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Jeon, G. Bayer pattern CFA demosaicking based on multi-directional weighted interpolation and guided filter. IEEE Signal Process. Lett. 2015, 22, 2083–2087. [Google Scholar] [CrossRef]
- Kim, Y.; Jeong, J. Four-direction residual interpolation for demosaicking. IEEE Trans. Circuits Syst. Video Technol. 2016, 26, 881–890. [Google Scholar] [CrossRef]
- Monno, Y.; Kiku, D.; Tanaka, M.; Okutomi, M. Adaptive residual interpolation for color and multispectral image demosaicking. Sensors 2017, 17, 2787. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Sun, J.; Tang, X. Guided image filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1397–1409. [Google Scholar] [CrossRef] [PubMed]
- Monno, Y.; Kiku, D.; Kikuchi, S.; Tanaka, M.; Okutomi, M. Multispectral demosaicking with novel guide image generation and residual interpolation. In Proceedings of the IEEE International Conference on Image Processing, Paris, France, 27–30 October 2014; pp. 645–649. [Google Scholar]
- Oh, P.; Lee, S.; Kang, M.G. Colorization-based RGB-white color interpolation using color filter array with randomly sampled pattern. Sensors 2017, 17, 1523. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Wu, X.; Buades, A.; Li, X. Color demosaicking by local directional interpolation and nonlocal adaptive thresholding. J. Electron. Imaging 2011, 20, 1–16. [Google Scholar]








| Direction | G Channel Interpolation | R and B Channels Interpolation |
|---|---|---|
| Horizontal | ||
| Vertical |
| Image | DLMMSE [9] | LDI-NAT [29] | LDI-NLM [29] | VDI [18] | RI [19] | MLRI [21] | Proposed |
|---|---|---|---|---|---|---|---|
| Figure 6a | 27.51 | 32.66 | 32.31 | 32.57 | 32.37 | 32.39 | 32.64 |
| Figure 6b | 31.91 | 39.00 | 39.09 | 38.95 | 39.44 | 39.24 | 39.47 |
| Figure 6c | 34.46 | 35.46 | 35.50 | 35.44 | 36.75 | 36.68 | 36.38 |
| Figure 6d | 36.80 | 40.40 | 38.99 | 41.31 | 42.14 | 41.16 | 43.15 |
| Figure 6e | 32.48 | 38.05 | 37.61 | 38.13 | 37.86 | 37.69 | 38.73 |
| Figure 6f | 33.09 | 43.36 | 41.87 | 42.49 | 42.16 | 41.85 | 43.12 |
| Figure 6g | 40.54 | 37.24 | 37.58 | 36.63 | 38.77 | 39.34 | 37.34 |
| Figure 6h | 40.43 | 40.15 | 40.32 | 39.60 | 41.37 | 41.73 | 40.36 |
| Figure 6i | 32.27 | 41.63 | 41.49 | 41.90 | 41.62 | 41.54 | 41.97 |
| Figure 6j | 31.15 | 42.66 | 42.24 | 42.47 | 42.07 | 41.98 | 42.95 |
| Figure 6k | 31.87 | 42.73 | 42.00 | 41.78 | 42.03 | 42.05 | 41.97 |
| Figure 6l | 31.55 | 41.52 | 41.52 | 41.65 | 42.24 | 42.04 | 42.38 |
| Figure 6m | 33.54 | 44.80 | 45.50 | 45.38 | 45.10 | 44.87 | 45.77 |
| Figure 6n | 30.89 | 42.80 | 42.62 | 42.96 | 43.05 | 42.78 | 43.71 |
| Figure 6o | 32.19 | 42.65 | 42.51 | 42.54 | 42.67 | 42.48 | 43.00 |
| Figure 6p | 26.70 | 35.60 | 35.10 | 35.20 | 35.16 | 35.28 | 35.35 |
| Figure 6q | 29.28 | 37.74 | 37.49 | 37.86 | 37.38 | 36.90 | 38.16 |
| Figure 6r | 30.43 | 37.66 | 37.74 | 36.36 | 37.68 | 37.89 | 36.89 |
| Average | 32.62 | 39.78 | 39.53 | 39.62 | 39.99 | 39.88 | 40.19 |
| Image | DLMMSE [9] | LDI-NAT [29] | LDI-NLM [29] | VDI [18] | RI [19] | MLRI [21] | Proposed |
|---|---|---|---|---|---|---|---|
| Figure 6a | 24.12 | 29.01 | 28.70 | 28.02 | 28.98 | 28.87 | 29.37 |
| Figure 6b | 28.39 | 35.01 | 34.86 | 34.16 | 35.00 | 35.09 | 35.17 |
| Figure 6c | 31.78 | 32.57 | 33.08 | 32.63 | 33.71 | 33.79 | 33.72 |
| Figure 6d | 34.13 | 35.95 | 36.47 | 36.00 | 37.88 | 37.48 | 38.56 |
| Figure 6e | 28.55 | 34.10 | 33.77 | 32.63 | 33.92 | 33.79 | 34.59 |
| Figure 6f | 29.24 | 37.86 | 37.12 | 35.64 | 38.32 | 38.29 | 38.62 |
| Figure 6g | 38.38 | 35.98 | 36.28 | 36.03 | 36.97 | 37.43 | 36.00 |
| Figure 6h | 36.64 | 37.46 | 37.82 | 37.41 | 36.98 | 36.83 | 38.20 |
| Figure 6i | 28.85 | 36.91 | 36.98 | 35.96 | 35.92 | 36.53 | 36.69 |
| Figure 6j | 27.76 | 38.73 | 38.36 | 37.26 | 38.15 | 38.55 | 38.92 |
| Figure 6k | 28.66 | 39.47 | 39.19 | 37.96 | 39.43 | 39.96 | 39.74 |
| Figure 6l | 27.35 | 38.89 | 38.59 | 37.10 | 39.64 | 39.67 | 39.58 |
| Figure 6m | 29.10 | 40.78 | 40.85 | 39.41 | 40.31 | 40.53 | 40.71 |
| Figure 6n | 27.25 | 38.68 | 38.48 | 37.32 | 38.95 | 38.74 | 39.16 |
| Figure 6o | 28.78 | 38.93 | 38.94 | 37.85 | 38.35 | 38.92 | 39.27 |
| Figure 6p | 24.23 | 33.50 | 32.98 | 31.41 | 35.15 | 35.16 | 35.30 |
| Figure 6q | 26.39 | 32.83 | 32.54 | 31.16 | 32.39 | 32.48 | 33.26 |
| Figure 6r | 27.83 | 34.98 | 35.21 | 34.24 | 36.48 | 36.23 | 35.95 |
| Average | 29.30 | 36.20 | 36.12 | 35.12 | 36.47 | 36.57 | 36.82 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, K.; Wang, C.; Yang, S.; Lu, Z.; Zhao, D. An Effective Directional Residual Interpolation Algorithm for Color Image Demosaicking. Appl. Sci. 2018, 8, 680. https://doi.org/10.3390/app8050680
Yu K, Wang C, Yang S, Lu Z, Zhao D. An Effective Directional Residual Interpolation Algorithm for Color Image Demosaicking. Applied Sciences. 2018; 8(5):680. https://doi.org/10.3390/app8050680
Chicago/Turabian StyleYu, Ke, Chengyou Wang, Sen Yang, Zhiwei Lu, and Dan Zhao. 2018. "An Effective Directional Residual Interpolation Algorithm for Color Image Demosaicking" Applied Sciences 8, no. 5: 680. https://doi.org/10.3390/app8050680
APA StyleYu, K., Wang, C., Yang, S., Lu, Z., & Zhao, D. (2018). An Effective Directional Residual Interpolation Algorithm for Color Image Demosaicking. Applied Sciences, 8(5), 680. https://doi.org/10.3390/app8050680