Manufacturing of Non-Stick Molds from Pre-Painted Aluminum Sheets via Single Point Incremental Forming
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
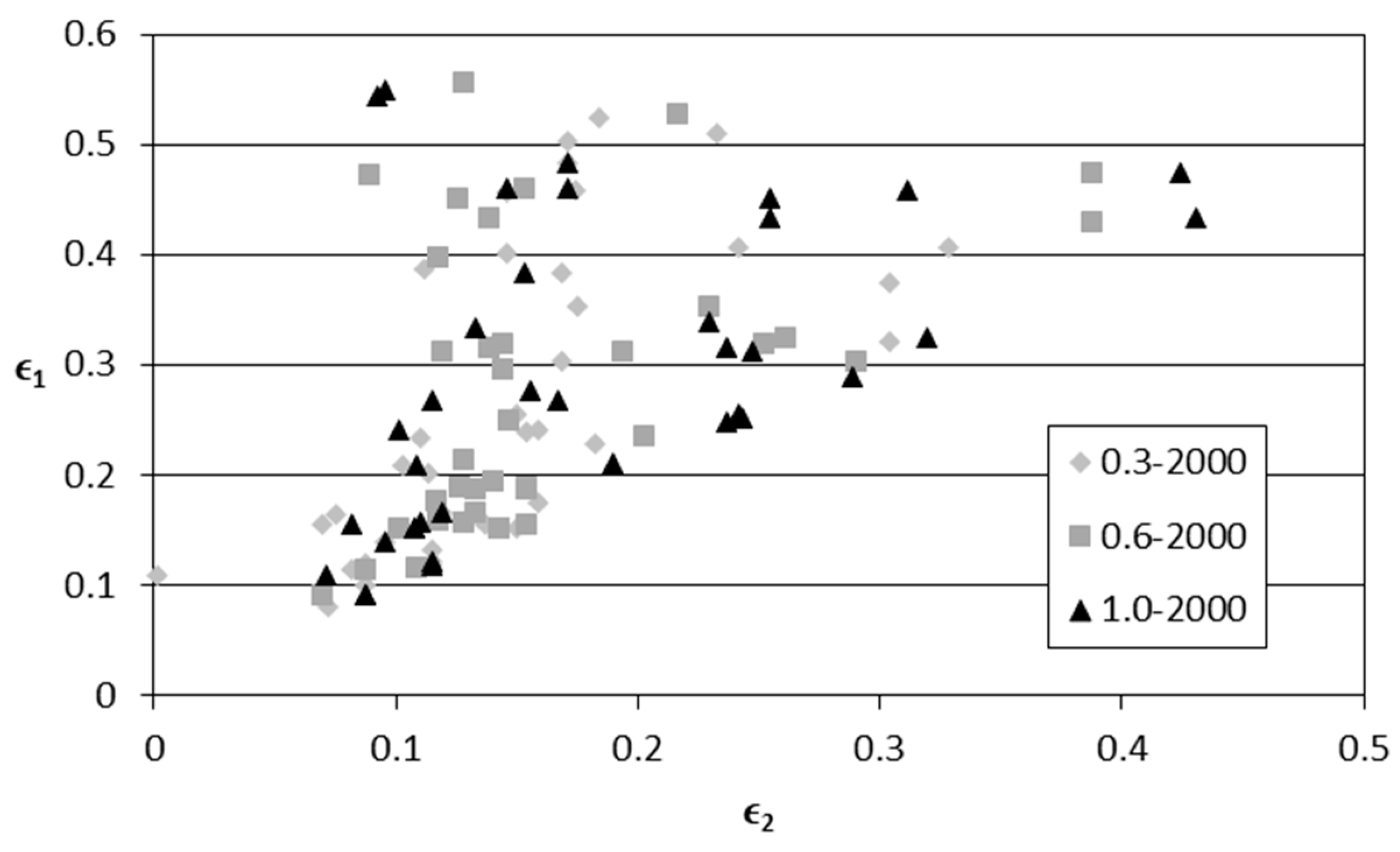
3. Results
4. Discussion
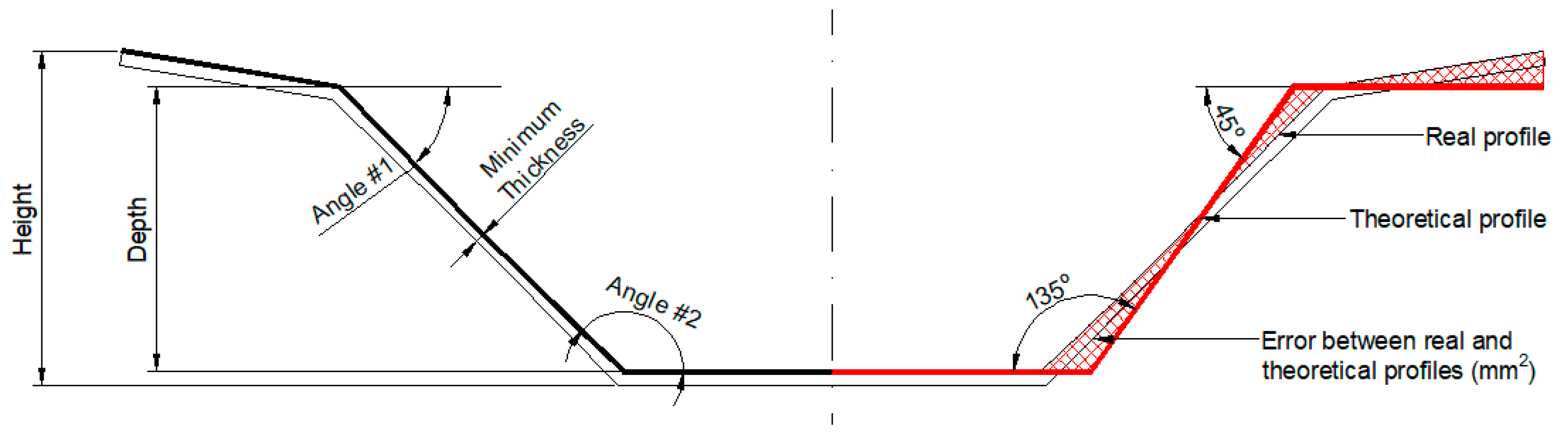
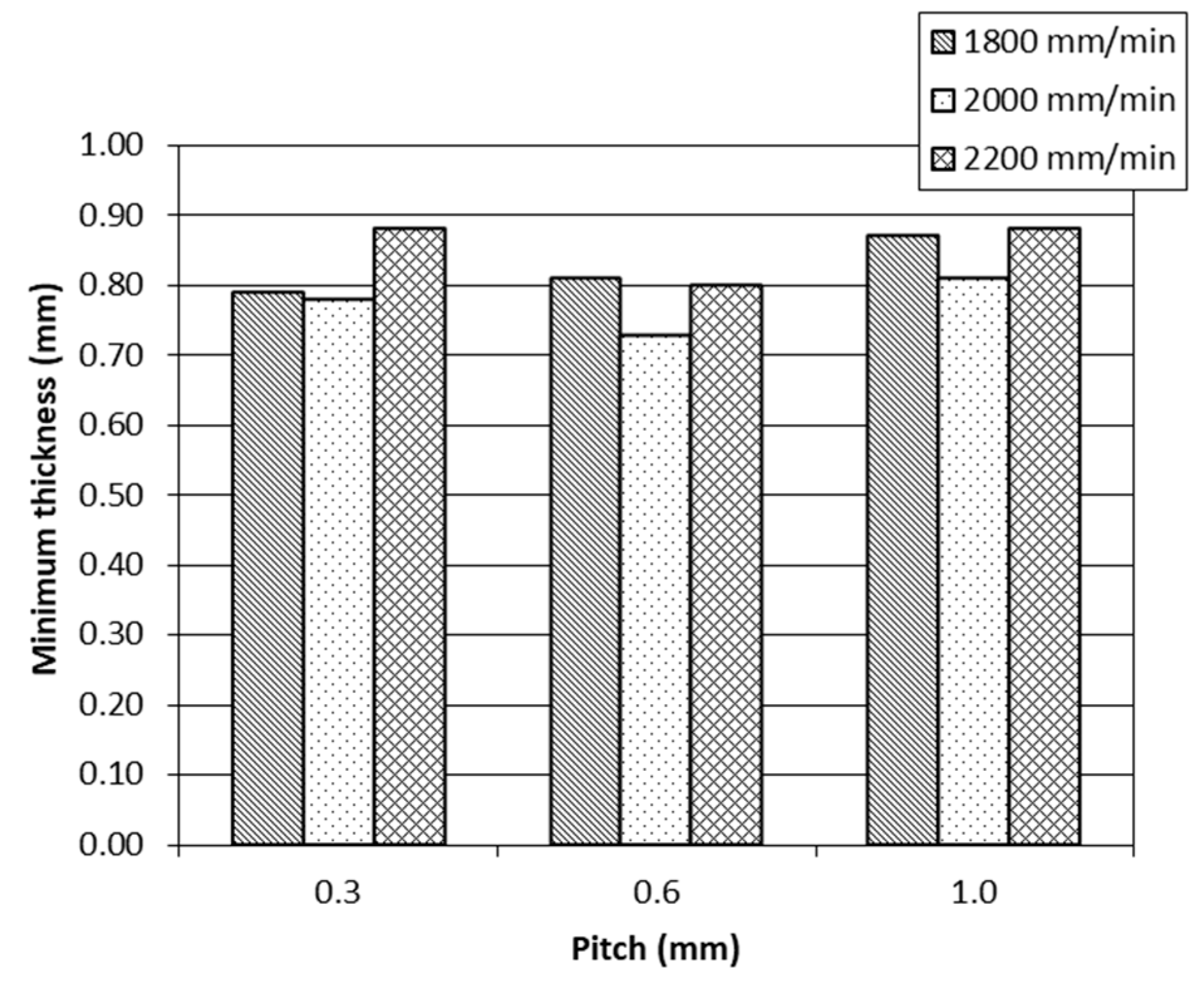
- The minimum thickness appears to show no relation to any of the technological parameters studied (Figure 7). This result is coherent with the law of sine [47]. According to this law, the theoretical thickness can be calculated as a product of the initial thickness (1.20 mm) and the sine of the angle (45°). The theoretical value calculated (0.84 mm) coincides with the value measured experimentally.
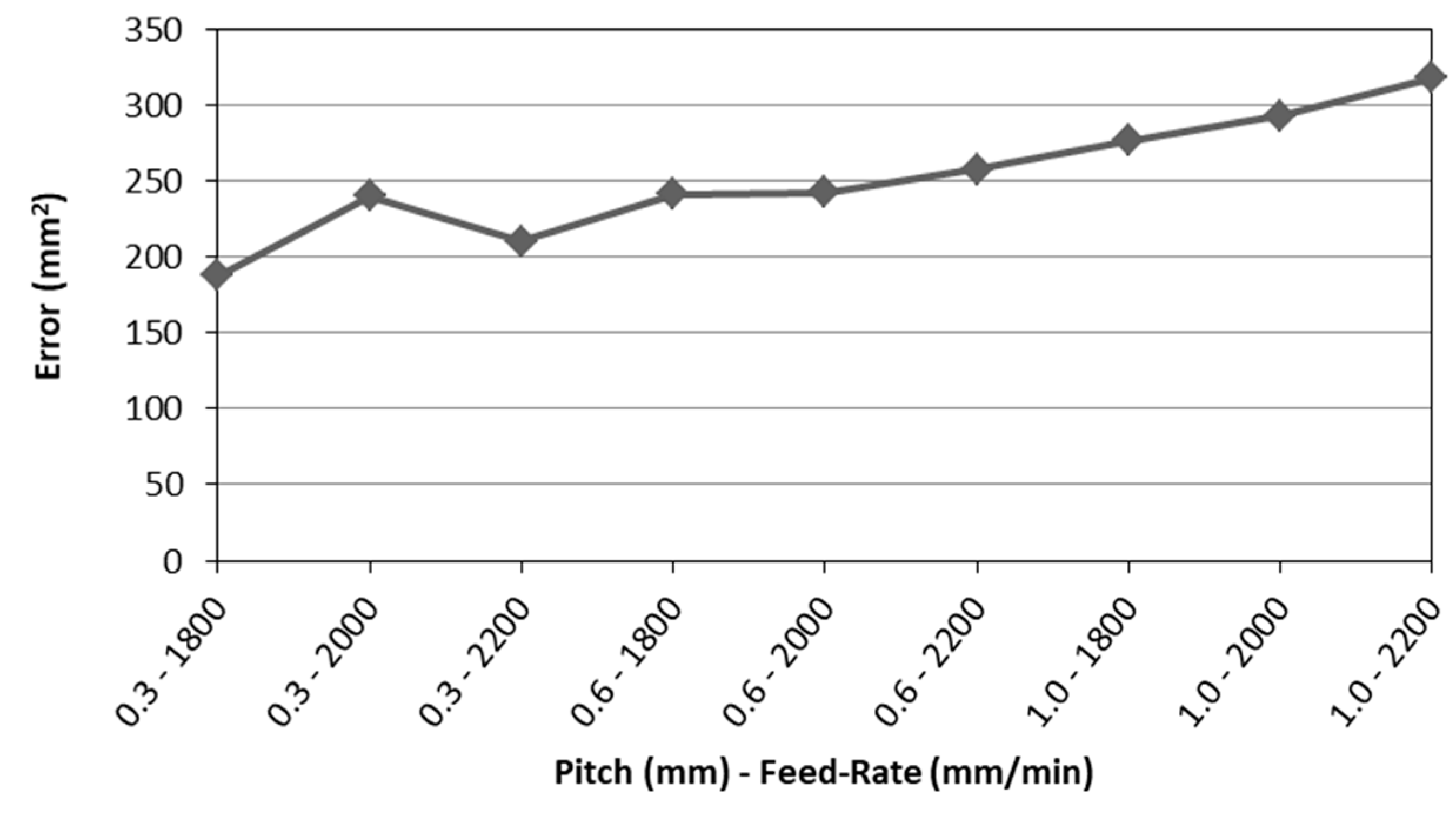
- The differences between the theoretical profile and the real profile of the mold are minor, in general terms, when using low values of pitch and feed-rate (Figure 10). These results coincide with those obtained by Hussain, Lin & Hayat [48] (greater pitches provoke greater deviations), Maqbool & Bambach [49] (lower pitches provoke lower geometrical accuracy) and Radu & Cristea [50] (high values of the feed-rate lead to a low-dimensional accuracy).
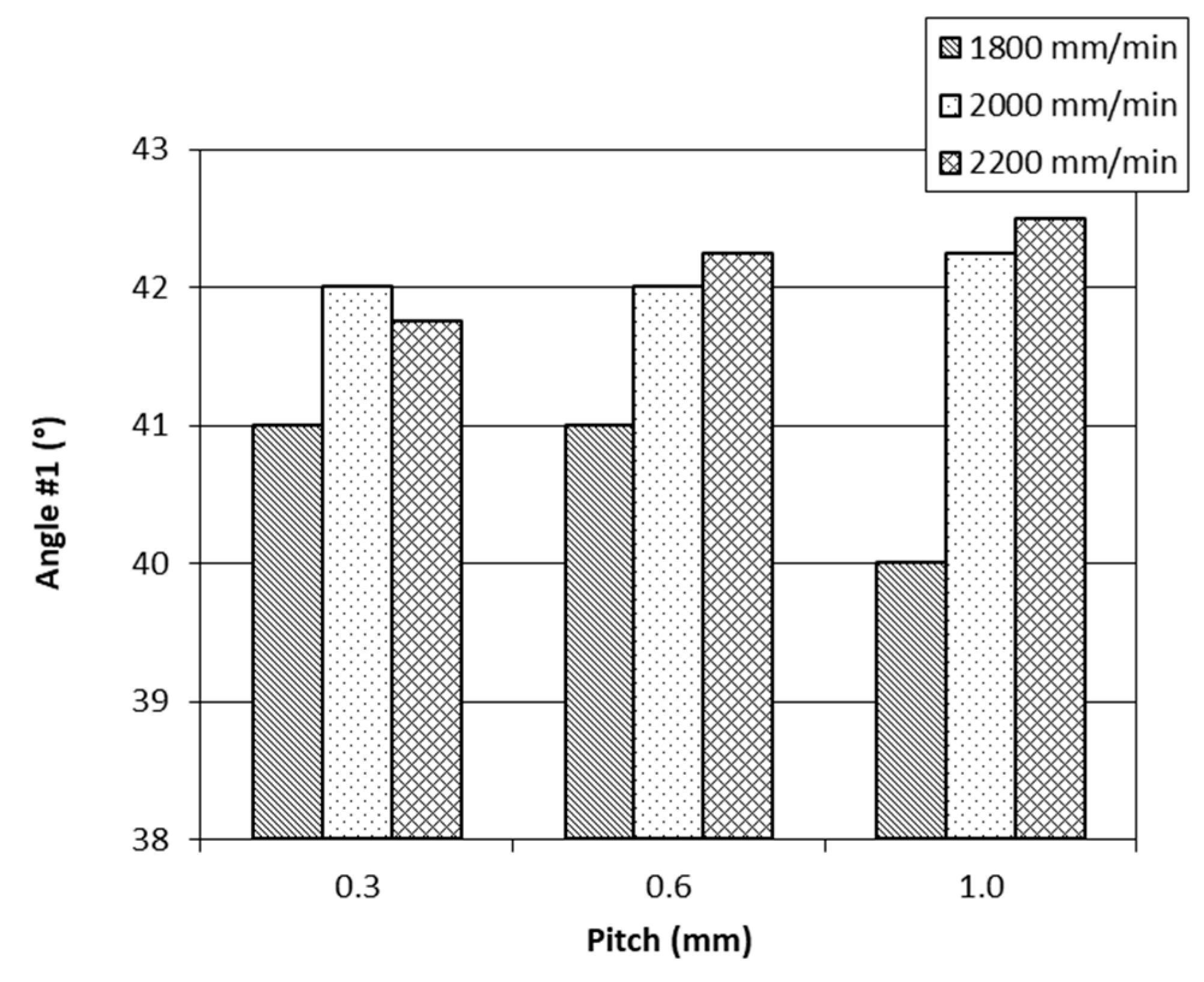
- However, low values of pitch and feed-rate result in certain geometrical features (depth, height, angle #1, normalized springback, angle #2) moving away from the sought-after theoretical values:
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Leszak, E. Apparatus and Processs for Incremental Dieless Forming. U.S. Patent 3342051, 19 September 1967. [Google Scholar]
- Matsubara, S. Incremental backward bulge forming of a sheet metal with a hemispherical head tool. Jpn. Soc. Technol. Plast. 1994, 35, 1311–1316. [Google Scholar]
- Kitazawa, K.; Wakabayashi, A.; Murata, K.; Yaejima, K. Metal-flow phenomena in computerized numerically controlled incremental stretch-expanding of aluminum sheets. J. Jpn. Inst. Light Met. 1996, 46, 65–70. [Google Scholar] [CrossRef]
- Jeswiet, J.; Micari, F.; Hirt, G.; Bramley, A.; Duflou, J.; Allwood, J. Asymmetric Single Point Incremental Forming of Sheet Metal. CIRP Ann. Manuf. Technol. 2005, 54, 88–114. [Google Scholar] [CrossRef]
- Afonso, D.; de Sousa, R.; Torcato, R. Integration of design rules and process modelling within SPIF technology—A review on the industrial dissemination of single point incremental forming. Int. J. Adv. Manuf. Technol. 2018, 94, 4387–4399. [Google Scholar] [CrossRef]
- McAnulty, T.; Jeswiet, J.; Doolan, M. Formability in single point incremental forming: A comparative analysis of the state of the art. CIRP J. Manuf. Sci. Technol. 2017, 16, 43–54. [Google Scholar] [CrossRef]
- Martins, P.A.F.; Kwiatkowski, L.; Franzen, V.; Tekkaya, A.E.; Kleiner, M. Single point incremental forming of polymers. CIRP Ann. Manuf. Technol. 2009, 58, 229–232. [Google Scholar] [CrossRef] [Green Version]
- Petek, A.; Gantar, G.; Pepelnjak, T.; Kuzman, K. Economical and Ecological Aspects of Single Point Incremental Forming Versus Deep Drawing Technology. Key Eng. Mater. 2007, 344, 931–938. [Google Scholar] [CrossRef]
- Ingarao, G.; Ambrogio, G.; Gagliardi, F.; Di Lorenzo, R. A sustainability point of view on sheet metal forming operations: Material wasting and energy consumption in incremental forming and stamping processes. J. Clean. Prod. 2012, 29–30, 255–268. [Google Scholar] [CrossRef]
- Echrif, S.B.M.; Hrairi, M. Research and Progress in Incremental Sheet Forming Processes. Mater. Manuf. Process. 2011, 26, 1404–1414. [Google Scholar] [CrossRef]
- Behera, A.K.; de Sousa, R.A.; Ingarao, G.; Oleksik, V. Single point incremental forming: An assessment of the progress and technology trends from 2005 to 2015. J. Manuf. Process. 2017, 27, 37–62. [Google Scholar] [CrossRef] [Green Version]
- Zha, G.; Xu, J.; Shi, X.; Zhou, X.; Lu, C. Forming process of automotive body panel based on incremental forming technology. Metall. Min. Ind. 2015, 12, 350–357. [Google Scholar]
- Bambach, M.; Taleb Araghi, B.; Hirt, G. Strategies to improve the geometric accuracy in asymmetric single point incremental forming. Prod. Eng. 2009, 3, 145–156. [Google Scholar] [CrossRef]
- Governale, A.; Lo Franco, A.; Panzeca, A.; Fratini, L.; Micari, F. Incremental Forming Process for the Accomplishment of Automotive Details. Key Eng. Mater. 2007, 344, 559–566. [Google Scholar] [CrossRef]
- Romero, P.E.; Aguilar-Contreras, F.J.; Dorado, R.; Lopez-Garcia, R. Rapid prototyping for automotive industry via incremental sheet forming. DYNA 2013, 88, 581–590. [Google Scholar]
- Amino, M.; Mizoguchi, M.; Terauchi, Y.; Maki, T. Current status of “Dieless” Amino’s incremental forming. Procedia Eng. 2014, 81, 54–62. [Google Scholar] [CrossRef]
- Ambrogio, G.; De Napoli, L.; Filice, L.; Gagliardi, F.; Muzzupappa, M. Application of Incremental Forming process for high customised medical product manufacturing. J. Mater. Process. Technol. 2005, 162–163, 156–162. [Google Scholar] [CrossRef]
- Castelan, J.; Schaeffer, L.; Daleffe, A.; Fritzen, D.; Salvaro, V.; Da Silva, F.P. Manufacture of custom-made cranial implants from DICOM® images using 3D printing, CAD/CAM technology and incremental sheet forming. Rev. Bras. Eng. Biomed. 2014, 30, 265–273. [Google Scholar] [CrossRef]
- Centeno, G.; Bagudanch, I.; Morales-Palma, D.; García-Romeu, M.L.; Gonzalez-Perez-Somarriba, B.; Martinez-Donaire, A.J.; Gonzalez-Perez, L.M.; Vallellano, C. Recent Approaches for the Manufacturing of Polymeric Cranial Prostheses by Incremental Sheet Forming. Procedia Eng. 2017, 183, 180–187. [Google Scholar] [CrossRef]
- Duflou, J.R.; Lauwers, B.; Verbert, J. Study on the achievable accuracy in single point incremental forming. In Advanced Methods in Material Forming; Springer: Berlin/Heidelberg, Germany, 2007; pp. 251–262. [Google Scholar]
- Afonso, D.; Alves de Sousa, R.; Torcato, R.; Sousa, J.P.; Santos, R.; Valente, R. Case studies on industrial applicability of single point incremental forming. In Proceedings of the Ciência 2017—Encontro com Ciência e Tecnologia en Portugal, Lisbon, Portugal, 3–5 July 2017. [Google Scholar]
- Kalo, A. N-Bowls. Available online: www.ammarkalo.com (accessed on 4 April 2018).
- Fiorotto, M.; Sorgente, M.; Lucchetta, G. Preliminary studies on single point incremental forming for composite materials. Int. J. Mater. Form. 2010, 3, 951–954. [Google Scholar] [CrossRef]
- Appermont, R.; Van Mieghem, B.; Van Bael, A.; Bens, J.; Ivens, J.; Vanhove, H.; Behera, A.K.; Duflou, J. Sheet-metal based molds for low-pressure processing of thermoplastics. PMI 2008, 383–388. [Google Scholar]
- Afonso, D.; De Sousa, R.A.; Torcato, R. Testing single point incremental forming molds for thermoforming operations. AIP Conf. Proc. 2016, 1769, 060016. [Google Scholar] [CrossRef] [Green Version]
- Afonso, D.; Pires, L.; de Sousa, R.A.; Torcato, R. Direct rapid tooling for polymer processing using sheet metal tools. Procedia Manuf. 2017, 13, 102–108. [Google Scholar] [CrossRef]
- Ruiz-Cabello, F.J.M.; Rodríguez-Criado, J.C.; Cabrerizo-Vílchez, M.; Rodríguez-Valverde, M.A.; Guerrero-Vacas, G. Towards super-nonstick aluminized steel surfaces. Prog. Org. Coat. 2017, 109, 135–143. [Google Scholar] [CrossRef]
- Katajarinne, T.; Vihtonen, L.; Kivivuori, S. Incremental forming of colour-coated sheets. Int. J. Mater. Form. 2008, 1, 1175–1178. [Google Scholar] [CrossRef]
- Skjoedt, M.; Silva, M.B.; Bay, N.; Martins, P.A.F. Single point incremental forming using a dummy sheet. In Proceedings of the 2nd International Conference on New Forming Technologies, Bremen, Germany, 20–21 September 2007; pp. 267–276. [Google Scholar]
- Silva, M.B.; Skjoedt, M.; Vilaça, P.; Bay, N.; Martins, P.A.F. Single point incremental forming of tailored blanks produced by friction stir welding. J. Mater. Process. Technol. 2009, 209, 811–820. [Google Scholar] [CrossRef]
- Guerrero-Vacas, G. Comparative Analysis of the Removal Processes of Fluoropolymer Anti-Adherent Coatings on Metallic Surfaces between Laser and Pyrolytic Technologies; University of Malaga: Malaga, Spain, 2013. [Google Scholar]
- Verbert, J. Computer Aided Process Planning for Rapid Prototyping with Incremental Sheet Forming Techniques; Katholieke Universiteit Leuven: Leuven, Belgium, 2010. [Google Scholar]
- Behera, A.K. Shape Feature Taxonomy Development for Toolpath Optimization in Incremental Sheet Forming; Katholieke Universiteit Leuven: Leuven, Belgium, 2013. [Google Scholar]
- Gupta, P.; Jeswiet, J. Observations on Heat Generated in Single Point Incremental Forming. Procedia Eng. 2017, 183, 161–167. [Google Scholar] [CrossRef]
- Ambrogio, G.; Costantino, I.; De Napoli, L.; Filice, L.; Fratini, L.; Muzzupappa, M. Influence of some relevant process parameters on the dimensional accuracy in incremental forming: A numerical and experimental investigation. J. Mater. Process. Technol. 2004, 153–154, 501–507. [Google Scholar] [CrossRef]
- Ambrogio, G.; Cozza, V.; Filice, L.; Micari, F. An analytical model for improving precision in single point incremental forming. J. Mater. Process. Technol. 2007, 191, 92–95. [Google Scholar] [CrossRef]
- Guzmán, C.F.; Gu, J.; Duflou, J.; Vanhove, H.; Flores, P.; Habraken, A.M. Study of the geometrical inaccuracy on a SPIF two-slope pyramid by finite element simulations. Int. J. Solids Struct. 2012, 49, 3594–3604. [Google Scholar] [CrossRef]
- Skjoedt, M. Rapid Prototyping by Single Point Incremental Forming of Sheet Metal. Ph.D. Thesis, Technical University of Denmark, Kgs. Lyngby, Denmark, 2008. [Google Scholar]
- Jackson, K.; Allwood, J. The mechanics of incremental sheet forming. J. Mater. Process. Technol. 2009, 209, 1158–1174. [Google Scholar] [CrossRef]
- Franzen, V.; Kwiatkowski, L.; Martins, P.A.F.; Tekkaya, A.E. Single point incremental forming of PVC. J. Mater. Process. Technol. 2009, 209, 462–469. [Google Scholar] [CrossRef]
- Silva, M.B.; Alves, L.M.; Martins, P.A.F. Single point incremental forming of PVC: Experimental findings and theoretical interpretation. Eur. J. Mech. A/Solids 2010, 29, 557–566. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Zhang, S. Study on Process Parameters on Single Point Incremental Forming of PVC. Mater. Sci. Forum 2017, 878, 74–80. [Google Scholar] [CrossRef]
- Medina-Sánchez, G.; Torres-Jimenez, E.; Lopez-Garcia, R.; Dorado-Vicente, R.; Cazalla-Moral, R. Temperature influence on Single Point Incremental Forming of PVC parts. Procedia Manuf. 2017, 13, 335–342. [Google Scholar] [CrossRef]
- Ambrogio, G.; Ingarao, G.; Gagliardia, F.; Di Lorenzo, R. Analysis of energy efficiency of different setups able to perform single point incremental forming (SPIF) processes. Procedia CIRP 2014, 15, 111–116. [Google Scholar] [CrossRef]
- Aerens, R.; Duflou, J.R.; Eyckens, P.; van Bael, A. Advances in force modelling for SPIF. Int. J. Mater. Form. 2009, 2, 25–28. [Google Scholar] [CrossRef]
- Azevedo, N.G.; Farias, J.S.; Bastos, R.P.; Teixeira, P.; Davim, J.P.; Alves de Sousa, R.J. Lubrication aspects during Single Point Incremental Forming for steel and aluminum materials. Int. J. Precis. Eng. Manuf. 2015, 16, 589–595. [Google Scholar] [CrossRef]
- Jeswiet, J.; Hagan, E.; Szekeres, A. Forming parameters for incremental forming of aluminium alloy sheet metal. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2002, 216, 1367–1371. [Google Scholar] [CrossRef]
- Hussain, G.; Gao, L.; Hayat, N. Forming parameters and forming defects in incremental forming of an aluminum sheet: Correlation, empirical modeling, and optimization: Part A. Mater. Manuf. Process. 2011, 26, 1546–1553. [Google Scholar] [CrossRef]
- Maqbool, F.; Bambach, M. Dominant deformation mechanisms in single point incremental forming (SPIF) and their effect on geometrical accuracy. Int. J. Mech. Sci. 2018, 136, 279–292. [Google Scholar] [CrossRef]
- Radu, M.C.; Cristea, I. Processing metal sheets by SPIF and analysis of parts quality. Mater. Manuf. Process. 2013, 28, 287–293. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Y.; Meehan, P.A. Experimental investigation of mechanical properties, formability and force measurement for AA7075-O aluminum alloy sheets formed by incremental forming. Int. J. Precis. Eng. Manuf. 2013, 14, 1891–1899. [Google Scholar] [CrossRef]






| Advantages | Disadvantages |
|---|---|
| It can be done in a machining center | The equipment must be managed by experienced and qualified operators |
| The changes in design may be done easily and quickly | The processing time is longer |
| The strengths within the material are relatively low | Elastic recuperation is produced |
| The pieces are produced directly from a electronic file | The process is limited to medium to small batches |
| The dimensions of the pieces are only restricted by the dimensions of the tool machinery | The forming of angles of 90° tends to be limited |
| Authors | Material | Feed-Rate (mm/min) | Spindle Speed (RPM) | Pitch (mm) |
|---|---|---|---|---|
| Franzen et al. [40] | PVC | 1500 | Free | 0.5 |
| Silva, Alves & Martins [41] | PVC | 1000 | Free | 0.5 |
| Martins et al. [7] | PVC | 1500 | Free | 0.5 |
| Zhang, Wang & Zhang [42] | PVC | 2000 | 2000 | 0.5/1.0 |
| Medina-Sanchez et al. [43] | PVC | 1500 | 500 | 0.5 |
| Ambrogio et al. [44] | EN-AW 5754 | 2000/8000 | 2500 | 0.5 |
| Aerens et al. [45] | EN-AW 5754 | 2000 | – | 0.5 |
| Ingarao et al. [9] | EN-AW 5754 | 2000 | 200 | 1.0 |
| Gupta & Jeswiet [34] | EN-AW 5754 | 3000/7500 | 1000/2000 | 0.2 |
| Test | Angle (°) | Depth (mm) | Pitch (mm) | Spindle Speed (RPM) | Feed-Rate (mm/min) | Results |
|---|---|---|---|---|---|---|
| #1 | 50 | 60 | 1.2 | 750 | 2200 | PVC sheet breaks |
| #2 | 45 | 65 | 1.2 | 750 | 2200 | PVC sheet breaks |
| #3 | 45 | 60 | 1.2 | 750 | 2200 | OK |
| #4 | 55 | 50 | 1.2 | 750 | 2200 | Al sheet break |
| #5 | 50 | 50 | 1.2 | 750 | 2200 | OK |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodriguez-Alabanda, O.; Narvaez, M.A.; Guerrero-Vaca, G.; Romero, P.E. Manufacturing of Non-Stick Molds from Pre-Painted Aluminum Sheets via Single Point Incremental Forming. Appl. Sci. 2018, 8, 1002. https://doi.org/10.3390/app8061002
Rodriguez-Alabanda O, Narvaez MA, Guerrero-Vaca G, Romero PE. Manufacturing of Non-Stick Molds from Pre-Painted Aluminum Sheets via Single Point Incremental Forming. Applied Sciences. 2018; 8(6):1002. https://doi.org/10.3390/app8061002
Chicago/Turabian StyleRodriguez-Alabanda, Oscar, Miguel A. Narvaez, Guillermo Guerrero-Vaca, and Pablo E. Romero. 2018. "Manufacturing of Non-Stick Molds from Pre-Painted Aluminum Sheets via Single Point Incremental Forming" Applied Sciences 8, no. 6: 1002. https://doi.org/10.3390/app8061002






