Short-Term Fuzzy Load Forecasting Model Using Genetic–Fuzzy and Ant Colony–Fuzzy Knowledge Base Optimization

Abstract

The estimation of hourly electricity load consumption is highly important for planning short-term supply–demand equilibrium in sources and facilities. Studies of short-term load forecasting in the literature are categorized into two groups: classical conventional and artificial intelligence-based methods. Artificial intelligence-based models, especially when using fuzzy logic techniques, have more accurate load estimations when datasets include high uncertainty. However, as the knowledge base—which is defined by expert insights and decisions—gets larger, the load forecasting performance decreases. This study handles the problem that is caused by the growing knowledge base, and improves the load forecasting performance of fuzzy models through nature-inspired methods. The proposed models have been optimized by using ant colony optimization and genetic algorithm (GA) techniques. The training and testing processes of the proposed systems were performed on historical hourly load consumption and temperature data collected between 2011 and 2014. The results show that the proposed models can sufficiently improve the performance of hourly short-term load forecasting. The mean absolute percentage error (MAPE) of the monthly minimum in the forecasting model, in terms of the forecasting accuracy, is 3.9% (February 2014). The results show that the proposed methods make it possible to work with large-scale rule bases in a more flexible estimation environment.

1. Introduction

Electricity load forecasting has always had a significant position in relation to efficiently planning and managing the operations of power systems [1]. Especially, estimating short-term load consumption characteristics is critical in the maintenance, power production, and interchange of both power generation and distribution facilities [2]. From the view of economic and natural aspects, accurate load forecasting provides a chance to operate and generate electricity at a lower cost, and thus better protect the natural environment.

Most of the techniques that are used for electricity generation need to use non-storable resources; thus, planning and estimating demand-side changes are very important. There are several types of methods that have been applied to find the best forecasting model [3]. Recent studies have shown that load consumption patterns are highly related to exogenous factors such as weather conditions, temperature changes, and consumption time (working days, religious and official holidays, weekends, etc.). Load consumption is also affected by economic or political fluctuations [4].

There are many types of methods that deal with the above-mentioned difficulties. These approaches are divided into two individual categories: statistically-based traditional conventional methods, and artificial intelligence-based nature-inspired methods.

Traditional statistic-based methods are based on the existence of a relationship between electricity load consumption characteristic and exogenous factors [5]. Regression-based methods such as autoregressive (AR) models, autoregressive moving average (ARMA) models, and autoregressive integrated moving average (ARIMA) models are usually applied to make short-term load forecasting. Regression-based models are those affected by calendar effective datasets, and the obtained results are not promising at all [6]. Linear models are easier to use compared with regression-based models, but these models produce higher forecast errors. Nonlinear forecast models give a higher forecast accuracy than the linear models [7].

Swarm intelligence based and bio-inspired programming methods are glittering and have recently been seen much more in the literature. Especially swarm intelligence based techniques such as ant colony optimization (ACO), artificial bee colony (ABC), particle swarm optimization (PSO), cuckoo search optimization (CSO), and firefly optimization (FO) are seen as having many advantages compared with traditional solution methods. There are many different types of algorithms that have been used for solving engineering problems in the literature, but there is no individual algorithm that presents an exact solution for all [8]. Most of the algorithms mentioned before were used in the forecasting of short-term load consumption. Several researchers have proposed different various forecasting models.

Hernandez et al. (2013) proposed artificial neural network (ANN)-based short-term load forecasting model. They used historical load consumption data and exogenous factors such as air temperature, average wind speed, wind direction, relative humidity, and pressure. They proposed two-stage ANN forecasting models. The first stage consisted of data preparation, and the second stage consisted of hourly-based load consumption forecasting. The proposed two-stage forecasting model was succeeded with a 1.62% forecasting error [9]. Hassan et al. (2016) proposed a type-2 fuzzy logic forecasting model by utilizing an extreme learning machine for electricity load forecasting. They used an extreme learning strategy to find optimal fuzzy parameters, which were randomly defined at an initializing phase. They used nonlinear datasets from the Australian National Electricity Market for the Victoria region and the Ontario Electricity Market. The obtained results of their model were compared with some traditional models such as neural networks and adaptive neuro-fuzzy models [10]. Hernandez et al. (2014) proposed load forecasting models in a microgrid environment. They used two different datasets (Data Set A, Data Set B) in their ANN models. Their research was aimed at the comparison and observation of the effects of solar radiation on energy consumption in a microgrid environment [11]. Chatuverdi et al. (2015) used a generalized neural network model for short-term load forecasting to deal with the disadvantages of neural networks such as deciding network size, type, architecture, and long learning time. The proposed model was used to forecast an electricity consumption amount of 15 MVA, 33/11 KV station in Dayalbagh Institute. They used weekday data and a trained forecasting model [12]. Li et al. (2015) proposed a hybrid load forecasting model. They used wavelet transform (WT) to feature extraction and define load frequency characteristic. They also used the extreme learning machine (ELM) algorithm and the modified artificial bee colony algorithm (MABC) for the global searching of input weights of ELM. Their presented model was trained and tested with ISO New England and North American load datasets [13]. Abdoos et al. (2015) presented a hybrid short-term load forecasting model. They used WT and Gram–Schmidt techniques for data preparing and feature extraction. They proposed support vector machine (SVM)-based models for both weekends and weekdays [14]. Kouhi et al. (2014) proposed an artificial neural network model with an intelligent chaotic feature selection technique. The proposed feature selection technique was used to obtain the best-input dataset, and candidate data was prepared with the taken embedded theorem. Fitness values of the input dataset’s were calculated using correlation analysis. They used MLP (multi-layer perceptron) in the load-forecasting module [15]. Selakov et al. (2014) presented a PSO and SVM-based short-term hybrid load forecasting model. They used historical weather information with a load consumption dataset. The obtained results showed that the proposed model had given highly accurate results with highly changeable temperature periods [16]. Li et al. (2014) proposed a hybrid load forecasting model. The laws of quantum physics were employed in their quantum neural network models, and used with the genetic algorithm (GA) to optimize and find the best sub-optimal network structure. The results of the research showed that the HQENN (Hybrid Quantum Elman Neural Network) model has an acceptable high accuracy, and might be used for short-term load forecasting [17]. Mamlook et al. (2009) proposed a fuzzy logic short-term load forecasting model using historical weather temperature and a load dataset [18]. Srinivasan et al. (1994) used a hybrid neuro-fuzzy model for short-term load forecasting. They used fuzzy logic to obtain input information for the neural network forecasting model. Historical load and weather temperature data were used for training and testing the load forecasting model [19].

In Turkey, there a large number of studies aim to have the closest results in short-term load forecasting. Yukseltan et al. (2017) published an article about forecasting the electricity demand of Turkey. They developed an hourly demand forecasting method on annual, weekly, and daily horizons using a linear model. Their model was based on sinusoidal variations, without using any climatic or econometric information. Their proposed method was applied to the Turkish Power market data for the period 2012–2014, and the daily and weekly electricity demand horizons were predicted [20]. Çevik et al. (2015) presented fuzzy logic short-term load forecasting models. They used fuzzy, adaptive neuro-fuzzy, and hybrid models with historical weather temperature data, seasonal changes, and historical load consumption datasets [21]. Esener et al. (2013) proposed an artificial intelligence-based load forecasting method that used signal processing and artificial neural networks. Their dataset was independent of historical weather condition influences and changes [22]. Demiroren et al. (2006) presented an artificial neural network load forecasting model to predict the hourly load consumption amount of the Middle Anatolian region. They used historical weather temperature and a load consumption dataset, and the obtained results were compared with regression-based statistical models [23]. Topalli et al. (2006) proposed Elman’s recurrent neural network model, and compared their results with other recurrent intelligent architecture models [24].

To date, a considerable body of research has been sought to understand load consumption characteristics. Previous research has demonstrated that several types of exogenous factors such as weather conditions (air temperature, humidity, enlightenment time, etc.) or economic changes and fluctuations directly affect hourly-based electricity consumption. This paper contributes to recent literature on:

• Flexible forecasting environments and conditions with independently chosen training dataset period seasonal changes,
• Intelligent optimal knowledge base methods for modeling load fuzzy forecasting systems.
• Hybrid load forecasting approaches that use genetic algorithm and ant colony optimization methods with fuzzy logic techniques.

In this study, we present hybrid genetic ant colony-based fuzzy inference load consumption forecasting models, which are composed of fuzzy logic and nature-inspired optimization methods. One of the most important difficulties when developing a fuzzy logic-based forecasting model is the complexity of defining an optimal rule base when the numbers for the input and membership functions are getting larger. Both prediction models presented in the study use natural-inspired methods and provide a more flexible working environment for the researcher while modeling the forecasting system. The researcher can easily increase or decrease the number of the input–output dataset sizes and membership functions without considering the size of the knowledge base.

The paper is organized as follows: Section 2 presents the output and input variables of the forecasting model, the morphological content of the training and testing datasets, and the detailed forecasting model and nature-inspired optimization methods that will be used. In Section 3, the experimental results of the proposed forecasting models and comparisons between real consumption values and optimized results will be presented. Finally, in Section 4, the obtained results will be discussed, and planned works will be explained.

2. Materials and Methods

In this study, we present hybrid genetic ant colony-based fuzzy inference, which is composed of fuzzy logic and nature-inspired optimization methods. The ant colony rule-based optimization module was used for exploration (global search), and the preselected rule set was obtained. The genetic algorithm rule-based optimization module was used for exploitation (local search), and the best rule set that was found in this phase was used. The fuzzy inference module was used with both ant colony and genetic modules to get crisp hourly load consumption amounts. The general block diagram of the proposed load forecasting model is seen in Figure 1.

The proposed models were trained and tested with historical weather temperature and hourly load consumption data obtained from National Load Dispatch Centre for the period between 2011 and 2014.

2.1. Data Set

The electricity load consumption amount generally follows a routine. However, there are usually improbable changes and fluctuation. There may be countless reasons to explain these changes. Mostly, these are temperature changes, calendar effects such as formal or religious holidays, and economic and political fluctuation and crisis. The hourly-based electricity load consumption changes in 2013 are shown in Figure 2.

In 2013, the maximum load consumption was 38,116 MWh, the minimum load consumption was 14,800 MWh, and the average load consumption was 28,003.08 MWh. The consumption values show that there is wide range of consumption characteristics in Turkey. The consumption records show that in the summer and winter seasons, consumption values are higher compared with spring and autumn. The highest consumption was recorded on 29 August as 38,116 MWh between 1 pm and 2 pm.

The electricity load consumption values of Turkey between 2011 and 2013 are visualized as black and white images in Figure 3. The darker parts of the graphic are pointing out the lower consumption; nevertheless, the brighter parts are pointing out the higher consumption values. There are two areas that are darker than the others in all of the graphics; these show the religious holiday periods in Turkey. Most of the government facilities and the private sector don’t work these days; thus, electricity consumption is dramatically less than usual.

The graphics show us more valuable information about Turkey. The 2013 graphic that is shown in Figure 3–c is generally darker than the other graphics, because there was an economic crisis in Turkey in 2013. This economic crisis started to show its effects from the end of 2012, and all of these effects are seen in Figure 3a–c.

2.2. Last Day (Ldc)—Last Week (Lwc) Consumption

Daily electricity load consumption usually has a clear path, and studies show that there is a strong and direct relationship between load consumption and temperature changes [21]. The hourly-based day ahead normalized load consumption values in 2013 are seen in Figure 4.

The daily electricity consumption pattern doesn’t change in a wide range. The load curves follow similar consumption characteristics for each day; the rises and falls are mostly similar. This consumption pattern is a useful indicator, and most of the researchers used these parameters in their studies.

2.2.1. Calculated Load Consumption (L_cal)

Daily consumption changes are remarkable indicators, but it is not enough to have a flawless load forecasting. The least squares method is the mathematical equation form that determines and visualizes the relationship in the dataset. Each data reveals the relationship between the known independent and unknown dependent variables.

The least square method was developed in the late 1700s, and is used for estimating the unknown parameters between data and the model using squared deviations [25]. The least square method is one of the best analytical techniques for extracting valuable information from the dataset [26]. In this paper, day-ahead weekly load changes are used as forecasting parameters. A trend analysis for the day-ahead consumption changes has been calculated using the following mathematical equations:

$$\mathrm{Least}\mathrm{Square}\mathrm{Load}\mathrm{Trend}\mathrm{Equation}:L=a+b{x}_i$$

(1)

$$\mathrm{Slope}:b=\frac{{{\displaystyle \sum }}_{i=1}^n{x}_i{y}_i-n\overline{x}\overline{y}}{{{\displaystyle \sum }}_{i=1}^n{x}_i{}^2-n{\overline{x}}^2}$$

(2)

$$\mathrm{Load}\mathrm{Intercept}:a=\overline{y}-b\overline{x}$$

(3)

In Equation (1), L denotes the estimated hourly electricity load consumption, a denotes the load factor, b denotes the load slope, and $x_i$ denotes the period of load that will be estimated.

The calculated load curve (L_CAL) using the least square method is another important input parameter of the load forecasting system. Load estimation for 1 January 2012, using the data between 25 and 31 December 2011, is seen in

Table 1. 25 December 2011–31 December 2011 load consumption data.

Date	Time Period (Distance)	Load Consumption (MWh)	x2	x2y
25 December 2011	1	26,175	1	26,175
26 December 2011	2	24,386	4	97,544
27 December 2011	3	26,412	9	237,708
28 December 2011	4	26,493	16	423,888
29 December 2011	5	26,345	25	658,625
30 December 2011	6	26,463	36	952,668
31 December 2011	7	26,083	49	1,278,067
1 January 2012		26,595

. Each row of the data is the measured electricity load consumption value for the same hour period (12:00 a.m. to 1:00 a.m.).

The relationship of the weekly-based hourly dataset was analyzed using the least square method, and the load trend line was determined. The target load consumption value was calculated with the equations mentioned above. The hourly load consumption data and calculated values for between 25 December 2011 and 1 January 2012 are seen in Figure 5.

2.2.2. Temperature Data Set (T_eff)

The literature research shows that there is a very strong relationship between weather condition changes and the electricity consumption amount. Temperature changes directly affect electricity consumption [21]. The correlation between air temperature and load consumption for the period between 1 and 4 April 2013 is given in Figure 6.

Usually, there is a linear correlation between temperature and load consumption. When temperature increases, load consumption increases synchronously. Temperature changes are crucial factors for forecasting but are not the only indicators to use.

2.3. Fuzzy Inference System

Fuzzy logic has been one of the most commonly used methods for solving engineering problems recently. Fuzzy logic methods are especially used for the planning, control, and production scheduling of power systems, and system stability management. The fuzzy logic methods and control techniques are very effective and powerful optimization tools that have many advantages, such as robustness and an ease of implementing [27].

The fuzzy logic concept was introduced first by Zadeh in 1965 [28]. The fuzzy approach may be briefly described as a generalized form of classical set theory. In classical set theory, every argument must be classified in an individual set or not, and any element cannot be represented by the intersection of sets. Contrary to the classical approach, in fuzzy theory, the degree of membership of an element may continuously exist. Continuous data may be expressed with membership functions [29]. The Mamdani inference model is a well-known and used fuzzy model.

The basic fuzzy logic inference system has four main blocks, which are seen in Figure 7. The knowledge base block involves the rule base and database, which are generally created by an expert or an optimization method. The fuzzier block is used for the transformation of crisp values into linguistic terms. Linguistic terms with membership values are processed with knowledge information in the inference module, and the results are sent to the defuzzifier (purification) module to obtain the crisp output.

In the Mamdani fuzzy approach, the defuzzification phase is evaluated with rule sentences and conditions such as those seen below:

Rule 1: if x₁ is A₁ and y₁ is B₁ … then z is C₁

Rule 2: if x₂ is A₂ and y₂ is B₂ … then z is C₂

Rule 3: if x₃ is A₃ and y₃ is B₃ … then z is C₃

⋮

Rule k: if x_k is A_k and y_k is B_k … then z is C_k.

where x and y are the first and second input variables, respectively, z is the output variable, and k is the number of rules.

There are a few important points that need to be defined very well, such as the membership function size, type, and shape. Changes to these parameters critically affect the accuracy of the system. These parameters need to be defined by an expert or through the use of optimization techniques [30].

2.4. Genetic Algorithm

The genetic algorithm is a nature-inspired method that is based on Darwin’s evolution theory. The genetic approach became more popular through various studies and John Holland’s book “Adaptation in Natural and Artificial Systems” in the early 1970s [31]. The literature shows that genetic algorithm methods are useful and more successful than traditional methods in solving engineering problems. Its advantages include gradient independency, a high discovery rate, and solution parallelism [32,33].

Genetic methods have some basic operators such as selection, crossover, mutation, and recombination. Selection operation is an elitism technique. This operation is aimed at finding the best or more useful individuals for having new and better offspring or children. There are a few selection methods used in the genetic algorithm such as roulette-wheel selection, tournament selection, and truncation selection. Crossover is a move–replace operation that is aimed at generating a new breed from existing or selected parents’ selected (single or multipoint) parts. Mutation operation is changing operation and maintains genetic diversity to the system. The mutation occurs during evolutionary operation, and works according to a predefined probability variable. Generally, a randomly generated variable for each bit in a sequence determines whether an individual bit will be changed or not. The main purpose of the mutation is to improve the genetic diversity of the breed.

The working process of the genetic algorithm and population production process is given as a sample in Figure 8. Two different randomly generated parents (the solution function) are seen at the top. Each parent consists of 14 binary coded gene chromosomes. The crossover point is defined before the operation, and divides the chromosome into different sized parts. These parts are used to have new children (solutions). Each child carries the parents’ unique features and characteristics. The genetic diversity of the breed is held by mutation operation. The randomly selected genes of each chromosome are changed from 1 to 0 or 0 to 1, and the generation process ends. The exploration phase is performed with the crossover operator. Sub-solutions are produced through the crossover operation, which gains a high convergence capacity to the searching system. The mutation operator provides diversity, and prevents the system from being stuck in a local optimum. The exploitation phase is performed with the mutation operation, and has a larger searching space to look for a deserved solution.

GA–FL Load Forecasting Model

The proposed load forecasting model consists of a fuzzy inference module and a genetic algorithm-based rule base optimization module. A block diagram of the proposed model is given in Figure 9.

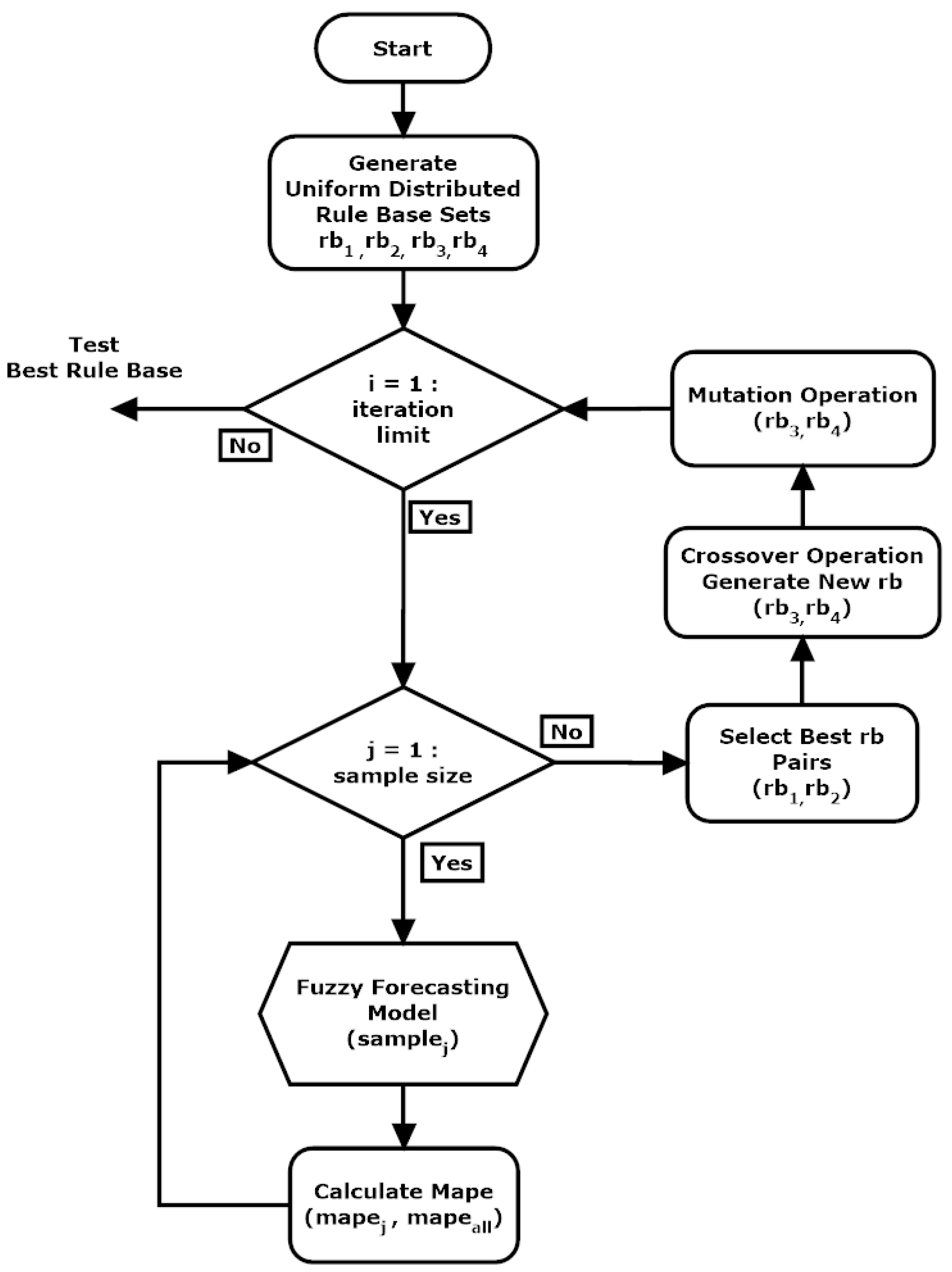
The genetic algorithm approach was applied to generate the optimal rule base set of the fuzzy load (FL) forecasting system. The rule bases were designed as five genes for all 625 chromosomes of each of four parents. Every chromosome consisted of five binary-coded genes. Uniformly distributed randomly created parent rule base sets and a genetic rule base optimization process is seen in Figure 10.

Rule base sets were produced and uniformly distributed in the rule base generator module at the first step of the optimization algorithm. These sets were applied to the fuzzy forecasting system, respectively. The generated rule base set was used in the fuzzy inference module with a randomly selected dataset, respectively. The mean absolute percentage error (MAPE) was calculated, and the error values were saved for each rule base set, as shown in Equation (4). The calculated MAPE values were the fitness values of the rule base sets.

$$\frac{1}{n}{\displaystyle \sum }_{t=1}^n\left(\left|\frac{A{L}_t-F{L}_t}{A{L}_t}\right|\times 100\right)$$

(4)

• $A{L}_t$ Actual Load
• $F{L}_t$ Forecasted Load

After the performance evaluation of each rule base set, the best two individuals were selected, and new candidate rule base sets were created. New rule bases were generated using crossing and mutation methods in the order of these two individuals. The evolution process continues until the iteration limit is reached.

2.5. Ant Colony Optimization

The ant colony optimization algorithm is a meta-heuristic search algorithm inspired by the strategies that ant colonies use to reach food resources [36]. Gross and Deneubourg showed that some ant species follow a ray-type path between food resource and nest in their experimental studies [37,38].

At the beginning of the research, the door is closed, and ants are waiting in the nest. There are two possible routes in the system, and just one of these routes is shorter than the other one. After opening the door, the ants follow a random route to the food source, and every individual ant leaves a pheromone behind. The pheromone amount left from the pioneer ant is a clue for the ants that are following to proceed more directly to the food source. After a while, researchers noticed that most of the ants that follow take a shorter path. An experimental setup of the research is given in Figure 11.

Dorigo et al. improved the artificial ant colony and artificial pheromone concept in their research, which was based on the experiments of Gross et al., and applied this technique to find a solution to the traveling salesman problem [39].

Nature-inspired optimization algorithms are also used to find the best search space. There are two main basic approaches in all of the methods: global search methods (exploration), and local search (exploitation) approaches. The new solution is based on local information and an existing solution in local search methods. The hill-climbing method is a marvelous example of the local search operation. With this method, the climbing position is changed to the closest peak point at each step of the iteration. This method gains a large convergence capacity to the search system, but there is also a risk of being stuck in a local optimum. The succession rate of this method is highly related to choosing a good starting position. In the global search method, the search space is analyzed from a global perspective. The new solution is possibly found in a location far from the existing solution’s location. With this method, the convergence rate falls and the searching time gets longer, but there is no risk of being stuck in a local optimum.

The balanced implementation of the searching methods mentioned above is the most crucial factor for determining the success of the algorithm. Greater exploitation may create a faster convergence rate, but the findings may be deceptive, and might not indicate the best solution. Using more exploration stretches out the searching time and slows the convergence rate. Balancing between these techniques is also a hyper-optimization problem [8].

AC–FL Load Forecasting Model

The proposed load forecasting model consists of a fuzzy inference module and an ant colony-based rule base optimization module. A block diagram of the proposed model is given in Figure 12.

The proposed forecasting model has four input variables, and each input variable has five different membership functions. Therefore, 625 different rules covering all of the possible situations were defined in the fuzzy load forecasting model. The rule base set that was used in the fuzzy model is seen in

Table 2. Randomly generated ant colony rule path.

Rules	VL	L	N	H	VH
Rule 1	0	1	0	0	0
Rule 2	0	0	1	0	0
Rule 3	1	0	0	0	0
Rule 4	0	0	0	1	0
Rule 5	0	0	1	0	0
Rule 6	0	0	0	0	1
Rule 7	1	0	0	0	0
Rule 8	0	0	1	0	0
Rule 9	0	1	0	0	0
	-	-	-	-	-
Rule 625	0	1	0	0	0

. These rules were then changed to the most appropriate rule base set for the system using the ant colony optimization technique. While using ant colony optimization, each rule that was used in the fuzzy inference engine is expressed as five bits of binary coded values. The binary coded rule set seems like a genetic algorithm model, but the rule set of the ant colony is unique, and only a single “1” value may be inside each rule. These positive values in each row (each rule) were used to generate a path that the ants then follow in each step of the iteration. Each column in Table 2 denotes the linguistic fuzzified terms of the output. A sample rule base set is seen in Table 2.

The agent operator ant follows a route that was generated and uniformly distributed in the first step of the iteration, and the selection possibility of all of the positions was defined in the same weight. A sample randomly created route at the first step of the iteration is given in Figure 13.

After the first step of the iteration, all of the samples were evaluated with the existing rule base set, and the MAPE (obtained in the i_th iteration) was calculated. The MAPE value of the existing rule base set was compared with the predefined tolerance value, and whether existing route would be punished or rewarded was decided. If the MAPE value of the existing rule base was lower than the best-recorded value of all, then the weights of the existing path increased, and the pheromones were updated. Otherwise, the weights of existing path decreased, and the pheromones were also updated. The updated weights and the new route are given in Figure 14.

Before the next step of the iteration started, a new route was created considering the new weights and new possibilities. Iteration continued until the iteration limit was reached or the success rate was lower than deserved.

3. Experimental Results and Discussions

In this paper, we developed two different artificial based load forecasting models. The fuzzy logic model is the main part of the system. The genetic algorithm and ant colony-based techniques were used to increase the performance of the fuzzy forecasting system.

Proposed GA–FL and AC–FL load forecasting models were trained with historical electricity load consumption and air temperature data between 2011 and 2014, as explained in Section 2. The training and testing datasets consist of four input variables (L_dc, L_wc, L_cal, and T_eff) and one output variable (L_forecasted). Membership function type and values were identified by annual changes in the load consumption and weather temperature. The average load consumption values of 2013 are given in Figure 15.

Load data was fuzzified through using five membership functions that considered the average values of 2013; the fuzzified input and output data (L_dc, L_wc, L_cal, and L_forecasted) are seen in Figure 16.

In Figure 16, VL denotes the lowest load value, which means very low consumption, L denotes a lower consumption than the normal level, N denotes normal consumption, H denotes a higher consumption than the normal level, and VH denotes the highest load consumption value.

Temperature data was also fuzzified using five membership functions. Membership function values were determined considering the thermal comfort values of TS EN ISO 7730, and the fuzzified temperature data is seen in Figure 17 [40].

In Figure 17, VL denotes the lowest temperature value, which means a very low temperature, L denotes a lower temperature than normal, N denotes a normal temperature, H denotes a higher temperature than normal, and VH denotes the highest temperature value.

Temperature data was provided from Turkish State Meteorological Service’s database. In this research, we observed a large scaled area in Turkey. Temperature data was collected from six different locations in Turkey. We tried to choose the best locations directly representing Turkey’s electricity consumption character. The hourly-based weather temperature data of the selected locations is given in

Table 3. Temperature data collected from the six selected stations for 1 December 2012.

Time (Hour)	Samsun 2%	Ankara 15%	Kırıkkale 2%	İzmir 10%	Adana 4%	İstanbul 67%	Weighted Avg.
00–01	5.8	−2.8	−3.7	4.3	5.3	4.7	3.41
01–02	5.9	−3.4	−4.1	4.1	4.5	4.4	3.06
02–03	5.9	−3.7	−4.9	3.3	5.3	4.1	2.75
03–04	5.9	−4.6	−5.6	3.8	4.9	3.6	2.30
04–05	5.0	−5.2	−6.0	3.0	4.2	3.4	1.95
05–06	5.0	−5.9	−6.6	3.1	4.3	2.8	1.44
06–07	4.7	−6.0	−7.1	3.2	5.0	2.5	1.25
07–08	5.2	−3.2	−6.0	5.0	6.8	2.7	2.09
08–09	7.7	0.4	−3.2	8.0	9.3	4.6	4.40
09–10	10.6	2.3	0.0	9.3	14.0	7.5	7.07
10–11	11.1	5.7	2.6	10.6	16.8	10.0	9.56
11–12	11.4	8.0	4.9	11.4	17.7	10.5	10.41
12–13	11.4	9.1	6.9	11.8	18.5	9.7	10.15
13–14	11.2	9.9	8.2	12.7	18.3	9.8	10.44
14–15	10.5	8.9	8.7	13.1	17.9	9.6	10.18
15–16	8.5	7.3	7.4	12.6	16.3	9.0	9.36
16–17	6.7	4.9	5.3	9.4	14.5	8.4	8.12
17–18	6.0	3.9	4.8	7.5	10.6	8.1	7.40
18–19	5.7	2.4	3.6	6.9	8.7	7.8	6.81
19–20	5.6	1.0	2.4	7.4	7.2	7.2	6.16
20–21	4.6	0.6	−0.6	6.5	6.0	6.6	5.48
21–22	4.5	−0.3	−1.0	5.5	6.7	6.1	4.93
22–23	4.5	−1.4	−1.2	4.5	5.7	5.4	4.15
23–00	4.7	−2.2	−2.6	4.0	6.0	5.1	3.77

.

The average temperature value was calculated with hourly-based temperature data collected from six different locations. The constants (% values in Table 3) that were used in the equation to calculate the average value were defined according to the level of economic development of the cities mentioned above, which was pointed out in the annually published report by the Ministry of Science, Industry, and Technology [41]. After averaging the calculations, the temperature values for the last seven days were used to calculate the temperature parameters as an input variable, while also using the trend analysis methods mentioned above in Section 2.2.1.

Both forecasting models were trained and tested with a day-ahead 24 h dataset. The input dataset consisted of the last day of consumption, the last week of consumption, and the consumption and weather temperature trends of the last seven days, which were calculated using the least square method mentioned in Section 2. As a sample, the input dataset used for the training of both proposed models is given in

Table 4. Input dataset used for the training of the proposed forecasting models (8 February 2013).

Hours	Last Day Consumption (MWh)	Last Week Consumption (MWh)	Consumption Trend (MWh)	Weighted Average Trend Temperature (°C)
00–01	28.700	28.459	28.872	2.72
01–02	26.856	26.740	27.065	2.31
02–03	25.823	25.451	26.146	1.99
03–04	25.273	24.769	25.555	1.96
04–05	25.072	24.546	25.423	1.70
05–06	25.465	24.706	25.969	1.54
06–07	26.038	24.804	26.678	1.30
07–08	26.865	25.141	28.009	1.88
08–09	31.587	28.708	33.508	3.91
09–10	34.511	31.389	36.684	5.74
10–11	35.395	32.464	37.483	7.69
11–12	35.637	32.955	37.427	9.22
12–13	32.974	32.184	34.902	9.78
13–14	33.726	32.256	35.447	10.68
14–15	33.727	31.980	35.717	10.13
15–16	33.229	31.221	35.163	9.35
16–17	33.304	31.215	35.376	8.43
17–18	34.505	32.192	36.547	7.20
18–19	34.255	32.131	35.874	6.12
19–20	32.965	31.130	34.265	5.45
20–21	32.057	30.292	33.400	4.68
21–22	31.486	29.739	32.603	4.00
22–23	31.698	30.205	32.790	3.69
23–00	30.494	28.959	31.645	3.43
Max.	35.637	32.955	37.483	10.68
Min.	25.072	24.546	25.423	1.30
Std. Dev.	361.576	298.789	425.341	3.13

.

In summary, the input dataset consists of load consumption information and weather temperature information. Load consumption data consists of the last day of consumption, the last week of consumption for the same hour, and the consumption trend, which is calculated using the trend analysis equation mentioned in Section 2.2.1.

Weather temperature information is obtained in a two-stage process. First, the weighted average air temperature is calculated using temperature data collected from six various locations in Turkey. Then, the air temperature trend is calculated using the trend analysis equation mentioned in Section 2.2.1. Lastly, the whole forecasting and optimization process uses the 24-h dataset.

3.1. GA–FL Simulation Results

The proposed GA–FL model was trained with a randomly chosen training set and tested data for a specific period, such as a monthly or weekly dataset. The results showed that the GA–FL model gives satisfying results for the specific part of the testing data, but couldn’t have full coverage. In other words, the final rule base set that was created with the optimization model didn’t fit for properly testing the entire dataset.

In order to reach the best rule base set, four different rule base sets consisting of 625 random rules were defined as a binary system to the optimization system in the initial phase. The performance value of each rule base was measured separately for the same training set for each step of the iteration. The results of this measurement are shown in

Table 5. MAPE (%) values for each GA–FL rule base set. GA: genetic algorithm, FL: fuzzy logic.

Iteration	MAPE (%)
	rb1	rb2	rb3	rb4
1	0.189	0.066	0.155	0.194
2	0.164	0.066	0.155	0.062
3	0.070	0.066	0.082	0.062
-	-	-	-	-
96	0.041	0.078	0.039	0.083
97	0.041	0.042	0.039	0.054
98	0.041	0.077	0.039	0.070
99	0.041	0.042	0.039	0.053
100	0.041	0.043	0.039	0.059

.

After each step of the iteration, selection, crossover and mutation operations that were designed in compliance with genetic algorithm methods were used, and a new rule base population was produced. The performance values of each rule base set and the optimization process are given in Figure 18.

The proposed GA–FL load forecasting model was trained with a monthly weekday dataset between 2011 and 2013, and tested with a monthly weekday dataset of 2014. Each rule base that was obtained at the last iteration of the optimization process was tested with the training dataset, and some of the forecasting results of the proposed forecasting model for the training and testing processes are shown in Figure 19 and Figure 20.

The proposed GA–FL model consisted of four individuals, and the mutation constant was 1%. The script was executed for more than 20 different runs with 100 iterations in order to have statistically meaningful results.

Each genetic rule base set after the optimization process was tested and compared with the actual data in Figure 19 for the same consumption period. The optimal rule base set was then tested with actual data, and the results are seen in Figure 20.

3.2. AC–FL Simulation Results

The proposed AC–FL model was trained with the data from 2012, and tested with the data from 2013 for the same monthly period. The simulation results showed a downward trend for the MAPE value of the optimization system since the first step. The system learned with both negative and positive information. When the MAPE value was worse, it showed that the existing choices on the ant path route were not proper for the fuzzy model, that this route was punished by giving fewer weight values, and that it consequently decreased the selection possibility of the path in the next step. When the MAPE value was better, it showed that the existing choices on the ant path route were more proper for the fuzzy model; thus, this route was rewarded with higher weight values, and it increased the selection possibility of the path in the next step.

After a while, in the late phase of the iteration process, as shown in Figure 21, differences in the MAPE values decreased dramatically. This situation showed that the route was optimized, the agent ants almost followed the same path, and similar rule sets were applied to the system in each step of the iteration process. The route optimization process and MAPE values of the ant rule base sets are seen in Figure 21.

The proposed AC–FL model was trained with 1000 virtual agent ants. In each step of the iteration, when an agent ant followed a route, which meant a new knowledge base of the fuzzy model, the weight matrix was updated. This route was also constantly updated with other pheromone amounts, which were calculated using the tolerance value that was defined at the beginning of the iteration process in the script. The pheromone constant in each iteration was calculated according to the performance of the virtual agent ant.

The training and testing values of the proposed AC–FL model are given in Figure 22 and Figure 23. The proposed model was trained with the monthly-based dataset for the same weekday periods in 2013 and 2014.

The ant colony optimization process is aimed at finding the best rule base set that will be used for testing with the target data. At the end of the optimization process, two different rule base sets were improved at the same time. One of these rule base sets gave the best training error value, which was saved and labeled as the best iteration. The other rule base set was obtained indirectly by measuring the maximum weights of each rule of the rule set’s weight table. A comparison of these rule sets is given in Figure 22. Comparative information on the rule sets helps choose the rule set that will be used for testing.

The compared results of the proposed models for the same testing dataset are given in

Table 6. Testing results of proposed GA–FL and AC–FL models for the same testing dataset for 8–9 February 2014.

Hours	Actual (MW)	GA–FL (MW)	AC–FL (MW)	GA–FL APE (%)	AC–FL APE (%)	Actual (MW)	GA–FL (MW)	AC–FL (MW)	GA–FL APE (%)	AC–FL APE (%)
00–01	27.270	26.445	27.123	3.03	0.54	27.207	27.007	27.433	0.74	0.83
01–02	25.614	25.221	26.506	1.53	3.48	25.639	24.983	26.428	2.56	3.08
02–03	24.771	26.165	22.816	5.63	7.89	24.600	25.590	24.857	4.02	1.04
03–04	24.291	26.052	21.703	7.25	10.65	24.188	25.912	22.249	7.13	8.02
04–05	24.063	25.473	22.655	5.86	5.85	24.108	25.795	22.156	7.00	8.10
05–06	24.649	25.446	22.910	3.23	7.06	24.747	24.436	25.932	1.26	4.79
06–07	25.397	25.768	26.446	1.46	4.13	25.342	25.985	26.878	2.54	6.06
07–08	26.624	24.461	25.042	8.12	5.94	26.490	24.727	24.609	6.66	7.10
08–09	30.455	31.896	31.897	4.73	4.73	30.510	32.195	32.207	5.52	5.56
09–10	32.764	32.124	32.124	1.95	1.95	32.410	32.488	32.489	0.24	0.24
10–11	33.187	32.363	32.363	2.48	2.48	33.052	32.540	32.552	1.55	1.51
11–12	33.234	32.392	32.395	2.53	2.52	32.840	32.486	32.531	1.08	0.94
12–13	31.204	31.903	31.903	2.24	2.24	30.995	31.734	31.881	2.38	2.86
13–14	31.661	31.959	31.959	0.94	0.94	31.467	31.930	32.108	1.47	2.04
14–15	31.598	31.769	31.765	0.54	0.53	31.715	31.691	31.962	0.07	0.78
15–16	31.239	31.722	31.721	1.55	1.54	31.231	31.811	31.954	1.86	2.32
16–17	31.196	31.977	31.977	2.50	2.50	31.556	32.097	32.146	1.71	1.87
17–18	32.476	32.360	32.360	0.36	0.36	32.860	32.518	32.524	1.04	1.02
18–19	32.968	32.514	32.514	1.38	1.38	32.987	32.614	32.615	1.13	1.13
19–20	31.954	32.377	32.377	1.32	1.32	31.945	32.508	32.508	1.76	1.76
20–21	31.308	32.201	32.201	2.85	2.85	31.296	32.362	32.362	3.41	3.41
21–22	30.316	31.995	32.000	5.54	5.56	30.373	32.068	32.103	5.58	5.70
22–23	30.832	32.073	32.074	4.03	4.03	30.800	32.234	32.235	4.66	4.66
23–00	29.276	31.609	31.895	7.97	8.95	29.751	30.438	31.951	2.31	7.39
	MAPE			3.29	3.73	MAPE			2.82	3.42

. Both models were trained and tested with the same monthly dataset. The training dataset included weekdays in February 2013, and the testing dataset included weekdays in February 2014.

The main reason for presenting the results from weekday periods in this paper is that weekday load consumption characteristics are more challenging than weekends. Therefore, the weekday results of the proposed models were presented. Also, the month of February is a kind of transition period of the year; it contains the features of four seasons, and thus was chosen as the case scenario period.

3.3. Comparative Results

The performance of the proposed forecasting models is compared with the multiple linear regression (MLR) model. The multiple linear regression (MLR) method is a well-known statistical based estimation method that is commonly used as a benchmark model for comparing forecasting models. Multiple linear regression analysis is a kind of simple linear regression analysis. MLR is used to define the correlation between two or more independent variables and a single continuous dependent variable. MLR is also used to identify whether a confounding influence exists. It ensures a way of adjusting for potentially confounding variables that have been included in the model.

Both the MLR and proposed forecasting models are trained and tested with same dataset. The statistical parameters and results of the proposed MLR model are given in

Table 7. Regression summary and statistics.

Regression Statistics
Multiple R	0.990516
R Square	0.981121
Adjusted R Square	0.980977
Standard Error	569.2768
Observations	528

and

Table 8. Regression table (ANOVA).

Summarize	df	SS	MS	F	Significance F
Regression	4	8.81 × 109	2.2 × 109	6794.925	0
Residual	523	1.69 × 108	32,4076
Total	527	8.98 × 109

.

MLR model has four independent variables: the last day of consumption (L_DC), the last week of consumption (L_WC), the weekly load trend (L_CAL), and the weekly air temperature trend (T_EFF). The proposed linear model is given in Equation 5. The proposed MLR model was trained with a training dataset, and after analysis, the coefficients of weights (w₀ to w₄) were determined. The analysis results and coefficients that were used in forecasting hourly-based consumption are summarized in

Table 9. Regression equation table.

Weights	Coefficients	Standard Error	t Stat	p-Value	Lower 95%	Upper 95%	Lower 95%	Upper 95%
Intercept (w0)	−499.735	188.3426	−2.65333	0.008213	−869.736	−129.734	−869.736	−129.734
w1	−0.02747	0.015863	−1.73172	0.083913	−0.05863	0.003693	−0.05863	0.003693
w2	0.920282	0.013497	68.18238	2.2 × 10−262	0.893766	0.946797	0.893766	0.946797
w3	0.139906	0.018693	7.484493	3.07 × 10−13	0.103184	0.176629	0.103184	0.176629
w4	−35.0648	6.56439	−5.34166	1.38 × 10−7	−47.9606	−22.1689	−47.9606	−22.1689

.

The linear forecasting model (LM) is:

L_dcw₁ + L_wcw₂ + L_estw₃ + T_effw₄ + w₀

(5)

A performance evaluation of each forecasting model has been conducted using the same dataset for training and testing. MAPE values have been calculated and used to determine the monthly forecasting performance of each model. Each model was trained using data obtained during the same period. Trained forecasting models were tested using data obtained during the same period. Training and testing phases were performed using the same monthly data sets for different years. The obtained results of the proposed models for the same period, 29–30 January 2013, are presented in

Table 10. Comparison of testing results of the proposed GA–FL, AC–FL, and MLR forecasting models for 29 January 2013.

Hours	LDC	LWC	LCAL	TEFF	Real Consumption	MLR	MLR APE %	GA-Fuzzy	GA-Fuzzy APE %	AC-Fuzzy	AC-Fuzzy APE %
00–01	24,234	26,540	24,776	3.75	26,788	26,594	0.725	27,642	3.188	26,249	2.012
01–02	22,646	24,890	23,130	3.03	24,960	24,914	0.185	24,136	3.301	24,835	0.502
02–03	21,777	24,041	22,064	2.88	23,912	24,013	0.420	23,592	1.340	23,703	0.875
03–04	21,308	23,465	21,466	2.80	23,167	23,414	1.068	22,649	2.235	22,503	2.864
04–05	21,183	23,434	21,206	3.00	23,135	23,346	0.912	22,494	2.771	22,362	3.341
05–06	21,592	23,600	21,449	3.16	23,284	23,516	0.996	23,305	0.090	23,315	0.134
06–07	22,218	24,543	21,518	3.33	23,907	24,370	1.938	23,788	0.496	23,751	0.651
07–08	23,278	25,648	21,649	3.42	24,816	25,373	2.245	25,316	2.014	25,887	4.317
08–09	28,115	29,155	24,877	3.14	29,074	28,929	0.498	30,602	5.256	30,252	4.050
09–10	31,601	31,497	27,791	3.26	31,967	31,392	1.798	31,614	1.104	31,879	0.276
10–11	32,762	31,904	29,287	3.38	32,741	31,940	2.447	32,495	0.752	31,562	3.600
11–12	33,590	32,167	30,324	3.97	33,490	32,284	3.603	33,416	0.220	31,780	5.106
12–13	32,564	30,763	29,778	3.95	32,445	30,944	4.627	33,246	2.470	31,572	2.691
13–14	32,768	31,086	29,914	4.33	32,727	31,241	4.539	33,343	1.882	31,645	3.306
14–15	33,036	31,347	29,872	4.12	32,944	31,476	4.457	33,319	1.138	31,639	3.960
15–16	32,578	31,032	29,461	3.95	32,574	31,147	4.381	32,848	0.842	31,485	3.344
16–17	32,900	31,447	29,819	3.46	33,135	31,587	4.672	33,284	0.451	33,632	1.499
17–18	33,311	32,461	30,485	3.50	33,762	32,601	3.439	33,423	1.004	33,822	0.179
18–19	32,333	31,658	30,122	3.49	32,574	31,838	2.259	33,401	2.539	31,730	2.590
19–20	31,143	30,637	29,243	3.29	31,328	30,815	1.637	32,380	3.357	31,507	0.571
20–21	30,211	30,082	28,356	3.02	30,443	30,216	0.747	31,132	2.262	31,442	3.282
21–22	29,331	29,172	27,806	2.95	29,702	29,328	1.260	29,518	0.619	28,874	2.787
22–23	29,741	29,576	28,218	2.55	30,093	29,760	1.107	29,724	1.227	30,298	0.683
23–00	28,609	28,395	27,249	2.22	28,924	28,580	1.188	28,118	2.785	29,544	2.144
						MAPE	2.13		1.81		2.28

and

Table 11. Comparison of testing results of proposed GA-FL, AC-FL and multiple linear regression (MLR) forecasting models for 30 January 2013.

Hours	LDC	LWC	LCAL	TEFF	Real Consumption	MLR	MLR APE %	GA-Fuzzy	GA-Fuzzy APE %	AC-Fuzzy	AC-Fuzzy APE %
00–01	26.788	25.966	25.577	2.25	26.710	26.160	2.060	27.598	3.325	26.274	1.631
01–02	24.960	24.766	23.699	1.81	25.054	24.858	0.781	25.778	2.891	26.274	4.871
02–03	23.912	23.748	22.679	1.92	24.061	23.804	1.069	23.578	2.007	24.107	0.190
03–04	23.167	23.302	21.929	1.81	23.512	23.313	0.847	23.271	1.024	23.702	0.806
04–05	23.135	23.230	21.773	1.96	23.338	23.220	0.504	23.199	0.594	24.372	4.431
05–06	23.284	23.566	21.929	2.23	23.657	23.538	0.503	23.339	1.342	23.177	2.027
06–07	23.907	24.310	22.217	2.14	24.131	24.249	0.488	23.119	4.194	24.878	3.095
07–08	24.816	25.410	22.597	2.51	25.019	25.276	1.028	27.613	10.369	25.160	0.562
08–09	29.074	29.028	26.336	2.22	29.397	29.022	1.275	28.758	2.174	28.298	3.737
09–10	31.967	31.525	29.394	2.40	32.355	31.662	2.142	32.727	1.150	31.516	2.593
10–11	32.741	32.125	30.607	2.45	33.381	32.361	3.056	33.431	0.149	32.852	1.586
11–12	33.490	32.563	31.632	2.36	34.045	32.890	3.392	33.431	1.803	33.960	0.249
12–13	32.445	31.221	31.063	3.05	32.980	31.580	4.245	33.429	1.361	32.927	0.160
13–14	32.727	31.437	31.209	3.07	33.335	31.791	4.632	33.427	0.276	31.934	4.204
14–15	32.944	31.536	31.343	3.02	33.574	31.897	4.996	33.429	0.432	31.936	4.879
15–16	32.574	31.363	30.900	2.78	33.312	31.694	4.858	33.431	0.356	31.904	4.227
16–17	33.135	31.974	31.302	2.30	33.605	32.314	3.842	33.428	0.526	31.962	4.889
17–18	33.762	32.736	31.932	2.36	34.075	33.084	2.909	33.430	1.892	33.961	0.335
18–19	32.574	31.685	31.213	2.20	32.917	32.054	2.621	33.428	1.551	31.952	2.932
19–20	31.328	30.593	30.191	1.95	31.603	30.949	2.068	33.392	5.660	31.698	0.300
20–21	30.443	29.647	29.353	1.75	30.879	29.993	2.869	30.965	0.277	30.335	1.762
21–22	29.702	29.005	28.634	1.66	30.061	29.325	2.449	29.006	3.510	30.167	0.352
22–23	30.093	29.600	29.023	1.15	30.326	29.934	1.292	29.897	1.414	30.390	0.212
23–00	28.924	28.423	27.996	0.77	29.447	28.753	2.357	28.170	4.335	29.687	0.813
						MAPE	2.28		2.04		2.33

.

Firstly, as seen in Table 10 and Table 11, the proposed mature-inspired technique-based forecasting model has smaller MAPE values compared with the statistical-based model MLR model. As seen in Figure 24, artificial intelligence-based models have better adaptation and yield more promising results than the statistical-based model in a nonlinear consumption zone. As with many statistical models, the MLR model provides more successful results, as expected in the linear zone.

4. Conclusions

Short-term electricity load forecasting has become one of the most popular research topic in recent years, and many inspiring types of research are seen in literature. Load forecasting has a leading role in the planning and management of power plants and production facilities. Research studies in the literature show that the load consumption pattern is highly related to air exogenous factors such as the weather condition, consumption time, day type (working, holiday etc.), seasonal effects, and economic or political changes. Therefore, several types of solution methods are required; here, these methods have also been improved in order to get better estimations.

In the literature, there are many studies on load forecasting that use fuzzy logic and artificial intelligence optimization algorithms and methods. Here, these fuzzy models have been improved with expert insight and adaptations. Therefore, the ability and knowledge depth of the experts has directly affected the succession rate of the system. When the input variable and membership function sizes get larger, the knowledge base, rule base size, and number of rules also enlarge. So, the fuzzy model needs to be optimized, whether classical or artificial intelligence methods are used.

In this paper, hybrid genetic–fuzzy and ant colony–fuzzy short-term load forecasting models were proposed. Artificial intelligence (AI)-based optimization methods were used to deal with the struggles in rule base definition that were mentioned above. The result show that intelligent optimization methods give promising results in load forecasting. The succession rate of the proposed system was measured by using MAPE, and the results showing that the proposed method has a 3.389% forecasting rate.

As a result, we developed fuzzy logic-based load forecasting models for estimating hourly-based electricity consumption. The literature research and observations showed that the definition of the knowledge base is a major factor in having a successful forecasting rate. Moreover, when the size of input variables and/or membership functions size grows, the knowledge base becomes dramatically more complex. We developed GA–FL and AC–FL hybrid models using nature-inspired optimization methods to deal with knowledge complexity. The obtained results showed that the proposed models are more successful than the standard fuzzy logic approach that is typically seen in the literature, and proved that Nature-Inspired (NI) based methods help when working in a more flexible estimation environment.

As a limitation of the proposed methods, in some cases, such as while working with a low-temperature period of time, some of the rules that are highly related to high-temperature periods may not be active in the optimization process. These inactive rules may cause an unnecessary increase in the optimization errors, and decrease optimization performance. In future studies, it is possible to develop new optimization techniques and algorithms for eliminating inactive rules.

In future works, we will use other nature-inspired optimization algorithms for optimizing fuzzy forecasting models. We will develop new hybrid forecasting models using fuzzy type-2, and these models will be optimized with meta-heuristic optimization methods. Proposed new forecasting models will be trained and tested with large, scaled datasets.